Lie symmetries and invariant solutions of $(2+1)$-dimensional breaking soliton equation

Abstract

The present article deals with the symmetry reductions and invariant solutions of breaking soliton equation by virtue of similarity transformation method. The equation represents the collision of a Riemann wave propagating along the y-axis with a long wave along the x-axis. The infinitesimal transformations under one parameter for the governing system have been derived by exploiting the invariance property of Lie group theory. Consequently, the number of independent variables is reduced by one and the system remains invariant. A repeated application transforms the governing system into systems of ordinary differential equations. These systems degenerate well-known soliton solutions under some limiting conditions. The obtained solutions are extended with numerical simulation resulting in dark solitons, lumps, compactons, multisolitons, stationary and parabolic profiles and are shown graphically.

1 Introduction

Nonlinear waves are time evolution phenomena described by nonlinear partial differential equations (PDEs). A wide variety of physical phenomena in soliton theory, fluid mechanics, plasma physics, solid-state physics, hydrodynamics, optical fibers etc. can be modelled by these nonlinear partial differential equations (NPDEs) [1–42]. Nonlinear equations generally do not follow the superposition principle and so it is difficult to analyse these equations. Investigation of exact solutions of these NPDEs is a very arduous task. Many methods such as inverse spectral transform technique [1], Bell polynomials approach [2], dressing method [3], variable separation approach [4, 5], a generalised expansion method [6], singular manifold method [7], Riccati equation method [8, 9], generalised auxiliary equation method [10], extended three-wave method [11], sine–cosine method [12], various symmetry methods [13,14,15,16,17,18,19,20,21,22,23,24,25], extended mapping method [26], Hirota’s method [27,28,29,30,31], $({G^{\prime }}/{G})$ expansion method [32], Bolotin method [33], unified method [34] and multiple exp-function method [35] have been developed for treating these PDEs.

The objective of this study is to construct the invariant solutions of breaking soliton (BS) equation of the form

$$\begin{aligned}&u_t+b\,{u_{xxy}}+4buv_x+4bu_xv=0, \end{aligned}$$

(1a)

$$\begin{aligned}&v_x=u_y, \end{aligned}$$

(1b)

where b is a real parameter. The BS equation governs the collision of the Riemann waves propagating along the y-axis with the long waves along the x-axis [36].

In soliton theory, nonlinear waves have quietly revolutionised the realm of research and gained a lot of attention due to their wide applications in the real world. A soliton is a localised solitary wave packet which maintains its shape and size while propagating with constant velocity. John Scott Russell, in 1834, first discovered the solitary waves in the context of hydrodynamics. Nonlinear interaction is one of the most important properties of solitons observed by Zabusky and Kruskal [37] in the collisionless plasma in the KdV equation and the solitons remain transparent during mutual collision except for phase shift. The soliton with infinite support is the outcome of the perfect balancing between the linear dispersion and nonlinear convection in KdV equation. Solitons have wide applications in various physical contexts like physical plasma, optical lattices, stratified fluid flows and biophysics [38,39,40].

Some dark solitons, compactons, lumps, stationary, parabolic and multisoliton profiles of solutions of system (1) are obtained in this research. The dark solitons are different types of envelope solitons arising in nonlinear dispersive media. These solitons mainly depend on the key factors, dispersion and nonlinearity. The same sign of dispersion and nonlinear terms results in dark solitons [41]. The compacton, a new class of solitary waves with finite wavelength, compact support and soliton-free exponential tails or wings, was first presented by Rosenau and Hyman [42]. It is completely supported in small finite core region and vanishes identically outside the region. Compactons exhibit elastic interaction after interacting with other compactons and re-emerge with a similar coherent structure.

A lot of evolution equations in mathematical physics and fluid mechanics can be derived from the generalised BS equation

$$\begin{aligned}&u_t+a\,{u_{xxx}}+b\,{u_{xxy}}+c\,uu_x+d\,uv_x+e\,u_xv=0,\nonumber \\&v_x=u_y. \end{aligned}$$

(2)

The BS equation (1) can be obtained by substituting $a=c=0$, $d=e=4b$ into eq. (2), while $c=6a$, $d=e=4b$ transforms eq. (2) into Bogoyavlensky–Konoplechenko equation [2]. A particular choice $c=6a$, $d=e=3b$ transforms eq. (2) into the generalised KdV equation [2] and $a=1$, $c=6$, $b=d=e=0$, into the well-known KdV equation [2].

Sufficient literature for BS equation (1) is provided here, notably Li and Zhang [3] constructed infinitely many symmetries of the BS equation with the aid of infinitesimal version of ‘dressing’ method, which constitutes infinite-dimensional Lie algebra containing Abelian and Virasoro subalgebras. Ruan [4] obtained localised coherent structures via a variable separation approach and generated some soliton solutions depending upon the appropriate choice of arbitrary functions. Continuing, Ma et al [5] derived periodic, rational function and soliton solutions of BS equation. Moreover, Chen et al [6] proposed a generalised expansion method of Riccati equation and used it to establish soliton-like solutions with the aid of symbolic computation. Later on, Peng and Krishnan [7] employed singular manifold method to the BS equation and obtained periodic wave solutions involving Jacobi elliptic functions. Some exact soliton-like solutions were examined in [8] by means of symbolic computation and generalised projective Riccati equation method.

Besides, Cao et al [9] extended the Riccati equations method and used it to extract analytic results of the BS equation. Zhang [10] studied eq. (1) and examined some travelling wave solutions by virtue of generalised auxiliary equation method. Also, some exact breather and periodic-type soliton solutions had been found by using extended three-wave method [11]. Moreover, Taşcan and Bekir [12] used sine–cosine method and obtained exact solutions. Recently, Kumar et al [13] employed similarity transformation method to BS equation and constructed various exact closed-form solutions.

Motivated by the aforementioned studies, the present study is done to generalise [12, 13] and obtain new invariant solutions using the similarity transformations method. The method is based on invariance property under one-parameter transformations of Lie groups. The symmetry groups are continuous groups of transformations, which reduce the independent variables and the corresponding PDEs remain invariant. Thus, Lie group analysis is a widely used mathematical tool to derive invariant solutions of the system of NPDEs with applications in different contexts [13,14,15,16,17,18,19,20,21,22,23,24,25].

The rest of the paper is structured as follows: Section 2 deals with symmetry reductions and invariant solutions of the BS equation. The graphical behaviour and physical analysis of the obtained solutions are presented in §3. The concluding remarks are given in §4.

2 Symmetry reductions and invariant solutions of breaking soliton equation

Consider a one-parameter ($\varepsilon$) Lie group of transformations

$$\begin{aligned} \displaystyle x_i^*&= x_i + \varepsilon \xi _i(x,u)+ O(\varepsilon ^2),\\ u_j^*&= u_j + \varepsilon \phi _j(x, u)+ O(\varepsilon ^2 ), \end{aligned}$$

where ${\xi }_1=\xi$, ${\xi }_2=\eta$, ${\xi }_3=\tau$, ${\phi }_1=\phi$ and ${\phi }_2=\psi$ are the infinitesimals corresponding to variables x, y, t, u and v respectively.

Then, the corresponding infinitesimal generator is

$$\begin{aligned} \displaystyle \mathbf{v}&=\xi {\partial }_x+\eta {\partial }_y+\tau {\partial }_t+\phi {\partial }_u+\psi {\partial }_v. \end{aligned}$$

(3)

The first and third prolongation formulae for the BS equation are given as

$$\begin{aligned}&\text{ pr }^{(1)}{} \mathbf v = \mathbf v +\phi ^{y}\frac{\partial }{\partial u_y}+\psi ^{x}\frac{\partial }{\partial v_x},\\&\text{ pr }^{(3)}{} \mathbf v = \mathbf v +\phi ^{t}\frac{\partial }{\partial u_t}+\phi ^{x}\frac{\partial }{\partial u_x} +\psi ^{x}\frac{\partial }{\partial v_x}+\phi ^{xxy}\frac{\partial }{\partial u_{xxy}}. \end{aligned}$$

Employing these prolongation formulae under invariance conditions to eqs (1), the symmetry conditions are obtained as

$$\begin{aligned}&{\phi }^t+b{\phi }^{xxy}+4b(u{\psi }^x+v_x{\phi }+v{\phi }^x+u_x{\psi })=0, \\&{\phi }^y-{\psi }^x=0. \end{aligned}$$

Making use of values of the extensions ${\phi }^t$, ${\phi }^x$, ${\phi }^y$, ${\phi }^{xxy}$, ${\psi }^x$ [15] and equating the coefficient of partial derivatives to zero, we obtain the system of determining equations as

$$\begin{aligned}&{\xi }_y=0,\quad {\xi }_u=0,\quad {\xi }_v=0,\quad {\xi }_{xx}=0,\quad \\&{\xi }_{xt}=0, \quad {\eta }_x=0,\\&{\eta }_u=0, \quad {\eta }_v=0,\quad {\tau }_x=0,\quad {\tau }_y=0,\quad \\&{\tau }_u=0, \quad {\tau }_v=0,\\&{\tau }_{tt}=0,\quad 2{\xi }_x+{\eta }_y-{\tau }_t=0,\quad \phi +2\,u\,{\xi }_x-\frac{{\eta }_t}{4\,b}=0,\\&\psi -v{\xi }_x+v{\tau }_t-\frac{{\xi }_t}{4\,b}=0. \end{aligned}$$

On solving the above system, the infinitesimals can be recorded as

$$\begin{aligned}&\xi = a_1f_1+a_2f_2+a_3f_3+a_4f_4+a_5(x+f_5), \nonumber \\&\eta = a_2+a_3t+a_4y-2a_5y, \nonumber \\&\tau =a_1+a_4t, \nonumber \\&\phi =\frac{a_3}{4b}-2a_5u, \nonumber \\&\psi =\frac{1}{4b}(a_1\bar{f_1}+a_2\bar{f_2}+a_3\bar{f_3}+a_4\bar{f_4} +a_5\bar{f_5})\nonumber \\&\qquad \quad +\,(a_5-a_4)v, \end{aligned}$$

(4)

where $\displaystyle f_i\,(1\le i \le 5)$ are arbitrary smooth functions of t, $\displaystyle a_i\,(1\le i \le 5)$ are arbitrary constants and bar is used for the derivative overall in the manuscript.

In order to get symmetry reductions of the BS equation, the characteristic equation is

$$\begin{aligned}&\frac{\mathrm {d}x}{a_1f_1+a_2f_2+a_3f_3+a_4f_4+a_5(x+f_5)} \nonumber \\&\quad =\frac{\mathrm {d}y}{a_2+a_3t+a_4y-2a_5y}=\frac{\mathrm {d}t}{a_1+a_4 t}=\frac{\mathrm {d}u}{({a_3}/{4b})-2a_5u}\nonumber \\&\quad =\frac{\mathrm {d}v}{({1}/{4b})(a_1\bar{f_1}+a_2\bar{f_2}+a_3\bar{f_3} +a_4\bar{f_4}+a_5\bar{f_5})+(a_5-a_4)v}. \end{aligned}$$

(5)

The solutions of eq. (5) can be split into the following cases:

Case I: Corresponding to $\displaystyle a_4=0$, $\displaystyle a_1\ne 0$ and $\displaystyle ({1}/{4ba_1}) (a_1f_1+a_2f_2+a_3f_3+a_5f_5)=g_1(t)$, eq. (5) reduces to

$$\begin{aligned} \displaystyle&\frac{\mathrm {d}x}{4bg_1(t)+A_{3}x} = \frac{\mathrm {d}y}{A_{1}+A_{2}t-2A_{3}y}=\frac{\mathrm {d}t}{1}\\&\quad =\frac{\mathrm {d}u}{({A_{2}}/{4b})-2A_{3}u} =\frac{\mathrm {d}v}{\bar{g_1}(t)+A_{3}v} \end{aligned}$$

which provides

$$\begin{aligned} u&=A_{5}+{U(X,Y)}{\mathrm {e}^{-2A_{3}t}}, \end{aligned}$$

(6)

$$\begin{aligned} v&=\mathrm {e}^{A_{3}t}\int \bar{g_1}(t)\mathrm {e}^{-A_{3}t}\mathrm {d}t+V(X,Y)\mathrm {e}^{A_{3}t}, \end{aligned}$$

(7)

where U and V are functions of X and Y, which are

$$\begin{aligned} X&=x\mathrm {e}^{-A_{3}t}-{4b}\int g_1(t)\mathrm {e}^{-A_{3}t}\,\mathrm {d}t \end{aligned}$$

and

$$\begin{aligned} Y&=(y+A_{4}-4bA_{5}t)\mathrm {e}^{2A_{3}t}, \end{aligned}$$

(8)

where

$$\begin{aligned}&A_{1}=\frac{a_2}{a_1}, \quad A_{2}=\frac{a_3}{a_1},\quad A_{3}=\frac{a_5}{a_1},\quad \\&A_{4}=\frac{A_{2}}{4A_{3}^2}-\frac{A_{1}}{2A_{3}},\quad A_{5}=\frac{A_{2}}{8b\,A_{3}}. \end{aligned}$$

Therefore, reduction of the BS equation (1) yields

$$\begin{aligned}&bU_{XXY}+4b(UV_X+VU_X)-A_{3}XU_X\nonumber \\&\quad +2A_{3}YU_Y-2A_{3}U=0, \end{aligned}$$

(9)

$$\begin{aligned}&U_Y=V_X. \end{aligned}$$

(10)

To proceed further, we find the infinitesimals $\hat{\xi }$, $\hat{\eta }$, $\hat{\phi }$ and $\hat{\psi }$ for eqs (9) and (10) as

$$\begin{aligned}&\hat{\xi }=a_{6}X+a_{7}, \;\; \hat{\eta }=-2a_{6}Y, \;\; \hat{\phi }=-2a_{6}U, \\&\psi =a_{6}V+\frac{a_{7}A_{3}}{4b}, \end{aligned}$$

where $a_{6}$ and $a_{7}$ are arbitrary constants. Then, we obtain

$$\begin{aligned} \displaystyle&\frac{\mathrm {d}X}{a_{6}X+a_{7}}=\frac{\mathrm {d}Y}{-2a_{6}Y}=\frac{\mathrm {d}U}{-2a_{6}U}=\frac{\mathrm {d}V}{a_{6}V+({a_{7}A_{3}}/{4b})}. \end{aligned}$$

For $\displaystyle a_{6}\ne 0$, the similarity form is

$$\begin{aligned}&U= YU_1(X_1) \end{aligned}$$

and

$$\begin{aligned}&V=-\frac{A_{3}A_{6}}{4b}+(X+A_{6})V_1(X_1), \end{aligned}$$

where $U_1$ and $V_1$ are functions of $X_1=Y(X+A_{6})^2$ with $A_6={a_7}/{a_6}$.

Substituting the values of U and V into eqs (9) and (10), one can obtain

$$\begin{aligned}&2X^2_1\bar{\bar{\bar{U}}}_1+7X_1\bar{\bar{U}}_1+2\bar{U}_1 \nonumber \\&\quad +2X_1(U_1+2V_1)\, \bar{U}_1+2{U}_1^2=0, \end{aligned}$$

(11)

$$\begin{aligned}&X_1(\bar{U}_1-2\bar{V}_1)+U_1-V_1=0. \end{aligned}$$

(12)

The primitive of which is

$$\begin{aligned}&U_1=\frac{c_1}{X_1} \;\; \text{ and } \;\; V_1=0. \end{aligned}$$

Eventually, the solution of BS equation is

$$\begin{aligned} u&=A_{5}+c_{1}{\Bigr [x+\mathrm {e}^{A_{3}t}\Bigr (A_{6}-{4b}\int g_1(t) \mathrm {e}^{-A_{3}t}\,\mathrm {d}t\Bigr )\Bigr ]^{-2}}, \end{aligned}$$

(13)

$$\begin{aligned} v&=\mathrm {e}^{A_{3}t}\int \bar{g}_1(t)\,\mathrm {e}^{-A_{3}t}\, \mathrm {d}t-\frac{A_{3}A_{6}}{4b}\mathrm {e}^{A_{3}t}. \end{aligned}$$

(14)

Also, another solution of eqs (11) and (12) is

$$\begin{aligned} U_1=0 \;\; \text{ and } \;\; V_1=\frac{c_{2}}{{X}_1^{\frac{1}{2}}}, \end{aligned}$$

which leads to the solution BS equation

$$\begin{aligned} u&=A_{5}, \end{aligned}$$

(15)

$$\begin{aligned} v&=\Bigr (\int \bar{g}_1(t)\,\mathrm {e}^{-A_{3}t}\,\mathrm {d}t-\frac{A_{3}A_{6}}{4b}\Bigr )\mathrm {e}^{A_{3}t}\nonumber \\&\quad +\,c_2(y+A_{4}-4bA_{5}t)^{-{1}/{2}}, \end{aligned}$$

(16)

where $c_{1}$ and $c_{2}$ are arbitrary constants of integration.

Case II: If $\displaystyle a_1\ne 0$, $a_4=0=a_5$ and $({1}/{4ba_1})(a_1f_1+a_2f_2+a_3f_3)=g_2(t),$ then eq. (5) can be rewritten as

$$\begin{aligned}&\frac{\mathrm {d}x}{4bg_2(t)} = \frac{\mathrm {d}y}{A_{1}+A_{2}t} =\frac{\mathrm {d}t}{1}=\frac{\mathrm {d}u}{{A_{2}}/{4b}} =\frac{\mathrm {d}v}{\bar{g}_2(t)}. \end{aligned}$$

The corresponding similarity form is

$$\begin{aligned}&u=\frac{A_{2}}{4b}t+U(X,Y) \;\;\nonumber \\&\text{ and } \;\;\nonumber \\&v=g_2(t)+V(X,Y), \end{aligned}$$

(17)

with similarity variables

$$\begin{aligned}&X=x-4b\int g_2(t)\,\mathrm {d}t \;\;\\&\hbox {and} \;\;\\&Y=y-A_{1}t-\frac{1}{2}A_{2}t^2. \end{aligned}$$

Making use of eqs (1) and (17), the original system reduces to the form

$$\begin{aligned}&bU_{XXY}+4b(UV_X+VU_X)-A_{1}V_X+\frac{A_{2}}{4b}=0, \end{aligned}$$

(18)

$$\begin{aligned}&U_Y=V_X. \end{aligned}$$

(19)

Further, applying similarity transformation method (STM) to (18) and (19), one can obtain

$$\begin{aligned} \frac{\mathrm {d}X}{a_{8}X+a_{9}}&=\frac{\mathrm {d}Y}{a_{10}-4a_{8}Y} =\frac{\mathrm {d}U}{-a_{8}(2U-({A_{1}}/{2b}))}\nonumber \\&=\frac{\mathrm {d}V}{3a_{8}V}, \end{aligned}$$

(20)

where $a_{8}$, $a_{9}$ and $a_{10}$ are arbitrary constants.

Case IIa: For $a_{8}\ne 0$, the similarity form is

$$\begin{aligned}&U=\frac{A_{1}}{4b}+\frac{U_1(X_1)}{(X+A_{7})^2} \;\;\\&\hbox {and}\;\; \\&V=\frac{V_1(X_1)}{(4Y-A_{8})^{{3}/{4}}}, \end{aligned}$$

where $U_1$ and $V_1$ are functions of $\displaystyle X_1=(X+A_{7})^4(4Y-A_{8})$ with $A_{7}={a_{9}}/{a_{8}}$ and $A_{8}={a_{10}}/{a_{8}}$.

Substituting the values of U and V into eqs (18) and (19), one can obtain

$$\begin{aligned}&8X^2_1\,\bar{\bar{\bar{U}}}_1+14X_1\bar{\bar{U}}_1+\bar{U}_1+2X_1^{{1}/{4}} (V_1\bar{U}_1+U_1\bar{V}_1)\nonumber \\&\quad -{{U_1}{V_1}}X^{-\frac{3}{4}}+\frac{A_{2}}{32b^2}=0, \end{aligned}$$

(21)

$$\begin{aligned}&\bar{U}_1-X^{{1}/{4}}\bar{V}_1=0. \end{aligned}$$

(22)

A particular solution of this can be obtained by taking $A_{2}=0$. Thus, we have

$$\begin{aligned}&U_1=c_{3}~~\text{ and }~~ V_1=0. \end{aligned}$$

Eventually, the solution of BS equation is given by

$$\begin{aligned} u&=\frac{A_{1}}{4b}+c_{3}\Bigr (x-4b\int g_2(t)\, \mathrm{d}t+A_{7}\Bigr )^{-2}, \end{aligned}$$

(23)

$$\begin{aligned} v&=g_2(t). \end{aligned}$$

(24)

Also, another solution of eqs (21) and (22) is

$$\begin{aligned} U_1=0~~ \text{ and } ~~ V_1=c_{4} \end{aligned}$$

Hence, the leading solution of BS equation is

$$\begin{aligned} u&=\frac{A_{1}}{4b}, \end{aligned}$$

(25)

$$\begin{aligned} v&=g_2(t)+c_{4}(4y-4A_{1}t-A_{8})^{-{3}/{4}}, \end{aligned}$$

(26)

where $c_{3}$ and $c_{4}$ are arbitrary constants of integration.

Case IIb: For $a_{10}\ne 0$ and $a_{8}=0$, the similarity form is

$$\begin{aligned}&U= U_2(X_2) \;\; \text{ and } \;\; V= V_2(X_2), \end{aligned}$$

(27)

with similarity variable $X_2=(X-A_{9}Y)$, where $\displaystyle A_{9}={a_{9}}/{a_{10}}$, which results in the following reduction:

$$\begin{aligned}&bA_{9}\bar{\bar{\bar{U}}}_2-4b(U_2\bar{V}_2+V_2\bar{U}_2)+A_{1}\bar{V}_2 -\frac{A_{2}}{4b}=0, \end{aligned}$$

(28)

$$\begin{aligned}&A_{9}\bar{U}_2+\bar{V}_2=0. \end{aligned}$$

(29)

Its integration provides

$$\begin{aligned}&V_2=-A_{9}(U_2+c_{5}). \end{aligned}$$

(30)

Substituting $V_2$ from eq. (30) in eq. (28), we obtain

$$\begin{aligned}&\bar{\bar{\bar{U}}}_2+4(2U_2\bar{U}_2+c_{5}\bar{U}_2)-\frac{A_{1}}{b} \bar{U}_2-\frac{A_{2}}{4b^2A_{9}}=0 \end{aligned}$$

integration of which gives

$$\begin{aligned}&\bar{\bar{U}}_2+4(U_2^2+c_{5}U_2)-\frac{A_{1}}{b} U_2-\frac{A_{2}}{4b^2A_{9}}X_2+\frac{4c_{6}}{3}=0. \end{aligned}$$

(31)

For $A_{2}=0$, the integration of (31) gives

$$\begin{aligned}&{\bar{U}}_2^2+\frac{8}{3}(U_2^3+3A_{10}U_2^2+c_{6}U_2+c_{7})=0, \end{aligned}$$

(32)

where $c_{5}$, $c_{6}$, $c_{7}$ and $A_{10}=({1}/{2})(c_{5}-({A_{1}}/{4b}))$ are arbitrary constants. A variety of solutions of eq. (32) has been obtained by considering proper choice of the arbitrary constants as follows:

Case II${\hbox {b}_1}$: Treating $c_{6}=({9}/{4})A^2_{10}$ and $c_{7}=0$, eq. (32) is transformed to

$$\begin{aligned}&\bar{U}_2^2+\frac{8}{3}U_2\left( U_2+\frac{3}{2}A_{10}\right) ^2=0. \end{aligned}$$

(33)

If $A_{10}=k_1^2$ (say) then solutions of eqs (28) and (29) are

$$\begin{aligned}&U_2=\displaystyle - \frac{3}{2}k^2_1\tanh ^2(k_1\,X_2+c_{8})\\&\text{ and } \\&V_2=\displaystyle A_{9}\Bigr [\frac{3}{2}k^2_1\tanh ^2(k_1X_2+c_{8})-c_{5}\Bigr ]. \end{aligned}$$

Thus, we have leading solution of BS equation as

$$\begin{aligned} u&=\displaystyle -\frac{3}{2} k^2_1\, \tanh ^2[k_1(X-A_{9}Y) +c_{8}], \end{aligned}$$

(34)

$$\begin{aligned} v&=g_2(t)+A_{9}\Bigr [\frac{3}{2}k^2_1\tanh ^2(k_1(X-A_{9}Y) +c_{8})-c_{5}\Bigr ]. \end{aligned}$$

(35)

Also, another solution of the BS equation can be furnished as

$$\begin{aligned} u&=\displaystyle -\frac{3}{2} k^2_1\, \coth ^2[k_1(X-A_{9}Y)+c_{9}], \end{aligned}$$

(36)

$$\begin{aligned} v&= g_2(t)+A_{9}\Bigr [\frac{3}{2}k^2_1\coth ^2(k_1(X-A_{9}Y)+c_{9})-c_{5}\Bigr ]. \end{aligned}$$

(37)

For $A_{10}=-k_2^2$, the solution of eqs (28) and (29) is

$$\begin{aligned}&U_2=\displaystyle -\frac{3}{2} k^2_2\tan ^2(k_2\,X_2+c_{10}) \\&\text{ and } \\&V_2=\displaystyle A_{9}\Bigr [\frac{3}{2}k^2_2\tan ^2(k_2X_2+c_{10})-c_{5}\Bigr ], \end{aligned}$$

which provides

$$\begin{aligned} u&=\displaystyle -\frac{3}{2} k^2_2\, \tan ^2[k_2(X-A_{9}Y)+c_{10}], \end{aligned}$$

(38)

$$\begin{aligned} v&=g_2(t)+A_{9}\Bigr [\frac{3}{2}k^2_2 \tan ^2(k_2(X-A_{9}Y)+c_{10})-c_{5}\Bigr ]. \end{aligned}$$

(39)

Case IIb$_2$: If $c_{6}=c_{7}=0$, eq. (32) is reduced to

$$\begin{aligned}&\bar{U}_2^2+\frac{8}{3}U_2^2(U_2+3A_{10})=0. \end{aligned}$$

(40)

For $A_{10}>0$, assume $A_{10}={k_3^2}/{2}$ and solution of eqs (28) and (29) is obtained as

$$\begin{aligned}&U_2=\displaystyle -\frac{3}{2} k^2_3\sec ^2(k_3\,X_2+c_{11})\\&\text{ and } \\&V_2=\displaystyle A_{9}\Bigr [\frac{3}{2}k^2_3\sec ^2(k_3X_2+c_{11})-c_{5}\Bigr ]. \end{aligned}$$

Finally, the solution of BS equation follows:

$$\begin{aligned} u&=\displaystyle -\frac{3}{2} k^2_3 \sec ^2[k_3(X-A_{9}Y)+c_{11}], \end{aligned}$$

(41)

$$\begin{aligned} v&= g_2(t)+A_{9}\Bigr [\frac{3}{2}k^2_3\sec ^2(k_3(X-A_{9}Y)+c_{11})-c_{5}\Bigr ]. \end{aligned}$$

(42)

For $A_{10}<0$, let $A_{10}=-{k_4^2}/{2}$ and solution of eqs (28) and (29) is obtained as

$$\begin{aligned}&U_2=\displaystyle \frac{3}{2} k^2_4\,\mathrm {sech}^2(k_4\,X_2+c_{12}) \;\; \\&\text{ and }\\&V_2=-\displaystyle A_{9}\Bigr [\frac{3}{2}k^2_4\,\mathrm {sech}^2(k_4X_2+c_{12})+c_{5}\Bigr ]. \end{aligned}$$

The solution of the BS equation yields

$$\begin{aligned} u&=\displaystyle \frac{3}{2} k^2_4\, \mathrm {sech}^2[k_4(X-A_{15}Y)+c_{12}], \end{aligned}$$

(43)

$$\begin{aligned} v&=g_2(t)-A_{9}\Bigr [\frac{3}{2}k^2_4\,\mathrm {sech}^2(k_4(X-A_{9}Y)+c_{12})+c_{5}\Bigr ]. \end{aligned}$$

(44)

Also, another solution is

$$\begin{aligned} u&=\displaystyle -\frac{3}{2} k^2_4 \,\mathrm {csch}^2[k_4(X-A_{9}Y)+c_{13}], \end{aligned}$$

(45)

$$\begin{aligned} v&= g_2(t)+A_{9}\Bigr [\frac{3}{2}k^2_4\,\mathrm {csch}^2(k_4(X-A_{9}Y)+c_{13})-c_{5}\Bigr ]. \end{aligned}$$

(46)

Case II${\hbox {b}_3}$: On setting $c_{6}=3A^2_{10}$ and $c_{7}=A^3_{10}$, eq. (32) converts to

$$\begin{aligned}&\bar{U}_2^2+\frac{8}{3}(U_2+A_{10})^3=0. \end{aligned}$$

(47)

The solution of eqs (28) and (29) is obtained as

$$\begin{aligned}&U_2=-A_{10}-\frac{3}{2}(X_2+c_{14})^{-2} \\&\text{ and } \\&V_2=A_{9}(A_{10}-c_{5})+\frac{3}{2}A_{9}(X_2+c_{14})^{-2}. \end{aligned}$$

Consequently, the outcome of the BS equation can be expressed as

$$\begin{aligned} u&=-A_{10}-\frac{3}{2}(X-A_{9}Y+c_{14})^{-2}, \end{aligned}$$

(48)

$$\begin{aligned} v&=g_2(t)+A_{9}(A_{10}-c_{5})+\frac{3}{2}A_{9}(X-A_{9}Y+c_{14})^{-2}, \end{aligned}$$

(49)

where $c_{i}s$ ($8\le i \le 14$) are arbitrary constants of integration with

$$\begin{aligned} X= x-4b\int g_2(t)~\mathrm {d}t\quad \text { and } \quad Y=y-A_{1}t. \end{aligned}$$

Fig. 1

Profiles (a) and (b) showing interaction of waves for components expressed in (34) and (35).

Fig. 2

Annihilation of multisoliton profile (a) in (c) and (b) in (d) for expressions (36) and (37).

Fig. 3

Elastic behaviour of multisoliton profiles (a) and (b) for the solution listed in eqs (38) and (39).

Deduction of previous results [12, 13]

• (i) Taking $\displaystyle g_2(t)=0$, $\displaystyle k_{3}=({1}/{2})\sqrt{{-c}/{\alpha }}$, $\displaystyle A_{1}=c$, $A_{9}=-1$, $\displaystyle c_{11}={\pi }/{2}$ and 0 into eq. (41), we can generate solutions (4.7) and (4.8) of [12] respectively.

• (ii) Taking $\displaystyle g_2(t)=0$, $\displaystyle k_{4}=({1}/{2})\sqrt{{c}/{\alpha }}$, $\displaystyle A_{1}=c$, $A_{9}=-1$, $\displaystyle c_{12}=0$ and $\displaystyle c_{13}=0$ into eqs (43) and (45), one can deduct solutions (4.10) and (4.9) of [12] respectively.

• (iii) Taking $\displaystyle g_2(t)=(b_3+t)^2$ in eqs (34) and (35), (38) and (39), one can obtain all the solutions corresponding to Case III(b$_1$) of table 6 of [13].

• (iv) Taking $\displaystyle g_2(t)=(b_3+t)^2$ and $\displaystyle c_{11}=({\pi }/{2})+c_{21}$ into eqs (41) and (42), (43) and (44), one can obtain all the solutions listed in Case III(b$_2$) of table 6 of [13].

• (v) The solution listed in Case III(b$_3$) of table 6 of [13] can be generated by taking particular choice of $\displaystyle g_2(t)=(b_3+t)^2$ into eqs (48) and (49).

Hence, we observed that various solutions are more general than previous findings [12, 13]. Moreover, to the best of the authors’ view, the obtained results have not been reported yet.

3 Analysis and discussions

The graphical representation of the BS equation produces the corporal information to interpret the phenomena physically. This section deals with the physical interpretation of the solutions given by eqs (34) and (35), (36) and (37), (38) and (39), (41) and (42), (43) and (44), (45) and (46), (48) and (49) depending upon their numerical simulations while the solutions listed in eqs (13) and (14), (15) and (16), (23) and (24), (25) and (26) are self-explanatory. The solutions contain various arbitrary constants and functions, and their appropriate choices are crucial to describe significant behaviour of the phenomena. The simulation is performed on MATLAB for $-10\le x,y \le 10$ and $-10\le x,t \le 10$. The authors fixed the value of arbitrary constants as: $a_{9}=0.824$, $a_{10}=0.982$, $b=1$, $b_2=0.022$, $A_{9}=0.839$ and arbitrary function $g_2(t)=(b_2+t)$ for all figures, while spatiotemporal profiles in figures 5 and 6 are traced by taking $g_2(t)=(b_2+t)^2$.

Fig. 4

Compacton profiles u in (a) and v in (b) for expressions (41) and (42).

Fig. 5

Lumps and parabolic profiles in (a) and (b) for expressions (43) and (44).

Fig. 6

Multisoliton profiles of u in (a) and v in (b) for expressions (45) and (46).

Fig. 7

Multisoliton profiles of u in (a) and v in (b) for the solution listed in eqs (48) and (49).

The interaction profiles for the waves expressed by the solution listed in eqs (34) and (35) are analysed in figure 1, which result into dark solitons. The suitable choice of constants is taken randomly as $k_1=0.276$, $A_{1}=0.429$, $c_{5}=0.260$, $c_{8}=0.968$ using the numerical simulation on MATLAB.

The multisoliton profiles corresponding to eqs (36) and (37) are shown in figure 2 at $t=0.450$. It is shown that the profile starts to annihilate to multisoliton after $t=6.698$ and become stationary. The adequate choices $k_1=0.276$, $A_{1}=0.429$, $c_{5}=0.260$ and $c_{9}=0.145$ are taken randomly by performing numerical simulation through MATLAB.

Figure 3 exhibits the elastic behaviour of multisoliton profiles eqs (38) and (39) by taking suitable choice of arbitrary constants as $k_2=0.276$, $A_{1}=0.429$, $c_{5}=-0.045$ and $c_{10}=0.964$. It is observed that the solitons do not change their shape and size when they interact with each other and show completely elastic nature.

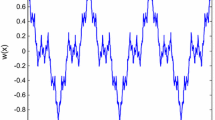
Figure 4 shows the physical behaviour of the explicit solution recorded in eqs (41) and (42) for $k_3=0.390$, $A_{1}=0.429$, $c_{5}=0.260$ and $c_{11}=0.528$. It exhibits the compacton behaviour of u and v when the argument of ‘$\cos$’ is less than $|{\pi }/{2}|$. It is concluded that compacton collides with another campacton without changing its shape and shows completely elastic behaviour. The decay in solution profiles is observed with time, which results in a straight strip.

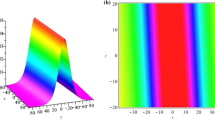
Figure 5 shows the spatiotemporal profiles reflecting the lumps and parabolic behaviour for the explicit solution given by eqs (43) and (44) at $y\,{=}\,0.631$. The adequate constants taken randomly are $k_4=0.390$, $A_{1}=0.429$, $c_{5}=-0.044$, $c_{12}=0.485$ and $g_2(t)=(b_2+t)^2$. It is observed that the amplitude of lumps oscillates periodically with the evolution of x and t. The lumps change its shape when the values of the above parameters are changed.

The spatiotemporal profiles for eqs (45) and (46) are plotted in figure 6 by taking arbitrary constants $k_4=0.390$, $A_{1}=0.429$, $c_{5}=-0.044$, $c_{13}=0.463$ and $g_2(t)=(b_2+t)^2$. The profile of u shows multisoliton while v shows multisoliton on curved surface.

Figure 7 shows the elastic behaviour of multisoliton profiles for (48) and (49) by taking $A_{1}=0.429$, $A_{6}=0.076$, $c_{5}=0.260$ and $c_{14}=0.653$. It is observed that the waves loose almost all the energy as time increases. Consequently, the multisoliton profiles start to decay and become stationary.

4 Concluding remarks

In this article, Lie symmetry analysis has been carried out to derive symmetry reductions of the BS equation. These reductions lead to invariant solutions in explicit form. The solutions are given by eqs (13) and (14), (15) and (16), (23) and (24), (25) and (26), (34) and (35), (36) and (37), (38) and (39), (41) and (42), (43) and (44), (45) and (46), (48) and (49). The solutions so obtained are more general than previous findings [12, 13] and never reported in the literature. The solutions are of great interest and have sufficient scope to describe various qualitative features of the soliton theory because of arbitrary constants and functions. To understand the phenomena physically, numerical simulation is performed on the obtained solutions. Thus, dark solitons, lumps, compactons, multisolitons and their elastic collisions are analysed. Also, these solutions can be used to verify the consistency and possible errors for newly developed numerical algorithms. Thus, similarity transformation method is a vital and crucial applicable tool to construct soliton solutions.