On Lie symmetries and soliton solutions of $(2+1)$-dimensional Bogoyavlenskii equations

Abstract

The present article is devoted to find some invariant solutions of the $(2+1)$-dimensional Bogoyavlenskii equations using similarity transformations method. The system describes $(2+1)$-dimensional interaction of a Riemann wave propagating along y-axis with a long wave along x-axis. All possible vector fields, commutative relations and symmetry reductions are obtained by using invariance property of Lie group. Meanwhile, the method reduces the number of independent variables by one, which leads to the reduction of Bogoyavlenskii equations into a system of ordinary differential equations. The system so obtained is solved under some parametric restrictions and provides invariant solutions. The derived solutions are much efficient to explain the several physical properties depending upon various existing arbitrary constants and functions. Moreover, some of them are more general than previously established results (Peng and Shen in Pramana 67:449–456, 2006; Malik et al. in Comput Math Appl 64:2850–2859, 2012; Zahran and Khater in Appl Math Model 40:1769–1775, 2016; Zayed and Al-Nowehy in Opt Quant Electron 49(359):1–23, 2017). In order to provide rich physical structures, the solutions are supplemented by numerical simulation, which yield some positons, negatons, kinks, wavefront, multisoliton and asymptotic nature.

1 Introduction

1.1 Scope

Nonlinear waves become intensively interesting since nonlinear phenomena has direct relevance and wide applications in real-life situations. These nonlinear phenomena can be described through nonlinear partial differential equations (NPDEs) [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32]. Such complex scientific phenomena frequently occurring in some physical systems like mathematical physics, chemistry, biology, fluid mechanics, plasma physics and some other real-life problems can be modeled by these NPDEs. The exact solutions provide the precise information of the physical systems described by these PDEs. During past five decades, a number of efficient techniques have been developed to obtain mathematical solutions of PDEs for their reliable treatment notably singular manifold method [2,3,4], traveling wave method [4], $\left( \frac{G^{'}}{G}\right)$-expansion method [5], modified extended tanh-function method [6], generalized Riccati equation mapping method [7], modified method of simplest equation [8], first integral method [9], Hirota’s method [10,11,12] and similarity transformations method (STM) [18,19,20,21,22,23,24,25,26,27,28,29,30,31,32].

The present article is addressed to generate Lie symmetries and derive solitary wave solutions of Bogoyavlenskii equations (BE)

$$\begin{aligned}&4\,u_t+u_{xxy}-4\,u^2\,u_y-4\,u_x\,v=0,\end{aligned}$$

(1a)

$$\begin{aligned}&u\,u_y=v_x,&\end{aligned}$$

(1b)

where u(x, y, t) and v(x, y, t) are the amplitude of relevant wave model. The system of Eqs. (1a)–(1b) is a modified version of a breaking soliton equation

$$\begin{aligned} 4\,u_{xt}+8\,u_x\,u_{xy}+4\,u_y\,u_{xx}+u_{xxxy} = 0, \end{aligned}$$

which describes $(2+1)$-dimensional interaction of a Riemann wave propagating along y-axis with a long wave along x-axis [1].

It is necessary to cite some importance of solitons in real-life situations before we discuss the related literature review for this problem. Solitons are nonlinear solitary wave packets with finite amplitude which retain their shapes and speed when interacting with each other. They also show completely elastic behavior. These are also possible outcome of perfect balancing between the nonlinear convection and linear dispersion in the well-known Korteweg-de Vries equation. Solitons are conspicuous manifestations of nonlinear interactions in diverse physical contexts including optical lattice, physical plasma, biophysics [14,15,16,17]. The nature of solitons is different for various systems and understanding of their properties is still a fundamental problem as in ultracold bosonic atoms in optical lattice [14] which are suitable for exploring quantum dynamics and their good isolation from the environment. Also, their frequencies and characteristic energies are very high, which are extremely advantageous for experimental investigations. These systems are unceasingly important to develop the experimental tools which allow to control system parameters in time and far from equilibrium initial states.

One of the applications of solitons is to carry the energy of hydrolysis of the molecules ATP along x-helical protein molecules without serious losses [16]. Solitons are also used in medical science to explain the contraction mechanism of animal muscles at the molecular level. Moreover, Davydov’s solitons [17] represent a composed state of an excitation of amide-I and hydrogen-bond distortion which describe a local conformational change of the DNA $\alpha$-helix.

Some positons, negatons, kinks, wavefront, multisoliton and asymptotic nature of the solutions of (1a)–(1b) are shown in this research. Positons are singular, oscillating, weakly localized, super-reflection less and completely transparent solutions with positive eigenvalue of the spectral parameter. Negatons are singular, weakly localized, exponentially decaying solutions having negative eigenvalue of spectral parameter which are absolutely intensive to the mutual collision. However, collision of positons–solitons results in solitons. Kink waves or Alfvén waves are the magneto hydrodynamic waves propagating in electrically conducting fluid along magnetic field lines, in which mass density of ions provides the inertia and the restoring force are provided by the magnetic field. Kink waves are widely used in the solar atmosphere and plasma physics. Moreover, a wavefront is the locus of points characterized by propagation of positions of identical phase. Wavefront is widely used to construct wavefront sensor for astronomical adaptive optics purpose due its flexibility to match the brightness of the source.

1.2 Related works

A literature review for the various forms of Bogoyavlenskii equations is reported here notably Bogoyavlenskii [1] presented Lax pair and a non-isospectral condition for the spectral parameter. Kudryashov and Pickering [2] obtained Eqs. (1a)–(1b) in terms of $(2+1)$-Schwarzian breaking soliton hierarchy to get rational solutions. In view of singular manifolds method, Estévez and Prada [3] generated BE (1a)–(1b) by promulgating that $(2+1)$-dimensional system of PDEs can be treated as a generalization of the sine-Gordon equation. Peng and Shen [4] reported some exact solutions of (1a)–(1b) with the help of the traveling wave and singular manifold method. Moreover, Malik et al. [5] extracted some exact traveling wave solutions with special type of solutions like kink shaped, anti kink shaped, bell type soliton solutions by employing $\left( \frac{G^{'}}{G}\right)$-expansion approach. Zahran and Khater [6] applied modified extended tanh-function method and hence derived some exact traveling wave solutions. Furthermore, Zayed and Nowehy [7] showed modified extended tanh-function method as a particular case of the generalized Riccati equation mapping method and then obtained a family of exact solutions of BE. Some exact traveling wave solutions of BE were constructed with the aid of modified method of simplest equation by Yu and Sun [8]. Besides, Eslami et al. [9] studied time fractional Bogoyavlenskii equations and constructed exact solutions by using first integral method. Some solutions of modified KdV-Calogero–Bogoyavlenskii–Schiff equation were yeilded by Wazwaz [10]. Continuing with same spirit, Wazwaz [11] constructed a integrable system combining recursion operator of the modified CBS equation and its inverse recursion operator, and hence some multiple-soliton solutions including peakons, kinks and cuspon were obtained.

1.3 Motivation

Nonlinear waves are fundamental time evolution phenomena characterized by nonlinear evolution equations. Basically, nonlinear waves or system are governed by nonlinear evolution equations (NLEES). The study of which has quietly revolutionized the realm of nonlinear science. Higher-order NLEEs describe the propagation of solitary waves on a continuous and fluctuating background with nonuniform velocities depending upon the solutions containing several arbitrary functions. Once if higher-order NLEEs integrated into closed form then many physical features existing into the system are naturally revealed. The NLEEs basically do not follow the superposition principle. Therefore, we have to search another tool to derive exact solution of a NLEE which is not always an easy task. Aim of this work is to bridge the gap made from previous findings [4,5,6,7] till date. We have derived more generalize soliton solutions of Eqs. (1a)–(1b) by using a reliable and efficient tool STM via Lie group theory under which system of PDEs remains invariant. The deductions of previously established solutions [4,5,6,7] prove the worthiness of this work. The theory of Lie symmetry has various applications to solve problems in diverse physical contexts including theoretical physics, optical lattice, physical plasma, biophysics [18,19,20,21,22,23,24,25,26,27,28,29,30,31,32].

1.4 Outline

The rest of the article is organized as follows: Sect. 2 deals with method of Lie symmetry analysis of BE. Symmetry reductions and invariant solutions are derived in Sect. 3, while Sect. 4 describes about analysis and discussions of the results. The research is accomplished with concluding remarks in Sect. 5.

2 Lie symmetry analysis

The objective of this section is to explain the basic terms to derive the infinitesimal symmetries and Lie algebra of Bogoyavlenskii equations (1) by using Lie group theory.

For BE system, one-parameter ($\epsilon$) transformations can be considered as

$$\begin{aligned} x^*&= x + \epsilon ~\xi (x, y, t, u, v)+ O(\epsilon ^2), [1]\\ y^*&= y + \epsilon ~\eta (x, y, t, u, v)+ O(\epsilon ^2),[1]\\ t^*&= t + \epsilon ~\tau (x, y, t, u, v)+ O(\epsilon ^2 ),[1]\\ u^*&= u + \epsilon ~\phi (x, y, t, u, v)+ O(\epsilon ^2 ),[1]\\ v^*&= v + \epsilon \,\psi (x, y, t, u, v)+ O(\epsilon ^2 ) ~\text{ etc. }, \end{aligned}$$

where $\xi$, $\eta$, $\tau$, $\phi$ and $\psi$ are coefficient functions of infinitesimal symmetries [19], which are to be determined.

The vector field $\mathbf {v}$ associated with the one-parameter transformations can be represented as

$$\begin{aligned} \displaystyle \mathbf{v}=\xi \,{\partial }_x+\eta \,{\partial }_y+\tau \,{\partial }_t +\phi \,{\partial }_u+\psi \,{\partial }_v. \end{aligned}$$

(2)

The corresponding first and third prolongations [19] are

$$\begin{aligned}&\text{ pr }^{(1)}{} \mathbf v = \mathbf v +\phi ^{y}\frac{\partial }{\partial u_y}+\psi ^{x}\frac{\partial }{\partial v_x}, \\ {}&\text{ pr }^{(3)}{} \mathbf v = \mathbf v +\phi ^{t}\frac{\partial }{\partial u_t}+\phi ^{x}\frac{\partial }{\partial u_x} +\phi ^{y}\frac{\partial }{\partial u_y}+\phi ^{xxy}\frac{\partial }{\partial u_{xxy}}. \end{aligned}$$

Applying invariance condition to Eqs. (1a)–(1b), we have

$$\begin{aligned}&\text{ pr }^{(3)}{} \mathbf v [4\,u_t+u_{xxy}-4\,u^2\,u_y-4\,u_x\,v]=0,\\ {}&\text{ pr }^{(1)}{} \mathbf v [u\,u_y-v_x]=0. \end{aligned}$$

which implies

$$\begin{aligned}&4\,{\phi }^t+{\phi }^{xxy}-4\,u^2\,{\phi }^y-8\,u\,u_y\,{\phi }\nonumber \\&\qquad -4\,v\,{\phi }^x-4\,u_x\,\psi =0, \end{aligned}$$

(3)

$$\begin{aligned}&u\,{\phi }^y+u_y\,\phi -{\psi }^x=0, \end{aligned}$$

(4)

where ${\phi }^t$, ${\phi }^x$, ${\phi }^y$, ${\phi }^{xxy}$ and ${\psi }^x$ can be expressed as

$$\begin{aligned} {\phi }^t&=D_t\phi -u_x\,D_t\xi -u_y\,D_t\eta -u_t\,D_t\tau \\ {\phi }^x&=D_x\,\phi -u_x\,D_x\xi -u_y\,D_x\eta -u_t\,D_x\tau \\ {\phi }^y&=D_y\phi -u_x\,D_y\xi -u_y\,D_y\eta -u_t\,D_y\tau \\ {\phi }^{xxy}&=D^2_x\,D_y\,\phi -u_x\,D^2_x\,D_y\,\xi -u_{xy}\,D^2_x\,\xi \\&\qquad -\,2\,u_{xx}\,D_x\,D_y\,\xi -\,2\,u_{xxy}\,D_x\xi \\&\qquad -u_{xxx}\,D_y\xi -u_y\,D^2_x\,D_y\eta -\,u_{yy}\,D^2_x\eta \\&\qquad -\,2\,u_{xy}\,D_x\,D_y\eta -2\,u_{xxy}\,D_x\eta -u_{xxy}\,D_y\eta \\&\qquad -\,u_t\,D^2_x\,D_y \tau -u_{yt}\,D^2_x\tau -2\,u_{xt}\,D_x\,D_y\tau \\&\qquad -\,2\,u_{xyt}\,D_x \tau -u_{xxt}\,D_y \tau \\ {\psi }^x&=D_x\,\psi -v_x\,D_x\xi -v_y\,D_x\eta -v_t\,D_x\tau , \end{aligned}$$

in which $D_t$, $D_x$ and $D_y$ denote the total derivatives. For illustration, one of them can be expressed as

$$\begin{aligned} D_t&=\frac{\partial }{\partial t}+u_t\frac{\partial }{\partial u}+v_t\frac{\partial }{\partial v}+u_{tx}\frac{\partial }{\partial u_x}+v_{tx}\frac{\partial }{\partial v_x}\\ \quad&+\,u_{tt}\frac{\partial }{\partial u_ t}+v_{tt}\frac{\partial }{\partial v_ t}+{\cdots }. \end{aligned}$$

Substituting above expressions into Eqs. (3)–(4) and equating the coefficient of various monomials, we get the set of overdetermining equations. Consequently, the following infinitesimal symmetries can be derived as

$$\begin{aligned} \xi&= a_1\,f_1+a_2\,f_2+a_3\,f_3+a_4\,(x+f_4),\nonumber [1]\\ \eta&= a_2+a_3\,y-2\,a_4\,y, \nonumber [1]\\ \tau&=a_1+a_3\,t, \nonumber [1]\\ \phi&=-\,a_4\,u,\nonumber [1]\\ \psi&=-\,(a_1\,\bar{f}_{1}+a_2\,\bar{f}_{2}+a_3\,\bar{f}_{3}+a_4\,\bar{f}_{4})+(a_4-a_3)\,v. \end{aligned}$$

(5)

where $f_i(t)$ ($1\le i\le 4$) are arbitrary smooth functions of t obtained by solving the system of overdetermining equations and $a_i$ ($1\le i\le 4)$ are arbitrary constants. The bar is used for the derivative overall in the manuscript.

For further processing, let us assume $a_1f_1+a_2f_2+a_3f_3+a_4f_4=g(t)$, then Eq. (5) becomes

$$\begin{aligned} \xi&= g(t)+a_4x, \eta = a_2+a_3y-2a_4y, \\ \tau&=a_1+a_3t, [1]\\ \phi&=-\,a_4u \psi =-\,\bar{g}(t)+(a_4-a_3)v, \end{aligned}$$

Thus, Lie symmetry analysis for system (1) is

$$\begin{aligned}&\mathbf{{v}}=\mathbf{{v_1}}(g)+\mathbf{{v_2}}+\mathbf{{v_3}}+\mathbf{{v_4}}+\mathbf{{v_5}} \end{aligned}$$

where

$$\begin{aligned} \mathbf{{v_1}}(g)&=g(t)\,\frac{\partial }{\partial x}-\bar{g}(t)\,\frac{\partial }{\partial v}, \mathbf{{v_2}}=\frac{\partial }{\partial t}, \mathbf{{v_3}}=\frac{\partial }{\partial y}, \\ \mathbf{{v_4}}&=y\,\frac{\partial }{\partial y}+t\,\frac{\partial }{\partial t}-v\,\frac{\partial }{\partial v}, \\ \mathbf{{v_5}}&=x\,\frac{\partial }{\partial x}-2\,y\,\frac{\partial }{\partial y}-u\,\frac{\partial }{\partial u}+v\,\frac{\partial }{\partial v}. \end{aligned}$$

Then Lie algebra and commutative relation of these vectors are calculated as

$$\begin{aligned} \begin{array}{ll} \mathbf{[v_1,v_2]}=-\,\mathbf{v_1}(\bar{g}),&{} \mathbf{[v_2,v_1]}=\mathbf{v_1}(\bar{g}), \\ \mathbf{[v_1,v_3]}=0, &{} \mathbf{[v_3,v_1]}=0,\\ \mathbf{[v_1,v_4]}=-\,\mathbf{v_1}(t\,\bar{g}), &{}\mathbf{[v_4,v_1]}=\mathbf{v_1}(t\,\bar{g}) \\ \mathbf{[v_1,v_5]}=\mathbf{v_1}(g), &{} \mathbf{[v_5,v_1]}=-\mathbf{v_1}(g),\\ \mathbf{[v_2,v_3]}=0, &{} \mathbf{[v_3,v_2]}=0, \\ \mathbf{[v_2,v_4]}=\mathbf{v_2}, &{} \mathbf{[v_4,v_2]}=-\,\mathbf{v_2},\\ \mathbf{[v_2,v_5]}=0, &{} \mathbf{[v_5,v_2]}=0,\\ \mathbf{[v_3,v_4]}=\mathbf{v_3}, &{} \mathbf{[v_4,v_3]}=-\,\mathbf{v_3},\\ \mathbf{[v_3,v_5]}=-\,2\,\mathbf{v_3}, &{} \mathbf{[v_5,v_3]}=2\,\mathbf{v_3},\\ \mathbf{[v_4,v_5]}=0, &{} \mathbf{[v_5,v_4]}=0, \end{array} \end{aligned}$$

Obviously, all the above vector fields are closed under Lie bracket.

3 Symmetry reductions and invariant solutions

In order to yield invariant solutions of BE (1a)–(1b), the corresponding characteristic equation is

$$\begin{aligned}&\frac{\mathrm{d}x}{a_1\,f_1+a_2\,f_2+a_3\,f_3+a_4\,(x+f_4)}\nonumber \\&\quad = \frac{\mathrm{d}y}{a_2+a_3\,y-2\,a_4\,y}\nonumber \\ {}&\quad = \frac{\mathrm{d}t}{a_1+a_3\,t}=\frac{\mathrm{d}u}{-\,a_4\,u}\nonumber \\ {}&\quad =\frac{\mathrm{d}v}{-\,(a_1\,\bar{f}_{1}+a_2\,\bar{f}_{2}+a_3\,\bar{f}_{3}+a_4\,\bar{f}_{4})+(a_4-a_3)\,v}. \end{aligned}$$

(6)

The adequate choice of arbitrary constants and functions appearing in Eq. (6) is chosen to proceed further integration. Consequently, the following cases arise:

• Case (I): If $a_3 \ne 0$ and $\displaystyle \frac{1}{a_3}\sum _{i=1}^4 a_if_i=g_1(t)$.

• Case (II): If $a_1\ne 0$ but $a_3=0$, and $\displaystyle \frac{1}{a_1}\sum _{i=1}^4 a_if_i=g_2(t)$.

• Case (III): If $a_1\ne 0$ but $a_3=a_4=0$ and $\displaystyle \frac{1}{a_1}\sum _{i=1}^4 a_if_i=g_3(t)$. For further process, we set $\displaystyle A_1=\frac{a_1}{a_3}, A_2=\frac{a_2}{a_3}$ and $\displaystyle A_3=\frac{a_4}{a_3}$.

Case (I) If $a_3\ne 0$ and $\displaystyle \frac{1}{a_3}(a_1f_1+a_2f_2+a_3f_3+a_4f_4)=g_1(t)$, then Eq. (6) can be rewritten as

$$\begin{aligned} \frac{\mathrm{d}x}{g_1(t)+A_3\,x}&= \frac{\mathrm{d}y}{A_2+(1-2A_3)\,y}=\frac{\mathrm{d}t}{A_1+t}=\frac{\mathrm{d}u}{-A_3\,u} \nonumber \\ {}&=\frac{\mathrm{d}v}{-\bar{g}_{1}(t)+(A_3-1)\,v}. \end{aligned}$$

(7)

Hence, similarity form of BE yields

$$\begin{aligned} u&=\displaystyle \frac{U(X,Y)}{(A_1+t)^{A_3}}, \end{aligned}$$

(8)

$$\begin{aligned} v&=\displaystyle \Bigg (V(X,Y)-\int \frac{\bar{g}_{1}(t)}{(A_1+t)^{A_3}}\,\mathrm{d}t\Bigg )(A_1+t)^{(A_3-1)}, \end{aligned}$$

(9)

where U(X, Y) and V(X, Y) are similarity functions of the variables X and Y, which can be expressed as

$$\begin{aligned} X&=\frac{x}{(A_1+t)^{A_3}}-\int \frac{g_1(t)}{(A_1+t)^{(A_3+1)}}\mathrm{d}t,\\ Y&=\Bigr (y-\frac{A_2}{2A_3-1}\Bigr )(A_1+t)^{(2\,A_3-1)},\qquad \left( \,A_3\ne \frac{1}{2}\right) . \end{aligned}$$

Therefore, first similarity reduction of the BE (1a)–(1b) produces

$$\begin{aligned}&\displaystyle U_{XXY}-4\,U^2\,U_Y-4\,V\,U_X-4\,A_3\,X\,U_X\nonumber \\&\quad \qquad +\,4\,(2A_3-1)\,Y\,U_Y-4\,A_3\,U=0, \end{aligned}$$

(10)

$$\begin{aligned}&U\,U_Y=V_X. \end{aligned}$$

(11)

For which, the infinitesimals ${\hat{\xi }}$, ${\hat{\eta }}$, ${\hat{\phi }}$ and ${\hat{\psi }}$ are given by

$$\begin{aligned} \nonumber \displaystyle&{\hat{\xi }}=a_5\,X+a_6, {\hat{\eta }}=-\,2\,a_5\,Y, {\hat{\phi }}=-\,a_5\,U, \nonumber \\ {}&{\hat{\psi }}=a_5\,V-a_6\,A_3. \end{aligned}$$

(12)

where $a_5$ and $a_6$ are arbitrary constants.

Thus, the characteristic equation for the system (10)–(11) is

$$\begin{aligned}&\displaystyle \frac{\mathrm{d}X}{a_5\,X+a_6}=\frac{\mathrm{d}Y}{-2\,a_5\,Y}=\frac{\mathrm{d}U}{-a_5\,U}=\frac{\mathrm{d}V}{a_5\,V-a_6\,A_3}. \end{aligned}$$

(13)

To solve further, following cases can be raised:

Case (I$a_1$) For $a_5\ne 0$ then Eq. (13) recasts

$$\begin{aligned}&\frac{\mathrm{d}X}{X+A_{4}}=\frac{\mathrm{d}Y}{-\,2\,Y}=\frac{\mathrm{d}U}{-\,U}=\frac{\mathrm{d}V}{V-A_3A_4}, \end{aligned}$$

where $A_{4}=\displaystyle \frac{a_6}{a_5 }$.

Then similarity form is

$$\begin{aligned}&U=\frac{U_1(X_1)}{X+A_4} \text{ and } V=A_3\,A_4+\frac{V_1(X_1)}{\sqrt{Y}}, \end{aligned}$$

where $U_1$ and $V_1$ are functions of $X_1=Y\,(X+A_4)^2$.

Substituting the values of U and V into Eqs. (10)–(11), one can obtain

$$\begin{aligned}&2\,X^2_1\,\bar{\bar{\bar{U_{1}}}}+3\,X_1\,\bar{\bar{U_{1}}}-2\,U_1^2\,\bar{U}_{1} +2\,\frac{U_1V_1}{\sqrt{X_1}}-4\,\sqrt{X_1}\,\bar{U}_{1}\,V_1\nonumber \\&\qquad -\,2\,X_1\,\bar{U}_{1}=0, \end{aligned}$$

(14)

$$\begin{aligned}&U_1\,\bar{U}_{1}=2\,\sqrt{X_1}\,\bar{V}_{1}. \end{aligned}$$

(15)

The primitives of which are

$$\begin{aligned}&U_1=c_1 \text{ and } V_1=0, \end{aligned}$$

(16)

Eventually, solution of BE is given by

$$\begin{aligned} u&=\frac{c_1}{\displaystyle x+\Bigr (A_4-\int \frac{g_1(t)}{(A_1+t)^{(A_3+1)}}\mathrm{d}t\Bigr )(A_1+t)^{A_3}}, \end{aligned}$$

(17)

$$\begin{aligned} v&=\Bigr (A_3\,A_4\,-\int \frac{\bar{g}_{1}(t)}{(A_1+t)^{A_3}}\,\mathrm{d}t\Bigr )\displaystyle (A_1+t)^{(A_3-1)}. \end{aligned}$$

(18)

where $c_{1}$ is an arbitrary constant of integration.

Case (I$a_2$) If $a_5=0$ and $a_6\ne 0$, then characteristic Eq. (13) recasts

$$\begin{aligned}&\frac{\mathrm{d}X}{a_6}=\frac{\mathrm{d}Y}{0}=\frac{\mathrm{d}U}{0}=\frac{\mathrm{d}V}{-\,a_6\,A_3}. \end{aligned}$$

On simplifying, we get similarity form

$$\begin{aligned}&U=U_2(Y) \text{ and } V=-A_3\,X+V_2(Y), \end{aligned}$$

(19)

where $U_2$ and $V_2$ both depend upon the same variable Y.

Therefore, the solution of BE is

$$\begin{aligned} u&=c_2, \end{aligned}$$

(20)

$$\begin{aligned} v&=\frac{V_2(Y)-g_1(t)}{(A_1+t)}, \end{aligned}$$

(21)

where $c_{2}$ is an arbitrary constant. Moreover, $V_2(Y)$ still remains arbitrary function of $\displaystyle Y=\frac{y+A_2}{A_1+t}$ and contributes to provide the general form of the exact solution.

On the other hand, if $A_3=\displaystyle \frac{1}{2}$, we proceed as

Case (Ib) For $2a_4=a_3$, characteristic Eq. (7) recasts

$$\begin{aligned} \displaystyle \frac{\mathrm{d}x}{g_1(t)+\frac{1}{2}\,x}&= \frac{\mathrm{d}y}{A_2}=\frac{\mathrm{d}t}{A_1+t}=-\frac{2\,\mathrm{d}u}{u}\\\quad&=-\frac{2\,\mathrm{d}v}{v+2\, \bar{g}_{1}(t)}. \end{aligned}$$

Therefore, we attain

$$\begin{aligned}&u=\displaystyle \frac{U(X,Y)}{(A_1+t)^{\frac{1}{2}}}, \end{aligned}$$

(22)

$$\begin{aligned}&v=-\frac{1}{(A_1+t)^{\frac{1}{2}}}\int \frac{\bar{g}_{1}(t)}{(A_1+t)^{\frac{1}{2}}}\mathrm{d}t +\frac{V(X,Y)}{(A_1+t)^\frac{1}{2}}, \end{aligned}$$

(23)

where similarity variables X and Y are

$$\begin{aligned}&X=\frac{x}{\displaystyle (A_1+t)^\frac{1}{2}}-\int \frac{g_1(t)}{(A_1+t)^{\frac{3}{2}}}\,\mathrm{d}t, \\&Y=y-A_{2}\,\log (A_1+t). \end{aligned}$$

Making use of u, v, X and Y into BE (1a)–(1b), one can get

$$\begin{aligned}&U_{XXY}-4\,U^2\,U_Y-4\,U_X\,V-2\,X\,U_X\nonumber \\&\qquad -4\,A_2\,U_Y-2\,U=0,\end{aligned}$$

(24)

$$\begin{aligned}&U\,U_Y=V_X. \end{aligned}$$

(25)

To solve above system, we shall require the corresponding infinitesimals ${\hat{\xi }}$, ${\hat{\eta }}$, ${\hat{\phi }}$ and ${\hat{\psi }}$ of Lie group, which are

$$\begin{aligned}&\displaystyle {{\hat{\xi }}=a_7, {\hat{\eta }}=a_8, {\hat{\phi }}=0, {\hat{\psi }}=-\frac{a_7}{2},} \end{aligned}$$

where $a_{7}$ and $a_{8}$ are arbitrary constants.

Then the characteristic equation for the system (24)–(25) is

$$\begin{aligned}&\displaystyle {\frac{\mathrm{d}X}{a_7}=\frac{\mathrm{d}Y}{a_8}=\frac{\mathrm{d}U}{0}=\frac{2\,\mathrm{d}V}{-a_7}}, \end{aligned}$$

which can be solved further treating $a_7\ne 0$ and then similarity form is

$$\begin{aligned}&U= U_1(X_1) \text{ and } V=-\frac{X}{2}+ V_1(X_1), \end{aligned}$$

(26)

where $\displaystyle X_1=Y-A_5\,X$ in which $A_{5}=\displaystyle \frac{a_8}{a_7}$.

Substituting U and V into Eqs. (24)–(25), one can obtain

$$\begin{aligned}&A_5^2\,\bar{\bar{\bar{U_{1}}}}-4\,U_1^2\,\bar{U}_{1}-4\,A_2\,\bar{U}_{1}+4\,A_5\,\bar{U}_{1}\,V_1-2\,U_1=0, \end{aligned}$$

(27)

$$\begin{aligned}&2\,U_1\,\bar{U}_{1}+2\,A_5\,\bar{V}_{1}+1=0. \end{aligned}$$

(28)

Eqs. (27)–(28) can be satisfied by

$$\begin{aligned}&U_1=\frac{A_5}{X_1}\quad \text{ and } \quad V_1=-\frac{A_5}{2X_1^2}+\frac{1}{2A _5}(2A_2-X_1). \end{aligned}$$

(29)

It helps to provide the solution of BE as

$$\begin{aligned} u&=\frac{A_5(A_1+t)^{-\frac{1}{2}} }{ \Bigg (y-A_2\log (A_1+t)-\frac{A_5x}{(A_1+t)^{\frac{1}{2}}}+A_5\int \frac{g_1(t)}{(A_1+t)^{\frac{3}{2}}}\mathrm{d}t\Bigg )} , \end{aligned}$$

(30)

$$\begin{aligned} v&=-\frac{1}{(A_1+t)^{\frac{1}{2}}}\int \frac{\bar{g}_{1}(t)}{(A_1+t)^{\frac{1}{2}}}\mathrm{d}t\nonumber \\\quad&-\frac{A_5(A_1+t)^{-\frac{1}{2}}}{2\Bigr (y-A_2\log (A_1+t)-\frac{A_5x}{(A_1+t)^{\frac{1}{2}}}+A_5\int \frac{g_1(t)}{(A_1+t)^{\frac{3}{2}}}\mathrm{d}t\Bigr )^2} \nonumber \\\quad&-\frac{y-A_2\Bigr (\log (A_1+t)+2\Bigr )}{2A_5(A_1+t)^{\frac{1}{2}}}. \end{aligned}$$

(31)

Case (II) For $\displaystyle a_1\ne 0$ and $a_3=0$, we have assumed $\displaystyle \frac{1}{a_1}\,(a_1\,f_1+a_2\,f_2+a_4\,f_4) =g_2(t)$, then characteristic Eq. (6) can be reformulated as

$$\begin{aligned} \nonumber \frac{\mathrm{d}x}{g_2(t)+A_{7}\,x}&= \frac{\mathrm{d}y}{A_6-2\,A_7\,y}=\frac{\mathrm{d}t}{1}=\frac{\mathrm{d}u}{-A_7\,u}\nonumber \\ {}&=\frac{\mathrm{d}v}{-\,\bar{g}_{2}(t)+A_{7}\,v}\,, \end{aligned}$$

(32)

where $A_6=\frac{a_2}{a_1}$, $A_7=\frac{a_4}{a_1}$ and leads to the following similarity reduction

$$\begin{aligned}&u=U(X,Y)\,{\displaystyle e^{-A_7\,t}}, \end{aligned}$$

(33)

$$\begin{aligned}&v={\displaystyle V(X,Y)\,e^{A_7\,t}} -e^{A_7\,t}\int e^{-A_7\,t}\bar{g}_{2}(t)\, \mathrm{d}t, \end{aligned}$$

(34)

with similarity variables X and Y as

$$\begin{aligned}&{\displaystyle X=x\,e^{-A_7\,t}-\int g_2(t)\,e^{-A_7\,t}\,\mathrm{d}t} \quad \text{ and } \\ {}&{\displaystyle Y=\Bigr (y-\frac{A_6}{2\,A_7}\Bigr )e^{2\,A_7\,t}}. \end{aligned}$$

Now, above values transform Eqs. (1a)–(1b) into the following system

$$\begin{aligned}&\displaystyle U_{XXY}-4\,U^2\,U_Y-4\,U_XV-4\,A_7\,X\,U_X +8\,A_7\,Y\,U_Y\nonumber \\ {}&\qquad -\,4\,A_7\,U=0, \end{aligned}$$

(35)

$$\begin{aligned}&U\,U_Y=V_X. \end{aligned}$$

(36)

For further reduction of the above system, we find the following infinitesimals of Lie group as

$$\begin{aligned}&\displaystyle {\hat{\xi }}=a_{9}\,X+a_{10}, {\hat{\eta }}=-2\,a_{9}\,Y, {\hat{\phi }}=-a_{9}\,U, \nonumber \\ {}&{\hat{\psi }}=a_{9}\,V-a_{10}\,A_{7}, \end{aligned}$$

where $a_{9}$ and $a_{10}$ are arbitrary constants.

For $\displaystyle a_9\ne 0$, we can proceed further as

$$\begin{aligned}&\frac{\mathrm{d}X}{X+A_8}=\frac{\mathrm{d}Y}{-2\,Y}=\frac{\mathrm{d}U}{-U}=\frac{\mathrm{d}V}{V-A_7\,A_8}, \end{aligned}$$

(37)

where $\displaystyle A_8=\frac{a_{10}}{a_9}$ and the similarity forms are

$$\begin{aligned}&U=\frac{U_1(X_1)}{X+A_8} \text{ and } V=A_7\,A_8+\frac{V_1(X_1)}{\sqrt{Y}}, \end{aligned}$$

with $\displaystyle X_1=Y\,(X+A_8)^2$.

Making use of the values of U and V into Eqs. (35)–(36), we have

$$\begin{aligned}&2\,X^2_1\bar{\bar{\bar{U_{1}}}}+3\,X_1\bar{\bar{U_{1}}}-2\,U_1^2\bar{U}_{1}-4\sqrt{X_1}\,\bar{U}_{1}V_1\nonumber \\&\quad \ +\frac{2\,U_1V_1}{\sqrt{X_1}} =0, \end{aligned}$$

(38)

$$\begin{aligned}&U_1\,\bar{U}_{1}=2\,\sqrt{X_1}\,\bar{V}_{1}. \end{aligned}$$

(39)

The primitive of the system is

$$\begin{aligned}&U_1=c_3 \text{ and } V_1=0, \end{aligned}$$

(40)

In this way, the solution of BE can be attained as follows

$$\begin{aligned} u&=\frac{c_3\,e^{-A_7\,t}}{\displaystyle x\,e^{-A_7\,t}-\int g_2(t)\,e^{-A_7\,t}\,\mathrm{d}t+A_8}, \end{aligned}$$

(41)

$$\begin{aligned} v&=-\,e^{A_7\,t}\int e^{-A_7\,t}\bar{g}_{2}(t) \,\mathrm{d}t+A_7\,A_8\,e^{A_7\,t}. \end{aligned}$$

(42)

This case terminates here and remaining solutions can be obtained further as

Case (III) For $a_1\ne 0$, $a_3=0=a_4$ and assuming $\displaystyle \frac{1}{a_1}\,(a_1\,f_1+a_2\,f_2)=g_3(t)$, then Eq. (6) provides

$$\begin{aligned}&\frac{\mathrm{d}x}{g_3(t)} = \frac{\mathrm{d}y}{A_{6}}=\frac{\mathrm{d}t}{1}=\frac{\mathrm{d}u}{0}=\frac{\mathrm{d}v}{-\bar{g}_{3}(t)}, \end{aligned}$$

which leads to similarity reduction of BE (1a)–(1b) as

$$\begin{aligned}&u=U(X,Y) \text{ and } v=-g_3(t)+V(X,Y), \end{aligned}$$

(43)

where U and V are functions of

$$\begin{aligned}&X=x-\int g_3(t)\,\mathrm{d}t \text{ and } Y=y-A_6t. \end{aligned}$$

Application of similarity transformations yields the following reductions

$$\begin{aligned}&U_{XXY}-4\,U^2\,U_Y-4\,A_6\,U_Y-4\,V\,U_X=0, \end{aligned}$$

(44)

$$\begin{aligned}&U\,U_Y=V_X. \end{aligned}$$

(45)

Moreover, the infinitesimals for the system (44)–(45) are

$$\begin{aligned}&{\hat{\xi }}=1, {\hat{\eta }}=F_1(Y), {\hat{\phi }}=0, {\hat{\psi }}=-V\,\bar{F}_{1}(Y). \end{aligned}$$

Then, the similarity form can be written as

$$\begin{aligned}&U=U_1(X_1) \text{ and } V=\frac{V_1(X_1)}{F_1(Y)}, \end{aligned}$$

(46)

where $\displaystyle X_1=X-\int \frac{1}{F_1(Y)}\mathrm{d}Y$.

Substituting the values of U and V into Eqs. (44)–(45), one can obtain

$$\begin{aligned}&\bar{\bar{\bar{U_{1}}}}-4\,U_1^2\,\bar{U}_{1}-4\,A_6\,\bar{U}_{1}+4\,V_1\,\bar{U}_{1}=0, \end{aligned}$$

(47)

$$\begin{aligned}&U_1\,\bar{U}_{1}+\bar{V}_{1}=0. \end{aligned}$$

(48)

Integrating Eq. (48) w.r.t $X_1$, one can obtain

$$\begin{aligned}&V_1=c_4-\frac{1}{2}U^2_1. \end{aligned}$$

(49)

Making use of this value of $V_1$ into Eq. (47), we obtain

$$\begin{aligned}&\bar{\bar{\bar{U_{1}}}}-6\,U_1^2\,\bar{U}_{1}+4\,(c_4-A_6)\,\bar{U}_{1}=0. \end{aligned}$$

(50)

Integrating, we obtain

$$\begin{aligned}&{\bar{U}_{1}}^2-U^4_1-2\,A_9\,U_1^2-c_5\,U_1-c_6=0, \end{aligned}$$

(51)

where $c_4$, $c_5$, $c_6$ and $A_9=2(A_6-c_4)$ are arbitrary constants.

Various solutions of Eq. (51) can be derived in the following manner:

Case (IIIa) Treating $c_5=0$ and adjusting $c_6=A_9^2$, then Eq. (51) can be written as

$$\begin{aligned}&\bar{U}_{1}^2-(U_1^2+A_9)^2=0. \end{aligned}$$

If $A_{9}=k_1^2$, then solution of Eqs. (47)–(48) is

$$\begin{aligned}&U_1=\displaystyle \pm \,k_1\tan (k_1\,X_1+c_{7}), \nonumber \\ {}&V_1=\displaystyle c_4-\frac{1}{2}k_1^2 \,\tan ^2(k_1\,X_1+c_{7}). \end{aligned}$$

(52)

The solution of BE is

$$\begin{aligned} u&=\displaystyle \pm \,k_1\, \tan \Bigg [k_1\Bigr (X-\int \frac{1}{F_1(Y)}\,\mathrm{d}Y\Bigr )+c_{7}\Bigg ], \end{aligned}$$

(53)

$$\begin{aligned} v&= \frac{\displaystyle 2c_4-k_1^2 \tan ^2\Bigg [k_1\Bigr (X-\int \frac{1}{F_1(Y)}\,\mathrm{d}Y\Bigr )+c_{7}\Bigg ]}{2F_1(Y)}-g_3(t). \end{aligned}$$

(54)

We fix $A_{9}=-k_2^2$ for getting another solution, which results

$$\begin{aligned}&U_1=\pm \, k_2\,\tanh \,(k_2\,X_1+c_{8}),\nonumber \\ {}&V_1=c_4-\frac{1}{2}\displaystyle k_2^2 \tanh ^2\,(k_2\,X_1+c_{8}), \end{aligned}$$

(55)

which implies

$$\begin{aligned} u=&\displaystyle \pm \, k_2\, \tanh \Bigr [k_2\Bigr (X-\int \frac{1}{F_1(Y)}\,\mathrm{d}Y\Bigr )+c_{8}\Bigr ], \end{aligned}$$

(56)

$$\begin{aligned} v=&\frac{\displaystyle 2\,c_4-k_2^2 \tanh ^2\Bigr [k_2\, \Bigr (X-\int \frac{1}{F_1(Y)}\mathrm{d}Y\Bigr )+c_{8}\Bigr ]}{2F_1(Y)}\nonumber \\ {}&\qquad -g_3(t). \end{aligned}$$

(57)

We also find another solution of Eqs. (47)–(48) as

$$\begin{aligned}&U_1=\pm \, k_2\, \coth (k_2\,X_1+c_{9}),\nonumber \\ {}&V_1=c_4-\frac{1}{2}k_2^2\, \coth ^2(k_2\,X_1+c_{9}). \end{aligned}$$

(58)

Therefore, the solution of BE is furnished as

$$\begin{aligned} u=&\displaystyle \pm \, k_2\, \coth \,\Bigg [k_2\,\Bigr (X-\int \frac{1}{F_1(Y)}\,\mathrm{d}Y\Bigr )+c_{9}\Bigg ], \end{aligned}$$

(59)

$$\begin{aligned} v=&\frac{\displaystyle 2c_4-k_2^2\, \coth ^2\,\Bigg [k_2\,\Bigr (X-\int \frac{1}{F_1(Y)}\mathrm{d}Y\Bigr )+c_{9}\Bigg ]}{2F_1(Y)}\nonumber \\ {}&\qquad -\,g_3(t). \end{aligned}$$

(60)

where $c_{7}$, $c_{8}$ and $c_{9}$ are the arbitrary constants of integration.

Deductions of some previously established results:

• (i) Treating $F_1(Y)=-1$, $g_3(t)=0$, $\displaystyle k_1=\sqrt{2c}$, $A_6=c$ in Eq. (53), we get two results of Zahran and Khater [6]; first by taking $c_7=0$ and second by $\displaystyle \frac{\pi }{2}$.

• (ii) Taking $F_1(Y)=-1$, $g_3(t)=0$, $c_4=0$ in Eqs. (53)–(54) lead to the deduction two results of Malik et al. [5], the first is obtained treating $\displaystyle k_1=\frac{\sqrt{4\mu -\lambda ^2}}{2}$, $A_6=c$, $\displaystyle c_7={\xi }_0+\frac{\pi }{2}$, while another for $k_1=1$, $A_6=\frac{1}{2}$, $c_7=0$.

• (iii) Assuming $\displaystyle F_1(Y)=-\frac{k}{l}$, $g_3(t)=0$, $k_2=k$, $\displaystyle A_6=-\frac{1}{2l}(k^2l+2c_1)$, $\displaystyle c_4=-\frac{c_1}{l}$, $c_8=0$ in Eqs. (56)–(57), one can derive previously established results by Peng and Shen [4].

• (iv) Treating $F_1(Y)=-1$, $g_3(t)=0$, $k_2=\sqrt{-2c}$, $A_6=c$, $c_8=0$ in Eq. (56), we can derive results of [6].

• (v) For $F_1(Y)=-1$, $g_3(t)=0$, $c_4=0$ in Eqs. (56)–(57), then one can deduce the three results of [5], first by setting $\displaystyle k_2=\frac{\lambda }{2}$, $A_6=c$, $c_8=0$, second by choosing $\displaystyle k_2=\frac{\sqrt{\lambda ^2-4\mu }}{2}$, $A_6=c$, $c_8={\xi }_0$ and last by assuming $k_2=1$, $\displaystyle A_6=-\frac{1}{2}$, $c_8=0$.

• (vi) Treating $F_1(Y)=-1$, $g_3(t)=0$, $\displaystyle k_2=\sqrt{-2c}$, $A_6=c$, $c_9=0$ in Eq. (59), we can derive results of [6].

• (vii) Putting $F_1(Y)=-1$, $g_3(t)=0$, $c_4=0$ in Eqs. (59)–(60), one can deduce the three previously established results in [5]; the first can be obtained by taking $\displaystyle k_2=\frac{\lambda }{2}$, $A_6=c$, $c_9=0$; second by taking $\displaystyle k_2=\frac{\sqrt{\lambda ^2-4\mu }}{2}$, $A_6=c$, $c_9={\xi }_0$ and third by $k_2=1$, $\displaystyle A_6=-\frac{1}{2}$, $c_9=0$.

• (viii) The solutions reported by Eqs. (51) and (52) derived in [7] can be deduced by setting $\displaystyle k_1=\sqrt{\frac{2c}{m}}$, $\displaystyle F_1(Y)=-\frac{l}{m}$, $g_3(t)=0$, $\displaystyle A_6=\frac{c}{m}$, $c_4=0$, $c_7=0$ and $\displaystyle \frac{\pi }{2}$, respectively, in Eqs. (53)–(54) of this article.

• (ix) Assuming ${\displaystyle k_2=\sqrt{\frac{-2c}{m}}}$, $\displaystyle F_1(Y)=-\frac{l}{m}$, $g_3(t)=0$, $\displaystyle A_6=\frac{c}{m}$, $c_4=c_8=c_9=0$ into Eqs. (56)–(57) and (59)–(60), the solutions (41) and (42) of [7] can be deduced, respectively.

Case (IIIb) If $c_{5}=c_{6}=0$, Eq. (51) is reduced to

$$\begin{aligned}&\bar{U}_{1}^2-U_1^2(U^2_1+2A_{9})=0, \end{aligned}$$

For $A_{9}=2k_3^2$, the solution of Eqs. (47)–(48) is obtained as

$$\begin{aligned}&U_1=\pm \, k_3\tanh (k_3X_1+c_{10})\mp k_3\coth (k_3X_1+c_{10})\nonumber \\&V_1=c_4-\frac{1}{2}k_3^2 \Bigr [\tanh (k_3X_1+c_{10})-\coth (k_3X_1+c_{10}) \Bigr ]^2, \end{aligned}$$

(61)

Consequently, the solution of BE is attained as

$$\begin{aligned} u=&\pm \, k_3\tanh \Bigr [\displaystyle k_3\Bigr (X-\int \frac{\mathrm{d}Y}{F_1(Y)}\Bigr )+c_{10}\Bigr ] \nonumber \\ {}&\mp k_3\coth \Bigr [k_3\Bigr (X-\int \frac{\mathrm{d}Y}{F_1(Y)}\Bigr )+c_{10}\Bigr ], \end{aligned}$$

(62)

while $A_{9}=-2k_4^2$ leads to the solution as

$$\begin{aligned}&U_1=\displaystyle \pm \, k_4\tan (k_4X_1+c_{11})\pm \, k_4\cot (k_4X_1+c_{11})\nonumber \\&V_1=c_4-\displaystyle \frac{1}{2}k_4^2 \Bigr [\tan (k_4X_1+c_{11})+\cot (k_4X_1+c_{11}) \Bigr ]^2. \end{aligned}$$

(64)

Ultimately, the solution of BE is obtained as

$$\begin{aligned} u=&\pm \, k_4\, \tan \,\Bigr [\displaystyle k_4\,\Bigr (X-\int \frac{\mathrm{d}Y}{F_1(Y)}\Bigr )+c_{11}\Bigr ]\nonumber \\ {}&\pm \, k_4\,\cot \Bigr [k_4\Bigr (X-\int \frac{\mathrm{d}Y}{F_1(Y)}\Bigr )+c_{11}\Bigr ], \end{aligned}$$

(65)

where $c_{10}$ and $c_{11}$ are the arbitrary constants of integration.

Deductions of some previously established results:

• (x) Taking $F_1(Y)=-1$, $g_3(t)=0$, $A_6=c$, $c_{10}=0$, $k_3=\sqrt{c}$ and $\displaystyle \sqrt{\frac{-c}{2}}$, respectively, in Eq. (62), we can derive two results of [6].

• (xi) For $F_1(Y)=\displaystyle -\frac{k}{l}$, $g_3(t)=0$, $k_4^2=-\displaystyle \frac{k}{2}$, $A_6=\displaystyle \frac{1}{4l}(k^2l-4c_1)$, $c_4=\displaystyle -\frac{c_1}{l}$, $c_{11}=\displaystyle \frac{\pi }{4}$ in Eqs. (65)–(66), one can derive the solutions of [4]. This endorses worthiness of this work over the previous findings [4].

• (xii) Substituting $F_1(Y)=-1$, $g_3(t)=0$, $A_6=c$, $c_{11}=0$, $k_3=\sqrt{-c}$ and $\displaystyle \sqrt{ \frac{c}{2}}$, respectively, in Eq. (65), we can derive previously established results of [6].

• (xiii) Assuming $\displaystyle k_3=\sqrt{\frac{c}{m}}$, $\displaystyle k_4=\sqrt{\frac{-c}{m}}$, $\displaystyle F_1(Y)=-\frac{l}{m}$, $g_3(t)=0$, $\displaystyle A_6=\frac{c}{m}$, $c_4=c_{10}=c_{11}=0$ in Eqs. (62)–(63) and (65)–(66), one can derive results (82), (87) and (88), (94), respectively, of [7], while $c_{11}=\frac{\pi }{2}$ provides the solution (95) of [7].

Case (IIIc) If $A_{9}=c_{5}=c_{6}=0$, then Eq. (51) is reduced to

$$\begin{aligned}&\bar{U}_{1}^2-U^4_1=0 \end{aligned}$$

The solution of Eqs. (47)–(48) is obtained as

$$\begin{aligned}&U_1=\pm \, \frac{1}{(X_1+c_{12})} \text{ and } V_1=A_6-\frac{1}{2(X_1+c_{12})^2}, \end{aligned}$$

(67)

where $c_{12}$ is an arbitrary constant and leads to

$$\begin{aligned} u&=\pm \, \frac{1}{\displaystyle \Bigr (X-\int \frac{\mathrm{d}Y}{F_1(Y)}+c_{12}\Bigr )}, \end{aligned}$$

(68)

$$\begin{aligned} v&=\frac{\displaystyle 2A_6\Bigr (X-\int \frac{\mathrm{d}Y}{F_1(Y)}+c_{12}\Bigr )^2-1}{2\Bigr (\displaystyle X-\int \frac{\mathrm{d}Y}{F_1(Y)}+c_{12}\Bigr )^2F_1(Y)}-g_3(t). \end{aligned}$$

(69)

where $X=\displaystyle x-\int g_3(t)~\mathrm{d}t \text{ and } Y=y-A_{6}t$.

Deductions of some previously established results:

• (xiv) Taking $F_1(Y)=-1$, $g_3(t)=0$, $A_6=c$ and $c_{12}=0$ in Eq. (68), one can derive the results of [6].

• (xv) Treating $F_1(Y)=-1$, $g_3(t)=0$, $A_6=0$ and $c_{12}=\displaystyle \frac{A_1}{A_2}$ in Eqs. (68)–(69), we can deduce the results of [5].

Fig. 1

Elastic behavior of multisoliton profile for the solution (30)–(31)

Fig. 2

Positon profile for the wave components listed in Eqs. (53)–(54)

Fig. 3

Kink wave profile for the expressions (56)–(57)

Fig. 4

Negaton profile for the solutions represented by Eqs. (59)–(60)

Fig. 5

Annihilation of multisoliton for solutions represented in Eqs. (62)–(63)

Fig. 6

Asymptotic and multisoliton profile for the solutions expressed by Eqs. (65)–(66)

Fig. 7

Multisoliton and wavefront profile of u and v for the solutions listed in Eqs. (68)–(69)

4 Analysis and discussions

The mathematical expressions of the invariant solutions can be analyzed physically on the basis of their graphical representation. The graphical structure provides the corporal information to understand the phenomena physically. In this section, the solutions listed in Eqs. (30)–(31), (53)–(54), (56)–(57), (59)–(60), (62)–(63), (65)–(66), (68)–(69) are analyzed graphically based on numerical simulation, while solutions given by Eqs. (17)–(18), (20)–(21), (41)–(42) are self-explanatory. The derived solutions involve arbitrary functions as well as arbitrary constants. The simulation is performed by taking appropriate choice of arbitrary constants and functions using the MATLAB code in the space range $-\,20 \le x,y \le 20$ and $-\,20 \le x,t \le 20$. Authors have taken $g_3(t)=a+t$, $a=0.9880$, $b=0.2199$, $a_1=0.0228$, $a_2=0.4494$ and $A_6=19.7105$ throughout the simulation. It is widely known that solitons are solitary wave packets with elastic scattering property that they do not change their shapes and amplitude after the mutual collision. It arises in many contexts like the intensity of light in optical fibers and the surface of water. The analysis of graphical behavior of solutions are described in the following manner:

Figure 1: The multisoliton profile corresponding to solution listed in Eqs. (30)–(31) is traced in this figure. It reveals that the nonlinear behavior of the wave is outcome of interaction of Riemann wave and long wave. The appropriate choice of arbitrary function $\displaystyle g_1(t)=(2b_1t+b_2)\,\exp (b_1t^2+b_2t+b_3)$ and constants $a_3=0.1635$, $A_1=0.1396$, $A_2=2.7486$, $A_5=0.8628$, $b_1=0.5773$, $b_2=0.4400$, $b_3=0.2576$ are taken on the basis of numerical simulation. The figure reflects that solitons do not change their amplitude after mutual collision and show completely elastic behavior.

Figure 2: The physical quantities given in Eqs. (53)–(54) are traced via this figure, which shows positon profile at $t=0.0318$. The adequate choice of arbitrary function $\displaystyle F_1(Y)=\frac{\cosh ^2(b_4Y^2+b_5Y+b_6)}{2b_4Y+b_5}$ and constants $c_4=0.9037$, $c_7=0.9293$, $k_1=6.1330$, $b_4=0.3540$, $b_5=0.2662$, $b_6=0.2194$ are taken with the help of numerical simulation on MATLAB, while rest of them are same as mentioned above. For integer n, when the amplitude of $\tan$ in Eqs. (53)–(54) is $(n+\frac{1}{2})\pi$, then the solution shows their singularity. The positons as a function of space variables has poles and zeros on real axis. Thus, positons are singular, weakly localized and super-reflectionless solitons, which retain their shape and size after interacting with each other and show completely elastic behavior. While carrier waves of positons and its envelope experience additional phase shift.

Figure 3: The intensive behavior of kink wave profile of wave components u and v for the solution listed in Eqs. (56)–(57) is shown in this figure at $t=0.1537$ by taking suitable choice of arbitrary function and constants as $F_1(Y)=\displaystyle \frac{\cosh ^2(b_4Y^2+b_5Y+b_6)}{2b_4Y+b_5}$ and $c_4=38.5218$, $c_8=0.7378$, $k_2=6.1330$, $b_4=0.3540$, $b_5=0.2662$, $b_6=0.2194$. The kink solution approaches to constants as $x \rightarrow \pm \, \infty$ for fixed y and t.

Figure 4: The physical behavior of wave components u and v expressed in Eqs. (59)–(60) are represented via this figure, which shows the negaton profile at $t=0.4076$. The suitable choice of arbitrary function $\displaystyle F_1(Y)=-(2b_4Y+b_5)^{-1}$ and arbitrary constants $c_4=38.5218$, $c_9=0.8199$, $k_2=6.1330$, $b_4=0.3540$, $b_5=0.2662$, $b_6=0.2194$ are taken randomly, while remaining are same as mentioned above. The negatons are singular solutions having singularities on imaginary axis. Negatons decay exponentially as $x \rightarrow \pm \, \infty$. The intensive behavior of negatons are observed, i.e., the negatons remain unchanged after mutual collision except finite phase shift.

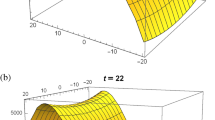
Figure 5: The transition of multisoliton profile into straight strip is observed here. The wave components expressed in Eqs. (62)–(63) show the completely elastic nonlinear behavior of multisoliton at $t=0.0252$. The appropriate choice of arbitrary function $\displaystyle F_1(Y)=-\frac{(b_7Y^2+b_8Y+b_9)^2}{(2b_7Y+b_8)}$ and constants $c_4=0.9037$, $c_{10}=0.8422$, $k_3=4.3367$, $b_7=0.3329$, $b_8=0.4671$, $b_9=0.6482$ is taken on the basis of numerical simulation. The decay in soliton profile with time is pointed out. The wave nature dissipates its almost energy as time passes over $t=4.04$ and profile becomes stationary.

Figure 6: The asymptotic behavior of u and multisoliton profile of v through Eqs. (65)–(66) are exhibited in this figure by taking $F_1(Y)=1$, $c_4=37.9774$, $c_{11}=0.1389$, $k_4=4.3367$, $b_{10}=1$. It is remarkable that as time passes over wider range, the wave profile looses its nonlinearity and becomes straight strip.

Figure 7: The graphical behavior of wave components u and v are analyzed via this figure. The profile of u represents elastic behavior of multisoliton, while wavefront profile is shown by v, which basically depend upon the appropriate choice $F_1(Y)=\sin Y\tan Y$, $c_{12}=0.3504$ in Eqs. (68)–(69). If the values of functions and constants are changed, then the profile changes its nature accordingly.

5 Concluding remarks

In this article, authors have well performed the invariance property and symmetry analysis of Bogoyavlenskii equations with the aid of Lie group theory. All the possible vector fields and the similarity reductions are constructed systematically. Moreover, a variety of closed-form solutions has been obtained by utilizing the STM successfully. The obtained solutions are represented in Eqs. (17)–(18), (20)–(21), (30)–(31), (41)–(42), (53)–(54), (56)–(57), (59)–(60), (62)–(63), (65)–(66), (68)–(69). These solutions are never reported yet and more general than previous findings [4,5,6,7]. The solutions are of great interest as some of them are helpful to generate the previous findings [4,5,6,7] by taking particular choice of arbitrary constants and functions. To provide precise insights into these invariant solutions, numerical simulation is performed on the basis of suitable choice of arbitrary constants and functions. Eventually, some positons, negatons, kinks, wavefront, multisoliton and asymptotic behavior of the solutions are presented in this work. These closed-form solutions can be applicable for comparative study of numerical results and forecasting the error in the newly proposed algorithm. These solutions may provide a substantial platform for the further study. Thus, the STM is a reliable and efficient tool to get closed-form solutions of PDEs. This is the big importance over the other methods.