1 Introduction

Considering its significance in engineering and business, the investigation of heat and mass transference is a particularly significant subject for researchers. It is used in biomedical and manufacturing processes, together with food preparation and tissue conduction. Because of the many applications of non-Newtonian fluids, investigators have expressed a strong interest in studying them. The main reason for this is the prevalence of these fluids in nature. Non-Newtonian performance is widely employed in industries like mining, where slurries and muck are regularly controlled, and in services like lubricating and biomedical flows. Although non-Newtonian fluids have been the subject of a sizable amount of research, non-Newtonian fluid models still need a great deal of work. Williamson fluid is classified as a non-Newtonian fluid having shear-thinning characteristics, meaning that its viscosity gets thinner as shear stress intensity rises.

Nanofluids have emerged as one of the most sought-after research fields due to their low heat resistance and efficient thermal properties. In addition, it's crucial to maintain the chilling of technical items like CPUs, laptops, power electronics, engines, and high-powered emissions in order for them to operate as intended. Choi [1] studied the thermal conductivity’s properties of different types of nanofluids. Kuznetsov and Nield [2] inspected a study on a vertical plate of natural convection boundary layer nanofluid flow. Khan and Pop [3] discussed fluid flow with nanomaterials over an extending surface. Haddad et al. [4] inspected the impressions of thermophoresis and the Brownian of nanofluid flow. A study on a stretchy sheet of Williamson fluid flow with nanomaterials was discussed by Nadeem et al. [5]. Khan et al. [6] inspected the Oldroyd-B fluid flow with the impacts of motile organisms and the active Prandtl approach. Bilal et al. [7] elucidate the flow characteristics of the Non-Newtonian Carreau fluid model within a square chamber. The Carreau fluid model describes the relationship between stress and strain for a non-elastic material, considering both infinite and zero stress magnitudes. Bilal et al. [8] investigate the physical properties of Carreau nanofluid on a linearly extensible cylinder, as well as its potential application in bioconvection phenomenon.

Fourier's law [9] also revealed the heat transfer mechanism in 1822. This law serves as the foundation for the hypothesis that the mode under investigation may detect the actual temperature quickly. Cattaneo [10] corrected this problem by adding a thermal relaxation time to Fourier's law. This expression denotes the amount of time required for a mode to transfer heat to the nearby elements. Christov [11] improved this model as well. The innovative model (C–C) is recognized as the Cattaneo-Christov heat flow model. The C–C model and the second-order slip, reaction rate, and double diffusion impacts on hydromagnetic convective Oldroyd-B liquid flow approaching an extensible surface were examined by Loganathan et al. [12]. Imtiaz et al. [13] inspected the fluid flow and heat transference impact of third-grade fluid in the presence of C–C models and reaction rates. Ramadevi et al. [14] inspected the hydromagnetic mixed convection micropolar fluid flow over a stretchy surface using a modified Fourier’s heat flux model. The impressions of heat transference and entropy creation of time-dependent MHD fluid flow over a stretchy revolving disk solved via an artificial neural system and particle swarm optimization procedure were discussed by Rashidi et al. [15]. Khan and Alzahrani [16] conducted a study on the flow of a non-Newtonian nanofluid (specifically, the Jeffrey fluid) towards a stretched surface, focusing on the Cattaneo-Christov double diffusion. López et al. [17] analyzed the entropy creation and non-linear thermal radiation impacts of hydromagnetic fluid flow with nanomaterials over a porous, erect microchannel. Khan et al. [18] considered the non-linear mixed convective nanofluid flow to analyze the entropy creation in the existence of Joule heating and slipping situations. Qing et al. [19] inspected the entropy creation study of hydromagnetic Casson fluid flow with nanomaterials over a porous extending or reducing surface. Sheikholeslami and Ganji [20] discussed the MHD nanofluid flow to optimize the entropy creation solved via the Lattice Boltzmann method. Liao and Tan [21] discussed a generic approach to searching out the series outcomes of non-linear PDEs.

The classification of the elements that cause the loss of useful energy makes the entropy computation of flow and heat transfer systems crucial. Energy loss may jeopardize the thermally designed system's efficiency. Reducing the entropy-producing variables can increase the system's output. Loganathan et al. [22] inspected the Williamson nanofluid flow over a slipping stretchy surface to control the passive situation of nanomaterials. Khan and Alzahrani [23] investigated the phenomenon of nonlinear mixed convection in a dissipative convective flow of micropolar fluid towards a stretched surface. Mixed convection refers to the simultaneous occurrence of forced and natural convection mechanisms. Eswaramoorthi et al. [24] discussed the double diffusion and chemical reaction impact of a radiative visco-elastic fluid flow over a stretchy surface. Aquino and Bo-ot [25] investigated the Homotopy analysis scheme to address the two-level set of equations and provide conclusions that would identify turbulent activity. The study conducted by Chu et al. [26] focuses on analyzing the entropy production in an inclined channel that is filled with Rabinowitsch fluid. Hayat et al. [27] discussed the radiative third-grade fluid flow over a radiative surface with Joule heating impact. Ghasemi et al. [28] inspected the hydromagnetic blood nanofluid flow that passes through porous arteries. Wang [29] discussed the natural convection fluid flow over an erect, stretchy surface. Reddy and Sidawi [30] studied the suction and blowing impacts on the erect stretchy surface of natural convection fluid flow. Khan and Pop [31] considered a boundary layer fluid flow with nanomaterials over a stretchy surface. Makinde and Aziz [32] inspected the convective boundary layer fluid flow with nanomaterials over a stretchy surface. Gorla and Gireesha [33] studied the dual results for Williamson fluid flow with nanomaterials over a stretchy/shrinking sheet and stagnation point.

As far as we know, no research has been done on how entropy building with C–C and zero mass flux affects the MHD 2D non-linear mixed convection flow of a Williamson nano-liquid caused by a stretchable surface. There are still few studies involving the C–C heat flux and entropy creation. Although there are a number of techniques for studying extremely non-linear equations, the homotopy analysis scheme is considered to be the best. The goal of the current essay is to mathematically formulate such flows with the help of the HAM approach. Upon completing our investigation, we furnish the solutions to the subsequent inquiries for additional research:

  • How the non-linear mixed convection affects the flow rate?

  • What are the impacts of embedded variables on entropy and Bejan number profile like Weissenberg number, Eckert number, and Brinkman number?

  • How thermos phoresies and Brownian motion affects the nanoparticle concentration?

2 Flow analysis

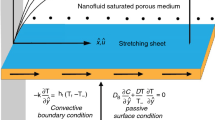
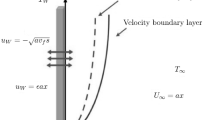
The current study enclosed with time-independent 2-D flow of incompressible, viscid and radiative Williamson fluid with nanomaterials over a flat stretchy surface. The bottom of the plate induces the convective heating temperature \(T_{f}\). The perpendicular direction of the plate is subjected to the imposition of a uniform transverse magnetic field \(B_{0}\). Assume that \(\hat{u} = \hat{u}_{{\text{w}}} = \hat{a}\hat{x}\) is the stretchy velocity and that \(^{\prime}\hat{a}{\prime}\) is the stretching rate. While the \(\hat{y}\)-track is moving vertically, the \(\hat{x}\)-track is stretched out. Nadeem et al. [5] present the Williamson fluid Cauchy stress tensor.

$$\delta = - pI + \Phi$$
(1)
$$\Phi = \left( {\mu_{\infty } + \frac{{\mu_{0} - \mu_{\infty } }}{1 - \beta \alpha }} \right)\varepsilon$$
(2)

where \(\Phi , \mu_{0}\), \(\mu_{\infty }\) is the extra stress tensor, viscosities at zero and endless shear stresses, respectively, time invariable is defining as \(\beta > 0\) i, \(\varepsilon\) is the initial Rivilin-Erickson tensor and shear rate \(\alpha\) is stated as

$$\alpha = \sqrt {\frac{1}{2}\pi } \cdot \pi = trace \left( {\varepsilon^{2} } \right)$$
(3)

After Gorla and Gireesha [33], we have researched

$${\rm M}_{\infty } = 0, \beta \alpha < 1.$$
(4)

So, we obtain

$$\Phi = \left( {\frac{{\mu_{0} }}{1 - \beta \alpha }} \right)\varepsilon$$
(5)

otherwise using binomial expansion

$$\Phi = \mu_{0} \left( {1 + \beta \alpha } \right)\varepsilon$$
(6)
$${\rm A} = \left[ {\left( {\frac{{\partial \hat{u}}}{{\partial \hat{x}}}} \right)^{2} + \left( {\frac{{\partial \hat{u}}}{{\partial \hat{y}}}} \right)^{2} + \frac{1}{2}\left( {\frac{{\partial \hat{v}}}{{\partial \hat{x}}} + \frac{{\partial \hat{u}}}{{\partial \hat{y}}}} \right)^{2} } \right]^{\frac{1}{2}}$$
(7)
$$\Phi_{{\hat{x}\hat{x}}} = 2\mu_{0} \left( {1 + \beta \alpha } \right)\frac{{\partial \hat{u}}}{{\partial \hat{x}}}$$
(8)
$$\Phi_{{\hat{x}\hat{y}}} = \Phi_{{\hat{y}\hat{x}}} = \mu_{0} \left( {1 + \beta \alpha } \right)\left( {\frac{{\partial \hat{v}}}{{\partial \hat{x}}} + \frac{{\partial \hat{u}}}{{\partial \hat{y}}}} \right)$$
(9)
$$\Phi_{{\hat{y}\hat{y}}} = 2\mu_{0} \left( {1 + \beta \alpha } \right)\frac{{\partial \hat{v}}}{{\partial \hat{y}}}$$
(10)

Figure 1 displays a physical structure of the model construction.

Fig. 1
figure 1

Flow diagram

Full size image

The governing flow equations are [22]:

$$\frac{{\partial \hat{u}}}{{\partial \hat{x}}} + \frac{{\partial \hat{v}}}{{\partial \hat{y}}} = 0$$
(11)
$$\hat{u}\frac{{\partial \hat{u}}}{{\partial \hat{x}}} + \hat{v}\frac{{\partial \hat{u}}}{{\partial \hat{y}}} = \nu \frac{{\partial^{2} \hat{u}}}{{\partial \hat{y}^{2} }} + \sqrt 2 \nu \beta \frac{{\partial \hat{u}}}{{\partial \hat{y}}}\frac{{\partial^{2} \hat{u}}}{{\partial \hat{y}^{2} }} - \frac{{\sigma B_{0}^{2} }}{\rho }\hat{u} + \frac{g}{\rho }\left( {\lambda_{1} \left( {T - T_{\infty } } \right) + \lambda_{2} \left( {\left( {T - T_{\infty } } \right)^{2} } \right)} \right) + \frac{g}{\rho }\left( {\lambda_{3} \left( {C - C_{\infty } } \right) + \lambda_{4} \left( {\left( {C - C_{\infty } } \right)^{2} } \right)} \right)$$
(12)
$$\hat{u}\frac{\partial T}{{\partial \hat{x}}} + \hat{v}\frac{\partial T}{{\partial \hat{y}}} = \frac{k}{{\rho c_{p} }}\frac{{\partial^{2} T}}{{\partial \hat{y}^{2} }} - \frac{1}{{\rho c_{p} }}\frac{{\partial q_{r} }}{{\partial \hat{y}}} + \frac{{Q_{0} }}{{\rho c_{p} }}\left( {T - T_{\infty } } \right) + \tau \left[ {D_{B} \frac{\partial C}{{\partial \hat{y}}}\frac{\partial T}{{\partial \hat{y}}} + \frac{{D_{T} }}{{T_{\infty } }}\left( {\frac{\partial T}{{\partial \hat{y}}}} \right)^{2} } \right] + \frac{{\sigma B_{0}^{2} }}{{\rho c_{p} }}\hat{u}^{2} + \frac{{\mu_{0} }}{{\rho c_{p} }}\left( {\frac{{\partial \hat{u}}}{{\partial \hat{y}}}} \right)^{2} + \frac{{\mu_{0} }}{{\rho c_{p} }}\beta \left( {\frac{{\partial \hat{u}}}{{\partial \hat{y}}}} \right)^{3}$$
(13)
$$\hat{u}\frac{{\partial {\text{C}}}}{{\partial \hat{x}}} + \hat{v}\frac{{\partial {\text{C}}}}{{\partial \hat{y}}} = {\text{D}}_{{\text{B}}} \frac{{\partial^{2} {\text{C}}}}{{\partial \hat{y}^{2} }} + \frac{{{\text{D}}_{{\text{T}}} }}{{{\text{T}}_{\infty } }}\frac{{\partial^{2} {\text{T}}}}{{\partial \hat{y}^{2} }} - k_{m} \left( {C - C_{\infty } } \right)$$
(14)
$$\hat{u} = \hat{u}_{{\text{w}}} \left( {\hat{x}} \right) = \hat{a}\hat{x} + {\text{L}}\frac{{\partial \hat{u}}}{{\partial \hat{y}}},{ }\hat{v} = \hat{v}_{{\text{w}}} ,{ } - k\frac{{\partial {\text{T}}}}{{\partial \hat{y}}} = {\text{h}}_{f} \left( {{\text{T}}_{f} - {\text{T}}_{\infty } } \right),{ }$$
$${ }D_{B} \frac{\partial C}{{\partial \hat{y}}} + \frac{{D_{T} }}{{T_{\infty } }}\frac{\partial T}{{\partial \hat{y}}} = 0{\text{ at }}\hat{y} = 0$$
$$\hat{u} \to 0,{\text{ T}} \to {\text{T}}_{\infty } { },{\text{ C}} \to {\text{C}}_{\infty } {\text{ as }}\hat{y} \to \infty$$
(15)

The heat flux \(\hat{q}\) is provided by [10, 11].

$$\hat{q} + \lambda_{T} \left( {\frac{{\partial \hat{q}}}{\partial t} + \left( {{\mathbb{V}} \cdot \nabla \hat{q} - \hat{q} \cdot \nabla {\mathbb{V}}} \right) + \left( {\nabla \cdot {\mathbb{V}}} \right)\hat{q}} \right) = - k\nabla T$$
(16)

For \(\lambda_{T} = 0\), Eq. (16) reduces to Fourier's law. The necessity for incompressible fluids is \(\nabla { } \cdot {\mathbb{V}} = 0\) and we achieve,

$$\hat{q} + \lambda_{T} \left( {\frac{{\partial \hat{q}}}{\partial t} + \left( {{\mathbb{V}} \cdot \nabla \hat{q} - \hat{q} \cdot \nabla { }{\mathbb{V}}} \right)} \right) = - k\nabla T$$
(17)

Removing \(\hat{q}\) between Eqns. (13) and (17), we arrive at the subsequent energy equation

$$\begin{gathered} \hat{u}\frac{\partial T}{{\partial \hat{x}}} + \hat{v}\frac{\partial T}{{\partial \hat{y}}} + \lambda_{T} \left( {\hat{u}^{2} \frac{{\partial^{2} T}}{{\partial \hat{x}^{2} }} + \hat{v}^{2} \frac{{\partial^{2} T}}{{\partial \hat{y}^{2} }} + \left( {\hat{u}\frac{{\partial \hat{u}}}{{\partial \hat{x}}}\frac{\partial T}{{\partial \hat{x}}} + \hat{v}\frac{{\partial \hat{u}}}{{\partial \hat{y}}}\frac{\partial T}{{\partial \hat{x}}}} \right) + 2\hat{u}\hat{v}\frac{{\partial T^{2} }}{{\partial \hat{x}\partial \hat{y}}}} \right) \hfill \\ + \left( {\hat{u}\frac{{\partial \hat{v}}}{{\partial \hat{x}}}\frac{\partial T}{{\partial \hat{y}}} + \hat{v}\frac{{\partial \hat{v}}}{{\partial \hat{y}}}\frac{\partial T}{{\partial \hat{y}}}} \right) = \frac{k}{{\rho c_{p} }}\frac{{\partial^{2} T}}{{\partial \hat{y}^{2} }} - \frac{1}{{\rho c_{p} }}\frac{{\partial q_{r} }}{{\partial \hat{y}}} + \frac{{Q_{0} }}{{\rho c_{p} }}\left( {T - T_{\infty } } \right) \hfill \\ + \tau \left[ {D_{B} \frac{\partial C}{{\partial \hat{y}}}\frac{\partial T}{{\partial \hat{y}}} + \frac{{D_{T} }}{{T_{\infty } }}\left( {\frac{\partial T}{{\partial \hat{y}}}} \right)^{2} } \right] + \frac{{\sigma B_{0}^{2} }}{{\rho {\text{c}}_{{\text{p}}} }}\hat{u}^{2} + \frac{{\mu_{0} }}{{\rho {\text{c}}_{{\text{p}}} }}\left( {\frac{{\partial \hat{u}}}{{\partial \hat{y}}}} \right)^{2} + \frac{{\mu_{0} }}{{\rho {\text{c}}_{{\text{p}}} }}\beta \left( {\frac{{\partial \hat{u}}}{{\partial \hat{y}}}} \right)^{3} \hfill \\ \end{gathered}$$
(18)

The transformations are [22],

$$\psi = \sqrt {\hat{a}\nu } \hat{x}f\left( { \eta } \right), \hat{u} = \frac{\partial \psi }{{\partial \hat{y}}}, \hat{v} = - \frac{\partial \psi }{{\partial \hat{x}}}, \eta = \sqrt {\frac{{\hat{a}}}{\nu }} \hat{y}, \hat{v} = - \sqrt {\hat{a}\nu } f\left( { \eta } \right),\hat{u} = \hat{a}\hat{x}f^{\prime}\left( { \eta } \right)$$
$$\theta \left( { \eta } \right) = \frac{{T - T_{\infty } }}{{T_{f} - T_{\infty } }},\phi \left( { \eta } \right) = \frac{{C - C_{\infty } }}{{C_{\infty } }}.$$
(19)

We have,

$$f^{\prime \prime \prime } + Wef^{\prime \prime } f^{\prime \prime \prime } - f^{{\prime}{2}} + ff^{\prime \prime } - Mf^{\prime } + \lambda \theta \left( {1 + \beta_{t} \theta } \right) + \lambda \phi N^{*} \left( {1 + \beta_{c} \phi } \right) = 0$$
(20)
$$\theta^{\prime \prime } + Rd\left( {\left( {\theta \left( {\theta_{w} - 1} \right) + 1} \right)} \right)^{2} \left( {3\theta^{\prime 2} \left( {\theta_{w} - 1} \right) + \left( {\theta \left( {\theta_{w} - 1} \right) + 1} \right)\theta^{\prime \prime } } \right) + Prf\theta^{\prime } + PrS\theta - Pr\gamma \left( {f^{2} \theta^{\prime \prime } + ff^{\prime } \theta^{\prime } } \right) + Pr\left( {Nb \theta^{\prime } \phi^{\prime } + Nt\theta^{\prime 2} } \right) + Pr\left( {MEcf^{\prime 2} + Ecf^{\prime \prime 2} + \frac{We}{{\sqrt 2 }}Ecf^{\prime \prime 3} } \right) = 0$$
(21)
$$\phi^{\prime\prime} + Lef\phi^{\prime} + \frac{Nt}{{Nb}}\theta^{\prime\prime} - LeCr\phi = 0$$
(22)

with limitations \(f\left( 0 \right) = f_{w}\), \(f{\prime} \left( 0 \right) = 1 + \Gamma \frac{We}{{\sqrt 2 }}f^{\prime \prime } \left( 0 \right)\), \(\theta^{\prime } \left( 0 \right) = - Bi\left( {1 - \theta \left( 0 \right)} \right)\), \(Nb \phi^{\prime } \left( 0 \right) + Nt \theta^{\prime } \left( 0 \right) = 1\)

$$f^{\prime}\left( \eta \right) \to 0, \theta \left( \eta \right) \to 0,\phi \left( \eta \right) \to 0\;{\text{as}}\;\eta \to \infty$$
(23)

The variables are stated as \(We = \sqrt {\frac{{2\hat{a}^{3} }}{\upsilon }} {\beta }\hat{x}\), \(\Gamma = L\sqrt {\frac{{\hat{a}}}{\nu }}\), \(M = \sigma B_{0}^{2} /\rho \hat{a}\), \(Pr = \rho c_{p} /k\), \(Ec = \frac{{\hat{a}^{2} \hat{x}^{2} }}{{c_{p} \left( {T_{f} - T_{\infty } } \right)}}\), \(Rd = \left( {4\sigma^{*} T_{\infty }^{3} } \right)/\left( {kk^{*} } \right)\), \(S = \frac{{Q_{0} }}{{\rho c_{p} }}\), \(\gamma = \lambda_{T} a\), \(Bi = \frac{{h_{f} }}{k}\sqrt {{\raise0.7ex\hbox{$\nu $} \!\mathord{\left/ {\vphantom {\nu {\hat{a}}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\hat{a}}$}}}\), \(Nb = \frac{{\tau D_{B} }}{\nu }C_{\infty } , Nt = \frac{{\tau D_{T} }}{\nu }\left( {T_{f} - T_{\infty } } \right)\), \(Cr = \frac{{k_{m} }}{a}\). \(\beta_{t} = \frac{{\lambda_{2} \left( {T_{f} - T_{\infty } } \right)}}{{\lambda_{2} }}\), \(\beta_{C} = \frac{{\lambda_{4} \left( {C_{\infty } } \right)}}{{\lambda_{3} }}\).

The following physical quantities are those of relevance to engineers:

$$C_{f} Re^{0.5} = \left[ {f^{\prime\prime}\left( 0 \right) + f^{{^{{\prime\prime}{2}} }} \frac{We}{2}\left( 0 \right)} \right]$$
(24)
$$NuRe^{ - 0.5} = = - \left( {1 + \frac{3}{4}Rd\left( {\left( {\theta_{w} - 1} \right)\left( {\theta \left( 0 \right)} \right)^{3} } \right)} \right)\theta^{\prime}\left( 0 \right)$$
(25)

In zero mass flux state, the local Sherwood number turns identically zero, as demonstrated in [22]:

$$ShRe^{ - 0.5} = \frac{Nt}{{Nb}}\theta^{\prime}\left( 0 \right)$$
(26)

3 Formulation of entropy generation

The entropy creation is stated as

$$S_{gen}^{{\prime\prime\prime}} = \frac{{K_{0} }}{{T_{\infty }^{2} }}\left[ {\left( {\frac{\partial T}{{\partial \hat{x}}}} \right)^{2} + \left( {\frac{\partial T}{{\partial \hat{y}}}} \right)^{2} + \frac{{16\sigma^{*} T_{\infty }^{3} }}{{3kk^{*} }}\left( {\frac{\partial T}{{\partial \hat{y}}}} \right)^{2} } \right] + \frac{\mu }{{T_{\infty } }}\left[ {\left( {\frac{{\partial \hat{u}}}{{\partial \hat{y}}}} \right)^{2} + \beta \left( {\frac{{\partial \hat{u}}}{{\partial \hat{y}}}} \right)^{3} } \right] + \left[ {\frac{{\partial \hat{u}}}{{\partial \hat{y}}} + \frac{{\partial \hat{v}}}{{\partial \hat{x}}}} \right]^{2} + \frac{RD}{{C_{\infty } }}\left[ {\left( {\frac{\partial C}{{\partial \hat{y}}}} \right)^{2} } \right] + \frac{RD}{{T_{\infty } }}\left[ {\left( {\frac{\partial T}{{\partial \hat{y}}}} \right)\left( {\frac{\partial C}{{\partial \hat{y}}}} \right)} \right] + \frac{{\sigma B_{0}^{2} }}{{T_{\infty } }} \hat{u}^{2} + \frac{\nu }{{k_{p} }} \hat{u}^{2}$$
(27)
$$N_{T} = \frac{{K_{0} }}{{T_{\infty }^{2} }}\left[ {\left( {\frac{\partial T}{{\partial \hat{y}}}} \right)^{2} + \frac{{16\sigma^{*} T_{\infty }^{3} }}{{3kk^{*} }}\left( {\frac{\partial T}{{\partial \hat{y}}}} \right)^{2} } \right] = {\text{Contribution of entropy due to thermal transfer}}.$$
$$N_{f} = \frac{\mu }{{T_{\infty } }}\left[ {\left( {\frac{{\partial \hat{u}}}{{\partial \hat{y}}}} \right)^{2} + \beta \left( {\frac{{\partial \hat{u}}}{{\partial \hat{y}}}} \right)^{3} } \right] = {\text{Contribution \, of \, entropy \, due \, to \, fluid \, friction}}.$$
$$N_{C} = \frac{RD}{{C_{\infty } }}\left( {\frac{\partial C}{{\partial \hat{y}}}} \right)^{2} + \frac{RD}{{T_{\infty } }}\left( {\frac{\partial T}{{\partial \hat{y}}}} \right)\left( {\frac{\partial C}{{\partial \hat{y}}}} \right) = {\text{Contribution of entropy due to mass transfer}}.$$
$$N_{m} = \left( {\frac{{\sigma B_{0}^{2} }}{{T_{\infty } }} + \frac{\nu }{{k_{p} }}} \right) \hat{u}^{2} = {\text{ Contribution of entropy due to magnetic field and porous medium}}.$$

where the following is a description of the characteristic entropy generation rate \(S_{0}^{{\prime\prime\prime}}:\)

$$S_{0}^{\prime \prime \prime } = \frac{{K_{0} }}{{T_{\infty }^{2} }}\frac{{\left( {\Delta T} \right)^{2} }}{{l^{2} }}$$

As a result, the following is the value of the non-dimensional entropy creation number:

$$E_{G} = \frac{{S_{gen}^{\prime \prime \prime } }}{{S_{0}^{\prime \prime \prime } }}$$
$$E_{G} = Re\left( {1 + Rd\left( {1 + \left( {\theta \left( {\theta_{w} - 1} \right) + 1} \right)^{2} } \right)} \right)\theta^{\prime 2} + Re\frac{Br}{\Omega }\left( {f^{\prime \prime 2} + \frac{We}{{\sqrt 2 }}f^{\prime \prime 3} } \right) + Re\left( {\frac{\zeta }{\Omega }} \right)^{2} \lambda \phi^{\prime 2} + Re\frac{\zeta }{\Omega }\lambda \phi^{\prime } \theta^{\prime } + \frac{Br}{\Omega }Mf^{{^{{\prime}{2}} }}$$
(28)

Bejan number is written as

$${\text{Be}} = \frac{{\text{Entropy creation due to heat and mass transmission }}}{{\text{Total entropy creation}}}$$
(29)
$${\text{Be}} = \frac{{Re\left( {1 + Rd\left( {1 + \left( {\theta \left( {\theta_{w} - 1} \right) + 1} \right)^{2} } \right)} \right)\theta^{\prime 2} + Re\left( {\frac{\zeta }{\Omega }} \right)^{2} \lambda \phi^{\prime 2} + Re\frac{\zeta }{\Omega }\lambda \phi^{\prime } \theta^{\prime } }}{{Re\left( {1 + \frac{4}{3}Rd} \right)\theta^{\prime 2} + Re\frac{Br}{\Omega }\left( {f^{\prime \prime 2} + \frac{We}{{\sqrt 2 }}f^{\prime \prime 3} } \right) + Re\left( {\frac{\zeta }{\Omega }} \right)^{2} \lambda \phi^{\prime 2} + Re\frac{\zeta }{\Omega }\lambda \phi^{\prime } \theta^{\prime } + \frac{Br}{\Omega }\left( {M + K_{P} } \right)f^{\prime 2} }}$$
(30)

4 HAM solutions

The main hypotheses for the homotopy process are described as

$$f_{0} = f_{w} + \left( {\frac{1}{1 + \Gamma }} \right)1 - e^{ - \eta } ,\theta_{0} = \frac{{Bi*e^{ - \eta } }}{1 + Bi}\;{\text{and}}\;\phi_{0} = - \left( {\frac{Nt}{{Nb}}} \right)*\frac{{Bi*e^{ - \eta } }}{1 + Bi}$$
(31)

The auxiliary linear operators \(L_{f}\), \(L_{\theta }\) and \(L_{\phi }\) are obtained as

$$L_{f} = f^{\prime \prime \prime } \left( \eta \right) - f^{\prime } \left( \eta \right),L_{\theta } = \theta^{\prime \prime } \left( \eta \right) - \theta \left( \eta \right)\;{\text{and}}\;L_{\phi } = \phi^{\prime \prime } \left( \eta \right) - \phi \left( \eta \right)$$
(32)

The above linear operators satisfying

$${\mathcal{L}}_{f} \left[ {A_{1} + A_{2} e^{\eta } + A_{3} e^{ - \eta } } \right] = 0,{\mathcal{L}}_{\theta } \left[ {A_{4} e^{\eta } + A_{5} e^{ - \eta } } \right] = 0\;{\text{and}}\;{\mathcal{L}}_{\phi } \left[ {A_{6} e^{\eta } + A_{7} e^{ - \eta } } \right] = 0$$
(33)

here \(A_{j} \left( {j = 1 - 7} \right)\) denote the licentious conditions.

Zeroth order deformation:

$$\left( {1 - p} \right){\mathcal{L}}_{f} \left[ {f\left( {\eta ;p} \right) - f\left( \eta \right)} \right] = p h_{f} {\mathcal{N}}_{f} \left[ {f\left( {\eta ;p} \right)} \right]$$
(34)
$$\left( {1 - p} \right){\mathcal{L}}_{\theta } \left[ {\theta \left( {\eta ;p} \right) - \theta_{0} \left( \eta \right)} \right] = p h_{\theta } {\mathcal{N}}_{\theta } \left[ {\theta \left( {\eta ;p} \right), f\left( {\eta ;p} \right),\phi \left( {\eta ;p} \right)} \right]$$
(35)
$$\left( {1 - p} \right){\mathcal{L}}_{\phi } \left[ {\phi \left( {\eta ;p} \right) - \phi_{0} \left( \eta \right)} \right] = p h_{\phi } {\mathcal{N}}_{\phi } \left[ {\phi \left( {\eta ;p} \right),\theta \left( {\eta ;p} \right), f\left( {\eta ;p} \right)} \right]$$
(36)

where \(p \varepsilon \left[ {0,1} \right]\) and \(h_{f}\), \(h_{\theta }\) and \(h_{\phi }\) are the non-zero auxiliary constants and \({\mathcal{N}}_{f}\), \({\mathcal{N}}_{\theta }\) and \({\mathcal{N}}_{\phi }\) are the nonlinear operators given by

$${\mathcal{N}}_{f} \left[ {f\left( {\eta ;p} \right), \theta \left( {\eta ;p} \right)} \right] = \frac{{\partial^{3} f\left( {\eta ;p} \right)}}{{\partial \eta^{3} }} + We\frac{{\partial^{2} f\left( {\eta ;p} \right)}}{{\partial \eta^{2} }}\frac{{\partial^{3} f\left( {\eta ;p} \right)}}{{\partial \eta^{3} }} + f\left( {\eta ;p} \right)\frac{{\partial^{2} f\left( {\eta ;p} \right)}}{{\partial \eta^{2} }} - M\frac{{\partial f\left( {\eta ;p} \right)}}{\partial \eta } + \lambda \theta \left( {\eta ;p} \right)\left( {1 + \beta_{t} \theta \left( {\eta ;p} \right)} \right) + \lambda \phi \left( {\eta ;p} \right)N^{*} \left( {1 + \beta_{c} \phi \left( {\eta ;p} \right)} \right)$$
(37)
$$\begin{aligned} & {\mathcal{N}}_{\theta } \left[ { f\left( {\eta ;p} \right),\theta \left( {\eta ;p} \right), \phi \left( {\eta ;p} \right)} \right] \\ & = \frac{{\partial^{2} \theta \left( {\eta ;p} \right)}}{{\partial \eta^{2} }} + Rd\left( {\left( {\theta \left( {\eta ;p} \right)\left( {\theta_{w} - 1} \right) + 1} \right)} \right)^{2} \left( {3\left( {\frac{{\partial \theta \left( {\eta ;p} \right)}}{\partial \eta }} \right)^{2} \left( {\theta_{w} - 1} \right) + \left( {\theta \left( {\eta ;p} \right)\left( {\theta_{w} - 1} \right) + 1} \right)\frac{{\partial^{2} \theta \left( {\eta ;p} \right)}}{{\partial \eta^{2} }}} \right) \\ & + \Pr f\left( {\eta ;p} \right)\frac{{\partial \theta \left( {\eta ;p} \right)}}{\partial \eta } + S\theta \left( {\eta ;p} \right) - \Pr \gamma \left[ {[f\left( {\eta ;p} \right)} \right]^{2} \frac{{\partial^{2} \theta \left( {\eta ;p} \right)}}{{\partial \eta^{2} }} - \Pr \gamma f\left( {\eta ;p} \right)\frac{{\partial f\left( {\eta ;p} \right)}}{\partial \eta }\frac{{\partial \theta \left( {\eta ;p} \right)}}{\partial \eta } \\ & + \Pr Nb\frac{{\partial \theta \left( {\eta ;p} \right)}}{\partial \eta }\frac{{\partial \phi \left( {\eta ;p} \right)}}{\partial \eta } + \Pr Nt\left[ {\frac{{\partial \theta \left( {\eta ;p} \right)}}{\partial \eta }} \right]^{2} + \Pr MEc\left[ {\frac{{\partial f\left( {\eta ;p} \right)}}{\partial \eta }} \right]^{2} + \Pr Ec\left[ {\frac{{\partial^{2} f\left( {\eta ;p} \right)}}{{\partial \eta^{2} }}} \right]^{2} \\ & + \Pr Ec\frac{We}{{\sqrt 2 }}\left[ {\frac{{\partial^{2} f\left( {\eta ;p} \right)}}{{\partial \eta^{2} }}} \right]^{3} \\ \end{aligned}$$
(38)
$${\mathcal{N}}_{\phi } \left[ { f\left( {\eta ;p} \right),\theta \left( {\eta ;p} \right), \phi \left( {\eta ;p} \right)} \right] = \frac{{\partial^{2} \phi \left( {\eta ;p} \right)}}{{\partial \eta^{2} }} + Le f\left( {\eta ;p} \right)\frac{{\partial \phi \left( {\eta ;p} \right)}}{\partial \eta } + \frac{Nt}{{Nb}}\frac{{\partial^{2} \theta \left( {\eta ;p} \right)}}{{\partial \eta^{2} }} - LeCr\phi \left( {\eta ;p} \right)$$
(39)
$$f\left( {0;p} \right) = f_{w} ,f^{\prime } \left( {0;p} \right) = 1 + {\Gamma }\frac{We}{{\sqrt 2 }}f^{\prime \prime } \left( {0:p} \right),f^{\prime } \left( {\infty ;p} \right) = 0,\theta^{\prime } \left( {0;p} \right) = - Bi\left( {1 - \theta \left( {\eta ;p} \right)} \right),\theta \left( {\infty ;p} \right) = 0,\phi^{\prime } \left( {0;p} \right) = - \frac{Nt}{{Nb}}\theta^{\prime } \left( {0;p} \right),\phi^{\prime } \left( {\infty ;p} \right) = 0$$
(40)

\(m{\text{th}}\) order deformation:

$${\mathcal{L}}_{f} \left[ {f_{m} \left( \eta \right) - \chi_{m} f_{m - 1} \left( \eta \right)} \right] = h_{f} R_{f,m} \left( \eta \right)$$
(41)
$${\mathcal{L}}_{\theta } \left[ {\theta_{m} \left( \eta \right) - \chi_{m} \theta_{m - 1} \left( \eta \right)} \right] = h_{\theta } R_{\theta ,m} \left( \eta \right)$$
(42)
$${\mathcal{L}}_{\phi } \left[ {\phi_{m} \left( \eta \right) - \chi_{m} \phi_{m - 1} \left( \eta \right)} \right] = h_{\phi } R_{\phi ,m} \left( \eta \right)$$
(43)

where

$$\chi_{m} = \left\{ {\begin{array}{*{20}c} {0, m \le 1} \\ {1, m > 1} \\ \end{array} } \right.$$
(44)
$$R_{f,m} \left( \eta \right) = f_{m - 1}^{{\prime\prime\prime}} + \mathop \sum \limits_{k = 0}^{m - 1} We\left( {f_{m - 1 - k}^{{\prime\prime\prime}} f_{k}^{{\prime\prime}} } \right) - \mathop \sum \limits_{k = 0}^{m - 1} f_{m - 1 - k}{\prime} f_{k}{\prime} + \mathop \sum \limits_{k = 0}^{m - 1} f_{m - 1 - k} f_{k}^{{\prime\prime}} - \left( M \right)f_{m - 1 - k}{\prime} \lambda \theta_{m - 1} \left( {1 + \beta_{t} \theta_{m - 1} } \right) + \lambda \phi_{m - 1} N^{*} \left( {1 + \beta_{c} \phi_{m - 1} } \right)$$
(45)
$$\begin{aligned} & R_{\theta ,m} \left( \eta \right) = \theta_{m - 1}^{{\prime\prime}} + Rd\left( {\left( {\theta_{m - 1} \left( {\theta_{w} - 1} \right) + 1} \right)} \right)^{2} \left( {3\left( {\theta_{w} - 1} \right)\mathop \sum \limits_{k = 0}^{m - 1} \theta_{m - 1 - k}{\prime} \theta_{k}{\prime} + \left( {\theta_{m - 1} \left( {\theta_{w} - 1} \right) + 1} \right)\theta_{m - 1}^{{\prime\prime}} } \right) \\ & + Pr\mathop \sum \limits_{k = 0}^{m - 1} \left[ {\theta_{m - 1 - k}{\prime} f_{k} } \right] \\ & \quad - Pr\gamma \left[ {\left( {f_{m - l - 1} \mathop \sum \limits_{j = 0}^{l} f_{1 - j}{\prime} \theta_{j}{\prime} + f_{m - l - 1} \theta_{l}^{{\prime\prime}} } \right)} \right] + PrNb\mathop \sum \limits_{k = 0}^{m - 1} \theta_{m - 1 - k}{\prime} \phi_{k} + PrNt\mathop \sum \limits_{k = 0}^{m - 1} \theta_{m - 1 - k}{\prime} \theta_{k}{\prime} + S\theta_{m - 1} \\ & + PrEc \left[ {f_{m - 1 - k}{\prime} } \right]^{2} + PrEc\left[ {f_{m - 1 - k}^{{\prime\prime}} } \right]^{2} + \frac{1}{\sqrt 2 } PrEcWe\left[ {f_{m - 1 - k}^{{\prime\prime}} } \right]^{3} \\ \end{aligned}$$
(46)
$$R_{\phi ,m} \left( \eta \right) = \phi_{m - 1}^{{\prime\prime}} + Le\mathop \sum \limits_{k = 0}^{m - 1} \phi_{m - 1 - k}{\prime} f_{k} + \frac{Nt}{{Nb}}\mathop \sum \limits_{k = 0}^{m - 1} \theta_{m - 1 - k}{\prime} \theta_{k}{\prime} - LeCr\phi_{m - 1}$$
(47)
$$f_{m} \left( 0 \right) = 0,f_{m}{\prime} \left( 0 \right) - \Gamma \frac{We}{{\sqrt 2 }}f_{m}^{\prime \prime } \left( 0 \right) = 0,\theta_{m}{\prime} \left( 0 \right) - Bi\theta_{m} \left( 0 \right) = 0, \phi_{m}{\prime} + \frac{Nt}{{Nb}}\theta_{m}{\prime} \left( 0 \right) = 0$$
$$f_{m}{\prime} \left( \eta \right) \to 0, \theta_{m}{\prime} \left( \eta \right) \to 0, \phi_{m} \left( \eta \right) \to 0\;{\text{as}}\;\eta \to \infty .$$
(48)

with boundary conditions

$$f_{m}{\prime} \left( 0 \right) = f_{m} \left( 0 \right) = f_{m}{\prime} \left( \infty \right) = \theta_{m} \left( 0 \right) = \theta_{m} \left( \infty \right) = \phi_{m} \left( 0 \right) = \phi_{m} \left( \infty \right) = 0.$$
(49)

The appropriate solutions \(\left[ {f_{m}^{*} ,\theta_{m}^{*} , \phi_{m}^{*} } \right]\) are

$$f_{m} \left( \eta \right) = f_{m}^{*} \left( \eta \right) + A_{1} + A_{2} e^{\eta } + A_{3} e^{ - \eta }$$
(50)
$$\theta_{m} \left( \eta \right) = \theta_{m}^{*} \left( \eta \right) + A_{4} e^{\eta } + A_{5} e^{ - \eta }$$
(51)
$$\phi_{m} \left( \eta \right) = \phi_{m}^{*} \left( \eta \right) + A_{6} e^{\eta } + A_{7} e^{ - \eta }$$
(52)

5 Convergence analysis

The above-mentioned HAM algorithm was computed by MATHEMATICA software platform. Significant contributions from the auxiliary constants \({\text{h}}_{f}\), \({\text{h}}_{\theta }\), and \({\text{h}}_{\phi }\) were made to the convergence series solutions. Figure 2 shows the h-curves of \(f^{\prime\prime}\left( 0 \right)\), \(\theta^{\prime}\left( 0 \right)\), and \(\phi^{\prime}\left( 0 \right)\). The h-curve, which is a straight line, is noted from these charts. The straight line representing the curves is used to select the convergent approximation. Up to four decimal places, the convergent series solution for the 15th order of approximations is shown in Table 1.

Fig. 2
figure 2

Curves for \(h_{f} , h_{\theta }\) and \(h_{\phi }\).

Full size image
Table 1 Code justification of \(- f^{\prime\prime}\left( 0 \right)\) for confining case \(M = \Gamma = f_{w} = 0\)
Full size table

6 Computational results and discussion

This section demonstrates the physical justification for velocity, nanomaterial volume percentage, temperature, Bejan impact, and entropy creation rate for a variety of flow parameters. The non-linear ODEs are cracked via HAM.

The impressions of the mass suction/blowing parameter (\(f_{w}\)) on the velocity outline is exposed in Fig. 3a. Figure 3a shows that as the \(f_{w}\) is improved, the velocity profiles drop, thickening the momentum boundary layer. As the dimensionless constant rises, the velocity profile also rises, as shown in Fig. 3b.

Fig. 3
figure 3

a–d Impressions of \(f_{w} , \lambda , \rho_{t}\) and \(N^{*}\) on velocity graph

Full size image

Figure 3c illustrates how the fluid flow velocity value grows. The velocity increases as the mixed convection parameter (\(\beta_{t}\)) value rises. This is because mixed convection happens when the buoyancy of free convection increases significantly. Consequently, the growing mixed convection parameter will result in a growth in buoyancy. Together with the buoyancy force, the flow velocity increases. The velocity graph increases as the ratio of concentration to thermal buoyancy increases, as shown in Fig. 3d. The buoyancy force affects the thermal buoyancy parameter. Stronger buoyancy forces result from larger buoyancy parameters. Such a stronger buoyancy force acts as a catalyst, causing the fluid velocity to rise.

In Fig. 4a, it is depicted that as the \(\theta_{w}\) rises, so does the temperature profile. Figure 4b demonstrates that as the quantity of \(We\) increases, the temperature curve and thermal boundary layer both improve. The impression of Prandtl number, \(Pr\), on temperature distribution was shown in Fig. 4c. It is clear that the Prandtl number has a negative connection with the temperature distribution. This is owing to the fact that larger amount of \(Pr\) causes the fluid thermal diffusivity to drop, which further causes the thermal boundary layer thickness to decrease.

Fig. 4
figure 4

a–d Impact of \(\theta_{w} , We, Pr\) and \(Ec\) on temperature profile

Full size image

For Eckert numbers \(\left( {Ec = 0.0, 0.3, 0.6, 0.9} \right),\) Fig. 4d forecasts \(Ec\) impact on the temperature graph, in which we can observe that temperature increases clearly. \(Ec\) calculates the energy loss resulting from flow arrangement. Enthalpy variance and the kinetic energy of fluid elements are correlated. We can see from \(Ec\) data that the bigger temperature differences are reduced at the sheet's surface. Frictional heating causes the liquid particles to have more kinetic energy than usual. This component caused the thermal boundary layer to expand for a greater \(Ec.\)

As seen in Fig. 5a, the fluid concentration falls as \(Nb\) upsurges because Brownian motion reasons the boundary layer to warm and cause the elements to leave the fluid regime. On the other hand, the movement of nanoparticles causes thermal conduction to rise with an increase in Nb, and this effect becomes stronger with smaller particles. The fluid concentration rises as the thermophoresis parameter rises, as shown in Fig. 5b. This is because, for smaller values of \(Pr\), thermophoresis heats the boundary layer, slowing the fluid's ability to transmit heat and mass.

Fig. 5
figure 5

a, b Impressions of \(Nt\) and \(Nb\) on Concentration Graph

Full size image

The impacts of different factors on the entropy generation graph and Bejan number are highlighted in Fig. 6a–h. The relationship between the entropy generation rate and Weissenberg parameter is described in Fig. 6a. Entropy production first appears at the microscopic level when heat transfer increases. Further actions brought by heat transfers cause heat energy to be lost and converted to work. Chaos develops as a result of the additional movement created both inside the structure and outside. Entropy is specifically mentioned as a amount of chaos; "\(We\)" is directly inversely related to relaxation time. As a result, fluid particle motion slows down for longer periods of relaxation, which prevents the system's entropy from increasing. As seen in Fig. 6b, the profile of the Bejan number grows as the quantities of the Weissenberg number \(\left( {We} \right)\) grow.

Fig. 6
figure 6

a–h Impact of \(We, Ec, \lambda\) and \(Br\) on Entropy and Bejan number profile

Full size image

The range of the entropy generation initially decreases as Ec increases in Fig. 6c, but it begins to expand as \(Ec\) reaches a value of \(\eta > 0.4\). According to Fig. 6c and d, the kinetic energy and enthalpy of the boundary layer in the fluid flow physically rise with an rise in the Eckert parameter. As a result, the rate of irreversibility increases. Entropy and Bejan number increase as a result for Eckert number. The impact of the dimensionless constant \(\left( \lambda \right)\) on the Bejan number and entropy generation profile is seen in Fig. 6e and f. In Fig. 6e, increasing values of \(\lambda\) cause the range of the Bejan number to initially decrease; but, after it reaches a value of \(\eta > 0.6\), it starts to increase. As Fig. 6f illustrates, the dimensionless constant (λ) tends to reduce the Bejan number.

When the Brinkman number rises, the outcome in Fig. 6g and h are inverted. In terms of physics, the Brinkman number predominates the disregarding of heat over viscous heating in comparison to heat transmission in the existence of molecular conduction. Heat transfer by molecular conduction close to the sheet is more efficient at transferring heat than the viscous effect. As a result, a significant amount of heat is produced amid the layers of moving fluid elements. Consequently, the Bejan number dropped and the rate of entropy generation increased.

Figures 7, 8, 9, 10, 11 and 12 show how various fluid parameter effects on skin friction, local heat transfer, and mass transference rates. Figures 7 and 8 show that for the combined settings of \(We\) & \(f_{w}\) and \(We\) & \(M\), the skin-friction rate decreases. From Fig. 9, it can be seen that the greater radiation impacts is an rise in the rate of heat transference. The outcome of \(We vs Nb\) on the Nusselt and Sherwood numbers will be examined in Figs. 10 and 11. These charts highlight the declining influence of increasing \(We\) values. Additionally, Fig. 10 shows that the Nusselt number quickly decrease as the amount of \(Nb\) grow, whereas the amount of the Sherwood number sharply increase with enhancement, as seen in Fig. 11. Positive Nusselt number indicate that heat is being transported physically from a hot object to a cool fluid. Figure 12 displays the mass transference rate for the joint parameters \(We\) and \(Nt\). Therefore, we infer from this graph that the mass transference rate decreases as \(We\) and \(Nt\) increase.

Fig. 7
figure 7

3-D plot of \(Re^{0.5} Cf\) for \(We \& fw\)

Full size image
Fig. 8
figure 8

3-D plot of \(Re^{0.5} Cf\) for \(We \& M\)

Full size image
Fig. 9
figure 9

3-D plot of \(Re^{ - 0.5} Nu\) for \(We \& Rd\)

Full size image
Fig. 10
figure 10

3-D plot of \(Re^{ - 0.5} Nu\) for \(We \& Nb\)

Full size image
Fig. 11
figure 11

3-D plot of \(Re^{ - 0.5} Sh\) for \(We \& Nb\)

Full size image
Fig. 12
figure 12

3-D plot of \(Re^{ - 0.5} Sh\) for \(We \& Nt\)

Full size image

7 Code validation

This section covers code validation of current results. With the exception of the exceptional case \(M = K_{P} = {\Gamma } = f_{w} = 0\), a comparative analysis of the order of approximation of HAM for \(- f^{\prime\prime}\left( 0 \right)\) and skin friction \(\left( { - Re^{0.5} Cf} \right)\) is completed by Nadeem et al. [5] (Consult Tables 1 and 2). Early findings of code validation for lower Nusselt number are presented in [29,30,31,32]. In Table 3, the validation is displayed. The validation results show a good degree of consistency with previously published findings. As a result, there is maximum confidence in the current simulations.

Table 2 Code justification of skin-friction \(\left( { - Re^{0.5} Cf} \right)\) for limiting case \(M = \Gamma = f_{w} = 0\)
Full size table
Table 3 Evaluation between the specific case with the lowered Nusselt number \(Rd = Ec = M = Nt = Nb = We = \gamma = S = {\Gamma } = f_{w} = 0\), \(Bi \to \infty\)
Full size table

8 Final outcomes

In the current study, a stretchable sheet with zero mass flux and Christov-Cattaneo heat flux was used to generate a non-linear mixed convective Williamson nanofluid flow. The governing nonlinear equations are dealt with using the homotopy progress technique. Following discussion of the physical clarification of various physical characteristics related to entropy creation, Bejan number, concentration, velocity, and temperature:

  • The velocity graph is increased by the thermal buoyancy parameter and the dimensionless constant, but the suction/blowing parameter exhibits the reverse trend.

  • When Eckert number and Weissenberg parameter are strong, the temperature profiles rise.

  • The Weissenberg number has an inverse relationship with the range of the heat and mass transfer rate.

  • For increased magnetic, suction/injection, and Weissenberg numbers, skin friction rate decreases.

  • Thermophoresis and Brownian motion parameters' inverse effects on the mass transfer rate and nanoparticle volume fraction are clearly visible.

  • Eckert parameter, dimensionless constant, and Brinkman number all cause a rise in entropy formation, however bigger values of the Weissenberg parameter have the opposite effect.

  • It is expected that in the future, several scientific and practical applications will rely on the dynamics of the stream across a stretching plate. The findings of the present study can be applied to various model investigations. The current issue's findings are particularly thrilling in various fields of science and technology, such as microchips, electronic cooling systems, heat exchangers, and more.