Steady flow of Burgers’ nanofluid over a stretching surface with heat generation/absorption

Abstract

Analysis has been conducted to analyze the steady free convection boundary layer flow of a Burgers’ nanofluid near a linear stretched sheet. The effects of the heat generation/absorption and nanoparticles on the flow are considered. Similarity transformations are presented to convert the coupled nonlinear partial differential equations into coupled nonlinear ordinary differential equations. The reduced coupled transformed boundary layer equations of Burgers’ nanofluid model are then solved analytically using the homotopy analysis method. The variations of the dimensionless velocity, temperature, and nanoparticle with various physical parameters, namely the Deborah numbers $\beta_{1}$, $\beta_{2},$ and $\beta_{3}$, the Prandtl number $\Pr$, the Brownian motion parameter $N_{\text{b}}$, the thermophoresis parameter $N_{\text{t}},$ and the Lewis number ${\text{Le}}$ are graphed and discussed.

1 Introduction

The study of the boundary layer flow of non-Newtonian fluids over a continuously moving surface is a topic of great interest to the researchers due to its wide range of practical applications in industrial and engineering. The Burgers’ fluid model is the class of rate type fluids. The Burgers’ fluid model was proposed to predict the properties of relaxation and retardation time. Hayat et al. [1] analyzed the influence of Hall current on the rotating flow of a Burgers’ fluid through a porous space. The accelerated flow of a viscoelastic fluid with the fractional Burgers’ model was investigated by Khan et al. [2]. Khan et al. [3] presented the exact solutions for some oscillating motions of a fractional Burgers’ fluid. Fetecau et al. [4] investigated a note on longitudinal oscillations of a generalized Burgers fluid in cylindrical domains. Exact solutions for the unsteady flow of a Burgers’ fluid between two sidewalls perpendicular to the plate was studied by Khan et al. [5]. The helical flow of a Burgers’ fluid with fractional derivative was examined by Shah [6]. The exact solution for rotating flows of a generalized Burgers’ fluid in cylindrical domains was investigated by Jamil and fetecau [7].

Recently, the researchers have been focusing on the study of nanofluids because nanofluids attract with their enormous potential to provide enhancement performance properties, especially with respect to heat transfer rate. Choi [8] investigated convection heat transfer fluids as nanofluid having substantially higher thermal conductivities to study the enhancement in heat transfer phenomenon. Chamkha and Aly [9] performed MHD free convective boundary layer flow of a nanofluid along a permeable isothermal vertical plate in the presence of heat source or sink. Meatin et al. [10] investigated the MHD mixed convective flow of a nanofluid over a stretching sheet. Aziz et al. [11] analyzed MHD flow over an inclined radiating plate with temperature-dependent thermal conductivity, variable reactive index, and heat generation. Aziz and Khan [12] investigated natural convective flow of a nanofluid over a convectively heated vertical plate. Kuznetsov and Nield [13] elaborated the natural convective flow of a nanofluid past a vertical plate. Khan and Pop [14] studied the laminar flow of nanofluid past a stretching sheet. Nadeem et al. [15] analyzed the optimized analytical solution for oblique flow of Casson-nanofluid with convective boundary conditions. Narayana and Sibanda [16] investigated the effects of laminar flow of a nanofluid over an unsteady stretching sheet. Hamad and Ferdows [17] presented the similarity solutions to viscous flow and heat transfer of a nanofluid over a nonlinear stretching sheet. Studies on heat generation/absorption effects for boundary layer flow of nanofluids are very limited. Alsaedi et al. [18] investigated the effects of heat generation/absorption on a stagnation-point flow of nanofluid over a surface with convective boundary conditions. Chemical reaction and uniform heat generation/absorption effects on MHD stagnation-point flow of a nanofluid over a porous sheet were presented by Anwar et al. [19]. Nandy and Mahapatra [20] examined the effects of slip and heat generation/absorption on MHD stagnation-point flow nanofluid past a stretching/shrinking surface with convective boundary conditions. Khan et al. [21] analyzed three-dimensional flow of an Oldroyd-B nanofluid toward a stretching sheet with heat generation/absorption.

The basic theme of this paper is to discuss the steady two-dimensional flow of Burgers’ nanofluid over a stretching sheet in the presence of heat generation/absorption effects. To our knowledge, no studies have been made to analyze the simultaneous effects of heat generation/absorption on heat and mass transfer of Burgers’ nanofluid over a linear stretching sheet. The governing coupled nonlinear partial differential equations are reduced to a system of coupled ordinary differential equations using appropriate transformations, and then the resulting equations are solved analytically by the homotopy analysis method (HAM). A parametric study is conducted to investigate the influence of various physical parameters on the velocity, temperature, and concentration profile.

2 Governing equations

The equations governing the steady flow of an incompressible Burgers’ nanofluid in the presence of heat generation/absorption

$$ {\text{div }}{\mathbf{V}} = 0,\, $$

(1)

$$ \rho a_{i} = - {\mathbf{\nabla }}p + {\text{div }}{\mathbf{S}},\, $$

(2)

$$ \left( {{\mathbf{V}} \cdot {\mathbf{\nabla }}} \right)\,T = \alpha {\mathbf{\nabla }}^{2} T + \frac{{Q_{0} }}{{\rho c_{p} }}(T - T_{\infty } ) + \tau \left( {D_{\text{B}} {\mathbf{\nabla }}C \cdot {\mathbf{\nabla }}T + \frac{{D_{\text{T}} }}{{T_{\infty } }}{\mathbf{\nabla }}T \cdot {\mathbf{\nabla }}T} \right),\, $$

(3)

$$ \left( {{\mathbf{V}} \cdot {\mathbf{\nabla }}} \right)\,C = D_{\text{B}} {\mathbf{\nabla }}^{2} C + \frac{{D_{\text{T}} }}{{T_{\infty } }}{\mathbf{\nabla }}^{2} T. $$

(4)

$$ \left( {1 + \lambda_{1} \frac{D}{Dt} + \lambda_{2} \frac{{D^{2} }}{{Dt^{2} }}} \right)\,{\mathbf{S}} = \mu \left( {1 + \lambda_{3} \frac{D}{Dt}} \right)\,{\mathbf{A}}_{1} . $$

(5)

In the above equations, ${\mathbf{V}}$ is the velocity vector, $T$ the temperature of the fluid, $C$ the concentration of the fluid, $\rho$ the fluid density, $p$ the pressure, $\alpha$ the thermal diffusivity, $Q_{0}$ the heat generation/absorption parameter, $T_{\infty }$ the ambient fluid temperature, $c_{p}$ the specific heat of fluid at constant temperature, $\tau =$ $\tfrac{{\left( {\rho c} \right)_{p} }}{{\rho c_{p} }}$ the ratio of effective heat capacity of the nanoparticle material to the heat capacity of the fluid, $D_{\text{B}}$ the Brownian diffusion coefficient, and $D_{\text{T}}$ the thermophoresis diffusion coefficient. Moreover, ${\mathbf{S}}$ is the extra stress tensor, ${\mathbf{A}}_{1} = ({\mathbf{\nabla V}}) + ({\mathbf{\nabla V}})^{ * }$ the first Rivlin–Ericksen tensor, $\mu$ the dynamic viscosity, $\lambda_{1},$ and $\lambda_{3} ( \le \lambda_{1} )$ the relaxation and retardation times, respectively, $\lambda_{2}$ the material parameter of the Burgers’ fluid and $\tfrac{D}{Dt}$ denotes the upper convected derivative defined by.

$$ \frac{{Da_{i} }}{Dt} = \frac{{\partial a_{i} }}{\partial t} + u_{r} a_{i,\,r} - \, u_{i,\,r} a_{i} ,\, $$

(6)

For a two-dimensional flow in Cartesian coordinates, we assume the velocity, temperature, concentration, and stress fields of the form

$$ {\mathbf{V}} = [u\left( {x,\,y} \right),\,v\left( {x,\,y} \right),\,0],\, \, T = T(x,\,y),\, \, C = C(x,\,y),\, \, {\mathbf{S = S}}(x,\,y). $$

(7)

By inserting Eq. (7) into Eqs. (1)–(5), having in mind Eq. (6), a lengthy but straight forward calculation results in the relevant governing equations for the steady flow of Burgers’ nanofluid, as follows:

$$ \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0,\, $$

(8)

$$ \begin{aligned} & u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} + \lambda_{1} \left( {u^{2} \frac{{\partial^{2} u}}{{\partial x^{2} }} + v^{2} \frac{{\partial^{2} u}}{{\partial y^{2} }} + 2uv\frac{{\partial^{2} u}}{\partial x\partial y}} \right)\, \\ & + \lambda_{2} \left[ {\begin{array}{*{20}c} {u^{3} \tfrac{{\partial^{3} u}}{{\partial x^{3} }} + v^{3} \tfrac{{\partial^{3} u}}{{\partial y^{3} }} + u^{2} \left( {\tfrac{{\partial^{2} u}}{{\partial x^{2} }}\tfrac{\partial u}{\partial x} - \tfrac{\partial u}{\partial y}\tfrac{{\partial^{2} v}}{{\partial x^{2} }} + 2\tfrac{\partial v}{\partial x}\tfrac{{\partial^{2} u}}{\partial x\partial y}} \right)} \\ { + 3v^{2} \left( {\tfrac{\partial v}{\partial y}\tfrac{{\partial^{2} u}}{{\partial y^{2} }} + \tfrac{\partial u}{\partial y}\tfrac{{\partial^{2} u}}{\partial x\partial y}} \right) + 3uv(u\tfrac{{\partial^{3} u}}{{\partial x^{2} \partial y}} + v\tfrac{{\partial^{3} u}}{{\partial x\partial y^{2} }})} \\ { + 2uv\left( {\tfrac{\partial u}{\partial y}\tfrac{{\partial^{2} u}}{{\partial x^{2} }} + \tfrac{\partial v}{\partial x}\tfrac{{\partial^{2} u}}{{\partial y^{2} }} + \tfrac{\partial v}{\partial y}\tfrac{{\partial^{2} u}}{\partial x\partial y} - \tfrac{\partial u}{\partial y}\tfrac{{\partial^{2} v}}{\partial x\partial y}} \right)} \\ \end{array} } \right]\, \\ = & - \frac{1}{\rho }\frac{\partial p}{\partial x} + \nu \left[ {\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{{\partial^{2} u}}{{\partial y^{2} }} + \lambda_{3} \left( {u\frac{{\partial^{3} u}}{{\partial x\partial y^{2} }} + v\frac{{\partial^{3} u}}{{\partial y^{3} }} - \frac{\partial u}{\partial x}\frac{{\partial^{2} u}}{{\partial y^{2} }} - \frac{\partial u}{\partial y}\frac{{\partial^{2} v}}{{\partial y^{2} }}} \right)} \right],\, \\ \end{aligned} $$

(9)

$$ \begin{aligned} & u\frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y} + \lambda_{1} \left( {u^{2} \frac{{\partial^{2} v}}{{\partial x^{2} }} + v^{2} \frac{{\partial^{2} v}}{{\partial y^{2} }} + 2uv\frac{{\partial^{2} v}}{\partial x\partial y}} \right)\, \\ & + \lambda_{2} \left[ {\begin{array}{*{20}c} {u^{3} \tfrac{{\partial^{3} v}}{{\partial x^{3} }} + v^{3} \tfrac{{\partial^{3} v}}{{\partial y^{3} }} + 2uv\left( {\tfrac{{\partial^{2} v}}{{\partial x^{2} }}\tfrac{\partial u}{\partial y} + \tfrac{\partial v}{\partial x}\tfrac{{\partial^{2} v}}{{\partial y^{2} }} - \tfrac{\partial v}{\partial x}\tfrac{{\partial^{2} v}}{\partial x\partial y} - \tfrac{\partial v}{\partial y}\tfrac{{\partial^{2} v}}{\partial x\partial y}} \right)} \\ { + u^{2} \left( {\tfrac{{\partial^{2} v}}{{\partial x^{2} }}\tfrac{\partial v}{\partial x} - 3\tfrac{\partial v}{\partial y}\tfrac{{\partial^{2} v}}{{\partial x^{2} }} + 3v\tfrac{{\partial^{3} v}}{{\partial x^{2} \partial y}} - \tfrac{\partial v}{\partial y}\tfrac{{\partial^{2} v}}{\partial x\partial y} + 2\tfrac{\partial v}{\partial x}\tfrac{{\partial^{2} v}}{\partial x\partial y}} \right)} \\ { + v^{2} \left( {2\tfrac{\partial v}{\partial y}\tfrac{{\partial^{2} v}}{{\partial y^{2} }} - \tfrac{\partial v}{\partial x}\tfrac{{\partial^{2} v}}{{\partial y^{2} }} + 2u\tfrac{{\partial^{3} v}}{{\partial x\partial y^{2} }} + 2\tfrac{\partial u}{\partial y}\tfrac{{\partial^{2} v}}{\partial x\partial y} + u\tfrac{{\partial^{3} v}}{{\partial x\partial y^{2} }}} \right)} \\ { + 2uv\left( {\tfrac{\partial u}{\partial y}\tfrac{{\partial^{2} u}}{{\partial x^{2} }} + \tfrac{\partial v}{\partial x}\tfrac{{\partial^{2} u}}{{\partial y^{2} }} + \tfrac{\partial v}{\partial y}\tfrac{{\partial^{2} u}}{\partial x\partial y} - \tfrac{\partial u}{\partial y}\tfrac{{\partial^{2} v}}{\partial x\partial y}} \right)} \\ \end{array} } \right]\, \\ = & - \frac{1}{\rho }\frac{\partial p}{\partial y} + \nu \left[ {\frac{{\partial^{2} v}}{{\partial x^{2} }} + \frac{{\partial^{2} v}}{{\partial y^{2} }} + \lambda_{3} \left( {\begin{array}{*{20}c} {u\tfrac{{\partial^{3} v}}{{\partial x\partial y^{2} }} + u\tfrac{{\partial^{3} v}}{{\partial x^{3} }} + v\tfrac{{\partial^{3} v}}{{\partial x^{2} \partial y}} + v^{3} \tfrac{{\partial^{3} v}}{{\partial y^{3} }}} \\ { - \tfrac{\partial v}{\partial x}\tfrac{{\partial^{2} u}}{{\partial x^{2} }} - \tfrac{\partial v}{\partial x}\tfrac{{\partial^{2} u}}{{\partial y^{2} }} - \tfrac{\partial v}{\partial y}\tfrac{{\partial^{2} v}}{{\partial x^{2} }} - \tfrac{\partial v}{\partial y}\tfrac{{\partial^{2} v}}{{\partial y^{2} }}} \\ \end{array} } \right)} \right],\, \\ \end{aligned} $$

(10)

$$ \begin{aligned} & u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} = \alpha \left( {\frac{{\partial^{2} T}}{{\partial x^{2} }} + \frac{{\partial^{2} T}}{{\partial y^{2} }}} \right) + \frac{{Q_{0} }}{\rho c}(T - T_{\infty } ) \\ & + \tau \left[ {D_{\text{B}} \left( {\frac{\partial C}{\partial x}\frac{\partial T}{\partial x} + \frac{\partial C}{\partial y}\frac{\partial T}{\partial y}} \right) + \frac{{D_{\text{T}} }}{{T_{\infty } }}\left( {\left( {\frac{\partial T}{\partial x}} \right)^{2} + \left( {\frac{\partial T}{\partial y}} \right)^{2} } \right)} \right],\, \\ \end{aligned} $$

(11)

$$ u\frac{\partial C}{\partial x} + v\frac{\partial C}{\partial y} = D_{\text{B}} \left( {\frac{{\partial^{2} C}}{{\partial x^{2} }} + \frac{{\partial^{2} C}}{{\partial y^{2} }}} \right) + \frac{{D_{\text{T}} }}{{T_{\infty } }}\left( {\frac{{\partial^{2} T}}{{\partial x^{2} }} + \frac{{\partial^{2} T}}{{\partial y^{2} }}} \right),\, $$

(12)

where $\nu = \tfrac{\mu }{\rho }$ is the kinematic viscosity. Under the usual boundary layer approximations [22], the above governing equations become

$$ \begin{aligned} & u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} + \lambda_{1} \left( {u^{2} \frac{{\partial^{2} u}}{{\partial x^{2} }} + v^{2} \frac{{\partial^{2} u}}{{\partial y^{2} }} + 2uv\frac{{\partial^{2} u}}{\partial x\partial y}} \right)\, \\ & + \lambda_{2} \left[ {\begin{array}{*{20}c} {u^{3} \tfrac{{\partial^{3} u}}{{\partial x^{3} }} + v^{3} \tfrac{{\partial^{3} u}}{{\partial y^{3} }} + u^{2} \left( {\tfrac{{\partial^{2} u}}{{\partial x^{2} }}\tfrac{\partial u}{\partial x} - \tfrac{\partial u}{\partial y}\tfrac{{\partial^{2} v}}{{\partial x^{2} }} + 2\tfrac{\partial v}{\partial x}\tfrac{{\partial^{2} u}}{\partial x\partial y}} \right)} \\ { + 3v^{2} \left( {\tfrac{\partial v}{\partial y}\tfrac{{\partial^{2} u}}{{\partial y^{2} }} + \tfrac{\partial u}{\partial y}\tfrac{{\partial^{2} u}}{\partial x\partial y}} \right) + 3uv(u\tfrac{{\partial^{3} u}}{{\partial x^{2} \partial y}} + v\tfrac{{\partial^{3} u}}{{\partial x\partial y^{2} }})} \\ { + 2uv\left( {\tfrac{\partial u}{\partial y}\tfrac{{\partial^{2} u}}{{\partial x^{2} }} + \tfrac{\partial v}{\partial x}\tfrac{{\partial^{2} u}}{{\partial y^{2} }} + \tfrac{\partial v}{\partial y}\tfrac{{\partial^{2} u}}{\partial x\partial y} - \tfrac{\partial u}{\partial y}\tfrac{{\partial^{2} v}}{\partial x\partial y}} \right)} \\ \end{array} } \right]\, \\ = & \nu \left[ {\frac{{\partial^{2} u}}{{\partial y^{2} }} + \lambda_{3} \left( {u\frac{{\partial^{3} u}}{{\partial x\partial y^{2} }} + v\frac{{\partial^{3} u}}{{\partial y^{3} }} - \frac{\partial u}{\partial x}\frac{{\partial^{2} u}}{{\partial y^{2} }} - \frac{\partial u}{\partial y}\frac{{\partial^{2} v}}{{\partial y^{2} }}} \right)} \right],\, \\ \end{aligned} $$

(13)

$$ u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} = \alpha \frac{{\partial^{2} T}}{{\partial y^{2} }} + \frac{{Q_{0} }}{\rho c}(T - T_{\infty } ) + \tau \left[ {D_{\text{B}} \frac{\partial C}{\partial y}\frac{\partial T}{\partial y} + \frac{{D_{\text{T}} }}{{T_{\infty } }}\left( {\frac{\partial T}{\partial y}} \right)^{2} } \right],\, $$

(14)

$$ u\frac{\partial C}{\partial x} + v\frac{\partial C}{\partial y} = D_{\text{B}} \frac{{\partial^{2} C}}{{\partial y^{2} }} + \frac{{D_{\text{T}} }}{{T_{\infty } }}\frac{{\partial^{2} T}}{{\partial y^{2} }}. $$

(15)

3 Mathematical formulation

Consider a steady, two-dimensional (x, y) boundary layer flow of an incompressible Burgers’ nanofluid over a stretching sheet coinciding with the plane $y > 0$. The flow is confined to the region $y > 0$ and is generated due to the stretching of the sheet along the x-axis with velocity $ax$, where $a$ is a positive constant. It is also assumed that the temperature and concentration at the surface of the sheet are $T_{w}$ and $C_{w}$, respectively, which are greater than the ambient fluid temperature $T_{\infty }$ and concentration $C_{\infty }$. The governing equations for the steady conservation of mass, momentum, thermal energy, and concentration are (8), (13), (14), and (15) subject to the boundary conditions

$$ u = U_{w} = ax,\, \, v = 0,\, \, T = T_{w} ,\, \, C = C_{w} \quad {\text{ at }}y = 0, $$

(16)

$$ u \to 0,\, \, v \to 0,\, \, T \to T_{\infty } ,\, \, C \to C_{\infty } \quad {\text{ as }}y \to \infty . $$

(17)

The above governing problem can be expressed in a simpler form by introducing the following transformation.

$$ \begin{aligned} \psi =\, & x\sqrt {a\nu } f(\eta ),\, \quad \eta\,=\,y\sqrt {\frac{a}{\nu }} ,\, \\ \, \theta \left( \eta \right)\,=\,& \frac{{T - T_{\infty } }}{{T_{w} - T_{\infty } }},\, \quad \varphi \left( \eta \right) = \frac{{C - C_{\infty } }}{{C_{w} - C_{\infty } }},\, \\ \end{aligned},$$

(18)

where $\eta$ is the similarity variable and $\psi (x,\,y)$ is the Stokes stream function.

By employing the similarity variables (18), the above problem reduces to

$$ \begin{aligned} & f^{\prime\prime\prime} + ff^{\prime\prime} - f^{\prime 2} + \beta_{1} \left[ {2ff^{\prime}f^{\prime\prime} - f^{2} f^{\prime\prime\prime}} \right] + \beta_{2} \left[ {f^{3} f^{iv} - 2ff^{\prime 2} f^{\prime\prime} - 3f^{2} f^{\prime \prime 2} } \right]\, \\ & + \beta_{3} \left[ {f^{\prime \prime 2} - ff^{iv} } \right] = 0,\, \\ \end{aligned} $$

(19)

$$ \theta^{\prime\prime} + \mathop {\Pr }\limits f\theta^{\prime} + \mathop {\Pr }\limits N_{\text{b}} \varphi^{\prime}\theta^{\prime} + \mathop {\Pr }\limits N_{\text{t}} \theta^{\prime 2} + \mathop {\Pr }\limits \lambda \theta = 0,\, $$

(20)

$$ \varphi^{\prime\prime} + \mathop {\Pr }\limits {\text{Le}}f\varphi^{\prime} + \frac{{N_{\text{t}} }}{{N_{\text{b}} }}\theta^{\prime\prime} = 0,\, $$

(21)

$$ f = 0,\, \, f^{\prime} = 1,\, \, \theta = 1,\, \, \varphi = 1 \quad {\text{ at }}\eta = 0, $$

(22)

$$ \, f^{\prime} \to 0,\, \, \theta \to 0,\, \, \varphi \to 0 \quad {\text{ as }}\eta \to \infty , $$

(23)

in which prime denotes differentiation with respect to $\eta$. Further, the non-Newtonian parameters $\beta_{1}$, $\beta_{2},$ and $\beta_{3}$, the generalized Prandtl number $\Pr$, the heat source $(\lambda > 0),$ and the heat sink $(\lambda < 0)$ parameter, the Brownian motion parameter $N_{\text{b}}$, the thermophoresis parameter $N_{\text{t}}$ and the Lewis number ${\text{Le}}$ are defined by

$$ \begin{aligned} \beta_{1} = & \lambda_{1} a,\, \, \beta_{2} = \lambda_{2} a^{2} ,\, \, \beta_{3} = \lambda_{3} a , { }\lambda = \frac{{Q_{0} }}{{\rho ac_{p} }},\, \, \mathop {\Pr }\limits = \frac{\nu }{\alpha },\, \\ N_{\text{b}} = & \frac{{\tau D_{\text{B}} (C_{w} - C_{\infty } )}}{\nu } ,\quad N_{\text{t}} = \frac{{\tau D_{T} (T_{w} - T_{\infty } )}}{{T_{\infty } \nu }} , {\text{ Le = }}\frac{\alpha }{{D_{\text{B}} }}. \\ \end{aligned}. $$

(24)

When $N_{\text{b}} = N_{t} = 0$, the present problem reduces to a regular Burgers’ fluid and the concentration Eq. (21) becomes ill-posed and is of no physical significance.

The local Nusselt number ${\text{Nu}}_{x}$ and local Sherwood numbers ${\text{Sh}}_{x}$ are given by

$$ {\text{Nu}}_{x} = - \frac{x}{{\left( {T - T_{\infty } } \right)}}\left. {\left( {\frac{\partial T}{\partial y}} \right)} \right|_{y = 0} ,\,{\text{ Sh}}_{x} = - \frac{x}{{\left( {C_{w} - C_{\infty } } \right)}}\left. {\left( {\frac{\partial C}{\partial y}} \right)} \right|_{y = 0} . $$

(25)

In terms of dimensionless quantities, we obtain

$$ Re^{{ - \tfrac{1}{2}}} Nu_{x} = - \theta^{\prime}\left( 0 \right),\, \, Re^{{ - \tfrac{1}{2}}} Sh_{x} = - \varphi^{\prime}\left( 0 \right),\, $$

(26)

in which $Re = U_{w} x/\nu$ is local Reynolds number.

4 Convergence of the homotopy solutions

The solutions of nonlinear coupled ordinary differential Eqs. (19)–(22) subjected to boundary conditions (22)–(23) are obtained with the help of well-known homotopy analysis technique (HAM). The homotopy analysis technique (HAM) provides a way to check and adjust the convergence of the obtained solution with the help of the auxiliary parameters ħ _f , ħ _θ , and ħ _ϕ and the base functions. These auxiliary parameters ħ _f , ħ _θ , and ħ _ϕ have a key role to control the convergence of the series solutions. The appropriate values of ħ _f , ħ _θ , and ħ _ϕ are determined by considering minimum square which is defined as

$$ F_{f,\,m} = \frac{1}{N + 1}\mathop \sum \limits_{j = 0}^{N} \left[ {N_{f} \mathop \sum \limits_{i = 0}^{m} F_{J} \left( {i\varDelta \eta } \right)} \right]^{2} . $$

(27)

Table 1 ensures the convergence of the series solution which shows that convergent solution for the velocity is obtained at 15th-order of approximation; whereas, such a convergence for temperature and concentration is achieved at 30th-order of approximation.

Table 1 Convergence of homotopy solutions when $\beta_{1} = \beta_{2} = \beta_{3} = 0.2,\,\Pr = 1.4,\,N_{\text{b}} = N_{\text{t}} = 0.1$, λ = 0.2 and ${\text{Le}} = 1.0$ are fixed

5 Numerical results and discussion

This section is focused to analyze the influence of various physical parameters on the temperature and concentration field, respectively. The coupled set of Eqs. (19)–(21) with boundary conditions (22) and (23) are solved analytically by means of the homotopy analysis technique (HAM). The results for the skin-friction coefficient, reduced Nusselt, and sherwood numbers are tabulated.

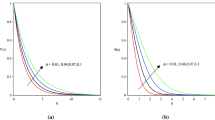
Figures 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, and 14 are plotted to see the variation of the Deborah numbers $\beta_{1}$, $\beta_{2},$ and $\beta_{3}$, Prandtl number Pr, heat source $(\lambda > 0)$ or sink $(\lambda < 0)$, Lewis number ${\text{Le}}$, Brownian motion parameter $N_{\text{b}},$ and thermophoresis parameter $N_{\text{t}}$ on the fluid temperature and concentration profile. The effect of the Deborah numbers $\beta_{1}$ and $\beta_{2}$ on the temperature profile is shown in Figs. 1 and 2. It is found that with the increase in the Deborah numbers $\beta_{1}$ and $\beta_{2},$ the temperature profile and the associated thermal boundary layer thickness increase. Figure 3 provides the analysis for the variation of the Deborah number $\beta_{3}$ on the temperature profile. It is noticed that the temperature and the thermal boundary layer become smaller for the large value of the Deborah number $\beta_{3}$. Figure 4 shows the behavior of the Prandtl number $\Pr$ on the temperature profile. It is noticed that a decrease in the temperature profile and the associated thermal boundary layer thickness is observed as the Prandtl number $\Pr$ is increased. Obviously, from the definition of the Prandtl number $\Pr \left( { = \tfrac{\nu }{\alpha }} \right),$ it is clear that when the value of the Prandtl number $\Pr$ increases, the thermal conductivity decreases and so the temperature profile decreases. Higher the value of the Prandtl number $\Pr$ implies the slow rate of the thermal diffusion. Figure 5 presents the effects of the thermophoresis parameter $N_{t}$ on the temperature profile $\theta (\eta )$. The temperature profile and the associated thermal boundary layer thickness are detected to increase with an increase in the thermophoresis parameter $N_{\text{t}}$. In fact with an increase of the thermophoresis parameter $N_{\text{t}},$ difference between the wall temperature and the reference temperature increases which increases the temperature profile. Figure 6 depicts the variations of the Brownian motion parameter $N_{\text{b}}$ on the temperature profile $\theta (\eta )$. Increase in the Brownian motion parameter $N_{\text{b}}$ has an increasing behavior on the temperature profile and the thermal boundary thickness. It occurs because with the increase of the Brownian motion parameter $N_{\text{b}}$ random motion of the particles increases which results in an enhancement in the temperature profile. Figure 7 indicates the effect of the heat generation phenomenon $\left( {\lambda > 0} \right)$ on the temperature profile. It is noticed that the increase in the heat generation phenomenon $\left( {\lambda > 0} \right),$ the temperature profile and the thermal boundary layer thickness increase. Because the heat generation phenomenon $\left( {\lambda > 0} \right)$ gives more heat to the fluid that corresponds to an increase in the temperature profile and the thermal boundary layer thickness. Figure 8 describes the effect of the heat absorption phenomenon $\left( {\lambda < 0} \right)$ on the temperature profile. We can see that the fluid temperature and thermal boundary layer thickness reduce with an increase in the heat absorption phenomenon $\left( {\lambda < 0} \right)$.

Fig. 1

Influence of the Deborah number β ₁ on θ(η) when β ₂ = β ₂ = 0.2, Pr = 1.2, λ = 0.2, N _t = N _b = 0.1, and Le = 1.0 are fixed

Fig. 2

Influence of the Deborah number β ₂ on θ(η) when β ₁ = β ₂ = 0.2, Pr = 1.2, λ = 0.2, N _t = N _b = 0.1, and Le = 1.0 are fixed

Fig. 3

Influence of the Deborah numbers β ₂ on θ(η) when β ₁ = β ₂ = 0.2, Pr = 1.2, λ = 0.2, N _t = N _b = 0.1m and Le = 1.0 are fixed

Fig. 4

Influence of the Prandtl numbers Pr on θ(η) when β ₁ = β ₂ = β ₂ = 0.2, λ = 0.2, N _t = N _b = 0.1, and Le = 1.0 are fixed

Fig. 5

Influence of the thermophoresis parameter N _t on θ(η) when β ₁ = β ₂ = β ₂ = 0.2, Pr = 1.2, λ = 0.2, N _b = 0.1, and Le = 1.0 are fixed

Fig. 6

Influence of the Brownian motion parameter N _b on θ(η) when β ₁ = β ₂ = β ₂ = 0.2, Pr = 1.2, λ = 0.2, N _t = 0.1, and Le = 1.0 are fixed

Fig. 7

Influence of the heat generation parameter λ(>0) on θ(η) when β ₁ = β ₂ = β ₂ = 0.2, Pr = 1.2, N _t = N _b = 0.1, and Le = 1.0 are fixed

Fig. 8

Influence of the heat absorption parameter λ(<0) on θ(η) when β ₁ = β ₂ = β ₂ = 0.2, Pr = 1.2, N _t = N _b = 0.1, and Le = 1.0 are fixed

Fig. 9

Influence of the Deborah numbers β ₁ on φ(η) when β ₂ = β ₂ = 0.2, Pr = 1.2, λ = 0.2, N _t = N _b = 0.1, and Le = 1.0 are fixed

Fig. 10

Influence of the Deborah number β ₂ on φ(η) when β ₁ = β ₂ = 0.2, Pr = 1.2, λ = 0.2, N _t = N _b = 0.1, and Le = 1.0 are fixed

Fig. 11

Influence of the Deborah number β ₂ on φ(η) when β ₁ = β ₂ = 0.2, Pr = 1.2, λ = 0.2, N _t = N _b = 0.1, and Le = 1.0 are fixed

Fig. 12

Influence of the Lewis number Le on φ(η) when β ₁ = β ₂ = β ₂ = 0.2, Pr = 1.2, λ = 0.2, N _t = 0.1, and N _b = 0.1 are fixed

Fig. 13

Influence of the thermophoresis parameter N _t on φ(η) when β ₁ = β ₂ = β ₂ = 0.2, Pr = 1.2, λ = 0.2, N _b = 0.1, and Le = 1.0 are fixed

Fig. 14

Influence of the Brownian motion parameter N _b on φ(η) when β ₁ = β ₂ = β ₂ = 0.2, Pr = 1.2, λ = 0.2, N _t = 0.1, and Le = 1.0 are fixed

Figures 9 and 10 are plotted to see the effects of the Deborah numbers $\beta_{1}$ and $\beta_{2}$ on the concentration profile $\varphi (\eta )$. It shows that the concentration profile and concentration boundary layer thickness are increasing functions of the Deborah numbers $\beta_{1}$ and $\beta_{2}$. Figure 11 elucidates that an increase in Deborah number $\beta_{3}$ corresponds to the decrease in the concentration profile and concentration boundary layer thickness. Figure 12 depicts the variation of the Lewis number ${\text{Le}}$ on the concentration profile. Decrease in the concentration profile and the concentration boundary layer thickness take place with the increase in the Lewis number ${\text{Le}}$. Obviously from the definition of the Lewis number ${\text{Le}}\left( { = \tfrac{\alpha }{{D_{\text{B}} }}} \right),$ it is clear that a large value of the Lewis number ${\text{Le}}$ has relatively lower Brownian diffusion coefficient. Thus, there is a reduction in the concentration profile, and concentration boundary layer thickness takes place for large value of the Lewis number${\text{Le}}$. The effect of the thermophoresis parameter $N_{\text{t}}$ on the concentration profile is described in Fig. 13. We explore that the increase in the thermophoresis parameter $N_{\text{t}}$ results in an increase in the concentration profile and the associated concentration boundary layer thickness. Figure 14 reveals the variation of the Brownian motion parameter $N_{\text{b}}$ on the concentration profile. It is seen that the increase in the Brownian motion parameter $N_{\text{b}}$ causes the concentration profile and the concentration boundary layer thickness to reduce.

Table 2 presents the numerical values of the skin friction coefficient, local Nusselt number, and local Sherwood number for different values of $\;\Pr ,\,\lambda ,\,N_{\text{b}} ,\,N_{\text{t}},$ and ${\text{Le}}.$.

Table 2 Values of Local Nusselt number and Sherwood number for different values of the parameters $\Pr ,\,\lambda ,\,N_{\text{b}} ,\,N_{\text{t}},$ and ${\text{Le}}$ when $\beta_{1} = \beta_{2} = \beta_{3} = 0.2$

6 Concluding remarks

In this paper, an analysis is presented for the two-dimensional boundary layer flow of Burgers’ nanofluid over a stretching surface. The governing coupled nonlinear ordinary differential equations are solved analytically using homotopy analysis technique (HAM). The important observations of the paper are as follows:

• Effects of the Deborah numbers $\beta_{1}$ and $\beta_{3}$ on the temperature and mass fraction function $\varphi (\eta )$ are quite opposite.

• Effects of $\lambda$ on the temperature profile is quite opposite for $\lambda > 0$ and $\lambda < 0$.

• Effects of Brownian motion and thermophoresis parameters correspond to an increase in the temperature profile.

• Effects of Brownian motion and thermophoresis parameters for mass fraction function are opposite.