Entropy generation optimisation in the nanofluid flow of a second grade fluid with nonlinear thermal radiation

Abstract

The flow of a second grade fluid by a rotating stretched disk is considered. Brownian motion and thermophoresis characterise the nanofluid. Entropy generation in the presence of heat generation / absorption, Joule heating and nonlinear thermal radiation is discussed. Homotopic convergent solutions are developed. The behaviour of velocities (radial, axial, tangential), temperature, entropy generation, Bejan number, Nusselt number, skin friction and concentration is evaluated. The radial, axial and tangential velocities increase for larger viscoelastic parameters while the opposite trend is noted for temperature. Concentration decreases when Schmidt number and Brownian diffusion increase. Entropy generation increases when the Bejan number increase while the opposite is true for the Brinkman number and the magnetic parameter.

1 Introduction

The requirements for the development in the heat transfer rate cannot be achieved by ordinary fluids like water, kerosene oil, ethylene glycol, etc. Several experiments have been carried out by the researchers for improving heat exchange. Many techniques have been proposed in this direction by enhancing micrometre-sized particles for the thermal conductivity of convectional fluids. The major drawbacks in heat transfer components and high-pressure drops are blockage and erosion. To overcome such issues, the idea of nanofluids is introduced. Nanofluids is a suspension of particles of size 1–100 nm in base fluids. It is very effective as the suspension of these particles can enhance the thermal conductivity of base fluids and thus is useful in increasing the heat transfer rate. The enhancement of the thermophysical properties of conventional fluids using nanoparticles suspension is first examined by Choi [1]. Nanofluids have many applications in fields such as nanocryosurgery, environment engineering, chemical industry, heat control systems, heat exchangers, energy storage, power production, refrigeration process, etc. Due to these noteworthy applications, many researchers have already worked on this topic [1,2,3,4,5,6,7,8,9,10]. Many materials in nature have diverse properties. All such materials cannot be handled by the Navier–Stokes theory. These materials are viscoelastic. Food stuff, care products, ketchup, shampoo, many fuel and oils are a few examples of such fluids. Many models like Maxwell, Williamson, Sisko, Jeffrey, Oldroyd-B, Burgers, generalised Burgers, etc. are developed for describing these fluids. Some contributions in this direction have already been made [11,12,13,14,15,16,17,18,19].

The irreversibility process in the system is called entropy. In thermodynamics, the transfer of heat is related to the minimum change of entropy. To enhance the ability of machines, entropy generation minimisation (EGM) is utilised. Some applications of EGM include spin moment, internal molecular friction, kinetic energy and vibration. This type of loss of energy cannot be regained without extra work. That is why entropy is called the measure of irreversibility through heat transfer, mass transfer or viscous dissipation. Several scientists used this process of minimisation in many systems like natural convection, fuel cells, cooling by evaporation, gas turbines, etc. Qayyum et al [20] analysed entropy generation in radiative and Von Karman’s swirling flow with Soret and Dufour effects. Berdichevsky [21] studied the effect of crystal plasticity in the presence of entropy. Khan et al [22] worked on disorderedness of the system for nanofluid flow after considering Arrhenius activation energy. An increase in the efficiency of thermal power plants through entropy generation is examined by Haseli [23]. Hayat et al [24] discussed the entropy generation of a flow with nonlinear thermal radiation. The generation of entropy in a gaseous phosphorus dimer is discussed by Jia et al [25]. The simulation of entropy generation by a similar method can be seen in [25] and Gibbs free energy and enthalpy generation in nitrogen monoxide and gaseous phosphorus dimer can be seen in refs [26,27,28].

This paper examines entropy generation optimisation for the flow of a second-grade nanofluid. Nonlinear thermal radiation, heat generation / absorption and Joule heating in formulation are considered. The relevant nonlinear problems are computed for the convergent series solutions by the homotopy analysis method [7, 29,30,31,32,33,34,35]. The effects of sundry variables on velocity, temperature, Bejan number, entropy generation, skin friction coefficients and concentration are examined.

2 Formulation

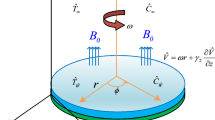
The flow of a second-grade nanofluid by a stretchable rotating disk is examined. Entropy generation for viscous dissipation, Joule heating and nonlinear thermal radiation is also discussed. A magnetic field of constant strength ($B_0$) is exerted in the z-direction. The disk at $z=0$ rotates at an angular velocity ($\Omega _1$) (see figure 1). The stretching velocity of the disk is a (with a being the stretching rate). The disk and ambient temperature are denoted by $\hat{{T}}_w$ and $\hat{{T}}_\infty$, respectively. The surface and ambient concentrations are $\hat{{C}}_w$ and $\hat{{C}}_\infty .$

Fig. 1

Flow geometry.

The governing equations in component form are

$$\begin{aligned}&\frac{\partial \hat{{w}}}{\partial z}+\frac{\hat{{u}}}{r}+\frac{\partial \hat{{u}}}{\partial r}=0, \end{aligned}$$

(1)

$$\begin{aligned}&\frac{\partial \hat{{u}}}{\partial z}\hat{{w}}-\frac{\hat{{v}}^{2}}{r}+\frac{\partial \hat{{u}}}{\partial r}\hat{{u}}\nonumber \\&\quad = \frac{\alpha _1 }{\rho _f }\left( {{\begin{array}{l} {\dfrac{\partial ^{3}\hat{{u}}}{\partial r \partial z^{2}}\hat{{u}}-\dfrac{1}{r}\left( {\dfrac{\partial \hat{{u}}}{\partial z}} \right) ^{2}+2\dfrac{\partial \hat{{u}}}{\partial r}\dfrac{\partial ^{2}\hat{{u}}}{\partial z^{2}}} \\ {\dfrac{\partial ^{3}\hat{{u}}}{\partial z^{3}}\hat{{w}}+\dfrac{\partial \hat{{v}}}{\partial r}\dfrac{\partial ^{2}\hat{{v}}}{\partial z^{2}}+\dfrac{\partial ^{2}\hat{{u}}}{\partial z^{2}}\dfrac{\partial \hat{{w}}}{\partial z}} \\ {\quad \quad +\dfrac{\partial \hat{{v}}}{\partial z}\dfrac{\partial ^{2}\hat{{v}}}{\partial r \partial z}+3\dfrac{\partial \hat{{u}}}{\partial z}\dfrac{\partial ^{2}\hat{{u}}}{\partial r \partial z}-\dfrac{\partial ^{2}\hat{{v}}}{\partial z^{2}}\dfrac{\hat{{v}}}{r}} \\ \end{array} }} \right) \\&+\nu _f \frac{\partial ^{2}\hat{{u}}}{\partial z^{2}} -\frac{\sigma _f B_0^2 }{\rho _f }\hat{{u}}, \end{aligned}$$

(2)

$$\begin{aligned}&\frac{\partial \hat{{v}}}{\partial z}\hat{{w}}+\frac{\partial \hat{{v}}}{\partial r}\hat{{u}}+\frac{\hat{{v}}\hat{{u}}}{r}\nonumber \\&\quad = \dfrac{\alpha _1 }{\rho _f }\left( {{\begin{array}{l} {\dfrac{\partial ^{2}\hat{{v}}}{\partial z^{2}}\dfrac{\hat{{u}}}{r}-2\dfrac{\partial \hat{{v}}}{\partial z}\dfrac{\partial ^{2}\hat{{u}}}{\partial r \partial z}} \\ {\dfrac{\partial ^{3}\hat{{v}}}{\partial r \partial z^{2}}\hat{{u}}+\dfrac{\partial ^{3}\hat{{v}}}{\partial z^{3}}\hat{{w}}-\dfrac{1}{r}\dfrac{\partial \hat{{u}}}{\partial z}\dfrac{\partial \hat{{v}}}{\partial z}} \\ \end{array} }} \right) +\nu _f \dfrac{\partial ^{2}\hat{{v}}}{\partial z^{2}} \nonumber \\&\ \qquad -\frac{\sigma _f B_0^2 }{\rho _f }\hat{{v}}, \end{aligned}$$

(3)

$$\begin{aligned}&\left( {\rho c_p } \right) _f \left( {\frac{\partial \hat{{T}}}{\partial z}\hat{{w}}+\frac{\partial \hat{{T}}}{\partial r}\hat{{u}}} \right) \nonumber \\&=\left. k_f \frac{\partial ^{2}\hat{{T}}}{\partial z^{2}}+Q^{{*}}( {\hat{{T}}-\hat{{T}}_\infty } )\right. \nonumber \\&\qquad +\sigma _f B_0^2 (\hat{{v}}^{2}+\hat{{u}}^{2})\nonumber \\&\qquad -\frac{16\sigma ^{{*}}}{3 k^{{*}}}\left[ {\hat{{T}}^{3}\frac{\partial ^{2}\hat{{T}}}{\partial z^{2}}+3\hat{{T}}^{2}\left( {\frac{\partial \hat{{T}}}{\partial z}} \right) ^{2}} \right] \nonumber \\&\qquad +\left( {\rho c_p } \right) _s \left[ {\frac{D_T }{T_\infty }\left( {\frac{\partial \hat{{T}}}{\partial z}} \right) ^{2}+D_B \left( {\frac{\partial \hat{{T}}}{\partial z}\frac{\partial \hat{{C}}}{\partial z}} \right) } \right] , \end{aligned}$$

(4)

$$\begin{aligned}&\frac{\partial \hat{{C}}}{\partial r}\hat{{u}}+\frac{\partial \hat{{C}}}{\partial z}\hat{{w}}=D_B \frac{\partial ^{2}\hat{{C}}}{\partial z^{2}}+\frac{D_T }{T_\infty }\left( {\frac{\partial ^{2}\hat{{T}}}{\partial z^{2}}} \right) , \end{aligned}$$

(5)

with boundary conditions

$$\begin{aligned}&\hat{{u}}= ra,\quad \hat{{v}}=r\Omega _1 ,\quad \hat{{w}}=0,\nonumber \\&\hat{{C}}=\hat{{C}}_w ,\quad \hat{{T}}=\hat{{T}}_w ,\quad \hat{{p}}\rightarrow 0\;\hbox { at }\;z=0\hbox {,} \nonumber \\&\hat{{u}}= 0,\quad \hat{{v}}=0,\quad \hat{{C}}\rightarrow \hat{{C}}_\infty \nonumber \\&\hat{{T}}=\hat{{T}}_\infty \;\hbox {when}\;z\rightarrow \infty . \end{aligned}$$

(6)

Here $(\hat{{u}}, \hat{{v}}, \hat{{w}})$ are velocities in the $(\hat{{r}}, \hat{{\theta }}, \hat{{z}})$ directions of the disk, $\alpha _1$ is the material parameter, $\nu _f$ is the kinematic viscosity, $\rho _f$ is the density, $\hat{{p}}$ is the pressure, $k_f$ is the thermal conductivity, $c_p$ is the specific heat, $Q^{{*}}$ is the heat generation / absorption coefficient and $D_{\!B}$ is the coefficient of diffusion species. Considering [18]

$$\begin{aligned}&\hat{{u}}= r\Omega _1 {{\tilde{f}}}'(\xi ),\quad \hat{{v}}=r\Omega _1 {\tilde{g}}(\xi ),\quad {\tilde{w}}=-2h\Omega _1 {\tilde{f}}(\xi ),\nonumber \\&\hat{{\varphi }}=\frac{\hat{{C}}-\hat{{C}}_\infty }{\hat{{C}}_w -\hat{{C}}_\infty },\quad \hat{{\theta }}= \frac{\hat{{T}}-\hat{{T}}_\infty }{\hat{{T}}_w -\hat{{T}}_\infty },\nonumber \\&\hat{{p}}=\rho _f \Omega _1 v_f \left( {P(\xi )+\frac{1}{2}\frac{r^{2}}{h^{2}}\varepsilon } \right) ,\quad \xi =\frac{z}{h}, \end{aligned}$$

(7)

the continuity equation is satisfied and eqs (2)–(6) are reduced in the dimensionless form as

$$\begin{aligned} {{\tilde{f}}}'''+ & {} \hbox {We Re}\big ( {2{\tilde{f}}^{{\prime \prime 2}}+{\tilde{g}}^{\prime 2}-2{\tilde{f}} {\tilde{f}}^{( {iv} )}+{\tilde{f}}' {{\tilde{f}}}'''} \big ) \nonumber \\- & {} \hbox {Re}\big ( {{{\tilde{f}}}'^{2}-2{\tilde{f}}{\tilde{f}}''-{\tilde{g}}^{2}} \big )-M{{\tilde{f}}}'=0, \end{aligned}$$

(8)

$$\begin{aligned} {{\tilde{g}}}''+ & {} \hbox {We Re}\big ( {2{f}' {{\tilde{g}}}''-2{\tilde{f}} {{\tilde{g}}}'''-3{{\tilde{f}}}'' {{\tilde{g}}}'} \big )\nonumber \\- & {} \hbox {Re}\big ( {2{{\tilde{f}}}' {\tilde{g}}-2{\tilde{f}}{{\tilde{g}}}'} \big ) -M{\tilde{g}}=0, \end{aligned}$$

(9)

$$\begin{aligned} {{\tilde{\theta }}}''+ & {} 2\hbox {Re}\mathop {\Pr }{\tilde{f}}{{\tilde{\theta }}}'+\hbox {Re}\mathop {\Pr }Q\tilde{\theta }+N_{\mathrm{b}} \mathop {\Pr }{{\tilde{\theta }}}'{\tilde{\varphi }}' \nonumber \\+ & {} N_{\mathrm{t}}\,{\Pr }{{\tilde{\theta }}}'^{2}+R_d \big ( 3(\theta _w -1)\big ( {{\tilde{\theta }}}'^{2}+\tilde{\theta }^{2}{{\tilde{\theta }}}'^{2}(\theta _w -1)^{2}\nonumber \\+ & {} 2\tilde{\theta }{{\tilde{\theta }}}'^{2}(\theta _w -1) \big ) +{{\tilde{\theta }}}''+(\theta _w -1)^{3}\tilde{\theta }^{3}{{\tilde{\theta }}}''\nonumber \\+ & {} 3(\theta _w -1)\tilde{\theta }{{\tilde{\theta }}}''+3(\theta _w -1)^{2}{\tilde{\theta }}^{2}{\tilde{\theta }}'' \big ) \nonumber \\+ & {} M\,{\Pr }\,{\mathrm{Ec}}\big ( {{\tilde{f}}'^{2}+{\tilde{g}}^{2}} \big )=0 , \end{aligned}$$

(10)

$$\begin{aligned} {{\tilde{\varphi }}}''+ & {} 2\hbox {Re}\, \, \hbox {Sc}{\tilde{f}}{\tilde{\varphi }}'+\frac{N_{\mathrm{t}} }{N_{\mathrm{b}} }{{\tilde{\theta }}}''=0 \end{aligned}$$

(11)

with

$$\begin{aligned}&{\tilde{f}}(0)= 0,\;{{\tilde{f}}}'(0)=A,\;\hbox { }{\tilde{f}}'(\infty )=0,\; {\tilde{g}}(0)=1,\nonumber \\&{\tilde{g}}(\infty )=0,\; {\tilde{\theta }}(0)= 1,\;{\tilde{\theta }}(\infty )=0,\;\tilde{\varphi }(0)=1,\nonumber \\&{\tilde{\varphi }}(\infty )=0,\;p(0)=0, \end{aligned}$$

(12)

where

$$\begin{aligned}&\hbox {We}= \frac{\alpha _1 }{\rho h^{2}},\quad \hbox {Re}=\frac{\Omega _1 h^{2}}{\nu _f },\quad {\Pr } =\frac{(\rho c_p )_f \nu _f }{k_f }, \nonumber \\&A=\frac{a}{\Omega _1 }, \quad Q= \frac{Q^{{*}}}{\rho c_p \Omega _1 },\quad \hbox {Sc}=\frac{\upsilon }{Dc^{{*}}},\quad \nonumber \\&\delta =\frac{D_d^{*} }{Dc^{{*}}},\quad N_{\mathrm{b}} =\frac{{{\tau }D_B} (C_w -C_\infty )}{\upsilon }, \nonumber \\&N_{\mathrm{t}} = \frac{{\tau }D_B (T_w -T_\infty )}{T_\infty \upsilon },\quad M=\frac{\sigma B_0^2 }{\rho \Omega _1 }, \nonumber \\&R_d = \frac{16\sigma ^{{*}}T_\infty ^3 }{3k_{f}pk^{{*}}},\nonumber \\&\theta _w =\frac{T_w }{T_\infty },\quad \hbox {Ec}=\frac{r^{2}\Omega _1^2 }{c_p (T_w -T_\infty )}, \end{aligned}$$

(13)

in which We, Re, Pr, A, Q, Sc, $\delta$, $N_{\mathrm{b}}$, $N_{\mathrm{t}}$, M, $R_d$, $\theta _w$ and Ec represent the Weissenberg number, Reynolds number, Prandtl number, stretching parameter, heat generation / absorption parameter, Schmidt number, ratio of diffusion coefficient, Brownian parameter, thermophoresis parameter, magnetic parameter, radiation parameter, temperature difference and the Eckert number, respectively.

We have $C_{f\theta }$ and $C_{fr}$ as skin friction coefficients in the tangential and radial direction, i.e.

$$\begin{aligned} \left. {{\begin{array}{l} {C_{f\theta } =\displaystyle \frac{\tau _{zr} }{\rho (r\Omega _1 )^{2}}} \\ {C_{fr} =\displaystyle \frac{\tau _{z\theta } }{\rho (r\Omega _1 )^{2}}} \\ \end{array} }} \right\} , \end{aligned}$$

(14)

where shear stresses$\;\tau _{zr}$ and $\tau _{z\theta }$ are

$$\begin{aligned} \tau _{zr}= & {} \mu \left( {\frac{\partial \hat{{w}}}{\partial r}+\frac{\partial \hat{{u}}}{\partial z}} \right) +\alpha _1\left[ +2\left( {\frac{\partial \hat{{v}}}{\partial r}-\frac{\hat{{v}}}{r}} \right) \frac{\partial \hat{{v}}}{\partial z}\right. \nonumber \\&\left. +\left( {\frac{\partial \hat{{u}}}{\partial z}+\frac{\partial \hat{{w}}}{\partial r}} \right) \left( {\frac{\partial }{\partial r}\hat{{u}}+\frac{\partial }{\partial z}\hat{{w}}} \right) \right. \nonumber \\&{\left. {+\frac{\partial \hat{{w}}}{\partial z}\frac{\partial \hat{{u}}}{\partial z}+\frac{\partial \hat{{u}}}{\partial r}\frac{\partial \hat{{w}}}{\partial r}+3\left( {\frac{\partial \hat{{w}}}{\partial r}\frac{\partial \hat{{w}}}{\partial z}+\frac{\partial \hat{{u}}}{\partial z}\frac{\partial \hat{{u}}}{\partial r}} \right) } \right] } \nonumber \\&-\alpha _1 \left( \left( {\frac{\partial \hat{{v}}}{\partial r}-\frac{\hat{{v}}}{r}} \right) \frac{\partial \hat{{v}}}{\partial z}\right. \nonumber \\&\left. +\left( {\frac{\partial \hat{{u}}}{\partial r}+\frac{\partial \hat{{w}}}{\partial z}} \right) \left( {\frac{\partial \hat{{u}}}{\partial z}+\frac{\partial \hat{{w}}}{\partial r}} \right) \right) , \end{aligned}$$

(15)

$$\begin{aligned} \tau _{z\theta }= & {} \mu \frac{\partial \hat{{v}}}{\partial z}+\left. \alpha _1 \left( \frac{\partial ^{2}v}{\partial z^{2}}\hat{{w}}-\frac{\hat{{v}}}{r}\frac{\partial \hat{{u}}}{\partial z}+\frac{\partial \hat{{v}}}{\partial z}\frac{\partial \hat{{w}}}{\partial z}\right. \right. \nonumber \\&\left. +\frac{\partial ^{2}\hat{{v}}}{\partial r\partial z}\hat{{u}}+\frac{\partial \hat{{u}}}{\partial z}\frac{\partial \hat{{v}}}{\partial r}+3\frac{\hat{{u}}}{r}\frac{\partial \hat{{v}}}{\partial z} \right) \nonumber \\&-\alpha _1 \left( \frac{\partial \hat{{u}}}{\partial z}\frac{\partial \hat{{v}}}{\partial r}+2\frac{\hat{{u}}}{r}\frac{\partial \hat{{v}}}{\partial z}+2\frac{\partial \hat{{v}}}{\partial z}\frac{\partial \hat{{w}}}{\partial z}-\frac{\hat{{v}}}{r}\frac{\partial \hat{{w}}}{\partial r}\right. \nonumber \\&\left. -\frac{\hat{{v}}}{r}\frac{\partial \hat{{u}}}{\partial z}+\frac{\partial \hat{{w}}}{\partial r}\frac{\partial \hat{{v}}}{\partial r} \right) . \end{aligned}$$

(16)

Skin friction coefficients in the dimensionless form are

$$\begin{aligned}&\hbox {Re}_{r}\,{C}_{fr} ={{\tilde{f}}}''(0)\nonumber \\&\quad +\hbox {We Re}\left( {3{{\tilde{f}}}'(0){\tilde{f}}''(0)-2{\tilde{f}}(0){\tilde{f}}'''(0)} \right) , \end{aligned}$$

(17)

$$\begin{aligned}&\hbox {Re}_{r}\,{C}_{f\theta } ={{\tilde{g}}}'(0)\nonumber \\&\quad +\hbox {We Re}\big ( {4{{\tilde{f}}}'(0){\tilde{g}}'(0)-2{\tilde{f}}(0){\tilde{g}}''(0)} \big )\!, \end{aligned}$$

(18)

where $\hbox {Re}_r = r\Omega _1 h/\nu$ depicts the local Reynolds number.

The heat transfer rate is

$$\begin{aligned} \hbox {Nu}_x =\frac{hq_{{w}} }{k(\hat{{T}}_w -\hat{{T}}_\infty )}. \end{aligned}$$

(19)

The wall heat flux ($q_{{w}}$) is defined as

$$\begin{aligned} q_{{w}} |_{z = 0} =\left. {-k\frac{\partial \hat{{T}}}{\partial z}} \right| _{z = 0} -\left. {\frac{16\sigma ^{{*}}\hat{{T}}^{3}}{3k^{{*}}}\frac{\partial \hat{{T}}}{\partial z}} \right| _{z = 0} . \end{aligned}$$

(20)

The Nusselt number in the dimensionless form is

$$\begin{aligned} \hbox {Nu}_x =-{\tilde{\theta }}^{\prime }(0)\left( {1+R_d \theta _w^3 } \right) \!. \end{aligned}$$

(21)

2.1 Entropy generation

Entropy generation in the nanofluid flow of a second-grade fluid with nonlinear thermal radiation irreversibility, viscous dissipation irreversibility and Joule heating irreversibility is discussed here. The dimensional form is defined as

$$\begin{aligned} S_G= & {} \frac{k_f }{\hat{{T}}_\infty ^{\!2} }\left[ {1+\frac{16\sigma ^{{*}}\hat{{T}}^{3}}{3k_f k^{{*}}}} \right] \left( {\frac{\partial \hat{{T}}}{\partial z}} \right) ^{2}+\frac{\Phi }{\hat{{T}}_\infty }\nonumber \\&+\frac{\sigma _f }{\hat{{T}}_\infty }B_0^2 \left( {\hat{{v}}^{2}+\hat{{u}}^{2}} \right) +\frac{RD}{\hat{{T}}_\infty }\left( {\frac{\partial \hat{{T}}}{\partial z}\frac{\partial \hat{{C}}}{\partial z}} \right) \nonumber \\&+\frac{RD}{\hat{{C}}_\infty }\left( {\frac{\partial \hat{{C}}}{\partial z}} \right) ^{\!\!2}, \end{aligned}$$

(22)

where

$$\begin{aligned} \Phi= & {} \mu _f \left[ {\left( {\frac{\partial \hat{{u}}}{\partial z}} \right) ^{2}+\left( {\frac{\partial \hat{{v}}}{\partial z}} \right) ^{2}} \right] \nonumber \\&+\alpha _1 \left[ {-\frac{\hat{{v}}}{r}\frac{\partial \hat{{v}}}{\partial z}\frac{\partial \hat{{u}}}{\partial z}-\frac{\partial \hat{{v}}}{\partial r}\frac{\partial \hat{{v}}}{\partial z}\frac{\partial \hat{{u}}}{\partial z}} \right. \nonumber \\&+2\frac{\partial \hat{{u}}}{\partial r}\left( {\frac{\partial \hat{{u}}}{\partial z}} \right) ^{2}+\hat{{u}}\frac{\partial \hat{{u}}}{\partial z}\frac{\partial ^{2}\hat{{u}}}{\partial r\partial z}\nonumber \\&+\frac{\partial \hat{{w}}}{\partial z}\left( {\frac{\partial \hat{{u}}}{\partial z}} \right) ^{2}+\hat{{w}}\frac{\partial \hat{{v}}}{\partial z}\frac{\partial ^{2}\hat{{v}}}{\partial z^{2}} \nonumber \\&\left. {+\frac{\hat{{v}}}{r}\left( {\frac{\partial \hat{{u}}}{\partial z}} \right) ^{2}-\frac{\partial \hat{{v}}}{\partial r}\left( {\frac{\partial \hat{{u}}}{\partial z}} \right) ^{2}} \right] . \end{aligned}$$

(23)

The above two equations yield

$$\begin{aligned} S_G= & {} \frac{k_f }{\hat{{T}}_\infty ^{2} }\left[ {1+\frac{16\sigma ^{{*}}\hat{{T}}^{3}}{3k_f k^{{*}}}} \right] \left( {\frac{\partial \hat{{T}}}{\partial z}} \right) ^{2}\nonumber \\&+\frac{1}{\hat{{T}}_\infty }\left[ {\mu _f \left[ {\left( {\frac{\partial \hat{{u}}}{\partial z}} \right) ^{2}+\left( {\frac{\partial \hat{{v}}}{\partial z}} \right) ^{2}} \right] } \right. \nonumber \\&\left. +\alpha _1 \left[ 2\frac{\partial \hat{{u}}}{\partial r}\left( {\frac{\partial \hat{{u}}}{\partial z}} \right) ^{2}-\frac{\hat{{v}}}{r}\frac{\partial \hat{{v}}}{\partial z}\frac{\partial \hat{{u}}}{\partial z} -\frac{\partial \hat{{v}}}{\partial r}\frac{\partial \hat{{v}}}{\partial z}\frac{\partial \hat{{u}}}{\partial z} \right. \right. \nonumber \\&\left. \left. +\hat{{u}}\frac{\partial \hat{{u}}}{\partial z}\frac{\partial ^{2}\hat{{u}}}{\partial r \partial z} \right. \right] \left. \left. +\hat{{w}}\frac{\partial \hat{{v}}}{\partial z}\frac{\partial ^{2}\hat{{v}}}{\partial z^{2}}+\frac{\partial \hat{{w}}}{\partial z}\left( {\frac{\partial \hat{{u}}}{\partial z}} \right) ^{2}\right. \right. \nonumber \\&\left. \left. -\frac{\partial \hat{{v}}}{\partial r}\left( {\frac{\partial \hat{{u}}}{\partial z}} \right) ^{2}+\frac{\hat{{v}}}{r}\left( {\frac{\partial \hat{{u}}}{\partial z}} \right) ^{2} \right] \right. \nonumber \\&+\frac{\sigma _f }{\hat{{T}}_\infty }B_0^2 \left( {\hat{{u}}^{2}+\hat{{v}}^{2}} \right) +\frac{RD}{\hat{{C}}_\infty }\left( {\frac{\partial \hat{{C}}}{\partial z}} \right) ^{2}\nonumber \\&+\frac{RD}{\hat{{T}}_\infty }\left( {\frac{\partial \hat{{T}}}{\partial z}\frac{\partial \hat{{C}}}{\partial z}} \right) . \end{aligned}$$

(24)

Equation (24) consists of four factors: (i) heat transfer irreversibility, (ii) fluid friction irreversibility, (iii) Joule heating irreversibility and (iv) diffusive irreversibility. Now, eq. (24) in the dimensionless form is

$$\begin{aligned} N_G= & {} \alpha _1 \big [ {1+R_d \big ( {1+{\tilde{\theta }}\big ( {\theta _w -1} \big )} \big )^{3}} \big ]{\tilde{\theta }}^{\prime 2}\nonumber \\&+\hbox {Br}\big ( {{\tilde{f}}^{\prime \prime {2}}+\tilde{g}^{\prime 2}} \big ) \nonumber \\&+\hbox {We Re Br}\big ( {{{\tilde{f}}}' {\tilde{f}}''^{2}-2{{\tilde{f}}}''{\tilde{g}}{{\tilde{g}}}'-2{\tilde{f}}{\tilde{g}}'{{\tilde{g}}}''} \big ) \nonumber \\&+\hbox {Br}M\big ( {{{\tilde{f}}}'^{2}+{\tilde{g}}^{2}} \big )+L^{{*}}{{\tilde{\theta }}}'{\tilde{\varphi }}'+L^{{*}}\frac{\alpha _2 }{\alpha _1 }{{\tilde{\varphi }}}'^{2}, \end{aligned}$$

(25)

in which the dimensionless parameters are

$$\begin{aligned} N_G= & {} \frac{S_G \hat{{T}}_\infty h^{2}}{\big ( {\hat{{T}}_w -\hat{{T}}_\infty } \big )k_f },\quad L^{{*}}=\frac{\hbox {RD}(\hat{{C}}_w -\hat{{C}}_\infty )}{k_f }{,}\nonumber \\ \alpha _1= & {} \frac{\hat{{T}}_w -\hat{{T}}_\infty }{\hat{{T}}_\infty }, \alpha _2 = \frac{\hat{{C}}_w -\hat{{C}}_\infty }{\hat{{C}}_\infty },\nonumber \\ \hbox {Br}= & {} \frac{\mu _f r^{2}\Omega _1^2 }{k_f (\hat{{T}}_w -\hat{{T}}_\infty )}\hbox { }, \end{aligned}$$

(26)

where $N_G$ indicates entropy generation, Br is the Brinkman number, $\alpha _1$ is the temperature ratio, $\alpha _2$ is the concentration ratio and $L^{{*}}$ is the diffusive parameter. The Bejan number is defined as

$$\begin{aligned} \hbox {Be}= & {} \frac{\hbox {Entropy}\;\hbox {generation}\;\hbox {due}\;\hbox {to}\;\hbox {heat}\;\hbox {and}\;\hbox {mass}\;\hbox {transfer}\;\hbox {irreversibility}}{\hbox {Total}\;\hbox {entropy}\;\hbox {generation}}, \end{aligned}$$

(27)

$$\begin{aligned} \hbox {Be}= & {} \frac{\alpha _1 [1+R_d (1+\tilde{\theta }(\theta _w -1))^{3}]{{\tilde{\theta }}}'^{^{2}}+L^{{*}}\tilde{\theta }{{\tilde{\varphi }}}'+L^{{*}}(\alpha _2 /\alpha _1 ){\tilde{\varphi }}'^{2}}{\left[ {{\begin{array}{l} {\alpha _1 [1+R_d (1+{\tilde{\theta }}(\theta _w -1))^{3}]{\tilde{\theta }}'^{2}+\hbox {Br(}{\tilde{f}}+{{\tilde{g}}}'^{2}\hbox {)}} {+\hbox {We Re Br}({{\tilde{f}}}'{{\tilde{f}}}''^{2}-2{\tilde{f}}''{\tilde{g}}{{\tilde{g}}}'} \\ {-2{\tilde{f}}{{\tilde{g}}}'{\tilde{g}}'')+\hbox {Br}M\hbox {(}{{\tilde{f}}}'^{2}+\tilde{g}^{2}\hbox {)}+L^{{*}}{{\tilde{\theta }}}'{\tilde{\varphi }}'+L^{{*}}(\alpha _2 /\alpha _1 ){{\tilde{\varphi }}}'^{2}} \\ \end{array} }} \right] }. \end{aligned}$$

(28)

3 Homotopic solutions

3.1 Zeroth-order deformation equations

The required linear operators and initial guesses are defined as

$$\begin{aligned} {\tilde{f}}_0 (\xi )= & {} \left( {1-\exp (-\xi )} \right) A,\;\tilde{g}_0 (\xi )=\exp (-\xi ), \nonumber \\ {\tilde{\theta }}_0 (\xi )= & {} \exp (-\xi ),\;{\tilde{\varphi }}_0 (\xi )=\exp (-\xi ), \end{aligned}$$

(29)

$$\begin{aligned}&{{{\mathbf {\mathtt{{L}}}}}}_{{\tilde{f}}} ({\tilde{f}})={{\tilde{f}}}'''-{\tilde{f}}',\quad {{{\mathbf {\mathtt{{L}}}}}}_{{\tilde{g}}} ({{\tilde{g}}})={\tilde{g}}''-{\tilde{g}},\nonumber \\&{{{\mathbf {\mathtt{{L}}}}}}_{{\tilde{\theta }}} ({\tilde{\theta }})={\tilde{\theta }}''-{\tilde{\theta }}, \quad {{{\mathbf {\mathtt{{L}}}}}}_{{\tilde{\varphi }}} ({{\tilde{\varphi }}})={\tilde{\varphi }}''-{\tilde{\varphi }} \end{aligned}$$

(30)

with

$$\begin{aligned}&{{{\mathbf {\mathtt{{L}}}}}}_{{\tilde{f}}} ({{\tilde{f}}})\left[ {c_1 +c_2 \hbox {e}^{-\xi }+c_3 \hbox {e}^{\xi }} \right] =0,\nonumber \\&{{{\mathbf {\mathtt{{L}}}}}}_{{\tilde{g}}} ({{\tilde{g}}})\left[ {c_4 \hbox {e}^{-\xi }+c_5 \hbox {e}^{\xi }} \right] =0, \nonumber \\&{{{\mathbf {\mathtt{{L}}}}}}_{{\tilde{\theta }}} ({{\tilde{\theta }}})\left[ {c_6 \hbox {e}^{-\xi }+c_7 \hbox {e}^{\xi }} \right] =0,\nonumber \\&{{{\mathbf {\mathtt{{L}}}}}}_{{\tilde{\varphi }}} ({{\tilde{\varphi }}})\left[ {c_8 \hbox {e}^{-\xi }+c_9 \hbox {e}^{\xi }} \right] =0, \end{aligned}$$

(31)

where $c_i \quad (i=1-9)$ are constants.

If $q\in [0, 1]$ and $( {\hbar _{{\tilde{f}}} ,\;\hbar _{\tilde{g}} ,\;\hbar _{{\tilde{\theta }}} \;\hbox {and}\;\hbar _{\tilde{\varphi }} } )$ are the auxiliary parameters, then the zeroth-order deformation problems are

$$\begin{aligned}&(1-q){{{\mathbf {\mathtt{{L}}}}}}_{{\tilde{f}}} \left\{ {{\tilde{f}}(\xi , q)-{\tilde{f}}_0 (\xi )} \right\} \nonumber \\&\quad =q\hbar _{{\tilde{f}}} {{{\mathbf {\mathtt{{N}}}}}}_{{\tilde{f}}} \left\{ {\tilde{f}(\xi ,q),\;{\tilde{g}}(\xi ,q)} \right\} , \end{aligned}$$

(32)

$$\begin{aligned}&(1-q){{{\mathbf {\mathtt{{L}}}}}}_{{\tilde{g}}} \left\{ {{\tilde{g}}(\xi , q)-\tilde{g}_0 (\xi )} \right\} \nonumber \\&\quad =q\hbar _{{\tilde{g}}} {{{\mathbf {\mathtt{{N}}}}}}_{{\tilde{g}}} \left\{ {[{\tilde{g}}(\xi ,q),\;{\tilde{f}}(\xi , q)} \right\} , \end{aligned}$$

(33)

$$\begin{aligned}&(1-q){{{\mathbf {\mathtt{{L}}}}}}_{{\tilde{\theta }}} \left\{ {{\tilde{\theta }}(\xi ,q)-{\tilde{\theta }}_0 (\xi )} \right\} \nonumber \\&\quad =q\hbar _{{\tilde{\theta }}} {{{\mathbf {\mathtt{{N}}}}}}_{{\tilde{\theta }}} \left\{ {{\tilde{\theta }}(\xi , q), {\tilde{f}}(\xi , q), {\tilde{g}}(\xi , q), {\tilde{\varphi }}(\xi , q)} \right\} , \end{aligned}$$

(34)

$$\begin{aligned}&(1-q){{{\mathbf {\mathtt{{L}}}}}}_{{\tilde{\varphi }}} \left\{ {{\tilde{\varphi }}(\xi , q)-\tilde{\varphi }_0 (\xi )} \right\} \nonumber \\&\quad =q\hbar _{{\tilde{\varphi }}} {{{\mathbf {\mathtt{{N}}}}}}_{{\tilde{\varphi }}} \left\{ {{\tilde{\varphi }}(\xi , q), {\tilde{f}}(\xi , q), {\tilde{\theta }}(\xi , q)} \right\} , \end{aligned}$$

(35)

$$\begin{aligned}&{\tilde{f}}(0, q)=0,\;\hbox { }{{\tilde{f}}}'(0, q)=A,\;\hbox { }{{\tilde{f}}}'(\infty , q)=0, \end{aligned}$$

(36)

$$\begin{aligned}&{\tilde{g}}(0, q)=1, \quad \hbox { }{{\tilde{g}}}'(0, q)=0, \end{aligned}$$

(37)

$$\begin{aligned}&{\tilde{\theta }}(0, q)=1, \quad {\tilde{\theta }}(\infty , q)=0, \end{aligned}$$

(38)

$$\begin{aligned}&{\tilde{\varphi }}(0, q)=1,\quad {\tilde{\varphi }}(\infty , q)=0 \end{aligned}$$

(39)

with operators ${{{\mathbf {\mathtt{{N}}}}}}_{{\tilde{f}}} , {{{\mathbf {\mathtt{{N}}}}}}_{{\tilde{g}}} , {{{\mathbf {\mathtt{{N}}}}}}_{\tilde{\theta }}$ and ${{{\mathbf {\mathtt{{N}}}}}}_{{\tilde{\varphi }}}$ in the forms

(40)

$$\begin{aligned} {{{\mathbf {\mathtt{{N}}}}}}_{{\tilde{g}}}= & {} \frac{\partial ^{2}{\tilde{g}}(\xi , q)}{\partial \xi ^{2}}+\hbox {We Re}\left( {2\frac{\partial {\tilde{f}}(\xi , q)}{\partial \xi }\frac{\partial ^{2}{\tilde{g}}(\xi , q)}{\partial \xi ^{2}}} \right. \nonumber \\&\left. {-2{\tilde{f}}(\xi , q)\frac{\partial ^{3}{\tilde{g}}(\xi , q)}{\partial \xi ^{3}}-3\frac{\partial ^{2}{\tilde{f}}(\xi , q)}{\partial \xi ^{2}}\frac{\partial {\tilde{g}}(\xi , q)}{\partial \xi }} \right) \nonumber \\&-\hbox {Re}\left( {2\frac{\partial {\tilde{f}}(\xi , q)}{\partial \xi }{\tilde{g}}(\xi , q)-2{\tilde{f}}(\xi , q)\frac{\partial \tilde{g}(\xi , q)}{\partial \xi }} \right) \nonumber \\&-M{\tilde{g}}(\xi , q), \end{aligned}$$

(41)

$$\begin{aligned} {{{\mathbf {\mathtt{{N}}}}}}_{{\tilde{\theta }}}= & {} \frac{\partial ^{2}{{\tilde{\theta }}}(\xi , q)}{\partial \xi ^{2}}+2\hbox {Re } {\Pr }{{\tilde{f}}}(\xi , q)\frac{\partial {{\tilde{\theta }}}(\xi , q)}{\partial \xi }\nonumber \\&+\hbox {Re } {\Pr } Q{{\tilde{\theta }}}(\xi , q) \nonumber \\&+ N_{\mathrm{t}}\, {\Pr }\left( {\frac{\partial {{\tilde{\theta }}}(\xi , q)}{\partial \xi }} \right) ^{2}+N_\mathrm{b } {\Pr }\frac{\partial {{\tilde{\theta }}}(\xi , q)}{\partial \xi } \frac{\partial {{\tilde{\varphi }}}(\xi , q)}{\partial \xi } \nonumber \\&+M {\Pr } {{\hbox { Ec}}}\left\{ {\left( {\frac{\partial {\tilde{f}}(\xi , q)}{\partial \xi }} \right) ^{2}+\left( {\tilde{g}(\xi , q)} \right) ^{2}} \right\} \nonumber \\&+R_d \left\{ 3(\theta _w -1)\left( {\frac{\partial \tilde{\theta }(\xi , q)}{\partial \xi }} \right) ^{2}\right. \nonumber \\&\left. \times \left[ {1+\left( {{\tilde{\theta }}(\xi , q)} \right) ^{2}(\theta _w -1)^{2}} \right. +2{\tilde{\theta }}(\xi , q)(\theta _w -1) \right] \nonumber \\&+\frac{\partial ^{2}{\tilde{\theta }}(\xi , q)}{\partial \xi ^{2}} \Big [ {1+(\theta _w -1)^{3}( {{\tilde{\theta }}(\xi , q)} )^{3}} \nonumber \\&+3(\theta _w -1)^{2}( {{\tilde{\theta }}(\xi , q)} )^{2}\left. \left. +3(\theta _w -1){\tilde{\theta }}(\xi , q) \right] \right\} ,\nonumber \\ \end{aligned}$$

(42)

$$\begin{aligned} {{{\mathbf {\mathtt{{N}}}}}}_{{\tilde{\varphi }}}= & {} \frac{\partial ^{2}\tilde{\varphi }(\xi , q)}{\partial \xi ^{2}}+2\hbox {Sc Re}\,{\tilde{f}}(\xi , q)\frac{\partial {\tilde{\varphi }}(\xi , q)}{\partial \xi }\nonumber \\&+\frac{N_\mathrm{t} }{N_\mathrm{b} }\frac{\partial ^{2}\tilde{\theta }(\xi , q)}{\partial \xi ^{2}}. \end{aligned}$$

(43)

We now expand ${\tilde{f}}(\xi , q), \quad {\tilde{g}}(\xi , q), \quad {\tilde{\theta }}(\xi , q)$ and ${\tilde{\varphi }}(\xi , q)$ by using the Taylor series about $q=0$ as

$$\begin{aligned}&{\tilde{f}}(\xi , q)={\tilde{f}}_0 (\xi )+\mathop \sum \limits _{m=1}^\infty {\tilde{f}}_m (\xi ) q^{m}; \nonumber \\&{\tilde{f}}_m (\xi )=\frac{1}{m}\frac{\partial ^{m}{\tilde{f}}}{\partial q^{m}}\Bigg |_{q=0} , \end{aligned}$$

(44)

$$\begin{aligned}&{\tilde{g}}(\xi , q)={\tilde{g}}_0 (\xi )+\mathop \sum \limits _{m=1}^\infty {\tilde{g}}_m (\xi ) q^{m};\nonumber \\&{\tilde{g}}_m (\xi )=\frac{1}{m!}\frac{\partial ^{m}{\tilde{g}}}{\partial q^{m}}\Bigg |_{q=0} , \end{aligned}$$

(45)

$$\begin{aligned}&{\tilde{\theta }}(\xi , q)={\tilde{\theta }}_0 (\xi )+\mathop \sum \limits _{m=1}^\infty {\tilde{\theta }}_m (\xi )q^{m};\nonumber \\&{\tilde{\theta }}_m (\xi )=\frac{1}{m!}\frac{\partial ^{m}{\tilde{\theta }}}{\partial q^{m}}\Bigg |_{q=0} , \end{aligned}$$

(46)

$$\begin{aligned}&{\tilde{\varphi }}(\xi , q)={\tilde{\varphi }}_0 (\xi )+\mathop \sum \limits _{m=1}^\infty {\tilde{\varphi }}_m (\xi ) q^{m};\nonumber \\&{\tilde{\varphi }}_m (\xi )=\frac{1}{m!}\frac{\partial ^{m}{\tilde{\varphi }}}{\partial q^{m}}\Bigg |_{q=0} . \end{aligned}$$

(47)

3.2 mth-order deformation equations

The $m\hbox {th}$-order problems are

$$\begin{aligned}&{{{\mathbf {\mathtt{{L}}}}}}_{{\tilde{f}}} \big [ {{\tilde{f}}_m (\xi )-\chi _m {\tilde{f}}_{m-1} (\xi )} \big ]=\hbar _{{\tilde{f}}} {{{\mathbf {\mathtt{{R}}}}}}_{{\tilde{f}}}^m (\xi ), \end{aligned}$$

(48)

$$\begin{aligned}&{{{\mathbf {\mathtt{{L}}}}}}_{{\tilde{g}}} \left[ {{\tilde{g}}_m (\xi )-\chi _m {\tilde{g}}_{m-1} (\xi )} \right] =\hbar _{{\tilde{g}}} {{{\mathbf {\mathtt{{R}}}}}}_{\tilde{g}}^m (\xi ), \end{aligned}$$

(49)

$$\begin{aligned}&{{{\mathbf {\mathtt{{L}}}}}}_{{\tilde{\theta }}} \big [ {{\tilde{\theta }}_m (\xi )-\chi _m {\tilde{\theta }}_{m-1} (\xi )} \big ]=\hbar _{\tilde{\theta }} {{{\mathbf {\mathtt{{R}}}}}}_{{\tilde{\theta }}}^m (\xi ), \end{aligned}$$

(50)

$$\begin{aligned}&{{{\mathbf {\mathtt{{L}}}}}}_{{\tilde{\varphi }}} \left[ {{\tilde{\varphi }}_m (\xi )-\chi _m {\tilde{\varphi }}_{m-1} (\xi )} \right] =\hbar _{{\tilde{\varphi }}} {{{\mathbf {\mathtt{{R}}}}}}_{{\tilde{\varphi }}}^m (\xi ), \end{aligned}$$

(51)

$$\begin{aligned}&{\tilde{f}}_m (0)= \frac{\partial {\tilde{f}}_m (0)}{\partial \xi }=\frac{\partial {\tilde{f}}_m (\infty )}{\partial \xi }=0,\nonumber \\&{\tilde{\theta }}(0)={\tilde{\theta }}(\infty )=0, \nonumber \\&{\tilde{g}}_m (0)= {\tilde{g}}_m (\infty )=0,\nonumber \\&\tilde{\varphi }(0)={\tilde{\varphi }}(\infty )=0, \end{aligned}$$

(52)

where the functions ${{{\mathbf {\mathtt{{R}}}}}}_{{\tilde{f}}}^m (\xi ), {{{\mathbf {\mathtt{{R}}}}}}_{{\tilde{g}}}^m (\xi )$, ${{{\mathbf {\mathtt{{R}}}}}}_{{\tilde{\theta }}}^m (\xi )$ and ${{{\mathbf {\mathtt{{R}}}}}}_{{\tilde{\varphi }}}^m (\xi )$ are

$$\begin{aligned} {{{\mathbf {\mathtt{{R}}}}}}_{{\tilde{f}}}^m (\xi )= & {} {{\tilde{f}}}'''_{m-1}\nonumber \\&+\hbox {We Re}\left( {2\sum _{k=0}^{m-1} {{{\tilde{f}}}''_{m-1-k} {{\tilde{f}}}''_k } +\sum _{k=0}^{m-1} {{{\tilde{g}}^\prime }_{m-1-k} {{\tilde{g}}^\prime }_k } } \right. \nonumber \\&\left. {-2\sum _{k=0}^{m-1} {{\tilde{f}}_{m-1-k} {\tilde{f}}_k^{iv} } +\sum _{k=0}^{m-1} {{\tilde{f}}}'_{m-1-k} {{\tilde{f}}}'''_k } \right) \nonumber \\&-\hbox {Re}\left( \mathop \sum \limits _{k=0}^{m-1} {{\tilde{f}}}'_{m-1-k} {{\tilde{f}}}'_k -\mathop \sum \limits _{k=0}^{m-1} {\tilde{f}}_{m-1-k} {{\tilde{f}}}''_k \right. \nonumber \\&\left. -\mathop \sum \limits _{k=0}^{m-1} \tilde{g}_{m-1-k} {\tilde{g}}_k \right) -M{{\tilde{f}}}'_{m-1} , \end{aligned}$$

(53)

$$\begin{aligned} {{{\mathbf {\mathtt{{R}}}}}}_{{\tilde{g}}}^m (\xi )= & {} {{\tilde{g}}}''_{m-1} +\hbox {We Re}\left( 2\mathop \sum \limits _{k=0}^{m-1} {f}'_{m-1-k} {{\tilde{g}}}''_k \nonumber \right. \\&\left. -2\mathop \sum \limits _{k=0}^{m-1} \tilde{f}_{m-1-k} {{\tilde{g}}}'''_k -3\mathop \sum \limits _{k=0}^{m-1} {{\tilde{f}}}''_{m-1-k} {{\tilde{g}}}'_k \right) \nonumber \\&-\hbox {Re}\left( {2\mathop \sum \limits _{k=0}^{m-1} {\tilde{f}}'_{m-1-k} {\tilde{g}}_k -2\mathop \sum \limits _{k=0}^{m-1} \tilde{f}_{m-1-k} {{\tilde{g}}}'_k } \right) \nonumber \\&-M{\tilde{g}}_{m-1} , \end{aligned}$$

(54)

$$\begin{aligned} {{{\mathbf {\mathtt{{R}}}}}}_{{\tilde{\theta }}}^{m} (\xi )= & {} {{\tilde{\theta }}}''_{m-1} {+}2\hbox {Re}\mathop {\Pr }\mathop \sum \limits _{k=0}^{m-1} {{\tilde{f}}}_{m-1-k} {{\tilde{\theta }}}'_k\nonumber \\&+\hbox {Re } { \Pr } Q\mathop \sum \limits _{k=0}^{m-1} {{\tilde{\theta }}}_{m-1} +N_\mathrm{b} \mathop {\Pr }\mathop \sum \limits _{k=0}^{m-1} {{\tilde{\theta }}}'_{m-1-k} {\tilde{\varphi }}'_k \nonumber \\&+N_\mathrm{t }\,{ \Pr } \mathop \sum \limits _ {k=0}^{m-1} {{\tilde{\theta }}}{'}_{m-1}^2 \nonumber \\&+M\,{\Pr }\,{\mathrm{Ec}}\mathop \sum \limits _{k=0}^{m-1} \left( {{\tilde{f}}{'}_{m-1-k}^2 +g_{m-1-k}^2 } \right) \nonumber \\&+{{R}}_d \left( 3(\theta _w -{1})\left( {\tilde{\theta }}{'}_{m-1}^2 \right. \right. \nonumber \\&{+}\sum _{k=0}^{m-1} {{\tilde{\theta }}_{m-1-k}^2 {\tilde{\theta }}{'}_k^2 (\theta _w {-}1)^{2}} \nonumber \\&\left. {+2\sum _{k=0}^{m-1} {{\tilde{\theta }}_{m-1-k} {\tilde{\theta }}{'}_k^2 (\theta _w -1)} } \right) +{{\tilde{\theta }}}''_{m-1}\nonumber \\&+(\theta _w -1)^{3}\sum _{k=0}^{m-1} {{\tilde{\theta }}_{m-1-k}^3 {{\tilde{\theta }}}''_k } \nonumber \\&\left. +3(\theta _w -1)\sum _{k=0}^{m-1} {\tilde{\theta }_{m-1-k} {{\tilde{\theta }}}''_k } \right. \nonumber \\&\left. +3\sum _{k=0}^{m-1} {(\theta _w -1)^{2}{\tilde{\theta }}_{m-1-k}^2 {{\tilde{\theta }}}''_k } \right) , \end{aligned}$$

(55)

$$\begin{aligned} {{{\mathbf {\mathtt{{R}}}}}}_{{\tilde{\varphi }}}^m (\xi )= & {} {\tilde{\varphi }}''_{m-1} +2\hbox {Re Sc}\mathop \sum \limits _{k=0}^{m-1} \tilde{f}_{m-1-K} {{\tilde{\varphi }}}'_K +\frac{N_\mathrm{t} }{N_\mathrm{b} }{{\tilde{\theta }}}''_{m-1} ,\nonumber \\ \end{aligned}$$

(56)

$$\begin{aligned} \chi _m= & {} \left\{ {{\begin{array}{l} {0,\quad m\le 1,} \\ {1,\quad m>1.} \\ \end{array} }} \right. \end{aligned}$$

(57)

The general solutions can be written as

$$\begin{aligned} {\tilde{f}}_m (\xi )= & {} {\tilde{f}}_m^{*} (\xi )+c_1 +c_2 \hbox {e}^{-\xi }+c_3 \hbox {e}^{\xi }, \end{aligned}$$

(58)

$$\begin{aligned} {\tilde{g}}_m (\xi )= & {} {\tilde{g}}_m^{*} (\xi )+c_4 \hbox {e}^{-\xi }+c_5 \hbox {e}^{\xi }, \end{aligned}$$

(59)

$$\begin{aligned} {\tilde{\theta }}_m (\xi )= & {} {\tilde{\theta }}_m^{*} (\xi )+c_6 \hbox {e}^{-\xi }+c_7 \hbox {e}^{\xi }, \end{aligned}$$

(60)

$$\begin{aligned} {\tilde{\varphi }}_m (\xi )= & {} {\tilde{\varphi }}_m^{*} (\xi )+c_8 \hbox {e}^{-\xi }+c_9 \hbox {e}^{\xi }, \end{aligned}$$

(61)

where the constants $c_i\, (i=1-9)$ by using the boundary conditions (52) have the values

$$\begin{aligned} c_1= & {} -c_2 -{\tilde{f}}_m^{*} (0),\quad c_2 =\frac{\partial \tilde{f}_m^{*} (0)}{\partial \xi },\nonumber \\ c_4= & {} -\frac{\partial \tilde{g}_m^{*} (0)}{\partial \xi }, \quad c_6 =-\frac{\partial \tilde{\theta }_m^{*} (0)}{\partial \xi }, \nonumber \\ c_8= & {} -\frac{\partial {\tilde{\varphi }}_m^{*} (0)}{\partial \xi },\quad c_3 =c_5 =c_7 =c_9 =0. \end{aligned}$$

(62)

4 Convergence analysis

With the help of auxiliary parameters $\hbar _{{\tilde{f}}}$, $\hbar _{{\tilde{g}}} ,\hbar _{{\tilde{\theta }}}$ and $\hbar _{\tilde{\varphi }}$, we can regulate the convergence region. By using the homotopy analysis method (HAM), we can solve the system of equations. Figure 2 shows the $\hbar$-curves at the 25th order of deformation. Convergence regions for these parameters are $-2\le \hbar _{{\tilde{f}}} \le -1$, $-2\le \hbar _{{\tilde{g}}} \le -0.1, -2\le \hbar _{{\tilde{\theta }}} \le -0.5$ and $-1.5\le \hbar _{{\tilde{\varphi }}} \le -0.5$. Table 1 demonstrates the convergence order for ${{\tilde{f}}}''(0), {{\tilde{g}}}'(0), {{\tilde{\theta }}}'(0)$ and ${{\tilde{\varphi }}}'(0)$ which converges at the 12th, 11th, 28th and 28th order of approximations, respectively.

Fig. 2

h curve at ${{\tilde{f}}}''(0)$, $\tilde{g}^{\prime }(0)$, ${{\tilde{\theta }}}'(0)$ and ${\tilde{\varphi }}'(0)$.

Table 1 Solution convergence occurs when $\hbox {Re}=0.3$, $\hbox {We}=0.01, R_d =0.01, \theta _w =0.1, A=0.4, \Pr =1.5, Q=0.01, \hbox {Ec}=0.4, \hbox {Sc}=1, N_\mathrm{b} =0.3, N_\mathrm{t} =0.01, M=0.2$.

5 Results and discussion

In this section, the behaviour of influential variables on velocity, temperature, concentration, coefficients of skin friction and the Nusselt number is analysed. In figures 3–23, we fixed $\hbox {We}=0.3, \quad \hbox {Re}=0.9=0.9 =0.7, \hbox {Ec}=0.4, Q=0.7, N_\mathrm{t} =0.3, N_\mathrm{b} =0.3, R_d =0.5, \theta _w =0.2,\;\hbox {Sc}=1\,\, \mathrm{and}\;M=0.5$.

5.1 Dimensionless velocities

Figures 3–10 illustrate the velocities of various parameters. In figures 3 and 4, the effects of viscoelastic parameter $(\xi )$ $\big ( {\hbox {when We}=0,0.4,0.8,1.2} \big )$ on axial $\big ( {\tilde{f}(\xi )} \big )$ and radial $({{\tilde{f}}'(\xi )})$ velocities are shown. We know that the Weissenberg number (We) is inversely proportional to the fluid viscosity because of which the motion of the fluid increases with larger We. The effect of the Reynolds number Re on $\big ( {{\tilde{f}}(\xi ), {\tilde{g}}(\xi )} \big )$ is shown in figures 5 and 6. Here, for increasing values of the Reynolds number (Re) $\left( {\hbox {Re}=0,0.5,1,1.5} \right)$, $( {{\tilde{f}}(\xi ), {\tilde{g}}(\xi )} )$ decreases because inertial forces become stronger for higher $\hbox {Re}$. The behaviour of velocities $( {{\tilde{f}}(\xi ), {\tilde{g}}(\xi )})$ for the stretching parameter (A) is discussed in figures 7 and 8. For larger values of A (${A=0,\;0.2,\;0.4,\;0.6}$), momentum boundary layer and ${\tilde{f}}(\xi )$ rise for a longer stretching rate (see figure 7). On the other hand, the reverse trend is noticed for ${\tilde{g}}(\xi )$ because the angular velocity $(\Omega _1$) reduces. Figures 9 and 10 show the effect of magnetic parameter M on $\big ( {{{\tilde{f}}}'(\xi ), {\tilde{g}}(\xi )} \big )$. We know that the Lorentz force is related to the magnetic field which causes resistance to the flow, and so $\big ( {{\tilde{f}}^{\prime }(\xi ),\;{\tilde{g}}(\xi )} \big )$ reduces for M.

Fig. 3

Graph of $f({\xi })$ against We.

Fig. 4

Graph of${{f^\prime }(\xi )}$ against We.

Fig. 5

Graph of$f({\xi })$ against Re.

Fig. 6

Graph of$g({\xi })$ against Re.

Fig. 7

Graph of $f({\xi })$ against A.

Fig. 8

Graph of $g({\xi })$ against A.

Fig. 9

Graph of ${f^\prime }(\xi )$ against M.

Fig. 10

Graph of $g({\xi })$ against M.

Fig. 11

Graph of $\theta ({\xi })$ against Pr.

Fig. 12

Graph of $\theta ({\xi })$ against Q.

Fig. 13

Graph of $\theta ({\xi })$ against $\theta _{w}$.

Fig. 14

Graph of $\theta ({\xi })$ against $N_{\mathrm{b}}$.

Fig. 15

Graph of $\theta ({\xi })$ against M.

Fig. 16

Graph of $\theta ({\xi })$ against $N_{\mathrm{t}}$.

5.2 Temperature

The analysis of temperature distribution ${\tilde{\theta }(\xi )}$ against different parameters is deliberated in figures 11–16. The behaviour of Pr with ${\tilde{\theta }(\xi )}$ is discussed in figure 11. As Pr is inversely proportional to thermal diffusivity, for large values of Pr $(\Pr =0.4, 0.8, 1.2, 1.6)$, the temperature of the fluid decreases. The effect of Q on the temperature is shown in figure 12. Clearly, ${\tilde{\theta }}(\xi )$ boosts up for larger Q (${Q=0,0.4,0.8,1.2}$) because heat generation / absorption coefficient increases. Figure 13 demonstrates the behaviour of ${{\tilde{\theta }}(\xi )}$ against $\theta _w$. The thermal state of the fluid enhances by increasing $\theta _w$ ($\theta _w =1.1, 1.3, 1.5, 1.7$) due to which the temperature is enhanced. Figure 14 illustrates the effect of $N_\mathrm{b}$ on ${\tilde{\theta }}(\xi )$. Temperature increases for higher $N_\mathrm{b}$. Figure 15 shows the behaviour of the magnetic field (M) on temperature distribution. An increase in M ($M=0, 0.5, 1, 1.5$) gives rise to ${\tilde{\theta }}(\xi )$. It is for larger Lorentz force. In figure 16, both $\tilde{\theta }(\xi )$ and the thermal layer thickness are increased for $N_\mathrm{t} =0,0.5,1,1.5$. An enhancement in $N_\mathrm{t}$ results in a stronger thermophoretic force due to which nanoparticles are transferred from warm to cold regions, and hence ${{\tilde{\theta }}(\xi )}$ rises.

Fig. 17

Graph of $\varphi ({\xi })$ against Sc.

Fig. 18

Graph of $\varphi ({\xi })$ against $N_{\mathrm{t}}$.

Fig. 19

Graph of $\varphi ({\xi })$ against $N_{\mathrm{b}}$.

5.3 Concentration

The behaviour of the concentration is portrayed in figures 17–19. The influence of the Schmidt number $({\hbox {Sc}})$ on ${{\tilde{\varphi }}(\xi )}$ is described in figure 17. Large values of Sc $(\hbox {Sc}=0,0.3,0.6,0.9)$ decrease the concentration. In fact, higher values of Sc result in low molecular diffusivity. The impacts of ${N_\mathrm{t}}$ and ${N_\mathrm{b}}$ on ${{\tilde{\varphi }}(\xi )}$ are shown in figures 18 and 19. With an enhancement of $N_\mathrm{t} =0,0.5,1,1.5$, thermophoresis force rises. Such force tends to move nanoparticles from warm to cold regions and hence ${{\tilde{\varphi }}(\xi )}$ rises. Moreover, the concentration layer thickness is also enhanced for larger $N_\mathrm{t}$. The higher the values of $N_{\mathrm{b}}\, (N_\mathrm{b} =0.3,\;0.6,\;0.9,\;1.2)$, the smoother is the distribution of nanoparticles concentration in the fluid system, which eventually decreases ${{\tilde{\varphi }}(\xi )}$.

5.4 Nusselt number

Figures 20 and 21 demonstrate the effect of the viscoelastic parameter $(\hbox {We})$ and the thermophoresis parameter $( {N_\mathrm{t}})$ on the rate of heat transfer. These figures show that the Nusselt number increases for higher values of We while a reverse behaviour is noticed for $N_\mathrm{t}$.

5.5 Skin friction coefficients

Figures 22 and 23 indicate the effects of A and We on the skin friction coefficients. Here, the magnitude of the surface drag force in radial and tangential directions is more for larger A and $\hbox {We}$.

Fig. 20

Graph of $\hbox {Nu}_{x}$ against We.

Fig. 21

Graph of $\hbox {Nu}_{x}$ against $N_{\mathrm{t}}$.

Fig. 22

Graph of $Cf_{r}\hbox { Re}_{r}$ and $Cf_{\theta }\hbox { Re}_{\theta }$ against We.

Fig. 23

Graph of $Cf_{r}\hbox { Re}_{r}$ and $Cf_{\theta }\hbox { Re}_{\theta }$ against A.

Fig. 24

Graph of $N_{G}$ against Br.

5.6 Entropy generation and Bejan number

Figures 24–33 illustrate the trends of ${N_G}$ and Be for different parameters. Figures 24 and 25 show the behaviour of $N_G$ and Be on the Brinkman number $({\hbox {Br}})$. Br is associated with the heat transfer from a disk to the flow of a viscous fluid. Figure 24 indicates more entropy generation rate for larger ${\hbox {Br}}$ because by dissipation, the conduction rate is slowly created. Figure 25 shows the behaviour of ${\hbox {Br}}$ on Be as entropy generation is more for large Br. It means viscosity is dominant over heat transfer irreversibility, and hence $\hbox {Be}$ decreases. In figures 26 and 27, the influence of the magnetic variable (M) on $N_G$ and Be is noticed. In figure 26, the entropy generation rate is addressed for large values of M. The entropy generation rate is enhanced for large M because drag force is higher for larger M. Figure 27 shows the decaying behaviour of Be for a larger magnetic variable M. Figures 28 and 29 describe the behaviour of the diffusion parameter $(L^{{*}})$ on $N_G$ and Be. It is noticed that for $L^{{*}}$, both $N_G$ and Be are increasing functions. The diffusion rate of nanoparticles enhances for larger $L^{{*}}$. That is why the total entropy of the system and $\hbox {Be}$ are enhanced. Figures 30 and 31 show the impact of $\theta _w$ on $N_G$ and Be. Here, both $N_G$ and Be are increasing functions of $\theta _w$.As the disk is heated, for larger values of the temperature ratio $({\theta _w})$, the disorderedness near the disk is high and so $N_G$ increases (see figure 30). Here, the irreversibility of the mass and heat transfer prevail over the irreversibility of the friction of the fluid for higher $\theta _w$, and so Be also rises (see figure 31). Trends of $N_G$ and Be vs. $\hbox {We}$ are displayed in figures 32 and 33. Disorderedness in the system is more for larger We (see figure 32). $\hbox {Be}$ decays for increasing We (see figure 33).

Fig. 25

Graph of Be against Br.

Fig. 26

Graph of $N_{G}$ via M.

Fig. 27

Graph of Be via M.

Fig. 28

Graph of $N_{G}$ via $L^{*}$.

Fig. 29

Graph of Be via $L^{*}$.

Fig. 30

Graph of $N_{G}$ via $\theta _w$.

Fig. 31

Be via $\theta _w$.

Fig. 32

Graph of $N_{G}$ against We.

Fig. 33

Graph of Be against We.

6 Conclusions

Major findings of this study are:

• For larger viscoelastic parameter $(\hbox {We})$, the velocities (radial $( {{\tilde{f}}(\xi )})$, axial $({{{\tilde{f}}}'(\xi )})$ and tangential $({{\tilde{g}}(\xi )}))$ are increased.

• Temperature $({{\tilde{\theta }}(\xi )})$ against ${\theta _w}$, ${N_\mathrm{t}}$, M and Q enhances.

• Concentration reduces for $A,{N_\mathrm{b}},{\hbox {Re}}$ and ${\hbox {Sc}}$.

• Entropy generation $(N_G)$ enhances for We and Br while the opposite trend is noticed against We.

• Both ${N_G}$ and Be are enhanced for larger ${L^{{*}}}$ and ${\theta _w }$.