Entropy generation on double-diffusive MHD slip flow of nanofluid over a rotating disk with nonlinear mixed convection and Arrhenius activation energy

Abstract

The present study deals with the swirling flow problem for the nanoliquid over a radially stretchable rotating disk with the consideration of nonlinear mixed convection and chemical reaction defined by Arrhenius model. The surface of the stretchable rotating disk concedes with the Navier’s velocity slip condition. The temperature jump condition due to imperfect liquid–solid energy interaction is also considered. The flow model is established by incorporating the well-known Buongiorno’s nanofluid model and therefore, Brownian motion and thermophoretic diffusion are incorporated in the mathematical modeling. Heat transport is performed taking into account the heat generation owing to viscous and Joule dissipations and internal energy generation/absorption of the fluid. The coupled nonlinear partial differential equations (PDEs) are converted to the non-dimensional ordinary differential equations (ODEs) through the similarity transformation. These ODEs together with the physical conditions are then solved by the “bvp4c” technique. The impact of present flow characteristics on the entropy generation and Bejan number, flow fields (axial and radial velocities), temperature and concentration profiles are presented graphically. Moreover, the surface drag force, strength of energy and mass transport are calculated and presented in tabular forms. The outcomes show that an increase in magnetic and slip parameter values decrease the fluid velocities (axial and radial). Entropy generation gets improved with the increase in either Brinkman number or magnetic parameter values.

1 Introduction

Considering various technical processes, it is possible to highlight that heat transfer from one mechanical unit to another one occurs. Fluid heating/cooling phenomena are involved during the liquid movement in such types of processes. Therefore, the development of better cooling techniques is essential for such processes. Nanoliquids have a much better heat transfer rate as compared to other conventional liquids (water, engine oil, ethylene glycol, etc). Hence, nanoliquids can be utilized to enhance the energy transference rate. The colloidal suspension of tiny particles with nanoscale measurement in the host liquid is defined as the nanoliquids. Moreover, the movement of nanoliquids in presence of the external magnetic can be observed in a large number of engineering systems and has many applications in biomedical applications including wound treatment, sterilized setup, gastric medications, tumors elimination, treatment of asthma, etc. Therefore, across the globe, many researches have performed several studies on the nanofluid motion with magnetic field effect. Turkyilmazoglu [1] presented an analytical study on the hydromagnetic slip flow of nanoliquid with four different types of the nano-sized particles dispersed uniformly in the host liquid. Kumar et al. [2] examined the unsteady hydromagnetic circulation of Brinkman type nanoliquid with TiO₂, Cu, Al₂O₃ as the nanoparticles in the base fluid, due to an exponentially accelerated vertical surface. Theoretical analysis for the motion of nanoliquid having carbon nanotubes as nano-size particles within the two co-axial rotating disks with Cattaneo–Christov heat flux was performed by Bhattacharyya et al. [3]. Tayebi and Chamkha [4] numerically investigated the hydromagnetic nanofluid flow of water-based Al₂O_3-Cu hybrid nanoliquid in a square enclosure. Some of the important investigations on this topic can be found [5,6,7,8,9,10].

It is established fact that disk type geometries appear widely in rotating machineries, like centrifugal pumps, liquid metal pumping engines, designs of a multi-pore distributor, rotating heat exchangers, marine or gas turbines, electric power generating system, rotating disk reactors for biofuels production and many more. One common occurrence of this type of situation is the rotating disk electrode (RDE) used in electrochemical reaction and generally associated with redox chemistry. In order to control the flow rate of the chemical reaction, the angular velocity of the rotating disk electrode (RDE) has an essential influence. The first analysis in this regard was done by Von-Karman [11] by introducing the similarity solution for the circulation due to a rotating disk of a large radius. The earlier investigation of the motion encouraged by a rotating disk under various conditions was done by Griffiths [12] where the author performed an analysis to study the boundary layer motion of viscous and incompressible liquid due to a rotating disk, using the generalized non-Newtonian fluid models (viz. power-law model, Bingham model and Carreau model). Ming et al. [13] presented a computational analysis for the laminar and axis-symmetric motion of power-law liquid, where the circulation was driven solely by an infinite rotating disk with generalized diffusion. Doh and Muthtamilselvan [14] studied the time-dependent, viscous and axis-symmetric swirling flow for non-Newtonian micropolar fluid, caused by a disk which was placed within the non-rotating cylinder, but the disk was rotating with a fixed angular velocity about its own vertical axis. Hayat et al. [15] considered the von-Karman swirling circulation of non-Newtonian Sisko liquid owing to a stretchable rotating disk. They implemented the homotopy analysis technique to find the solution of the highly nonlinear coupled ordinary differential equations. Gholinia et al. [16] developed a mathematical model to study the chemically reactive circulation of non-Newtonian Eyring–Powell liquid over a rotating plate with homogeneous-heterogeneous reactions. Bhat and Katagi [17] employed the Keller-box method to find the numerical solution of the flow of micropolar liquid between two parallel disks, in which the upper plate is considered as permeable while the lower plate is non-porous. Turkyilmazoglu [18] studied the two-phase energy transport analysis for the fluid motion on a stretchable rotating disk with the suspension of the dusty particles.

The first analysis for the entropy generation on the irreversible process was done by Bejan [19] and this research familiarized with the concept of strength of entropy generation for energy transference flows. Thereafter, researchers are actively engaged to study the entropy generation in technological processes. Rashidi et al. [20] performed the entropy investigation for the hydromagnetic motion of nanoliquid with three various types of particles (Al₂O₃, CuO, Cu) in the base liquid over a porous rotating disk. Arikoglu et al. [21] studied a mathematical approach to investigate the application of irreversibility for the MHD Von-Karman swirling motion of viscous fluid above a single rotating plate. Renuka et al. [22] presented an analytical solution for the flow of nanofluid between two stretched rotating disks within the porous environment, considering the entropy generation. In their analysis, they conclude that Bejan number increases with higher temperature ratio parameter values, while the opposite nature is defined for the entropy production strength. Qayyum et al. [23] examined the influence of various characteristics on the entropy production and Bejan number for the axis-symmetric motion of non-Newtonian fluid (Williamson liquid) between two stretchable rotating plates where both the plates have various angular velocities and stretching rates. Abbas et al. [24] presented an analysis of the entropy production influence on MHD fully developed slip circulation of nanoliquid with second-order velocity slip and convectively heating boundary conditions at the disk plate. Chen et al. [25] presented a review on entropy in the convective heat transference which summarizes the applications of entropy theory and theoretical frameworks. Theoretical investigation for the radiative motion of nanofluid having carbon nanotubes as nano-size particles within the two co-axial rotating disks with the production of entropy was performed by Khan et al. [26]. Authors concluded that entropy production intensity is effectively controlled by the Brinkman parameter and rate of entropy generation has increasing nature for the higher Brinkman parameter. Tayebi and Chamkha [27, 28] presented an entropy generation analysis on the hydromagnetic natural convection flow of hybrid nanofluid in cavity. Other important investigations in this context are explained in [29,30,31,32,33].

Activation energy is the minimum energy volume used to generate a chemical reaction in a technical system. Arrhenius, a Swedish scientist first defined such approach in 1889. Activation energy is absent in the case of reaction between the elements, while for the beginning of such reaction process some energy is necessary. Activation energy can be considered as a fence between the reacted and unreacted energy states of atoms and molecules. A reaction will be initiated when this barrier is removed. Taking into account the Maxwell model, only those tiny particles will overcome such a barrier which have energy higher than the barrier. Hence, we can consider the activation energy as a barrier height. Khan et al. [34] considered MHD flow of radiative liquid above a stretchable rotating disk with the consideration of Arrhenius activation energy. Hayat et al. [35] established a mathematical approach to study the physical behavior of the activation energy on the motion of nanofluid between two rotating plates. Khan et al. [36] scrutinized the radiative non-Newtonian flow of nanofluid above a radially stretchable rotating disk under the vertically applied magnetic field and estimated the impact of the activation energy for such circulation. Effect of activation energy on the hydromagnetic mixed convective nanoliquid motion above a rotating disk with chemical reaction between species was investigated numerically using the shooting technique by Alghamdi [37]. Asma et al. [38] investigated chemically reactive MHD nanoliquid motion above rotating disk considering the chemical reaction of second-order between the species, triggered by the activation energy. Ahmad et al. [39] investigated the chemically reactive radiative circulation of non-Newtonian (third-grade liquid), incorporating the effect of Arrhenius activation energy above a rotating disk using the homotopic analysis method. They found that an increase in activation energy is mainly responsible for a decrease in the species concentration. Kumar et al. [40] studied the motion of nanofluid by incorporating the Casson model of non-Newtonian liquid with the consideration of activation energy effect in the concentration equation.

Dissipation factors, i.e., Joule and viscous dissipations are phenomena of practical importance in numerous engineering devices. Due to the effect of viscous dissipation, the temperature distribution varies significantly. So, the consideration of viscous dissipation effect is of utmost importance in heat transport investigation, when the liquid is adequately viscous, as accounted in the current study. There has a large number of engineering processes where we can use this fact for our benefit for instance: immersion heaters and electrical irons, etc. However, sometimes this occurrence becomes a burden for us, where this unnecessarily produced energy may result in the downgrading of the system. Therefore, dissipation factor effects work as a volumetric heat source and the investigation of heat transference becomes essential in several physical situations.

In this present research, we have scrutinized the MHD [41,42,43,44,45] nanoliquid circulation over a stretchable rotating disk under the heat generation/absorption, viscosity and Joule heating impacts. The influence of the binary chemical reaction among varied species stimulated by providing activation energy is also accounted for the current flow situation. Although some research articles have been published recently in reputed journals by many researchers discussing the entropy generation, but none of them have discussed the nonlinear mixed convection for such flow with Navier’s velocity slip and the temperature jump condition at the surface of the disk. Therefore, the present research work focuses on filling-up this gap.

2 Mathematical modeling of the problem

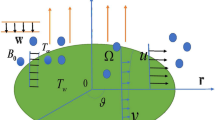
We have considered the MHD steady flow problem of viscous nanomaterial over a stretchable (in radial direction) rotating disk of large radius with the consideration of nonlinear mixed convection. At the disk plate, the partial slip conditions of fluid are taking place under the consideration that the scale of roughness is insignificant with compare to the thickness of boundary layer. The temperature jump condition is also accounted at the disk surface. A schematic diagram of the problem is sketched in Fig. 1 in which disk is located at the position $z = 0$. The area which is above the surface of the disk $(z > 0)$ is occupied by the nanoliquid. It is assumed that the disk is rotating in its own plane (i.e., about z axis) in the anti-clockwise direction with fixed angular velocity $\omega$ which sets up the von-Karman swirling motion to the neighboring liquid layers. The whole domain of the flow is pervaded by an unvarying magnetic field of strength $B_0$ as shown in Fig. 1 (which is parallel to z axis). It is considered that the concentration and temperature at the disk are maintained at ${{\hat{C}}_{{\hat{W}}}}$ and ${{\hat{T}}_{{\hat{W}}}}$, respectively. Far above the disk surface or in the free stream, concentration and temperature take the values ${{\hat{C}}_\infty }$ and ${{\hat{T}}_\infty }$, respectively. Due to low magnetic Reynolds number $\left( {{{{\text {Re}} }^m}< < 1} \right)$ [46], the induced magnetic influence is weak, where ${{\text {Re}} ^m} = R\omega /{D_m}$ and $R,\,\,{D_m}$ are radius of the disk and diffusivity of the magnetic field, respectively.

Fig. 1

Geometry of the problem

Considering the aforementioned assumptions, the control flow narrating differential equations describing the motion of nanomaterial with energy and mass transport presented as

$$\begin{aligned}&\frac{{\partial {\hat{U}}}}{{\partial {r}}} + \frac{{{\hat{U}}}}{\partial {r}} + \frac{{\partial {\hat{W}}}}{{\partial z}} = 0, \end{aligned}$$

(1)

$$\begin{aligned}&\left. \begin{array}{l} {\hat{U}}\frac{{\partial {\hat{U}}}}{{\partial r}} - \frac{{{{{\hat{V}}}^2}}}{r} + {\hat{W}}\frac{{\partial {\hat{U}}}}{{\partial z}} = {\upsilon _f}\frac{{{\partial ^2}{\hat{U}}}}{{\partial {z^2}}} + g\left[ {{\lambda _1}\left( {{\hat{T}} - {{{\hat{T}}}_\infty }} \right) + {\lambda _2}{{\left( {{\hat{T}} - {{{\hat{T}}}_\infty }} \right) }^2}} \right] \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + g\left[ {{\lambda _3}\left( {{\hat{C}} - {{{\hat{C}}}_\infty }} \right) + {\lambda _4}{{\left( {{\hat{C}} - {{{\hat{C}}}_\infty }} \right) }^2}} \right] - \frac{{{\sigma _f}B_0^2}}{{{\rho _f}}}{\hat{U}}, \\ \end{array} \right\} \end{aligned}$$

(2)

$$\begin{aligned}&{\hat{U}}\frac{{\partial {\hat{V}}}}{{\partial r}} + \frac{{{\hat{U}}{\hat{V}}}}{r} + {\hat{W}}\frac{{\partial {\hat{V}}}}{{\partial z}} = {\upsilon _f}\frac{{{\partial ^2}{\hat{V}}}}{{\partial {z^2}}} - \frac{{{\sigma _f}B_0^2}}{{{\rho _f}}}{\hat{V}}, \end{aligned}$$

(3)

$$\begin{aligned}&\left. \begin{array}{l} {\hat{U}}\frac{{\partial {\hat{T}}}}{{\partial r}} + {\hat{W}}\frac{{\partial {\hat{T}}}}{{\partial z}} = \frac{{{k_f}}}{{{{\left( {\rho {c_p}} \right) }_f}}}\frac{{{\partial ^2}{\hat{T}}}}{{\partial {z^2}}} + \Upsilon \left[ {\frac{{{D_{{\hat{T}}}}}}{{{{{\hat{T}}}_\infty }}}{{\left( {\frac{{\partial {\hat{T}}}}{{\partial z}}} \right) }^2} + {D_B}\left( {\frac{{\partial {\hat{T}}}}{{\partial z}}} \right) \left( {\frac{{\partial {\hat{C}}}}{{\partial z}}} \right) } \right] + \frac{{{\sigma _f}B_0^2}}{{{{\left( {\rho {c_p}} \right) }_f}}}\left( {{{{\hat{U}}}^2} + {{{\hat{V}}}^2}} \right) \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \frac{{Q'}}{{{{\left( {\rho {c_p}} \right) }_f}}}({\hat{T}} - {{{\hat{T}}}_\infty }) + \frac{{{\mu _f}}}{{{{\left( {\rho {c_p}} \right) }_f}}}\left[ {{{\left( {\frac{{\partial {\hat{U}}}}{{\partial z}}} \right) }^2} + {{\left( {\frac{{\partial {\hat{V}}}}{{\partial z}}} \right) }^2}} \right] , \\ \end{array} \right\} \end{aligned}$$

(4)

$$\begin{aligned}&{\hat{U}}\frac{{\partial {\hat{C}}}}{{\partial r}} + {\hat{W}}\frac{{\partial {\hat{C}}}}{{\partial z}} = \frac{{{D_{{\hat{T}}}}}}{{{{{\hat{T}}}_\infty }}}\frac{{{\partial ^2}{\hat{T}}}}{{\partial {z^2}}} + {D_B}\frac{{{\partial ^2}{\hat{C}}}}{{\partial {z^2}}} - k_r^2\left( {{\hat{C}} - {{{\hat{C}}}_\infty }} \right) {\left( {\frac{{{\hat{T}}}}{{{{{\hat{T}}}_\infty }}}} \right) ^s}\exp \left[ {\frac{{ - {A_c}}}{{\varepsilon {\hat{T}}}}} \right] . \end{aligned}$$

(5)

In Eqs. (1)–(5), $\left( {{\hat{U}},\,\,{\hat{V}}} \right)$ are the velocities in $\left( {r,\,\,\phi } \right)$ directions, respectively, while the velocity in $z-$ direction is represented by ${\hat{W}}$. Furthermore, ${\upsilon _f},\,\,{\hat{T}},\,\,{\sigma _f},\,\,{\rho _f},\,\,g,\,\,{{\hat{T}}_\infty },\,\,{B_0},\,\,{{\hat{C}}_\infty },$ ${c_p},\,\,{D_B},\,\,{k_r},\,\,{\hat{C}},\,\,{D_{{\hat{T}}}},\,\,{k_f},\,\,s,\,\,{A_c},\,\,\omega ,\,\,Q',\,\,{\mu _f}$ are the kinematic viscosity, temperature, the electrical conductivity, the density, the gravitational acceleration, the ambient temperature, magnetic field strength, the ambient concentration, the heat capacitance, the Brownian diffusion, the chemical reaction strength, concentration, the thermophoresis coefficient, thermal conductivity, the constant of fitted rate, the coefficient of activation energy, the angular velocity, the heat generation/absorption parameter and the dynamic viscosity, respectively. ${\lambda _1},\,\,{\lambda _2}$ are linear and nonlinear heat expansion parameters, ${\lambda _3},\,\,{\lambda _4}$ are linear and nonlinear concentration expansion parameters, $\varepsilon = 8.61 * {10^{ - 5}}eV/K$ is the Boltzmann constant.

In Eq. (4), $\Upsilon = \frac{{{{\left( {\rho {c_p}} \right) }_p}}}{{{{\left( {\rho {c_p}} \right) }_f}}}$ illustrates the ratio of volumetric heat capacity of particles to the volumetric heat capacity of host liquid.

The boundary conditions for the swirling flow above the rotating disk are

$$\begin{aligned} {\hat{U}}&= br + {\gamma _1}\frac{{\partial {\hat{U}}}}{{\partial z}},\,\,{\hat{V}} = \omega r + {\gamma _2}\frac{{\partial {\hat{V}}}}{{\partial z}}, \,\,{\hat{W}} = 0, \nonumber \\ {\hat{T}}&= {{\hat{T}}_w} + {\gamma _3}\frac{{\partial {\hat{T}}}}{{\partial z}},\,\,{\hat{C}} = {{\hat{C}}_{{\hat{W}}}}\,\,\,\,\,at\,\,z = 0, \end{aligned}$$

(6)

$$\begin{aligned}&\quad {\hat{U}} \rightarrow 0,\,\,{\hat{V}} \rightarrow 0,\,\,{\hat{T}} \rightarrow {{\hat{T}}_\infty },\,\,{\hat{C}} \rightarrow {{\hat{C}}_\infty }\,\,\,\,\,\,\,\,\,\,as\,\,\,\,\,z \rightarrow \infty \end{aligned}$$

(7)

In Eq. (6), $\left( {{\gamma _1},\,\,{\gamma _2}} \right)$ represent the slip coefficient for velocity components $\left( {{\hat{U}},\,\,{\hat{V}}} \right)$, respectively, whereas ${\gamma _3}$ is the thermal slip coefficient. Parameter b characterizes the stretching constant.

To transform the PDEs defined in Eqs. (2)–(5) into ODEs, we introduced the following similarity transformation

$$\begin{aligned} \left. {\begin{array}{*{20}{c}} {{\hat{U}} = \omega rf'\left( \xi \right) ,\,\,{\hat{T}} = \left( {{{{\hat{T}}}_{{\hat{W}}}} - {{{\hat{T}}}_\infty }} \right) \theta \left( \xi \right) + {{{\hat{T}}}_\infty },\,\,{\hat{W}} = - 2\omega hf\left( \xi \right) ,} \\ {\xi = \frac{z}{h},\,\,{\hat{V}} = \omega rg\left( \xi \right) ,\,\,\,\,{\hat{C}} = \left( {{{{\hat{C}}}_{{\hat{W}}}} - {{{\hat{C}}}_\infty }} \right) \Phi \left( \xi \right) + {{{\hat{C}}}_\infty }.} \\ \end{array}} \right\} \end{aligned}$$

(8)

Implementing Eq. (8) into Eqs. (2)–(5), we obtained the following set of coupled dimensionless ODEs

$$\begin{aligned}&f''' + {\mathrm{Re}} \left( {2ff'' + {g^2} - {{f'}^2}} \right) - M{\mathrm{Re}} f' + \chi \left( {1 + {B_t}\theta } \right) \theta \nonumber \\&\quad + N\chi \left( {1 + {B_c}\Phi } \right) \Phi , \end{aligned}$$

(9)

$$\begin{aligned}&g'' + {\mathrm{Re}} \left( {2fg' - 2gf'} \right) - M{\mathrm{Re}} g = 0, \end{aligned}$$

(10)

$$\begin{aligned}&\frac{1}{{\Pr }}\theta '' + 2{\mathrm{Re}} f\theta ' + Nt{\theta '^2} + Nb\Phi '\theta ' \nonumber \\&\quad + {\mathrm{Ec}}M\left( {{{f'}^2} + {g^2}} \right) + {\mathrm{Ec}}\left( {{{f''}^2} + {{g'}^2}} \right) + Q\theta = 0, \end{aligned}$$

(11)

$$\begin{aligned}&\Phi '' + \left( {\frac{{Nt}}{{Nb}}} \right) \theta '' + {\mathrm{Sc}}f\Phi ' - {K_c}{\mathrm{Sc}}{\left( {1 + \delta \theta } \right) ^s}\Phi \exp \nonumber \\&\qquad \left( {\frac{{ - A}}{{1 + \delta \theta }}} \right) = 0. \end{aligned}$$

(12)

The dimensionless boundary conditions are

$$\begin{aligned}&f'\left( 0 \right) = B + {l_1}f''\left( 0 \right) ,\,\,f\left( 0 \right) = 0,\,\,g\left( 0 \right) = 1 + {l_2}g'\left( 0 \right) , \nonumber \\&\qquad \theta \left( 0 \right) = 1 + {l_3}\theta '\left( 0 \right) ,\,\,\Phi \left( 0 \right) = 1, \end{aligned}$$

(13)

$$\begin{aligned}&f'\left( \infty \right) \rightarrow 0,\,\,g\left( \infty \right) \rightarrow 0,\,\,\theta \left( \infty \right) \rightarrow 0,\,\,\Phi \left( \infty \right) \rightarrow 0. \end{aligned}$$

(14)

In Eqs. (13) and (14), $\left( {{l_1},\,\,{l_2}} \right)$ are velocity slip parameters, whereas $l_3$ denotes the thermal slip coefficient. B is the stretching constant.

Dimensionless physical parameters appeared in Eqs. (9)–(14) are

$$\begin{aligned} \left. \begin{array}{l} {\mathrm{Re}} = \frac{{\omega {r^2}}}{{{\upsilon _f}}},\,\,M = \frac{{{\sigma _f}}}{{{\rho _f}\omega }}B_0^2,\,\,\,\,\chi = \frac{{g{\lambda _1}}}{{{\omega ^2}r}}\left( {{{{\hat{T}}}_{{\hat{W}}}} - {{{\hat{T}}}_\infty }} \right) ,\,\,\,\,\,\\ N = \left( {\frac{{{\lambda _3}}}{{{\lambda _1}}}} \right) \left( {\frac{{{{{\hat{C}}}_{{\hat{W}}}} - {{{\hat{C}}}_\infty }}}{{{{{\hat{T}}}_{{\hat{W}}}} - {{{\hat{T}}}_\infty }}}} \right) ,\,\,\,\,{\mathrm{Sc}} = \frac{{{\upsilon _f}}}{{{D_B}}}, \\ A = \frac{{{A_c}}}{{\varepsilon {{{\hat{T}}}_\infty }}},\,\,Nt = \frac{{{D_{{\hat{T}}}}\Upsilon }}{{{\upsilon _f}}}\frac{{\left( {{{{\hat{T}}}_{{\hat{W}}}} - {{{\hat{T}}}_\infty }} \right) }}{{{{{\hat{T}}}_\infty }}},\,\,{\mathrm{Ec}} = \frac{{{r^2}{\omega ^2}}}{{{c_p}\left( {{{{\hat{T}}}_{{\hat{W}}}} - {{{\hat{T}}}_\infty }} \right) }},\,\, \\ Nb = \frac{{{D_B}\Upsilon }}{{{\upsilon _f}}}\left( {{{{\hat{C}}}_{{\hat{W}}}} - {{{\hat{C}}}_\infty }} \right) ,\,\,{l_3} = \frac{{{\gamma _3}}}{h} \\ B = \frac{b}{\omega },\,\,Q = \frac{{Q'}}{{{{\left( {\rho {c_p}} \right) }_f}\omega }},\,\,\,\,\,\delta = \frac{{\left( {{{{\hat{T}}}_{{\hat{W}}}} - {{{\hat{T}}}_\infty }} \right) }}{{{{{\hat{T}}}_\infty }}},\,\,\,\,\, \\ {B_t} = \left( {\frac{{{\lambda _2}}}{{{\lambda _1}}}} \right) \left( {{{{\hat{T}}}_{{\hat{W}}}} - {{{\hat{T}}}_\infty }} \right) ,\,\,{l_1} = \frac{{{\gamma _1}}}{h},\,\,\,\,\,{l_2} = \frac{{{\gamma _2}}}{h}, \\ {B_c} = \left( {\frac{{{\lambda _4}}}{{{\lambda _3}}}} \right) \left( {{{{\hat{C}}}_{{\hat{W}}}} - {{{\hat{C}}}_\infty }} \right) ,\,\,\,\,\,\,{K_c} = \frac{{k_r^2}}{\omega }\,\,\,\,\,\,\,\,\Pr = \frac{{{\upsilon _f}{{\left( {\rho {c_p}} \right) }_f}}}{{{k_f}}}. \\ \end{array} \right\} \end{aligned}$$

(15)

Here, Re is the Reynolds number, M is magnetic parameter, $\chi$ is mixed convection variable, $B_t$ is nonlinear convection parameters due to temperature, Pr is the Prandtl number, Nt is thermophoretic parameter, Q is heat generation/absorption parameter, Ec is the Eckert number, Sc is the Schmidt number, B is the ratio between the stretching parameter and angular velocity, Nb is Brownian motion parameter, Kc is chemical reaction parameter, $\delta$ is temperature ratio parameter, $B_c$ is nonlinear convection parameters due to concentration, A is activation energy parameter, N is ratio of concentration to temperature buoyancy force.

3 Quantity of physical interest

Skin friction coefficient $\left( {{\mathrm{{C}}_f}} \right)$ is an important physical quantity, and it is measured at the surface of disk. Other significant quantities such as heat transference rate $\left( {N{u_x}} \right)$ as well as mass transference rate $\left( {S{h_x}} \right)$ are also calculated at the disk surface as

$$\begin{aligned} {C_f}&= \frac{{{\tau _w}}}{{{\rho _f}{{\left( {r\omega } \right) }^2}}} \end{aligned}$$

(16)

$$\begin{aligned} {\mathrm{Nu}}&= {\left. {\frac{{{\Upsilon _w}h}}{{{k_f}\left( {{{{\hat{T}}}_w} - {{{\hat{T}}}_\infty }} \right) }}} \right| _{z = 0}} \end{aligned}$$

(17)

$$\begin{aligned} {\mathrm{Sh}}&= {\left. {\frac{{h{\Upsilon _m}}}{{{D_B}\left( {{{{\hat{C}}}_w} - {{{\hat{C}}}_\infty }} \right) }}} \right| _{z = 0}} \end{aligned}$$

(18)

Substituting Eqs. (8) into (16) to (18), we get the above physical dimensionless quantities

$$\begin{aligned} {C_f}&= \frac{1}{{{\mathrm{Re}} }}\sqrt{{{\left( {f''\left( 0 \right) } \right) }^2} + {{\left( {g'\left( 0 \right) } \right) }^2}} \end{aligned}$$

(19)

$$\begin{aligned} {\mathrm{Nu}}&= - \left( {{{{\mathrm{Re}} }^{0.5}}} \right) \theta '\left( 0 \right) \end{aligned}$$

(20)

$$\begin{aligned} {\mathrm{Sh}}&= - \left( {{{{\mathrm{Re}} }^{0.5}}} \right) \Phi '\left( 0 \right) \end{aligned}$$

(21)

Here, ${\tau _w} = {\left. {\left( {\sqrt{\tau _{zr}^2 + \tau _{z\theta }^2} } \right) } \right| _{z = 0}},$ $\,\,{\Upsilon _w} = - {k_f}{\left. {\frac{{\partial {\hat{T}}}}{{\partial z}}} \right| _{z = 0}},\,\,{\mathrm{Re}} = \left( {\frac{h}{{{\upsilon _f}}}} \right) \left( {\omega r} \right) ,\,\,{\Upsilon _m} = - {D_B}{\left. {\frac{{\partial {\hat{C}}}}{{\partial z}}} \right| _{z = 0}}$ are shear, heat flux, Reynolds number and mass flux, respectively.

4 Analysis of entropy generation

According to the results presented by Bejan [47], for the nanofluid flow, the volumetric entropy generation rate influenced by the heat and mass transference, fluid friction, etc., is given in the mathematical form as

$$ \left. {\begin{array}{*{20}c} {\Omega ^{\prime}_{{{\text{gen}}}} = \underbrace {{\frac{{k_{f} }}{{\hat{T}_{\infty }^{2} }}\left( {\frac{{\partial ^{2} \hat{T}}}{{\partial z^{2} }}} \right)^{2} }}_{{\begin{array}{*{20}c} {Thermal} \\ {{\text{irreversibility}}} \\ \end{array} }} + \underbrace {{\frac{{\mu _{f} }}{{\hat{T}_{\infty } }}\left\{ {\left( {\frac{{\partial \hat{U}}}{{\partial z}}} \right)^{2} + \left( {\frac{{\partial \hat{V}}}{{\partial z}}} \right)^{2} } \right\}}}_{{\begin{array}{*{20}c} {Fluid\;Friction} \\ {{\text{irreversibility}}} \\ \end{array} }} + \underbrace {{\frac{{\sigma _{f} \left( {\hat{U}^{2} + \hat{V}^{2} } \right)}}{{\hat{T}_{\infty } }}}}_{{\begin{array}{*{20}c} {Joule{\text{ }}dissipation} \\ {{\text{irreversibility}}} \\ \end{array} }}B_{0}^{2} } \\ {\underbrace {{\frac{{RD}}{{\hat{T}_{\infty } }}\left( {\frac{{\partial \hat{T}}}{{\partial z}}} \right)\left( {\frac{{\partial \hat{C}}}{{\partial z}}} \right) + \frac{{RD}}{{\hat{C}_{\infty } }}\left( {\frac{{\partial \hat{C}}}{{\partial z}}} \right)^{2} }}_{{\begin{array}{*{20}c} {Diffusive} \\ {{\text{irreversibility}}} \\ \end{array} }}.} \\ \end{array} } \right\} $$

(22)

In the right hand side of the above equation, the first term is contributed owing to the energy transference across the boundary layer in the entropy production, 2nd term represents the entropy production owing to viscous dissipation or liquid friction irreversibility, 3rd term is contributed owing to the Joule dissipation in the entropy production and last term is added in the entropy production equation owing to the diffusive irreversibility.

After implementing the similarity variable introduced in Eq. (8), the entropy production Eq. (22) is metamorphosed in the following non-dimensional form as

$$\begin{aligned} Ng&= {\alpha _a}{\theta '^2} + {\mathrm{Br}}M\left( {{{f'}^2} + {g^2}} \right) + {\mathrm{Br}}\left( {{{f''}^2} + {{g'}^2}} \right) + L\phi '\theta ' \nonumber \\&\quad + L\left( {\frac{{{\alpha _b}}}{{{\alpha _{a.}}}}} \right) . \end{aligned}$$

(23)

Here, $L\left( { = \frac{{RD}}{{{k_f}}}\left( {{\hat{C}} - {{{\hat{C}}}_\infty }} \right) } \right)$ denotes the diffusive variable, $Br\left( { = {\mu _f}\frac{{{r^2}{\omega ^2}}}{{{k_f}}}} \right)$ represents the Brinkman parameter, ${\alpha _b}\left( { = \frac{{\left( {{{{\hat{C}}}_{{\hat{W}}}} - {{{\hat{C}}}_\infty }} \right) }}{{{C_\infty }}}} \right)$ indicates the concentration difference parameter, ${\alpha _a}\left( { = \frac{{\left( {{{{\hat{T}}}_{{\hat{W}}}} - {{{\hat{T}}}_\infty }} \right) }}{{{C_\infty }}}} \right)$ is the temperature difference parameter, $Ng\left( { = \frac{{{{\Omega '}_{gen}}{{{\hat{T}}}_\infty }}}{{{k_f}\left( {{\hat{T}} - {{{\hat{T}}}_\infty }} \right) }}} \right)$ represents the entropy generation rate.

The mathematical expression for Bejan number Be (irreversibility distribution ratio) [36] in the non-dimensional form is as follows

$$\begin{aligned} {\mathrm{Be}} = \frac{{{\alpha _a}{{\theta '}^2} + L\Phi '\theta ' + L\left( {\frac{{{\alpha _b}}}{{{\alpha _a}}}} \right) }}{{{\alpha _a}{{\theta '}^2} + {\mathrm{Br}}M\left( {{{f'}^2} + {g^2}} \right) + {\mathrm{Br}}\left( {{{f''}^2} + {{g'}^2}} \right) + L\Phi '\theta ' + L\left( {\frac{{{\alpha _b}}}{{{\alpha _a}}}} \right) }} \end{aligned}$$

(24)

It is clear from the above expression that Bejan number is the ratio of irreversibility distribution [48] and therefore, it helps us to understand the irreversibility distribution caused by the energy transport and liquid friction, etc., Bejan number varies from 0 to 1.

5 Solution methodology

To get the numerical solution of the set of coupled ODEs (9) to (12) which are highly nonlinear with the corresponding boundary conditions (13) and (14), the bvp4c technique [49, 50] is employed. This technique is developed on a relaxation technique that makes employing the polynomial interpolation on a systematically defined mesh. Also, the bvp4c technique has an accuracy of fourth-order. In this method, the computational solutions are attained by transforming the boundary value problem into the set of ordinary differential equations (ODEs) of first order. To do this, we introduced the following variables

$$\begin{aligned} \left. \begin{array}{l} {g_1} = f,\,\,\,{g_2} = f',\,\,\,{g_3} = f'',\,\,\,{g^ * }{g_1} = f''',\,\,\,{g_4} = g, \\ {g_5} = g',\,\,\,{g^ * }{g_2} = g'', \\ {g_6} = \theta ,\,\,\,{g_7} = \theta ',\,\,\,{g^ * }{g_3} = \theta '',\,\,\,{g_8} = \Phi , \\ {g_9} = \Phi ',\,\,\,{g^ * }{g_4} = \Phi ''. \\ \end{array} \right\} \end{aligned}$$

(25)

By incorporating the above-mentioned substitutions in Eqs. (9)–(12) along with the boundary conditions (13) and (14), one has

$$\begin{aligned} {g^ * }{g_1}&= {\mathrm{Re}} \left( {g_2^2 - 2{g_1}{g_3} - g_4^2} \right) + M{\mathrm{Re}} {g_2} \nonumber \\&\quad - \chi \left( {1 + {B_t}{g_6}} \right) {g_6} - N\chi \left( {1 + {B_c}{g_8}} \right) {g_8}, \end{aligned}$$

(26)

$$\begin{aligned} {g^ * }{g_2}&= {\mathrm{Re}} \left( {2{g_2}{g_4} - 2{g_1}{g_5}} \right) + M{\mathrm{Re}} {g_4}, \end{aligned}$$

(27)

$$\begin{aligned} {g^ * }{g_3}&= - \Pr \left[ {2{\mathrm{Re}} {g_1}{g_7} + Ntg_7^2 + Nb{g_9}{g_7} + MEc\left( {g_2^2 + g_4^2} \right) + Ec\left( {g_{_3}^2 + g_5^2} \right) + Q{g_6}} \right] , \end{aligned}$$

(28)

$$\begin{aligned} {g^ * }{g_4}&= - \left( {\frac{{Nt}}{{Nb}}} \right) {g^ * }{g_3} - Sc{g_1}{g_9} + {K_c}Sc{\left( {1 + \delta {g_6}} \right) ^s}{g_8} \nonumber \\&\qquad \exp \left( {\frac{{ - A}}{{1 + \delta {g_8}}}} \right) . \end{aligned}$$

(29)

Based on the above efforts, to do the computations feasible, a range of similarity variable is studied. Throughout the numerical computations for $\xi = 10;$ the entropy generation, velocities, thermal, Bejan number and concentration distributions are converging to their corresponding magnitudes in free stream area. Moreover, the selection of mesh and error control are based on the residual of the continuous solution. In this present study, the tolerance of relative error is set as 10⁻⁶. The suitable mesh determination is formed and returned in the field sol.x. Though, solution values can be fetched from the array called sol.y, corresponding to the field sol.x.

6 Validation of results

In order to verify the accuracy of the numerical method used in this paper, a comparison between our results and a previously published research paper is presented in Table 1. It presents the values of Nusselt number $\theta '\left( 0 \right)$ obtained by present model and that of Hayat et al. [51] for different values of magnetic parameter M. The values of the parameters involved in the governing equations are adjusted accordingly. As evident from the table, a very good agreement is perceived between the numerical values of physical entity obtained by Hayat et al. [51] and by us.

Table 1 Comparison of the numerical values of Nusselt number with Hayat et al. [51]

7 Results and discussion

In this segment, the influence of various significant flow characteristics on velocities, i.e., radial $f'\left( \xi \right)$ and axial $f\left( \xi \right)$ , temperature distributions $\theta \left( \xi \right)$ , concentration distributions $\Phi \left( \xi \right)$, Bejan number Be and entropy production $Ng\left( \xi \right)$ are discussed and presented graphically in Figs. 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32 together with Tables 2, 3 and 4 to analyze the quantities of physical interest.

7.1 Velocity profiles

The effect of stretching parameter B, magnetic parameter M, nonlinear convection parameter due to temperature $B_t$, velocity slip parameters $\left( {{l_1}\,\,{l_2}} \right)$, mixed convection characteristic $\chi$ and ratio of concentration to temperature buoyancy force N on velocities (axial and radial) are represented in Figs. 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13. The relationship between the fluid velocities (axial, radial) and the stretching parameter is established in Figs. 2 and 3, respectively. Both the velocities, i.e., $f\left( \xi \right)$ and $f'\left( \xi \right)$ increase for high stretching parameters B. Since a growth of stretching characteristic results in an increment in the stretching rate, as a result, additional disturbance is added in the fluid, which will ultimately increase axial $f\left( \xi \right)$ as well as radial $f'\left( \xi \right)$ velocities. As observed from Figs. 4 and 5, both the velocities are decreased for larger estimation of velocity slip parameters $\left( {{l_1}\,\,{l_2}} \right)$. Physically, this happening can be justified with the fact that disk which is rotating with fixed angular velocity exerts a centrifugal force on the layers of the fluid neighboring to the disk surface, consequently, liquid particles are being thrown away from the disk. As slip mechanism rises, less and less liquid particles move out from the surface and as a result, very small circumferential momentum of the disk is transported to the fluid, therefore, there is very small fluid movement in the axial and radial directions. The effect of $B_t$ on axial $f\left( \xi \right)$ and radial $f'\left( \xi \right)$ velocities is presented in Figs. 6 and 7. These fluid velocity profiles are accelerated for larger estimation of $B_t$. Since high magnitudes of $B_t$ result in a diminution of the viscous force which provides less resistance within the particles of the fluid and the velocity profiles are enlarged. The effect of magnetic parameter M on velocities, i.e., $f\left( \xi \right)$ and $f'\left( \xi \right)$, is presented in Figs. 8 and 9, respectively. As found from these figures, M has tendency to decline both the velocity profiles, i.e., axial as well as radial velocities. This nature of the fluid velocities is in agreement with the fact that the presence of the magnetic influence encourages a hindering body force that opposes the motion of the fluid. Consequently, a reduction in both the velocities is detected. The effect of parameter N, i.e., the ratio of concentration to temperature buoyancy force on the velocities of the fluid (axial and radial) is illustrated in Figs. 10 and 11, respectively. It is obtained that axial and radial velocities are increasing functions of N, i.e., both are increasing for larger values of N. The impact of $\chi$ on $f\left( \xi \right)$ and $f'\left( \xi \right)$ is depicted in Figs. 12 and 13. Both velocities have an increasing behavior, i.e., for larger estimation of $\chi$, $f\left( \xi \right)$ and $f'\left( \xi \right)$ increase since buoyancy force increases.

Fig. 2

Graph of $f(\xi )$ against B

Fig. 3

Graph of $f'(\xi )$ against B

Fig. 4

Graph of $f(\xi )$ against $l_1, l_2$

Fig. 5

Graph of $f'(\xi )$ against $l_1, l_2$

Fig. 6

Graph of $f(\xi )$ against $B_t$

Fig. 7

Graph of $f'(\xi )$ against $B_t$

Fig. 8

Graph of $f(\xi )$ against M

Fig. 9

Graph of $f'(\xi )$ against M

Fig. 10

Graph of $f(\xi )$ against N

Fig. 11

Graph of $f'(\xi )$ against N

Fig. 12

Graph of $f(\xi )$ against $\chi$

Fig. 13

Graph of $f'(\xi )$ against $\chi$

7.2 Temperature profiles

To understand the changes in the nature of fluid temperature against the variations in magnetic parameter M, thermophoretic characteristic Nt, thermal generation/absorption characteristic Q, Eckert number Ec, Brownian motion characteristic Nb and thermal slip parameter $l_3$, the influences of these parameters are presented in Figs. 14, 15, 16, 17, 18, 19, 20. Figure 14 represents the change in the temperature profile against Eckert number Ec. It is found that temperature rises with a growth in Ec. Since this non-dimensional number signifies the ratio of moving energy of the fluid particles (kinetic energy) to enthalpy, the increase in Ec ultimately rise $\theta \left( \xi \right)$. The behavior of liquid temperature against M is demonstrated in Fig. 15. It is noted from this Figure that there is an elevation in temperature of fluid when there is a rise in the intensity of the magnetic field. Since existence of magnetic field encourages an obstructing body force which is acting in the opposite direction of the liquid circulation. This, in turn, produces energy owing to which temperature of the fluid is growing. The nature of liquid temperature against Nt and Nb is demonstrated in Figs. 16 and 17, respectively. There is a rise in $\theta \left( \xi \right)$ when there is an increment in both the parameters, i.e., Nt and Nb. It is noted from Fig. 16 that $\theta \left( \xi \right)$ is getting increased with increasing Nt. Tiny solid particles diffuse due to temperature difference and this occurrence is generally referred to thermophoresis. A rise in this non-dimensional parameter influences the movement of nano-particles, and therefore on the warmer region, the momentum of nana-particles increases. Due to increase in the momentum, the kinetic energy of these nano particles moves in the direction of cooler region, and as a result, region becomes heated up rapidly and $\theta \left( \xi \right)$ improves. Likewise, in Fig. 17, $\theta \left( \xi \right)$ increases for larger Nb. Since Brownian motion signifies the random circulation of nano particles which are dispersed uniformly in the base fluid. Due to the increment in Nb, random motion of nano particles has larger intensity, which leads to a rise in the kinetic energy of these particles and consequently, fluid temperature increases. The change in the nature of fluid temperature $\theta \left( \xi \right)$ against Q is revealed in Figs. 18 and 19, respectively. There is a rise in $\theta \left( \xi \right)$ for positive values of $(Q > 0)$ (see Fig. 18), since an additional energy is produced in the area for larger magnitudes of Q, while temperature profile is reduced for $(Q < 0)$ (see Fig. 19). The relation between the fluid temperature and thermal slip parameter is established in Fig. 20. The increment in thermal slip parameter decreases the temperature of the fluid. Temperature follows such behavior because a rise of $l_3$ results to reduce the rate of heat transference from the disk to the neighboring layers of the fluid, consequently decreases the temperature of the fluid.

Fig. 14

Graph of $\theta (\xi )$ against Ec

Fig. 15

Graph of $\theta (\xi )$ against M

Fig. 16

Graph of $\theta (\xi )$ against Nt

Fig. 17

Graph of $\theta (\xi )$ against Nb

Fig. 18

Graph of $\theta (\xi )$ against $(Q>0)$

Fig. 19

Graph of $\theta (\xi )$ against $(Q<0)$

Fig. 20

Graph of $\theta (\xi )$ against $l_3$

7.3 Concentration profiles

The exploration of various parameters, such as activation energy parameter, Brownian motion characteristic, chemical reaction characteristic, thermophoresis characteristic, Schmidt number and nonlinear convection parameters due to concentration on concentration profile $\Phi \left( \xi \right)$, which can be seen in Figs. 21, 22, 23, 24, 25, 26. Figure 21 is drawn to illustrate the behavior of concentration profile for varied activation energy parameter A. In this Figure, it is witnessed that $\Phi \left( \xi \right)$ is raised due to a growth of A. Physically, this is justified, since increment in activation energy parameter A leads to a reduction in modified Arrhenius function $\left( {{{\left( {\frac{{{\hat{T}}}}{{{{{\hat{T}}}_\infty }}}} \right) }^s}\exp \left[ {\frac{{ - {A_c}}}{{\varepsilon {\hat{T}}}}} \right] } \right)$, which ultimately encourages the chemical reaction. Figure 22 shows how the chemical reaction parameter $K_c$ affects the concentration profile $\Phi \left( \xi \right)$. It can be noted that increase in $K_c$ decreases the concentration profile. Physically, the reaction rate within the species is improved for higher estimation of chemical reaction characteristic, consequently, concentration declines. The changes in concentration distribution against the parameters Nt and Nb are plotted in Figs. 23 and 24, respectively. There is a rise in $\Phi \left( \xi \right)$ when there is an increment in Nt. On the contrary, the liquid concentration is decreasing with increasing Nb (see Fig. 24). The effect of Sc on $\Phi \left( \xi \right)$ is highlighted in Fig. 25. It is found that $\Phi \left( \xi \right)$ is reducing with increasing Schmidt number Sc. An enhancement in this non-dimensional parameter Sc leads to a reduction in the diffusivity of mass. Figure 26 shows how the nonlinear convection parameter due to concentration $B_c$ affects the concentration profile $\Phi \left( \xi \right)$. It is noted from this figure that enhancing in $B_c$, concentration profile.

Fig. 21

Graph of $\Phi (\xi )$ against A

Fig. 22

Graph of $\Phi (\xi )$ against $K_c$

Fig. 23

Graph of $\Phi (\xi )$ against Nt

Fig. 24

Graph of $\Phi (\xi )$ against Nb

Fig. 25

Graph of $\Phi (\xi )$ against Sc

Fig. 26

Graph of $\Phi (\xi )$ against $B_c$

7.4 Entropy Production and Bejan number

To understand the changes in the nature of entropy production $Ng\left( \xi \right)$ and Bejan number Be against the variations in Brinkman parameter Br, magnetic characteristic M, velocity slip parameters $\left( {{l_1},\,\,{l_2}} \right)$, temperature and concentration ratio parameter $\left( {{\alpha _a},\,\,{\alpha _b}} \right)$ and diffusive variable L are studied in Figs. 27, 28, 29, 30, 31, 32. The nature of $Ng\left( \xi \right)$ and Be against the parameters $\alpha _a$ is demonstrated in Figs. 27. There is a rise in $Ng\left( \xi \right)$ when there is a growth in $\alpha _a$. Due to larger values of $\alpha _a$, an additional disturbance is created within the nano particles, as a result, more disorderedness will be there in the system, which increases the entropy generation $Ng\left( \xi \right)$. Likewise, Be increases for higher estimation of $\alpha _a$. Along with the increase in $\alpha _a$, the effect of heat transference is more significant than viscous effects and hence, Be boosts. Figure 28 is drawn to illustrate the change in $Ng\left( \xi \right)$ and Be for varied $\alpha _b$. It is witnessed that $Ng\left( \xi \right)$ as well as Be are increased due to increasing $\alpha _b$. Figure 29 is drawn to see the change in the nature of $Ng\left( \xi \right)$ and Be for varied Br. Here, $Ng\left( \xi \right)$ is found to be improving for larger Br. Physically, this behavior of $Ng\left( \xi \right)$ valid, because Br is ratio of heat release by viscous warming to energy transference by molecular conduction. Therefore, for higher estimation of Br, additional energy is produced in the region which leads to a growth of the disorderedness of the whole system, and as a result, $Ng\left( \xi \right)$ is getting enhanced for higher Br. While Be reduces for higher estimation of Br. Owing to increment in Br, viscous effects are dominating over heat transference effects, and therefore, Bejan number is declining. An impact of L on $Ng\left( \xi \right)$ and Be is displayed in Fig. 30. $Ng\left( \xi \right)$ as well as Be are increasing function for diffusion parameter L. Diffusivity in the liquid particles is improved for high L, which results in an enhancement in the disorderedness within the entire system that causes $Ng\left( \xi \right)$ to be enlarged. Moreover, Variation in Be for enhancing L is demonstrated in Fig. 30 and it increases for higher L. For varied values of magnetic parameter, the change in $Ng\left( \xi \right)$ and Be is illustrated in Fig. 31. It is noted that $Ng\left( \xi \right)$ is found to be improving for larger value of this parameter. Physically, for larger M, additional resistance is produced within the system as a result $Ng\left( \xi \right)$ is improving. On the other hand, Be is declining since the dominance of viscous effect over heat and mass transference for larger estimation of this parameter. Figure 32 is drawn to see the change in the nature of $Ng\left( \xi \right)$ and Be for varied values of the velocity slip parameter $\left( {{l_1},\,{l_2}} \right)$. In this Figure, $Ng\left( \xi \right)$ and Be have opposite nature, i.e., $Ng\left( \xi \right)$ is reducing while Be is improving for larger values of $\left( {{l_1},\,{l_2}} \right)$.

Fig. 27

Graph of Ng, Be against $\alpha _a$

Fig. 28

Graph of Ng, Be against $\alpha _b$

Fig. 29

Graph of Ng, Be against Br

Fig. 30

Graph of Ng, Be against L

Fig. 31

Graph of Ng, Be against M

Fig. 32

Graph of Ng, Be against $l_1, l_2$

7.5 Quantities of physical interest

The numerical computations for velocity $f\left( \infty \right)$, tangential and radial wall stresses $\left( {\mathrm{{g'}}\left( 0 \right) ,\,\,\mathrm{{f''}}\left( 0 \right) } \right)$, respectively, under the influence of the parameters $M, B_t, B_c$ and $\left( {{l_1},\,{l_2}} \right)$ have been studied and are presented in Table 2. As per the observation from Table 2, it is noted that the skin friction parameter increases with the increase in the nonlinear convection parameter due to temperature $B_t$, magnetic parameter and nonlinear convection parameter due to concentration $B_c$, while totally reverse trend is observed for the velocity slip parameters $\left( {{l_1},\,{l_2}}\right)$, i.e., comparatively smaller skin fraction parameter is found for high $\left( {{l_1},\,{l_2}}\right)$. Table 3 shows the change in the rate of heat transference against the various significant parameters. It is witnessed that an augmentation in either of energy generation/absorption characteristic, Eckert number and magnetic parameter uplift the magnitude of rate of heat transference, while it is reduced for larger estimation for thermal slip parameter $l_3$. Table 4 is prepared to see the behavior of the rate of mass transference for chemical reaction, activation energy, Brownian and thermophoresis parameters. From this table, it is noted that mass transference rate is reduced with the growth in activation energy parameter, while it increases for chemical reaction, Brownian and thermophoresis parameters.

Table 2 Computations for skin friction parameter at various coefficients

Table 3 Numerical computation for Nusselt number $\theta '\left( 0 \right)$ at various parameters

Table 4 Computation for Sherwood number $\Phi '\left( 0 \right)$ at various parameters

8 Conclusions

In this work, we aimed to study the MHD flow of nanoliquid over a rough disk that is rotating with fixed angular velocity, under the consideration of nonlinear mixed convection, activation energy and partial slip effects. Noteworthy conclusions based on the results achieved are summarized as:

• Axial as well as radial velocities are accelerating for stretching parameter, nonlinear convection parameters due to temperature and mixed convection variable, whereas an increment in the magnetic and slip parameters decelerates these fluid velocities.

• The fluid temperature decreases with the improvement in the thermal slip characteristic and heat absorption characteristic, while it increases with increasing heat generation parameter, Eckert number, thermophoresis and magnetic coefficients.

• Concentration profile gets weakened with rising chemical reaction coefficient, Brownian diffusion parameter, and nonlinear convection parameters, while it increases with increasing value of activation energy parameter.

• Increase in temperature and concentration difference coefficients, magnetic coefficient, diffusion parameter and Brinkman parameter lead to an enhancement in entropy generation.

• Skin friction parameter increases with increasing magnetic coefficient, while decreases with on increasing velocity slip parameters.

• A reduction in the strength of energy transference is observed when thermal slip coefficient is improved. Strengthening the activation energy parameter leads to a decline in the rate of mass transference.