Non-linear heat and mass transfer in a thermal radiated MHD flow of a power-law nanofluid over a rotating disk

Abstract

The steady MHD flow of a power law nanofluid due to a uniform rotation of an infinite disk is studied with heat and mass transfer. The viscous dissipation has been comprised in the energy equation. The governing PDEs are reduced to a set of ODEs; using the generalized Von Karman similarity transformations; for which finite difference numerical scheme is implemented along with the associated boundary conditions. The non-Newtonian fluid characteristics affect the fluid velocity, temperature and concentration of suspended nanoparticles. The significant effects of thermal radiation, Brownian motion and thermophoresis diffusion are involved. The skin friction coefficients in addition to the heat and mass transfer rates are defined and calculated considering the variation of all flow parameters. The present results are verified and compared with literature.

1 Introduction

Rotating disk flows are of both theoretical and practical value. The boundary layer induced by a rotating disk is of great scientific importance owing to its relevance to applications in many areas such as rotating machinery, computer storage devices, viscometry, turbo-machinery, lubrication, oceanography, crystal growth processes, and chemical vapor deposition reactor [1]. The problem of the motion of a fluid due to the rotation of an infinitely extended disk was firstly illustrated by von Karman [2], who introduced a set of generalized similarity transformations to reduce the governing PDEs to ODEs.

Many authors studied the heat transfer behavior from a rotating disk in different ways [3,4,5]. Batista [6] succeeded in finding a closed form for the velocity components regarding the fluid flow between two uniformly co-rotating disks. Also, explicit solutions have been presented for generalized non-Newtonian fluids at different conditions with both mechanical and biological applications [7,8,9]. The flow of non-Newtonian power-law fluids considering the influence of a magnetic field has been studied [10,11,12] using the extensions of Karman analysis which discussed in [13, 14]. MHD flows regarding power-law fluids over a rotating disk are of great impact because of the absence of the magnetic force field outside the viscous boundary layer, which means that the fluid flow only affected inside the boundary layer. Applying an external uniform magnetic field on a power-law fluid flow over a rotating disk was proved to serve in the process of flow control [15,16,17].

The steady flow of a nanofluid due to a rotating disk was studied by Bachok et al. [18]. The thermal radiation effect on the motion of an electrically conducting fluid over an infinite rotating porous disk was studied with heat and mass transfer [19]. Ming et al. [20] gave extreme illustrations to the steady flow and heat transfer of an incompressible viscous fluid of a power-law type over a rotating infinite disk. They assumed that the thermal conductivity obeys the same nonlinear formula as the definition of the viscosity function. Osalusi [21] provided a continuum of the fluid motion over a rotating disk considering the Reiner–Rivlin model. Andersson et al. [22] demonstrated the characteristics of the power-law fluid flow over a rotating disk by introducing the boundary layer approximations and extending the power-law index in the range of (1.5, 2). Later, Andersson and de Korte [15] expanded their research work to account for the MHD flow; they obtained asymptotic solutions and solved numerically for magnetic parameter values up to 4.0. They concluded that imposing the magnetic field is more effective for shear-thinning than for shear-thickening fluids where a distinctive behavior has been obtained compared with the non-magnetic case.

Nanofluids provide an important class of fluids because of their enormous energetic applications. This kind of fluids composes of a base liquid with suspended nanoparticles. The fluid thermal conductivity is enhanced because of the addition of small amount of nanoparticles according to the experimental verification made by Choi [23]. Buongiorno [24] worked out his famous mathematical model that addresses the flow of nanofluids along with the incorporation of both the Brownian motion and thermophoretic diffusion of nanoparticles. Nanofluids aroused a great interest because of enhancing the thermal conductivity of the base fluid which is necessary for several applications; especially in nuclear reactors [25,26,27].

Bachok et al. [18] interpreted the nanofluid flow and heat transfer characteristics because of the rotation of an infinitely extended porous disk. The steady magnetohydrodynamic flow of a nanofluid due to a rotating porous disk has been richly discussed considering the entropy generation phenomenon [28]. This simulation proved the high impact of using a magnetic rotating disk in novel nuclear space propulsion engines in addition to its several applications in heat transfer enhancement. Turkyilmazoglu [29] illustrated the flow and heat transfer of many water-based nanofluids over a rotating disk. The phenomenon of nanoparticles precipitation; accompanying to the arising motion of power-law nanofluids due to a rotating disk has been studied numerically using the Homotopy analysis method (HAM) [30]. The obtained solutions agreed with the experimental results; which reflects the importance of such mathematical formulations. Mustafa et al. [31] proposed a numerical study of a two-phase Bödewadt nanofluid flow with heat transfer over a stationary stretching disk. Later, many authors [32,33,34,35] have presented extensive research work regarding the flow of nanofluids between two rotating disks under different physical assumptions. The usage of such nanofluids enhancing the heat transfer performance and leads to many updatable energetic applications [36].

The present work ventilates the effectiveness of thermal radiation on the nonlinear heat and mass transfer across a steady MHD flow of a power-law nanofluid over a rotating disk; as a continuation of the problems discussed previously in [15, 22]. The governing nonlinear PDEs of fluid flow, temperature and nanoparticles concentration in the prescribed boundary layer are solved numerically using finite differences. The effects of characteristics of non-Newtonian power-law fluid have been accentuated and a full parametric study has been conducted.

2 Physical model and governing equations

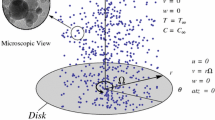
This problem considers the arising steady motion of a fluid due to the rotating behavior of an insulated infinite disk about the z-axis with angular velocity ω. The cylindrical polar coordinates (r, φ, z) are used in modeling this phenomenon as presented in Fig. 1. The disk has been positioned in the plane z = 0. The utilized non-Newtonian power law nanofluid occupies the space z > 0. The pressure gradient in the z-direction vanishes (∂p/∂z = 0) according to the boundary layer derivation represented by Andersson and de Korte [15]. In addition, the similarity transformations of Karman implied (∂p/∂r = 0), which provides a constant pressure inside the boundary layer. The disk is maintained at a constant temperature T_w, while, the fluid out of the boundary layer is kept at a uniform ambient temperature T_∞. The concentration of the nanoparticles at the disk is set to a constant value C_w differs from that far from the disk C_∞. This physical geometry can be found in many realistic situations such as rotating and turbo-machinery.

Fig. 1

Rotating disk flow configuration

The governing PDEs of continuity, momentum, energy and concentration are given; respectively, as follows:

$$\frac{\partial u}{\partial r} + \frac{u}{r} + \frac{\partial w}{\partial z} = 0$$

(1)

$$\rho \left( {u\frac{\partial u}{\partial r} + w\frac{\partial u}{\partial z} - \frac{{v^{2} }}{r}} \right) = - \frac{\partial p}{\partial r} + \frac{\partial }{\partial z}\left( {\mu \frac{\partial u}{\partial z}} \right) - \sigma B_{o}^{2} \,u$$

(2)

$$\rho \left( {u\frac{\partial v}{\partial r} + w\frac{\partial v}{\partial z} + \frac{uv}{r}} \right) = \frac{\partial }{\partial z}\left( {\mu \frac{\partial v}{\partial z}} \right) - \sigma B_{o}^{2} \,v$$

(3)

$$\begin{aligned} & u\frac{\partial T}{\partial r} + w\frac{\partial T}{\partial z} = \frac{k}{\rho c}\frac{{\partial^{2} T}}{{\partial z^{2} }} + \frac{\mu }{\rho c}\left[ {\left( {\frac{\partial u}{\partial z}} \right)^{2} + \left( {\frac{\partial v}{\partial z}} \right)^{2} } \right] \\ & \quad + \,R\,\left[ {\frac{{D_{t} }}{{T_{w} }}\,\left( {\frac{\partial T}{\partial z}} \right)^{2} + D_{B} \,\left( {\frac{\partial T}{\partial z}\frac{\partial C}{\partial z}} \right)} \right] + \frac{{\sigma B_{o}^{2} }}{\rho c}\,(u^{2} + v^{2} ) - \frac{1}{\rho c}\,\frac{{\partial q_{r} }}{\partial z} \\ \end{aligned}$$

(4)

$$u\frac{\partial C}{\partial r} + w\frac{\partial C}{\partial z} = D_{B} \left( {\frac{{\partial^{2} C}}{{\partial z^{2} }}} \right) + \frac{{D_{t} }}{{T_{w} }}\left( {\frac{{\partial^{2} T}}{{\partial z^{2} }}} \right)$$

(5)

The non-Newtonian fluid considered in the present work obeys the power law model, where, the viscosity has been assumed to depend on the velocity gradients as follows [15]:

$$\mu = \mu_{o} \,\left[ {\left( {\frac{\partial u}{\partial z}} \right)^{2} + \left( {\frac{\partial v}{\partial z}} \right)^{2} } \right]^{(n - 1)/2}$$

(6)

In the last term of the right hand side of Eq. (4), q_r accounts for the radiated heat flux [37],

$$q_{r} = - \frac{{4\,\sigma^{*} }}{{3\,k^{*} }}\,\frac{{\partial T^{4} }}{\partial z}$$

(7)

where, σ^* is the Stefan–Boltzmann constant and k^* is the mean absorption coefficient. The term T⁴ is expressed as a linear Taylor expansion of temperature about T_∞ with neglecting the second and higher order terms,

$$T^{4} \cong 4T_{\infty }^{3} \,T - 3T_{\infty }^{4}$$

(8)

The boundary conditions are given by:

$$u = \, 0,v = r\omega ,w = \, 0,T = T_{w} \,{\text{and}}\,C = C_{w} \,{\text{at}}\,z = \, 0$$

(9)

$$u \to \, 0,v \to \, 0,T \to T_{\infty } \,{\text{and}}\,C \to C_{\infty } \,{\text{as}}\,z \to \infty.$$

(10)

The following Von Karman generalized transformations are modified in order to fit the present power law flow problem [13, 15]:

$$\left\{ {\begin{array}{*{20}l} {u = r\,\omega \,F(\zeta ),\quad v = r\,\omega \,G(\zeta ),\quad w = \left( {\frac{{\omega^{1 - 2n} }}{{\mu_{o} /\rho }}} \right)^{ - 1/(1 + n)} r^{(n - 1)/(n + 1)} H(\zeta ),} \hfill \\ {p - p_{\infty } = - \rho \,\omega \,\upsilon \,P(\zeta ),\quad \zeta = z\,\left( {\frac{{\omega^{2 - n} }}{{\mu_{o} /\rho }}} \right)^{1/(1 + n)} r^{(1 - n)/(n + 1)} ,} \hfill \\ {\theta = \left( {T(\zeta ) - T_{\infty } } \right) /\left( {T_{w} - T_{\infty } } \right),\quad \phi \,{ = }\,\left( {C(\zeta ) - C_{\infty } } \right) /\left( {C_{w} - C_{\infty } } \right).} \hfill \\ \end{array} } \right.$$

(11)

With the definitions illustrated in (6) and (11); the Eqs. (1–5) are transformed to Eqs. (12–16):

$$H^{{\prime }} + 2F + \left( {\frac{1 - n}{1 + n}} \right)\zeta F^{{\prime }} = 0$$

(12)

$$F^{2} - G^{2} + \left( {H + \left( {\frac{1 - n}{1 + n}} \right)\zeta F} \right)F^{{\prime }} = \left( {((F^{{\prime }} )^{2} + (G^{{\prime }} )^{2} )^{(n - 1)/2} F^{{\prime }} } \right)^{{\prime }} - m\,F\,$$

(13)

$$2FG + \left( {H + \left( {\frac{1 - n}{1 + n}} \right)\zeta F} \right)G^{{\prime }} = \left( {\left[ {(F^{{\prime }} )^{2} + (G^{{\prime }} )^{2} } \right]^{(n - 1)/2} G^{{\prime }} } \right)^{{\prime }} - m\,G$$

(14)

$$\begin{aligned} \left[ {\left( {\frac{1 - n}{1 + n}} \right)\,\eta \,F + H} \right]\theta^{{\prime }} & = \frac{1}{\Pr }\,\left[ {\left( {1 + \frac{4}{{3\,R_{d} }}} \right)\,\theta^{{\prime \prime }} + N_{t} \,\,\theta^{{{\prime }2}} + N_{b} \,\theta^{{\prime }} \phi^{{\prime }} } \right] \\ & \quad + \,Ec\left[ {\left( {F^{{{\prime }2}} + G^{{{\prime }2}} } \right)^{(n + 1)/2} \, + \,m\left( {F^{2} + G^{2} } \right)} \right] \\ \end{aligned}$$

(15)

$$\left[ {\left( {\frac{1 - n}{1 + n}} \right)\,\eta \,F + H} \right]\,\phi^{{\prime }} = \frac{1}{Le\,\Pr }\left( {\phi^{{\prime \prime }} + \frac{{N_{t} }}{{N_{b} }}\theta^{{\prime \prime }} } \right)$$

(16)

where, the differentiation is with respect to the variable $\zeta$.

The dimensionless boundary conditions are expressed as:

$$F = \, 0,G = \, 1,H = \, 0,\theta = \, 1\,{\text{and}}\,\phi = 1\,{\text{at}}\,\zeta = \, 0$$

(17)

$$F \to \, 0,G \to \, 0,\theta \to 0\,{\text{and}}\,\phi \to 0\,{\text{as}}\,\zeta \to \infty$$

(18)

The parameters that govern the fluid flow are defined in the following manner:

$$\left\{ {\begin{array}{*{20}l} {m = \frac{{\sigma \,B_{o}^{2} }}{\rho \,\omega \,},\quad \Pr = \mu_{0}^{2/(n + 1)} c_{p} (\omega^{3} r^{2} \rho )^{{\frac{n - 1}{n + 1}}} /k,\quad Ec = \omega^{2} r^{2} /c_{p} (T_{w} - T_{\infty } ),\quad Le = \frac{k}{{\rho \,c\,D_{B} }},} \hfill \\ {N_{B} = \frac{{R\,D_{B} \,\rho \,c\,(C_{w} - C_{\infty } )}}{k},\quad N_{t} = \frac{{R\,\,D_{t} \,\rho \,c\,(T_{w} - T_{\infty } )}}{{T_{w} \,k}},\quad R_{d} = \frac{{k\,k^{*} }}{{4\,\sigma^{*} T_{\infty }^{3} }}.} \hfill \\ \end{array} } \right.$$

(19)

Below, One can find the definitions of the interesting physical quantities $C_{{f_{t} }}$, $C_{{f_{r} }}$, Nu_r and Sh_r [38]:

$$C_{{f_{t} }} = \frac{{\tau_{t} }}{{\rho \,r^{2} \omega^{2} }},\quad C_{{f_{r} }} = \frac{{\tau_{r} }}{{\rho \,r^{2} \omega^{2} }},\quad Nu_{r} = \frac{{r\,q_{w} }}{{k\,\left( {T_{w} \, - \,T_{\infty } } \right)}},\quad Sh_{r} = \frac{{r\,q_{m} }}{{D_{b} \,\left( {C_{w} - C_{\infty } } \right)}}$$

(20)

where, the tangential and radial skin frictions τ_t and τ_r; as well as the heat and mass fluxes q_w and q_m are expressed, respectively, as follows:

$$\left\{ {\begin{array}{*{20}l} {\tau_{t} = \left[ {\mu \,\,\left( {\frac{\partial v}{\partial z} + \frac{1}{r}\,\frac{\partial w}{\partial \varphi }} \right)} \right]_{z = 0} ,} \hfill \\ {\tau_{r} = \left[ {\mu \,\,\left( {\frac{\partial u}{\partial z} + \frac{\partial w}{\partial \varphi }} \right)} \right]_{z = 0} ,} \hfill \\ {q_{w} = - \,\left[ {\left( {\frac{{16\,\sigma^{*} \,T_{\infty }^{3} }}{{3\,k^{*} }} + k} \right)\,\,\left( {\frac{\partial T}{\partial z}} \right)} \right]_{z = 0} ,} \hfill \\ {q_{m} = - \,D_{b} \,\left( {\frac{\partial C}{\partial z}} \right)_{z = 0} .} \hfill \\ \end{array} } \right.$$

(21)

The quantities $C_{{f_{t} }}$, $C_{{f_{r} }}$, Nu_r and Sh_r are given in their dimensionless forms as below:

$$\left\{ {\begin{array}{*{20}l} {\text{Re}_{r}^{{\frac{1}{1 + n}}} \,C_{{f_{t} }} = \left[ {F^{{{\prime }2}} (0) + G^{{{\prime }2}} (0)} \right]^{{\frac{n - 1}{2}}} G^{{\prime }} (0),} \hfill \\ {\text{Re}_{r}^{{\frac{1}{1 + n}}} \,C_{{f_{r} }} = \left[ {F^{{{\prime }2}} (0)\, + \,G^{{{\prime }2}} (0)} \right]^{{\frac{n - 1}{2}}} F^{{\prime }} (0),} \hfill \\ {\text{Re}_{r}^{{\frac{ - 1}{1 + n}}} \,Nu_{r} = - \left[ {1 + \frac{4}{{3\,R_{d} }}} \right]\,\theta^{{\prime }} (0),} \hfill \\ {\text{Re}_{r}^{{\frac{ - 1}{1 + n}}} Sh_{r} = - \phi^{{\prime }} (0).} \hfill \\ \end{array} } \right.$$

(22)

where, $\text{Re}_{r} = \frac{{r^{2} \,\omega^{2 - n} }}{{{{\mu_{o} } \mathord{\left/ {\vphantom {{\mu_{o} } \rho }} \right. \kern-0pt} \rho }}}$ is the rotational Reynolds number.

3 Numerical solution

Equations (12–16) are solved numerically using finite differences [39] under the boundary conditions given by Eqs. (17) and (18) to determine the velocity, temperature and nanoparticles concentration distributions for different values of the governing parameters n, m, R_d, N_t and N_b with various values of Pr, Ec and Le numbers. The Crank–Nicolson implicit method [40] is applied.

The variables D = −0.5(dF/dζ), E = −0.5(dG/dζ), $M = d\theta /d\zeta$ and $N = d\phi /d\zeta$ have been defined to reduce the second order differential Eqs. (12–16) to first order ones as follows;

$$\frac{dH}{d\zeta } + 2\,F - 2\,\left( {\frac{1 - n}{1 + n}} \right)\zeta D = 0$$

(23)

$$F^{2} - G^{2} - \,2\,\,\left( {H + \left( {\frac{1 - n}{1 + n}} \right)\zeta F} \right)D = - 2^{n} \left( {\left( {D^{2} + E^{2} } \right)^{(n - 1)/2} D} \right)^{\prime } - m\,F$$

(24)

$$2FG - 2\left( {H + \left( {\frac{1 - n}{1 + n}} \right)\zeta F} \right)\,\,E = - 2^{n} \left( {\left( {D^{2} + E^{2} } \right)^{(n - 1)/2} \,E} \right)^{\prime } - m\,G$$

(25)

$$\begin{aligned} \left[ {H + \left( {\frac{1 - n}{1 + n}} \right)\,\zeta \,F} \right]M & = \frac{1}{\Pr }\,\left[ {\left( {1 + \frac{4}{{3\,R_{d} \,}}} \right)\,M^{{\prime }} + N_{t} \,M^{2} + N_{b} \,M\,N} \right] \\ & \quad + \,Ec\left[ {2^{n + 1} \,\left( {D^{2} + E^{2} } \right)^{(n + 1)/2} +\,m\,\left( {F^{2} + G^{2} } \right)} \right] \\ \end{aligned}$$

(26)

$$\left[ {H + \left( {\frac{1 - n}{1 + n}} \right)\,\zeta \,F} \right]\,N = \frac{1}{Le\,\Pr }\left( {N^{{\prime }} + \frac{{N_{t} }}{{N_{b} }}M^{{\prime }} } \right).$$

(27)

The finite difference scheme is implemented by writing Eqs. (23–27) at the mid-point of the computational cell and then replacing the difference terms by their second order central difference approximation in ζ direction. A quasi-linearization technique is firstly applied to replace the non-linear terms at a linear stage, with the corrections incorporated in subsequent iterative steps until convergence. Finally, the resulting block tri-diagonal system is solved using the generalized Thomas-algorithm [39,40,41].

The finite difference representations for the resulting first order differential Eqs. (23–27) take the form:

$$\frac{{H_{i + 1} - H_{i} }}{{\Delta \zeta }} + 2\left( {\frac{{F_{i + 1} + F_{i} }}{2}} \right) - 2\,\left( {\frac{1 - n}{1 + n}} \right)\,\left( {\frac{{\zeta_{i + 1} + \zeta_{i} }}{2}} \right)\,\left( {\frac{{D_{i + 1} + D_{i} }}{2}} \right) = 0$$

(28)

$$\begin{aligned} & \frac{{F_{i + 1} \,\bar{F}_{i + 1} + F_{i} \bar{F}_{i} }}{2} - \frac{{G_{i + 1} \bar{G}_{i + 1} + G_{i} \bar{G}_{i} }}{2} - \frac{{H_{i} \bar{D}_{i} + \bar{H}_{i} D_{i} }}{2} - \frac{{H_{i + 1} \bar{D}_{i + 1} + \bar{H}_{i + 1} D_{i + 1} }}{2} \\ & \quad - \,\frac{1}{2}\,\left( {\frac{1 - n}{1 + n}} \right)\,\left[ {\zeta_{i} \,\left( {F_{i} \bar{D}_{i} + \bar{F}_{i} D_{i} } \right) + \zeta_{i + 1} \,\left( {F_{i + 1} \bar{D}_{i + 1} + \bar{F}_{i + 1} D_{i + 1} } \right)} \right] \\ & \quad + \,\frac{m}{2}\left( {F_{i} + F_{i + 1} } \right) + \frac{{2^{n} }}{\Delta \zeta }\left[ {\left( {\bar{D}_{i + 1}^{2} + \bar{E}_{i + 1}^{2} } \right)^{(n - 1)/2} D_{i + 1} - \left( {\bar{D}_{i}^{2} + \bar{E}_{i}^{2} } \right)^{(n - 1)/2} D_{i} } \right] = 0 \\ \end{aligned}$$

(29)

$$\begin{aligned} & \frac{{G_{i + 1} \bar{F}_{i + 1} + \bar{G}_{i + 1} F_{i + 1} }}{2} + \frac{{G_{i} \bar{F}_{i} + \bar{G}_{i} F_{i} }}{2} - \frac{{H_{i} \bar{E}_{i} + \bar{H}_{i} E_{i} }}{2} - \frac{{H_{i + 1} \bar{E}_{i + 1} + \bar{H}_{i + 1} E_{i + 1} }}{2} \\ & \quad - \,\frac{1}{2}\,\left( {\frac{1 - n}{1 + n}} \right)\,\left[ {\zeta_{i} \,\left( {F_{i} \bar{E}_{i} + \bar{F}_{i} E_{i} } \right) + \zeta_{i + 1} \,\left( {F_{i + 1} \bar{E}_{i + 1} + \bar{F}_{i + 1} E_{i + 1} } \right)} \right] \\ & \quad + \,\frac{m}{2}\left( {G_{i} + G_{i + 1} } \right) + \frac{{2^{n} }}{\Delta \zeta }\left[ {\left( {\bar{D}_{i + 1}^{2} + \bar{E}_{i + 1}^{2} } \right)^{(n - 1)/2} E_{i + 1} - \left( {\bar{D}_{i}^{2} + \bar{E}_{i}^{2} } \right)^{(n - 1)/2} E_{i} } \right] = 0 \\ \end{aligned}$$

(30)

$$\begin{aligned} & \frac{{H_{i} \bar{M}_{i} + \bar{H}_{i} M_{i} }}{4} + \frac{{H_{i + 1} \bar{M}_{i + 1} + \bar{H}_{i + 1} M_{i + 1} }}{4} \\ & \quad + \frac{1}{4}\,\left( {\frac{1 - n}{1 + n}} \right)\,\left[ {\zeta_{i} \,\left( {F_{i} \bar{M}_{i} + \bar{F}_{i} M_{i} } \right) + \zeta_{i + 1} \,\left( {F_{i + 1} \bar{M}_{i + 1} + \bar{F}_{i + 1} M_{i + 1} } \right)} \right] \\ & \quad - \,2^{(n + 1)/2} Ec\,\,\left[ {\left( {D_{i + 1} \,\bar{D}_{i + 1} + D_{i} \bar{D}_{i} } \right) + \left( {E_{i + 1} \bar{E}_{i + 1} + E_{i} \bar{E}_{i} } \right)} \right]^{(n + 1)/2} \\ & \quad - \,m\,Ec\,\left( {\frac{{F_{i + 1} \,\bar{F}_{i + 1} + F_{i} \bar{F}_{i} }}{2} + \frac{{G_{i + 1} \bar{G}_{i + 1} + G_{i} \bar{G}_{i} }}{2}} \right) \\ & \quad - \frac{1}{\Pr }\,\left[ \begin{aligned} \left( {1 + \frac{4}{{3\,R_{d} \,}}} \right)\,\left( {\frac{{M_{i + 1} - M_{i} }}{\Delta \zeta }} \right) + N_{t} \,\,\left( {\frac{{M_{i + 1} \,\bar{M}_{i + 1} + M_{i} \bar{M}_{i} }}{2}} \right) \hfill \\ + \,N_{b} \,\left( {\frac{{N_{i} \bar{M}_{i} + \bar{N}_{i} M_{i} }}{4} + \frac{{N_{i + 1} \bar{M}_{i + 1} + \bar{N}_{i + 1} M_{i + 1} }}{4}} \right) \hfill \\ \end{aligned} \right] = 0 \\ \end{aligned}$$

(31)

$$\begin{aligned} & \frac{{H_{i} \bar{N}_{i} + \bar{H}_{i} N_{i} }}{4} + \frac{{H_{i + 1} \bar{N}_{i + 1} + \bar{H}_{i + 1} N_{i + 1} }}{4} \\ & \quad + \,\frac{1}{4}\left( {\frac{1 - n}{1 + n}} \right)\,\left[ {\zeta_{i} \,\left( {F_{i} \bar{N}_{i} + \bar{F}_{i} N_{i} } \right) + \zeta_{i + 1} \,\left( {F_{i + 1} \bar{N}_{i + 1} + \bar{F}_{i + 1} N_{i + 1} } \right)} \right] \\ & \quad - \,\frac{1}{Le\,\Pr }\left[ {\left( {\frac{{N_{i + 1} - N_{i} }}{{\Delta \zeta }}} \right) + \frac{{N_{t} }}{{N_{b} }}\left( {\frac{{M_{i + 1} - M_{i} }}{\Delta \zeta }} \right)} \right] = 0 \\ \end{aligned}$$

(32)

The bars in the above equations refer to the previous iteration.

The computational domain 0 < ζ < ζ _∞ can be divided into intervals of 0.001 step size each. The independence of the results from the length of the finite domain and the grid density was ensured and successfully checked by various trial and error numerical experimentations. The value ζ_∞ = 20 is adequate for all the ranges of the studied parameters. The scheme convergence is satisfied when the variables H, F, G, D, E, θ, ϕ, M and N; have an absolute difference of 10⁻⁶ for the last two approximations for all values of ζ in the specified interval 0 < ζ < ζ _∞. These results are found to be reduced to those given in [14, 15, 20, 22] considering a clear fluid with different flow modes; which, assures the solutions accuracy and correctness.

4 Results and discussion

Figures 2, 3 and 4 show that the augmentation of the magnetic parameter m results in reducing the radial, tangential and axial velocities F, G and H; respectively, where the movement of the rotating disk axially draws the surroundings toward the surface to compensate the radial outflow. Also, it is extremely obvious that the boundary layer thickness becomes thinner with increasing the power-law index n. The inclusion of the magnetic force field provides the same influence of velocity reduction considering different values of n expressed for shear-thinning fluids (n < 1), Newtonian fluids (n = 1) and shear-thickening fluids (n > 1). It is worthwhile to infer that raising m causes the boundary layer to be thinner; and that the variations of the velocities F, G and H with m is more pronounced in case of non-Newtonian shear-thinning fluids. Moreover, Fig. 5 indicates that the values of the temperature θ(ζ) and the nanoparticles concentration ϕ(ζ) increase with boosting m for different n values. This influence is due to the presence of Lorentz force caused by the acting magnetic field that decelerates the flow around the disk.

Fig. 2

Variation of the radial velocity F with different values of m and n

Fig. 3

Variation of the tangential velocity G with different values of m and n

Fig. 4

Variation of the axial velocity H with different values of m and n

Fig. 5

Variation of both θ(ζ) and ϕ(ζ) with different values of m and n (Ec = 0.2, R_d = Pr = Le = 1, N_t = N_b = 0.5)

Figure 6 exhibits a raise in the temperature profiles; while, a depression is obtained in the concentration profiles with increasing Ec for different kinds of fluids. This illustrates the fact that when the friction increases due to fluid viscosity, a large amount of heat is obtained where the viscous dissipation provides an important internal heat source because of the viscous stresses action; and hence, the nanofluid temperature increases. Figure 7 displays the influence of the thermal radiation parameter R_d on both θ(ζ) and ϕ(ζ) for different n. Increasing R_d elevates the behavior of ϕ(ζ) but, decreases θ(ζ) and the thickness of the thermal boundary layer due to the reduction of energy transport into fluid.

Fig. 6

Variation of both θ(ζ) and ϕ(ζ) with different values of Ec and n (m = R_d = Pr = Le = 1, N_t = N_b = 0.5)

Fig. 7

Variation of both θ(ζ) and ϕ(ζ) with different values of R_d and n (Ec = 0.2, m = Pr = Le = 1, N_t = N_b = 0.5)

Figure 8 accentuates the reduction behavior of both θ(ζ) and ϕ(ζ) with increasing Pr; which is physically verified due to the dependence of Pr on the ratio of the fluid kinematic viscosity to thermal diffusivity. In this study, the values of Pr have been chosen according to the categories; (Pr ≪ 1) for liquid metals which have high thermal conductivity but low viscosity and (Pr ≫ 1) for high-viscosity oils. It should be mentioned that the specific used values Pr = 0.72, 1.0 and 7.0 correspond to air, electrolyte solution, and water; respectively. Figure 9 elucidates that increasing Le; increases the Newtonian fluid temperature, while, a lessening in the temperature values is recognized for non-Newtonian fluids (n ≠ 1). Nevertheless, a diminishment attitude of ϕ(ζ) is obtained due to the increase of Le. This may be attributed to the physical definition of Le as the ratio of thermal diffusivity to nanoparticle mass diffusivity; where it is used to characterize the heat and mass transfer through nanofluids flows.

Fig. 8

Variation of both θ(ζ) and ϕ(ζ) with different values of Pr and n (Ec = 0.2, R_d = m = Le = 1, N_t = N_b = 0.5)

Fig. 9

Variation of both θ(ζ) and ϕ(ζ) with different values of Le and n (Ec = 0.2, R_d = Pr = m = 1, N_t = N_b = 0.5)

Figure 10 clarifies that the distributions of θ(ζ) and ϕ(ζ) put up with increasing the thermophoretic parameter N_t and that the influence of thermophoresis phenomenon is the same for different values of n. Physically; enhancing the thermophoretic effect results in a larger mass flux due to temperature gradient which in turn raises the concentration. This mechanism therefore, assists the diffusion of the nanoparticles and elevates the concentration profile. On the other hand, Fig. 11 is prepared to present the effect of the Brownian motion on both θ(ζ) and ϕ(ζ). The temperature of the fluid decreases with increasing N_b for Newtonian fluids; while, an elevation in θ(ζ) profiles is obtained with increasing N_b regarding the class of non-Newtonian fluids (n ≠ 1). Furthermore, ϕ(ζ) decreases with increasing N_b for all n values. This reflects the great impact of following up the influence of the Brownian motion of the particles at nanoscale level; which highly affects the thermal behaviors of the surrounding liquids by transporting energy directly by nanoparticles. The parameters N_b and N_t may vary in (0, ∞); however, the distinctive profiles can be obtained in the range (0, 2) [42].

Fig. 10

Variation of both θ(ζ) and ϕ(ζ) with different values of N_t and n (Ec = 0.2, m = R_d = Pr = Le = 1, N_b = 0.5)

Fig. 11

Variation of both θ(ζ) and ϕ(ζ) with different values of N_b and n (Ec = 0.2, m = R_d = Pr = Le = 1, N_t = 0.5)

Table 1 provides a comparison between the present values of the flow characteristics F′(0), − G′(0) and − H(∞) with those obtained in [15, 43]. These numerical results have been calculated for the particular case of a Newtonian fluid (n = 1). The wall gradient F′(0) and the axial inflow − H(∞) showed a reduction behavior with respect to the growth of m; while an increase in − G′(0) is obtained. Tables 2, 3 and 4 clarify the variation of both the radial and tangential skin frictions F′(0), − G′(0) as well as the axial inflow − H(∞) with varying n. The calculations agree with those presented in [14, 20, 22] for the non-magnetic flow (m = 0). It is shown that the values of the wall gradient F′(0) increase with increasing n, while a diminishment attitudes are obtained for both − G′(0) and − H(∞). Table 5 indicates the effectiveness of thermal radiation on the heat and mass transfer for different values of Pr considering a magnetic Newtonian fluid flow with n = m = Le = 1, Ec = 0.2 and N_t = N_b = 0.5. Increasing R_d and Pr has a marked influence in enhancing the magnitudes of both the Nusselt and Sherwood numbers.

Table 1 Variation of F′(0), − G′(0) and − H(∞) with m for (n = 1)

Table 2 Variation of F′(0) with n for (m = 0)

Table 3 Variation of − G′(0) with n for (m = 0)

Table 4 Variation of − H(∞) with n for (m = 0)

Table 5 Variation of Nu_r and Sh_r with R_d and Pr

Table 6 elucidates the variations of the radial and tangential skin frictions, in addition to the Nusselt and Sherwood numbers for different m considering different types of fluids with Pr = R_d = Le = 1, Ec = 0.2 and N_t = N_b = 0.5. It is obvious that the radial skin friction coefficient decrease with increasing m for all n values, while, a raise in the magnitude of the tangential skin friction coefficient is recognized with increasing m and decreasing n. Also, increasing n, enhances the value of the radial skin friction coefficient for (m > 0) and reduces it in the nonmagnetic flow case (m = 0). It is observed that for different kind of fluids, the magnitudes of both the local Nusselt number and the local Sherwood number increase with increasing the magnetic parameter (m > 1), while a reduction is obtained with increasing m, where (m < 1). Table 7 accentuates the variation of Sh_r for different values of Le, N_t and N_b where, m = Pr = R_d = 1 and Ec = 0.2. It is shown that Sh_r increases with increasing the parameters Le, N_t and N_b which accompany the flow of a nanofluid with simultaneous heat and mass transfer.

Table 6 Variation of $C_{{f_{t} }}$, $C_{{f_{r} }}$, Nu_r and Sh_r for various values of n and m

Table 7 Variation of Sh_r with different values of Le, N_t and N_b

5 Conclusions

This research work deals with the analysis of a steady MHD flow of a non-Newtonian power law nanofluid due to the rotation of an infinite disk. The effect of thermal radiation has been enrolled together with both the Brownian motion and thermophoretic diffusion phenomena. It is concluded that increasing the magnetic parameter reduces the radial, tangential and axial velocities for all n values and that the boundary layer thickness becomes thinner with increasing n. The augmentation of m causes the boundary layer to be thinner; and the velocities variation with m is more pronounced in case of non-Newtonian shear-thinning fluids. Moreover, θ(ζ) and ϕ(ζ) increase with boosting m and N_t for different n values. Increasing Pr and R_d decreases θ(ζ) and the thickness of the thermal boundary layer, while, increasing Ec enhances the temperature values.

Furthermore, the temperature of the fluid decreases with increasing N_b for Newtonian fluids; while, an elevation in θ(ζ) profiles is obtained with increasing N_b regarding the class of non-Newtonian fluids (n ≠ 1), which totally opposes the effect of Le on θ(ζ). On the other hand, a diminishment attitude of ϕ(ζ) is obtained due to the increase of Ec, Pr, Le and N_b, while, an elevation of the behavior of ϕ(ζ) is observed with increasing R_d for different n values. The wall gradient F′(0) and the axial inflow − H(∞) decrease; while, the values of − G′(0) increase with increasing m. The values of F′(0) increase, while, a diminishment attitudes are obtained for both − G′(0) and − H(∞) with increasing n. Increasing R_d and Pr has a marked influence in enhancing the magnitudes of both Nu_r and Sh_r. The radial skin friction coefficient decreases with increasing m for all n values, while, the magnitude of the tangential skin friction coefficient raises with increasing m and decreasing n. Also, increasing n enhances the radial skin friction coefficient for (m > 0) and reduces it in the nonmagnetic flow case (m = 0). The magnitudes of both Nu_r and Sh_r increase with increasing the magnetic parameter (m > 1), while a reduction is obtained with increasing m, where (m < 1). Moreover, increasing the parameters Le, N_t and N_b put up the values of Sh_r.