1 Introduction

The investigation of soliton propagation through nonlinear optical fibres as a theory of optical solitons has become one of the interesting research areas [1, 2]. It is well known that optical solitons represent a treasure trove of research in the field of nonlinear optics. Optical solitons play vital roles in the field of fibre optics, photonics, quantum electronics, optoelectronics and so on [3]. Various integral schemes have been used to investigate different kinds of nonlinear Schrödinger equations (NLSE) [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32].

For the past two decades, the study of fractional differential equations has attracted the attention of many scientists [33, 34]. Several definitions of fractional differential equations have been submitted to the literature, such as Riemann–Liouville, Grunwald–Letnikov, the Caputo, Atangana–Baleanu derivative in Caputo sense, Atangana–Baleanu fractional derivative in Riemann–Liouville sense and modified Riemann–Liouville [35,36,37,38]. Recently, Khalil et al [39] developed the conformable fractional derivative, which can simply be used to transform fractional nonlinear partial differential equations to nonlinear ordinary equations.

This paper is devoted for obtaining optical solitons and singular periodic wave solutions to the conformable space–time fractional complex Ginzburg–Landau (GL) equation [2, 3] by utilising the powerful extended sinh-Gordon equation expansion method (ShGEEM) [40,41,42,43,44]:

$$\begin{aligned}&\mathrm {i}D_{t}^{\alpha }\Psi +aD_{x}^{2\beta }\Psi +bF(|\Psi |^{2})\Psi \nonumber \\&\quad -(|\Psi |^{2}\Psi ^{*})^{-1} [\nu |\Psi |^{2}D_{x}^{2\beta }(|\Psi |^{2})\quad \nonumber \\&\quad -\varrho (D_{x}^{\beta }(|\Psi |^{2}))^{2}]-\gamma \Psi =0, \end{aligned}$$
(1)

where x and t are the non-dimensional distance along the fibre and time in dimensionless form, respectively. The unknown function \(\Psi \) is the complex-valued function of x and t, the symbol \(*\) stands for the complex conjugate of the unknown function \(\Psi \), a and b are the coefficients of the group velocity dispersion and nonlinearity, respectively. The real-valued constants \(\nu ,\;\varrho ,\;\gamma \) are coefficients from the perturbation effects [45, 46]. F is a real-valued algebraic function which must have the smoothness of the function \(F(|\Psi |^{2})\Psi {:}\mathbb {C}\rightarrow \mathbb {C}\). When the complex plane \(\mathbb {C}\) is considered as 2D linear space \(\mathbb {R}^{2}\), the function \(F(|\Psi |^{2})\Psi \) is k times continuously differentiable [47].

$$\begin{aligned} F(|\Psi |^{2})\Psi \in \bigcup _{\sigma ,\delta =1}^{\infty }\mathbb {C}^{k}\big ((-\delta ,\delta )\times (\sigma ,\sigma );\mathbb {R}^{2}\big ). \end{aligned}$$
(2)

2 The conformable fractional derivative

In this section, basic definition, properties and theorem about conformable fractional derivative are discussed [39].

DEFINITION 1

Let \(g: (0,\infty )\rightarrow \mathbb {R}\), then the conformable fraction derivative of g of order \(\alpha \) is defined as

$$\begin{aligned} T_{\alpha }(g)(t)= & {} \lim _{\epsilon \rightarrow 0} \frac{g(t+\epsilon t^{1-\alpha })-g(t) }{\epsilon },\nonumber \\&t>0,~ 0<\alpha <1. \end{aligned}$$
(3)

Here, some basic properties of the conformable fractional derivative [39] are presented:

  1. 1.

    \(T_{\alpha }(bg+ch)=bT_{\alpha }(g)+cT_{\alpha }(h)\), \(b, c\in \mathbb {R}\).

  2. 2.

    \(T_{\alpha }(t^{\lambda })=\lambda t^{\lambda -\alpha }\), \(\lambda \in \mathbb {R}\).

  3. 3.

    \(T_{\alpha }(gh)=gT_{\alpha }(h)+hT_{\alpha }(g)\).

  4. 4.

    \(T_{\alpha }(g/h)={((hT_{\alpha }(g)-gT_{\alpha }(h))}/{h^{2}})\).

  5. 5.

    If g is differentiable, then \(T_{\alpha }(g)(t)=t^{1-\alpha }({{\mathrm {d}}g}/{{\mathrm {d}}t})\).

Theorem 1

Let \(g,h: (0,\infty )\rightarrow \mathbb {R}\) be differentiable and also \(\alpha \) differentiable functions. Then the following rule holds:

$$\begin{aligned} T_{\alpha }(g\circ h)(t)=t^{1-\alpha }h{'}(t)g{'}(h(t)). \end{aligned}$$
(4)

3 The extended ShGEEM

Consider the following space–time fractional sinh-Gordon equation [40]:

$$\begin{aligned} D_{x}^{\beta }(D_{t}^{\alpha }\Psi )=\lambda \sinh (\Psi ), \quad 0<\alpha ,~\beta \le 1, \end{aligned}$$
(5)

where \(\lambda \) is a non-zero constant.

Substituting the fractional travelling wave transformations

$$\begin{aligned} \Psi (x,t)=\psi (\eta ),\quad \eta =\frac{x^{\beta }}{\beta }-\upsilon \frac{t^{\alpha }}{\alpha }, \end{aligned}$$
(6)

into eq. (5), we obtain the following nonlinear ordinary differential equation (NODE):

$$\begin{aligned} \psi {''}=-\frac{\lambda }{\upsilon }\sinh (\psi ), \end{aligned}$$
(7)

where \(\upsilon \) is the velocity of the travelling wave.

Integrating eq. (7) once, we obtain

$$\begin{aligned} \Bigg (\frac{\psi {'}}{2}\Bigg )^{2}=-\frac{\lambda }{\upsilon }\sinh ^{2}\Bigg (\frac{\psi }{2}\Bigg )+c, \end{aligned}$$
(8)

where c is the constant of integration. Setting \(-({\lambda }/{\upsilon })=b\) and \({\psi }/{2}=\Theta \), eq. (8) becomes

$$\begin{aligned} \Theta {'}=\sqrt{b\sinh ^{2}(\Theta )+c}. \end{aligned}$$
(9)

For different values of parameters a and b, eq. (9) possesses the following sets of solutions:

Set I: When \(c=0\), \(b=1\), eq. (9) becomes

$$\begin{aligned} \Theta {'}=\sinh (\Theta ). \end{aligned}$$
(10)

Simplifying eq. (10), the following solutions are secured:

$$\begin{aligned} \sinh (\Theta )=\pm {\mathrm {csch}}(\eta )\;\;\;\text{ or }\;\;\;\sinh (\Theta )=\pm \;\mathrm {i}\; {\mathrm {sech}}(\eta ) \end{aligned}$$
(11)

and

$$\begin{aligned} \cosh (\Theta )=\pm \coth (\eta )\;\;\;\text{ or }\;\;\;\cosh (\Theta )=\pm \tanh (\eta ), \end{aligned}$$
(12)

where \(\mathrm {i}=\sqrt{-1}\).

Set II: When \(c=1\), \(b=1\), eq. (9) becomes

$$\begin{aligned} \Theta {'}=\cosh (\Theta ). \end{aligned}$$
(13)

Simplifying eq. (13), the following solutions are obtained:

$$\begin{aligned} \sinh (\theta )=\tan (\eta )\;\;\;\text{ or }\;\;\;\sinh (\Theta )=-\cot (\eta ) \end{aligned}$$
(14)

and

$$\begin{aligned} \cosh (\Theta )=\pm \sec (\eta )\;\;\;\text{ or }\;\;\;\cosh (\Theta )=\pm \;\; \csc (\eta ). \end{aligned}$$
(15)

For a given nonlinear space–time fractional partial differential equation, say

$$\begin{aligned}&P(\Psi ,\;D_{x}^{\beta }\Psi ,\;D_{x}^{\beta }(D_{t}^{\alpha }\Psi ),\;\Psi ^{2}D_{x}^{\alpha }\Psi _{t}, \ldots )=0,\nonumber \\&\quad 0<\alpha ,\beta \le 1, \end{aligned}$$
(16)

the following steps are followed to secure various wave solutions to (16):

Step 1: We first transform eq. (16) into the following NODE by using eq. (6):

$$\begin{aligned} Q(\psi ,\;\psi {'},\;\psi {''},\;\psi ^{2}\psi {'}, \ldots )=0. \end{aligned}$$
(17)

Step 2: We assume that eq. (17) has a new ansatz solution of the form

$$\begin{aligned} \psi (\Theta )=\sum _{k=1}^{m}\big [B_{k}\sinh (\Theta )+A_{k}\cosh (\Theta )\big ]^{k}+A_{0}, \end{aligned}$$
(18)

where \(\Theta \) is a function of \(\eta \) and it satisfies eq. (9), and \(A_{0},\;A_{k},\;B_{k}\) \((k=1,2,\ldots ,m)\) are constants to be determined later. To obtain the value of m, the homogeneous balance principle is used on the highest derivatives and highest power nonlinear term in eq. (17).

Step 3: We substitute eq. (28) and its derivatives with a fixed value of m along with eq. (10) or (13) into eq. (17) to obtain a polynomial equation in \(\Theta {'^s}\sinh ^{j}(\Theta )\cosh ^{k}(\Theta )\) \((s=0,1\; \text{ and }\;j,k=0,1,2,\ldots )\). We collect a set of overdetermined nonlinear algebraic equations in \(A_{0},\;A_{k},\;B_{k},\;\upsilon \) by summing the coefficients of \(\Theta {'^s}\sinh ^{j}(\Theta )\cosh ^{k}(\Theta )\) with the same power and setting each summation to zero.

Step 4: The obtained set of overdetermined nonlinear algebraic equations is then solved with the aid of symbolic software to determine the values of the parameters \(A_{0},A_{k},B_{k}\, {\mathrm {and}}\ \upsilon \).

Step 5: Using the results obtained in eqs (11), (12), (14) and (15), we have the wave solutions to the given nonlinear partial differential equation in the following forms:

$$\begin{aligned} \psi (\eta )= & {} \sum _{k=1}^{m}\big [\pm B_{k}\;\mathrm {i}\;{\mathrm {sech}}(\eta ) \pm A_{k}\tanh (\eta )\big ]^{k} +A_{0},\nonumber \\ \end{aligned}$$
(19)
$$\begin{aligned} \psi (\eta )= & {} \sum _{k=1}^{m}\big [\pm B_{k}\;{\mathrm {csch}}(\eta )\pm A_{k}\coth (\eta )\big ]^{k} +A_{0},\nonumber \\ \end{aligned}$$
(20)
$$\begin{aligned} \psi (\eta )= & {} \sum _{k=1}^{m}\big [\pm B_{k}\sec (\eta )+A_{k}\tan (\eta )\big ]^{k}+A_{0} \end{aligned}$$
(21)

and

$$\begin{aligned} \psi (\eta )=\sum _{k=1}^{m}\big [\pm B_{k}\csc (\eta )-A_{k}\cot (\eta )\big ]^{k}+A_{0}. \end{aligned}$$
(22)

4 Application

In this section, we obtain various solutions to the complex GL equation [3] by using the extended ShGEEM.

Consider the following complex fractional travelling wave transformation:

$$\begin{aligned}&\Psi (x,t)=\psi (\eta )\mathrm{e}^{\mathrm{i}\phi },\quad \phi =-\vartheta \frac{x^{\beta }}{\beta }+\omega \frac{t^{\alpha }}{\alpha }+\Phi ,\nonumber \\&\eta =\frac{x^{\beta }}{\beta }-\upsilon \frac{t^{\alpha }}{\alpha }, \end{aligned}$$
(23)

where \(\psi (\eta )\) stands for the pulse shape, \(\upsilon \) is the velocity of the soliton, \(\phi \) is the phase component, \(\vartheta \) is the soliton frequency, \(\omega \) is the soliton wave number and \(\Phi \) is the phase constant.

Substituting eq. (23) into eq. (1) yields the following NODE:

$$\begin{aligned}&-\omega \psi +a(\psi {''}-\vartheta ^{2}\psi )+bF(\psi ^{2})\psi \nonumber \\&-2(\nu -2\varrho )\frac{(\psi {'})^{2}}{\psi }-2\nu \psi {''}-\gamma \psi =0 \end{aligned}$$
(24)

from the real part and the relation \(\upsilon =-2a\vartheta \) from the imaginary part.

Setting \(\nu =2\varrho \), eqs (1) and (24) become

$$\begin{aligned}&\mathrm{i}D_{t}^{\alpha }\Psi +aD_{x}^{2\beta }\Psi +bF(|\Psi |^{2})\Psi \nonumber \\&\quad -\varrho (|\Psi |^{2}\Psi ^{*})^{-1} [2|\Psi |^{2}D_{x}^{2\beta }(|\Psi |^{2})\quad \nonumber \\&\quad -(D_{x}^{\beta }(|\Psi |^{2}))^{2}]-\gamma \Psi =0 \end{aligned}$$
(25)

and

$$\begin{aligned} (a-4\varrho )\psi {''}-(\omega +a\vartheta ^{2}+\gamma )\psi +bF(\psi ^{2})\psi =0, \end{aligned}$$
(26)

respectively.

For the Kerr law nonlinearity, \(F(\psi )=\psi \) [3]. Therefore, eq. (26) becomes

$$\begin{aligned} (a-4\varrho )\psi {''}-(\omega +a\vartheta ^{2}+\gamma )\psi +b\psi ^{3}=0. \end{aligned}$$
(27)

The Kerr law nonlinearity arises from the fact that light wave in an optical fibre encounters nonlinear responses from the non-harmonic motion of electrons with an external electric field [2].

Balancing the terms \(\psi {''}\) and \(\psi ^{3}\) in eq. (27) yields \(m=1\).

With \(m=1\), eqs (28)–(32) take the following forms:

$$\begin{aligned}&\Psi (\Theta )=B_{1}\sinh (\Theta )+A_{1}\cosh (\Theta )+A_{0}, \end{aligned}$$
(28)
$$\begin{aligned}&\psi (\eta )=\pm B_{1}\;\mathrm {i}\;{\mathrm {sech}}(\eta )\pm A_{1}\tanh (\eta )+A_{0}, \end{aligned}$$
(29)
$$\begin{aligned}&\psi (\eta )=\pm B_{1}\;{\mathrm {csch}}(\eta )\pm A_{1}\coth (\eta )+A_{0}, \end{aligned}$$
(30)
$$\begin{aligned}&\psi (\eta )=\pm B_{1}\sec (\eta )+A_{1}\tan (\eta )+A_{0} \end{aligned}$$
(31)

and

$$\begin{aligned} \psi (\eta )=\pm B_{1}\csc (\eta )-A_{1}\cot (\eta )+A_{0}, \end{aligned}$$
(32)

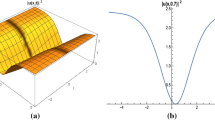
respectively (figure 1).

Fig. 1
figure 1

The 3D graphics of eq. (35) when (a) \(\alpha =\beta =0.7\) and (b) \(\alpha =\beta =0.6\).

Full size image

Putting eq. (28) and its second derivative into eq. (27) give a polynomial in the power hyperbolic functions. We get a set of algebraic equations by equating each summation of the coefficients of the hyperbolic functions of the same power to zero. We solve the set of algebraic equations to get the values of the parameters involved. To explicitly secure the solutions of eq. (1), we insert the values of the parameters into each of eqs (29)–(32).

Set 1: When

$$\begin{aligned}&A_{0},\;A_{1}=-\sqrt{\frac{4\varrho -a}{2b}},\quad B_{1}=A_{1},\\&\vartheta =-\sqrt{-\frac{(a+2(\gamma -2\varrho +\omega ))}{2a}}, \end{aligned}$$

eq. (1) possesses the following combined dark–bright and combined singular optical solitons:

$$\begin{aligned}&\Psi _{1}(x,t)=\pm \sqrt{\frac{4\varrho -a}{2b}}\Bigg (\mathrm {i}\;{\mathrm {sech}}\Bigg [\frac{x^{\beta }}{\beta }+2a\vartheta \frac{t^{\alpha }}{\alpha }\Bigg ]\nonumber \\&\quad +\tanh \Bigg [\frac{x^{\beta }}{\beta }{+}2a\vartheta \frac{t^{\alpha }}{\alpha }\Bigg ]\Bigg )\mathrm{e}^{\mathrm{i}\left( -\vartheta ({x^{\beta }}/{\beta })+\omega ({t^{\alpha }}/{\alpha }){+}\Phi \right) } \end{aligned}$$
(33)

and

$$\begin{aligned}&\Psi _{2}(x,t)=\pm \sqrt{\frac{4\varrho -a}{2b}}\Bigg ({\mathrm {coth}}\Bigg [\frac{x^{\beta }}{\beta }+2a\vartheta \frac{t^{\alpha }}{\alpha }\Bigg ]\nonumber \\&\quad +{\mathrm {csch}}\Bigg [\frac{x^{\beta }}{\beta }+2a\vartheta \frac{t^{\alpha }}{\alpha }\Bigg ]\Bigg )\mathrm{e}^{\mathrm{i}\left( -\vartheta {(x^{\beta }}/{\beta )}+\omega {(t^{\alpha }}/{\alpha )}+\Phi \right) }, \end{aligned}$$
(34)
Fig. 2
figure 2

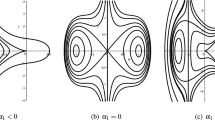
The 3D graphics of eq. (43) when (a) \(\alpha =\beta =0.7\) and (b) \(\alpha =\beta =0.6\).

Full size image
Fig. 3
figure 3

The 3D graphics of eq. (44) when (a) \(\alpha =\beta =0.7\) and (b) \(\alpha =\beta =0.6\).

Full size image

respectively, where \(b(4\varrho -a)>0\) and \(a(a+2(\gamma -2\varrho +\omega ))<0\) for the existence of valid solitons (figure 2).

Set 2: When

$$\begin{aligned}&A_{0}=0,\quad A_{1}=-\sqrt{\frac{2(4\varrho -a)}{b}},\quad B_{1}=0,\\&\vartheta =-\sqrt{\frac{8\varrho -2a-\gamma -\omega }{a}}, \end{aligned}$$

eq. (1) possesses the following dark and singular optical solitons:

$$\begin{aligned}&\Psi _{3}(x,t)=\pm \sqrt{\frac{2(4\varrho -a)}{b}}\nonumber \\&\quad \times \tanh \Bigg [\frac{x^{\beta }}{\beta }+2a\vartheta \frac{t^{\alpha }}{\alpha }\Bigg ] \mathrm{e}^{\mathrm{i}(-\vartheta ({x^\beta }/\beta )+\omega ({t^\alpha }/\alpha )+\Phi )} \end{aligned}$$
(35)

and

$$\begin{aligned}&\Psi _{4}(x,t)=\pm \sqrt{\frac{2(4\varrho -a)}{b}}\nonumber \\&\quad \times \coth \left[ \frac{x^{\beta }}{\beta }+2a\vartheta \frac{t^{\alpha }}{\alpha }\right] \mathrm{e}^{\mathrm{i}(-\vartheta ({x^\beta }/{\beta })+\omega ({t^\alpha }/{\alpha })+\Phi )}, \end{aligned}$$
(36)

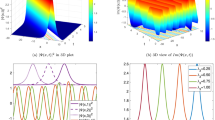
respectively, where \(b(4\varrho -a)>0\) and \(a(8\varrho -2a-\gamma -\omega )>0\) for the existence of valid solitons (figure 3).

Set 3: When

$$\begin{aligned}&A_{0}=0,\;A_{1}=0,\;B_{1}=-\sqrt{-\frac{2(4\varrho -a)}{b}},\;\\&\vartheta =\sqrt{\frac{a-\gamma -4\varrho -\omega }{a}}, \end{aligned}$$

eq. (1) possesses the following bright and singular optical solitons:

$$\begin{aligned}&\Psi _{5}(x,t)=\pm \sqrt{-\frac{2(4\varrho -a)}{b}}\nonumber \\&\times \,{\mathrm {sech}}\left[ \frac{x^{\beta }}{\beta }+2a\vartheta \frac{t^{\alpha }}{\alpha }\right] \mathrm{e}^{\mathrm{i}(-\vartheta ({x^\beta }/{\beta })+\omega ({t^\alpha }/{\alpha })+\Phi )}\nonumber \\ \end{aligned}$$
(37)

and

$$\begin{aligned}&\Psi _{6}(x,t)=\pm \sqrt{\frac{2(4\varrho -a)}{b}}\nonumber \\&\times \,{\mathrm {csch}}\left[ \frac{x^{\beta }}{\beta }+2a\vartheta \frac{t^{\alpha }}{\alpha }\right] \mathrm{e}^{\mathrm{i}(-\vartheta ({x^\beta }/{\beta })+\omega ({t^\alpha }/{\alpha })+\Phi )},\nonumber \\ \end{aligned}$$
(38)

respectively.

Valid solitons exist for both \(b(4\varrho -a)<0\) or \(b(4\varrho -a)>0\) and \(a(a-\gamma -4\varrho -\omega )>0\).

Set 4: When

$$\begin{aligned}&A_{0}=0,\quad A_{1}=-\sqrt{\frac{4\varrho -a}{2b}},\quad B_{1}=A_{1},\\&\omega =-\frac{1}{2}a(1+2\vartheta ^{2})-\gamma +2\varrho , \end{aligned}$$

eq. (1) possesses the following combined dark–bright and combined singular optical solitons:

$$\begin{aligned}&\Psi _{7}(x,t)=\pm \sqrt{\frac{4\varrho -a}{2b}} \Bigg (\mathrm{i}\;{\mathrm {sech}}\Bigg [\frac{x^{\beta }}{\beta }+2a\vartheta \frac{t^{\alpha }}{\alpha }\Bigg ]\nonumber \\&\quad +\tanh \Bigg [\frac{x^{\beta }}{\beta }+2a\vartheta \frac{t^{\alpha }}{\alpha }\Bigg ]\Bigg )\nonumber \\&\quad \times \mathrm{e}^{\mathrm{i}\left( -\vartheta {(x^{\beta }}/{\beta )}-\left( {1}/{2}a(1+2\vartheta ^{2})+\gamma -2\varrho \right) {(t^{\alpha }}/{\alpha )}+\Phi \right) } \end{aligned}$$
(39)

and

$$\begin{aligned}&\Psi _{8}(x,t)=\pm \sqrt{\frac{4\varrho -a}{2b}}\Bigg (\coth \Bigg [\frac{x^{\beta }}{\beta }+2a\vartheta \frac{t^{\alpha }}{\alpha }\Bigg ]\nonumber \\&\quad +{\mathrm {csch}}\Bigg [\frac{x^{\beta }}{\beta }+2a\vartheta \frac{t^{\alpha }}{\alpha }\Bigg ]\Bigg )\nonumber \\&\quad \times \mathrm{e}^{\mathrm{i}(-\vartheta ({x^\beta }/{\beta })-(({1}/{2})a(1+2\vartheta ^{2})+\gamma -2\varrho ) ({t^\alpha }/{\alpha })+\Phi )}, \end{aligned}$$
(40)

respectively, where \(b(4\varrho -a)>0\) for valid solitons.

Set 5: When

$$\begin{aligned}&A_{0}=0,\quad A_{1}=-\sqrt{\frac{2(4\varrho -a)}{b}},\quad B_{1}=0,\\&\omega =-a(2+\vartheta ^{2})-\gamma +8\varrho , \end{aligned}$$

eq. (1) possesses the following dark and singular optical solitons:

$$\begin{aligned}&\Psi _{9}(x,t)=\pm \sqrt{\frac{2(4\varrho -a)}{b}}\tanh \Bigg [\frac{x^{\beta }}{\beta }+2a\vartheta \frac{t^{\alpha }}{\alpha }\Bigg ]\nonumber \\&\quad \times \mathrm{e}^{\mathrm{i}\left( -\vartheta {(x^{\beta }}/{\beta )}-(a(2+\vartheta ^{2})+\gamma -8\varrho ) {(t^{\alpha }}/{\alpha )}+\Phi \right) } \end{aligned}$$
(41)

and

$$\begin{aligned}&\Psi _{10}(x,t)=\pm \sqrt{\frac{2(4\varrho -a)}{b}}\coth \Bigg [\frac{x^{\beta }}{\beta }+2a\vartheta \frac{t^{\alpha }}{\alpha }\Bigg ]\nonumber \\&\quad \times \mathrm{e}^{\mathrm{i}\left( -\vartheta {(x^{\beta }}/{\beta )}-(a(2+\vartheta ^{2})+\gamma -8\varrho ) {(t^{\alpha }}/{\alpha )}+\Phi \right) }, \end{aligned}$$
(42)

respectively, where \(b(4\varrho -a)>0\) for valid solitons.

Set 6: When

$$\begin{aligned}&A_{0}=0,\quad A_{1}=0,\quad B_{1}=-\sqrt{\frac{2(4\varrho -a)}{b}},\\&\omega =a(1-\vartheta ^{2})-\gamma -4\varrho , \end{aligned}$$

eq. (1) possesses the following bright and singular optical solitons:

$$\begin{aligned}&\Psi _{11}(x,t)=\pm \sqrt{\frac{2(a-4\varrho )}{b}}{\mathrm {sech}}\Bigg [\frac{x^{\beta }}{\beta }+2a\vartheta \frac{t^{\alpha }}{\alpha }\Bigg ]\nonumber \\&\quad \times \mathrm{e}^{\mathrm{i}\left( -\vartheta {(x^{\beta }}/{\beta )}+(a(1-\vartheta ^{2})-\gamma -4\varrho ) {(t^{\alpha }}/{\alpha )}+\Phi \right) } \end{aligned}$$
(43)

and

$$\begin{aligned}&\Psi _{12}(x,t)=\pm \sqrt{\frac{2(4\varrho -a)}{b}}{\mathrm {csch}}\Bigg [\frac{x^{\beta }}{\beta }+2a\vartheta \frac{t^{\alpha }}{\alpha }\Bigg ]\nonumber \\&\quad \times \mathrm{e}^{\mathrm{i}\left( -\vartheta {(x^{\beta }}/{\beta )}+(a(1-\vartheta ^{2})-\gamma -4\varrho ) {(t^{\alpha }}/{\alpha )}+\Phi \right) }, \end{aligned}$$
(44)

respectively, where \(b(a-4\varrho )>0\) or \(b(a-4\varrho )<0\) for valid solitons.

Set 7: When

$$\begin{aligned}&A_{0}=0,\quad A_{1}=-\sqrt{\frac{2(\gamma +4\vartheta ^{2}\varrho +\omega )}{b(2+\vartheta ^{2})}},\\&B_{1}=0,\quad a=-\frac{(\gamma -8\varrho +\omega )}{2+\vartheta ^{2}}, \end{aligned}$$

eq. (1) possesses the following dark and singular optical solitons:

$$\begin{aligned}&\Psi _{13}(x,t)=\pm \sqrt{\frac{2(\gamma +4\vartheta ^{2}\varrho +\omega )}{b(2+\vartheta ^{2})}}\nonumber \\&\quad \times \tanh \Bigg [\frac{x^{\beta }}{\beta }-\frac{2\vartheta (\gamma -8\varrho +\omega )}{2+\vartheta ^{2}} \frac{t^{\alpha }}{\alpha }\Bigg ]\nonumber \\ {}&\quad \times \mathrm{e}^{\mathrm{i}\left( -\vartheta \frac{(x^{\beta })}{(\beta )}+\omega \frac{(t^{\alpha })}{(\alpha )}+\Phi \right) } \end{aligned}$$
(45)

and

$$\begin{aligned}&\Psi _{14}(x,t)=\pm \sqrt{\frac{2(\gamma +4\vartheta ^{2}\varrho +\omega )}{b(2+\vartheta ^{2})}}\nonumber \\&\times \coth \Bigg [\frac{x^{\beta }}{\beta }-\frac{2\vartheta (\gamma -8\varrho +\omega )}{2+\vartheta ^{2}} \frac{t^{\alpha }}{\alpha }\Bigg ]\nonumber \\ {}&\times \mathrm{e}^{\mathrm{i}\left( -\vartheta {(x^{\beta }}/{\beta )}+\omega {(t^{\alpha }}/{\alpha )}+\Phi \right) }, \end{aligned}$$
(46)

respectively, where \(b(2+\vartheta ^{2})(\gamma +4\vartheta ^{2}\varrho +\omega )>0\) for valid solitons.

Set 8: When

$$\begin{aligned}&A_{0}=0,\quad A_{1}=0,\\&B_{1}=\sqrt{\frac{2(\gamma +4\vartheta ^{2}\varrho +\omega )}{b(\vartheta ^{2}-1)}},\quad a=\frac{\gamma +4\varrho +\omega }{1-\vartheta ^{2}}, \end{aligned}$$

eq. (1) possesses the following bright and singular optical solitons:

$$\begin{aligned}&\Psi _{15}(x,t)=\pm \sqrt{\frac{-2(\gamma +4\vartheta ^{2}\varrho +\omega )}{b(\vartheta ^{2}-1)}}\nonumber \\&\quad \times {\mathrm {sech}}\Big [\frac{x^{\beta }}{\beta }+\frac{(\gamma +4\varrho +\omega )}{1-\vartheta ^{2}} \frac{t^{\alpha }}{\alpha }\Big ]\nonumber \\ {}&\quad \times \mathrm{e}^{\mathrm{i}\left( -\vartheta {(x^{\beta }}/{\beta )}+\omega {(t^{\alpha }}/{\alpha )}+\Phi \right) } \end{aligned}$$
(47)

and

$$\begin{aligned}&\Psi _{16}(x,t)=\pm \sqrt{\frac{2(\gamma +4\vartheta ^{2}\varrho +\omega )}{b(\vartheta ^{2}-1)}}\nonumber \\&\quad \times {\mathrm {csch}}\Bigg [\frac{x^{\beta }}{\beta }+\frac{(\gamma +4\varrho +\omega )}{1-\vartheta ^{2}} \frac{t^{\alpha }}{\alpha }\Bigg ]\nonumber \\ {}&\quad \times \mathrm{e}^{\mathrm{i}\left( -\vartheta {(x^{\beta }}/{\beta )}+\omega {(t^{\alpha }}/{\alpha )}+\Phi \right) }, \end{aligned}$$
(48)

respectively, where \(b(\vartheta ^{2}-1)(\gamma +4\vartheta ^{2}\varrho +\omega )>0\) or \(b(\vartheta ^{2}-1)(\gamma +4\vartheta ^{2}\varrho +\omega )<0\) for valid solitons.

Set 9: When

$$\begin{aligned}&A_{0}=0,\quad A_{1}=-\sqrt{\frac{4\varrho -a}{2b}},\\&B_{1}=A_{1},\quad \vartheta =-\sqrt{\frac{a-2(\gamma +2\varrho +\omega )}{2a}}, \end{aligned}$$

eq. (1) possesses the following singular periodic solutions:

$$\begin{aligned}&\Psi _{17}(x,t)=\pm \sqrt{\frac{4\varrho -a}{2b}}\Bigg (\sec \Bigg [\frac{x^{\beta }}{\beta }+2a\vartheta \frac{t^{\alpha }}{\alpha }\Bigg ]\nonumber \\&\quad +\tan \Bigg [\frac{x^{\beta }}{\beta }+2a\vartheta \frac{t^{\alpha }}{\alpha }\Bigg ]\Bigg )\mathrm{e}^{\mathrm{i}\left( -\vartheta {(x^{\beta }}/{\beta )}+\omega {(t^{\alpha }}/{\alpha )}+\Phi \right) } \end{aligned}$$
(49)

and

$$\begin{aligned}&\Psi _{18}(x,t)=\pm \sqrt{\frac{4\varrho -a}{2b}}\Bigg (\cot \Bigg [\frac{x^{\beta }}{\beta }+2a\vartheta \frac{t^{\alpha }}{\alpha }\Bigg ]\nonumber \\&\quad +\csc \Bigg [\frac{x^{\beta }}{\beta }+2a\vartheta \frac{t^{\alpha }}{\alpha }\Bigg ]\Bigg )\mathrm{e}^{\mathrm{i}\left( -\vartheta {(x^{\beta }}/{\beta )}+\omega {(t^{\alpha }}/{\alpha )}+\Phi \right) }, \end{aligned}$$
(50)

where \(b(4\varrho -a)>0\) or \(b(4\varrho -a)<0\) and \(a(a-2(\gamma +2\varrho +\omega ))>0\) for valid solitons.

Set 10: When

$$\begin{aligned}&A_{0}=0,\quad A_{1}=-\sqrt{\frac{4\varrho -a}{2b}},\\&B_{1}=A_{1},\quad \omega =\frac{1}{2}(a-2a\vartheta ^{2}-2(\gamma +2\varrho )), \end{aligned}$$

eq. (1) possesses the following singular periodic solutions:

$$\begin{aligned}&\Psi _{20}(x,t)=\pm \sqrt{\frac{4\varrho -a}{2b}}\Bigg (\sec \Bigg [\frac{x^{\beta }}{\beta }+2a\vartheta \frac{t^{\alpha }}{\alpha }\Bigg ]\nonumber \\&\quad +\tan \Bigg [\frac{x^{\beta }}{\beta }+2a\vartheta \frac{t^{\alpha }}{\alpha }\Bigg ]\Bigg )\nonumber \\&\quad \times \mathrm{e}^{\mathrm{i}(-\vartheta ({x^\beta }/{\beta })+({1}/{2})(a-2a\vartheta ^{2}-2(\gamma +2\varrho )) ({t^\alpha }/{\alpha })+\Phi )} \end{aligned}$$
(51)

and

$$\begin{aligned}&\Psi _{21}(x,t)=\pm \sqrt{\frac{4\varrho -a}{2b}}\Bigg (\cot \Bigg [\frac{x^{\beta }}{\beta }+2a\vartheta \frac{t^{\alpha }}{\alpha }\Bigg ]\nonumber \\&\quad +\csc \Bigg [\frac{x^{\beta }}{\beta }+2a\vartheta \frac{t^{\alpha }}{\alpha }\Bigg ]\Bigg )\nonumber \\&\quad \times \mathrm{e}^{\mathrm{i}(-\vartheta ({x^\beta }/{\beta })+({1}/{2})(a-2a\vartheta ^{2}-2(\gamma +2\varrho )) ({t^\alpha }/{\alpha })+\Phi )}, \end{aligned}$$
(52)

where \(b(4\varrho -a)>0\) or \(b(4\varrho -a)<0\) for valid solitons.

5 Conclusions

This study used the powerful extended ShGEEM in constructing the dark, bright, combined dark–bright, singular, combined singular optical solitons and singular periodic wave solutions to the conformable space–time fractional complex GL equation. The constraint conditions for the existence of a valid soliton to each of the obtained solutions are stated. Under suitable choice of parameters, the 3D graphics of some of the obtained solutions are also plotted. The results reported may be useful in explaining the physical meaning of the studied equation in this paper and other complex nonlinear models arising in various fields of nonlinear science.

The computations in this paper provide a lot of encouragement to the future findings. It can be seen that the integral scheme used in this study is a powerful and efficient mathematical tool, which produces a family of solutions when applied to a complex nonlinear model. In our future research, we are going to consider investigating the conformable space–time fractional complex GL with a different type of nonlinearity. Its numerical solutions will also be computed.