1 Introduction

For the past two decades, the investigation of the solutions to the various types of nonlinear evolution equations (NEEs) has attracted the attentions of many researchers. Nonlinear evolution equations are often used to express some models that describe complex physical aspects which arise in the various fields on nonlinear sciences, especially in mathematical physics, chemical physics, plasma wave, biology and fluid mechanics. Various analytical techniques have been developed, modified and applied to explore search of the various solutions to such equations, this include the sine-Gordon expansion method (Baskonus et al. 2017; Bulut et al. 2016, 2017), the simple equation method (Nofal 2016), the generalized tanh function method (Inan and Kaya 2007), the Cole-Hopf transformation method (Wazwaz 2015), the improved F-expansion method with Riccati equation (Akbar and Ali 2017; Zhao 2013), the improved Bernoulli sub-equation function method (Baskonus and Bulut 2016), the extended mapping approach (Fang et al. 2005), the simplified homogeneous balance method (Wang and Li 2014), the modified exp \((-\Omega (\xi ))\)-expansion function method (Ozpinar et al. 2015; Baskonus et al. 2016), the He’s variational iteration method (Momani and Abuasad 2006; Dehghan and Shakeri 2008), the generalized tanh-function type method (Zhang 2013) and so on. In general, various analytical techniques for finding new solutions to different types of NEEs have been formulated (Noor et al. 2011; Bulut et al. 2017, 2018; Khan et al. 2014; Naher and Abdullah 2012; Rawashdeh 2014; Alquran et al. 2011; Yokus et al. 2018; Seadawy 2017; Rizvi and Ali 2017; Cattani and Rushchitskii 2003; Haq et al. 2017; Cattani 2003; Eslami et al. 2012, 2017; Seadawy 2015; Seadawy et al. 2017; Akbar et al. 2013; Mirzazadeh 2014; Sulaiman et al. 2017).

However, this study uses the extended sinh-Gordon equation expansion method (ShGEEM) (Xian-Lin and Jia-Shi 2008; Bulut et al. 2017; Baskonus et al. 2018) in extracting some solitary wave solutions to the longitudinal wave equation in a magneto-electro-elastic (MEE) circular rod (Baskonus et al. 2016). The longitudinal wave equation is an equation with dispersion caused by the transverse Poisson’s effect in a MEE circular rod which and it was derived by Xue et al. (2011).

The longitudinal wave equation in a MEE circular rod is given by Baskonus et al. (2016);

$$\begin{aligned} \psi _{tt}-v_{0}^{2}\psi _{xx}-\Big (\frac{v_{0}^{2}}{2}\psi ^{2}+p\psi _{tt}\Big )_{xx}=0, \end{aligned}$$
(1.1)

where \(v_{0}\) is the linear longitudinal wave velocity for a MEE circular rod and p is the dispersion parameter, all of them depend on the material property and the geometry of the rod (Xue et al. 2011). Different computational approaches have been used to investigate the solutions of the longitudinal wave equation in a magneto-electro-elastic MEE circular rod (Ma et al. 2013; Khan et al. 2016; Younis and Ali 2015).

2 The extended ShGEEM

In this sections, the general facts of the sinh-Gordon equation expansion method are presented.

To apply the ShGEEM, the following steps are followed:

Step 1 Consider the following nonlinear partial differential equation and the travelling wave transformation:

$$\begin{aligned} P(\psi _{x},\;\psi ^{2}\psi _{xx},\;\psi _{t},\;\psi _{xt},\;\ldots )=0, \end{aligned}$$
(2.1)

where P is a polynomial in \(\psi\), the subscripts indicate the partial derivative of \(\psi\) with respect to x or t, and

$$\begin{aligned} \psi =\Psi (\zeta ),\;\;\; \zeta =x-kt, \end{aligned}$$
(2.2)

respectively.

Substituting Eq. (2.2) into Eq. (2.1), we get the following nonlinear ordinary differential equation (NODE):

$$\begin{aligned} Q(\Psi ,\;\Psi ^{'},\;\Psi ^{''},\;\Psi ^{2}\Psi ^{'},\; \ldots )=0, \end{aligned}$$
(2.3)

where Q is a polynomial in \(\Psi\) and the superscripts indicate the ordinary derivative of \(\Psi\) with respect to \(\zeta\).

Step 2 We assume that Eq. (2.3) has the solution of the form Yan and Zhang (1999)

$$\begin{aligned} \Psi (\omega )=\sum _{j=1}^{m}cosh^{j-1}(\omega )\big [B_{j}sinh(\omega )+A_{j}cosh(\omega )\big ]+A_{0}, \end{aligned}$$
(2.4)

where \(A_{0},\;A_{j},\;B_{j}\) \((j=1,\;2,\;\ldots ,\;m)\) are constants to be determine later and \(\omega\) is a function of \(\zeta\) that satisfies the following ordinary differential equation:

$$\begin{aligned} \omega ^{\prime}=sinh(\omega ). \end{aligned}$$
(2.5)

To obtain the value of m, the homogeneous balance principle is used on the highest derivatives and highest power nonlinear term in Eq. (2.3).

Equation (2.5) has been extracted from the popularly known sinh-Gordon equation (Xian-Lin and Jia-Shi 2008) given as

$$\begin{aligned} \psi _{xt}=\lambda sinh(\psi ). \end{aligned}$$
(2.6)

Equation (2.5) has the following solutions (Xian-Lin and Jia-Shi 2008):

$$\begin{aligned} sinh(\omega )=\pm \, csch(\zeta )\;\;\;\text{ or }\;\;\;sinh(\omega )=\pm \;i\; sech(\zeta ) \end{aligned}$$
(2.7)

and

$$\begin{aligned} cosh(\omega )=\pm \, coth(\zeta )\;\;\;\text{ or }\;\;\;cosh(\omega )=\pm \;\; tanh(\zeta ), \end{aligned}$$
(2.8)

where \(i=\sqrt{-1}\).

Step 3 We substitute Eq. (2.4), its derivative with fixed value of m along with Eq. (2.5) into Eq. (2.3) to get a polynomial in \(\omega ^{'s}sinh^{i}(\omega )cosh^{j}(\omega )\) \((s=0,1\; \text{ and }\;i,\;j=0,\;1,\;2,\;\ldots )\). We collect a group of over-determined nonlinear algebraic equations in \(A_{0},\;A_{j},\;B_{j},\;k\) by setting the coefficients of \(\omega ^{'s}sinh^{i}(\omega )cosh^{j}(\omega )\) to zero.

Step 4 The obtained set of over-determined nonlinear algebraic equations is then solved with aid of symbolic software to determine the values of the parameters \(A_{0},\;A_{j},\;B_{j},\;k\).

Step 5 Based on Eqs. (2.7) and (2.8), solutions of Eq. (2.1) have the following forms:

$$\begin{aligned} \Psi (\zeta )= & {} \sum _{j=1}^{m}tanh^{j-1}(\zeta )\big [\pm iB_{j}\;\;sech(\zeta )\pm A_{j}tanh(\zeta )\big ]+A_{0}, \end{aligned}$$
(2.9)
$$\begin{aligned} \Psi (\zeta )= & {} \sum _{j=1}^{m}coth^{j-1}(\zeta )\big [\pm B_{j}\;csch(\zeta )\pm A_{j}coth(\zeta )\big ]+A_{0}. \end{aligned}$$
(2.10)

3 Applications

In this section, the application of ShGEEM to Eq. (1.1) is presented.

Consider the the longitudinal wave equation (Eq. 1.1) given in Sect. 1. Substituting the travelling wave transformation

$$\begin{aligned} \psi =\Psi (\zeta ), \zeta= & {} \mu (x-kt) \end{aligned}$$
(3.1)
$$\begin{aligned} 2pk^{2}\mu ^{2}\Psi ^{''}-2(k^{2}-c_{0}^{2})\Psi +c_{0}^{2}\Psi ^{2}= & {} 0. \end{aligned}$$
(3.2)

We get \(m=2\) by balancing \(\Psi ^{''}\) and \(\Psi ^{2}\) in Eq. (3.2).

With \(m=2\), Eqs. (2.4), (2.9) and (2.10) take the form

$$\begin{aligned} \Psi (\omega )= & {} B_{1}sinh(w)+A_{1}cosh(\omega )+B_{2}cosh(\omega )sinh(\omega )+A_{2}cosh^{2}(\omega )+A_{0}, \end{aligned}$$
(3.3)
$$\begin{aligned} \Psi (\zeta )= & {} \pm iB_{1}\;sech(\zeta )\pm A_{1}tanh(\zeta )\pm iB_{2}tanh(\zeta )sech(\zeta )\pm A_{2}tanh^{2}(\zeta )+A_{0} \end{aligned}$$
(3.4)

and

$$\begin{aligned} \Psi (\zeta )=\pm \, B_{1}\;csch(\zeta )\pm A_{1}coth(\zeta )\pm B_{2}coth(\zeta )csch(\zeta )\pm coth^{2}(\zeta )+A_{0}, \end{aligned}$$
(3.5)

respectively.

Putting Eq. (3.3) and its second derivative along with Eq. (2.5) into Eq. (3.3), yields a polynomial in the power of hyperbolic functions. We collect a system of algebraic equations from the polynomial by equating each summations of the coefficients of the hyperbolic functions with the same power to zero. To obtain the values of the parameters involved, we simplify the system of the algebraic equations with aid of symbolic software. To get the new solutions to Eq. (1.1), we insert the obtained values of the parameters in each case into Eqs. (3.4) and (3.5).

Case 1 When

$$\begin{aligned} A_{0}=-3+\frac{3k^{2}}{v_{0}^{2}},\;A_{1}=0,\;B_{1}=0,\;A_{2}=3-\frac{3k^{2}}{v_{0}^{2}},\;B_{2}=0,\;\mu =\frac{\sqrt{k^{2}-v_{0}^{2}}}{2k\sqrt{p}}, \end{aligned}$$

we have

$$\begin{aligned} \psi _{1}(x,t)= & {} \frac{3(k^{2}-v_{0}^{2})}{v_{0}^{2}}sech^{2}\Big [\frac{\sqrt{k^{2}-v_{0}^{2}}}{2k\sqrt{p}}(x-kt)\Big ], \end{aligned}$$
(3.6)
$$\begin{aligned} \psi _{2}(x,t)= & {} 3\Big (1-\frac{k^{2}}{v_{0}^{2}}\Big )csch^{2}\Big [\frac{\sqrt{k^{2}-v_{0}^{2}}}{2k\sqrt{p}}(x-kt)\Big ]. \end{aligned}$$
(3.7)

Case 2 When

$$\begin{aligned} A_{0}=\frac{k^{2}-v_{0}^{2}-2\sqrt{(v_{0}^{2}-k^{2})^{2}}}{v_{0}^{2}},\;A_{1}=0,\;B_{1}=0,\;A_{2}=\frac{3\sqrt{(v_{0}^{2}-k^{2})^{2}}}{v_{0^{2}}},\;B_{2}=0, \end{aligned}$$

\(p=-\frac{\sqrt{(v_{0}^{2}-k^{2})^{2}}}{4k^{2}\mu ^{2}}\), we have

$$\begin{aligned} \psi _{3}(x,t)= & {} \frac{k^{2}-v_{0}^{2}+\sqrt{(v_{0}^{2}-k^{2})^{2}}-3\sqrt{(v_{0}^{2}-k^{2})^{2}}}{v_{0}^{2}}sech^{2}[\mu (x-kt)], \end{aligned}$$
(3.8)
$$\begin{aligned} \psi _{4}(x,t)= & {} \frac{k^{2}-v_{0}^{2}+\sqrt{(v_{0}^{2}-k^{2})^{2}}+3\sqrt{(v_{0}^{2}-k^{2})^{2}}}{v_{0}^{2}}csch^{2}[\mu (x-kt)]. \end{aligned}$$
(3.9)

Case 3 When

$$\begin{aligned} A_{0}=4-\frac{4}{1+p\mu ^{2}},\;A_{1}=0,\;B_{1}=0,\;A_{2}=-6+\frac{6}{1+p\mu ^{2}},\;B_{2}=-\frac{6p\mu ^{2}(p\mu ^{2}-1)}{\sqrt{(p^{2}\mu ^{4}-1)^{2}}}, \end{aligned}$$

\(v_{0}=k\sqrt{1+p\mu ^{2}},\) we have

$$\begin{aligned} \begin{aligned} \psi _{5}(x,t)&=4-\frac{4}{1+p\mu ^{2}}-\frac{6p\mu ^{2}(p\mu ^{2}-1)}{\sqrt{(p^{2}\mu ^{4}-1)^{2}}}i\;sech[\mu (x-kt)]tanh[\mu (x-kt)]\\&+\Big (-6+\frac{6}{1+p\mu ^{2}}\Big )tanh^{2}[\mu (x-kt)], \end{aligned} \end{aligned}$$
(3.10)
$$\begin{aligned} \begin{aligned} \psi _{6}(x,t)&=4-\frac{4}{1+p\mu ^{2}}-\frac{6p\mu ^{2}(p\mu ^{2}-1)}{\sqrt{(p^{2}\mu ^{4}-1)^{2}}}coth[\mu (x-kt)]csch[\mu (x-kt)]\\&+\Big (-6+\frac{6}{1+p\mu ^{2}}\Big )coth^{2}[\mu (x-kt)]. \end{aligned} \end{aligned}$$
(3.11)

Case 4 When

$$\begin{aligned} A_{0}=-3+\frac{3}{1-4p\mu ^{2}},\;A_{1}=0,\;B_{1}=0,\;A_{2}=3+\frac{3}{4p\mu ^{2}-1},\;B_{2}=0,\;v_{0}=k\sqrt{1-4p\mu ^{2}}, \end{aligned}$$

we have

$$\begin{aligned} \begin{aligned} \psi _{7}(x,t)=\frac{12p\mu ^{2}}{1-4p\mu ^{2}}sech^{2}[\mu (x-kt)], \end{aligned} \end{aligned}$$
(3.12)
$$\begin{aligned} \begin{aligned} \psi _{8}(x,t)=\frac{12p\mu ^{2}}{4p\mu ^{2}-1}csch^{2}[\mu (x-kt)]. \end{aligned} \end{aligned}$$
(3.13)

Case 5 When

$$\begin{aligned} A_{0}=4-\frac{4}{1+p\mu ^{2}},\;A_{1}=0,\;B_{1}=0,\;A_{2}=-6+\frac{6}{1+p\mu ^{2}},\;B_{2}=\frac{6p\mu ^{2}\sqrt{1-\frac{2}{1+p\mu ^{2}}}}{\sqrt{p^{2}\mu ^{4}-1}}, \end{aligned}$$

\(k=-\frac{v_{0}}{\sqrt{1+p\mu ^{2}}},\) we have

$$\begin{aligned} \psi _{9}(x,t)= & {} 2p\mu ^{2}\Bigg (\frac{3i\sqrt{1-\frac{2}{1+p\mu ^{2}}}}{\sqrt{p^{2}\mu ^{4}-1}}sech\Big [\mu \Big (x+\frac{v_{0}}{\sqrt{1+p\mu ^{2}}}t\Big )\Big ]\nonumber \\&\times tanh\Big [\mu \Big (x+\frac{v_{0}}{\sqrt{1+p\mu ^{2}}}t\Big )\Big ]+\frac{2-3tanh^{2}\Big [\mu \Big (x+\frac{v_{0}}{\sqrt{1+p\mu ^{2}}}t\Big )\Big ]}{1+p\mu ^{2}}\Bigg ), \end{aligned}$$
(3.14)
$$\begin{aligned} \psi _{10}(x,t)= & {} 4-\frac{4}{1+p\mu ^{2}}+6coth\Big [\mu \Big (x+\frac{v_{0}}{\sqrt{1+p\mu ^{2}}}t\Big )\Big ]\nonumber \\&\times \Bigg (\Big (-1+\frac{1}{1+p\mu ^{2}}\Big )coth\Big [\mu \Big (x+\frac{v_{0}}{\sqrt{1+p\mu ^{2}}}t\Big )\Big ]\nonumber \\&+\frac{p\mu ^{2}\sqrt{1-\frac{2}{1+p\mu ^{2}}}}{\sqrt{p^{2}\mu ^{4}-1}}csch\Big [\mu \Big (x+\frac{v_{0}}{\sqrt{1+p\mu ^{2}}}t\Big )\Big ]\Bigg ). \end{aligned}$$
(3.15)

Case 6 When

$$\begin{aligned} A_{0}=1+\frac{1}{-1-4p\mu ^{2}},\;A_{1}=0,\;B_{1}=0,\;A_{2}=-3+\frac{3}{1+4p\mu ^{2}},\;B_{2}=0,\;k=-\frac{v_{0}}{\sqrt{1+4p\mu ^{2}}}, \end{aligned}$$

we have

$$\begin{aligned} \begin{aligned} \psi _{11}(x,t)=\frac{4p\mu ^{2}}{1+4p\mu ^{2}}\Big (1-3tanh^{2}\Big [\mu \Big (x+\frac{v_{0}}{\sqrt{1+4p\mu ^{2}}}t\Big )\Big ]\Big ), \end{aligned} \end{aligned}$$
(3.16)
$$\begin{aligned} \begin{aligned} \psi _{12}(x,t)=\frac{4p\mu ^{2}}{1+4p\mu ^{2}}\Big (1-3coth^{2}\Big [\mu \Big (x+\frac{v_{0}}{\sqrt{1+4p\mu ^{2}}}t\Big )\Big ]\Big ). \end{aligned} \end{aligned}$$
(3.17)
Fig. 1
figure 1

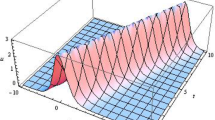
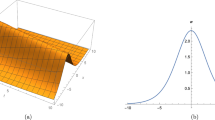
The a 3D, 2D surfaces b contour plot of the non-topological soliton [Eq. (3.6)]

Full size image
Fig. 2
figure 2

The a 3D, 2D surfaces b contour plot of the singular soliton [Eq. (3.7)]

Full size image
Fig. 3
figure 3

The a 3D, 2D surfaces b contour plot of the non-topological bell type soliton [imaginary part of Eq. (3.10)]

Full size image
Fig. 4
figure 4

The a 3D, 2D surfaces b contour plot of the topological soliton [real part of Eq. (3.10)]

Full size image
Fig. 5
figure 5

The a 3D, 2D surfaces b contour plot of the topological soliton [Eq. (3.16)]

Full size image

4 Conclusions

In this study, we constructed some topological, non-topological, non-topological bell type and singular soliton solutions to the longitudinal wave equation in a magneto-electro-elastic circular rod by using the extended sinh-Gordon equation expansion method. Under the choice of suitable parameters, the 2D, 3D and the contour graphs to some of the obtained solution are presented. The reported results in this study have some physical meanings which are related to the studied model, such as; the hyperbolic tangent that arises in the calculation of magnetic moment and rapidity of special relativity, the hyperbolic cotangent that arises in the Langevin function for magnetic polarization and the hyperbolic secant that arises in the profile of a laminar jet (Weisstein 2002). All the computations and the graphics plots in this study are carried out with help of the Wolfram Mathematica 11. Baskonus et al. (2016) secured various complex hyperbolic function solutions to Eq. (1.1) by utilizing the modified exp \((-\varphi (\zeta ))\)-expansion function method. Ma et al. (2013) obtained some hyperbolic and trigonometric function solutions to Eq. (1.1) by using the modified \((G^{'}/G)\)-expansion method. Younis and Ali (2015) obtained some dark, bright and singular solitons to Eq. (1.1) by utilizing the the solitary wave ansatz scheme. When we compare our results with the reported results in the literature, we observed that using the presented technique, the solution to Eq. (1.1) are reduced to topological, non-topological, non-topological bell type and singular soliton solutions. The extended sinh-Gordon equation expansion method is an efficient and simple computational scheme which provides good results when applied to various nonlinear evolution equations (Figs. 1, 2, 3, 4 and 5).