1 Introduction

The interaction between a structure and a fluid in which it is submerged or surrounding fluid flow is generally known as Fluid Structure Interaction (FSI). FSI problems exist in numerous applications of engineering such as the stability and response of aircraft wings, the flow of blood through arteries, the response of bridges and tall buildings to wind, the vibration of turbine and compressor blades, the oscillation of heat exchangers. The complexity of current engineering problems leads engineers to model all the elements of their environment with ever greater precision in order to improve the performance of systems [1]. Visual fluid models have many obvious applications in the industry including special effects and interactive games. Ideally, good computer graphics fluid model should both be easy to use and produce highly realistic results. The simulation of a fluid can be split into four main parts: advection, surface tracking, pressure projection and fluid–solid interaction. Each of these parts has been the focus of many research papers. The modeling of fluid flows is essential for mechanics and engineering, especially the fully developed turbulent flow which is the most common flow in circular pipes. Turbulence is an uncertain, chaotic, unsteady and unpredictable phenomenon [2]. Simulating physically realistic complex fluid behaviors in a distributed interactive simulation (DIS) presents a challenging problem for computer graphics researchers. In many applications, such as simulations involving a dynamic terrain, fluid flow interacts with the environment. Therefore, fluid conservation and the interaction of the flowing fluid with its environment are important issues to address. In addition to high visual quality and stability, simulation algorithms used in interactive applications must have predictable and constant computation time and robustness to all possible user inputs. Recently, Direct Numerical Simulations (DNS) has examined high-speed turbulent mixing layers and the interaction of shock waves with turbulence [3]. The main purpose of DNS is to solve (to best of our ability) for the turbulent velocity field without the use of “turbulent modeling”.

The subject of fluid–structure interaction is immensely vast and can cover almost any field of modern engineering. The main factors, which characterize fluid–structure interaction, are the geometry of the tube, the incompressibility of the fluid and the rigidity of the tube. The numerical solution of the resulting equations of the fluid–structure interaction problem poses great challenges since it includes the features of structural mechanics, fluid dynamics and their coupling. García et al. [4]. performed CFD simulation of complex phenomena in batch mode on large high performance computing (HPC) systems. Cucinotta et al. [5]. investigated, with a preliminary numerical study by means of Computational Fluid Dynamics (CFD), the Air Cavity Ships technology. Cherrad and Benchabane [6] proposed an interactive numerical process to control the evaporating temperature of refrigerant for solar adsorption cooling machine with a new correlation. Bahar et al. [7]. presented a CAD transfer method to visualize thermal simulation results in a virtual environment in order to optimize building design determined by energy efficiency. Amaya et al. [8]. developed a mathematical and numerical model of flow and combustion process for spark ignition engines using the principles of the first and second law of thermodynamics. Zhang et al. [9]. simulated the temperature change of the sinusoidal surface milling process by using the three-dimensional modeling software, Matlab and finite element analysis software.

Afzal [10] analyzed the open equations of thermal turbulent boundary layer subjected to pressure gradient by the method of matched asymptotic expansions at large Reynolds number. Gbadebo et al. [11]. developed an empirical correlation for local and average Nusselt numbers in the thermal entrance region of steady and pulsating turbulent air-flows in a pipe. Yan et al. [12]. investigated theoretically the turbulent flow in rectangular channels in ocean environment using CFD code FLUENT. Yan et al. [13]. investigated theoretically with CFD code FLUENT, the turbulent flow and heat transfer in triangular rod bundles. Weigand and Wrona [14] analyzed the heat transfer characteristics in the thermal entrance region of concentric annuli for laminar and turbulent internal flow. Habib et al. [15]. experimentally investigated heat transfer characteristics to turbulent pulsating pipe flows under a wide range of Reynolds number and pulsation frequency under uniform heat flux condition. Hui and Liejin  [16] investigated numerically a three-dimensional turbulent developing flow in a helical square duct with large curvature. Roy et al. [17]. conducted a numerical study of turbulent axisymmetric radial compressible channel flow between a nozzle and a flat plate. Eiamsa-ard and Changcharoen [18] also investigated numerically the heat transfers and flow characteristics in a channel with repeated ribs on one broad wall.

Taler [19] analyzed the heat transfers in turbulent pipe flow. Tian et al. [20]. analyzed the effects of Prandtl numbers on heat transfers of supercritical pressure fluids. In Taler’s later works resulted in a valid engineering model for flows subjected to uniform heat flux through a circular tube [21] for different Reynolds numbers Re Prandtl Pr, of which the number of Nusselt Nu was expressed as a function of friction factor ξ (Re). Belhocine and Wan Omar [22], and Belhocine [23] conducted a study to investigate the distribution of temperature in the pipes for a fully developed laminar flow. More recently, Belhocine and Wan Omar [24] solved the problem of convective heat transfers in circular pipes, whose solutions were in the form of the hypergeometric series. Belhocine and Abdullah [25] then used a similarity solution and Runge–Kutta method to visualize analytically the thermal boundary layer in the vicinity of the inlet of the circular pipe.

In this paper, a two-dimensional heat transfer in a fully developed turbulent flow in a circular duct is numerically investigated. The work utilizes a FORTRAN code which applied the finite difference method to solve thermal problems on two boundary conditions. The situation is relevant as an asymptotic case in several application fields in engineering design, as heat transfer and chemical catalysis. The interaction between a simple circular conduit and a fluid flow under turbulent, well-defined, uniform and fully developed inlet and outlet flow conditions was investigated. The work consisted of studies with constant wall temperature and surface heat flux with fully turbulent axisymmetric flow. The numerical results of the model were validated by comparing them with some results available in specialized literatures. The comparisons give good agreements with published data.

2 The flow governing equations

In a flow, the governing equations are the continuity, momentum and energy equations:

$$ \frac{{\partial \left( {\rho u_{i} } \right)}}{{\partial x_{i} }} = 0 $$
(1)
$$ \frac{\partial }{\partial t}\left( {\rho u_{i} } \right) + \frac{\partial }{{\partial x_{j} }}\left( {\rho u_{i} u_{j} } \right) = - \frac{\partial P}{{\partial x_{i} }} + \frac{\partial }{{\partial x_{j} }}\left[ {\mu \left( {\frac{{\partial u_{i} }}{{\partial x_{j} }} + \frac{{\partial u_{j} }}{{\partial x_{i} }} - \frac{2}{3}\delta_{ij} \frac{{\partial u_{j} }}{{\partial x_{i} }}} \right)} \right] + \frac{\partial }{{\partial x_{j} }}\left( { - \rho \overline{{u_{i}^{\prime } u_{j}^{\prime } }} } \right) $$
(2)
$$ \frac{\partial }{{\partial x_{i} }}\left[ {u_{i} \left( {\rho E + P} \right)} \right] = \frac{\partial }{{\partial x_{i} }}\left[ {\left( {\lambda + \frac{{c_{p} \mu_{t} }}{{\Pr_{t} }}} \right)\frac{\partial T}{{\partial x_{j} }} + \mu \mu_{t} \left( {\frac{{\partial u_{i} }}{{\partial x_{j} }} + \frac{{\partial u_{j} }}{{\partial x_{i} }} - \frac{2}{3}\delta_{ij} \frac{{\partial u_{j} }}{{\partial x_{i} }}} \right)} \right] $$
(3)

where \( \lambda \) is the thermal conductivity and E is the total energy expressed by.

$$ E = c_{p} T - P/\rho + u^{2} /2 $$

From the momentum equation a transport equation for the Reynolds stress tensor can be derived [26] as

$$ \frac{{\partial \left( {\rho \overline{{u_{i}^{\prime } u_{j}^{\prime } }} } \right)}}{\partial t} + C_{ij} = D_{T,ij} + D_{I,ij} + P_{ij} +\Phi _{ij} + \varepsilon_{ij} $$
(4)

where \( C_{ij} \), \( D_{T,ij} \), \( D_{I,ij} \), \( P_{ij} \), \( \Phi _{ij} \) and \( \varepsilon_{ij} \) are respectively the terms of convection, turbulent diffusion, molecular diffusion, shear stress production, stress–strain and viscosity dissipation.

$$ C_{ij} = \frac{\partial }{{\partial x_{k} }}\left( {\rho u_{k} \overline{{u_{i}^{\prime } u_{j}^{\prime } }} } \right) $$
(5)
$$ D_{T,ij} = - \frac{\partial }{{\partial x_{k} }}\left( {\rho \overline{{u_{i}^{\prime } u_{j}^{\prime } u_{k}^{'} }} + \overline{{P^{\prime } u_{i}^{'} }} \delta_{kj} + \overline{{P^{\prime } u_{j}^{'} }} \delta_{ik} } \right) $$
(6)
$$ D_{I,ij} = \frac{\partial }{{\partial x_{k} }}\left[ {\mu \frac{\partial }{{\partial x_{k} }}\left( {\overline{{u_{i}^{\prime } u_{j}^{\prime } }} } \right)} \right] $$
(7)
$$ P_{ij} = - \rho \left( {\overline{{u_{i}^{'} u_{k}^{'} }} \frac{{\partial u_{j} }}{{\partial x_{k} }} + \overline{{u_{j}^{'} u_{k}^{'} }} \frac{{\partial u_{i} }}{{\partial x_{k} }}} \right) $$
(8)
$$ \Phi _{ij} = \overline{{P^{\prime}\left( {\frac{{\partial u_{i}^{'} }}{{\partial x_{j} }} + \frac{{\partial u_{j}^{'} }}{{\partial x_{i} }}} \right)}} $$
(9)
$$ \varepsilon_{ij} = - 2\mu \overline{{\frac{{\partial u_{i}^{'} }}{{\partial x_{k} }}\frac{{\partial u_{i}^{'} }}{{\partial x_{k} }}}} $$
(10)

For computational stability, \( D_{T,ij} \), \( \Phi _{T,ij} \) and \( \varepsilon_{T,ij} \) which are defined as follows.

$$ D_{T,ij} = \frac{\partial }{{\partial x_{k} }}\left( {\frac{{\mu_{t} }}{{\sigma_{k} }}\frac{{\partial \overline{{u_{i}^{'} u_{j}^{'} }} }}{{\partial x_{k} }}} \right) $$
(11)

where \( \sigma_{k} = 0.82 \) and \( \mu_{t} \) is the turbulent viscosity, and

$$ \phi_{ij} = \phi_{ij,1} + \phi_{ij,2} + \phi_{ij,w} $$
(12)

with \( \phi_{ij,w} \), \( \phi_{ij,1} \) and \( \phi_{ij,2} \) are respectively the surface reflection term, slow term, and the rapid term. The last two terms are defined as follows

$$ \phi_{ij,1} = - C_{1} \rho \frac{\varepsilon }{k}\left( {\overline{{u_{i}^{'} u_{j}^{'} }} - \frac{2}{3}\delta_{ij} k} \right) $$
(13)
$$ \phi_{ij,2} = - C_{2} \left( {P_{ij} - \frac{2}{3}P \delta_{ij} } \right) $$
(14)

where C1 = 1.8 and C2 = 0.6.

As for the viscosity dissipation, the large-scale vortex is essentially engaged in the transport of momentum. Nevertheless, it was considered that dissipation was generated only in a small-scale isotropic vortex. So the equation for εi,j has been reduced to the following expression

$$ \varepsilon_{ij} = \frac{2}{3}\rho \varepsilon \delta_{ij} $$
(15)

3 Simplifying assumptions used in the turbulent flow analysis

The governing equations for convective heat transfer flow as presented above together form a very complex set of simultaneous partial differential equations. Analytical solutions to this set of equations could be realized for a few, relatively very simple cases. Numerical solutions for these equations for three-dimensional flow solutions may be relatively large and would require substantial computer resources.

The following two types of flow are, from a practical viewpoint, are probably the most important. For these two flows, some simplifying assumptions can be adopted.

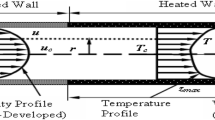
In the case of flow inside a duct, it can be assumed that the flow is fully developed. Basically, this means that it can be assumed that certain properties of the flow do not change with distance along the duct. Real duct flows well away from the entrance or other fittings could be said to be fully developed. Understanding the entrance length is important for the design and analysis of flow systems. The entrance region will have different velocity, temperature, and other profiles than exist in the fully developed region of the pipe.

For fully developed duct flows, it can be assumed that the fluid properties are constant, and the form of the velocity and temperature profiles does not change with distance along the duct. Such a condition could be presented in Fig. 1. If the velocity and temperature profiles are expressed in the form, then in fully developed flow, the velocity and temperature profile functions f and g are independent of the distance along the duct.

$$ \left( {\frac{u}{{u_{c} }}} \right) = f\left( {\frac{r}{D}} \right), \left( {\frac{{T - T_{c} }}{{T_{\omega } - T_{c} }}} \right) = g\left( {\frac{r}{D}} \right) $$
(16)
Fig. 1
figure 1

Thermally developing pipe flow

Full size image

This means that the velocity at any distance y from the center line of the duct remains constant with distance along the duct, and that the temperature at the same position, will vary relative to the center line and wall temperatures.

As such \( (T - T_{c} )/\left( {T_{\omega } - T_{c} } \right) \) remains constant. In fully developed flow, since u does not change, it follows that the velocity components in the radial and tangential directions will be zero.

4 Numerical procedure of the thermal problem

4.1 Thermally developing pipe flow

In this analysis, there is initially no thermal transfer until the flow is fully developed. Then only the heat transfer would begin, but the properties of the fluid are initially assumed to be constant [27]. Thus, the velocity field will not vary in this region. In our simulation, we had limited the thermal problem to the case of constant fluid properties, such that the corresponding equation for turbulent flow in the tube is given as [28]:

$$ \bar{u}\frac{{\partial \bar{T}}}{\partial z} + \bar{v}\frac{{\partial \bar{T}}}{\partial r} = \frac{1}{r}\frac{\partial}{\partial r}\left[{r\left({\epsilon_{H} + \alpha} \right)\frac{{\partial \bar{T}}}{\partial r}} \right] $$
(17)

The radial velocity component (\( \bar{\upsilon } \)) is zero as explained before. The energy equation describing the thermal problem is then given by the following form:

$$ \bar{u}\frac{{\partial \bar{T}}}{\partial z} = \frac{1}{r}\frac{\partial}{\partial r}\left[{r\left({\epsilon_{H} + \alpha} \right)\frac{{\partial \bar{T}}}{\partial r}} \right] $$
(18)

4.2 Boundary and initial conditions

The form of the governing equations used is quite parabolic while neglecting the longitudinal heat flux and considering only the radial flux. The mean velocity, \( \bar{u} \) is independent of z and varies according to r. We can then write Eq. (18) in this form

$$ \bar{u}\frac{{\partial \bar{T}}}{\partial z} = \frac{1}{r}\frac{\partial}{\partial r}\left[{r\left({\frac{\epsilon}{{Pr_{T}}} + \frac{\upsilon}{Pr}} \right)\frac{{\partial \bar{T}}}{\partial r}} \right] $$
(19)

The initial and boundary conditions applied to this equation are such that

when z = 0, \( \bar{T} = T_{i} \)

when r = d/2, \( \bar{T} = T_{\omega } \),

when r = 0, \( \frac{{\partial \bar{T}}}{\partial r} = 0 \).

4.3 Derivation of dimensionless formulas

For simplification purposes, it is important to convert this equation to a dimensionless form in order to solve the problem. For this reason, we will use the following variables:

$$ R = \frac{r}{D},\quad U = \frac{{\bar{u}}}{{\bar{u}_{m}}},\quad E = \frac{\epsilon}{\upsilon},\quad Z = \frac{z/D}{{Re_{D} Pr}} $$
(20)

where ReD is the Reynolds number of the average velocity \( \bar{u}_{m} \) through a tube of diameter D, defined as

$$ Re_{D} = \frac{{\bar{u}_{m} D}}{\upsilon } $$
(21)

The wall temperature is considered uniform and equal to \( T_{\omega } \). Thus the dimensionless temperature is defined as

$$ \theta = \frac{{\bar{T} - T_{i} }}{{T_{\omega } - T_{i} }} $$
(22)

where \( {\text{T}}_{\text{i}} \) is the initial fluid temperature before the heating is triggered. The substitution of dimensionless variables into Eq. (19) gives

$$ U\frac{\partial \theta }{\partial Z} = \frac{1}{R}\frac{\partial }{\partial R}\left[ {R\left( {E\frac{Pr}{{Pr_{T} }} + 1} \right)\frac{\partial \theta }{\partial R}} \right] $$
(23)

For our problem, we obtained the following boundary and initial condition

$$ Z = 0:\theta = 0 ,\quad R = 0.5:\theta = 1,\quad R = 0: \frac{\partial \theta }{\partial R} = 0. $$
(24)

4.4 The Thomas algorithm

The tridiagonal matrix algorithm is used for the resolution of a system with a tridiagonal matrix that was first developed by Llevellyn Thomas who bears his name (Thomas algorithm) and is a way to solve implicitly three diagonal system equations. We seek to solve a tridiagonal matrix system of the form:

$$ MU = D $$
(25)

where \( M \) is a matrix of dimensions N × N tridiagonal, that is to say a matrix whose all elements are null except on the main diagonal, the diagonal upper and the diagonal lower.

$$ \left( {\begin{array}{*{20}l} {b_{1} } \hfill & {c_{1} } \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill \\ {a_{2} } \hfill & {b_{2} } \hfill & {c_{2} } \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill \\ {} \hfill & {a_{3} } \hfill & {b_{3} } \hfill & {c_{3} } \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill \\ {} \hfill & {} \hfill & \ddots \hfill & \ddots \hfill & \ddots \hfill & {} \hfill & 0 \hfill & {} \hfill & {} \hfill \\ {} \hfill & {} \hfill & {} \hfill & \ddots \hfill & \ddots \hfill & \ddots \hfill & {} \hfill & {} \hfill & {} \hfill \\ {} \hfill & {} \hfill & 0 \hfill & {} \hfill & \ddots \hfill & \ddots \hfill & \ddots \hfill & {} \hfill & {} \hfill \\ {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & \ddots \hfill & \ddots \hfill & \ddots \hfill & {} \hfill \\ {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {a_{N - 1} } \hfill & {b_{N - 1} } \hfill & {c_{N - 1} } \hfill \\ {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {a_{N} } \hfill & {b_{N} } \hfill \\ \end{array} } \right). $$
(26)

The vectors \( U \) and \( D \), of dimension NX1, are written:

$$ U = \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} {u_{1} } \\ {u_{2} } \\ {u_{3} } \\ \end{array} } \\ {\begin{array}{*{20}c} \vdots \\ \vdots \\ \vdots \\ \end{array} } \\ {\begin{array}{*{20}c} \vdots \\ {u_{N - 1} } \\ {u_{N} } \\ \end{array} } \\ \end{array} } \right)\quad {\text{and}}\quad D = \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} {d_{1} } \\ {d_{2} } \\ {d_{3} } \\ \end{array} } \\ {\begin{array}{*{20}c} \vdots \\ \vdots \\ \vdots \\ \end{array} } \\ {\begin{array}{*{20}c} \vdots \\ {d_{N - 1} } \\ {d_{N} } \\ \end{array} } \\ \end{array} } \right) $$
(27)

In this algorithm, we first calculate the following coefficients:

$$ c_{1}^{\prime } = \frac{{c_{1} }}{{b_{1} }} $$
(28)
$$ c_{i}^{\prime } = \frac{{c_{i} }}{{b_{i} - a_{i} c_{i - 1}^{,} }}\quad {\text{for}}\;i = 2,3, \ldots ,N - 1 $$
(29)

And

$$ d_{1}^{\prime } = \frac{{d_{1} }}{{b_{1} }} $$
(30)
$$ d_{i}^{\prime } = \frac{{d_{i} - a_{i} d_{i - 1}^{\prime } }}{{b_{i} - a_{i} c_{i - 1}^{\prime } }}\quad {\text{for}}\quad i = 2,3, \ldots ,N $$
(31)

The unknowns \( u_{1} \), \( u_{2} \), …., \( u_{N} \) are then obtained by the formulas:

$$ u_{N} = d_{N}^{\prime } $$
(32)
$$ u_{i} = d_{i}^{\prime } - c_{i}^{\prime } u_{i + 1} \quad {\text{for}}\;i = N - 1,\;N - 2, \ldots ,2,1 $$
(33)

In CFD solution techniques, the algorithm in question is directly coded in the resolution process in contrast to machine-optimized subroutines that are used on a specific computer. A simple example of a FORTRAN program to adapt this algorithm is well illustrated in Fig. 2.

Fig. 2
figure 2

Subroutine Thomas written in FORTRAN 95

Full size image

4.5 The numerical method

Notice that the variations of the quantities U and E with R are known, as long as the fluid velocity is fully developed. The equation obtained will now be processed numerically by the finite difference method since it is better adapted to a medium with a wall temperature that varies according to the longitudinal coordinate Z. This method is simple in its concept but effective in its results, as such it is often used in heat transfer problems.

Figure 3 represents the nodal points used in the numerical simulation. Here, the finite difference method of approximations is introduced, and an explicit backward order of order 1 in the direction (i) is used where the variable U does not change, to evaluate values at the spatial coordinate (Z).

$$ U \left. {\frac{\partial \theta }{\partial Z}} \right|_{i,j} = U_{j} \left[ {\frac{{\theta_{i,j} - \theta_{i - 1,j} }}{{\Delta Z}}} \right]. $$
(34)
$$ \begin{aligned} &\left. \frac{1}{R}\frac{\partial }{\partial R} \left[ {R\left( {E\frac{Pr}{{Pr_{T} }} + 1} \right) \frac{\partial \theta }{\partial R}} \right] \right|_{i,j} = \frac{1}{{R_{j} }} \frac{2}{{\Delta R_{j + 1} + \Delta R_{j} }}\hfill \\ &\quad \times\,\left\{ \left[ {\frac{{R_{j + 1} \left( {E_{j + 1} Pr/Pr_{T} + 1} \right) + R_{j} \left( {E_{j} Pr/Pr_{T} + 1} \right)}}{2}} \right] \left( {\frac{{\theta_{i,j + 1} - \theta_{i,j} }}{{\Delta R_{j + 1} }}} \right)\right.\hfill \\ &\quad\left.- \left[ {\frac{{R_{j} \left( {E_{j} Pr/Pr_{T} + 1} \right) + R_{j - 1} \left( {E_{j - 1} Pr/Pr_{T} + 1} \right)}}{2}} \right]\left( {\frac{{\theta_{i,j} - \theta_{i,j - 1} }}{{\Delta R_{j} }}} \right) \right\}.\end{aligned} $$
(35)
Fig. 3
figure 3

Nodal points used in obtaining finite-difference solution

Full size image

By replacing the derivatives by its finite difference approximations obtained from Eq. (23), we obtain an equation in the following form:

$$ A_{j} \theta_{i,j} + B_{j} \theta_{i,j + 1} + C_{j} \theta_{i,j - 1} = D_{j} $$
(36)

The coefficients Aj, Bj, Cj and Dj resulting from the calculations are obtained from the mining form

$$ A_{j} = \frac{{U_{j} }}{{\Delta Z}} + \frac{1}{{R_{j} }} \frac{2}{{\Delta R_{j + 1} +\Delta R_{j} }} \times \left\{ {\begin{array}{*{20}c} {\left[ {\frac{{R_{j + 1} \left( {E_{j + 1} \Pr /\Pr_{T} + 1} \right) + R_{j} \left( {E_{j} \Pr /\Pr_{T} + 1} \right)}}{2}} \right] \times } \\ {\left( {\frac{1}{{\Delta R_{j + 1} }}} \right) + \left[ {\frac{{R_{j} \left( {E_{j} \Pr /\Pr_{T} + 1} \right) + R_{j - 1} \left( {E_{j - 1} \Pr /\Pr_{T} + 1} \right)}}{2}} \right]\left( {\frac{1}{{\Delta R_{j} }}} \right)} \\ \end{array} } \right\} $$
(37)
$$ B_{j} = - \frac{1}{{R_{j} }} \frac{2}{{\Delta R_{j + 1} +\Delta R_{j} }} \times \left\{ {\left[ {\frac{{R_{j + 1} \left( {E_{j + 1} \Pr /\Pr_{T} + 1} \right) + R_{j} \left( {E_{j} \Pr /\Pr_{T} + 1} \right)}}{2}} \right]\left( {\frac{1}{{\Delta R_{j + 1} }}} \right)} \right\} $$
(38)
$$ C_{j} = - \frac{1}{{R_{j} }} \frac{2}{{\Delta R_{j + 1} +\Delta R_{j} }} \times \left\{ {\left[ {\frac{{R_{j} \left( {E_{j} \Pr /\Pr_{T} + 1} \right) + R_{j - 1} \left( {E_{j - 1} \Pr /\Pr_{T} + 1} \right)}}{2}} \right]\left( {\frac{1}{{\Delta R_{j} }}} \right)} \right\} $$
(39)
$$ D_{j} = \frac{{U_{j} \theta_{i - 1,j} }}{{\Delta Z}} $$
(40)

Insertion of boundary conditions into the equations for this problem leads to \( \theta_{i,2} = \theta_{i,1} \) and \( \theta_{i,N} = 1 \). By exploiting this boundary conditions and applying at all “internal” points (j = 1, 2, 3, …, N − 2, N − 1) in Eq. (36), a system of N equations for N unknown \( \theta \) could be summarized in the following form.

$$ \begin{array}{*{20}c} {\theta_{i,1} - \theta_{i,2} = 0} \\ {A_{2} \theta_{i,2} + B_{2} \theta_{i,3} + C_{2} \theta_{i,1} = D_{2} } \\ {A_{3} \theta_{i,3} + B_{3} \theta_{i,4} + C_{3} \theta_{i,2} = D_{3} } \\ {A_{4} \theta_{i,4} + B_{4} \theta_{i,5} + C_{4} \theta_{i,3} = D_{4} } \\ \vdots \\ {A_{N - 1} \theta_{i,N - 1} + B_{N - 1} \theta_{i,N} + C_{N - 1} \theta_{i,N - 2} = D_{N - 1} } \\ {\theta_{i,N} = 1} \\ \end{array} $$
(41)

Or in matrix form

$$ \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} 1 & { - 1} & 0 \\ {C_{2} } & {A_{2} } & {B_{2} } \\ 0 & {C_{3} } & {A_{3} } \\ \end{array} } & {\begin{array}{*{20}c} 0 & 0 & \ldots \\ 0 & 0 & \ldots \\ {B_{3} } & 0 & { \ldots } \\ \end{array} } & { \begin{array}{*{20}c} {0 } & 0 & 0 \\ {0 } & 0 & { 0} \\ {0 } & 0 & { 0} \\ \end{array} } \\ {\begin{array}{*{20}c} 0 & { 0} & {C_{4} } \\ \vdots & { \vdots } & \vdots \\ 0 & 0 & 0 \\ \end{array} } & {\begin{array}{*{20}c} {A_{4} } & {B_{4} } & \ldots \\ \vdots & \vdots & \ddots \\ 0 & 0 & \ldots \\ \end{array} } & {\begin{array}{*{20}c} 0 & 0 & { 0} \\ \vdots & \vdots & \vdots \\ {C_{N - 1} } & {A_{N - 1} } & {B_{N - 1} } \\ \end{array} } \\ {\begin{array}{*{20}c} 0 & { 0} & { 0} \\ \end{array} } & {\begin{array}{*{20}c} {0 } & 0 & { \ldots } \\ \end{array} } & {\begin{array}{*{20}c} {0 } & 0 & { 0} \\ \end{array} } \\ \end{array} } \right] \times \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\theta_{i,1} } \\ {\theta_{i,2} } \\ {\theta_{i,3} } \\ \end{array} } \\ {\begin{array}{*{20}c} {\theta_{i,4} } \\ \vdots \\ {\theta_{i,N - 1} } \\ \end{array} } \\ {\theta_{i,N} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ {D_{2} } \\ {D_{3} } \\ \end{array} } \\ {\begin{array}{*{20}c} {D_{4} } \\ \vdots \\ {D_{N - 1} } \\ \end{array} } \\ 1 \\ \end{array} } \right] $$
(42)
$$ Q \theta_{i,j} = R $$
(43)

where Q is a tridiagonal matrix. This can be effectively solved by Thomas’s algorithm for tridiagonal matrix. For any value of Z, we can estimate the local heat transfer rate as follows:

$$ q_{\omega } = k \left. {\frac{{\partial \bar{T}}}{\partial r}} \right|_{r = R} $$
(44)

where \( q_{\omega } \) is derived from

$$ \frac{{q_{\omega } D}}{{k\left( {T_{\omega } - T_{i} } \right)}} = \left. {\frac{\partial \theta }{\partial R}} \right|_{R = 0.5} $$
(45)

This implies that

$$ Nu_{iD} = \left. {\frac{\partial \theta }{\partial R}} \right|_{R = 0.5} $$
(46)

where \( Nu_{iD} \) is the local number. Then

$$ Nu_{iD} = \frac{{q_{\omega } D}}{{k\left( {T_{\omega } - T_{i} } \right)}}. $$
(47)

However

$$ \left. {\frac{\partial \theta }{\partial R}} \right|_{i,1} = \frac{{\theta_{i,N} - \theta_{1,N - 1} }}{{\Delta R_{N} }}, $$
(48)

which means replacing Eq. (48) into Eq. (46) would result in

$$ Nu_{iD} = \frac{{\theta_{i,N} - \theta_{1,N - 1} }}{{\Delta R_{N} }} $$
(49)

This Nusselt number is based on the spacing between wall temperatures and local average temperatures, the flow via the pipe is practically considered, so we draw

$$ Nu_{D} = \frac{{q_{\omega } D}}{{k\left( {T_{\omega } - \bar{T}_{m} } \right)}} = \frac{{q_{\omega } D}}{k}Nu $$
(50)

where Nu is the averaged local Nusselt number. This can be expressed as \( Nu = \frac{1}{{T_{\omega } - \bar{T}_{m} }} \).

Substituting Eq. (47) into Eq. (50), allows us to write

$$ Nu_{D} = Nu_{iD} \frac{{T_{\omega } - T_{i} }}{{T_{\omega } - \bar{T}_{m} }} = \frac{{Nu_{iD} }}{{\theta_{m} }} $$
(51)

with

$$ \theta_{m} = \frac{{T_{\omega } - \bar{T}_{m} }}{{T_{\omega } - T_{i} }}. $$
(52)

We can then define the bulk temperature through the tube which is the temperature of the fluid that can be calculated by

$$ T_{b} = \frac{{\mathop \int \nolimits_{0}^{D/2} \rho 2\pi rdr\bar{u}c_{p} \bar{T}}}{{\mathop \int \nolimits_{0}^{D/2} \rho 2\pi rdr\bar{u}c_{p} }} $$
(53)

In this expression, the denominator indicates the multiplication of the specific heat integrated in the flow zone with the mass flow, while the numerator indicates that the total energy flowing through the tube. This results in the following expression

$$ \bar{T}_{m} = \frac{{\mathop \int \nolimits_{0}^{D/2} \bar{u}\bar{T}rdr}}{{\mathop \int \nolimits_{0}^{D/2} \bar{u}rdr}} $$
(54)

which can be written as

$$ \theta_{m} = \mathop \int \limits_{0}^{0.5} U\theta RdR/\mathop \int \limits_{0}^{0.5} URdR. $$
(55)

By using a pre-determined numeric value of θ with R for any value of Z, the values \( \theta_{m} \) can be drawn. So, we can determine the value of \( Nu_{D} \) at this value of Z.

The solution to this problem can then be obtained such that, we must specify the variations of U and E = (\( \epsilon/\upsilon_{\epsilon}/\upsilon \)) in which the distribution of E is given by the following equations

$$ \begin{array}{*{20}c} {y^{ + } < 5 : E = 0} \\ {5 \le y^{ + } \le 30 : E = \frac{{y^{ + } }}{5} - 1} \\ {y^{ + } > 30 : E = 1.6R\left( {y^{ + } } \right)^{6/7} - 1} \\ \end{array} $$
(56)

with

$$ y^{ + } = \frac{y}{\upsilon }\sqrt {\frac{{\tau_{\omega } }}{\rho }} = \left( {0.5 - R} \right)Re_{D} \sqrt {\frac{f}{8}} $$

in which f is the friction factor

$$ f = \frac{0.305}{{Re_{D}^{0.25} }}. $$
(57)

This is valid for hydraulically smooth pipe with turbulent flow up to the Reynolds number 105(Re < 105) giving

$$ \frac{{\bar{u}}}{{u_{c} }} = \left( {\frac{D - 2r}{D}} \right)^{1/7} $$
(58)

where \( \bar{u}_{c} \) means the center line speed. Now the value of \( \bar{u}_{m} \) becomes

$$ \bar{u}_{m} = \frac{8}{{D^{2} }}\mathop \int \limits_{0}^{D/2} \bar{u}rdr $$
(59)

which tends towards

$$ \frac{{\bar{u}_{m} }}{{\bar{u}_{C} }} = 8 \mathop \int \limits_{0}^{0.25} \left( {1 - 2R} \right)^{1/7} RdR = \frac{49}{60}. $$
(60)

By comparing the two equations, we can draw the following result

$$ U = \frac{49}{60}\left( {1 - 2R} \right)^{1/7} . $$
(61)

This equation finally yields the average values of the dimensionless velocity U as a function of the radius of tube R. A program in FORTRAN 95 was used to solve the thermal values in fully developed turbulent flow inside a cylindrical tube with uniform wall temperature. The program was based on the finite difference method.

5 Results and discussions

5.1 Uniform wall temperature

The average Nusselt number NuD along the pipe is shown in Fig. 4 for different Reynolds number ReD at Prandtl number Pr = 0.7. The Nu number helps to determine whether the flow is hydrodynamically fully developed, or otherwise. The decrease in Nu for Re = 100000 to 50000 is very significant such that it is suggests different flow regimes occurred at these two Reynolds number values. There is also a high gradient of Nu changes for axial positions near the entrance to the tube. These high gradients are caused by high friction in the flow near the entrance to the pipe.

Fig. 4
figure 4

Variation of Nusselt number NuDfor Pr = 0.7 at the thermal input entrance region and various values of ReD

Full size image

Using the results obtained from the calculation codes, the the Nusselt number variations for different Prandtl numbers are plotted against the pipe axial position as shown in Fig. 5. From an approximation of the distances from the tube thermal entrance, it has been found that variations in Prandtl number has significant effects on the Nusselt number values. This distance is defined as the thermal entrance length, which is important for engineers to design efficient heat transfer processes. In fact, although it is hard to see in the presented scale, different Prandtl values also yielded different Nu values for the isothermal wall condition.

Fig. 5
figure 5

Variation of Nusselt number NuD in the thermal entrance region for ReD = 105 for various values of Pr

Full size image

Dimensionless temperature results are plotted against dimensionless radial positions for the constant wall temperature case, for Reynolds numbers 50, 800, 3000, and 6000, are presented in Fig. 6. Figure 6 shows that when the Reynolds number is low, the temperature of the fluid varied markedly from the centre of the tube (equal to the inlet temperature) to the wall. This variation reduces as the Re is increased, to equal the wall temperature when as Re reaches 3000. Re being the ratio of inertial to frictional forces, which is related to the viscosity of the fluid, would increase gradually as the temperature of the heating fluid increases from the inlet values to the wall temperature values.

Fig. 6
figure 6

Dimensionless temperature profile (θ) along radial coordinate for different values of Reynolds numbers

Full size image

The dimensionless axial velocity profile, as a function of radial position for turbulent flow at Prandtl number Pr = 0.7 is depicted in Fig. 7. Fully developed laminar flow would produce the parabolic profile, while a turbulent flow would produce a much steeper slope near the wall. The axial velocity is maximum at the centerline and gradually decreases towards the wall, and as it nears the wall (dimensionless radius of 0.45) it reduces sharply to satisfy the no-slip boundary condition for viscous flow. This effect is a slight decrease of the shear stresses at the wall and an overall decrease of the pressure-drop.

Fig. 7
figure 7

Dimensionless axial velocity profile (U) for Pr = 0.7

Full size image

The dimensionless eddy viscosity distribution (E) along the dimensionless radius of the pipe at different values of the Reynolds numbers (Re) is shown in Fig. 8. It can be seen that the dimensionless eddy viscosity profiles also have a more uniform and almost coincide with the symmetric parabolic distribution. The concavity of this parabola varies with the Reynolds number. We see a significant change in maximum eddy viscosity towards the central part of the pipe at Reynolds number values above 6000. The turbulent regime begins in the pipe (Re˃4000). Indeed, the turbulent flow consists of eddies of various size ranges, which increase with increasing Reynolds number. The kinetic energy of the flow would cascade down from large to small eddies of interactional forces between the eddies.

Fig. 8
figure 8

Dimensionless eddy viscosity distribution (E) along the dimensionless radius (R) for Pr = 0.7 for various Reynolds numbers of the flow

Full size image

5.2 Wall heat flux uniform

Figure 9 shows the Nusselt number variations at the thermal entrance region for Pr = 0.7 plotted for different values of ReD in the case of uniform wall heat flux, in order to represent the augmentation in the heat transfer.

Fig. 9
figure 9

Variation of Nusselt number NuD in thermal entrance region for Pr = 0.7 for various values of ReD

Full size image

It can be seen that as Re increases above 10,000 the average Nusselt number for the circular tube starts to increase significantly. Axially the Nu values decreased rapidly from the entrance to a point of about Z = 5 × 10−5, after which the reduction is of lower and constant values as shown with the straight line graphs. The straight lines also show that the turbulent flow is fully developed. The development of the turbulent flow is significantly affected by the large Reynolds number values.

Nusselt number NuD variations with axial variations at Reynolds number 6000 and Prandtl number 0.7 as obtained from the program codes for fully developed turbulent flow in the tube with constant wall heat flux are shown in Table 1.

Table 1 Summarized results of the FORTRAN 95 code for uniform wall heat flux for Re = 6000 and Pr = 0.7
Full size table

The dimensionless temperature profiles along the dimensionless radius are plotted in Fig. 10 for Prandtl number 0.7 and various Reynolds numbers. Note that the effects of increasing the Reynolds number is to give a more “square” temperature profile, while a low Reynolds number yields a more rounded profile similar to that of laminar flow. As the Reynolds number increases to more than 3000 the dimensionless temperatures approach a constant value of 0.8, except at points near the wall of the tube.

Fig. 10
figure 10

Temperature behavior (θ) versus dimensionless radius (R) for various values of Reynolds number

Full size image

5.3 Comparison of constant wall temperature and heat flux cases

The calculations of the heat transfers in fully developed turbulent flow inside a circular pipe, the Nusselt numbers results for the case of constant wall temperature and the case of constant heat flux at constant Reynolds number of 104 (shown in Fig. 11) are compared. The Nusselt numbers in the case of uniform wall temperature are more than the numbers for wall in uniform heat flux. This Nu values decreased sharply exponentially at the entrance but as the flow moved away from the entrance, the Nu decreased at lower rates, resulting in two distinct values for the two thermal cases.

Fig. 11
figure 11

Comparison of Nu profile along the pipe for uniform wall temperature (UWT) and constant heat flux (UWH) for Re = 10,000

Full size image

5.4 Comparison of the present numerical model to previously published data

The results of this thermal problem simulation are compared to the work recently performed by Taler [21] using the finite difference method. Taler evaluated the Nu variations with Re for different Prandtl numbers. In addition, Nu were obtained for fully developed turbulent flow in tubes with constant wall heat flux after solving the energy conservation equation.

The variations of the Nu to Re for Pr = 0.7 from this work were compared to the results of Taler and shown in Fig. 12. The two results matched very well, with variations of not more than 2%. This shows that the model used in this work is verified and validated, and thus confirms the reliability of the numerical method and model for turbulent flow inside a circular tube used in this work.

Fig. 12
figure 12

Comparison of the results from the present work to those from Taler [21] for turbulent air flow in circular tube with constant wall heat flux

Full size image

6 Conclusions

The impact of our contribution on the prediction of the heat transfer rate at the wall of a pipe towards a fluid in turbulent flow is presented. Main attention was given to two dimensional and axi-symmetric flows through circular pipes. The analysis is based on the thermal equations of turbulent flow models which was solved using finite-difference method. The equations were adapted for any thermal boundary conditions, so long as the velocity profile is fully developed at the point where heat transfer starts. A FORTRAN program simulating the fully developed turbulent fluid flow through a circular tube, together with heat flow model, was developed. The program was then used to analyze two thermal boundary conditions of uniform wall temperature and constant heat flux. It was found that the surface temperature is higher with higher Reynolds numbers, due to the free convection dominant in the combined heat transfer process. The mean axial velocity and temperature profiles were found to increase and extend farther in the outer layer with increasing Reynolds numbers. This consequently made the local Nu numbers to be higher for high Re numbers. This is due to the forced convection that dominates the heat transfer process. The thermal flux results show the influences and sensitivities of some of the parameters involved in the calculations. The results obtained agree well with available literature with uncertainties of less than 2%. In the fully developed turbulent flow, the Nusselt number, as well as the dimensionless temperatures increase with increasing Reynolds numbers.

The results of Nu were also compared to published results,

It is also necessary to compare the numerical results of this work, especially the Nusselt numbers variations, temperature and velocity profiles with experimental data, but this could be done for now for the lack of the said data.

It should also be mentioned that the same solution procedure can be used for any dynamically developed velocity profiles and turbulent models in other conduit configurations such as channel geometries and rectangular, triangular or other tube sections. Different wall heating conditions, and viscous and other flows conditions could also be evaluated for different heating effects.