First and second thermodynamic law analyses applied to spark ignition engines modelling and emissions prediction

Abstract

A mathematical and numerical model of flow and combustion process for spark ignition engines is developed using the principles of the first and second law of thermodynamic. Availability (exergy) analysis is applied to cylinder of a spark ignition engine during the combustion process using a two-zone combustion model. Special attention is given to identification and quantification of irreversibility of combustion process and energy available basing on the isooctane fuel explosion. To predict emissions generation (greenhouse gases) a skeletal mechanism including 32 species and 61 reactions was developed and tested for different engine operations and exergy destructions.

1 Introduction

The best-known and most widely used internal combustion motor engine in the world is the spark-ignition gasoline engine. Therefore, many efforts have been done to optimize the combustion engine process to achieve: (1) rational use of fossil fuels, (2) minimization of noxious emissions and (3) reduction of greenhouse gases. However, optimization processes for internal combustion engines requires application of advanced software. In addition to experimental methods, numerical modeling calculations are needed to obtain an insight into this complex phenomenon. In engineering, modeling a process means developing and using the appropriate combination of assumptions and equations that allows modeling of critical features of the process to be analyzed. The modeling of engine processes continues to develop as our basic understanding of the physics and chemistry of the phenomena that occur inside the engine improves allowing to understand and optimize its operation. For the processes that govern engine performance and emissions, two basic types of models have been developed: (1) Thermodynamic based on energy conservation and (2) fluid dynamics, based on a full analysis of fluid motion. Thermodynamic energy conservation models are themselves categorized as: zero-dimensional (where geometric features of the fluid motion cannot be predicted), phenomenological (where additional details beyond the energy conservation equations are added for each phenomenon), and quasi-dimensional (where specific geometric features, (e.g., the spark-ignition engine flame) are added to the basic thermodynamic approach) [9]. Fluid-dynamic based models are often called multidimensional models due to their inherent ability to provide detailed geometric information on the flow field based on solution of the governing flow equations. Currently, it is not possible to construct models that predict engine operation from the basic governing equations alone. Therefore, the objectives of any model development should be clearly defined with its structure and detailed content appropriate to fulfill these objectives. It is impractical to construct models that attempt to describe all aspects of the operation of the engine because computational costs would be very high. Due to this complexity of engine processes and lack of robust numerical computational methods to solve all phenomenology governing equations, most engine models are incomplete and need empirical relations and approximations to solve the differential and algebraic equations systems and enable modeling and optimize the process. From the above, it is well understood that the multidimensional models are useful for predicting the detailed information of the cylinder charge during the engine cycle but are not practical for parametric studies of the effects of changes in design and operating variables on engine performance, efficiency and emissions. Therefore is developed a quasi-dimensional and phenomenological model from the first thermodynamic law and analyses of the energy quality in the combustion cycle from the second thermodynamic law are done. Profiles of thermodynamic and kinetic variables are obtained for each engine cycle and techniques for energy and environmental optimization are proposed based on the properties behavior.

2 First law analysis

These models are called quasi-dimensional and are phenomenological since additional details beyond the energy conservation equations are added for each phenomenon.

The quasi-dimensional model used is a hybrid one, meaning that it uses phenomenological sub-models to describe the various processes taking place inside the combustion chamber: heat transfer through the cylinder walls, fuel injection rate, fuel spray penetration, evaporation, combustion, and pollutants formation.

Many thermodynamic cycle models developed for the optimization of engine design and operating parameters use the turbulent combustion mechanism developed by the Soviet Academy of Sciences, Institute of Chemical Physics (ICP) for an ideal gas law [19, 23].Other authors have presented mathematical and numerical models of flow for four stroke spark ignition engines, based on a quasi-dimensional thermodynamic cycle model [11, 14] and others have used empirical correlations for heat release and combustion duration coupled with the quasi-dimensional model [1, 2], all of them have showed goods results for engine simulation. This type of models described correctly the properties fields compared with more accurate models (CFD) with a minimum error percent, allowing a very low computational time (6 min face 20h to CFD models) [25].

This work presents a model based on the energy conservation equation for a control volume and the assumption of spatially uniform to pressure, velocity, temperature and emissions concentration is taken. The basic equation for the engine model is derived from the conservation of energy (first thermodynamic law) applied to the cylinder control volume:

$$\begin{aligned} dU=\sum \limits _i h_i dm_i -dQ-dW \end{aligned}$$

(1)

Here, U is the internal energy of the cylinder gas mixture, Q the heat exchange of the cylinder contents with the environment (walls), W the work on the piston, $\hbox {h}_{\mathrm{i}}$ the specific enthalpy of in- or out-flowing gas, and dmi the mass flow into (+) or out of (-) the cylinder. Here the changes of kinetic and potential energy have despised.

The first thermodynamic law principle is applied to four engine cycles, since the process variables have different behavior in each stroke and must be modeled with different (Fig. 1) governing equations. Below are presented the energy conservation equations applied to each cycle (admission, compression, combustion and expansion).

Fig. 1

Four stroke cycle for spark ignition engines. (Wikipedia@, 2014)

2.1 Compression and expansion process

From the general conservation equation energy, equation (1) is expressed as:

$$\begin{aligned} \frac{d(mu)}{d\theta }=-\frac{dQ}{d\theta }-\frac{dW}{d\theta }+h\frac{dm}{d\theta } \end{aligned}$$

(2)

With $\hbox {du}/\hbox {d}\uptheta =\hbox {c}_{\mathrm{v}}\hbox {dT}/\hbox {d}\uptheta$ and h = u+RT for ideal gases, the following equation for temperature change is obtained:

$$\begin{aligned} \frac{dT}{d\theta }=\frac{1}{mc_v }\left[ {-\frac{dQ}{d\theta }-p\frac{dV}{d\theta }+RT\frac{dm}{d\theta }} \right] \end{aligned}$$

(3)

For the compression and expansion process the mass change is around zero. For obtain the pressure expression change, the ideal gas equation is differentiated:

$$\begin{aligned} V\frac{dp}{d\theta }+p\frac{dV}{d\theta }=RT\frac{dm}{d\theta }+mT\frac{dR}{d\theta }+mR\frac{dT}{d\theta } \end{aligned}$$

(4)

During compression, the cylinder gas composition can be assumed constant, during expansion it can be assumed to change only slowly, or $\hbox {dR}/\hbox {d}\uptheta = 0$ resulting in the following expression for the pressure profile:

$$\begin{aligned} \frac{dp}{d\theta }=\frac{1}{V}\left[ {mR\frac{dT}{d\theta }-p\frac{dV}{d\theta }} \right] \end{aligned}$$

(5)

2.2 Combustion process

During the process of combustion two discrete regions (two zone model) need to be accounted for to model the process: a region of the unburned fuel-air mixture (u) and a region where combustion has already taken place (b) with only fully burned gases or products of combustion (i.e: $\hbox {CO}_{2};\, \hbox {H}_{2}\hbox {O},\,\hbox {NO}_{\mathrm{x}}$). Two different sets of equations need to be developed in order for combustion to be correctly modeled. Conservation of energy is applied to the unburned gas zone resulting in the following equation:

$$\begin{aligned} \frac{d(m_u u_u )}{d\theta }=-\frac{dQ_u }{d\theta }-p\frac{dV_u }{d\theta }-h_u \frac{dm_b }{d\theta } \end{aligned}$$

(6)

Here, $\hbox {Q}_{\mathrm{u}}$ is the heat exchange between the unburned zone and the cylinder walls, $\hbox {V}_{\mathrm{u}}$ is the volume of the unburned zone, $\hbox {dm}_{\mathrm{b}}/\hbox {d}\uptheta$ is the mass burning rate. Conservation of energy for the burned gas zone is:

$$\begin{aligned} \frac{d(m_b u_b )}{d\theta }=-\frac{dQ_b }{d\theta }-p\frac{dV_b }{d\theta }+h_u \frac{dm_b }{d\theta } \end{aligned}$$

(7)

The total internal energy balance is obtained as the sum of the balances for burned and unburned zones (6) and (7):

$$\begin{aligned}&m_b c_{vb} \frac{dT_b }{d\theta }+m_u c_{vu} \frac{dT_u }{d\theta }+\left( {u_b -u_u } \right) \frac{dm_b }{d\theta } \nonumber \\&\quad =-\frac{dQ}{d\theta }-p\frac{dV}{d\theta } \end{aligned}$$

(8)

Differentiating the ideal gas equation for the two zones leads to:

$$\begin{aligned}&p\frac{dV_u }{d\theta }+V_u \frac{dp}{d\theta }=R_u T_u \frac{dm_u }{d\theta }+m_u R_u \frac{dT_u }{d\theta } \end{aligned}$$

(9)

$$\begin{aligned}&p\frac{dV_b }{d\theta }+V_b \frac{dp}{d\theta }=R_b T_b \frac{dm_b }{d\theta }+m_b R_b \frac{dT_b }{d\theta } \end{aligned}$$

(10)

Here $\hbox {R}_{\mathrm{b}}$ and $\hbox {R}_{\mathrm{u}}$ are the universal constant gas for burned and unburned zones. Using the correlation for ideal gases [$\hbox {c}_{\mathrm{vu}} + \hbox {R}_{\mathrm{u}} = \hbox {c}_{\mathrm{pu}}$] and combining Eqs. (6) and (9) one obtains and expression for the change of unburned zone gas temperature:

$$\begin{aligned} \frac{dT_u }{d\theta }=\frac{1}{m_u c_{pu} }\left( {V_u \frac{dp}{d\theta }-\frac{dQ_u }{d\theta }} \right) \end{aligned}$$

(11)

Using [$\hbox {c}_{\mathrm{vb}} + \hbox {R}_{\mathrm{b}} = \hbox {c}_{\mathrm{pb}}$] and substituting $\hbox {dV}_{\mathrm{u}}/\hbox {d}\uptheta$ and $\hbox {dV}_{\mathrm{b}}/\hbox {d}\uptheta$ from Eqs. (9) and (10) in the expression [$\hbox {dV}/\hbox {d}\uptheta = \hbox {dV}_{\mathrm{u}}/\hbox {d}\uptheta + \hbox {dV}_{\mathrm{b}}/\hbox {d}\uptheta$] gives:

$$\begin{aligned} \frac{dV}{d\theta }&= \frac{R_u T_u }{p}\frac{dm_u }{d\theta }+\frac{m_u R_u }{p}\frac{dT_u }{d\theta }-\frac{V_u }{p}\frac{dp}{d\theta }\nonumber \\&+\frac{R_b T_b }{p}\frac{dm_b }{d\theta }+\frac{m_b R_b }{p}\frac{dT_b }{d\theta }-\frac{V_b }{p}\frac{dp}{d\theta } \end{aligned}$$

(12)

Rearranging this equation and substituting Eq. (11) into (12), an equation for the rate of change of the burned gas temperature is obtained:

$$\begin{aligned} \frac{dT_b }{d\theta }&= \frac{1}{m_b R_b }\left( \frac{dV}{d\theta }p+\frac{dp}{d\theta }-\left( {R_b T_b -R_u T_u } \right) \frac{dm_b }{d\theta }\right. \nonumber \\&\left. -\frac{R_u }{c_{pu} }\left( {V_u \frac{dp}{d\theta }-\frac{dQ_u }{d\theta }} \right) \right) \end{aligned}$$

(13)

Finally substituting (11) and (13) in Eq. (8) is obtained an expression for the pressure change:

$$\begin{aligned} p=\frac{A}{B} \end{aligned}$$

(14)

where:

$$\begin{aligned} A&= \left( {1+\frac{c_{vb} }{R_b }} \right) p\frac{dV}{d\theta }+ \left[ \left( {u_b -u_u } \right) \right. \\&\left. -c_{vb} \left( {T_b -\frac{T_u R_u }{R_b }} \right) \right] \frac{dm_b }{d\theta } \\&+\left[ {\frac{c_{vu} }{c_{pu} }-\frac{c_{vb} R_u }{c_{pu} R_b }} \right] \frac{dQ_u }{d\theta }-\frac{dQ}{d\theta } \\ B&= -\left( {V_u \frac{c_{vu} }{c_{pu} }-\frac{c_{vb} }{c_{pu} }\frac{R_u }{R_b }V_u +\frac{Vc_{vb} }{R_b }} \right) \end{aligned}$$

For obtain more information about the flow features in the explosion cycle, is proposed a turbulent combustion sub-model which gives more details of geometric and parameters of combustion process.

2.2.1 Combustion burn rate sub-model

A functional form often used to represent the mass fraction burned versus crank angle is used the Wiebe Function Heywood et al. [15]:

$$\begin{aligned} x_b =1-\exp \left[ {-\alpha \left( {\frac{\theta -\theta _0 }{\Delta \theta }} \right) ^{m+1}} \right] \end{aligned}$$

(15)

where $\uptheta$ is the crank angle, $\uptheta _{0}$ is the angle where the start of combustion occurs, $\Delta \uptheta$ is the total combustion duration and $\upalpha$ and m are adjustable parameters. Actual mass fraction burned curves was fitted with $\upalpha = 4.6$ and $m = 2$ [16]. The mass fraction that remains unburned is given by $(1 - x_{\mathrm{b}})$. Differentiation of Eq. (15) with respect to crank angle (CA) yields the burning rate:

$$\begin{aligned} \frac{dx_b }{d\theta }=\left( {1-x_b } \right) \frac{a\left( {m+1} \right) }{\Delta \theta _b }\left( {\frac{\theta -\theta _0 }{\Delta \theta _b }} \right) ^{m} \end{aligned}$$

(16)

During combustion, close to the flame front turbulent eddies of characteristic radius $\hbox {l}_{\mathrm{t}}$ are developed. These eddies are entrained into the flame zone at a characteristic time $\tau _b$. To compute the burned and unburned mass rate was followed the same procedure proposed by Bayraktar et al. [2] with the following equations for turbulent combustion:

$$\begin{aligned} \frac{dm_e }{d\theta }=\rho _u A_f \left( {U_t +S_t } \right) \end{aligned}$$

(17)

Then, the rate of change of mass of the burned fraction is:

$$\begin{aligned} \frac{dm_b }{dt}=\rho _u A_f U_t +\frac{m_e -m_b }{\tau _b } \end{aligned}$$

(18)

where $\tau _b =\frac{l_t }{S_t }$ is the characteristic reaction time to burn the mass of an eddy of size $\hbox {l}_{\mathrm{t}},\,\hbox {m}_{\mathrm{e}}$ is the mass entrained by the flame front, $\hbox {U}_{\mathrm{t}}$ is the characteristic speed, $\hbox {A}_{\mathrm{f}}$ is the flame front area, ${\uprho }_{\mathrm{u}}$ is the unburned gas density and $\hbox {S}_{\mathrm{l}}$ is the laminar flame speed. The laminar flame speed is calculated with the Gülder et al. [12] and Keck et al. [18] correlation:

$$\begin{aligned} S_l =\frac{B}{\Delta \theta /\left( \frac{2\pi n}{60}\right) } \end{aligned}$$

(19)

Here n is the frequency of rotation of the crankshaft (rpm); B is the cylinder bore and $\Delta \theta$ the combustion duration. The enflame volume $\hbox {V}_{\mathrm{f}}$ is given by the following equation and it’s used to compute the flame front area $\hbox {A}_{\mathrm{f}}$:

$$\begin{aligned} V_f =V_b +\frac{m_e -m_b }{\rho _u } \end{aligned}$$

(20)

The parameter $\hbox {U}_{\mathrm{t}}$ is given by the Eq. (21):

$$\begin{aligned} U_t =0.08U_i \left( \frac{\rho _i }{\rho _u }\right) ^{\frac{1}{2}} \end{aligned}$$

(21)

$\hbox {l}_{\mathrm{t}}$ is empirically calculated depending on the maximum intake valve lift $\hbox {l}_{\mathrm{iv}}$ and the density ratio ${\uprho }_{\mathrm{i}}/{\uprho }_{\mathrm{u}}$ as follows:

$$\begin{aligned} l_t =0.8l_{iv} \left( \frac{\rho _i }{\rho _u }\right) ^{\frac{3}{4}} \end{aligned}$$

(22)

The burned and unburned fraction volumes are taken as:

$$\begin{aligned}&V_b =x_b V \end{aligned}$$

(23)

$$\begin{aligned}&V_u =\left( {1-x_b } \right) V \end{aligned}$$

(24)

where:

$$\begin{aligned} \dot{V}_{b} = - \dot{V}_{u} \quad \dot{m}_{b} = - \dot{m}_{u} \end{aligned}$$

(25)

A heat transfer sub-model is necessary apply in the combustion model to take account the heat losses of the gas to the cylinder walls and the consequent effect in the temperature and pressure distribution.

2.2.2 Heat transfer sub-model

Heat transfer between the two zones was neglected in the model; only the heat loss due to convection and radiation of burned and unburned gases with the surrounding combustion chamber walls is accounted, using the Annand’s formula [28]:

$$\begin{aligned}&\frac{dQ_u }{d\theta }=K_u A_u \left( {T_u -T_w } \right) +h_R \left( {T_u ^{4}-T_w ^{4}} \right) \end{aligned}$$

(26)

$$\begin{aligned}&\frac{dQ_b }{d\theta }=K_b A_b \left( {T_b -T_w } \right) +h_R \left( {T_b ^{4}-T_w ^{4}} \right) \end{aligned}$$

(27)

Here $\hbox {K}_{\mathrm{u}}$ and $\hbox {K}_{\mathrm{b}}$ are the heat transfer coefficients for burned and unburned zone and depend of the Reynolds number and the thermal conductivity of each zone. $\hbox {h}_{\mathrm{R}}$ is the radiation transfer coefficient, $\hbox {A}_{\mathrm{u}}$ and $\hbox {A}_{\mathrm{b}}$ are the areas of each zone and $\hbox {T}_{\mathrm{w}}$ is the transfer wall temperature which is taken as 420 K [16].The heat transfer for compression and expansion could be calculated with an easier expression

$$\begin{aligned} \frac{dQ}{d\theta }=KA\left( {T-T_w } \right) +h_R \left( {T^{4}-T_w ^{4}} \right) \end{aligned}$$

(28)

3 Second law analysis

Investigations and reports that have used the second law of thermodynamics to analyze the combustion process in internal combustion engines have been published for more than 40 years. For several decades, various authors have been trying to optimize processes in the internal combustion engine, where energy degradations occur during combustion. It is essential to get a better insight and understanding of the sources for this energy degradation to avoid or diminish them, striving to achieve higher efficiencies of internal combustion engines as the most effective heat engine. One of the most suitable ways in research of energy degradation is the application of the second law of thermodynamics in the analysis of the process in internal combustion engines. Furthermore, in the few past decades, it has been clearly understood that the first law of thermodynamics is not capable of providing a suitable insight into engine operations. For this reason, the use of the second law of thermodynamics has been intensified in internal combustion engines. A series of papers have been published on second law or exergy analysis applied to internal combustion engines lately. A review study on the application of exergy analysis with simple empirical combustion equations to SI engines was published by Kumar et al. [21] and Caton et al. [4, 5, 7] and was extended by Rakopoulos et al. [26] and Ismet Sezer et al. [3] whose performed studies with detailed combustion models.

In this work is used the second law to get a better insight into combustion chamber, and the basic energy equation for a closed system has been applied:

$$\begin{aligned} A=E+p_0 V-T_0 S \end{aligned}$$

(29)

Here E is the total energy, which is the sum of the internal, kinetic and potential energies, V and S are the volume and entropy of the system, respectively; and $\hbox {p}_{0}$ and $\hbox {T}_{0}$ are the fixed pressure and temperature of the dead state, respectively. Availability (or exergy) is defined as the maximum theoretical work that can be obtained from a combined system when the system comes into equilibrium with the environment. The availability balance for a closed system for any process can also be written as:

$$\begin{aligned} \Delta A=A_Q -A_W -A_{dest} \end{aligned}$$

(30)

where $\Delta \hbox {A}$ is the variation of the total system availability; $\hbox {A}_{\mathrm{Q}}$ is the availability transfer due to heat transfer interactions; $\hbox {A}_{\mathrm{W}}$ is the availability transfer due to work interactions; and $\hbox {A}_{\mathrm{dest}}$ is the destroyed availability by irreversible processes. Considering fuel chemical exergy, the exergy balance equation for the engine cylinder can be written as:

$$\begin{aligned} \frac{dA}{d\theta }&= \left( {1-\frac{T_0 }{T}} \right) \frac{dQ}{d\theta }-\left( {\frac{dW}{d\theta }-p_0 \frac{dV}{d\theta }} \right) \nonumber \\&+\frac{m_f }{m}\frac{dx_b }{d\theta }a_{f,ch} -\frac{dI_c }{d\theta } \end{aligned}$$

(31)

The fuel chemical exergy is calculated using the correlation developed by Ismet Sezer et al. [3] for liquid fuels:

$$\begin{aligned} a_{f,ch} m_f&= Q_{HLV} \left( 1.04+0.01728\frac{h}{c} \right. \nonumber \\&\left. +0.0432\frac{o}{c}+0.2196\frac{s}{c}( {1-2.06\frac{h}{c}}) \right) \end{aligned}$$

(32)

where $\hbox {Q}_{\mathrm{HLV}}$ is the lower heating value of the fuel and the quantities c, h, o, s represent the mass fractions of the elements carbon, hydrogen, oxygen and sulphur in the fuel, respectively. The last term on the right-hand side of Eq. (31) illustrates exergy destruction in the cylinder due to combustion. It is calculated as:

$$\begin{aligned} \frac{dI_c }{d\theta }=T_0 \frac{dS_{comb} }{d\theta } \end{aligned}$$

(33)

The rate of entropy generation due to combustion irreversibility’s is calculated from the two-zone combustion model depending on entropy balance and first law analysis:

$$\begin{aligned} \frac{dS_{comb} }{d\theta }=\frac{d(m_u s_u )}{d\theta }+\frac{d(m_b s_b )}{d\theta } \end{aligned}$$

(34)

where $\hbox {m}_{\mathrm{b}}$ and $\hbox {m}_{\mathrm{u}}$ are the masses and $\hbox {s}_{\mathrm{b}}$ and $\hbox {s}_{\mathrm{u}}$ are the specific entropy values of the burned and unburned gases respectively. The exergy destruction from the heat transfer process is calculated as:

$$\begin{aligned} \frac{dI_Q }{d\theta }=T_0 \frac{dS_Q }{d\theta } \end{aligned}$$

(35)

Entropy production sourced from heat transfer depends of the contribution of both zones [8]:

$$\begin{aligned} \frac{dS_Q }{d\theta }=\frac{Q_b }{T_b }+\frac{Q_u }{T_u } \end{aligned}$$

(36)

4 Geometric sub-model

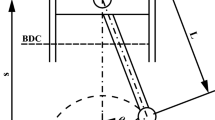
From the first and second thermodynamic law analysis can be seen that the change of properties depends of the volume gas profile (Fig. 2) in each cycle. Therefore is imperative developing a geometric sub-model to determinate an expression for V ($\uptheta$). A study of the rod-crank cylinder system was performed:

Fig. 2

Scheme of the rod-crank-slipper system proposed for the combustion cylinder rate volume

From the law of sine’s and complementary angles can be obtained relations between L, R and D:

$$\begin{aligned} \frac{R}{\sin \alpha }=\frac{L}{\sin \beta }=\frac{D}{\sin \gamma } \end{aligned}$$

(37)

with $\beta =180^{\circ }-\theta \quad \gamma =180^{\circ }-\left( {\alpha +\beta } \right)$ and $\gamma =\theta -\alpha$

$$\begin{aligned}&\sin (\beta )=\sin (180^{\circ }-\theta )=\sin (\theta ) \\&\cos (\beta )=\cos (180^{\circ }-\theta )=-\cos (\theta ) \end{aligned}$$

From these equations:

$$\begin{aligned} D=\sqrt{L^{2}-R^{2}\sin ^{2}(\beta )}+R\cos (\beta ) \end{aligned}$$

(38)

Then with S = (L+R) – D

$$\begin{aligned} \frac{S}{R}=\left( {\frac{L}{R}} \right) +\left( {1+\cos (\theta )} \right) -\sqrt{\left( {\frac{L}{R}} \right) ^{2}-\sin ^{2}\left( \theta \right) } \end{aligned}$$

(39)

The following expressions relate S with V, $\hbox {V}_{\mathrm{min}},\,\hbox {V}_{\mathrm{max}}$:

$$\begin{aligned}&\!\!\! \left( {\frac{\hbox {V}}{\hbox {V}_{\hbox {min}} }} \right) =1+\left( {\frac{\Delta \hbox {V}}{\hbox {V}_{\hbox {min}} }} \right) \end{aligned}$$

(40)

$$\begin{aligned}&\!\!\! \Delta V=S.A_p =\frac{S\pi D_p^2 }{4} \end{aligned}$$

(41)

$$\begin{aligned}&\!\!\! \Delta V_{\max } =S_{\max } .A_p =\frac{S_{\max } \pi D_p^2 }{4} \end{aligned}$$

(42)

With $\hbox {S}_{\mathrm{max}} =\hbox {2R}$.Then:

$$\begin{aligned}&\left( {\frac{V}{V_{\min } }} \right) =1+\left( {\frac{S\pi D_p^2 }{4V_{\min } }} \right) =1+\left( {\frac{S}{R}} \right) \left( {\frac{\pi D_p^2 R}{4V_{\min } }} \right) \end{aligned}$$

(43)

$$\begin{aligned}&\frac{\Delta V_{\max } }{V_{\min } }=\left( {rc-1} \right) \end{aligned}$$

(44)

Replacing Eq. (39) and (42) in (43) is obtained an expression to relate the cylinder gas volume with crank angle:

$$\begin{aligned} \frac{V\left( \theta \right) }{V_{min} }&= 1+\left( {\frac{r_c -1}{2}} \right) \left[ 1+\cos \left( \theta \right) +\left( {\frac{L}{R}} \right) \right. \nonumber \\&\left. -\sqrt{\left( {\frac{L}{R}} \right) ^{2}-\sin ^{2}\left( \theta \right) } \right] \end{aligned}$$

(45)

Here $\hbox {V}_{\mathrm{min}}$ is the combustion chamber volume.

To predict unburned and burned zone areas in contact with combustion chamber these areas were approximated using their respective mass fractions as weighting factors [26]:

$$\begin{aligned}&A_u =A_{cyl} \left( {1-\sqrt{x_b }} \right) \end{aligned}$$

(46)

$$\begin{aligned}&A_b =A_{cyl} \sqrt{x_b } \end{aligned}$$

(47)

Here $\hbox {A}_{\mathrm{cyl}}$ is the total area in contact with combustion gases:

$$\begin{aligned} A_{cyl} =\left( {\frac{\pi }{2}B^{2}} \right) +\left( {\frac{4V}{B}} \right) \end{aligned}$$

(48)

The start of combustion is initialized assuming the instantaneous formation of an ignition kernel at or shortly after the ignition timing. The ignition kernel for the simulation was taken with the assumptions done by Verhelst et al. [30]:

• $\hbox {m}_{\mathrm{b}}=0.01\hbox {m}_{\mathrm{tot}}$. The initial burned mass is one percent of the total cylinder mass.

• $\hbox {V}_{\mathrm{b}}=\hbox {V}_{\mathrm{cyl}}$/1,000. With $\hbox {V}_{\mathrm{b}}$ the inicial burn zone volume and $\hbox {V}_{\mathrm{cyl}}$ the maximum cylinder volume.

• $\hbox {r}_{\mathrm{f}}= 1/2$ mm. The initial flame Kernel radius

5 Chemical kinetic model

The necessity of predict the main emissions of internal combustion engines have led to many researches to perform chemical kinetics models for the oxidation of primary reference fuels as gasoline and it’s surrogates. However, at first the reduced chemistry used includes only the low temperature reactions required to describe the ignition process and couldn’t describe the complete combustion process responsible for the major energy release (Fig. 3). The first model developed was the shell model [13] that is a generalized model, in which the two stage ignition character of high carbon fuel is realized by an eight-step chain branching scheme including only five species. In order to avoid this drawback and make the fuel reaction kinetics closer to real process, many kinetic models have added additional information about high hydrocarbon oxidation. Tanaka et al. [27] extended the Hu and Keck model including two-stage ignition process and developed a reduced chemical kinetic model that included 32 species and 61 reactions taking into account the effects of wall heat transfer. Similar to Tanaka et al. [27], Jia et al. [17], Machrafi et al. [22] and Mehl et al. [24] developed reduce kinetic models for different fuel surrogates containing n-heptane, iso-octane and toluene and studied the effect of fuel composition in the auto ignition of gasoline. Those mechanisms were validated numerically against more detailed mechanisms models and experimentally against experimental shock tube and rapid compression machine data varying input variables as inlet temperature and pressure, equivalence ratio, compression ratio and spark timing. Small differences in the air/fuel ratio significantly influenced the total ignition timing, while the low temperature step was scarcely affected. On the contrary, the effect of model parameters (e.g., temperature distribution profiles) resulted to be of less importance in the considered condition. Likewise relatively high compression ratios were needed in order to auto-ignite the gasoline. Respect to the mixture fuel composition they found that the aromatics that are present in gasoline cause the so-called obstructed pre-ignition, followed by a delayed final ignition. This phenomenon can be explained by the competition generated between the consumption of the fuel and the formation of stable benzyl radicals from toluene. These models helped to Surushima et al. [29] to developed a more complete model including high temperature mechanism reactions, intermediates as olefins and aldehydes, and the consideration of beta-scission of alkyl radicals in parallel with the low-temperature reactions taken from Refs. [17, 22, 24, 27]. High temperature reactions mechanisms performed by Surushima et al. [29] were very simple and consist of the thermal decomposition of alkyl radicals to ethylene and the oxidation of ethylene and formaldehyde to products. The Beta-scission and thermal decomposition of alkyl radicals to ethylene consist of five elementary reactions and one global reaction, and oxidations of ethylene and formaldehyde consist of 10 elementary reactions and two additional global reactions. Shock tube ignition delay data and intermediate profiles from gas-sampling experiments in a HCCI (homogeneous charge compression ignition engine) were used to develop and validate the new model. Finally lately have been developed multi-zone models to improve the fluid dynamic understanding and the emissions prediction. The principle of these types of models is the division of the combustion chamber into zones based on geometrical considerations. Heat and mass is exchanged between zones and the cylinder wall according to their spatial configuration, throughout the engine strokes operation. Kominos et al. [20] and Chin et al. [29] considered the piston crevice and the area of fluid close to the cylinder walls as responsible largely for emissions and improved numerical models dividing the combustion chamber in several areas. With the assumption of equal pressure for all zones, analytical models were developed for the mass transfer between the core fluids and those in the piston crevice. The numerical model was solved for the coupled mass, energy, and species equations simultaneously leading to consistent solutions at every time step. Comparisons of the calculated results were made between this multi-zone code, a 3-D CFD model coupled with multiple zones, and experimental data showing good agreement.

To model completely the isooctane combustion process and minimize gas emissions is needed to model chemical reactions and achieve profiles of combustions gases in the crank angle domain. A skeletal mechanism including 32 species and 61 reactions was developed, which could predict satisfactorily ignition timing, burn rate and the emissions of HC, CO, $\hbox {CO}_{2}$ and $\hbox {NO}_{x}$ for our quasi-dimensional model. There are two approaches in the construction of the fuel kinetic oxidation. The first is based on mathematical analysis, and a typical example is the Shell model. Because this type of mechanism is far from the real reaction process, so the details of the reactions cannot be described, was used the second category named the hierarchical approach which built sequentially reaction mechanism for complex fuels and establish sub-mechanisms for simple fuel molecules and high temperatures reactions.

The low temperature mechanism was taken from the skeletal mechanism of Tanaka et al. [27], including the following reactions:

$$\begin{aligned} \hbox {C}_8 \hbox {H}_{18} +\hbox {O}_2 \leftrightarrow \hbox {C}_8 \hbox {H}_{17} +\hbox {HO}_2 \end{aligned}$$

(R1)

$$\begin{aligned} \hbox {C}_8 \hbox {H}_{17} +\hbox {O}_2 \leftrightarrow \hbox {C}_8 \hbox {H}_{17} \hbox {OO} \end{aligned}$$

(R2)

$$\begin{aligned} \hbox {C}_8 \hbox {H}_{17} \hbox {OO} \leftrightarrow \hbox {C}_8 \hbox {H}_{16} \hbox {OOH} \end{aligned}$$

(R3)

$$\begin{aligned} \hbox {C}_8 \hbox {H}_{16} \hbox {OOH}+\hbox {O}_2 \rightarrow \hbox {OOC}_8 \hbox {H}_{16} \hbox {OOH} \end{aligned}$$

(R4)

$$\begin{aligned} \hbox {OOC}_8 \hbox {H}_{16} \hbox {OOH} \rightarrow \hbox {OC}_8 \hbox {H}_{15} \hbox {OOH}+\hbox {OH} \end{aligned}$$

(R5)

$$\begin{aligned} \hbox {C}_8 \hbox {H}_{18} +\hbox {OH} \rightarrow \hbox {C}_8 \hbox {H}_{17} +\hbox {H}_2 \hbox {O} \end{aligned}$$

(R6)

$$\begin{aligned} \hbox {OC}_8 \hbox {H}_{15} \hbox {OOH} \rightarrow \hbox {OC}_8 \hbox {H}_{15} \hbox {O}+\hbox {OH} \end{aligned}$$

(R7)

$$\begin{aligned} \hbox {C}_8 \hbox {H}_{17} +\hbox {O}_2 \leftrightarrow \hbox {C}_8 \hbox {H}_{16} +\hbox {HO}_2 \end{aligned}$$

(R8)

This mechanism is followed by the reaction:

$$\begin{aligned} \hbox {HO}_2 +\hbox {HO}_2 \leftrightarrow \hbox {H}_2 \hbox {O}_2 +\hbox {O}_2 \end{aligned}$$

(R9)

Reactions (R8) and (R9) lower the reactivity of the system, producing that the temperature of the system rises slowly until the reaction (R10) becomes important and the thermal explosion is initiated.

$$\begin{aligned} \hbox {H}_2 \hbox {O}_2 +\hbox {M} \rightarrow \hbox {OH}+\hbox {OH}+\hbox {M} \end{aligned}$$

(R10)

The main products of the reactions (R1)–(R8) were $\hbox {C}_{8}\hbox {H}_{16}$ and $\hbox {OC}_{8}\hbox {H}_{15}\hbox {O}$. In order to describe the whole oxidation process, was taken the Jia et al. [17] sub-model that include three global reactions and directly decompose $\hbox {C}_{8}\hbox {H}_{16}$ and $\hbox {OC}_8 \hbox {H}_{15} \hbox {O}$ into CO and $\hbox {H}_{2}\hbox {O}$.

$$\begin{aligned} \hbox {OC}_8 \hbox {H}_{15} \hbox {O}+\hbox {O}_2 \rightarrow \hbox {C}_2 \hbox {H}_3 +2\hbox {CH}_2 \hbox {O}+\hbox {C}_3 \hbox {H}_4 \!+\!\hbox {CH}_3 \!+\!\hbox {HO}_2 \end{aligned}$$

(R11)

$$\begin{aligned} \hbox {C}_8 \hbox {H}_{17} \rightarrow \hbox {C}_4 \hbox {H}_8 +\hbox {C}_3 \hbox {H}_6 +\hbox {CH}_3 \end{aligned}$$

(R12)

$$\begin{aligned} \hbox {C}_8 \hbox {H}_{16} \rightarrow \hbox {C}_4 \hbox {H}_8 +\hbox {C}_3 \hbox {H}_5 +\hbox {CH}_3 \end{aligned}$$

(R13)

In these reactions the large molecules formed during the low temperature stage break up into smaller molecules. After these three reactions the isobutene $(\hbox {C}_{4}\hbox {H}_{8})$ was one of the major intermediates formed. Isobutene is decomposed further by the following reaction into smaller molecules [17].

$$\begin{aligned} \hbox {C}_4 \hbox {H}_8 +\hbox {O}_2 \rightarrow \hbox {C}_2 \hbox {H}_3 +\hbox {C}_2 \hbox {H}_4 +\hbox {HO}_2 \end{aligned}$$

(R14)

Tanaka et al. [27] ignore the process of the break into low carbon hydrocarbons, therefore it is difficult for Tanaka mechanism predict HC and CO emissions. In order to take account the break of high carbon hydrocarbons into low carbon hydrocarbons and predict HC (non burned hydrocarbon) and CO emissions a mechanism of 44 reactions of C1-C3 hydrocarbon oxidation developed by Patel et al. [18] was taken. With this complete mechanism could be predict no burned hydrocarbons as $\hbox {C}_{2}\hbox {H}_{3},\, \hbox {C}_{2}\hbox {H}_{4},\,\hbox {CH}_{4},\,\hbox {CH}_{3}$ and CO.

In the combustion of fuels that contain Nitrogen, nitric oxid ($\hbox {NO}_{\mathrm{X}}$) can be formed by three chemical routes: the termal or Zeldovivh mechanism,the Fenimore or prompt mechanism and the $\hbox {N}_{2}\hbox {O}$-intermediate mechanism. The thermal mechanism dominates in high temperature combustion over a fairly wide range of equivalence ratios, while the Fenimore mechanism is important in rich combustion. For the features of the system and high temperature chamber combustion the $\hbox {NO}_{\mathrm{X}}$ formation was modeled using the Zeldovich mechanism [10, 15].This mechanism consists of three reversible chain reactions:

$$\begin{aligned} \hbox {O}+\hbox {N}_2 \leftrightarrow \hbox {N}+\hbox {NO} \end{aligned}$$

(R59)

$$\begin{aligned} \hbox {O}_2 +\hbox {N} \leftrightarrow \hbox {O}+\hbox {NO} \end{aligned}$$

(R60)

$$\begin{aligned} \hbox {N}+\hbox {OH} \leftrightarrow \hbox {H}+\hbox {NO} \end{aligned}$$

(R61)

This mechanism was coupled to the fuel combustion chemistry though the $\hbox {O}_{2}$,O,H,OH species resulting in a complex and stiff kinetic model.

To model combustion reactions, a mole balance component was done into combustion chamber in temporal state without spatial variation. The most of the combustion reactions were considered elementary with some exceptions of no–elementary reactions. Hence the mole rate expression was:

$$\begin{aligned} \frac{dF_i }{d\theta }=\frac{(r_i .V)}{\omega } \end{aligned}$$

(49)

where $\hbox {F}_{\mathrm{i}}$ is the molar accumulation and $r_i$ represent the generation or consumption of each specie for the 61 combustion reactions. Hence the molar accumulation has a strong dependence of the reactions kinetic and the angular velocity of the crankshaft $\omega$.

$$\begin{aligned} r_i = \sum \limits _{j=1}^n r_{ij} \end{aligned}$$

(50)

The term $r_{ij}$ represents the kinetic of each reaction and depends of the cylinder temperature and the concentration of the species. The expression for $r_{ij}$ can be more simple for the elementary reactions since the concentration dependence is relate with the stoichiometric coefficients of the reaction. The temperature dependence was express with the Arrhenius expression.

$$\begin{aligned} k_{ij} =A_j T^{b}e^{\frac{-E_{aj} }{RT}} \end{aligned}$$

(51)

Here $A_j$ is a constant termed the pre-exponential factor or the frequency factor, $\hbox {E}_{\mathrm{a}}$ is the activation energy and b is an empirical parameter, all of them give for each combustion reaction.

6 Contribution of this article

This work presents a new general procedure for analyses the energetic efficiency and the thermal degradation of the combustion process in an internal combustion engine coupled with a hierarchical fuel kinetic model. An energetic and mechanical model is developed from the first and second law of thermodynamic coupled with a kinetic model including 32 species and 61 chemical reactions. The solution of the non-linear coupled ordinary differential system equations for combustion needs the construction of robust numerical techniques. The Non-linear stiff system equations are solved using a modified fourth order Runge-Kutta method computing the Jacobian matrix by finite differences in Matlab. The mathematical model is validated against other authors and are studied the effect of engine operation parameters over energy destruction and greenhouse gases production.

7 Numerical applications

7.1 Computing program and solution procedure

A computer code has been written in Matlab for the presented S.I. engine model. Input parameters in the software were $\hbox {r}_{\mathrm{c}}$, A/F relation, $\upomega$ (angular engine velocity), ${\uptheta }_{0}$, L/R engine relation, properties of the fuel and ambient pressure and temperature. The composition and Thermodynamic properties of the cylinder content (specific heat, enthalpy, internal energy and entropy) as functions of temperature were curve fitted to polynomials agree with a compilation published by the National Bureau of Standards, called the JANAF tables (1971).The compression and expansion process is modeled solving the ordinary differential Eqs. (3) and (5) coupled with the geometric sub model for the volume change expression Eq. (45). Profiles for the temperature, pressure and volume change were obtained in the compression and expansion cycle. For model the combustion cycle were solved the ordinary differential system Eqs. (11), (13), (14), (17), (18), (26) and (27) coupled with the algebraic equations of the heat transfer, geometric and combustion burn rate sub model. Profiles for $\hbox {T}_{\mathrm{u}},\,\hbox {T}_{\mathrm{b}}$, P, $\hbox {m}_{\mathrm{u}},\,\hbox {m}_{\mathrm{b}},\,\hbox {Q}_{\mathrm{u}},\, \hbox {Q}_{\mathrm{b}}$ variables in the two zone combustion model were obtained. The second law analysis was modeled simultaneously with the combustion first law model and the differential Eqs. (31), (33), (34), (35), and (36) were added to the system. Profiles for total, heat transfer and work energy availability were obtained in the combustion cycle coupled with profiles for chemical and heat transfer exergy destruction. The kinetic model was simulated coupled with the first law combustion model. Chemical species balances (Eq. 49) were solved coupled with Arrhenius Temperature dependence equations and a numerical method using an ode 13s subroutine was developed for the solution of the 93 stiff algebraic differential equations system. Profiles for air and fuel consumption were obtained with the production of pollutant gases and intermediaries of the hydrocarbon oxidation.

Fig. 3

Comparisons of computed and experimental cylinder pressures at 750 rpm

7.2 Validation of the model

To demonstrate the reliability of the presented cycle model, the predicted values are compared with the results presented by Hongquing et al. [16] regard with the engine specifications given in Table 1. Cylinder pressure (Fig. 3) and mean temperature (Fig. 4) were selected as the comparison parameters, and predictions for pressure and temperature are in good agreement with the experimental data obtained by Hongquing et al. [16]. Therefore, it can be said that the presented model has a sufficient level of confidence for the analysis of engine performance and parametric investigation since the error percent is below of 5 %.

Fig. 4

Comparisons of computed and experimental cylinder mean temperature at 750 rpm

Table 1 Specifications of engines (mm)

8 Results and discussion

Initially, some first law results are presented.Then is presented second law and chemical kinetic analysis. First results from geometric sub-model are presented in Figs. 5 and 6. In Fig. 5 is showed the change of cylinder gas volume for each engine cycle (admission-compression-combustion-exhaust),where combustion duration is 55$^{\circ }$CAD(-15$^{\circ }$ to 45$^{\circ }$CAD).The analysis is focused in the combustion cycle since during this process occur the most of energetic irreversibility’s and emissions production.

Fig. 5

Cylinder volume profile

In Fig. 6 is showed the volume gas profile for the unburned and burned zone from the geometric sub-model. It can be seen that as the fuel is burned decrease the volume of unburned area and increase the burned volume zone up to fill the combustion cylinder.

Fig. 6

Burned and unburned gas cylinder volume

The results for combustion sub-model (Sect. 2.2.1) and heat transfer sub-model (Sect. 2.2.2) can be seen bellow. Figure 7 shows the profile for burned and unburned mass gas cylinder for turbulent combustion. The mass for the unburned zone is consumed as combustion proceeds, while the mass for the burned zone increased during the combustion duration (55$^{\circ }$CAD).The burned mass gas fraction is showed in Fig. 8, which is calculated using the Wiebe function and becomes one at the end of combustion. The heat transfer process between the gases and wall cylinder is presented in Fig. 9 and becomes approximately 1,600 J taking account the contribution of the burned and unburned gas zone.

Fig. 7

Burned and unburned mass gas cylinder volume

Fig. 8

Burned mass gas fraction from the Wiebe Function

Fig. 9

Heat released from gas zones to wall cylinder

Figures 10 and 11 show the burned gas temperature and the unburned gas temperature as a function of crank angle for the combustion period. Before the top dead center (TDC, 0$^{\circ }$CAD) the temperature of the burned zone increased drastically due to the initial compression conditions (temperature and heat transfer). After the TDC the temperature begins to decreased due to the expansion process and work transfer. The change of the unburned temperature is similar to burned temperature and decreased at the end of combustion and the start of expansion.

Fig. 10

Temperature of burned gas zone

Fig. 11

Temperature of unburned gas zone

Figures 12, 13 and 14 show the second law analysis. The total availability of the cylinder charge is presented in Fig. 12, and its initial value (2,000 J) has two contributions: thermo-mechanical and chemical exergy (depends of the lower heating value of the fuel). With the burning, significant destruction of availability occurs, which is basically due to the irreversible process of the combustion and the heat transfer. At the end of combustion, the residual availability is about 52.5 % of the total availability. Figure 13 depicts the regularity for change of the availability associated with work and heat transfer as a function of crank angle. Before the TDC, the availability associated with work is negative, due to the compression effect of the piston travel as it moves towards the top dead center (TDC) position. After the TDC, the availability associated with work increases, and at the end of the combustion, it is up to the 205 J, about 10.25 % of the total fuel availability. At the same time, the heat transfer between the working medium and cylinder walls increased coming to 385 J, about 19.25 % of the total fuel availability. The availability associated with heat transfer continues to increase along with combustion process, since the temperature of the working medium is always higher than the cylinder walls. In Fig. 14 is shown the cumulative combustion and heat transfer irreversibility’s. This result shows that (369 J) 18.45 % of the total fuel availability is lost due to combustion irreversibility and 215 J (10.75 %) is lost for heat transfer irreversibility. The availability destruction due to the combustion increases sharply in the initial period of the burning process. Therefore postponed ignition or increased combustion duration help to reduce availability combustion destruction. However with the increased of the crank angle of combustion duration the availability destruction due to heat transfer increase at the higher temperature in the combustion chamber and the posterior increment in entropy occur.

Fig. 12

Instantaneous availability as a function of crank angle

Fig. 13

Availiability changes as a function of crank angle

Fig. 14

Availability destruction due to combustion and heat transfer

Figures 15 and 16 present the results for the mechanical model. Before the TDC, the availability associated with work is negative, due to the compression effect. After the TDC, the transfer work increases, and at the end of the combustion, it is up to the 350 J.The mean effective pressure (Fig. 15) is a key parameter to evaluate engine performance and gives an indication of the thrust of the gases during combustion and expansion phases, as well as heat and friction losses during an operation cycle. The maximum mean effective pressure is achieved at 25$^{\circ }$CAD.Advance the ignition crank angle and increase combustion duration improved the power and work transfer achieving higher thermal efficiency of the machine. This result is due at the greater pressure and temperature reached in the combustion chamber.

Fig. 15

Mean effective Power as a function of crank angle

Fig. 16

Work transfer during combustion

The results of the kinetic model are shown in Figs. 17, 18, 19, 20, 21, 22 and 23. The isooctane (fuel) and oxygen consumption are shown in Fig. 17. Fuel oxidation is initiated when H atoms are abstracted by oxygen molecules, and alkyl radicals and $\hbox {HO}_{2}$ are produced [Reaction (R1)]. At low temperature, in the sequence of reactions: an alkyl radical is oxidated by an oxygen addition [Reaction (R2)], an internal hydrogen is rearranged [Reaction (R3)], a second oxygen is added to a hydroperoxy alkyl radical [Reaction (R4)], and the product decomposes irreversibly [Reaction (R5)], as a result, an OH radical and a ketohydroperoxide are formed. The profile for OH and O radicals are shown in Fig. 23, both play an important role in fuel oxidation and in the $\hbox {CO}_{\mathrm{X}}$ and $\hbox {NO}_{\mathrm{x}}$ mechanisms been excellent catalysts.

Fig. 17

Fuel and oxygen consumption during the combustion cycle

Fig. 18

Unburned hydrocarbon production during the combustion cycle

Fig. 19

Modeling results for some species concentration during the combustion cycle

Fig. 20

Modeling results for Carbon monoxide production

Fig. 21

Modeling results for some species concentration

Exhaust gases leaving the combustion chamber of an SI engine contain up to 6,000 ppm of hydrocarbon components, the equivalent of 1–1.5 % of the fuel. About 40 % of this is unburned gasoline fuel components. The other 60 % consists of partially reacted components that were not present in the original fuel [15]. These consist of small non-equilibrium molecules which are formed when large fuel molecules break up (thermal cracking) during the combustion reaction. The HC (unburned hydrocarbon) production depends of gasoline blend, combustion chamber geometry and engine operating parameters as air-fuel relation, combustion duration and spark advance. The most considerable unburned hydrocarbon specie formed was the alkyl radical $\hbox {C}_{2}\hbox {H}_{3}$, which is produce for the incomplete isobutene oxidation [Reaction (R14)] reaching a concentration of 2,500 $\hbox {mg}/\hbox {m}^{3}$ at the end of combustion (Fig. 18).With a fuel-rich mixture there is no enough oxygen to react with all the carbon and hydrogen, resulting in high levels of HC in the exhaust products. Likewise if the mixture is too lean poorer combustion and misfire occur, resulting in high HC emissions. Hence if fuel and air enter at ideal stoichiometric relation (A/F = 14.7) a good combustion occur and HC emissions are minimized. The spark advance and the increase in the combustion duration generate a better collision between fuel and oxygen improving combustion and minimizing HC emissions.

If the combustion were perfect the only products would be the $\hbox {CO}_{2}$ (from the perfect oxidation of hydrocarbon), $\hbox {H}_{2}\hbox {O}$ and $\hbox {N}_{2}$ (atmospheric nitrogen without oxygen reaction). The results for $\hbox {N}_{2},\,\hbox {CO}_{2}$ and $\hbox {H}_{2}\hbox {O}$ concentrations whose are the main combustion products are shown in Fig. 19.

Results for carbon monoxide (CO) and acetaldehyde acid (HCO) concentration are presented in Figs. 20 and 21. Cabon monoxide emissions from internal combustion engines are controlled mainly by the fuel/air equivalence ratio. For fuel-rich mixtures, CO concentration in the exhaust increase by the excess of fuel and incomplete oxidation. Hence spark-ignition engines often operate close to stoichiometric air-fuel relation(14.7),causing that the production of HCO and CO during combustion are very low, indicating that the fuel carbon atoms are almost completely oxidized to $\hbox {CO}_{2}$ as it can be observed in Figs. 20 and 21,only a 5 mg/$\hbox {m}^{3}$ concentration is obtained by CO concentration without HCO production.

While nitric oxide (NO) and nitrogen dioxide ($\hbox {NO}_{2}$) are usually grouped as together as $\hbox {NO}_{\mathrm{x}}$ emissions, nitric oxid is the predominant oxide of nitrogen produce inside the engine cylinder. The principal source of NO is the oxidation of atmospheric nitrogen ($\hbox {N}_{2}$).The mechanism of NO formation from atmospheric nitrogen has been studied by the Zeldovich mechanism [R(59),R(60),R(61)].The results for NO formation is presented in Fig. 22, here the maximum value of NO concentration is reached at the ignition explosion(-15$^{\circ }$ to 0 $^{\circ }$CAD) when the temperature of the burned zone increase drastically due to the initial compression conditions. After the TDC the temperature of the burned zone fall causing the decrease in nitrogen oxides. At the end of combustion (40$^{\circ }$CAD) the NO concentration becomes 2,000 $\hbox {mg}/\hbox {m}^{3}$.Spark timing affects significantly NO emissions levels. The spark advance increased the peak cylinder pressure resulting in higher peak burned gas temperature and hence higher NO formation rates. For lower peak cylinder pressures, lower NO formation rates result.

Fig. 22

Modeling results for nitrogen oxides production

Fig. 23

Modeling results for some species concentration

9 Conclusions

In this work, a mathematical and numerical model was presented for a four stroke spark ignition engine, based on a quasi-dimensional thermodynamic cycle model. Simulations were performed for each cycle of the engine and the obtained results were in reasonable agreement with theoretical results. In thisstudy, second law analysis is applied to cylinder using a two zone combustion model and a kinetic model was developed for the isooctane oxidation for analyze the causes of greenhouse production. The following general conclusions can be written:

• 1. Results show that during the whole combustion process shortened combustion duration and postponed ignition are all helpful to reduce availability destruction.

• 2. Advance the ignition crank angle and increase combustion duration improved the power and work transfer achieving higher thermal efficiency of the machine.

• 3. Improving engine power increases the exergy destroyed and the entropy production. Therefore the mechanical engine optimization goes against the environmental principles.

• 4. Cabon monoxide emissions from internal combustion engines are controlled mainly by the fuel/air equivalence ratio. For fuel-rich mixtures, CO concentration in the exhaust increase by the excess of fuel and incomplete oxidation. Therefore a stoichiometric relation always is needed.

• 5. Spark timing affects significantly NO emissions levels. The spark advance and the increase of combustion duration result in higher peak burned gas temperature and hence higher NO formation rates. Entropy generation is directly related with NO levels.