Introduction

The turbulent flow is a state of a fluid moving in the direction of the flow guide, but with non-rectilinear trajectories. There will be trajectory crossing for all layers of fluid volume in motion which causes interactions between the fluid volumes and collisions on the walls of the flow guide. These collisions can cause noise. This type of flow is very hard to analyze. Turbulent flows of fluids are of importance in mechanical and engineering fields. They are encountered in a variety of engineering applications, e.g., drilling hydraulics, sewage transport, processing of mineral oil and polymer products, blood flow in arteries, and applications involving relatively high heat transfer rates. The fully developed turbulent flows of fluids in a stationary cylindrical tube have been studied numerically by several authors where they used the simulation of computer-based computation codes at different Reynolds numbers to better understand and analyze thermal problems. Jinnah [1] investigated the shock-induced turbulent flow fields and shock/turbulent-boundary layer interaction at the nozzle divergent. Jinnah and Takayama [2] solved Reynolds-averaged Navier–Stokes equations with k–ε turbulence model for numerical study of turbulent length scales. Majumder et al. [3] studied experimentally the turbulent fluid flow through a rectangular diffuser. Kumar et al. [4] analyzed the laminar hydrodynamically developed and thermally developing flow using finite volume method. Several studies [5,6,7,8,9,10,11] whether digital or experimental on fully developed turbulent channel flow were conducted actively. Gnielinski [12] developed the equation describing both the fully developed region of flow and the transition region through channels and pipes using an experimental data for high Prandtl and large Reynolds numbers. Taler [13] developed a correlation for the Nusselt number Nu in terms of the friction factor ξ (Re), Reynolds number Re, and also Prandtl number Pr, which is valid for transitional and fully developed turbulent flow in a circular tube subject to a uniform heat flux. Badus’haq [14] conducted an experimental study to determine steady-state local heat transfer characteristics for air flowing turbulently inside an electrically heated pipe.

Belhocine and Wan Omar [15], Belhocine [16] conducted an analysis to predict the distribution of the dimensionless temperature in a fully developed laminar flow in a cylindrical pipe. Recently, Belhocine and Wan Omar [17] were able to develop the analytical solution of the problem of convective heat transfer within a pipe whose solution obtained is in the form of the hypergeometric series. Belhocine and Wan Omar [18] used a similarity solution and Runge–Kutta method to analyze thermal boundary layer model at the entrance region of a circular tube.

In this paper, a two-dimensional fully developed mean turbulent fluid flow and heat transfer in a circular duct are numerically investigated using FORTRAN code which applies the finite difference method to solve the thermal problem for the two thermal boundary conditions, constant surface temperature, constant heat rate (constant surface heat flux), and steady, axisymmetric flow. Finally, the numerical results of our model developed in the document have been validated in good accuracy by comparing them with some correlation results available in the specialized literature.

Governing Equations

The governing equations are the continuity, momentum, and energy equations:

$$\frac{{\partial \left( {\rho u_{i} } \right)}}{{\partial x_{i} }} = 0$$
(1)
$$\begin{aligned} & \frac{\partial }{\partial t}\left( {\rho u_{i} } \right) + \frac{\partial }{{\partial x_{j} }}\left( {\rho u_{i} u_{j} } \right) = - \frac{\partial P}{{\partial x_{i} }} \\ & \quad + \frac{\partial }{{\partial x_{j} }}\left[ {\mu \left( {\frac{{\partial u_{i} }}{{\partial x_{j} }} + \frac{{\partial u_{j} }}{{\partial x_{i} }} - \frac{2}{3}\delta_{ij} \frac{{\partial u_{j} }}{{\partial x_{i} }}} \right)} \right] + \frac{\partial }{{\partial x_{j} }}\left( { - \rho \overline{{u_{i}^{'} u_{j}^{'} }} } \right) \\ \end{aligned}$$
(2)
$$\begin{aligned} & \frac{\partial }{{\partial x_{i} }}[u_{i} (\rho E + P)] \\ & \quad = \frac{\partial }{{\partial x_{i} }}\left[ {\left( {\lambda + \frac{{c_{\rm p} \mu_{t} }}{{Pr_{t} }}} \right)\frac{\partial T}{{\partial x_{j} }}} \right] + \mu \mu_{t} \left( {\frac{{\partial u_{i} }}{{\partial x_{j} }} + \frac{{\partial u_{j} }}{{\partial x_{i} }} - \frac{2}{3}\delta_{ij} \frac{{\partial u_{j} }}{{\partial x_{i} }}} \right) \\ \end{aligned}$$
(3)

where \(\lambda\) is the thermal conductivity and E is the total energy expressed by

$$E = c_{\rm p} T - P/\rho + u^{2} /2$$

From the momentum equation, a transport equation for the Reynolds stress tensor can be derived [19] as;

$$\frac{{\partial \left( {\rho \overline{{u_{i}^{'} u_{j}^{'} }} } \right)}}{\partial t} + C_{ij} = D_{T,ij} + D_{I,ij} + P_{ij} +\Phi _{ij} + \epsilon_{ij}$$
(4)

where \(C_{ij}\), \(D_{T,ij}\), \(D_{I,ij}\), \(P_{ij}\), \(\Phi _{ij}\), and \(\epsilon_{ij}\) are, respectively, the terms of convection, turbulent diffusion, molecular diffusion, shear stress production, stress–strain, viscosity dissipation

$$C_{ij} = \frac{\partial }{{\partial x_{k} }}\left( {\rho u_{k} \overline{{u_{i}^{'} u_{j}^{'} }} } \right)$$
(5)
$$D_{T,ij} = - \frac{\partial }{{\partial x_{k} }}\left( {\rho \overline{{u_{i}^{'} u_{j}^{'} u_{k}^{'} }} + \overline{{P^{{\prime }} u_{i}^{'} }} \delta_{kj} + \overline{{P^{{\prime }} u_{j}^{'} }} \delta_{ik} } \right)$$
(6)
$$D_{I,ij} = \frac{\partial }{{\partial x_{k} }}\left[ {\mu \frac{\partial }{{\partial x_{k} }}\left( {\overline{{u_{i}^{'} u_{j}^{'} }} } \right)} \right]$$
(7)
$$P_{ij} = - \rho \left( {\overline{{u_{i}^{'} u_{k}^{'} }} \frac{{\partial u_{j} }}{{\partial x_{k} }} + \overline{{u_{j}^{'} u_{k}^{'} }} \frac{{\partial u_{i} }}{{\partial x_{k} }}} \right)$$
(8)
$$\Phi_{ij} = \overline{{P^{{\prime }} \left( {\frac{{\partial u_{i}^{'} }}{{\partial x_{j} }} + \frac{{\partial u_{j}^{'} }}{{\partial x_{i} }}} \right)}}$$
(9)
$$\epsilon_{ij} = - 2\mu \overline{{\frac{{\partial u_{i}^{'} }}{{\partial x_{k} }}\frac{{\partial u_{i}^{'} }}{{\partial x_{k} }}}}$$
(10)

For computational stability, it has been used other expressions of the equations \(D_{T,ij}\), \(\Phi_{T,ij}\) and \(\epsilon_{T,ij}\) which are defined as this;

$$D_{T,ij} = \frac{\partial }{{\partial x_{k} }}\left( {\frac{{\mu_{t} }}{{\sigma_{k} }}\frac{{\partial \overline{{u_{i}^{'} u_{j}^{'} }} }}{{\partial x_{k} }}} \right)$$
(11)

Where \(\sigma_{k} = 0.82\) and \(\mu_{t}\) is the turbulent viscosity,

$$\phi_{ij} = \phi_{ij,1} + \phi_{ij,2} + \phi_{ij,w}$$
(12)

with \(\phi_{ij,w}\), \(\phi_{ij,1}\), and \(\phi_{ij,2}\) are, respectively, the surface reflection term, slow term, and the rapid term, where the last two are defined as follows:

$$\phi_{ij,1} = - C_{1} \rho \frac{\epsilon }{k}\left( {\overline{{u_{i}^{'} u_{j}^{'} }} - \frac{2}{3}\delta_{ij} k} \right)$$
(13)
$$\phi_{ij,2} = - C_{2} \left( {P_{ij} - \frac{2}{3}P \delta_{ij} } \right)$$
(14)

where C1 = 1.8 and C2 = 0.6.

With regard to viscosity dissipation, the large-scale vortex is essentially engaged in the transport of momentum. Nevertheless, it was considered that dissipation was generated only in a small-scale isotropic vortex (Fig. 1).

Fig. 1
figure 1

Flow in pipe

Full size image

So the equation for εi,j has been reduced to the following expression

$$\epsilon_{ij} = \frac{2}{3}\rho \epsilon \delta_{ij}$$
(15)

Simplifying Assumptions Used in the Turbulent Flow Analysis

The general equations governing convective heat transfer, i.e., the continuity, Navier–Stokes, and energy equations, together form a very complex set of simultaneous partial differential equations. Analytical solutions to this set of equations have only been found in a few, relatively very simple cases. Numerical solutions of these equations can be obtained using relatively moderately sized computers although the computer time involved with three-dimensional flow solutions may be relatively large.

The following two types of flow are, from a practical viewpoint, probably the most important in which such simplifying assumptions can be adopted.

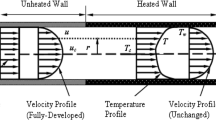
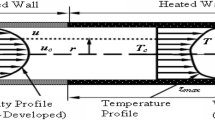
  • In the case of flow inside a duct, it can be assumed that the flow is fully developed. Basically, this means that it can be assumed that certain properties of the flow do not change with distance along the duct. Real duct flows well away from the entrance or other fittings are very nearly fully developed in many cases.

For fully developed duct flows in which it can be assumed that the fluid properties are constant, the form of the velocity and temperature profiles does not change with distance along the duct, i.e., considering the variables as defined in Fig. 2, if the velocity and temperature profiles are expressed in the form then in fully developed flow, the velocity and temperature profile functions f and g are independent of the distance along the duct.

$$\left( {\frac{u}{{u_{\text{c}} }}} \right) = f\left( {\frac{r}{D}} \right),\quad \left( {\frac{{T - T_{\text{c}} }}{{T_{\omega } - T_{\text{c}} }}} \right) = g\left( {\frac{r}{D}} \right)$$
(16)

This will mean that the velocity at any distance y from the center line of the duct will remain constant with distance along the duct and that the temperature at this position will vary in such a way relative to the center line and wall temperatures that \((T - T_{\text{c}} )/\left( {T_{\omega } - T_{\text{c}} } \right)\) remains constant. In fully developed flow because u is not changing, it follows that the velocity components in the radial and tangential coordinate directions will be zero.

Fig. 2
figure 2

Velocity and temperature profiles in a pipe flow

Full size image

Numerical Procedure of the Thermal Problem

Thermally Developing Pipe Flow

We are interested here in a thermal problem with an initially unheated elongated section for a flow inside a long pipe. For speed to be in this problem, fully developed before the beginning of the heating phase, this unheated section is considered sufficiently long. The temperature field develops when heating begins in this thermally developed region for a fluid with constant properties [20], whose velocity field will not be variable in this region. Figure 3 clearly shows the schematization of the flow considered.

Fig. 3
figure 3

Thermally developing pipe flow

Full size image

In our simulation, we will limit the thermal problem to the case of constant fluid properties; the corresponding equation for a turbulent flow in a tube is given as [21]:

$$\bar{u}\frac{{\partial \bar{T}}}{\partial z} + \bar{v}\frac{{\partial \bar{T}}}{\partial r} = \frac{1}{r}\frac{\partial}{\partial r}\left[{r\left({\epsilon_H + \alpha} \right)\frac{{\partial \bar{T}}}{\partial r}} \right]$$
(17)

The radial velocity component (\(\bar{\upsilon }\)) is zero because here the velocity profile is fully developed.

The energy equation describing the thermal problem we are dealing with is given in the following form:

$$\bar{u}\frac{{\partial \bar{T}}}{\partial z} = \frac{1}{r}\frac{\partial}{\partial r}\left[{r\left({\epsilon_{H} + \alpha} \right)\frac{{\partial \bar{T}}}{\partial r}} \right]$$
(18)

Boundary and Initial Conditions

The used form of the governing equations is quite parabolic while neglecting the longitudinal heat flux and considering only the radial flux. The mean velocity, \(\bar{u}\), is independent of z and varies according to r. We can write Eq. (18) like this

$$\bar{u}\frac{{\partial \bar{T}}}{\partial z} = \frac{1}{r}\frac{\partial}{\partial r}\left[{r\left({\frac{\epsilon}{{\Pr_{T}}} + \frac{\upsilon}{\Pr}} \right)\frac{{\partial \bar{T}}}{\partial r}} \right]$$
(19)

The initial and boundary conditions on the solution to this equation are:

$$\begin{aligned} & {\text{When}}\;z = 0,\;\bar{T} = T_{i} \\ & {\text{When}}\;r = D/2,\;\bar{T} = T_{\omega } \\ & {\text{When}}\;r = 0,\;\frac{{\partial \bar{T}}}{\partial r} = 0 \\ \end{aligned}$$

Derivation of Dimensionless Formulas

For simplification purposes, it is important to convert this equation to a dimensionless form in order to solve the problem. For this reason, we will use the following variables:

$$R = \frac{r}{D},\quad U = \frac{{\bar{u}}}{{\bar{u}_{m}}},\quad E = \frac{\epsilon}{\upsilon},\quad Z = \frac{z/D}{{\text{Re}_{D} \Pr}}$$
(20)

where ReD is the Reynolds as a of the average velocity \(\bar{u}_{m}\) through a tube of diameter D, is defined by

$$Re_{D} = \frac{{\bar{u}_{m} D}}{\upsilon }$$
(21)

The wall temperature is considered uniform and equal to \(T_{\omega }\). We will introduce the dimensionless temperature in the following; we can define it as follows:

$$\theta = \frac{{\bar{T} - T_{i} }}{{T_{\omega } - T_{i} }}$$
(22)

where \(T_{i}\) is the initial fluid temperature before the heating triggers. The substitution of dimensionless variables in Eq. (19), gives us

$$U\frac{\partial \theta }{\partial Z} = \frac{1}{R}\frac{\partial }{\partial R}\left[ {R\left( {E\frac{Pr}{{Pr_{T} }} + 1} \right)\frac{\partial \theta }{\partial R}} \right]$$
(23)

For our problem, this equation is subject to the following initial and boundary conditions

$$Z = 0:\theta = 0,\;R = 0.5:\theta = 1,\;R = 0: \frac{\partial \theta }{\partial R} = 0$$
(24)

The Thomas Algorithm

The tridiagonal matrix algorithm is used for the resolution of a system with a tridiagonal matrix that was first developed by Llewellyn Thomas who bears his name (Thomas algorithm) and is a way to solve implicitly three diagonal system equations.

We seek to solve a tridiagonal matrix system of the form:

$$MU = D$$
(25)

where M is a matrix of dimensions N × N tridiagonal, that is to say a matrix whose all elements are null except on the main diagonal, the diagonal upper and the diagonal lower.

$$\left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} {b_{1} } & {c_{1} } & {} \\ {a_{2} } & {b_{2} } & {c_{2} } \\ {} & {a_{3} } & {b_{3} } \\ \end{array} } & {\begin{array}{*{20}c} {} & {} & {} \\ {} & {} & {} \\ {c_{3} } & {} & {} \\ \end{array} } & {\begin{array}{*{20}c} {} & {} & {} \\ {} & {} & {} \\ {} & {} & {} \\ \end{array} } \\ {\begin{array}{*{20}c} {} & {} & \ddots \\ {} & {} & {} \\ {} & {} & 0 \\ \end{array} } & {\begin{array}{*{20}c} \ddots & \ddots & {} \\ \ddots & \ddots & \ddots \\ {} & \ddots & \ddots \\ \end{array} } & {\begin{array}{*{20}c} 0 & {} & {} \\ {} & {} & {} \\ \ddots & {} & {} \\ \end{array} } \\ {\begin{array}{*{20}c} {} & {} & {} \\ {} & {} & {} \\ {} & {} & {} \\ \end{array} } & {\begin{array}{*{20}c} {} & {} & \ddots \\ {} & {} & {} \\ {} & {} & {} \\ \end{array} } & {\begin{array}{*{20}c} \ddots & \ddots & {} \\ {a_{N - 1} } & {b_{N - 1} } & {c_{N - 1} } \\ {} & {a_{N} } & {b_{N} } \\ \end{array} } \\ \end{array} } \right)$$
(26)

and where the vectors \(U\) and \(D\), of dimension N, are written:

$$U = \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} {u_{1} } \\ {u_{2} } \\ {u_{3} } \\ \end{array} } \\ {\begin{array}{*{20}c} \vdots \\ \vdots \\ \vdots \\ \end{array} } \\ {\begin{array}{*{20}c} \vdots \\ {u_{N - 1} } \\ {u_{N} } \\ \end{array} } \\ \end{array} } \right)\;{\text{and}}\;D = \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} {d_{1} } \\ {d_{2} } \\ {d_{3} } \\ \end{array} } \\ {\begin{array}{*{20}c} \vdots \\ \vdots \\ \vdots \\ \end{array} } \\ {\begin{array}{*{20}c} \vdots \\ {d_{N - 1} } \\ {d_{N} } \\ \end{array} } \\ \end{array} } \right)$$
(27)

In this algorithm, we first calculate the following coefficients:

$$c_{1}^{{\prime }} = \frac{{c_{1} }}{{b_{1} }}$$
(28)
$$c_{i}^{{\prime }} = \frac{{c_{i} }}{{b_{i} - a_{i} c_{i - 1}^{{\prime }} }}\quad {\text{for}}\;i = 2,3, \ldots ,N - 1$$
(29)

And

$$d_{1}^{{\prime }} = \frac{{d_{1} }}{{b_{1} }}$$
(30)
$$d_{i}^{{\prime }} = \frac{{d_{i} - a_{i} d_{i - 1}^{{\prime }} }}{{b_{i} - a_{i} c_{i - 1}^{{\prime }} }}\quad {\text{for}}\;i = 2,3, \ldots ,N$$
(31)

The unknowns \(u_{1}\), \(u_{2}\), …, \(u_{N}\) are then obtained by the formulas:

$$u_{N} = d_{N}^{{\prime }}$$
(32)
$$u_{i} = d_{i}^{{\prime }} - c_{i}^{{\prime }} u_{i + 1} \quad {\text{for}}\;i = N - 1,\;N - 2, \ldots , 2,1$$
(33)

In CFD solution techniques, the algorithm in question is directly coded in the resolution process in contrast to machine-optimized subroutines that are used on a specific computer. A simple example of a FORTRAN program to adapt this algorithm is well illustrated in Fig. 4.

Fig. 4
figure 4

Subroutine Thomas written in FORTRAN 95

Full size image

The Numerical Method

Let us know the variations of the quantities U and E with R as long as the speed is fully developed. The equation obtained will now be processed numerically by the finite difference method since it is better adapted to a medium with a wall temperature that varies according to the longitudinal coordinate Z. This method is simple in its concept but effective in its results; it is often used in heat transfer problems.

Figure 5 represents the nodal points used in the numerical simulation. We introduce here the finite difference method of approximations, and we use an explicit backward order of order 1 in the direction (i) where the variable U does not change to evaluate the spatial coordinate (Z)

$$U \left. {\frac{\partial \theta }{\partial Z}} \right|_{i,j} = U_{j} \left[ {\frac{{\theta_{i,j} - \theta_{i - 1,j} }}{\Delta Z}} \right]$$
(34)
$$\begin{aligned} & \left. {\frac{1}{R}\frac{\partial }{\partial R}\left[ {R\left( {E\frac{\Pr }{{\Pr_{T} }} + 1} \right)\frac{\partial \theta }{\partial R}} \right]} \right|_{i,j}\quad = \frac{1}{{R_{j} }} \frac{2}{{\Delta R_{j + 1} + \Delta R_{j} }} \\ & \quad \left\{ {\left[ {\frac{{R_{j + 1} \left( {E_{j + 1} \Pr /\Pr_{T} + 1} \right) + R_{j} \left( {E_{j} \Pr /\Pr_{T} + 1} \right)}}{2}} \right]\left( {\frac{{\theta_{i,j + 1} - \theta_{i,j} }}{{\Delta R_{j + 1} }}} \right)} \right. \\ & \quad \left. { - \left[ {\frac{{R_{j} \left( {E_{j} \Pr /\Pr_{T} + 1} \right) + R_{j - 1} \left( {E_{j - 1} \Pr /\Pr_{T} + 1} \right)}}{2}} \right]\left( {\frac{{\theta_{i,j} - \theta_{i,j - 1} }}{{\Delta R_{j} }}} \right)} \right\} \\ \end{aligned}$$
(35)
Fig. 5
figure 5

Nodal points used in obtaining finite difference solution

Full size image

By replacing in Eq. (23), the derivatives by its finite difference approximations, we obtain an equation of the following form:

$$A_{j} \theta_{i,j} + B_{j} \theta_{i,j + 1} + C_{j} \theta_{i,j - 1} = D_{j}$$
(36)

The coefficients Aj, Bj, Cj, and Dj resulting from the calculations are obtained from the mining form

$$\begin{aligned} A_{j} & = \frac{{U_{j} }}{\Delta Z} + \frac{1}{{R_{j} }} \frac{2}{{\Delta R_{j + 1} + \Delta R_{j} }} \\ & \quad \times \left\{ {\left[ {\frac{{R_{j + 1} \left( {E_{j + 1} Pr/Pr_{T} + 1} \right) + R_{j} \left( {E_{j} Pr/Pr_{T} + 1} \right)}}{2}} \right]} \right. \times \left( {\frac{1}{{\Delta R_{j + 1} }}} \right) \\ & \quad \left. { + \left[ {\frac{{R_{j} \left( {E_{j} Pr/Pr_{T} + 1} \right) + R_{j - 1} \left( {E_{j - 1} Pr/Pr_{T} + 1} \right)}}{2}} \right]\left( {\frac{1}{{\Delta R_{j} }}} \right)} \right\} \\ \end{aligned}$$
(37)
$$\begin{aligned} B_{j} & = - \frac{1}{{R_{j} }} \frac{2}{{\Delta R_{j + 1} + \Delta R_{j} }} \\ & \quad \times \left\{ {\left[ {\frac{{R_{j + 1} \left( {E_{j + 1} Pr/Pr_{T} + 1} \right) + R_{j} \left( {E_{j} Pr/Pr_{T} + 1} \right)}}{2}} \right]\left( {\frac{1}{{\Delta R_{j + 1} }}} \right)} \right\} \\ \end{aligned}$$
(38)
$$\begin{aligned} C_{j} & = - \frac{1}{{R_{j} }} \frac{2}{{\Delta R_{j + 1} + \Delta R_{j} }} \\ & \quad \times \left\{ {\left[ {\frac{{R_{j} \left( {E_{j} Pr/Pr_{T} + 1} \right) + R_{j - 1} \left( {E_{j - 1} Pr/Pr_{T} + 1} \right)}}{2}} \right]\left( {\frac{1}{{\Delta R_{j} }}} \right)} \right\} \\ \end{aligned}$$
(39)
$$D_{j} = \frac{{U_{j} \theta_{i - 1,j} }}{\Delta Z}$$
(40)

Insertion of boundary conditions of the problem leads us to \(\theta_{i,2} = \theta_{i,1}\) and \(\theta_{i,N} = 1\). By exploiting boundary conditions while applying all “internal” points (j = 2.3,…, N − 2, N − 1) in equation Eq. (36). We get a system of N equations for N unknowns \(\theta\) summarized from the following form

$$\begin{aligned} & \theta_{i,1} - \theta_{i,2} = 0 \\ & A_{2} \theta_{i,2} + B_{2} \theta_{i,3} + C_{2} \theta_{i,1} = D_{2} \\ & A_{3} \theta_{i,3} + B_{3} \theta_{i,4} + C_{3} \theta_{i,2} = D_{3}\\& A_{4} \theta_{i,4} + B_{4} \theta_{i,5} + C_{4} \theta_{i,3} = D_{4} \\ & \vdots \\ & A_{N - 1} \theta_{i,N - 1} + B_{N - 1} \theta_{i,N} + C_{N - 1} \theta_{i,N - 2} = D_{N - 1} \\ & \theta_{i,N} = 1 \\ \end{aligned}$$
(41)

Or else, in the following matrix form

$$\begin{aligned} \left[ {\begin{array}{*{20}c} 1 & { - 1} & 0 & 0 & 0 & \ldots & 0 & 0 & 0 \\ {C_{2} } & {A_{2} } & {B_{2} } & 0 & 0 & \ldots & 0 & 0 & 0 \\ 0 & {C_{3} } & {A_{3} } & {B_{3} } & 0 & \ldots & 0 & 0 & 0 \\ 0 & 0 & {C_{4} } & {A_{4} } & {B_{4} } & \ldots & 0 & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots \\ 0 & 0 & 0 & 0 & 0 & \ldots & {C_{N - 1} } & {A_{N - 1} } & {B_{N - 1} } \\ 0 & 0 & 0 & 0 & 0 & \ldots & 0 & 0 & 0 \\ \end{array} } \right] \times \left[ {\begin{array}{*{20}c} {\theta_{i,1} } \\ {\theta_{i,2} } \\ {\theta_{i,3} } \\ {\theta_{i,4} } \\ \vdots \\ {\theta_{i,N - 1} } \\ {\theta_{i,N} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 0 \\ {D_{2} } \\ {D_{3} } \\ {D_{4} } \\ \vdots \\ {D_{N - 1} } \\ 1 \\ \end{array} } \right] \hfill \\ \hfill \\ \end{aligned}$$
(42)
$$Q \theta_{i,j} = R$$
(43)

where Q is a tridiagonal matrix. This can be effectively solved by Thomas’s algorithm for tridiagonal matrix.

For any value of Z, we can estimate the local heat transfer rate as follows:

$$q_{\omega } = k \left. {\frac{{\partial \bar{T}}}{\partial r}} \right|_{r = R}$$
(44)

from where

$$\frac{{q_{\omega } D}}{{k\left( {T_{\omega } - T_{i} } \right)}} = \left. {\frac{\partial \theta }{\partial R}} \right|_{R = 0.5}$$
(45)

which implies

$$Nu_{iD} = \left. {\frac{\partial \theta }{\partial R}} \right|_{R = 0.5}$$
(46)

where \(Nu_{iD}\) is the local number of Nusselt, based on the difference between the inlet temperature and that of the wall, then

$$Nu_{iD} = \frac{{q_{\omega } D}}{{k\left( {T_{\omega } - T_{i} } \right)}}$$
(47)

However,

$$\left. {\frac{{\partial \theta }}{{\partial R}}} \right|_{{i,1}} = \frac{{\theta _{{i,N}} - \theta _{{1,N - 1}} }}{{\Delta R_{N} }}$$
(48)

Replacing Eqs. (6) into (4), we obtain

$$Nu_{iD} = \frac{{\theta_{i,N} - \theta_{1,N - 1} }}{{\Delta R_{N} }}$$
(49)

We use the Nusselt number based on the difference between the local average temperatures and that of the wall because the flow via the pipe is practically considered, so we draw

$$Nu_{D} = \frac{{q_{\omega } D}}{{k\left( {T_{\omega } - \bar{T}_{m} } \right)}} = \frac{{q_{\omega } D}}{k}Nu$$
(50)

Where Nu is the averaged local Nusselt number can be expressed as: \(Nu = \frac{1}{{T_{\omega } - \bar{T}_{m} }}\)

By substituting the previous Eqs. (47) in (50), this allows us to write

$$Nu_{D} = Nu_{iD} \frac{{T_{\omega } - T_{i} }}{{T_{\omega } - \bar{T}_{m} }} = \frac{{Nu_{iD} }}{{\theta_{m} }}$$
(51)

With

$$\theta_{m} = \frac{{T_{\omega } - \bar{T}_{m} }}{{T_{\omega } - T_{i} }}$$
(52)

We can define the bulk temperature through the tube which is the temperature of the medium energy fluid that we can calculate it like this

$$T_{\rm b} = \frac{{\mathop \int \nolimits_{0}^{D/2} \rho 2\pi r{\text{d}}r\bar{u}c_{\rm p} \bar{T}}}{{\mathop \int \nolimits_{0}^{D/2} \rho 2\pi r{\text{d}}r\bar{u}c_{\rm p} }}$$
(53)

In this expression, the denominator indicates the product of the mass flow and the specific heat integrated on the flow zone, while the numerator indicates the total energy flow through the tube. Now, we have the following expression

$$\bar{T}_{m} = \frac{{\mathop \int \nolimits_{0}^{D/2} \bar{u}\bar{T}r{\text{d}}r}}{{\mathop \int \nolimits_{0}^{D/2} \bar{u}r{\text{d}}r}}$$
(54)

We can write so

$$\theta_{m} = \int_{0}^{0.5} {U \theta R{\text{d}}R} /\int_{0}^{0.5} {U R{\text{d}}R}$$
(55)

By using determined numeric value of θ with R for any value of Z, the values \(\theta_{m}\) can be drawn. So, we can determine the value of \(Nu_{D}\) at this value of Z. To use the process of the solution in question, we must specify via the flow the variations of U and E = (\(\epsilon/\upsilon\)) on which the distribution of E is considered quite described by the following equations

$$\begin{aligned} & y^{ + } < 5 : E = 0 \\ & 5 \le y^{ + } \le 30 : E = \frac{{y^{ + } }}{5} - 1 \\ & y^{ + } > 30 : E = 1.6R\left( {y^{ + } } \right)^{6/7} - 1 \\ \end{aligned}$$
(56)

with

$$y^{ + } = \frac{y}{\upsilon }\sqrt {\frac{{\tau_{\omega } }}{\rho }} = \left( {0.5 - R} \right)Re_{D} \sqrt {\frac{f}{8}}$$

In which f is the friction factor

$$f = \frac{0.305}{{Re_{D}^{0.25} }}$$
(57)

This is valid for hydraulically smooth pipe and the turbulent flow up to the Reynolds number 105(Re < 105)

$$\frac{{\bar{u}}}{{\bar{u}_{c} }} = \left( {\frac{D - 2r}{D}} \right)^{1/7}$$
(58)

The distribution of the average speed is presumed to be appreciable as follows. Where \(\bar{u}_{c}\) is the meaning center line speed.

Now knowing the value of \(\bar{u}_{m}\), like this

$$u_{m} = \frac{8}{{D^{2} }}\mathop \int \limits_{0}^{D/2} \bar{u}r{\text{d}}r$$
(59)

which tends toward

$$\frac{{\bar{u}_{m} }}{{\bar{u}_{C} }} = 8 \mathop \int \limits_{0}^{0.25} \left( {1 - 2R} \right)^{1/7} R{\text{d}}R = \frac{49}{60}$$
(60)

by comparing the two equations, we can draw the following result

$$U = \frac{49}{60}\left( {1 - 2R} \right)^{1/7}$$
(61)

This equation finally gives us the variation of the average dimensionless velocity U as a function of the radius of tube R.

The program was coded in the FORTRAN 95 language using the finite difference method to solve a thermal problem in fully developed turbulent flow inside circular cylindrical tube with a uniform wall temperature

Results and Discussion

Uniform Wall Temperature

Figure 6 illustrates the variation in the case of a uniform temperature wall of the function of the dimensionless temperature derivative with respect to the variable R for various Reynolds number values in the thermal development region. We can notice in the fully developed zone that the behavior of the values of this one is related to the number of Reynolds whose correlation to this number becomes very noticeable as one advances in the thermal input region, the values of this function tend to increase with increasing Nusselt.

Fig. 6
figure 6

Variation of dimensionless temperature derivative (dθ/dR) in thermal entrance region for Pr = 0.7 for various values of ReD

Full size image

The average Nusselt number NuD is shown in Fig. 7 according to Reynolds number Re for Prandtl number Pr = 0.7 in order to determine whether or hydrodynamically fully developed flow has been reached at the inlet of the entrance section. The increase in the average number of Nusselt is very remarkable for the increase in the number of Reynolds which is maximum at the access of the tube because the friction factor is maximal there too; then, it decreases with constant and constant value.

Fig. 7
figure 7

Variation of Nusselt number NuD in the thermal entrance region for Pr = 0.7 for various values of ReD

Full size image

Using the results obtained from the calculation code, the evolution of the Nusselt number for various values of the number of Peclet was appreciated. Figure 8 shows the distribution of Nu in the developing thermal region for various Péclet number. With approximate distances from the tube entrance, it has been found that the Peclet number has a much greater effect on the Nusselt values. In fact, although hard to see in the presented scale, different Péclet values also yield different Nu values for the isothermal walls conditions

Fig. 8
figure 8

Variation of Nusselt number NuD in the thermal entrance region for ReD = 105 for various values of Pr

Full size image

The maximum Nusselt number versus Reynolds number was plotted in Fig. 9 for the constant wall temperature case. The results were calculated and plotted for Peclet numbers 0.7, 1, 6, 9, 10, and 13 to see how Peclet number affects the Nusselt number distribution in the flow. The more the number of Peclet increases, the more the Nusselt number increases with the increase in the Reynolds number which characterizes the flow. At Pr = 0, 7, the difference is perfectly very small, and at higher Prandtl numbers, the difference is still large and significant.

Fig. 9
figure 9

Variation of Nusselt number NuD versus Reynolds number for various values of Pr

Full size image

The dimensionless temperature was plotted versus dimensionless radial for the constant wall temperature case. The results were calculated and plotted for Reynolds numbers 50, 800, 3000, and 6000. As can be seen in Fig. 10, when the Reynolds number, inertial forces outweigh the frictional forces related to the viscosity of the fluid and the temperature of the heating fluid increases gradually from the inlet to the temperature of the fluid wall. When the Peclet number is 3000 and 6000, the fluid temperature at radial coordinate is almost equal to the entrance temperature.

Fig. 10
figure 10

Dimensionless temperature profile (θ) along radial coordinate for different values of Reynolds number

Full size image

The dimensionless axial velocity profile, as a function of radial position for turbulent flow at Peclet number Pr = 0.7, is depicted in Fig. 11. The parabolic profile for laminar flow is fully developed which it is clear that turbulent profile has a much steeper slope near the wall. The axial velocity is maximum at the centerline and gradually decreases towards the wall, and as it nears the wall (dimensionless radius of 0.45) it reduces sharply to satisfy the no-slip boundary condition for viscous flow. This effect results in a slight decrease in the shear stresses at the wall and an overall decrease in the pressure-drop.

Fig. 11
figure 11

Dimensionless axial velocity profiles (U) for Pr = 0.7

Full size image

The dimensionless eddy viscosity distribution (E) at different values of the Reynolds number (Re) is shown in Fig. 12. It can be seen that the dimensionless eddy viscosity profiles also have a more uniform and almost parabolic symmetric distribution whose concavity of this parabola is variable according to the Reynolds number. We see a significant change in maximum eddy viscosity toward the central part of the pipe for at the Reynolds number value of 6000 and up, up to 10000, where the turbulent regime begins in the pipe (Re > 4000). Indeed, turbulent flow consists of eddies of various size ranges, and the size ranges increase with increasing Reynolds number. The kinetic energy cascades down from large to small eddies of interactional forces between the eddies.

Fig. 12
figure 12

Dimensionless eddy viscosity distribution (E) versus dimensionless radius (R) for various Nusselt number

Full size image

Wall Heat Flux Uniform

Figure 13 shows Nusselt number in thermal entrance region for Pr = 0.7 plotted for different values of ReD in the case of wall heat flux uniform in order to represent the augmentation in the heat transfer. It can be seen that as Re increases, the average Nusselt number behaviors for the circular tube are increases. For lower values of Reynolds number, the behavior decreases rapidly with the increase in Z and tends to stabilize at a certain value which is termed the fully rough region. The effect of the turbulence aspect is quite remarkable is significant for large Reynolds number values.

Fig. 13
figure 13

Variation of Nusselt number NuD in thermal entrance region for Pr = 0.7 for various values of ReD

Full size image

Nusselt number NuD as a function of the Reynolds and Prandtl numbers is obtained from the solution of the energy conservation equation for fully developed turbulent flow in tubes with constant wall heat flux. It was evaluated for Reynolds Re = 6000 and Prandtl number Pr = 0.7, and the results are listed in Table 1.

Table 1 Summarized results of FORTRAN 95 code in wall heat flux uniform for Re = 6000 and Pr = 0.7
Full size table

The dimensionless temperature profiles are plotted on Fig. 14 for a single value of Prandtl number and high values of the Reynolds number. Note that the effect of increasing Reynolds number is to give a more “square” temperature profile, while a low Reynolds number yields a more rounded profile that is similar to that for laminar flow. Still higher and lower values of Reynolds number continue these trends. Note that as the Reynolds approaches very low values, the dimensionless temperature approaches a constant value that is approaching the threshold of 0.80.

Fig. 14
figure 14

Temperature behavior (θ) versus dimensionless radius (R) for various values of Reynolds number

Full size image

The dimensionless eddy viscosity distribution E as a function of dimensionless axial position plotted for one particular value of Peclet number in Fig. 15 at different Re numbers. As can be seen in this figure, the surface temperature increases from a certain value at the pipe center with the increase in the Reynolds number Re. Note that the eddy diffusivity is maximum at the tube centerline. Indeed, the relative viscosity increases from the pipe wall toward the pipe center because the fluid tends to behave like a solid rather than a liquid when approaching the core region of the pipe, due to the lower shear rate in this region. That is why the dimensionless Eddy viscosity, is related to the dimensionless shear rate and the Reynolds number.

Fig. 15
figure 15

Dimensionless eddy viscosity distributions (E) versus dimensionless radius (R) for various Nusselt number

Full size image

Comparison of Constant Wall Temperature and Heat Flux Cases

For a calculation of the heat transfer in a fully developed turbulent flow inside a circular pipe, we will compare the current numerical results for the Reynolds number (Re = 104) for the average Nusselt number obtained in the uniform wall temperature case with those in the uniform wall heat flux. The comparison between the two case numerical results for the Nusselt number versus dimensionless axial coordinate is displayed in Fig. 16. It can be seen that the numerical data of the Nusselt number in the case of uniform wall temperature lie above the data captured in that of a wall in uniform heat flux. The behavior of pace is the same and Nu decreases monotonously and exponentially whose distribution becomes significant with the increase in the axial coordinate Z. The same curve showing the same behavior in Fig. 17 is obtained for the comparison of Nusselt number profile in uniform wall temperature with the uniform wall heat flux for Pr = 0.7.

Fig. 16
figure 16

Comparison of Nusselt number profile in uniform wall temperature with the uniform wall heat flux for Re = 10000

Full size image
Fig. 17
figure 17

Comparison of Nusselt number profile in uniform wall temperature with the uniform wall heat flux for Pr = 0.7

Full size image

In Fig. 18, the effect of boundary conditions (constant wall temperature (CWT) and constant wall heat flux (CWHF)) on the dimensionless temperature in a pipe is shown for Re = 104. Constant heat flux and constant temperature surfaces do not give the same results (in terms of θ) when the flow becomes strongly unsteady and turbulent. Constant heat flux surfaces produce colder zones at high Re thus yielding a reduced Nu. Note that only at very low Prandtl number is there a significant difference between the constant-heat-rate and constant-surface temperature results.

Fig. 18
figure 18

Comparison of dimensionless temperature behavior in the two case for Re = 104

Full size image

Comparison of the Present Numerical Model and the Previous Correlation Data

In order to approve the numerical results of the simulation of our thermal problem treated, we found after research in the literature the work recently performed by Taler [13] using the finite difference method whose Nusselt number was evaluated for various Reynolds numbers and Prandtl. In addition, this Nusselt number was obtained for fully developed turbulent flow in tubes with constant wall heat flux after solving the energy conservation equation.

The comparison of the results of the Nusselt number (Nu) as a function of Reynolds number (Re) for the case of Prandtl number (Pr = 0.7) of the present study and that of the Taler correlation [13] for air flowing inside the circular heating pipe is well illustrated in Fig. 19. It can be observed that the deviation from the numerical solution is within 2% and the Nusselt number profiles at Pr = 0.7 were in good agreement with those carried out in the work of Taler [13]. The treated thermal model has been well verified and validated, and the comparison results confirm the reliability of the numerical apparatus.

Fig. 19
figure 19

Comparison of the numerical data predicted in the present paper and the correlation of Taler [13] obtained for turbulent air flow in a tube with constant wall heat flux

Full size image

Conclusions

The impact of our contribution was on the prediction of the heat transfer rate of the wall of a pipe toward a fluid in turbulent flow circulating in this one. The majority of the attention will be given to two-dimensional and axisymmetric flow through pipes. The methodology of the analysis was based here on the thermal equation of the moment using the turbulence models and finite difference methods, for any thermal boundary conditions, so long as the velocity profile was assumed to be fully developed at the point where heat transfer starts. For this reason, a numerical simulation using FORTRAN 95 of fluid flows in fully developed turbulent through a circular tube for the two thermal boundary conditions, uniform wall temperature, and constant heat rate, has been carried out in the present study. It was found that the surface temperature is higher for high Reynolds number Re than for low Re number due to the free convection domination on the combined heat transfer process. Mean axial velocity and temperature profiles were shown to increase and extend farther in the outer layer with increasing Reynolds number. This consequently makes the local Nu numbers to be higher for high Re number than for low Re number due to the forced convection domination on the heat transfer process. The current predictions in the thermal study, performed numerically, show the effluence and sensitivity of some of the parameters involved in the calculations, and the results of the available literature agree quite well. In the fully developed turbulent flow, the number of Nu Nusselt as well as the dimensionless temperature also increases with increasing Reynolds number. Nusselt numbers obtained in the numerical prediction model are in excellent agreement with the correlations results which found in the specialized literature. At the end and for the Navier–Stokes equations for fully developed axisymmetric turbulent flow, it is also necessary to compare the numerical results obtained during this simulation such as le Nusselt number, the temperature, and velocity profile with an experimental data.

Also, as final comments one should mention that the same solution procedure can be used for any dynamically developed velocity profile and turbulent models to other configurations such as other channel geometries and rectangular section, triangular and so on, different wall heating conditions, and vicious and other flow heating effect.