Introduction

Developing expert systems in some fields like medicine, science, and engineering is very important. An expert system is a kind of intellectual programming system which can solve problems in relevant fields with expert’s levels, use the experience and special knowledge that domain experts accumulated for many years, simulate the thought process of human experts, and solve the difficult problem that generally only experts can do [1]. The building of expert systems has been characterized by capturing expert knowledge in such a way that it is possible for non-experts to solve a particular problem using knowledge already captured and stored in the computer [2].

In the current technological complexity of modern systems, the product reliability constitutes the significant attribute to satisfy the demand and increase the quality toward sustainable production [3]. To satisfy the demand and increase the quality of life for human beings, the product reliability is an indispensable factor on both the academic research and practice. In real world, high-tech industry has enough complexity to be analyzed by varieties of risk assessment methods. Fault tree analysis (FTA) as a powerful risk assessment technique is usually used which is based on reliability, maintenance, and experts’ systems knowledge [4].

Expert systems (an expert system is a computer system that emulates the decision-making ability of a human expert [5]) development is an unavoidable issue in risk assessment procedure in varieties of fields such as science, engineering, and medicine. It is commonly engaged to solve the relevant problems of experts’ fields focusing on the intellectual programming system. In addition, it uses the experiences besides knowledge; in this case a group of employed expert accumulated their knowledge for many years. Employing expert system has been classified as apprehending expert knowledge in case of a possibility for non-experts. It helps considerably to solve a specific problem by previous captured knowledge, and then, it will be stored in the computer [2]. Two key issues in developing an expert system are the acquisition of domain experts’ professional knowledge and the representation and reasoning of the transformed knowledge rules. In an expert system, the inference engine usually serves as the tool for application of the proper parts of the knowledge base according to the input, and the output is a recommendation, for example, to take a set of actions [6, 7].

In general, knowledge can be categorized into explicit and tacit knowledge, as first introduced by Polanyi (1966) and accepted by many researchers [8]. Explicit knowledge is codified knowledge articulated in words, figures, and numbers. It is objective and relatively easy to share in the form of reports, standard operating procedures, and data. Tacit knowledge, in contrast, is the knowledge residing in the heads of people that is highly personal and hard to codify. Such knowledge is subjective and unstructured, which is acquired over a period of time through experience, reflection, and intuition. In the past, knowledge managers focused mainly on explicit knowledge since it is much easier to handle and share. This tendency to concentrate on explicit knowledge makes it important for practice and academia to examine the missed opportunities that may result from ignoring tacit knowledge [1, 9,10,11,12,13,14]. Tacit knowledge is established personally and depends on individual experience, perceptions, and insights while in an expert system, decision makers are willing to use the linguistic terms for representing their judgments. Obviously, in a group of experts, each of them has varying opinions according to their different background and experience. Additionally, experts are usually uncertain about their estimations in knowledge acquisition process. That is because of many reasons such as limitation of time, absence of experience, and data. In this context, fuzzy set theory introduced by Zadeh (1965) [15] can be utilized to handle tactic knowledge. With respect to the advantages of fuzzy set theory, some of them may be unclear, ambiguous, incomplete, or even uncertain. The information is to integrate into the knowledge acquisition by using existing conventional fuzzy set theory. However, in a parallel way, uncertainty treatment [16] can be utilized as a significant issue in knowledge acquisition procedure which is not the main goal of this study.

Regarding safety concept, in expert systems, the two main significant parts of any risk assessment procedure are identified: representation of knowledge and acquisition of domain experts. Firstly, as a promising tool for knowledge representation and reasoning in risk assessment, like FTA, even more conventional fuzzy FTA still suffers a couple of deficiencies. As an example, the available rules in the most existing knowledge inference frameworks cannot change dynamically according to propositions’ deviation as human cognition and thinking. Furthermore, the parameters in conventional fuzzy FTA models cannot exactly signify the increasingly complex knowledge-based systems. Secondly, due to the expert knowledge acquisition process, the domain expert board usually establishes diverse experience and knowledge from one another and produces various types of knowledge information including complete/incomplete, precise/imprecise, and known/unknown because of its cross functional and multi-disciplinary nature [16]. The latter shortages can be handled by the interval 2-tuple linguistic terms method. The 2-tuple intuitionistic fuzzy numbers (IFNs) and many of its considerable extension can overcome on the aforementioned limitation [17]. The substantial superiority of IFNs is that the experts can express their opinions using 2-tuple qualitative terms with variety of uncertainties and ambiguities. In addition, the numerous uncertainties in the judgments can be modeled by using IFNs [18]. The 2-tuple IFNs and its current extension have been widely used to solve many multi-criteria decision-making (MCDM) problems. At present, a hybrid method based on integration of analytical network process (ANP) and ELECTRE II methods in interval 2-tuple linguistic environment for supplier selection is conducted by Wan et al. (2017) [19]. In another study, Singh et al. (2017) [20] developed the PROMETHEE II method to interval-valued 2-tuple linguistic variables in order to address energy-planning problems. In a same way, Liu et al. (2014a) [21] coped with the problems of robot selection employing an interval 2-tuple linguistic MCDM method. Shan et al. (2016) [22] developed some interval 2-tuple linguistic harmonic mean operators and their application in material selection followed by Lin et al. (2015) [23] which utilized a novel interval linguistic aggregation operator for facility location selection based on optimal aggregation method. In risk assessment context, Bozdag et al. (2015) [24] ranked the failure modes in failure mode and effect analysis (FMEA) technique using an interval type-2 fuzzy sets. Further, Liu et al. (2014b) [25] applied intuitionistic fuzzy hybrid TOPSIS (Technique for Order of Preference by Similarity to Ideal Solution) approach to prioritize the identified failure modes concerning a 1.8-inch. color super twisted nematic. Yazdi (2018) [26] introduced a novel 2-tuple intuitionistic fuzzy-hybrid-modified TOPSIS approach for assessing hazards in a gas refinery for the welding and lamination task to represent the effectiveness and reliability of proposed model to compare with the conventional risk matrix. In the current year, Yazdi and Soltanali (2018) [27] used recently IFNs in order to compute the failure probability in fluid filling system and then compare the results employing an updating mechanism tool. In addition, Yazdi (2018) [28] applied the same procedure with different types of failure in automotive industry to compare the results with different approaches. Therefore, the model based on the interval 2-tuple linguistic terms method will be more flexible and precise to cope with expert judgments in the tacit knowledge acquisition process.

However, to the best of authors’ knowledge, there are few attempts that have been done to use 2-tuple linguistic terms in FTA, whereas many studies have been performed using conventional fuzzy FTA, such as Rajakarunakaran et al. (2015), Yazdi and Zarei (2018), and Kabir et al. (2018) [29,30,31]. As a prior study, an intuitionistic fuzzy set-based method has been engaged for the failure analysis of the printed circuit board assembly [32]. Authors directly computed the intuitionistic fuzzy FTA interval, old-fashioned reliability, and the intuitionistic fuzzy reliability interval. Chang et al. (2006) [33] introduced an algorithm of vague FTA to compute fault interval of system components from integrating expert’s knowledge. Cheng et al. (2009) [34] proposed an intuitionistic FTA procedure to compute the intuitionistic fuzzy reliability interval for liquefied natural gas terminal emergency shutdown system. Kumar and Yadav (2012) [35] applied the weakest t-norm-based intuitionistic fuzzy FTA to evaluate system reliability by finding the most critical system component that affects the system reliability. Therefore, one of the main objectives of current study is proposing tactic knowledge acquisition framework using 2-tuple interval qualitative terms, and fuzzy analytical hierarchy process (FAHP) to capture, store, share, leverage, and improve tactic knowledge based is increasing and sustaining in competitive merits of experts’ knowledge in FTA.

Pythagorean fuzzy sets (PFS) are an extension of intuitionistic fuzzy sets. It provides more freedom to experts in expressing their opinions about the vagueness and uncertainty of the considered risk assessment problem. In Pythagorean fuzzy sets, experts assign membership and non-membership degrees. Unlike intuitionistic fuzzy sets, sum of the assigned membership and non-membership degrees does not have to be at most 1. However, the sum of squares of these degrees must be at most 1. It has many advantages as follows [36]. As an example, it allows the experts to assign judgments to the hazards and associated risks with respect to two parameters of two-dimensional (2D) risk matrix method by means of linguistic terms, which are better interpreted by humans, fuzzy in nature and then transferred into Pythagorean fuzzy numbers. However, it has not been used for diagnostic analysis, whereas it is well applied currently in occupational safety concepts such as integration of PFS and AHP in risk assessment for occupational health and safety [37, 38] and PFS and TOPSIS [39].

In other side, to cope with dynamically changeable (first drawback), Bayesian network (BN) mechanism can be utilized to handle this lack in conventional FTA method. BN as a well-known graphical model illustrates the causal relationships between key factors (causes) and one or more final outcomes in a system. BN analysis may be qualitative, quantitative, or both, depending on the scope of the analysis as well as FTA, and it is popular in statistics, machine learning, artificial intelligence, and risk and reliability analyses. Additionally, BN has also been widely applied in numerous risk and reliability studies [40, 41], improving the safety performance of a system [42], updating failure probability [43], mapping static or dynamic FTs into corresponding BNs [44], using fuzzy evidence theory, and updating mechanism [45], and in recent work combining BN and Petri nets aimed to analyze dynamic safety system [46].

The main purpose of this paper is to provide a novel framework to improve knowledge acquisition for analyzing fault diagnosis in a FT and comparing the results with listing of approaches. In the next section, a new framework based on interval 2-tuple IFNs is presented to compute the failure probability (FP) of the top event (TE) in FTA. Firstly, a new knowledge acquisition technique based on interval 2-tuples and FAHP is introduced to model the variety and vagueness of information in tacit knowledge acquisition. Secondly, BN is used to handle the lack of conventional FTA in both crisp and fuzzy environments. In “Case Study” section, the practicality and usefulness of the proposed approach are demonstrated by a numerical example in an automotive manufacturing process fault. The concluding remarks and recommendation for further studies are presented in the last section.

Methodology

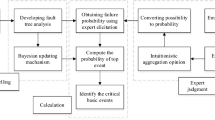
As it can be seen from Fig. 1, a new framework is proposed to improve the knowledge acquisition in failure diagnosis analysis. Expert judgment, modeling, and calculation are the three key stages in the proposed model. Once an event is selected as a TE, the modeling part using FTA and BN is constructed and developed. Next, a group of employed experts express their opinions for possibility of each basic event (BE) using linguistic terms. A reliable aggregation process is applied, which collects all possibilities in terms of linguistic opinions. Applying the aggregation result, the probability of each BE and subsequently TE is computed. Finally, critical BE is identified to obtain further corrective actions to reduce the probability of TE. The details of each stage are provided as follows.

Fig. 1
figure 1

Proposed framework

Full size image

Developing Fault Tree Analysis

FTA is a failure-oriented, deductive, and top-down approach, which considers an undesirable event associated with the system as the TE; the various possible combinations of fault events leading to the TE are represented with logic gates. Fault tree is a qualitative model which provides useful information on the various causes of undesired top events. However, quantification of fault tree provides top event occurrence probability and critical contribution of the basic causes and events [47, 48]. Fault tree approach is widely used in probability safety assessment. The faults can be the events that are associated with component hardware failure, software error, human errors, or any other relevant events which can lead to top events. The gates show the relationships of faults (or events) needed for the occurrence of a higher event. The gates those serve to permit or inhibit the fault logic up the tree. The gate symbol denotes the type of relationship of the input (lower) events required for the output (higher) event. Lack of proper understanding of objectives may lead to incorrect definition of top event, which will result in wrong decisions being made. Hence, it is extremely important to define and understand the objectives of the analysis. After identifying top event from the objectives, scope of the analysis is defined. The scope of the FTA specifies which of the failures and contributors to be included in the analysis. It mainly includes the boundary conditions for the analysis. The boundary conditions comprise the initial states of the subsystems and the assumed inputs to the system. Interfaces to the system such as power source or water supplies are typically included in the analysis; their states need to be identified and mentioned in the assumptions [49]. To compute the probability of TE in a quantitative analysis, the following conventional assumptions and mathematical operations can be performed:

$$P_{\text{OR}} = 1 - \mathop \prod \limits_{i = 1}^{n} \left( {1 - P_{i} } \right)$$
(1)
$$P_{\text{AND}} = \mathop \prod \limits_{i = 1}^{n} P_{i}$$
(2)

Once the probability of each BE is known, the probability of TE can be computed. Input data for BE are divided into five categories: non-repairable component, repairable component, periodically tested component, frequency, and on-demand probability in this accordance. However, in FTA sometimes there is a lack of information to obtain failure rate for all BEs. Therefore, three other ways such as expert judgment, extrapolation, and statistical may be engaged as a trustworthy alternative way. In this study, expert judgment is used to compute the probability of all BEs.

Bayesian Updating Mechanism

Since the equipment failure tends to be a rare event, empirical data for parameter estimation are generally sparse. Classical approach (FTA) is ill suited for this situation, leading to excessively wide confidence intervals. Partly because of this, most of the risk assessment community has turned to Bayesian analysis (because they employ so-called Bayes’ theorem), as a natural means to incorporate a wide variety of information (in addition to statistical data, i.e., r failures in n tests) in the estimation process.

The following four steps are to be followed in Bayesian estimation.

Step 1:

Identification of the parameter to be estimated

Step 2:

Development of a prior distribution that is obtained from generic data

Step 3:

Collection of evidence and construction of appropriate likelihood function

Step 4:

Derivation of the posterior distribution using Bayes’ theorem

Assuming the conditional dependencies among the variables, BN shows the joint probability distribution \(P(U):\)

$$P\left( U \right) = \mathop \prod \limits_{i = 1}^{n - 1} P\left( {X_{i} |X_{i + 1} , \ldots ,X_{n} } \right)$$
(3)

where \(U = \left\{ {X_{1} ,X_{2} , \ldots ,X_{n} } \right\}\) and \(X_{i + 1}\) is the parent of \(X_{i}\). Accordingly, the probability of \(X_{i}\) can be computed as:

$$P\left( {X_{i} } \right) = \mathop \sum \limits_{{U{ \setminus }X_{i} }} P\left( U \right)$$
(4)

The main advantage of BN is in a probability of updating. This information is commonly based on expert knowledge or becomes available in the lifecycle of processes, such as accidents, incidents, near misses and mishaps. Based on Bayes theorem, BN can be used to update the prior probability of an event (E), explanation of the updated or posterior probabilities:

$$P\left( {U \backslash E} \right) = \frac{{P\left( {U \cap E} \right)}}{P\left( E \right)} = \frac{{P\left( {U \cap E} \right)}}{{\mathop \sum \nolimits_{U} P\left( {U \cap E} \right)}}$$
(5)

To obtain more information, one can refer to the [50].

Expert Judgment

Expert knowledge is affected by individual visions and purposes [51]. Therefore, it is very difficult to assess the complete impartiality of expert knowledge. The main challenge is the selection of heterogeneous specialists (e.g., either scientists or workers) and homogenous specialists (it just includes scientists).

Individual experience on expert judgment is presumed to be smaller in the homogeneous group as compared to the heterogeneous one as a result of experience differences. Therefore, by considering all possible opinions, a group of heterogeneous specialists could have a privilege over the homogeneous group. Moreover, the weights of experts are different, so in real life, the heterogeneous group is more realistic [52, 53]. The criteria for the recognition of experts are established as follows: firstly, the period of learning and experience in the precise scope of knowledge. Secondly, the individual conditions in which experience is obtained, including either practical or theoretical conditions, are considered. Thus, using the FAHP method can handle this problem. Accordingly, each expert is evaluated based on the four criteria: education, job tenure, experience, and age. FAHP as a first preliminary is explained as follows.

Preliminary 1: Fuzzy Analytical Hierarchy Process (FAHP)

Conventional AHP as a well-known method is widely used in multi-criteria decision-making issues. AHP originally is introduced by Saaty (1977), to deal with the complexity of decision problems using hierarchy of decision layers [54]. In order to break a problem into the several layers (subproblem) and improve the subjectivity (capability of reflecting the human thinking), the FAHP has been developed to solve the AHP problems [55]. Additionally, the subjectivity should be avoided in order to achieve more credible and reliable results [56]. In this regard, the main extension of the FAHP techniques under trapezoidal and triangular memberships is introduced by Buckley (1985) and Change (1996) [57, 58].

  • Stage 1: Let \(\tilde{a}_{ij}^{k} = \left( {\tilde{a}_{ij1}^{k} ,\tilde{a}_{ij2}^{k} ,\tilde{a}_{ij3}^{k} } \right)\), \(\left( {i = 1,2, \ldots ,\left( {n - 1} \right),j = 2,3, \ldots ,n} \right)\) be the fuzzy relative importance by comparing criterion i with criterion j provided by kth expert. Then, the aggregated fuzzy relative importance \(\tilde{a}_{ij}\) is obtained as follows.

    $$\tilde{a}_{ij} = \left( {\mathop \sum \limits_{k = 1}^{K} \lambda_{k} \cdot \tilde{a}_{ij1}^{k} ,\mathop \sum \limits_{k = 1}^{K} \lambda_{k} \cdot \tilde{a}_{ij2}^{k} ,\mathop \sum \limits_{k = 1}^{K} \lambda_{k} \cdot \tilde{a}_{ij3}^{k} } \right)$$
    (6)

    where \(\lambda_{k} > 0 \left( {k = 1,2, \ldots ,K} \right)\) and satisfying \(\sum\nolimits_{k = 1}^{K} {\lambda_{k} = 1} .\)

  • Stage 2: Pairwise comparison matrices are made in the dimensions of the hierarchy procedure throughout all the defined criteria. Experts’ opinions in quantifiable terms are allocated by considering the importance of pairwise comparison.

    $$\tilde{A} = [\tilde{a}_{ij} ] = \left[ {\begin{array}{*{20}c} 1 & {\tilde{a}_{12} } & \cdots & {\tilde{a}_{1n} } \\ {1/\tilde{a}_{21} } & 1 & \cdots & {\tilde{a}_{2n} } \\ \vdots & \vdots & \ddots & \vdots \\ {1/\tilde{a}_{n1} } & {1/\tilde{a}_{n2} } & \cdots & 1 \\ \end{array} } \right]$$
    (7)

    when criterion i is of relative importance to criterion j, \(\tilde{a}_{ij} = \tilde{1},\tilde{3},\tilde{5},\tilde{7},\tilde{9}\). In contrast, when criterion j is of relative importance to criterion i, \(\tilde{a}_{ij} = \tilde{1},\tilde{3}^{ - 1} ,\tilde{5}^{ - 1} ,\tilde{7}^{ - 1} ,\tilde{9}^{ - 1}\). In a situation \(i = j, \,\tilde{a}_{ij} = 1\), where relative importance criterion j in qualitative terms and corresponding fuzzy numbers are provided in Fig. 2 and Table 1 as follows:

    Fig. 2
    figure 2

    Membership function for pairwise comparison importance of criterion j

    Full size image
    Table 1 Fuzzy corresponding number for relative importance comparison to criterion
    Full size table

  • Stage 3: Examine the consistency of fuzzy pairwise comparison matrix. Considering \(A = \left[ {a_{ij} } \right]\) as a positive mutual matrix and \(\tilde{A} = [\tilde{a}_{ij} ]\) is a fuzzy positive mutual matrix. As it discussed in [57], if \(A = \left[ {a_{ij} } \right]\) is consistent, \(\tilde{A} = [\tilde{a}_{ij} ]\) will also be consistent. Thus, this study used this procedure to examine the consistency of comparison matrix and validate the questionnaire provided for experts. In case of the inconsistency of the comparison matrix, the evaluation procedure should be repeated to improve the consistency [59].

  • Stage 4: Using the geometric mean method, the fuzzy weights of fuzzy comparison values between criteria are calculated by Eq 8 as follows;

    $$\tilde{r}_{i} = \left( {\tilde{a}_{i1} \otimes \tilde{a}_{i2} \otimes \cdots \otimes \tilde{a}_{in} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 n}}\right.\kern-0pt} \!\lower0.7ex\hbox{$n$}}}}$$
    (8)

    where \(\tilde{a}_{in}\) is a fuzzy comparison values of criterion i to criterion n.

  • Stage 5: For each criterion, the fuzzy weights are defined as follows:

    $$\tilde{w}_{i} = \tilde{r}_{i} \otimes \left( {\tilde{r}_{1} \oplus \tilde{r}_{2} \oplus \cdots \oplus \tilde{r}_{n} } \right)^{ - 1}$$
    (9)

    \(\tilde{w}_{i}\)is defined as a fuzzy weight of criterion i and \(\tilde{w}_{i} = \left( {l\tilde{w}_{i} ,m\tilde{w}_{i} ,u\tilde{w}_{i} } \right)\) which are included \(l\tilde{w}_{i} ,m\tilde{w}_{i} ,\;{\text{and}}\;u\tilde{w}_{i}\) justify the lower, middle, and upper values of the fuzzy weights of criterion i, respectively.

  • Stage 6: Defuzzification procedure. The significant step in fuzzy multi-criteria decision making is the defuzzification procedure which locates the best non-fuzzy performance (BNP) value. There are many techniques available for defuzzification, including center of area (CoA), mean of maximum (MoM), and a–cut. CoA is known as a more simple and practical technique; therefore, it is used to compute the BNP value of the fuzzy weights of each dimension.

    $$X^{*} = \frac{{\smallint \upsilon_{i} \left( x \right)x{\text{d}}x}}{{\smallint \upsilon_{i} \left( x \right){\text{d}}x}}$$
    (10)

    where X* = defuzzified output; \(\upsilon_{i} (x)\) = aggregated membership function; x = output variable.

Defuzzification of triangular fuzzy number \(\tilde{A}\) = (a1, a2, a3) is:

$$X^{*} = \frac{{\mathop \smallint \nolimits_{{a_{1} }}^{{a_{2} }} \frac{{x - a_{2} }}{{a_{2} - a_{1} }}x{\text{d}}x + \mathop \smallint \nolimits_{{a_{2} }}^{{a_{3} }} \frac{{a_{3} - x}}{{a_{3} - a_{2} }}x{\text{d}}x}}{{\mathop \smallint \nolimits_{{a_{1} }}^{{a_{2} }} \frac{{x - a_{2} }}{{a_{2} - a_{1} }}{\text{d}}x + \mathop \smallint \nolimits_{{a_{2} }}^{{a_{3} }} \frac{{a_{3} - x}}{{a_{3} - a_{2} }}{\text{d}}x}} = \frac{1}{3}\left( {a_{1} + a_{2} + a_{3} } \right)$$
(11)

where X* is the weight on expert j.

In this study, a heterogeneous group of experts expresses their opinions for possibility of each BE in linguistic terms. As it mentioned earlier, the linguistic terms are defined as IFNs because of improving knowledge acquisition. IFS is explained as follows.

Preliminary 2: Intuitionistic Fuzzy Set (IFS)

Atanassov (1986) [60] presented intuitionistic fuzzy set (IFS) to deal acceptably with ambiguity as an extension of the classical model introduced by Zadeh (1965) [15] which includes the membership and non-membership functions and hesitation margin groups. Xu (2011) [61] indicated that the IFS data are more comprehensive than the fuzzy conventional set with only a membership function. Chang and Cheng (2010) [62] and Chang et al. (2010) [63] showed that IFS is a proper approach to deal with ambiguities and uncertainties in FMEA as an efficient risk assessment technique. Figure 3 illustrates the interrelations among crisp sets, fuzzy sets, and IFS. The definition of IFS and the related issues is provided as follows:

Fig. 3
figure 3

Interrelations between crisp sets, fuzzy sets, and IFS [64]

Full size image

Definition 1

Considering X as a fixed set, intuitionistic fuzzy S in X is introduced:

$$S = \left\{ {x, \mu_{S} \left( x \right), \nu_{S} \left( x \right) \left| {x \in X} \right.} \right\},$$
(12)

where \(\mu_{S} \left( x \right)\) and \(\nu_{S} \left( x \right) \in \left[ {0,1} \right]\) are denoted as a degree of membership and non-membership functions, respectively, and satisfy \(0 \le \mu_{S} \left( x \right) + \nu_{S} \left( x \right) \le 1,\quad \forall x \in X.\)

In addition, the hesitation degree of \(x \in S\) indicates the degree of uncertainty of x to S and is given as \(\pi_{S} \left( x \right) = 1 - \mu_{S} \left( x \right) - \nu_{S} \left( x \right)\) and clearly satisfies \(0 \le \pi_{S} \left( x \right) \le 1, \quad \forall x \in X\).

It is obvious that the value of x is more uncertain or certain when the value of \(\pi_{S} \left( x \right)\) is large or small, respectively. Moreover, as illustrated in Fig. 4 considering both continuous functions of \(\mu_{S} \left( x \right)\) and \(\nu_{S} \left( x \right)\), IFS clearly regresses the conventional fuzzy set when \(\mu_{S} \left( x \right) = 1 - \nu_{S} \left( x \right)\). In addition, IFS reduces into a crisp set in special cases when the value of \(\mu_{S} \left( x \right) = 1 - \nu_{S} \left( x \right)\) is equal to 0 or 1.

Fig. 4
figure 4

Intuitionistic fuzzy sets [65]

Full size image

The set \(\left( { \mu_{S} \left( x \right),\nu_{S} \left( x \right)} \right)\) is called an intuitionistic fuzzy number in IFS and \(\alpha = \left( { \mu_{S} \left( x \right),\nu_{S} \left( x \right)} \right)\) simply represents each IFN, where \(\mu_{\alpha } \in \left[ {0,1} \right]\) and \(\nu_{\alpha } \in \left[ {0,1} \right],\) and also satisfy \(\mu_{\alpha } + \nu_{\alpha } \le 1.\) It should be noted that for an IFN \(\alpha = \left( { \mu_{\alpha } , \nu_{\alpha } } \right)\),\(\alpha^{ + } \left( {1, 0} \right)\) and \(\alpha^{ - } \left( {0, 1} \right)\) are nominated as the largest and smallest IFNs, respectively.

Definition 2

Let \(\alpha_{1} = \left( { \mu_{{\alpha_{1} }} ,\nu_{{\alpha_{1} }} } \right)\) and \(\alpha_{2} = \left( { \mu_{{\alpha_{2} }} ,\nu_{{\alpha_{2} }} } \right)\) be two IFNs, and the intuitionistic fuzzy distance (IFD) between a1 and a2 is illustrated as follows:

$$d_{\text{IFD}} \left( {\alpha_{1} ,\alpha_{2} } \right) = \left| {\alpha_{1} - \alpha_{2} } \right| = \frac{1}{2}\left( {\left| {\mu_{{\alpha_{1} }} - \mu_{{\alpha_{2} }} } \right| + \left| {\nu_{{\alpha_{1} }} - \nu_{{\alpha_{2} }} } \right|} \right)$$
(13)

The next stage of the procedure presents the aggregation of experts’ opinions in an intuitionistic fuzzy environment.

Aggregation Procedure

According to IFS, the linguistic terms are defined as IFNs for the possibility of each BE. The theoretical basis for the transformation between qualitative terms and IFNs in the following tables is provided in detail by Liu et al. (2014a) [25] and subsequently the detail reasons of why qualitative terms can be defined as IFNs are provided by Wang and Liu (2012) [66]; Xu and Zhao (2016) [67]. Thus, the employed experts express their opinions due to the possibility of occurrence for each BE using IFNs.

In recent years, Xu (2007) [68] has introduced an extension of the intuitionistic fuzzy-hybrid-weighted Euclidean distance (IFHWED) operator to aggregate experts’ opinions. Then, he ordered them when the linguistic terms are prepared with IFNs. IFHWED is integrated with the intuitionistic fuzzy-weighted Euclidean distance (IFWED) operator and the intuitionistic fuzzy-ordered-weighted Euclidean distance (IFOWED) operator. Both IFWED and IFOWED are developed by Zeng (2012) [69]. The principal superiority of IFHWED is that it cannot only integrate both of them by applying the degree of importance but can also reduce the effect of unreasonable small (or large) deviations on the aggregation outcomes by allocating them in different weights. The steps of aggregation procedure which is engaged in this study are provided as follows.

Aggregate the expert’s opinion using the intuitionistic fuzzy-weighted averaging (IFWA) operator for any BEs, \({\text{BE}}_{i} = \left( {i = 1, \ldots ,m} \right).\)

$$\begin{aligned} \alpha_{ij} & = IFWA\left( {\alpha_{ij}^{1} ,\alpha_{ij}^{2} , \ldots ,\alpha_{ij}^{n} } \right) = \mathop \sum \limits_{k = 1}^{n} \lambda_{k} \alpha_{ij}^{k} \\ & = \left[ {1 - \mathop \prod \limits_{k = 1}^{n} \left( {1 - \mu_{ij}^{k} } \right)^{{\lambda_{k} }} ,\mathop \prod \limits_{k = 1}^{n} \left( {\nu_{ij}^{k} } \right)^{{\lambda_{k} }} } \right] \\ \end{aligned}$$
(14)

where \(\alpha_{ij} = \left( {\mu_{ij} ,\nu_{ij} } \right)\) is the final aggregated subjective opinions in terms of IFN, \(\alpha_{ij}^{k} = \left( {\mu_{ij}^{k} ,\nu_{ij}^{k} } \right)\) is the IFN that is transferred by the corresponding linguistic terms according to an experts’ opinion, \(\lambda_{k}\) is the given weight to each expert according to FAHP that represents the importance of his/her opinion on BEi and satisfies \(\lambda_{k} > 0\)\(\left( {k = 1, \ldots ,n} \right)\) and \(\left( {\sum\nolimits_{k = 1}^{n} {\lambda_{k} = 1} } \right).\)

Next, to make reliable decisions with consideration of maintenance actions, the intuitionistic fuzzy output is converted into the crisp value using Eq 13. However, Boran et al. (2009) [70] showed that Eq 14 can be normalized to Eq 15. Additionally, Yazdi et al. (2019) [71] represented that Eq 15 can be considered as a defuzzification IFNs which is obtained by:

$$Val_{S} \left( x \right) = \frac{1}{2} \times \left( {1 + \mu_{S} \left( x \right) - \nu_{S} \left( x \right)} \right)$$
(15)

PFS is explained as follows.

Preliminary 3: Pythagorean Fuzzy Sets (PFS)

In the literature [72,73,74,75], Yager provided three basic representations for Pythagorean membership grades. The first one is \(\left( {a,b} \right)\) satisfying the conditions that \(\in \left[ {0,1} \right], b \in \left[ {0,1} \right] {\text{and }}a^{2} + b^{2} \le 1\). The second one is the polar coordinates \(\left( {r, \theta } \right)\) satisfying the conditions that \(\in \left[ {0,1} \right]\;{\text{and}}\; \theta \in \left[ {0,\pi /2} \right].\) The third one is \(\left( {r, d} \right)\) close to the second one satisfying the conditions that \(r \in \left[ {0,1} \right], d \in \left[ {0,\pi /2} \right],\) and \(d = 1 - 2\theta /c\). Their relationship is that \(a^{2} + b^{2} = r^{2} ,\;a = r\,{ \cos }\left( \theta \right)\) and \(b = r\;{\text{sin(}}\theta ).\) He referred to a fuzzy subset having these Pythagorean membership grades as a PFS. Similar to the definition of IFSs, in the following, we introduce the general definition of PFSs.

Let a set X be a universe of discourse. A PFS, P is an object having the form

$$P = \left\{ {\left\langle {x, P\left( {\mu_{P} \left( x \right), \nu_{P} \left( x \right)} \right)} \right\rangle |x \in X} \right\}$$
(16)

where the function \(\mu P : X \to \left[ {0, 1} \right]\) defines the degree of membership and \(\mu_{P} :X \to \left[ {0, 1} \right]\) defines the degree of non-membership of the element \(x \in X\) to P, respectively, and for every \(x \in X,\) it holds that:

$$\left( {\mu_{P} \left( x \right)} \right)^{2} + \left( {\nu_{P} \left( x \right)} \right)^{2} \le 1$$
(17)

For any PFS, P and \(x \in X\), \(\pi_{P} \left( x \right) = \sqrt {1 - \pi_{P}^{2} \left( x \right) - \nu_{P}^{2} \left( x \right)}\) is called the degree of indeterminacy of x to P. For simplicity, we call \(P\left( {\mu_{P} \left( x \right), \nu_{P} \left( x \right)} \right)\) a Pythagorean fuzzy number (PFN) denoted by \(\beta = P\left( {\mu_{\beta } , \nu_{\beta } } \right)\), where \(\mu_{\beta } \;{\text{and}}\;\nu_{\beta } \in \left[ {0,1} \right],\;\pi_{\beta } = \sqrt {1 - \mu_{\beta }^{2} - \nu_{\beta }^{2} } ,\) and \(\mu_{\beta }^{2} + \nu_{\beta }^{2} \le 1.\)

Given three PFNs \(\beta_{1} = P\left( {\mu_{{\beta_{1} }} , v_{{\beta_{1} }} } \right), \beta_{2} = P\left( {\mu_{{\beta_{2} }} , v_{{\beta_{2} }} } \right), {\text{and}}\, \beta = P\left( {\mu_{\beta } , v_{\beta } } \right),\) Yager [72,73,74,75] defined the basic operations on them, which can be described as follows:

  1. 1.

    \(\beta_{1} \cup \beta_{2} = P\left( {{ \hbox{max} }\left\{ {\mu_{{\beta_{1} }} ,\mu_{{\beta_{2} }} } \right\},\;{ \hbox{min} }\left\{ {v_{{\beta_{1} }} , v_{{\beta_{2} }} } \right\}} \right).\)

  2. 2.

    \(\beta_{1} \cap \beta_{2} = P\left( {{ \hbox{min} }\left\{ {\mu_{{\beta_{1} }} ,\mu_{{\beta_{2} }} } \right\},\;{ \hbox{max} }\left\{ {v_{{\beta_{1} }} , v_{{\beta_{2} }} } \right\}} \right).\)

  3. 3.

    \(\beta ^{c} = P\left( {v_{\beta } , \mu_{\beta } } \right).\)

On the basis of relationship between PFNs and IFNs, we further define some novel operations for PFNs as below:

  1. 4.

    \(\beta_{1} \oplus \beta_{2} = P\left( {\sqrt {\mu_{{\beta_{1} }}^{2} + \mu_{{\beta_{2} }}^{2} - \mu_{{\beta_{1} }}^{2} \mu_{{\beta_{2} }}^{2} } ,v_{{\beta_{1} }} v_{{\beta_{2} }} } \right).\)

  2. 5.

    \(\beta_{1} \otimes \beta_{2} = P\left( {\mu_{{\beta_{1} }} \mu_{{\beta_{2} }} ,\sqrt {v_{{\beta_{1} }}^{2} + v_{{\beta_{2} }}^{2} - v_{{\beta_{1} }}^{2} v_{{\beta_{2} }}^{2} } } \right).\)

  3. 6.

    \(\lambda \beta = P\left( {\sqrt {1 - \left( {1 - \mu_{\beta }^{2} } \right)^{\lambda } } ,(v_{\beta } )^{\lambda } } \right), \lambda \ge 0.\)

  4. 7.

    \(\beta^{\lambda } = P\left( {(\mu_{\beta } )^{\lambda } ,\sqrt {1 - \left( {1 - v_{\beta }^{2} } \right)^{\lambda } } } \right), \lambda \ge 0.\)

In order to aggregate PFNs, Yager [74] introduced the following weighted averaging aggregation operator.

Let \(\beta_{j} = P\left( {\mu_{{\beta_{1} }} ,v_{{\beta_{1} }} } \right)\left( {j = 1,2, \ldots ,n} \right)\) be a collection of PFNs and \(w = \left( {w_{1} ,w_{2} , \ldots ,n} \right)^{T}\) be the weight vector of \(\beta_{j}\), where \(w_{j}\) indicates the importance degree of \(\beta_{j}\), satisfying \(w_{j} \ge 0\) and \(\sum\nolimits_{j = 1}^{n} {w_{j} = 1}\), and let Pythagorean fuzzy-weighted averaging (PFWA): \(\Theta ^{n} \to\Theta\) if

$$PFWA = \left( {\beta_{1} ,\beta_{2} , \ldots ,\beta_{n} } \right) = \left( {\mathop \sum \limits_{j = 1}^{n} w_{j} \mu_{{\beta_{j} }} ,\mathop \sum \limits_{j = 1}^{n} w_{j} v_{{\beta_{j} }} } \right)$$
(18)

Same as IFNs, the aggregation process can be done using Eq 15.

The main difference between PFN and IFN is their different constraint conditions. According to their definitions introduced in “Developing Fault Tree Analysis” and “Bayesian Updating Mechanism” sections, we know that the constraint condition of IFN is \(0 \le \mu_{\alpha } + \nu_{\alpha } \le 1\), whereas the constraint condition of PFN is \(\left( {\mu^{\beta } } \right)^{2 } + \left( {v^{\beta } } \right)^{2 } \le 1\). Because the fact that for any point (a, b) \(\left( {a, b \in \left[ {0, 1} \right]} \right)\), if \(a + b \le 1\), then \(a _{2} + b _{2} \le 1\); Yager [74] showed that the space of the Pythagorean membership grade is greater than the space of the intuitionistic membership grade. In other words, if one is an IFN, then it must also be a PFN, but not all PFNs are the IFNs. This result can be easily shown in Fig. 5.

Fig. 5
figure 5

Comparison of spaces of the PFNs and the IFNs

Full size image

From the above comparison analysis, we can clearly know that the main advantage of PFN is that it cannot only model the decision situations in which the IFN can capture that the sum of the degree provided by the decision maker to which an alternative satisfies a criterion and the degree to which an alternative dissatisfies a criterion is equal to or < 1, but also model some other situations in which the IFN cannot describe that the sum of the degree to which an alternative satisfies a criterion and the degree to which an alternative dissatisfies a criterion is bigger than 1, but their square sum is equal to or < 1. Nevertheless, this advantage of PFN comes at the cost that the operations involving PFNs are generally more complex than those involving IFNs.

Computing the Failure Probability of BE and TE

Once the crisp value as a possibility of an BE is computed, then the possibility is converted to probability using Onisawa equations as follows [76]:

$${\text{FP}} = \left\{ {\begin{array}{*{20}l} {1/10^{K} , } \hfill & {{\text{CFP}} \ne 0} \hfill \\ {0,} \hfill &{{\text{CFP}} = 0} \hfill \\ \end{array} ,\quad K = \left[ {\left( {\frac{1}{\text{CFP}} - 1} \right)} \right]^{1/3}\times 2.301} \right.$$
(19)

where FP is denoted as failure probability of each BE and CFP is signified as corresponding crisp failure possibility extracted using IFS.

In order to compute the probability of TE, Eqs 1, 2 and Boolean algebra in FTA model and Eqs 3–5 in BN model are utilized.

Identifying the Critical BEs

Quantification of system risk/reliability only gives the overall system performance measure. In case of improvement in the system reliability or reduction in risk is required, one has to rank the components or in general the parameter of system model. Importance measures determine the change in the system metric due to change in parameters of the model. Based on these importance measures, critical parameters are identified. By focusing more resources on the most critical parameters, system performance can be improved effectively. Importance measure also provides invaluable information in prioritization of components for inspection and maintenance activities. Importance measures are useful in identification of critical components for the purpose of design modifications and maintenance. The Birnbaum measure of importance is defined as the change in system risk for a change in failure probability for a BE. The BE can be component failure or human error or a parameter of system risk model. It is mathematically expressed as:

$$I_{{{\text{BE}}_{i} }}^{\text{BIM}} = P\left( {{\text{TE}}|{\text{BE}}_{i} } \right) - P\left( {{\text{TE}}|{\text{BE}}_{i}^{*} } \right)$$
(20)

Based on BIM, first, the TE probability \(P\left( {{\text{TE}}|{\text{BE}}_{i} } \right)\) is computed by assuming that basic event i has occurred. Then, the TE probability \(\left( {{\text{TE}}|{\text{BE}}_{i}^{*} } \right)\) is computed when it is assumed that the BE has not occurred.

Case Study

In order to implement the proposed framework, a spherical storage hydrocarbon tank system as the most critical and complex equipment in an oil and gas production process was evaluated. This case study is selected from Yazdi (2019) [44] in order to make further comparisons. The reliability and safety guarantee of such system from operational and non-operational aspects are important. Considering the former, because of the importance of speedy nature in various operations, a low reliability leads to an increase in operational costs and equipment breakdown and ultimately a downtime in the process lines. Figure 6 shows the views of a spherical storage hydrocarbon tank system and its process description (flow diagram). The most important feature of the system is simultaneous activity of many devices in different blocks. In other words, any failure of a component in each block leads to not only system disability but downtime in the whole production line.

Fig. 6
figure 6

Process description

Full size image

According to the mentioned process description, failure in a spherical storage hydrocarbon tank system is considered as a TE, and accordingly FT is developed and illustrated in Fig. 7.

Fig. 7
figure 7

Fault tree for the failure in a spherical storage hydrocarbon tank system adopted after [44]

Full size image

The identified 34 BEs, which contribute directly and/or indirectly to the specified TE considering common cause failures (CCFs), are shown in Table 2. To compute the FP of BEs, an expert judgment method is employed. As it is mentioned earlier, in this study, because of advantages of heterogeneous group of expert to compare with homogenous one, three specialists as heterogeneous group of expert with different backgrounds were employed to compute the FP of all 34 BEs in which the qualitative terms based on experts’ opinions are shown in Table 2.

Expert No. 1:

An experienced safety auditor and risk assessor working as consultant for complex chemical plant

Expert No. 2:

An experienced technician working in different kinds of process industry

Expert No. 3:

A senior chemical process designer from process engineering department with master certificate

Expert No. 4:

An experienced safety officer working in a complex process plant with safety engineering certificate

Table 2 Details of the BEs of FT of Fig. 7
Full size table

FAHP method is used to compute each expert’s capability and assigning the respective weights. The system of expert information is illustrated in Fig. 8; the experts profile is shown in Table 3.

Fig. 8
figure 8

Fuzzy AHP index system of respective expert capabilities

Full size image
Table 3 Experts’ profile
Full size table

The FP and BIM of all BEs in both conventional approach [77] and the proposed model based on IFNs and PFNs are shown in Table 4.

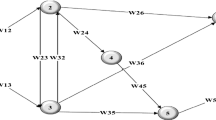
Table 4 Failure probability and importance measures of the BEs based on the proposed FTA approach and the conventional approach
Full size table

Once the data for all BEs are obtained, the FT (Fig. 7) is mapped to a BN (Fig. 9). The prior probability values of the root nodes of the BN are defined based on the values shown in Fig. 4, and corresponding values are provided in Table 4 in both conventional fuzzy set and IFNs. The conditional probability values of each intermediate node of the BN are populated based on the type of logic gate it represents. In this BN, G.1 is the node corresponding to the TE of the FT.

Fig. 9
figure 9

Bayesian network of the fault tree in Fig. 7

Full size image

Now running a query on this node would return the value of system unreliability. The value of system unreliability for the system obtained from the FTA-based approaches including fuzzy set theory, IFNs, and PFNs is 0.3016, 0.2988, and 0.2921, respectively. The system unreliability was also calculated using the BN-based using including fuzzy set theory, IFNs, and PFNs, and the value obtained was 0.1869, 0.1782, and 0.1711, respectively. To compare the unreliability results, both BN approaches are less than FT approaches. That is because the conventional FT approaches do not consider the statistical dependence among the events and also a number of CCF are available. However, it can be seen from the BN model that some events are statistically dependent on each other. As an example, the events represented by nodes G.6 and G.14 are statistically dependent on each other as they share a CCF and common BE is X.4. For a similar reason, nodes G.5, G.7, G.12, G.13, and G.16 are also statistically dependent. The effect of these dependences also propagates through the network to the node representing the TE. As it is mentioned earlier, the significant aspect of probabilistic risk assessment of a system is to determine the critical components based on their contribution to the occurrence of the system failure. This information will help to assessors and responsible decision makers to improve the system reliability by taking the necessary corrective actions or by putting more design determinations on the feeblest part of the system. Accordingly, the safety performance of the system will be improved by facing impressive reduction in probability of TE. As an example, if the assessors want to improve the reliability of the system, then they could substitute the above-mentioned critical components using components with higher reliability or they could introduce redundant components in parallel with the critical components.

The criticality of the BEs of the FT and corresponding BN in Figs. 7 and 9 are computed using Eq 20. The results of the evaluation are shown in Tables 4 and 5 for both FT- and BN-based approaches. According to the results shown in Table 4 which is FTA based, X.6 contributes the most to the TE probability based on fuzzy set theory and IFNs while using PFNs, X.4 has gotten the first critical ranking and thus ranked as the most critical component. According to BN-based approaches, X.3 contributes the most to the TE probability based on fuzzy set theory and PFNs while using IFNs, X.1 has gotten the first critical ranking and thus ranked as the most critical component. When the both BN and FT ranking are compared, it is obvious that both approaches agree on the ranking of most of the components. However, there are some disagreements between the four approaches regarding the ranking of BEs. For instance, the BN-based IFNs approach ranked X.33 as the least critical BE, whereas the conventional FT approached ranked X.30 as the least critical BE. Author surely with high confidence believes that these differences are because of the two reasons: firstly, the statistical independence supposition of the BEs and IEs in the conventional FT approaches and secondly, due to the improving knowledge acquisition which is collated from experts using linguistic terms and their corresponding IFNs and PFNs.

Table 5 Importance measures of the BEs based on the proposed BN approach and the conventional BN approach
Full size table

Figures 10 and 11 illustrate that the ranking of BEs obtained by the conventional method is completely different from those obtained by the proposed approaches when trying to eliminate, control, or substitute for obtaining further corrective actions. However, this comparison shows that the first priorities of BE using all methods are the same with consideration of different precedences among Bes, whereas the rest of BEs have considerable different priorities. In addition, it is vital to acquire corrective actions for at least the first 10 BEs on the ranking list to improve the safety performance of the company. Therefore, there is no difference to how the ranking list is considered for obtaining corrective actions. In addition, several studies have been done in the literature to represent the reliability of important measures as tools for recognizing the critical BEs. Author strongly believes that even though the integration of IFNs PFNs and BN method provides much more reliable information, it depends on the company’s conditions and the capacity to determine which ranking techniques are most appropriate for them.

Fig. 10
figure 10

Comparison between the three types of FTA-based ranking

Full size image
Fig. 11
figure 11

Comparison between the three types of BN-based ranking

Full size image

Conclusion

This study aimed to propose a new framework based on the 2-tuple intuitionistic fuzzy numbers to improve knowledge acquisition in failure diagnosis analysis using FTA. A Bayesian network mechanism is engaged in a same way to handle the shortages of conventional FTA as well. The study highlights an improvement in the completeness and enhancement in the probability computation for a spherical storage hydrocarbon tank system fault in a production process as a case study. Additionally, comparing the results of existing techniques [56, 77] and the proposed approaches showed that uncertainty factors about the reliability decreases and the result are much more exact besides having improvement and progressive in knowledge acquisition. Therefore, the proposed model has following attractions to compare the conventional ones:

  • It has the capability of allowing the natural modeling of incomplete knowledge. The approach uses IFS and PFS as a knowledge acquisition tool, thus reducing knowledge elicitation from the experts to a minimum. In this way, the knowledge acquisition bottleneck can be managed.

  • The proposed model has capability of allowing the natural modeling of incomplete knowledge. The approach uses IFNs; in this way, the knowledge acquisition bottleneck can be managed.

  • Fuzzy knowledge in expert systems, like human cognition and thinking, can be accustomed automatically following the changing environment through our BN model based on IFNs and PFNs. This is an innovation over other models.

  • Using BN has capability of letting to use historical data to update our risk analysis based on domestic information. FTA as a statistic analysis means that the assessors cannot analyze in deductive reasoning way, whereas the BN can deal with this considerable lack.

  • CCF and conditional dependencies between identified BEs are common fact in conventional FTA, and many methods are available such as using Beta factor to handle mentioned dependencies which seems that they are not more effective and efficient tools, whereas BN using conditional probability and graphical representation has high superiority to handle dependencies.

  • Fuzzy knowledge in expert systems, like human cognition and thinking, can be adjusted automatically following the changing environment through our fuzzy BN model. This is an innovation over other models.

At present, we use constant amount of probability for BEs. As a direction for further studies, we plan to use Bayesian updating mechanism for adding new possible probability data. In addition, we plan to apply the proposed model in dynamic system using dynamic FTA. The case study presented in this article provides assurance on the methodology and its competency in examining the failure of process components. Yet the current application was concentrated on automotive industry, the methodology could easily be extended to other processing systems. Furthermore, the IFNs which are used in this paper may be considered as traditional IFNs in fuzzy logic concepts. An argumentation on uncertainty treatment and comparing results using methods such as probability and Dempster–Shafer theory may consider for further studies.