Keywords

10.1 Introduction

Chemical process industries are one of the most hazardous sectors where the potential of occurrence of serious undesirable events, rare accidents, mishaps, or near misses is significant. Such unexpected events can directly or indirectly cause serious injuries like loss of life, serious and immutable environmental damage, loss of material and equipment assets, and decrease the forgotten factor as the reputation of the company. Fire and explosion, the release of toxic, and hazardous materials are common examples of the abovementioned events [1]. Catastrophic accidents such as the Piper Alpha fire and explosion in 1988, BP explosion in 2005, and Deepwater Horizon tragedy in 2010 reveal the tragic effects of major accidents in the chemical process industry [2]. Thus, the prediction of the occurrence of unexpected events and subsequent consequences has a high necessity to assure the safe operation of the system and to prevent the upcoming occurrence of similar events. In this regard, safety and risk analysis can help to prevent the occurrence of unwanted events and develop operational mitigation actions [3]. Several qualitative and quantitative methods, including fault tree analysis (FTA), event tree analysis (ETA), failure mode and effect analysis (FMEA), hazard and operability study (HAZOP), and risk matrix, have been widely used in the risk analysis of chemical process industries. Among the available techniques, FTA is a well-established technique, which can graphically describe the relationships between the cause and effects of different events in the form of Basic Events (BEs), Intermediates Events (IEs), and Top Event (TE). FTA can provide both qualitative and quantitative analysis by presenting undesired events and giving probabilistic analysis from root causes to the consequence [4].

FTA uses the probabilities of BEs (located at bottom of the tree) as quantitative input to calculate the probability of the undesired event as TE (located at the top of the tree). Therefore, the probability of all BEs as crisp values or probability density functions (PDF) is required for quantitative analysis [5]. However, in the real-world industry, because of the lack of knowledge and missing data or systematic bias, the availability of all necessary data cannot be guaranteed. Thus, collecting data from varieties of sources having different features such as dissimilar operating environments, industrial sectors, and experts from diverse backgrounds is an important solution, which has been widely used to obtain the known probability. In addition, even with consideration of exact probabilities or PDFs, intrinsic uncertainties may remain because of different failure modes, lack of knowledge of the mechanism of the failure process, and ambiguity of system experiences. Therefore, a robust method is required for calculating the probability of BEs and addressing the uncertainty among the data collection and analysis procedure [6, 7].

Experts’ knowledge has been used to obtain the BEs probability when objective data are limited, incomplete, imprecise, or unknown [8]. The fuzzy set theory (FST) introduced by Zadeh [9] has been demonstrated to be effective and efficient in data uncertainty handling and computing the probability of BEs utilizing multi-expert opinions. The previous studies generally used FST to acquire the probability of BEs from impression and subjectivity in expert judgment. For example, Yazdi and Kabir [10] proposed a framework to obtain the known failure rates from the reliability data handbook and the unknown failure rate according to the experts’ opinions. Due to the elicitation procedure considering the unavailability of sufficient data, fuzzy set theory is used to transform linguistic expressions provided by experts into fuzzy numbers. Subsequently, fuzzy possibility, crisp possibility, and failure probability of each BEs are calculated. The risk matrix analysis framework proposed by Yan et al. [11] considered potential risk influences such as controllability, manageability, criticality, and uncertainty. The likelihood in the risk matrix has been calculated by obtaining the probability of the TE of a fault tree. In the TE probability computation process, the probabilities of the BEs of the fault tree have been obtained through expert elicitation. The analytical hierarchy process (AHP) is utilized to improve the accuracy of the failure probability data by minimizing the subjective biases of the experts by quantifying their weightings. Yazdi and Kabir [12] revised Yan et al.’s methodology as a new framework using fuzzy AHP and similarity aggregation procedure (SAM) in the fuzzy environment to cope with available ambiguities of identified BEs. All mentioned papers used a combination of FST and multi-expert knowledge to approximate the BEs’ probabilities. However, the FST suffers from several shortages. The one worth mentioning is related to the uncertainty or hesitation about the degree of membership. The FST cannot include the hesitation in the membership functions. In this regard, Atanassov [13] extended conventional fuzzy set to propose the intuitionistic fuzzy set (IFS), in which non-membership degrees and hesitation margin groups have been included with the membership degrees. The IFS data are more complete than the conventional fuzzy data that considers membership function only [14]. In another example, it is demonstrated the use of IFSs to handle uncertainties in FMEA [15]. Yazdi [16] utilized IFS and specifically intuitionistic fuzzy numbers (IFNs) to develop a conventional risk matrix.

To the best of the authors’ knowledge, limited research has been conducted to combine IFNs and multi-expert knowledge to address the issues of data uncertainty in FTA. For instance, Shu et al. [17] utilized IFNs to analyze the failure behavior of the printed circuit board assembly. A vague FTA approach has been proposed [18] by integrating experts’ judgment into the analysis to calculate the fault interval of system components. Afterward, for fuzzy reliability evaluation of a “liquefied natural gas terminal emergency shutdown system”, Cheng et al. [19] used IFS with FTA. The weakest t-norm-based IFS has been used with FTA [20] to evaluate system reliability. Recently, Kabir et al. [21] have utilized IFS for dynamic reliability analysis.

On the other hand, traditional FTA as well as fuzzy FTA are well known to have a static structure and cannot consider the variation of risk due to the dynamic behavior of the system. In addition, BEs are assumed to be independent in both methods and they are considered to have binary states—failed and non-failed, whereas, in practice, events can be in more than two states. Moreover, the effects of common cause failure (CCF) in the reliability of systems are usually not considered in traditional FTA. Such mentioned issues are commonly named as model uncertainty in risk analysis [22]. Thus, model uncertainty is recognized as a considerable limitation of risk analysis methods. In this regard, a dependency coefficient method is introduced by Ferdous et al. [23] to evaluate the interdependencies of BEs in static FT. The joint likelihood function in the hierarchical Bayesian network is developed [24] to consider the interdependencies among BEs in conventional FT. Besides, Hashemi et al. [25] used the copula function technique to evaluate and model the interdependencies of BEs to improve uncertainty analysis.

Bayesian networks (BN) have become a popular method, which has been widely used to incorporate a variety of information types such as extrapolated data, experts’ judgment, or partially related data in risk analysis of process industries [26, 27]. Kabir and Papadopoulos [22] provided a review of the applications of BNs in reliability and risk assessment areas. Examples of such applications include risk analysis of fire and explosion [28, 29], leakage [30, 31], human error [32,33,34], maintenance activity [35, 36], and offshore and drilling operations [37,38,39] utilized BN as a probabilistic interface tool for reasoning under uncertainty. BN used a chain rule or d-separation to represent the causal relationships between a set of variables (in case of FTA is BEs) considering the dependencies [40]. BN is also able to cope with the limitations of conventional FTA as well as having a flexible structure. Several scholars have used BN in parallel with FTA and addressed the shortages of the conventional FTA by mapping FT into the corresponding BN [41,42,43,44]. Because of the modeling flexibility provided by BN, the interdependencies of BEs can be effortlessly modeled by using BN. BN can also model multiple states for BEs and common cause failure (CCF) scenarios. Furthermore, to deal with the model uncertainty, BN can perform the probability updating mechanism using Bayes’ theorem by adding new information about the system over time.

The novelty and contribution of this work are utilizing the advantages of IFNs over traditional FST to evaluate the TE probability of an FT. Besides, this chapter adopts BN to allow dynamic risk assessment under uncertainty, where the BEs’ probabilities are calculated based on the combination of subjective opinions and IFNs, and BN is used to take into account the interdependencies of BEs as well as CCF. The rest of the chapter is organized as follows. In Sect. 10.2, the uncertainty sources in chemical process industries are reviewed. A short overview of the IFS theory is presented in Sect. 10.2. In Sect. 10.3, the proposed methodology is described. Section 10.4 demonstrates the feasibility and efficiency of the proposed approach via a numerical example with sensitivity analysis. Lastly, the concluding statements are presented in Sect. 10.5.

10.2 Background

10.2.1 Uncertainty Sources in Chemical Process Industries

The term uncertainty is widely used with a different meaning in the literature on risk analysis. Several scholars claimed that uncertainty is equal to risk about the future and accordingly risk is equal to uncertainty. Others stated that uncertainty and risk are from two different schools and it has not been complicated to each other [40]. In this chapter, it is assumed the terms risk and uncertainty are two different concepts. There exist two distinct concepts of uncertainty in chemical process industries including (i) uncertainty caused by physical unpredictability (aleatory uncertainty) and (ii) uncertainty caused by insufficient knowledge (epistemic uncertainty) [45, 46].

The existence of aleatory and epistemic uncertainties in risk analysis of chemical process industries implies that the probability of numerous risk factors cannot be measured in an appropriate way when they are ambiguous and unknown. Referring to aleatory uncertainty, the random behavior of some parameters in a system or its environment should be stated such as inconsistency in weather conditions and experimental data variability for BEs in FT. In contrast, epistemic uncertainty is related to fuzziness, vagueness, or imprecision regarding the quality of chemical process safety, particularly in the accident scenario identification and consequence modeling. In reality, it is difficult to reduce aleatory uncertainty because of the intrinsic nature of a system, whereas it is possible to reduce epistemic uncertainty when more knowledge about the system is available over time. More information about the characteristics of aleatory and epistemic uncertainties can be found in [47]. This study concentrates on epistemic uncertainty.

During analysis, a certain explanation or assumption about the models leads to model uncertainty. Moreover, mathematical and other analytical tools are utilized to reduce properties of interest, ranging from structural, stochastic, human behavior, accident, evacuation, dispersion model, etc. This study concentrates on the model uncertainty caused by the independence assumptions among BEs in FTA. Thus, the modeling capability of BN is used to assess the dependency among events to address the abovementioned issue.

Parameter uncertainties are caused by the imprecisions and inaccuracies in the input data used in the process safety analysis. These uncertainties are intrinsic due to the imperfect nature of the available data, and the analysis process requires to be based on partial knowledge. Nonetheless, it is believed that parameter uncertainty is the easiest one to be quantified [48]. In the literature, to cope with parameter uncertainty, it is commonly expressed by PDFs and Monte Carlo simulation-based probability theory [49,50,51]. However, as mentioned earlier, PDFs are rarely easy to obtain. In this chapter, IFNs are utilized to deal with parameter uncertainty, where the probabilities of BEs are treated as IFNs that are derived from multi-experts’ knowledge.

10.2.2 IFS Theory

The concept of the classical fuzzy sets has been generalized by Atanassov [13] into IFS through the introduction of a non-membership function \(v_{{\tilde{A}}} \left( x \right)\) indicating the evidence against \(x \in X\) along with the membership value \(\mu_{{\tilde{A}}} \left( x \right)\) indicating evidence for \(x \in X\) and this admits an aspect of indeterminacy.

An IFS \(\tilde{A}\) in the universe of discourse X is given by

$$\tilde{A} = \left\{ {\left\langle {x,\mu_{{\tilde{A}}} \left( x \right),v_{{\tilde{A}}} \left( x \right)} \right\rangle :x \in X} \right\}$$
(10.1)

where \(\mu_{{\tilde{A}}} :X \to \left[ {0,1} \right]\) and \(v_{{\tilde{A}}} :X \to \left[ {0,1} \right]\) are membership and non-membership functions, respectively, where

$$0 \le \mu_{{\tilde{A}^{i} }} \left( x \right) + v_{{\tilde{A}^{i} }} \left( x \right) \le 1, \forall x \in X$$
(10.2)

For every value \(x \in X\), the values \(\mu_{{\tilde{A}}} \left( x \right)\) and \(v_{{\tilde{A}}} \left( x \right)\) represent, respectively, the degree of membership and degree of non-membership to \(\tilde{A} \subseteq X\) Moreover, the uncertainty level or hesitation degree of the membership of \(x\) in \(\tilde{A}\) is denoted as:

$$\pi_{{\tilde{A}}} \left( x \right) = 1 - \mu_{{\tilde{A}}} \left( x \right) - v_{{\tilde{A}}} \left( x \right)$$
(10.3)

If \(\pi_{{\tilde{A}}} \left( x \right) = 0,\forall x \in X\), then the IFS becomes a classical fuzzy set.

If the membership and non-membership functions of an IFS \(\tilde{A}\) (i.e., \(\mu_{{\tilde{A}}} \left( x \right)\) and \(v\left( {_{{\tilde{A}}} \left( x \right)} \right)\) satisfy the following conditions given by Eqs. (10.4) and (10.5), then \(\tilde{A}\) in X is considered as IF-convex

$$\mu_{{\tilde{A}}} \left( {\lambda x_{1} + \left( {1 - \lambda } \right)x_{2} } \right) \ge \min \left( {\mu_{{\tilde{A}}} \left( {x_{1} } \right),\mu_{{\tilde{A}}} \left( {x_{2} } \right)} \right) \forall x_{1} ,x_{2} \in X, 0 \le \lambda \le 1.$$
(10.4)
$$v_{{\tilde{A}}} \left( {\lambda x_{1} + \left( {1 - \lambda } \right)x_{2} } \right) \le \max \left( {v_{{\tilde{A}}} \left( {x_{1} } \right),v_{{\tilde{A}}} \left( {x_{2} } \right)} \right) \forall x_{1} ,x_{2} \in X, 0 \le \lambda \le 1.$$
(10.5)

If there exist at least two points \(x_{1} ,x_{2} \in X\) such that \(\mu_{{\tilde{A}}} \left( {x_{1} } \right) = 1\) and \(v_{{\tilde{A}}} \left( {x_{2} } \right) = 1\), then the IFS \(\tilde{A}\) in X is considered as IF-normal [52]:

An IFS \(\tilde{A} = \left\{ {\left\langle {x,\mu_{{\tilde{A}}} \left( x \right),v_{{\tilde{A}}} \left( x \right)} \right\rangle :x \in R} \right\}\) is called an IFN if

  1. (i)

    \(\tilde{A}\) is IF-normal and IF-convex.

  2. (ii)

    \(\mu_{{\tilde{A}}} \left( x \right)\) is an upper and \(v_{{\tilde{A}}} \left( x \right)\) is a lower semi-continuous.

  3. (iii)

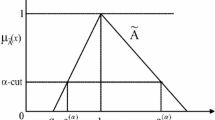
    \(Supp \tilde{A} = \left\{ {x \in X:v_{{\tilde{A}}} \left( x \right) < 1} \right\}\) is bounded (see Fig. 10.1).

    Fig. 10.1
    figure 1

    Graphical representation of IFNs

    Full size image

A Triangular-IFN is an IFN given by

$$\mu_{{\tilde{A}}} \left( x \right) = \left\{ {\begin{array}{*{20}l} {\frac{{x - a_{1} }}{{a_{2} - a_{1} }},} \hfill & {a_{1} \le x \le a_{2} } \hfill \\ {\frac{{a_{3} - x}}{{a_{3} - a_{2} }},} \hfill & {a_{2} \le x \le a_{3} } \hfill \\ {0,} \hfill & {{\text{otherwise}}} \hfill \\ \end{array} } \right.$$
(10.6)

and

$$v_{{\tilde{A}}} \left( x \right) = \left\{ {\begin{array}{*{20}l} {\frac{{a_{2} - x}}{{a_{2} - a_{1}^{\prime } }},} \hfill & {a_{1}^{\prime } \le x \le a_{2} } \hfill \\ {\frac{{x - a_{2} }}{{a_{3}^{\prime } - a_{2} }},} \hfill & {a_{2} \le x \le a_{3}^{\prime } } \hfill \\ {1,} \hfill & {{\text{otherwise}}} \hfill \\ \end{array} } \right.$$
(10.7)

where \(a_{1}^{\prime } \le a_{1} \le a_{2} \le a_{3} \le a_{3}^{\prime }\). This TIFN is denoted by \(\tilde{A} = \left( {a_{1} ,a_{2} ,a_{3} ; a_{1}^{\prime } ,a_{2} ,a_{3}^{\prime } } \right).\)

10.3 Material and Method

To introduce the methodology developed in this chapter, this section briefly describes the framework as can be seen in Fig. 10.2.

Fig. 10.2
figure 2

The structure of the proposed method

Full size image

10.3.1 Hazard Analysis

There are numerous methods available for hazard analysis in different types of industrial sectors. The initial step of all hazard analysis methods is identifying all possible hazards. Therefore, well understanding of process function has a high necessity for this purpose. All information about a process system should be collected to understand its functionality appropriately. Then, any hazards which have enough potential to destroy the industrial equipment, surrounding environment, or harm to the public should be considered [40]. HAZOP technique is based on the brainstorming method that has enough capability to recognize hazardous systems and sub-systems by employing a group of specialists, commonly a third-party company. Thus, this study considers the outcome of HAZOP as a highly probable and severe event. In fact, the HAZOP study is commonly in conducted process-based industries to identify the deviation as a pre-step fault tree analysis. However, considering the inherent features process, FMEA or other types of risk assessment method can also be carried out.

10.3.2 Developing a Fault Tree and Collecting Data

After identifying an event as the TE of a fault tree, the rest of the tree is developed from top to bottom in a downward direction. It should be noted that further analysis of the FT is performed based on the TE. Therefore, the TE of the FT must be chosen appropriately for further analysis. The TE is commonly specified as an accident or hazardous event which can potentially be a cause of asset loss or harm to the public. After finalizing the development of an FT, the BEs that are put at the bottom level of the tree (leaves) should be identified to facilitate further analysis. The logic relationship between BEs, IEs, and TE is defined using Boolean OR and AND gates.

The reliability data such as the ones from OREDA [53] can be used to obtain the failure rate of known BEs. Nevertheless, when there is a difficulty in using a reliability handbook to obtain failure rates of rare events with unknown or limited failure data, three popular methods, including expert judgment, extrapolation, and statistical methods, can be utilized to estimate the failure rates [54]. The statistical method estimates the failure rates by estimating the failure probabilities by performing a short test on the practical data. In addition, statistical methods can be distinguished with deterministic methods, which are suitable where observations are precisely reproducible or are expected to be in this manner. The extrapolation method denotes the utilization of a predicting model, equal condition, or the available reliability data sources. The expert judgment method directly calculates probabilities based on experts’ opinions on the occurrence of BEs. This study employs the expert judgment method to estimate BEs’ occurrence probability. In this regard, a combination of subjective opinions expressed by experts and IFNs can help assessors to deal with the uncertainty that may arise during the analysis. In the following subsection, the procedure of using an expert system is presented.

10.3.3 Use of the Expert System

Expert systems are convenient to use in quantitative analysis models in circumstances where the available situations make it difficult or even more impossible to make enough observation to quantify the models using real data. Thus, expert systems are commonly used to approximate the model parameter under ambiguous conditions. Expert systems can also be used to improve the estimation, which is gained from real data.

An expert provides his/her judgment about a subject based on knowledge and experience according to his/her background. Thus, an employed expert will require to respond to a predefined set of questions related to a subject, which can include personal information, probabilities, rating, weighting factor, uncertainty estimation, and so on. The experts’ opinions can be collected during an eliciting. An important issue related to the elicitation process is that experts’ opinions should not be used instead of rigorous reliability and risk analysis approaches, whereas it can be used to supplement them where reliability and risk analytical approaches are inconsistent or inappropriate.

10.3.3.1 Experts’ Opinion Elicitation

Due to the increased complexity of systems and the subjective nature of expert judgment, no officially renowned approach has been developed for treating expert opinion. Once the elicitation process is finished, opinions are analyzed by combining them to obtain an aggregated result to be used in the reliability analysis. Clemen and Winkler [55] divided the elicitation and aggregation processes into two categories—behavioral and mathematical methods. Behavioral methods aim to create some sort of group agreement between the employed experts. While, in mathematical methods, the experts expressed their opinion about an uncertain quantity in the form of subjective probabilities. Afterward, suitable mathematical methods are used to combine these opinions. The rationale behind using mathematical approaches for the processing of experts’ opinions was provided in [56, 57]. Hence, in this study, one of the mathematical methods is used to analyze experts’ opinions.

According to [58], probability can be considered as a numerical representation of uncertainty because it offers a way to quantify the likelihood of occurrence of an event. Therefore, it is much easier for the employed experts to use linguistic expressions like high probable, low probable, and so on to express their opinions. Three elicitation methods that have been widely used for subjective analysis are Indirect, Direct, and Delphi. The basis of the Indirect method is to utilize the betting rates of experts to reach a point of indifference between obtainable choices according to an issue. The Direct method is the direct estimation of the degree of confidence of an expert on some subject. The Delphi technique is the first organized tool for methodologically collecting opinions on a specific subject using a cautiously defined ordered set of questionnaires mixed with summarized information and feedback resulting from previously received responses [59, 60]. The selection of each method for a particular purpose should fulfill the rational consensus principles such as accountability and fairness. In this study, among the abovementioned methods, Delphi, because of having enough capacity for expert opinion elicitation, is selected for eliciting process.

10.3.3.2 Experts Weighting Evaluation

Once the experts’ opinion elicitation process is completed, the expert weighting calculation is started. This step is necessary because, in real life, each employed expert has a different weight according to his/her experience and background. Thus, to obtain realistic results for the probability of each BE, the weight (importance of the judgment outcome) of the employed experts should be identified. There are many methods such as simple averaging besides many unmethodical techniques that may be used for giving specific weighting to the experts. However, they cannot diminish subjective bias and help domain experts to carry out the eliciting procedure in an effective way.

AHP (analytical hierarchy process) introduced by Saaty [61] is a widely used process in multi-criteria decision-making. This process breaks large decision problems into smaller ones and then uses a hierarchy of decision layers to handle the complexity of the problems. This allows focusing on a smaller set of the decision at a time. There exist criticism regarding AHP’s use of lopsided judgmental scales and its inability to appropriately reflect the characteristic uncertainty and imprecision of pair comparisons [62]. The verbal statements provided by the decision-makers in AHP could be unclear. Moreover, they regularly would choose to provide their preferences as oral expressions instead of numerical quantities and the type of pair comparisons used cannot properly reflect their decisions about priorities [63,64,65,66]. The abovementioned shortages represent that in most cases, the nature of decision-making is full of ambiguities and complexities, and accordingly it is denoted that most decisions are made in a fuzzy environment.

Let \(O = \left\{ {o_{1} , o_{2} , \ldots , o_{n} } \right\}\) is a set of objects and \(W = \left\{ {w_{1} , w_{2} , \ldots , w_{m} } \right\}\) is a set of goals. Therefore, the extent analysis values for \(m\) goals for each object can be denoted as:

$$M_{gi}^{1} ,M_{gi}^{2} , \ldots ,M_{gi}^{m} \quad i = 1,2, \ldots n$$
(10.8)

where each of \(M_{gi}^{m}\) is a triangular fuzzy set.

Step 1. The fuzzy synthetic extent concerning the i-th object is denoted as:

$$\mathop \sum \limits_{j = 1}^{m} {\text{\rm M}}_{gi}^{j} \otimes \left[ {\mathop \sum \limits_{i = 1}^{n} \mathop \sum \limits_{j = 1}^{m} {\text{\rm M}}_{gi}^{j} } \right]^{ - 1}$$
(10.9)

To get \(\mathop \sum\nolimits_{j = 1}^{m} {\text{\rm M}}_{gi}^{j}\) the fuzzy addition operation of \(m\) extent analysis values for a particular matrix is achieved as:

$$\mathop \sum \limits_{j = 1}^{m} {\text{\rm M}}_{gi}^{j} = \left( {\mathop \sum \limits_{j = 1}^{m} l_{j} ,\mathop \sum \limits_{j = 1}^{m} m_{j} ,\mathop \sum \limits_{j = 1}^{m} u_{j} } \right)$$
(10.10)

and afterward, the inverse of the vector is calculated as follows:

$$\left[ {\mathop \sum \limits_{i = 1}^{n} \mathop \sum \limits_{j = 1}^{m} {\text{\rm M}}_{gi}^{j} } \right]^{ - 1} = \left( {\frac{1}{{\mathop \sum \nolimits_{j = 1}^{m} l_{j} }},\frac{1}{{\mathop \sum \nolimits_{j = 1}^{m} m_{j} }},\frac{1}{{\mathop \sum \nolimits_{j = 1}^{m} u_{j} }}} \right)$$
(10.11)

Step 2. The degree of likelihood of \({\text{\rm M}}_{2} = \left( {l_{2} ,m_{2} ,u_{2} } \right) \ge {\text{\rm M}}_{1} = \left( {l_{1} ,m_{1} ,u_{1} } \right)\) is calculated as:

$$V\left( {M_{2} \ge M_{1} } \right) = \sup_{y \ge x} \left[ {\min \left( {\mu_{{M_{1} }} \left( x \right),\mu_{{M_{2} }} \left( y \right)} \right)} \right]$$
(10.12)

It can be represented by Eq. (10.13).

$$V\left( {M_{2} \ge M_{1} } \right) = hgt\left( {M_{1} \cap M_{2} } \right) = \mu_{{M_{2} }} \left( d \right) = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {{\text{if}}\;m_{2} \ge m_{1} } \hfill \\ {0,} \hfill & {{\text{if}}\;l_{2} \ge u_{1} } \hfill \\ {\frac{{ l_{1} \ge u_{1} }}{{\left( {m_{2} - u_{2} } \right) - \left( {m_{1} - u_{1} } \right)}},} \hfill & { {\text{otherwise}}} \hfill \\ \end{array} } \right.$$
(10.13)

As seen in Fig. 10.3, \(d\) is the highest intersection point between \(\mu_{{M_{1} }}\) and \(\mu_{{M_{2} }}\).

Fig. 10.3
figure 3

The intersection between \(M_{1}\) and \(M_{2}\)

Full size image

Step 3. The degree of likelihood that a convex fuzzy number is greater than \(k\) convex fuzzy \(M_{i} \left( {i = 1,2, \ldots ,k} \right)\) numbers can be obtained by:

$$\begin{aligned} V\left( {M \ge M_{1} ,M_{2} , \ldots ,M_{k} } \right) & = V\left[ {\left( {M \ge M_{2} } \right)\;{\text{and}}\;\left( {M \ge M_{1} } \right){\text{and}}\; \ldots \;{\text{and}}\;\left( {M \ge M_{k} } \right)} \right] \\ & = {\text{min}}V\left( {M \ge M_{i} } \right), i = 1,2,3, \ldots k \\ \end{aligned}$$
(10.14)

Suppose that \(d^{\prime} ( A_{i} ) = \min V\left( {S_{i} \ge S_{k} } \right)\) for \(k = 1,2, \ldots ,n;k \ne i\). Now, the given weight vector is denoted by:

$$W^{\prime } = (d^{\prime } (A_{1} ),d^{\prime } (A_{2} ), \ldots ,d^{\prime } (A_{n} ))^{{\text{T}}}$$
(10.15)

where \(A_{i} \left( {i = 1,2, \ldots ,n} \right)\) are n elements.

Step 4. Using normalization, the normalized weight vectors are:

$$W_{{{\text{FAHP}}}} = d\left( {A_{1} } \right),d\left( {A_{2} } \right), \ldots , d\left( {A_{n} } \right))^{T}$$
(10.16)

where W is a non-fuzzy number.

The fuzzy linguistic variables are used to allow experts to provide their subjective opinions reflecting nine-point essential scale. In this chapter, the linguistic variables and their equivalent fuzzy numbers are used.

10.3.3.3 Experts’ Opinion Aggregation

The experts’ opinion aggregation process can be completed in three phases including (i) obtaining linguistic terms from experts describing the likelihood of occurrence of BEs, (ii) mapping linguistic variables into the corresponding fuzzy numbers, and (iii) applying an aggregation process under fuzzy environment.

Firstly, the engaged experts provided their judgements about the likelihood of occurrence of each BE in the fault tree. Their opinions can be obtained in the form of linguistic variables represented as IFNs.

As experts may have dissimilar opinions about a subject due to having a different level of experience, background, and expertise, it is essential to aggregate multi-expert opinions to reach an agreement. Different kinds of aggregation methods like the arithmetic averaging method and similarity aggregation method (SAM) can be utilized for this purpose. However, Yazdi and Zarei [56] pointed out the benefits of such methods in the context of fuzzy FTA. It is concluded that SAM has enough capability for this purpose. Therefore, an extension of SAM as described in [67] is used in this chapter for the aggregation of IFNs. The SAM method contains the following steps.

Step A. Mapping of linguistic variables into equivalent IFNs:

After each expert, \(E_{k} \left( {k = 1, 2, \ldots , n} \right)\) provides his/her judgment about the occurrence possibility of each BE in the form of linguistic variables; accordingly, it is transformed into the equivalent IFNs.

Step B. Degree of similarity computation:

The similarity \(S_{uv} \left( {\tilde{A}_{u} ,\tilde{A}_{v} } \right)\) between the opinions \(\tilde{A}_{u}\) and \(\tilde{A}_{v}\) of experts \(E_{u}\) and \(E_{v}\) is evaluated as:

$$S_{uv} \left( {\tilde{A}_{u} ,\tilde{A}_{v} } \right) = \left\{ {\begin{array}{*{20}c} {\frac{{EV_{u} }}{{EV_{v} }} if EV_{u} \le EV_{v} } \\ {\frac{{EV_{v} }}{{EV_{u} }} if EV_{v} \le EV_{u} } \\ \end{array} } \right.$$
(10.17)

where \(S_{uv} \left( {\tilde{A}_{u} ,\tilde{A}_{v} } \right) \in \left[ {0,1} \right]\) is the function to measure similarity, where \(\tilde{A}_{u}\) and \(\tilde{A}_{v}\) are two regular intuitionistic fuzzy numbers, \(EV_{u}\) and \(EV_{v}\) are the expectancy evaluation for \(\tilde{A}_{u}\) and \(\tilde{A}_{v}\). The \(EV\) of a triangular IFN \(\tilde{A} = \left( {a,b,c; a^{\prime}, b^{\prime}, c^{\prime} } \right)\) is calculated as:

$$EV\left( {\tilde{A}} \right) = \frac{{\left( {a + a^{\prime } } \right) + 4b + (c + c^{\prime } )}}{8}$$
(10.18)

A similarity matrix \(\left( {SM} \right)\) for m experts is defined as:

$$SM = \left[ {\begin{array}{*{20}c} 1 & {s_{12} } & {\begin{array}{*{20}c} {s_{13} } & {\begin{array}{*{20}c} \cdots & {s_{1m} } \\ \end{array} } \\ \end{array} } \\ {s_{21} } & 1 & {\begin{array}{*{20}c} {s_{23} } & {\begin{array}{*{20}c} \cdots & {s_{2m} } \\ \end{array} } \\ \end{array} } \\ {\begin{array}{*{20}c} \vdots \\ {s_{m1} } \\ \end{array} } & {\begin{array}{*{20}c} \vdots \\ {s_{m2} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} { \vdots } & {\begin{array}{*{20}c} { \ddots } & { \vdots } \\ \end{array} } \\ \end{array} } \\ {\begin{array}{*{20}c} {s_{m3} } & {\begin{array}{*{20}c} {... } & {1 } \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right]$$
(10.19)

where \(S_{uv} = s\left( {\tilde{A}_{u} ,\tilde{A}_{v} } \right)\), if \(u = v\) then \(S_{uv} = 1\).

Step C. Degree of agreement computation:

The average agreement degree \(AA\left( {E_{m} } \right)\) for each expert is calculated as

$${\text{AA}}\left( {E_{m} } \right) = \frac{1}{m - 1}\mathop \sum \limits_{{\begin{array}{*{20}c} {v = 1} \\ {v \ne 1} \\ \end{array} }}^{m} S_{uv}$$
(10.20)

where \(m = 1,2, \ldots ,n\).

Step D. The relative agreement computation:

The \({\text{RAD}} \left( {E_{m} } \right)\) is the relative agreement degree, which can be calculated as:

$${\text{RAD}} \left( {E_{m} } \right) = \frac{{{\text{AA}} \left( {E_{m} } \right)}}{{\mathop \sum \nolimits_{u = 1}^{n} {\text{AA}} \left( {E_{n} } \right)}}$$
(10.21)

where \(m = 1,2, \ldots ,n\).

Step E. Consensus degree computation:

The aggregation weight \(\left( {w_{m} } \right)\) of an expert \(E_{m}\) is computed using \({\text{RAD}} \left( {E_{m} } \right)\), and the weight of each expert (\(W_{{{\text{FAHP}}}}\)) is obtained by FAHP as follows.

$$w_{m} = \alpha \odot W_{{{\text{FAHP}}}} (E_{m} ) + \left( {1 - \alpha } \right) \odot {\text{RAD }}\left( {E_{m} } \right)$$
(10.22)

where \(\alpha \left( {0 \le \alpha \le 1} \right)\) is the weighting factor also known as a relaxation factor that can be assigned to \(W_{{{\text{FAHP}}}} \left( {E_{m} } \right)\) \({\text{RAD}} \left( {E_{m} } \right)\) to define their relative importance.

Step F. Aggregated result computation:

The aggregated result for each basic event can be computed as:

$$\tilde{P}_{j} = \mathop \sum \limits_{i = 1}^{n} w_{m} \otimes \tilde{P}_{ij}$$
(10.23)

where \(\tilde{P}_{j}\) is the aggregated possibility of basic event j in the form of IFNs.

So far, the aggregation possibility of each BE based on IFNs is computed. In the next section, the procedure of TE computation is explained.

10.3.4 Calculation of Probability of TE

Once the occurrence possibilities of all BEs are obtained, these values are translated into the equivalent probabilities using the following equation introduced by [68]:

$${\text{FP}} = \left\{ {\begin{array}{*{20}l} {1/10^{k} } \hfill & {{\text{FPS}} \ne 0} \hfill \\ 0 \hfill & {{\text{FPS}} = 0} \hfill \\ \end{array} } \right.$$
(10.24)

where FP and FPS represent failure probability and failure possibility, respectively, and

$$k = 2.301 \times \left[ {\left( {1 - {\text{FPS}}} \right)/{\text{FPS}}} \right]^{1/3}$$
(10.25)

Once the intuitionistic fuzzy failure probabilities of the BEs are obtained, they are used to calculate the IF probability of the TE. Intuitionistic fuzzy arithmetic operations are adopted to evaluate the probabilities of the minimal cut sets of the FT and the same for the TE probability.

A set of minimal cut sets of a fault tree can be denoted as:

$$S = C_{i} :i = 1,2, \ldots ,m$$
(10.26)

where \(C_{i}\) is the i-th minimal cut set of order \(k\) and is denoted as \(C_{i} = e_{1} .e_{2} \ldots e_{k}\).

Let the probability \(\tilde{P}_{j}\) of event \(e_{j} :i = 1,2, \ldots ,n\) be characterized by triangular IFNs \(\left( {a_{j} ,b_{j} ,c_{j} ;a_{j}^{\prime } ,b_{j} ,c_{j}^{\prime } } \right)\), then the failure probability of \(\tilde{P}_{{C_{i} }}\) of the minimal cut set \(C_{i}\) is estimated using the following expressions.

$$\begin{aligned} \tilde{P}_{{C_{i} }} & = {\text{AND}}\left( { \tilde{P}_{1} ,\tilde{P}_{2} , \ldots ,\tilde{P}_{k} } \right) = \tilde{P}_{1} \otimes \tilde{P}_{2} \otimes \ldots \otimes \tilde{P}_{k} \\ & = \left( {\mathop \prod \limits_{j = 1}^{n} a_{j} ,\mathop \prod \limits_{j = 1}^{n} b_{j} ,\mathop \prod \limits_{j = 1}^{n} c_{j} ;\mathop \prod \limits_{j = 1}^{n} a_{j}^{\prime } \mathop \prod \limits_{j = 1}^{n} b_{j} ,\mathop \prod \limits_{j = 1}^{n} c_{j}^{\prime } } \right) \\ \end{aligned}$$
(10.27)

As the TE of an FT is represented by an OR gate, the failure probability of the TE can be calculated using the following equation:

$$\begin{aligned} ~\tilde{P}_{{C_{i} }} = & {\text{OR}}\left( {~\tilde{P}_{{c1}} ,\tilde{P}_{{c2}} , \ldots ,\tilde{P}_{{cm}} } \right) = 1{ \ominus }\left( {1{ \ominus }~\tilde{P}_{{c1}} } \right) \otimes \left( {1{ \ominus }~\tilde{P}_{{c2}} } \right) \otimes \ldots \otimes \left( {1{ \ominus }~\tilde{P}_{{cm}} } \right) \\ = & \left( {1 - \mathop \prod \limits_{{j = 1}}^{n} \left( {1 - a_{j} } \right),1 - \mathop \prod \limits_{{j = 1}}^{n} \left( {1 - b_{j} } \right),1 - \mathop \prod \limits_{{j = 1}}^{n} \left( {1 - c_{j} } \right);} \right. \\ & \quad \left. {1 - \mathop \prod \limits_{{j = 1}}^{n} \left( {1 - a_{j}^{\prime } } \right),1 - \mathop \prod \limits_{{j = 1}}^{n} \left( {1 - b_{j} } \right),1 - \mathop \prod \limits_{{j = 1}}^{n} \left( {1 - c_{j}^{\prime } } \right)} \right) \\ \end{aligned}$$
(10.28)

where \(\tilde{P}_{{C_{1} }} , \tilde{P}_{{C_{2} }} , \ldots , \tilde{P}_{{C_{m} }}\) denoted the failure probabilities of all MCSs \(C_{i} :i = 1,2, \ldots ,m\).

Through IF-defuzzification process an IFN can be converted to a single scalar quantity. The failure probability of the TE obtained as triangular IFN \(\tilde{A} = \left( {a,b,c;\mathop {a,}\limits^{\prime } b,\mathop c\limits^{\prime } } \right)\) can be defuzzified as follows.

$$X = \frac{1}{3}\left[ {\frac{{\left( {c^{\prime } - a^{\prime } } \right)\left( {b - 2c^{\prime } - 2a^{\prime } } \right) + \left( {c - a} \right)\left( {a + b + c} \right) + 3\left( {c^{\prime 2} - a^{\prime 2} } \right)}}{{c^{\prime } - a^{\prime } + c - a}}} \right]$$
(10.29)

10.3.5 Different Approach Comparison

To understand the efficiency of the proposed model, the results are compared with the common approaches. Firstly, conventional FFTA based on the FST which is widely used in different engineering applications is applied. Then, an approach based on the integration of the BN and FST which was introduced in [12] is utilized.

As mentioned in the literature, the procedure of conventional FFTA is utilizing triangular or trapezoidal fuzzy numbers for the probability expression of all BEs in FT. Then, fuzzy arithmetic operations are utilized to compute the TE probability in terms of a fuzzy number.

In the second approach, after [69] that compared conventional FTA and BN, many studies have been performed by mapping FT into the corresponding BN for different applications. A list of such works can be found in literature [70], which makes use of the advantages of multi-expert opinions and FST for uncertainty handling in the data and BN for modeling dependency between events. According to their approach, the probability of each BE is computed in five key steps as collecting experts’ opinions in qualitative terms, fuzzification, aggregation, defuzzification, and probability computation. Once the probability of each BEs is obtained, then FT is mapped into the corresponding BN. According to the Bayes theorem, the TE probability can be calculated as follows.

In a BN, the joint probability distribution of a set of variables can be denoted using the conditional dependency of variables and chain rules as follows:

$$P\left( U \right) = \prod\limits_{i = 1}^{n} P \left( {X_{i} {\mid }X_{i + 1} , \ldots X_{n} } \right)$$
(10.30)

where \(U = \left\{ {X_{1} ,X_{2} , \ldots ,X_{n} } \right\}\) and \(X_{i + 1}\) is the parent of \(X_{i}\). Consequently, the probability of \(X_{i}\) can be calculated as:

$$P\left( {X_{i} } \right) = \sum\limits_{{U{ \setminus }X_{i} }} P \left( U \right)$$
(10.31)

Using Bayes theorem as seen in Eq. (10.32), the prior probability of an event (E) can be updated.

$$P\left( {U|E} \right) = \frac{{P\left( {U \cap E} \right)}}{P\left( E \right)} = \frac{{P\left( {U \cap E} \right)}}{{\mathop \sum \nolimits_{U} P\left( {U \cap E} \right)}}$$
(10.32)

To get further details, readers can refer to [71].

10.3.6 Sensitivity Analysis

Once the relative competency of each expert’s opinion is predicted, it is better to determine the consensus coefficient. Thus, the decision-maker needs to allocate a proper value for the relaxation factor \(\alpha\) in Eq. (10.22); otherwise, sensitivity analysis (SA) should be performed to evaluate the reliability of the system when \(\alpha\) has been given different values ranging from 0 to 1. In this study, the relaxation factor is considered as 0.5 to give equal weights to both factors on the right side of the Eq. (10.22). However, to identify the sensitivity of the BEs, we have performed the sensitivity analysis by varying the values of \(\alpha .\) This helped to understand which of the BEs are more sensitive to uncertainty.

Using BIM, the criticality of an event is identified as follows:

$${\text{BIM}} \left( {{\text{BE}}_{i} } \right) = P{\text{(Top}}\;{\text{Event|}}P\left( {{\text{BE}}_{i} } \right) = 1) - P{\text{(Top}}\;{\text{Event|}}P\left( {{\text{BE}}_{i} } \right) = 0)$$
(10.33)

As seen in the above equation, the criticality of the basic event \({\text{BE}}_{i}\) is computed by taking the difference between the top event probabilities when the \({\text{BE}}_{i}\) is assumed to have occurred and non-occurred, respectively.

10.4 Application to the Case Study

The developed methodology is applied to the risk analysis of an ethylene oxide (EO) production plant that is a component of an ethylene transportation line to demonstrate its effectiveness. The detail of the system is shown in Fig. 10.4. A prior study performed on the abovementioned system by [72] identified the most hazardous components of the system, including the ethylene oxide storage and reaction unit, ethylene oxide distillation column, transportation line, and ethylene re-boiler. It was recommended that further risk assessment is essential for the declared units. Therefore, Khan and Haddara [73] found optimal maintenance in the above case study using a risk-based maintenance method. Additionally, the ethylene transportation line component was recognized as the third key hazard in the available units. In this regard, [12] applied their proposed approach to EO Transportation line as a case study.

Fig. 10.4
figure 4

Schematic diagram of the EO plant [72]

Full size image

10.4.1 Probabilistic Risk Assessment

An ignition of vapor cloud that may lead to a fireball is selected as the TE of the FT. The developed FT is shown in Fig. 10.5. As seen in the fault tree, there are 25 BEs (represented as circles) and details of these BEs are presented in Table 10.1. To compute the occurrence probability of each BE, the heterogeneous group of experts used in [12] has been used in this chapter. Using the Delphi method, employed experts were asked to provide their judgements in relevant linguistic terms. The weights of experts have been computed using the FAHP method, and the calculated weights of experts 1, 2, 3, and 4 are 0.249, 0.126, 0.495, and 0.128, respectively [12].

Fig. 10.5
figure 5

FT for the ethylene transportation line (reworked and modified from [12])

Full size image
Table 10.1 Details of the BEs of FT of Fig. 10.5 and experts’ opinions
Full size table

To show the aggregation procedure of expert’s judgment; consider the case of BE24 (Corrosion) as an example. Concerning the characterization of IFNs, the linguistic variables, obtained from four experts, are categorized as “L”, “M”, “FH”, and “M”. The detailed computation of aggregation for BE24 is shown in Table 10.2. The aggregated results for all BEs are presented in Table 10.3.

Table 10.2 Aggregation calculations for the BE24
Full size table
Table 10.3 The fuzzy and crisp failure data of all BEs
Full size table

To calculate the TE of the FT of Fig. 10.5, it was qualitatively analyzed to obtain 102 MCSs. Each of the MCSs is a combination of a number of BEs that can cause the TE. Using the Eqs. (10.22), (10.23) and the IF-probabilities of the BEs from Table 10.3, the TE probability as IFN is calculated as: {3.296E-11, 8.270E-10, 1.132E-08, 1.804E-11, 8.270E-10, 1.922E-08}. After defuzzification, the crisp probability of the TE obtained is 5.715E-09. We have also used the crisp probabilities of the BEs (see the last column of Table 10.3) to evaluate the TE probability and the value obtained was 1.620E-09. As can be seen, this value is close to the value obtained through the defuzzification of the IF-probabilities.

According to step 11 of the framework shown in Fig. 10.2, the TE probability has been evaluated using the BN-based approach for comparison of the result. Figure 10.6 shows the BN model of the FT illustrated in Fig. 10.5. In this BN, the prior probabilities of the root nodes are specified based on the crisp probabilities of the BEs as shown in Table 10.3. Conversely, the conditional probabilities of nodes representing logic gates are characterized according to the specification of the gates. After running a query on this BN model, the probability of TE obtained was 1.576E-9, which is quite close to the value of TE probability calculated by the algebraic formulation.

Fig. 10.6
figure 6

BN model of the FT of Fig. 10.5

Full size image

10.4.2 Sensitivity Analysis

As discussed in Sect. 3.6, a SA can be applied to show the validity of the proposed method, as well as highlight some features of the method. By varying the value of \(\alpha\) from 0 to 1, the probability of each BE is computed. Accordingly, the TE probability is estimated using BN. The probabilities of all BEs based on the corresponding value of \(\alpha\) are provided in Table 10.4.

Table 10.4 The probability of BEs based on different relaxation factor
Full size table

It should be added that the sensitivity analysis assists experts to allocate priorities and make it flexible to perform the risk assessment. Figure 10.7 shows the results of the sensitivity analysis.

Fig. 10.7
figure 7

The probability of basic events based on the variation of \(\alpha\)

Full size image

The SA specifies that the estimated probability for all the basic events is not pretty sensitive to the variations in the value of \(\alpha\). Using different values of \(\alpha\) ranging from 0 to 1, we can see that the risk probability of only 4 of the 25 basic events (16%) is quite different and these BEs are BE4, BE9, BE11, and BE20. Therefore, in this study, the differences between the rankings concerning different \(\alpha\) values are low.

In addition, choosing an adequate value of \(\alpha\) illustrates an important role in the top event probability computation. The value of \(\alpha\) can have an effect on the probability of each BE and accordingly top event. Thus, the value of \(\alpha\) should be allocated taking into account the following issues. As an initial subject, decision-makers can consult any existing historical data from similar operation conditions and risk assessment, which have received feedback from them earlier. Next, using a questionnaire or other available methods, the value of \(\alpha\) can be obtained based on the decision-makers’ opinions. If a decision-maker has a high confidence regarding his/her judgment about the probability of basic events, the value of \(\alpha\) can be set to a higher value, on the contrary, a smaller value can be assigned to \(\alpha\). Finally, the value of \(\alpha\) can be assigned according to a realistic circumstance, meaning that the value of \(\alpha\) should be allocated a higher value when it is easy to get the consensus of decision-makers’ judgements on the probability of basic events or when the appropriately selected decision-makers are present.

The above SA illustrates that the presented model can offer vital data to analysts and other involved parties in the risk assessment process. Accordingly, the probability of the top event is computed by varying the value of \(\alpha\).

According to the new estimated probability of BEs, the probability of the TE is also updated and provided in Table 10.5.

Table 10.5 The probability of the top event based on different values of \(\alpha\)
Full size table

10.4.3 Identification of Critical BEs and Corrective Actions for the Most Critical BEs

As we all know, one of the important outputs of FTA and correspondingly BN is recognizing the critical basic events. Based on this recognition, decision-makers can provide corrective and/or preventive actions to reduce the probability of critical basic events. As a result, the TE probability will be reduced; subsequently, the probability reduction will lead to improved performance of the system.

By following the criticality calculation approach shown in Sect. 3.6, the criticality of the BEs is estimated and conveyed in Table 10.6. As seen in the table, Flame arrestor A failed (BE4), Flame arrestor B failed (BE5), Ignition source present (BE6), Flammable gas detector fail (BE1), Flow sensor failed (BE11), and Leak from bends (four bends) (BE9) are recognized to be the most critical events (in the descending order of criticality), which are also recognized as top six critical events in [12]. This chapter provides corrective actions for the first five critical basic events because in the realistic case, the system cannot apply any interpretative actions to all BEs. The existing control measures for the aforementioned BEs can fall into the process safety management system since the construction of the complex plant. However, the performance of the control measures needs to be upgraded based on all requirements and changed after a couple of years.

Table 10.6 Criticality ranking of the BEs of the FT of Fig. 10.5
Full size table

Several control measures as corrective actions are recommended for the critical basic events. It is believed that any corrective actions need to satisfy the three main criteria as (i) it should have acceptable efficiency, (ii) it should fall into the acceptable economic perspective, and (iii) the recommended corrective actions should be environmentally friendly. Keeping these criteria in our mind, to control the Flame arrestors A and B, increasing the number of inspection can effectively reduce the probability of failure. In addition, cleaning, as an important part of the Flame arrestor maintenance procedure, is required to be continuously considered. The Ignition source present event can properly be eliminated by providing natural or in some specific cases of a fireproof ventilation system. The ventilation system has been widely used and accepted method in the oil and gas industries. It can prevent smoke and fire propagation through the air ducts even in case of fire. To reduce the failure probability of a flammable gas detector, one possible and applicable way is using an updated version of a gas detector. The flammable gas detector may fail due to some identical causes. These causes also need to be identified. Thus, the failure can be eliminated only and only by some simple modifications. According to this, continual maintenance to preserve the detector in operational conditions is recommended. To deal with another critical basic event as “Flow sensor failed”, a potential acceptable solution is by introducing redundancy, i.e., changing the current system into the parallel one by adding one more sensor. In this case, one sensor is operating and the second sensor is in a standby mode. In case of the failure of the operating sensor, the standby sensor can take over the operational responsibility of the failed sensor, thus preventing the failure. Finally, the “Leak from bends” is controlled by bare-eye inspection. To cope with this failure, electrical testing such as voltage and resistance measurement, physical testing like drop test, bending test, and pull test can be applied. Also, such visual inspection including optical microscope and X-ray microscope is also possible to be used.

Adding to this, the risk assessment is a continuous procedure to improve the safety performance of the studied system. Therefore, continuous review and revision must be taken into account.

10.5 Conclusion

This chapter presents a framework for FTA and BN-based reliability analysis of process systems using IFS theory where there exists uncertainty with the availability of precise failure data. The proposed approach enables the gathering of uncertain data by combining IFS theory with expert elicitation. The IFS theory differs from the traditional fuzzy set theory in the sense that it considers both the membership and non-membership of an element in the set. Therefore, the utilization of the IFS theory would allow us to model situations where a varying level of confidence is associated with the fuzziness of numerical data. Therefore, by using IFS theory together with expert judgment as presented in this chapter, the analysts would get increased flexibility while expressing failure data in the form of fuzzy numbers.

The sensitivity analysis performed within the proposed framework would help the analysts to determine the events that are more sensitive to uncertainty, thus allowing to make informed decision to improve the data quality of the associated events. Furthermore, the criticality analysis of the events followed by the recommendation of corrective actions would greatly help to increase the reliability of the studied system. The efficiency of the proposed framework has been verified by applying it to a practical system. The experimentations illustrate that the IFS-based method offers a valuable way of reliability assessment of process systems when the fuzzy failure data of system components cannot be defined with high confidence. It should be added that, as a direction for future works, the same approach can be integrated using much more advanced fuzzy set theory such as but not limited PFS.