Fuzzy Petri nets and industrial applications: a review

Abstract

Fuzzy Petri net (FPN) provides an extremely competent basis for the implementation of computing reasoning processes and the modeling of systems with uncertainty. This paper reviews recent developments of the FPN and its industrial applications. Several important aspects of FPN’s background, history and formalisms are discussed, including the reasoning algorithm and relevant industrial applications; after which we present our conclusions and suggestions for future research.

1 Introduction

Net theory was described as a net-like model applied to relevant research in the automated communication field by Petri (1962). Petri nets (PNs) first mentioned in Petri’s 1965 talk of “Fundamentals on the description of discrete processes” to instead of net theory at the $3{\mathrm{rd}}$ Colloquium on Automata Theory in Hannover, 1966. A few years later, Holt and his group have contributed to popularize Petri Net (Holt et al. 1970). With rapid development of PNs and its applications, Plunnecke and Reisig (1991) undertook a difficult task to present a bibliography which is related to all relevant publications on Petri Nets and Petri applications. Brauer and Reisig reviewed Petri’s exceptional life and related work (Brauer and Reisig 2006). After half century of C. A. Petri’s Ph.D dissertation, Sliva systematical reviewed the development of PN theory (Silva 2013).

As a graphic mathematical modeling tool, PN offers a uniform environment for the description and analysis of inter-relations in discrete event systems such as process synchronization, asynchronous events, concurrent operations and conflicts or resource sharing (Urawski and Zhou 1994). Due to its remarkable advantages, PN and its application have attracted much research. In the past few decades, various high level PNs (HLPNs) have been presented for different research applications including the stochastic Petri net (SPN) (Molloy 1982); the colored Petri net (CPN) (Jensen 1981); the time Petri net (TPN) (Ramchandani 1974), etc. These have been widely applied for problem solving in multiple fields including software systems, communication protocols, workflow and manufacturing systems, batch processing, scheduling problems, etc., (Aura and Lilius 2000; Co et al. 2012; Garg 1987; Fenton et al. 2007; Gua and Bahri 2002; Ha and Suh 2008; Hugo and Pedro 2012; Jung and Lee 2012; Liu et al. 2002; Lee et al. 2004; Murata 1989; Pouyan et al. 2011; Pla et al. 2014; Shojafar et al. 2013; Van der Aalst 1994; Van der Aalst and Hee 1996; Wang et al. 2015; Zhang and Jiao 2009).

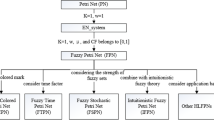
Although PN and HLPN research and applications have borne much fruit, a fatal flaw remained, namely, they were unable to represent fuzzy data applied in knowledge-based systems (KBS) or systems with uncertainty. To overcome this disadvantage, a novel HLPN model called fuzzy Petri net (FPN) was developed by Lipp (1984). In short, FPN is a formalism that models expert systems containing fuzzy data. The developmental track from PN to FPN is illustrated in Fig. 1.

Fig. 1

Development of the PN model family

It has proven easy to discover the various high level FPNs (HLFPNs) that combine different characteristics of HLPNs to overcome shortfalls based on unique applications from 1997 through 2009.

As an HLPN model, FPN inherited graphic descriptive and mathematical foundation features from the PN model, after which FPN was applied to build, compute and reason expert systems (Konar and Jain 2005). Based on the characteristics just cited, FPN provides an extremely competent basis for the implementation of computing reasoning processes and the modeling of systems with uncertainty. In recent years, FPN was consequently applied to a variety of industrial fields. Nonetheless, we could find no prior survey of these industrial applications. Hence, this paper reviews FPN development and its industrial applications with the following goals:

• 1. To analyze FPN’s reasoning algorithm.

• 2. To summarize typical applications in different industrial sectors.

The organization of this paper is as follows: General definitions for FPN and high level FPNs (HLFPNs) and related notions are discussed in Sect. 2. Section 3 summarizes and analyzes the most recently utilized reasoning algorithms for FPN. Section 4 highlights industrial FPN applications and discusses developmental trends. Section 5 presents conclusions along with suggestions for future work.

2 Fuzzy Petri net and high level fuzzy Petri nets

The process of industrial applications using FPN can be abstracted from the literature and summarized in three phases:

• Phase 1: Generate corresponding FPN models for KBS or systems with uncertainty.

• Phase 2: Design a reasoning algorithm based on different application backgrounds.

• Phase 3: Implement a reasoning algorithm with relevant parameters.

This section presents concepts related to an elementary net system, PN, FPN and HLFPNs as illustrated in Fig. 1.

2.1 Petri net and elementary net system

Summarizing, PN formalism is six-tuple as illustrated in Definition 1.

Definition 1

(Petri net) PN is six-tuple:$\textit{PN}=\{P,T,F,K,W,M_0 \}$, where

• 1. P is a finite set of places: the place is represented by a circle in the PN model;

• 2. T is a finite set of transitions: the transition is represented by a rectangle in the PN model;

• 3. $F\subseteq (P\times T)\cup (T\times P)$ is a finite set of arcs from ’place to transition’ or ’transition to place’;

• 4. $K=\{1,2,3,\ldots \}$ is the capacity function of p. K(p) represents the number of resources stored in place (p);

• 5. $W{:}F\rightarrow \{1,2,3,\ldots \}$ is a weight function that represents the number of resources consumed from a ’place to transition’ or created from a ’transition to place’;

• 6. $M_0{:}P\rightarrow \{0,1,2,\ldots \}$ is an initial marking $(M_0 )$ that represents the distribution of resources for each place in the initial statement of the PN model. Moreover, a resource is called ’token’ in PN theory.

Furthermore, a modified PN is called an elementary net system (EN_ system) when a PN model fulfills the following three conditions:

• 1. $\forall s\in S,K(s)=1$ (In PN theory, the place is marked (s), and a set of places is marked (S);

• 2. $\forall (x,y)\in F,W(x,y)=1$ ;

• 3. $\forall s\in S,M(s)=1$ ;

The EN_system is the most fundamental model of the PN family. In the EN_system, a set of places is considered conditions, represented by B. A set of transitions is considered events, represented by E (Thiagarajan 1987). EN_system formalism is given in Definition 2.

Definition 2

(EN_system) An EN_system is a four-tuple$EN\_system=(B,E,F,c)$, where

• 1. B is a finite set of places;

• 2. E is a finite set of transitions;

• 3. $F\subseteq (P\times T)\cup (T\times P)$ is a finite set of flow relations;

• 4. $c\in B$ is an EN_system case.

The status of conditions for B is divided into two classes: True condition $(M(s)=1)$, and false condition $(M(s)=0)$. On this basis, a subset of B (replaced by c) is used to represent all ’true’ conditions. Figure 2 illustrates a turbine fault diagnosis system modeled by an EN_system (in Fig. 2, each place only contains, at most, one token and each weight value equals one). Table 1 lists meanings for each place.

Fig. 2

Turbine fault diagnosis system modeled by an EN_system

Table 1 The meaning of each place in Fig. 2

2.2 Fuzzy Petri net

To model and analyze a system with uncertainty, Looney (1988) proposed a rough notion for a fuzzy Petri net to execute approximate reasoning. Up to the present time, there is no unified formalism for FPN (See Appendix 1: list of FPN definitions from 2000 through 2013). After discussing and comparing sixteen formalisms from twenty-four articles for FPN in “Appendix 1”, a developmental track was clearly discerned comprising the following three points.

• 1. The importance of parameters was realized step-by-step. For example, Chen et al. (1990) did not consider the influence of parameters in the reasoning process. The formalism was enhanced to 9-tuple, which added a weight factor to the FPN (Chen 2002). During the last five years, FPN formalism always included three main parameters: weight value, threshold value, and a certainty factor.

• 2. With further in-depth research, each parameter was divided into multi-subclasses that more accurately described FPRs in KBS. For instance, Wang et al. (2001) divided transitions into five types to control the scale of the FPN model and simplify the analytical process. Gniewek (2013) classified the set of places into two types connected with either process or resource modeling, which depend on place. A similar case was found by Liu et al. (2013a) where places were classified into three different sets: starting places, intermediate places, and terminating places. Liu et al. (2013b) divided the threshold into two modules: input threshold and output threshold.

• 3. With increasing numbers of applications for FPN, different formalisms were proposed to analyze and resolve issues of disassembly (Tang et al. 2006; Tang 2009). Cao and Chen (2010) proposed extensive formalism for FPN to analyze the issue of computing with words.

2.2.1 The formal definition of FPN

Definition 3 illustrates a general FPN formalism.

Definition 3

(General formalism:) The general formalism of FPN is viewed as a 2-tuple structure.

$$\begin{aligned} \hbox {FPN}={<}N,C{>} \end{aligned}$$

N is the FPN’s basic structure as $\hbox {N}=\{P,T,M,I,O,W,\mu ,CF\}$, where

• 1. The declaration of P, T is same as Definition 1;

• 2. $M=(m_1 ,m_2 ,\ldots ,m_n )^{T}$ is a vector of fuzzy marking; $m_i \in [0,1]$ is the truth degree of $p_i (i=1,2,\ldots ,n)$. The initial truth degree vector is denoted by $M_0$;

• 3. $I{:}P\times T\rightarrow \{0,1\}$is an $n\times m$ input matrix defining the directed arc from place to transition:

  $$\begin{aligned} \left\{ {{\begin{array}{lll} {{\begin{array}{lll} {I(p_i ,t_j )=1}&{} {\hbox {if there is a directed arc from p}_{\mathrm{i}} \,\hbox {to t}_{\mathrm{j}} } \\ \end{array} }} \\ {{\begin{array}{ll} {I(p_i ,t_j )=0}&{} { \hbox {else }} \\ \end{array} }} \\ \end{array} }} \right. (i=1,2,\ldots ,n;j=1,2,\ldots ,m) \end{aligned}$$

• 3. $O{:}P\times T\rightarrow \{0,1\}$ is an $n\times m$ output matrix defining the directed arc from transitions to place:

  $$\begin{aligned} \left\{ {{\begin{array}{ll} {{\begin{array}{ll} {O(p_i ,t_j )=1}&{} {\hbox {if there is a directed arc from t}_{\mathrm{j}}\, \hbox {to p}_{\mathrm{i}} } \\ \end{array} }} \\ {{\begin{array}{ll} {O(p_i ,t_j )=0}&{} { \hbox {else }} \\ \end{array} }} \\ \end{array} }} \right. (i=1,2,\ldots ,n;j=1,2,\ldots ,m) \end{aligned}$$

• 4. W(i, j) is the weight from $p_i$ to $t_j$;

• 5. $\mu {:}T\rightarrow (0,1]$ represents the threshold value of transition $(t_i )$;

• 6. $CF_{ji}$ is the support strength from $t_j$ to $p_i$, representing the credibility of post-condition(s) from precondition(s);

C is the correspondence between KBS and FPN as $C=(D,\beta )$, where

• 1. D is a finite set of propositions in the KBS. Moreover, $P\cap T\cap D=\emptyset ,|P|=|D|$;

• 2. $\beta {:}P\rightarrow D$ is an association function that reveals the relationship between places and propositions.

Figure 3 demonstrates the turbine fault diagnosis system as modeled by FPN.

Fig. 3

The turbine fault diagnosis system modeled by FPN

The characteristics of the FPN illustrated in Fig. 3 are given as follows:

• 1. The capacity for each place is one and the value of each token will not exceed one. The range of value for the token is [0–1];

• 2. According to the FPN definition, it is easy to find that concurrence and conflict do not exist in the FPN model;

• 3. The token for the proposition will not disappear after firing the rule,

2.2.2 Related notions of FPN

Other notions of FPN are given in Definitions 4 through 13.

Definition 4

(Pre-set and post-set:) For an $\hbox {FPN}\sum =\{P,T,M,I,O,W,\mu ,\lambda \}$, ${ }^{\bullet }x=\{x|(x,y)\in F\}$ is the pre-set or input set ofx, and $x^{*}=\{x|(y,x)\in F\}$ is the post-set or output set of $x(x,y\in P\cup T)$.

Definition 5

(Input Place and Output Place)

• Input place:   $P_{in} =\{p\in P|{ }^{\bullet }p=\emptyset \wedge p^{{\bullet }}\ne \emptyset \}$;

• Output place:   $P_{\mathrm{out}} =\{p\in P|{ }^{\bullet }p\ne \emptyset \wedge p^{{\bullet }}=\emptyset \}$.

Definition 6

(Enabled) For $\forall t\in T, \quad t$ is enabled if and only if $\forall p \in { }^{\bullet }p$; $M(p)\cdot w(i,j)\ge \mu (t)$, denoted by $M[t>$.

Definition 7

(Fired) A firing of an enabled transition $t_i$ removes token from each input place of $t_i$ and adds a new token to each output place of $t_i$. Value of the new token will be compute based on mechanisms in fuzzy reasoning with different industrial applications.

Definition 8

(Immediate Reachability Set) The set of places that is immediately reachable from place $p_i$ is called the immediate reachability set of $p_i$, denoted $IRS(p_i )$.

Definition 9

(Reachability Set) A set of places that is reachable from place $p_i$ is called the reachability set of $p_i$, denoted as $RS(p_i)$.

Definitions 8 and 9 are widely employed to generate the reachability tree of FPN model to implement reasoning operations. Table 2 shows the correspondence of $RS(P_i )$ and $\textit{IRS}(P_i )$ for each place demonstrated in Fig. 3.

Table 2 Correspondence of $RS(P_i)$ and $\textit{IRS}(P_i)$

Definition 10

(FPN Incidence Matrix) Incidence matrix H of a fuzzy Petri net N is defined as a $n\times m$ matrix for recording the flow relationship between places and transitions. Furthermore, each row corresponds to a place and each column corresponds to a transition, respectively. The incidence matrix H is defined as $H=\{h_{ij} \}(i=1,2,\ldots ,n;j=1,2,\ldots ,m)$, where

$$\begin{aligned} h_{ij} =\left\{ {{\begin{array}{ll} 1&{}\quad {if(p_i ,t_j )\in F} \\ {-1}&{}\quad {if(t_j ,p_i )\in F} \\ 0&{}\quad {else} \\ \end{array} }} \right. \end{aligned}$$

Definition 11

(Three Operators of Max Algebra) $\oplus : X\oplus Y=Z,z_{_{ij} } =\max \{x_{_{ij} } ,y_{_{ij} } \}.$ Where, X, Y and Zare $n\times m$-dimensional matrices;

$\otimes :X\otimes Y=Z,z_{ij} =\mathop {\max }\limits _{1\le k\le p} \{x_{ik} ,y_{kj} \}$. Where, X, Y and Z are $n\times p$, $p\times m$ and $n\times m$-dimensional matrices, respectively;

$\Theta : \Theta :X\Theta Y=Z.$ If $x_{ij} \ge y_{ij}$, $z_{ij} =x_{ij}$. Else, $z_{ij} =0$.

Definition 12

(Place Vector) $X=(x_1 ,x_2 ,\ldots ,x_n )^{T}$ is place vector, where $|X|=|P|$. If $p_i$ is the goal place or a place related to the goal place, $x_i =1$. Else, $x_i =0$.

Definition 13

(Transition Vector) $Y=(y_1 ,y_2 ,\ldots ,y_m )^{T}$ is transition vector, where $|Y|=|T|$. If $t_j$is the transition related to the goal place, $t_i =1$. Else, $t_i =0$.

2.3 Colored Petri net (CPN) and fuzzy colored Petri net (FCPN)

Colored Petri net (CPN) is presented by Jensen (1981) to fold the net system by classifying tokens as various types. In CPN, each token has attached a color for indicating the identity of the token (Jensen 1983, 1987, 1992, 1995, 1997; Jensen and Kristensen 2009). In general, CPN functions are:

• 1. To study, model and validate discrete-event systems.

• 2. To analyze and obtain structure and dynamic performance data for a modeled system.

The formal definition of a CPN is demonstrated below.

Definition 14

(Colored Petri net) CPN is a 6-tuple $\textit{CPN}=(P,T,C,I^{-},I^{+}M_0 )$, where

• 1. The declaration of $P,T,M_o$ is same as Definition 1

• 2. C is a color function that assigns a finite and non-empty set of colors to each place and a finite and non-empty set of modes to each transition.

• 3. $I^{-}$ and $I^{+}$ denote the backward and forward incidence functions defined by $P\times T$, such that

  $$\begin{aligned} I^{-}(p,t),I^{+}(p,t)\in [C(t)\rightarrow C(p)_{MS} ],\forall (p,t)\in P\times T \end{aligned}$$

Based on the notions of PN and CPN, Yeung et al. (1996) presented a kind of HLPNs, called fuzzy colored Petri net (FCPN), which is demonstrated as follows:

Definition 15

(Fuzzy colored Petri net) FCPN is a twelve-tuple $FCPN=(\sum ,P,T,D,A,N,C,G,E,\beta ,f,I)$, where

• 1. $\sum =\{\sigma _1 ,\sigma _2 ,\ldots ,\sigma _l \}(l\ge 0)$ denotes a finite set of non-empty types, called color sets .

• 2. $P=\{P_C ,P_F \}$ denotes a finite set of places:

  • $P_C =\{pc_1 ,pc_2 ,\ldots ,pc_m \}(m\ge 0)$ denotes a finite set of places that model the dynamic control behavior of a system, and is called control places;

  • $P_F =\{pf_1 ,pf_2 ,\ldots ,pf_n \}(n\ge 0)$ denotes a finite set of places that model the fuzzy production rules, and is called fuzzy places, and $P_C \cap P_F =\emptyset$.

• 3. $T=\{T_C ,T_F \}$denotes a finite set of transitions:

  • $T_C =\{tc_1 ,tc_2 ,\ldots ,tc_i \}(i\ge 0)$ denotes a finite set of transitions that are connected to and from control places, and is called control transition;

  • $T_C =\{tf_1 ,tf_2 ,\ldots ,tf_j \}(j\ge 0)$ denotes a finite set of transitions that are that are connected to or from fuzzy places, and is called fuzzy transition, and $T_C \cap T_F =\emptyset$;

• 4. $D=\{d_1 ,d_2 ,\ldots ,d_h \}$ denotes a finite set of propositions, $|PF|=|D|$;

• 5. $A=\{a_1 ,a_2 ,\ldots ,a_k \}(k\ge 0)$ denotes a finite set of arcs, and $P\cap T=P\cap A=T\cap A=\emptyset$;

• 6. $N{:}A\rightarrow P\times T\cup T\times P$ denotes a node function, and it maps each arc to a pair, where the first element is the source node and the second element is the destination node; the two nodes have to be of different kinds;

  • In: an input function that maps each node, x, to the set of nodes that are connected by an input $arc(x)\rightarrow x$;

  • Out: an output function that maps each node, x, to the set of its nodes that are connected to x by output $arc(x)\rightarrow x$.

• 7. $C{:}(P\cup T)\rightarrow \sum _{ss}$ is a color function, which maps each place and transition to a super-set of color sets.

• 8. $G{:}T\rightarrow$ expression which denotes a guard function:

  $$\begin{aligned} \forall t\in T:\left[ Type(G(t))=Boolean\wedge Type(Var(G(t)))\subseteq \sum \right] ,~\hbox {where} \end{aligned}$$

  Type(Vars) denotes the set of types, $\{Type(v)|v\in Vars\}$. Vars denotes the set of variables, and Var(G(t)) denotes the set of variables used in G(t);

• 9. $E{:}A\rightarrow$ expression which denotes an arc expression function:

  $$\begin{aligned} \forall a\in A:\left[ Type(E(A))=C(p(a))MS\wedge Type(Var(E(a)))\subseteq \sum \right] ,~\hbox {where} \end{aligned}$$

  p(a) is a place in N(a), and MS stands for multi-set.

• 10. $\beta {:}PE\rightarrow D$ denotes a bijective mapping from fuzzy places to a proposition.

• 11. $f{:}T\rightarrow [0,1]$ denotes an association function, which assigns a certainty value to each color used in each fuzzy transition.

• 12. I :  denotes an initialization of double$(\delta ,\alpha )$

  • $\delta :P\rightarrow$expression which denotes an initialization function:

    $$\begin{aligned} \forall p\in P:[Type(\delta (P))=C(p)MS]. \end{aligned}$$

  • $\alpha$ denotes an association function, which assigns a certainty value in the range [0, 1] to each token in the fuzzy places.

In the existing literature, FCPN net structure is similar to the general FPN model (Fig. 3). However, tokens are marked by different colors in the FCPN model.

2.4 Time Petri net (TPN) and fuzzy time Petri net (FTPN)

The earliest TPN formalism was proposed to analyze the recoverability of a computer system and communication protocol by Ramchandani (1974). Compared to the original PN, the TPN transition was labeled with correspondence time intervals. These intervals represented upper and lower limits of the time when a transition was enabled. TPN is a suitable technique to model and analyze a system with imperfect timing. The TPN formalism is given as follows:

Definition 16

(Time Petri Net) A time Petri net is a five-tuple, $TPN=(P,T,F,SI,M_0 )$, where,

• 1. The declaration of $P,T,F,M_0$ is same as Definition 1.

• 2. $SI{:}T\rightarrow R^{+}$ is a firing time function that assigns a positive real number to each transition on the net.

Normally, a general FPN is difficult to represent, model and resolve its sharing of abnormality propagation and temporal evolution. To overcome this shortage, Pedrycz and Camargo (2003) systematic illustrated how to add the time factor as an integral part of the models of transitions and place. A classical FTPN formalism was demonstrated as a 12- tuple by Definition 15 (Liu et al. 2011b).

Definition 17

(Fuzzy Time Petri Net) An FTPN is an 11- tuple $FTPN=\{P,T,E,I,O,f,\alpha ,\beta ,D,TS,M_0 \}$, where

• 1. The declaration of $P,T,I,O,M_0$ is same as Definition 3.

• 2. $E=\{e_1 ,e_2 ,\ldots ,e_n \}$ is a finite set of propositions where$|P|=|E|$;

• 3. $f:T\rightarrow [0,1]$ is a relationship function with respect to transition t, representing a mapping from t to a real number confined in [0, 1];

• 4. $\alpha :P\rightarrow [0,1]$ is a relationship function with respect to place p, representing a mapping from p to a real number bound by [0, 1];

• 5. $\beta :P\rightarrow E$ is a relationship function with respect to place p, representing a bidirectional mapping between p and the proposition set;

• 6. $D=\{d_1 ,d_2 ,\ldots ,d_n \},C(T)\rightarrow R^{+}$ is a time delay function associated with each transition;

• 7. TS is a finite set of transition states. $\forall TS_i \in TS,TS_i =\{0,1\}$; $TS_i =1$ implies the corresponding transition $(t_i )$ that is fired; otherwise, $TS_i =0$ implies $t_i$ is not fired.

Figure 4 shows the FTPN model for a turbine fault diagnosis system. Compared with FPN (Fig. 3), every transition of FTPN has two parameters (the threshold value and the time delay). For example, the transition $t_1$ Fig. 4 has two parameters 0.3(1). These two parameters represent the threshold value of $t_1$ is 0.3 and the time delay associated with the deduction of transition $t_1$ is 1.

Fig. 4

FTPN model for a Turbine fault diagnosis system

2.5 Stochastic Petri net (SPN) and fuzzy stochastic Petri net (FSPN)

SPN is an advanced PN form that describes the dynamic behaviors of discrete dynamic systems vis-à-vis isomorphic continuous-time Markov chains. A random variable, $\Lambda :T\rightarrow R^{+}$, is used to determine the probabilistic delay rate (Molloy 1982). A definition for SPN is given below.

Definition 18

(Stochastic Petri net) An SPN is a six-tuple $SPN=(P,T,I,O,M_0 ,\Lambda )$, where

• 1. The declaration of $P,T,I,O,M_0$ is same as Definition 3.

• 2. $\Lambda :T\rightarrow R^{-}$ is a firing function. Moreover, ith is the firing rate of the ith transition where $\lambda _i$ denotes the firing rate of $(t_i )$ and $R^{+}$ is the set of all positive real numbers.

In SPN, the description of uncertainty is based on the probability value. As it is not suitable to represent, describe or analyze various uncertainties except in terms of randomness, the concept of fuzzy mathematics was applied to SPN to improve its approach (Tuysuz and Kahraman 2010). A general FSPN formalism is introduced by Yuan et al. (2007) as follows.

Definition 19

(Fuzzy Stochastic Petri Net) An FSPN is a six-tuple $SPN=(P,T,I,O,M_0 ,\tilde{\lambda } )$, where

• 1. The declaration of $P,T,I,O,M_0$ is the same as in Definition 3;

• 2. $\tilde{\lambda }=(\tilde{\lambda }_{1} ,\tilde{\lambda }_{2} ,\ldots ,\tilde{\lambda }_{m} )$ is a fuzzy set of transition firing rates; $\tilde{\lambda }_{i}$ is a positive real number.

In the existing literature, FSPN net structure is similar to that of the general FPN model (Fig. 3). However, the fuzzy set is used for the transition firing rate.

2.6 Intuitionstic fuzzy Petri net (IFPN)

IFPN is kind of HLFPNs by combing FPN and intuitionistic fuzzy set to over the limitation of fuzzy Petri nets single membership (Shen et al. 2009). Compared with other traditional FPN, intuitionistic fuzzy number is widely employed to represent confidence degree, threshold and token value of each place in IFPN. A kind of general IFPN formalisms is introduced as follows.

Definition 20

(Intuitionstic Fuzzy Petri Net) An IFPN model is defined as 6-tuple, as $(P,T,I,O,\mu ,\theta )$, where

• 1. The declaration of $P,T,\mu$ is the same as in Definition 3;

• 2. $I=\{a_{ij} \}:P\times T\rightarrow [0,1]$ is an $n\times m$ weighted input matrix defining the directed arcs from places to transitions, $\sum \nolimits _{0\le i\le n} {a_{ij} =1} (i=1,2,\ldots ,n;j=1,2,\ldots ,m)$. If there is a directed arc from $p_i$ to $t_j$, then $a_{ij} =w_{ij}$ ($w_{ij}$ is the weight of $p_i$ to $t_j )$. Otherwise, $a_{ij} =0$.

• 3. $O=\{b_{ij} \}:P\times T\rightarrow [0,1]$ is an $n\times m$ weighted input matrix defining the directed arcs from transitions to places. If there is a directed arc from $t_j$ to $p_i$, then $b_{ij} =c_j$. Otherwise, $b_{ij} =(0,1)$.

  Where, $c_j =(C_{\mu _j } ,C_{\gamma _j } )(i=1,2,\ldots ,n;j=1,2,\ldots ,m)$ is an intuitionistic fuzzy number, $C_{\mu _j }$ means the support degree of $t_j$ and $C_{\gamma _j }$ means the nonsupport degree of $t_j$.

• 4. $\theta :P\rightarrow [0,1]$ is the function which assigns a token value to each place, also means fuzzy value of the proposition; the initial state vector $\theta ^{^{0}}=\{\theta _1^0 ,\theta _2^0 ,\ldots ,\theta _n^0 \}$

3 Reasoning algorithms using fuzzy Petri net

After generating the corresponding FPN for KBS, the relevant reasoning algorithm can be implemented under the FPN framework. These inference algorithms have some characteristics that include the reduction of searching steps; the improvement of search effectiveness; and their adaptation to real-time requirements. To give analysis and summary of existing reasoning algorithms, forty-one published papers were selected as discussed below.

3.1 The proposed algorithm reasoning using FPN

Looney (1988) proposed the ideas of FPN and forward reasoning. However, the formal definition of FPN was not presented. Based on Looney’s contribution, research in algorithm reasoning using FPN sharply increased and focused on algorithm analytics for FPN, FCPN, FTPN and IFPN.

3.1.1 Reasoning algorithms using FPN

Chen et al. (1990) built a corresponding FPN for each fuzzy production rule type and utilized$IRS(p_i ),RS(p_i )$with a sprouting tree to execute a forward reasoning algorithm. However, this algorithm did not consider influences from parameters such as weight, threshold and certainty in the inference process. Similarly, Chen (2000) developed a backward reasoning method. Compared to his previous work, the truth degree of any proposition was automatically evaluated by his novel algorithm which, however, was unable to perform weighted fuzzy reasoning. Meanwhile, certainty factors and true values were restricted and represented by real values between [0, 1]. To avoid these disadvantages, Chen (2002). proposed an improved weighted FPN and related reasoning algorithm. Compared to Chen’s other works, the cited parameters were added and represented by fuzzy rather than real values. His case study illustrated that a reasoning process using the novel FPN performed and informed more flexibly and with greater intelligence.

Based on Chen et al.’s work in (1990), Manoj et al. (1998) presented a modified form of Chen et al.’s reasoning algorithm, and proposed a hierarchical FPN for all types of data abstraction.

To cope with the FPN state explosion issue, Garg et al. (1991) proposed three reduction rules to control the scale of FPN which improved both the FPN model and reasoning algorithm by checking KBS consistency.

To calculate the accuracy value of atoken output place, two variables, global and local fuzzy variables, were applied in the reasoning process by Tiehua and Sanderson (1993). This reasoning algorithm’s key precedence relations were controlled by a global fuzzy variable through sequence operations. Hence, vague data was described by a local fuzzy variable.

Srinivasan and Gracanin (1993) proposed a novel fuzzy reasoning algorithm using ’fuzzy theory’. In this algorithm, the token was replaced by a membership function and the transition represented the distance the model could be fired.

Chun and Bien (1993) applied FPN asa rule-based decision support system. Their design’s inference approach comprised two phases: a forward strategy and a backward algorithm. Most importantly, an algebraic format was used to describe the state equation for the first time.

Yeung and Tsang (1994) discussed algorithm use to build reachability sets and sets of adjacent places by proposing an extended reasoning algorithm using Chen’s algorithm. In 1998, the same authors presented an expanded FPN that considered weight factors. Yeung and Tsang (1998) introduced a multilevel weighted reasoning strategy using the expanded model. Tsang et al. (1999) applied a learning algorithm with an artificial neural network (ANN) to the FPN framework. Their comparison and simulation demonstrated that some ANN theories and algorithms (such as learning algorithms and optimization strategies) also can be implemented in FPN.

Bugarin and Barro (1994a) focused on a series of reasoning algorithms and presented an enhanced FPN to describe KBS by using rule chaining and a data driven strategy that employed a sup-min compositional rule. Their computational complexity of the data driven strategy included the following equations and is worth a quick review:

$$\begin{aligned} O\left( \left( \frac{C}{2}+M+N\right) R^{2}\right) ~\hbox {and also}~O((M+N)R^{2})~\hbox {and}~O(2(M+N)R^{2}). \end{aligned}$$

where

• 1. R denotes number of fuzzy conditional statements in KBS;

• 2. M, N denote maximum numbers of antecedents and consequences, respectively;

• 3. C denotes the amount of chaining transitions in KBS.

Another reasoning algorithm usinga Goal-Driven mechanism was reported by Bugarin and Barro (1994b). This algorithm was implemented when chaining transitions in each production were incomplete. Bugarin et al. (1996) proposed an improved reasoning strategy based on their previous work to ensure the correct implementation of the reasoning algorithm under unknown situations. This proposed algorithm effectively executed inference when some KBS variables remained unknown.

Scarpelli and Gomide (1994) presented an integrity checking strategy using HLFPN and also proposed other algorithms capable of discerning inconsistencies at local and global levels. Their case study illustrated an automatic implementation of the verification process by their proposed algorithms. Scarpelli et al. (1996) introduced a novel structure that described HLFPN using a new variable (V). The major contribution of this proposed algorithm was that it implemented a specific process in answer to a specific query.

Yu (1995) presented an improved FPN to extend the representation range from prepositional logic to first-order predicate logic by using Pr/T net. The proposed mechanism was a profitable development of the reasoning in H-net.

After providing an analysis of the forward and backward reasoning mechanisms, Zhou and Wu (1996) proposed NNF and NNPrF, combined with FPN, ANN and the learning mechanism. Their case study demonstrated that NNF and NNPrF have learning abilities similar to ANN.

A new FPN model, the Adaptive weights FPN (AFPN), was proposed by Li and Lara-Rosano (1999) that explored the adjustment learning mechanism of FPN. AFPN applied a weight value that represented contributions from antecedent propositions and consequent propositions. They also considered a negative weight for AFPN along with a modified token transfer rule to train AFPN as an ANN. Li et al. (2000) extended their work and proposed a modified back propagation learning algorithm using AFPN. The convergence of weights was highlighted in their modified algorithm.

Wang and Wu (1999) presented a fuzzy reasoning technique to obtain potential conclusions for KBS with incomplete original data. A reachability set and a fuzzy backward reasoning algorithm were both utilized. Their simulation results showed that the reasoning conclusions protected maximized consistency with KBS under certain situations.

Gao et al. (2000) exploited maximum reasoning abilities by proposing a parallel reasoning algorithm based on max-algebra and the fuzzy reasoning Petri net (FRPN). The prominent feature of their proposed algorithm exploited potential maximum parallel reasoning by using a matrix equation expression as the traditional PN theory. An improved FRPN model and related reasoning algorithm were also proposed by Gao et al. (2003) and then implemented when the KBS contained negative literals.

Concentrating on large-scale systems, Wang et al. (2001) proposed an improved FPN model and related reasoning patterns using generating rules and PN descriptive semantics. The two patterns were applied in different situations. A forward reasoning algorithm was used in circumstances where the belief strength of an initial proposition was known and the belief strength of a non-initial propositions required computation. A backward reasoning algorithm was used in circumstances where the belief strength of a preliminary proposition was known and the belief strength of a goal proposition required computation.

To improve the flexibility of the inference process, Yang et al. (2002) proposed an algorithm that performed fuzzy inference in KBS using FPN. This algorithm automatically simulated the reasoning process from initial propositions to goal propositions. Moreover, structured formats for the improved FPN were more generalized and complex and better fit the requirements of expert systems.

To obtain more accurate reasoning results, Shen (2003) proposed a reinforced learning approach that simultaneously executed structure and parameter learning while introducing a high level fuzzy Petri net (HLFPN) structure. This HLFPN generated a corresponding model for KBS which had IF–THEN and IF–THEN–ELSE rules. Moreover, multiple heterogeneous output places also allowed appearances even though the data structure of this model was more compact. In 2006, an enhanced HLFPN model and corresponding reasoning algorithm were proposed by Shen (2006) that offered a more universal rule chaining technique. Related algorithms automatically implemented a reasoning process when data was imprecise, vague or ’fuzzy’. To study the supervised and unsupervised learning ability of FPN, Shih et al. (2010) presented a machine learning Petri net (MLPN) with related learning algorithms. Some properties of the proposed algorithms were discussed such as complexity, accuracy of learning consequences between two approaches, as well as the reachable property and convergences. Shen et al. (2012) carried out a novel learning evaluation model based on high-level fuzzy Petri net (HLFPN) and relevant fuzzy reasoning method to test educational grading system.

Hu et al. (2003) presented a reasoning algorithm that implemented the inference process using a modified FPN. This modified FPN performed inference when the inherent firing mechanism lacked an additional control mechanism. In addition, power and module replacement mechanisms enhanced the proposed model’s reasoning performance under difficult situations such as reasoning uncertainty and structure conflict.

Konar et al. (2005) proposed a supervised learning mechanism by FPN that allowed for the analysis of semantic justification in hidden layers with correspondence predecessor and successor layers. The proposed algorithm executed reasoning and learning processes in instances of noisy training. Convergence was also discussed in the process of training a feed-forward FPN.

Wang et al. (2005) reported an Interactive Weighted Fuzzy Petri net (IWFPN) and relevant reasoning algorithm. In this algorithm, fuzzy numbers were used to represent local weights. More importantly, the fuzzy number-valued fuzzy integral was utilized to describe a reasoning result in two instances. The fuzzy measure was replaced by a fuzzy number using the extended $g_\lambda$ measure, considered a non-additive, non-negative fuzzy number-valued set function specified by a domain expert.

For consequences from two or more propositions connected by “AND” or “OR” types in KBS, Ha et al. (2005) proposed a 17-tuple formal definition for a generalized fuzzy Petri net (GFPN). In GFPN, weights were classified as two types, input and output. Their case study demonstrated that the approach efficiently deduced synchronization. A GFPN was extended to 18-tuple by Ha et al. (2007) whose results showed that certainty factors and related inference results from their innovation were more accurate and reasonable compared to the pervious algorithm.

Yuan et al. (2008) proposed a backward concurrent reasoning algorithm to control the scale of the FPN model. A vector-computation approach was used that identified intermediate places. Man-machine interaction was applied to the inference process to reduce FPN complexity and scale. Compared to similar algorithms, theirs proved more efficient and less costly.

Zhang and Cui (2008) proposed a parallel backward reasoning algorithm to exploit multi-parallel reasoning. Their new algorithm included two steps: first, an AND-OR graph of goal places was introduced based on the FPN data table; second, their method for calculating the degree of truth value for the least solution place was based on four different scenarios.

Xu (2009) introduced an Interactive Weighted Fuzzy Petri net (IWFPN) and related reasoning algorithm to improve the efficiency of the multilevel weighted fuzzy reasoning algorithm. In their proposed algorithm, local weights in the antecedents of the rule were represented by fuzzy numbers. This algorithm also automatically calculated conclusions for fuzzy sets and related certainty factor values.

Yuan (2009) proposed a learning algorithm by using a taboo algorithm to optimize FPN parameters in which several fuzzy reasoning functions generated a corresponding FPN. The proposed model had self-adaptability and a strong generalization capability. Moreover, it proved to be an obvious improvement on accuracy of reasoning results after implementing the learning algorithm.

Qiao et al. (2011) proposed a fuzzy Petri net model for rescheduling (FPN-R) and related reasoning mechanism to overcome the uncertain production disturbances in rescheduling research. Case study revealed that the proposed formalism and reasoning algorithm paved a practicable way for discussing unstructured scheduling problems.

Hu et al. (2011) proposed a kind of backward reasoning strategies with reversed FPN to reduce the consequence-antecedent relationship between their manifestation and antecedent using max-algebra in fault diagnosis process of manufacturing.

To improve the feasibly of exception handling in workflow management, Ye et al. (2011) proposed two extended knowledge models, generalized fuzzy event-condition-action (GFECA) rule and typed fuzzy Petri net extended knowledge (TFPN-PK), to execute integraded representation and reasoning for both fuzzy knowledge and non-fuzzy knowledge for dynamic workflow management. Furthermore, a weighted reasoning algorithm combining forward and backward reasoning strategies was employed to solve two kinds of reasoning cases in workflow management, which are uncertain goal propositions and known goal concepts of exception handing.

To improve the capability of capturing the dynamic nature of fuzzy knowledge, Liu et al. (2013a) proposed a novel dynamic adaptive fuzzy Petri net to represent fuzzy information accurately and a max-algebra based parallel reasoning algorithm. Case study demonstrated that the proposed model has ability to depict the expert’s diverse knowledge accurately and the proposed reasoning algorithm can implement approximate reasoning dynamically. In the same year, Liu et al. (2013b) proposed a new KA& R approach using the fuzzy evidential reasoning (FER) approach and DAFPNs to execute knowledge acquisition and representation. Liu et al. (2013c) also proposed Fault diagnosis and cause analysis (FDCA) model to perform a bi-directional reasoning using forward fault diagnosis strategy and backward cause analysis method.

An and Liang (2013) proposed a novel fuzzy Petri net for unobservable system multi-fault diagnosis. In this formalism, fault class is determined by an unobservable transitions subset, and certain factor values of diagnosis results are defined by two fuzzy operators. Meanwhile, a bi-directional reasoning approach is also presented by combing forward reasoning and backward reasoning.

Amin and Shebl (2014) presented adaptive fuzzy high order Petri net based on considering the changes of weight of arc in the dynamic reasoning process and algorithm to automatically learn the weight. Meanwhile, a reasoning algorithm using algebraic forms were also proposed and applied into a weather forecast issue.

Zhao et al. (2014) proposed a decision-making model of product disassembly sequence with FPN and presented a reasoning mechanism using matrix operation for the end-of-life product recycling and remanufacturing. Results of case study illustrated that the proposed model and related reasoning algorithm owns some characteristics, such as parallel operation, intelligent decisions functions, and automatic clustering identification ability.

3.1.2 Reasoning algorithms using HLPN

Ouchi and Tazaki (1997) focused on large-scale systems and proposed learning and reasoning mechanisms using the fuzzy colored Petri net (FCPN). This was a useful attempt to combine highlights from FPN and other HLPNs. FCPN increased the ability to generate a large scale model and solve for uncertain factors in a complex system. Lee and Seong (2004) proposed employed fuzzy colored Petri net to enhance automated operating system for nuclear power plants. Yuan et al. (2010) also proposed a fuzzy colored Petri net (FCPN) with a related forward concurrent reasoning algorithm where the conformal partitioned matrix theory was integrated with the process of forward concurrent inference.

Fuzzy time Petri net (FTPN) was proposed to represent and decode various temporal data in KBS (Ribarik et al. 1999). The FTPN extended the application field for FPN with its ability to analyze and solve for temporal knowledge.

Shen et al. (2009) presented another HLFPN type called intuitionistic FPN (IFPN) and related algorithms. Compared to other FPN models, IFPN used a fuzzy member to replace both the confidence degree and threshold of the transition. Moreover, asymmetrical weight was mapped to one transition of a weighted parameter. The confidence degree was added to the output matrix and they reported that reasoning results from their proposed algorithm were more persuasive and precise than the non-membership parameter.

Table 3 summarizes the FPN reasoning algorithms used in the cited studies. The last column indicates reasoning strategies of three types:

• A: Reachability tree (also known as sprouting tree in some scholars’ work.);

• B: Algebraic form;

• C: HLFPN.

Table 3 Summary of reasoning algorithms using FPN

3.2 Analysis of reasoning algorithms

From the above analysis of the existing research result of reasoning algorithm using FPN, term “fuzziness in FPNs” could be understood from two viewpoints. At first, in a narrower sense, fuzzy logic is seen as a multi-valued logic, and a marking of the FPNs is illustrated by numbers from the interval [0,1]. More importantly, in a boarder sense, “fuzziness in FPNs” means the same as the fuzzy sets theory proposed in 1965 by L. Zadeh. Obviously, the narrower sense of this term is a special case of the fuzzy set theory (Cardoso 1999).

After understanding the fuzziness in FPN, the inference mechanisms are classified as three types: reasoning using the reachability tree (utilizing FPN’s graphic ability), reasoning using the algebraic form (utilizing FPN’s mathematical analytic ability); and reasoning using HLFPN (combined facilities of FPN and other HLPNs). This classification is illustrated in Fig. 5.

Fig. 5

Classification of existing reasoning algorithms

Figure 5 indicates that reasoning algorithms using FPN enable full advantages for the PN model such as graphical description, parallel operations by algebraic theory, and extensive capabilities offered by ANN and other HLPNs. Details for each type of reasoning algorithm are summarized in the next sections.

3.2.1 Reasoning algorithm using the reachability tree

The main objective of the reachability tree is to implement the inference process using FPN ’s capability for graphic description. This approach was discussed and applied widely during the 20th century. The complete mechanism comprises the following two phases.

• Phase 1: Generate the reachability tree for FPN based on $RS(P_i)$ and $IRS(P_i )$.

• Phase 2: Implement different reasoning strategies within the reachability tree.

Figure 6 demonstrated a modified algorithm to generate reachability tree using $RS(P_i )$and $IRS(P_i )$ based on Monaj et al.’s work (1998). Figure 7 shows the complete reasoning process using the reachability tree’s division into three phases.

Advantages and disadvantages of the reachability tree are summarized in Table 4.

Fig. 6

Monaj et al. proposed modified algorithm (1998)

3.2.2 Reasoning algorithm using the algebraic format

The algebraic reasoning algorithm was proposed for parallel operations utilizing algebraic representation. In this algorithm, all data is stored in different matrices and the core operational goal is to generate the incidence matrix. Based on Fig. 3, the incidence matrix is attained as follows.

$$\begin{aligned} H=\left[ {{\begin{array}{cccccc} 1&{} 0&{} 0&{} 0&{} 0&{} 0 \\ 0&{} 1&{} 0&{} 0&{} 0&{} 0 \\ 0&{} 0&{} 1&{} 0&{} 0&{} 0 \\ {-1}&{} 0&{} 1&{} 0&{} 0&{} 0 \\ 0&{} {-1}&{} 0&{} 1&{} 0&{} 0 \\ 0&{} 0&{} {-1}&{} 0&{} 1&{} 0 \\ 0&{} 0&{} 0&{} {-1}&{} 0&{} 1 \\ 0&{} 0&{} 0&{} 0&{} {-1}&{} {-1} \\ \end{array} }} \right] \end{aligned}$$

The incidence matrix is an important tool that records flow relationships in the FPN. It records transitions defined in Fig. 3. For example, there are two elements marked (1) in column 3. This indicates two arcs from place 3 and place 4 to transition 3, respectively. The incidence matrix is subsequently used to fire related transitions, step-by-step.

Fig. 7

Flowchart for reasoning algorithm using the reachability tree

Table 4 Advantages and disadvantages of reachability tree

These algebraic algorithms are classified as three types: forward, backward and bi-directional. Details for each mechanism are given in Table 5.

Table 5 Summary of algebraic reasoning mechanisms

General flowcharts for the forward and backward mechanisms are shown in Figs. 8 and 9, respectively. Figure 8 demonstrates a general flowchart for the FPN forward reasoning facility. Its core operational goal is to repeatedly compute the truth degree for each place until all related transitions are fired. This process depends on individual strategies based on the three main operations of Max Algebra (See: Definition 11) and the meaning of each symbol as stated in Definition 3.

Figure 9 illustrates the general idea of the backward reasoning mechanism. This facility is suitable for implementing the reasoning process when a goal output place is given. It is divided into two parts: (i) obtain the reasoning path for the goal output place; (ii) compute the truth degree for the goal output place.

Fig. 8

Flowchart of forward mechanism

Fig. 9

Flowchart of backward mechanism

3.2.3 Reasoning algorithm using HLFPNs

Various HLFPNs have been proposed to enhance the original FPN. Extensive ideas for this mechanism are based on two positions. First, the structure of FPN and ANN are similar and some ANN techniques were applied to the FPN model to improve properties such as self-adaption and generalization capability. Second, other HLFPNs were proposed to solve aspecific problem by combining FPN and HLPN. Moreover, the FTPN was also proposed to represent temporal data. The advantages and disadvantages of HLFPN algorithms are listed in Table 6.

Table 6 Summary of HLFPN reasoning algorithms

4 Fuzzy Petri net and industrial applications

During this period, FPN received increasing attention from researchers in various fields. This section addresses recent developments in fuzzy Petri net (FPN) applications in various industrial sectors. Forty journal articles are reviewed and discussed in the following subsections.

4.1 Several areas of industrial applications for FPN

In the robotic engineering sector, Wai and Liu (2009) developed a dynamic Petri recurrent fuzzy neural network to cope with a path-tracking control problem for a non-holonomic mobile robot. Tont et al. (2010) proposed a stochastic model to execute adaptive task assignment in non-stationary environments by using the non-homogeneous Markov chain and Fuzzy Petri net. Sharma et al. (2010) established an improved method for calculating fuzzy conflicting data using fuzzy Lambda-Tau methodology. Wai et al. (2010) proved that a Petri recurrent fuzzy neural network (DPRFNN) increased the accuracy of a robust path tracking control on a mobile robot model. Parhi and Mohanta (2011) applied a Petri-potential-fuzzy hybrid controller to implement a navigational control for mobile robotic agents. Sharma et al. (2012) proposed a novel method to compute reliability parameters for a multi-robotic system by using a genetic algorithm: PN and Fuzzy Lambda-Taumethodology. Table 7 summarizes FPN applications for robotic engineering.

Table 7 FPN applications in robotic engineering

In the power engineering sector, Luo and Kezunovic (2008) applied the FPN to implement fault estimation in a power system. Abdulkareem et al. (2011) proposed an artificial intelligence (AI) system by using Neural Net (NN), Fuzzy Neural Net (FNN), and Fuzzy Neural Petri Net (FNPN) to analyze fault detection in transmission lines. Pamuk and Uyaroglu (2012) presented an improved fault diagnosis mechanism using FPN to shorten the reasoning task for fault diagnosis in a complicated power system. He et al. (2014) proposed a estimation method using adaptive FPN to solve the complex power system fault-section estimation problem. Table 8 summarizes the applications of FPN in the power engineering sector.

Table 8 FPN applications in the power engineering Sector

In traffic engineering, Cheng and Yang (2009) used FPN to simulate a decision-making process for dispatchers. Their results provided calculations that validated dispatch options regarding train delays. Lee et al. (2009) proposed a hybrid artificial intelligent control scheme that optimized parking using a genetic algorithm (GA), PN, and fuzzy logic control. Asthana et al. (2011) proposed a real time traffic control mechanism using a Neural PN and Fuzzy Logic. Khan et al. (2011) presented an improved FPN and reachability graph to model and analyze railway crossings in a complicated environment. Barzegar et al. (2011) used a hybrid adaptive FCPN model to more efficiently and intelligently control traffic signals. Rajpurohit and Pai (2012) developed an FPN fuzzy rule–based motion prediction algorithm that predicted the next position instance of a moving object in a dynamic navigation environment. Table 9 summarizes FPN applications in the field of traffic engineering.

Table 9 FPN applications in traffic engineering

In the field of systems engineering, Sharma et al. (2008) presented a structured framework using fuzzy methodology and FPN to help maintenance engineers/managers/practitioners to model, analyze and predict systems’ behaviors. Zhong (2008) developed a fuzzy Petri net controller to solve for dead lock phenomenon in parallel and concurrent systems. Lee and Lee (2012) proposed an hybrid algorithm based on electromagnetism-like mechanisms (EM) and PSO to generate Petri recurrent fuzzy neural system (FLPRFNS) for nonlinear systems control. Table 10 summarizes FPN applications in systems engineering.

Table 10 FPN applications in system engineering

In civil engineering, Zhang et al. (2011) used a fuzzy-timed place Petri net to model and simulate the process of hull construction implementing a Triangular Fuzzy Number (TFN), a setting dummy place, and a reformative Minkowski subtraction. Table 11 summarizes FPN application use in civil engineering.

Table 11 FPN application in civil engineering

In chemical engineering, Liu et al. (2011b) used a timed fuzzy Petri net (TFPN) to monitor abnormal events in a chemical process. Table 12 summarizes FPN application in chemical engineering.

Table 12 FPN application in chemical engineering

In the ecosystem products sector, Xu et al. (2011) designed an improved modular colored fuzzy Petri net (MCFPN) model to capture causal relations between users’ affective responses and cognitive processes. Zhou et al. (2012) presented a novel fuzzy reasoning PN to solve the UX model with fuzzy dynamics factors. Table 13 summarizes the application of FPN in the ecosystem products sector.

Table 13 Applications of FPN in the field of product ecosystem

Yu et al. (2011) proposed a multi-level routing algorithm using FPN for wireless sensor networks. Table 14 summarizes FPN application use in sensor engineering.

Table 14 FPN application in sensor engineering

In medical engineering, Pantelopoulos and Bourbakis (2010) presented a novel physiological data fusion model for a multi-sensor, wearable Health-Monitoring System (WHMS) using fuzzy regular language and an SPN model. Shih et al. (2010) improved an embedded mobile ECG reasoning system using FPN to maintain the continual monitoring of vital signs for elderly patients. Chen et al. (2014) utilized FPNs to design a rule-based decision-making diagnosis system. This proposed diagnosis system is employed to monitor and evaluate the arteriovenous shunt (AVS) stenosis for long-term hemodialysis treatment of patients. Table 15 summarizes FPN applications in medical engineering.

Table 15 FPN applications in medical engineering

In soft engineering, Ting et al. (2008) established a fuzzy reasoning and verification Petri net model (FRVPNs) that was implemented for fault diagnosis in a large-scale, complex, fault-tolerant PC-controlled system. Liu et al. (2010) designed flight control software for an unmanned aerial vehicle (UAV) using weighted FPN. Wu and Hsieh (2012) proposed a novel approach utilizing fuzzy comprehensive evaluation and a fuzzy reasoning Petri net (FRPN) to research reliability for the distribution of a solar array. Wang et al. (2012) proposed a novel fuzzy technique to classify software evolution components using Petri Net. Table 16 summarizes FPN applications in software engineering.

Table 16 FPN applications in software engineering

In mechanical engineering, Wu et al. (2011) proposed a fuzzy reasoning Petri net (FRPN) and fault tree analysis (FTA) to increase solar array reliability. Liu et al. (2011a) proposed an improved weighted FPN strategy to develop a fault diagnosis model for a flight control system. Shi (2012) proposed a target fusion recognition system with fuzzy sets and FPN to execute target recognition tasks in a complex environment. Kumar et al. (2012) proposed a novel combination of real coded genetic Algorithms with fuzzy lambda tau methodology to analyze reliability analysis for a hazardous waste clean-up manipulator. Qiao et al. (2011) proposed a fuzzy Petri net model for rescheduling (FPN-R) along with a related reasoning algorithm to implement rescheduling decision-making. Table 17 summarizes FPN applications in mechanical engineering.

Table 17 FPN applications in mechanical engineering

In manufacturing engineering, Peters and Tagg (2009) defined rough places, rough tokens and rough transitions using rough theory to create an early warning system for workflow with missing data. Ye et al. (2011) proposed a hybrid exception handling approach by using the generalized fuzzy event–condition–action (GFECA) rule and a typed fuzzy Petri net (extended by process knowledge: TFPN-PK) to analysis and resolve the issue of exception handing in a dynamic workflow system. Hu et al. (2011) proposed an iterative reasoning algorithm by using a reversed FPN and algebraic form to execute fault diagnosis in a manufacturing system. Wu et al. (2012) proposed a real-time FPN framework to implement progressive fault diagnosis for discrete manufacturing systems. Pan et al. (2012) proposed a novel method to diagnose faults by using a neural network and weighted FPN. Gong and Wang (2012) proposed a self-adaptive weighted fuzzy fault diagnosis approach using PN and a fuzzy logical BP neural network to describe relationships between causes and phenomena in a complicated flexible manufacturing system. Table 18 summarizes FPN applications in manufacturing engineering.

Table 18 FPN applications in manufacturing engineering

4.2 Analysis of industrial applications

Based on the previous section’s review, Fig. 10 summarizes cited articles for FPN applications in various fields.

Fig. 10

Number of articles on FPN applications in various fields

Figure 10 shows the wide use of FPN in traditional industrial fields such as manufacturing engineering, software engineering and mechanical engineering. FPN was also applied in various complex systems such as medical engineering, traffic engineering, multi-robotic engineering, chemical engineering, civil engineering and product ecosystem. According to different application backgrounds, the FPN model has been broadly expanded from its basic formal definition. Figure 11 reveals the relationship between the FPN model and other members of the PN family.

Fig. 11

Relationship between FPN model and other members of the PN family

Figure 11 indicates that FPN is a bridge connecting each member of the PN family. FPN was transformed to EN_system and applied in several corresponding fields. Moreover, the FPN application process in various industrial fields involved four distinct phases as shown in Fig. 12.

Fig. 12

FPN application process for industry

5 Conclusions

This detailed review of FPN’s industrial application(s) contributes the following considerations to the literature. First, FPN general formalisms were obtained by analyzing different formal definitions offered by researchers from 2000 through 2013. Next, reasoning algorithms using FPN were discussed and a flowchart containing each reasoning mechanism was provided. Finally, various industrial applications based on FPN in the recent five years were presented and summarized.

Although FPN has made rapid progress over the last thirty years, issues requiring further study are as follows:

• 1. Compared to FPN application research, theoretical research lags far behind that of practice. For example, properties (especially dynamic properties) are not addressed in journals or conferences.

• 2. With the rapid development of modern technology, the scale of FPN is sharply increasing. Nevertheless, simplified or decomposed algorithms are not reported. A possible reason for this is that it is hard to analyze the consistency of properties between the original FPN model and a corresponding subnet due to a lack of research on dynamic properties such as liveness, boundedness, safeness, and fairness.

• 3. Recent research on the reasoning algorithm and applications using FPN has focused on the acyclic FPN model although the circle or loop structure is reflected in existing FPN models. However, the recycle thinking model is presently in wide use in the real world. Hence, research on how to analyze and reason using FPN with a circular structure remains a pressing need.

Appendix 1: formal definitions of FPN (2000 to 2013)

Formalism	Highlight
$\textit{FPN}=(P,T,D,I,O,f,\alpha ,\beta )$ (Chen 2000; Sun et al. 2004; Shih et al. 2010)	(P,T,D,I,O) is the basic net structure of FPN; $(\alpha ,\beta )$describes correspondence between KBS and FPN
$\textit{AFPN}=(P,T,D,I,O,\alpha ,\beta ,Th,W)$ (Li et al. 2000)	Weight and threshold considered and added to formalism
$\textit{FPN}=(P,T,F,M_0 ,D,H,\alpha ,\theta ,\lambda )$ (Wang et al. 2001)	Transitions classified into five types: $t^{1},^{and}t,^{or}t,^{and},t^{or};$ to control scale of FPN and simplify analysis
$\textit{WFPN}=(P,T,D,I,O,f,\alpha ,\beta ,W)$ (Chen 2002)	Chen considered the function of weight in his research and enhanced the proposed formalism
$\textit{HLFPN}=(P,T,F,C,V,\alpha ,\beta ,\delta )$ (Shen 2003, 2006; Shih et al. 2010)	This formalism extended the description range for FPN
$\textit{FRPN}=(P,R,I,O,H,\theta ,\gamma ,C)$ (Gao et al. 2003, 2004; Luo and Kezunovic 2008; Zhou et al. 2012; Guan and Kezunovic 2013)	This formalism used an algebraic form to explore parallel operation ability and used I, O, H to define relevance matrices
$\textit{FPN}=(P,R,D,G,R,\Delta ,\Gamma ,\Theta ,M_0 )$ (Gniewek and Kluska 2004)	This formalism focused on one-to-one correspondence between KBS and FPN
$\textit{FAPN}=(P,T,I,O,M,\tau ,\alpha ,\lambda )$ (Tang et al. 2006)	This formalism was based on the disassembly issue; human factors were considered. For example, places divided into two modules, one for operators, another for product subassembly or component
$\textit{IFPN}=(P,T,D,I,O,\mu ,f,w,H,\beta )$ (Heng et al. 2006)	This formalism considered parameters and correspondence between KBS and FPN. Moreover, dynamic certainty given and marked by f
$\textit{APN}=(P,T,S,D,\Lambda ,\Gamma ,I,O,C,\alpha ,\beta ,W,Th)$ (Shih et al. 2007)	This formalism derived from FPN. Compared with above, a special element, ’square’, was added in the APN model
$\textit{FPN}=(P,T,I,O,M,\theta ,\alpha ,\delta ,\tau ,\lambda )$ (Tang 2009)	This formalism also focused on the disassembly issue. Compared with the 8-tuple of FPN by Gao et al. (2004), this formalism used 10-tuple to describe the FPN
$\textit{FPN}=(P,T,I,O,\alpha ,\beta ,M_0 )$ (Cao and Chen 2010)	This formalism focused on computing with words, weight value of one for every situation
$\textit{FIPN}=(P,T,\Omega ,\Psi ,R,\Delta ,K,W,\Gamma ,\Theta ,M_0 ,e)$ (Gniewek 2013)	This formalism proposed a strategy to settle conflict. For instance, places were summarized in two modules, one associated with modeling a processes, another associated with modeling resources
$\hbox {WFSN P system}=(O,N_p ,N_r ,syn,IN,OUT)$ (Wang et al. 2013)	This formalism proposed to model weighted FPRs and implement weighted reasoning based on the SNP system model
$DAFPN=(P;T;I;O;D;\alpha ;\beta ;W;U;Th;M)$ (Liu et al. 2013a)	This formalism proposed to overcome unreasonable points in the defection of FPN
$\textit{DAFPN}=(P;T;I;O;D;\alpha ;\beta ;W;U;Th_I ;Th_O ;M)$ Liu (2013b)	This formalism divided the threshold in two: input and output values, respectively