Introduction

In neural systems, subthreshold signals are not detected by sensors because the membrane potential does remains below the detectable threshold. In addition, input signals are usually contaminated by external or internal random forces. In bistable neurons, weak signal detection can be enhanced by adding white Gaussian noise at a certain intensity range. Under these conditions, white Gaussian noise improves signal-to-noise ratios during detection of subthreshold periodic signals in nonlinear elements (Fauve and Heslot 1983; Bulsara et al. 1991; Longtin et al. 1991; Douglass et al. 1993; Moss et al. 1993). This phenomena is known as stochastic resonance (SR). Weak signals were also detected under sine-Wiener noise in the FitzHugh–Nagumo model (Yao and Ma 2018) and with high frequency inputs in a noisy neural network model (vibrational resonance) (Qin et al. 2018).

SR was previously detected in sensory peripheries that were forced by periodic inputs (Douglass et al. 1993; Longtin et al. 1994; Levin and Miller 1996; Shimozawa et al. 2003). With relevance to central nervous systems, SR has been reported in rat hippocampal slices and in a computer simulation of a CA1 pyramidal cell model (Stacey and Durand 2000, 2001, 2002). In these studies, action potentials synchronized with periodic synaptic inputs in the presence of random synaptic inputs, which contributed to recall of stored patterns in a hippocampal neural network model (Yoshida et al. 2002). In this neural network model, weak periodic synaptic inputs evoked an embedded pattern in CA1 pyramidal cell in cooperation with irregular synaptic inputs.

Spike synchronization has also been shown in coupled neural network models, such as the small-world network reported by Kim and Lim (2017) and in their subsequent free-scale network model (Kim and Lim 2018). In a noisy neural network model based on Izhikevich neuron models, SR was induced by a white Gaussian current (Zhao et al. 2017) and was supported by neural coupling following synchronization of neural spikes. Under these conditions, decoupling eliminated synchronization. Stochastic burst synchronization also appeared in a scale-free neural network model (Kim and Lim 2018) and the effects of synaptic plasticity of spike-times were examined.

Gaussian white noise induces synchronization in uncoupled nonlinear oscillators of theoretical models and in physiological experiments, and this process is known as noise-induced synchronization (Mainen and Sejnowski 1995; Teramae and Tanaka 2004; Goldobin and Pikovsky 2006; Galán et al. 2006). In rat neocortical slices, the timing of spike trains was precisely reproducible using low intrinsic noisy depolarization, whereas constant dc current induced fluctuations in spike times (Mainen and Sejnowski 1995). The precision of spike times between separate trials indicates synchronization between uncoupled neural oscillators following common noise inputs. Noise-induced synchronization has also been observed in neuron models that were driven by Poisson trains (Nagai et al. 2005; Nagai and Nakao 2009). Furthermore, in a pair of uncoupled neuron models, synchronization was induced by common random neural pulses that were generated by an exponential distribution with a negative slope (Tateno et al. 2011).

Currently available data indicates that noise-induced synchronization occurs even in pairs of non-identical neurons. In the electroreceptors of paddlefish, bursts of neural activities in electroreceptor afferents were synchronized by common Gaussian noise (Neiman and Russell 2002). Although afferent neurons oscillate at various intrinsic frequencies, the common noise contributes to convergence of interburst intervals. This convergence of firing frequencies is facilitated under conditions of greater noise intensity. Accordingly, noise-induced synchronization has been found in an ensemble of uncoupled non-identical Hodgkin–Huxley neuron models (Zhou and Kurths 2003).

In human brains, augmentation of phase synchronization by random signals potentially causes behavioral SR. In previous studies, detection of weak visual signals in the right eye was enhanced by random luminance signals applied to the left eye (Kitajo et al. 2003, 2007). Yet these noise inputs also augmented long-range phase synchronization of electro-encephalogram signals in human brains (Ward et al. 2006; Kitajo et al. 2007). These studies suggest that increases in phase synchronization increase signal transfer between neurons, and consequently induce behavioral SR.

Random forces reportedly induced SR and noise-induced synchronization simultaneously in a neural network (Yao and Ma 2018). Thus, we investigated the conditions under which similar concurrent phenomena between phase synchronization and SR are induced by random spiking inputs. To this end, we examined rhythmic synchronization of two uncoupled non-identical neuron models. We show that the common random pulse input contributes to noise-induced synchronization in the pair of neuron models, and SR was concurrently induced by common periodic pulse inputs with common random pulse inputs. Moreover, common random pulse inputs uncovered periodic responses in these neuron models, and the induced periodic responses facilitated phase synchronization.

In the present uncoupled non-identical neuron models, periodic responses were induced by common periodic input with the common random pulse, and these occurred in both neuron models, thus facilitating phase synchronization. In “Methods” section, we present the neuron model with stimulation patterns and data analysis. “Results” section describes noise-induced synchronization and SR induced by random pulses in the pair of non-identical neuron models. In “Discussion” section we discuss applications of these noise-related phenomena.

Methods

Mathematical neuron model

As shown in the schematic of the present system (Fig. 1), neuron models received common random and/or periodic pulse inputs. We introduced random or periodic pulses as the input layer, the output properties of the pair of neuron models were investigated. The output layer comprised two \(I_{{{\text{Na}},p}} + I_{\text{K}}\) neuron models, and both of these were the Hodgkin–Huxley type models proposed by Izhikevich (2007). No interconnection was presented between the two neurons. Pulse inputs were applied to both neuron models, either randomly or as a periodic pulse train.

Fig. 1
figure 1

An outline of the present system: the two Hodgkin–Huxley neuron models were uncoupled and were exposed to a common random pulse and/or a periodic pulse

Full size image

The \(I_{{{\text{Na}},p}} + I_{\text{K}}\) model comprises a persistent \({\text{Na}}^{ + }\) channel and a delayed rectified \({\text{K}}^{ + }\) channel and is represented by following equations:

$$\begin{aligned} C_{m} \frac{{dV_{i} }}{dt} & = \bar{g}_{\text{Na}} m_{\infty ,i} \left( {E_{\text{Na}} - V_{i} } \right) + \bar{g}_{{{\text{K}},i}} n_{i} \left( {E_{\text{K}} - V_{i} } \right) \\ & \quad + \,g_{l} \left( {E_{l} - V_{i} } \right) + I_{\text{com}} \left( t \right) +\upxi\left( {\text{t}} \right), \\ \frac{{dn_{i} }}{dt} & = \frac{{n_{\infty ,i} - n_{i} }}{{\tau_{n} }} \\ \end{aligned}$$

where i = 1 or 2. \(I_{\text{com}} \left( t \right)\) is a common pulse input current, and \(\xi \left( {\text{t}} \right)\) is the Gaussian noise. \(<\!\xi \left( t \right), \xi \left( {t^{\prime}} \right)\!> = \sigma^{2} \delta \left( {t - t^{\prime}} \right)\). \(\upsigma = 0.02\,\upmu{\text{A/cm}}^{2}\). Detailed input patterns of the common pulse input current are described in “Stimulation” section.

The rate functions of the persistent \({\text{Na}}^{ + }\) channel and the delayed rectified \({\text{K}}^{ + }\) channel current are calculated as follows:

$$\begin{aligned} m_{\infty ,i} \left( {V_{i} } \right) & = \frac{1}{{1 + \exp \left( {\frac{{ - 20 - V_{i} }}{15}} \right)}} \\ n_{\infty ,i} \left( {V_{i} } \right) & = \frac{1}{{1 + \exp \left( {\frac{{ - 25 - V_{i} }}{5}} \right)}} \\ \end{aligned}$$

The following parameters were used: \(C_{m} = 1 \,\upmu{\text{F/cm}}^{2}\), \(E_{\text{Na}}\) = 60 mV, \(E_{\text{K}}\) = − 90 mV, \(E_{l}\) = − 80 mV, \(\bar{g}_{\text{Na}}\) = 20 mS/\({\text{cm}}^{2}\), \(g_{l}\) = 8 mS/\({\text{cm}}^{2}\). \(\tau_{n}\) = 1 ms.

In this study, we set different \(g_{\text{K}}\) values in the neuron models but fixed \(\bar{g}_{{{\text{K}},1}}\) at 10 mS/\({\text{cm}}^{2}\) throughout the present simulations. Unless otherwise specified, \(\bar{g}_{{{\text{K}},2}}\) was fixed at 10.5 mS/\({\text{cm}}^{2}\). This parameter difference caused a difference in distances between resting and threshold states, thereby demonstrating that dc current induces different responses in spike frequencies.

Neuron model equations were integrated using the Euler scheme with a time step of 0.001 ms.

Stimulation

The common input current (Icom) was applied to the two neuron models with three stimulation patterns. The first, a random pulse, was applied to the neuron models and the interval \(y\) between the down stroke of the pulse and the upstroke of the next pulse was selected from the following gamma distribution:

$$f\left( y \right) = \frac{\theta }{\varGamma \left( k \right)}\left( {\theta y} \right)^{k - 1} e^{ - \theta y} \quad \left( {y \ge 0} \right)$$

where \(\varGamma \left( k \right)\) is the gamma function (\(k = 1, 2, 3, 4,\,{\text{or }}\,5\)). The shape parameter \(k\) and the scale parameter \(\theta\) determined the mean random pulse train frequency. When \(k = 1\), the gamma distribution is equivalent to the exponential distribution with a negative slope. Hence, by varying the shape parameter of the gamma distribution, the common pulses exhibit intermediate properties between random Poisson and periodic pulses. In these subthreshold simulations, the pulse duration was fixed at 5 ms and the pulse amplitude was fixed at 5.5 \(\upmu{\text{A/cm}}^{2}\).

In the second simulation pattern, the periodic pulse was applied to neuron models with varying input frequencies of the periodic pulse, but with a pulse duration of 5 ms.

In the third simulation pattern, periodic and random pulses were applied concurrently to the neuron models and the random pulse was selected from the gamma distribution. When two pulses were coincident, the pulse was simply superimposed on the other pulse with a constant pulse amplitude of 5.5 \(\upmu{\text{A/cm}}^{2}\).

The computation presented above was repeated 10 times with a computational time of 10 s.

Data analysis

In assessments of the phase differences between the present neuron models, degrees of synchronization in spiking of neuron models were quantified according to vector strength \(\rho\). We defined a phase variable for the spike train as follows:

$$\phi_{j} \left( t \right) = 2\pi i + 2\pi \frac{{t - T_{i} }}{{T_{i + 1} - T_{i} }}\quad \left( {j = 1 \,{\text{or}}\, 2} \right)$$

where \(T_{i}\) is the time of the \(i\)-th spike (Zhou and Kurths 2003) and the phase \(\phi_{j} \left( t \right)\) is increased by \(2\pi\) every time a spike occurs. The phase was interpolated linearly between sequential spikes, but the phase difference \(\Delta \phi \left( t \right) = \phi_{1} \left( t \right) - \phi_{2} \left( t \right)\) changed with time due to disturbances but plateaued when the spike timing was locked. The vector strength was calculated using the following equation:

$$\uprho^{2} = \left\langle {\sin \Delta \phi } \right\rangle^{2} + \left\langle {\cos \Delta \phi } \right\rangle^{2}$$

The brackets denote the average over time and \(\uprho = 1\) when phase synchronization continues during the computation. The mean value of the vector strength \(\uprho\) was obtained using the average of 10 trials with computation times of 10 s. Under these conditions, \(\uprho\) was not calculated if the mean spiking frequency was less than 2 Hz.

Periodicity of output spikes was assessed after applying the periodic pulse with the random pulse. Interpulse intervals were then collected from neuron #1 and periodicity was assessed using a histogram of the interpulse intervals. The bin size was 2 ms. The rate of periodic responses in all response events was quantified by the number of periodic spike events. For example, when the periodic pulse was 40 Hz, interspike intervals in the range of \(25 \pm 1\) ms were regarded as periodic responses and the common periodic pulse was applied for 15, 25, and 45 ms. The number of periodic spike events was then normalized by the total number of spike events in each trial, and the resulting value is the periodic event rate.

Results

Synchronization induced by the common random pulse

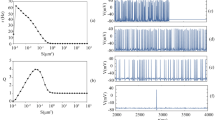
Figure 2 shows the vector strength \(\uprho\) induced by the common random pulse or the periodic pulse as a function of the mean input frequency. In these computations, \(\bar{g}_{{{\text{K}},1}}\) was fixed at 10 mS/\({\text{cm}}^{2}\) and \(\bar{g}_{{{\text{K}},2}}\) was varied. Figure 2a shows \(\uprho\) for \(\bar{g}_{{{\text{K}},2}} = 10.5\) mS/\({\text{cm}}^{2}\). For \(k\) = 1, \(\uprho\) was approximately 0.9 when the input frequency was above 30 Hz (Fig. 2a (filled circle)) and the vector strength \(\uprho\) was less dependent on the mean input frequency and decreased with increases in the shape parameter \(k\) (Fig. 2a). However, when \(k = 3\), \(\uprho\) was constant at around 0.7 with frequencies of greater than 90 Hz (Fig. 2a (filled square)). When \(k = 5\), \(\uprho\) was close to 0.6 at frequencies higher than 100 Hz (Fig. 2a (filled triangle)). The common periodic pulse led to a low vector strength (< 0.4) throughout the frequency range (Fig. 2a (triangle)). Because the stimulus amplitude was weak, several periodic input pulses were required to induce a spike and numbers of input pulses required for excitation were not constant because of the Gaussian noise. Moreover, phase differences jumped randomly and vector strength was consequently low.

Fig. 2
figure 2

Degrees of synchronization in output spikes of a pair of neuron models stimulated by a common random pulse; \(k = 1\) (filled circle), 2 (filled inverted triangle), 3 (filled square), 4 (filled diamond) and 5 (filled triangle) or a common periodic pulse (triangle); data are presented as means \(\pm\) standard errors of the mean (S.E.). a A common random pulse with a low shape parameter induced a higher vector strength \(\uprho\); \(\bar{g}_{{{\text{K}},1}}\) = 10 mS/\({\text{cm}}^{2}\) and \(\bar{g}_{{{\text{K}},2}}\) = 10.5 mS/\({\text{cm}}^{2}\). b Vector strengths \(\uprho\) were collected with the random pulse at 100 Hz and are plotted as a function of \(\bar{g}_{{{\text{K}},2}}\). Differences in \(\bar{g}_{\text{K}}\) reduce ρ. The roll-off slope with \(k\) = 1 is not symmetrical

Full size image

The vector strength \(\uprho\) at the mean random frequency of 100 Hz was plotted as a function of potassium channel conductance \(\bar{g}_{{{\text{K}},2}}\) (Fig. 2b). Difference in \(\bar{g}_{{{\text{K}},2}}\) caused decrements of \(\uprho\) and the slope of these depended on the shape parameter k. Specifically, when \(k\) = 1, a peak was found at \(\bar{g}_{{{\text{K}},1}}\) = \(\bar{g}_{{{\text{K}},2}}\) = 10 mS/\({\text{cm}}^{2}\), reflecting identical parameters (Fig. 2b (filled circle)). Differences between \(\bar{g}_{{{\text{K}},1}}\) and \(\bar{g}_{{{\text{K}},2}}\) increased asynchronous spiking of the neuron models. Yet, the roll-off slope of the vector strength was not symmetrical. Thus, if \(\bar{g}_{{{\text{K}},2}} < \bar{g}_{{{\text{K}},1}}\), the slope was steeper than that of the other side. Consequently, when \(\bar{g}_{{{\text{K}},2}} > \bar{g}_{{{\text{K}},1}}\), \(\uprho\) was maintained at a relatively high value. Accordingly, random inputs with \(k\) = 2 or higher induced lower ρ than those with k = 1 (Fig. 2b). For \(k\) = 2–5, differences in \(\bar{g}_{\text{K}}\) caused relatively symmetric decrements of \(\rho\). Under the periodic conditions, the vector strength was zero (Fig. 2b (triangle)), and was insensitive to differences in \(\bar{g}_{\text{K}}\). Although one of the neurons had a low threshold and excited by a few periodic pulses, the other needed a few more input pulses for excitation. These differences in excitability resulted in low degrees of synchronization and \(\bar{g}_{{{\text{K}},2}}\) was thereafter fixed at 10.5 mS/\({\text{cm}}^{2}\).

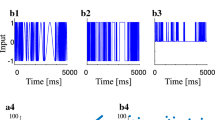
Figure 3a shows the membrane potential of neurons that were stimulated by the common random pulse with \(k\) = 1. In these simulations, the mean input frequency was 100 Hz (\(\theta\) = 0.2 \({\text{ms}}^{ - 1}\)) and the neurons fired spikes simultaneously, albeit with non-constant interspike intervals. Moreover, frequent bursts of pulses induced simultaneous excitation in the pair of neurons. Figure 3b depicts the temporal evolution of the phase difference \(\Delta \phi \left( t \right)\). In this simulation, the phase synchronization was detected by plateaus of \(\Delta \phi\). Specifically, \(\Delta \phi \left( t \right)\) slipped by \(2\pi\). To give the cyclic phase difference \(\Delta_{c} \phi\), \(\Delta \phi \left( t \right)\) was then remapped in the range of \(- \pi\) and \(\pi\) as described previously (Schäfer et al. 1998; Zhou and Kurths 2003). In Fig. 3c, we present the probability density of the cyclic phase difference \(\Delta_{c} \phi\), and the sharp peak in the distribution of \(\Delta_{c} \phi\) indicates that the random pulse induced phase synchronization.

Fig. 3
figure 3

Spikes of neurons after stimulation by random pulses with \(k\) = 1; a The mean input frequency of the random pulse was 100 Hz (\(\theta\) = 0.2 \({\text{ms}}^{ - 1}\)). Spikes are elicited simultaneously; vector strength \(\uprho\) = 0.88; b time course of phase differences; c probability density of cyclic phase differences \(\Delta_{c} \phi\); \(\Delta \phi\) was remapped in the range of \(- \pi\) and \(\pi\)

Full size image

Figure 4a shows the membrane potential of neurons after stimulation by the random pulse with \(k = 5\) and a mean input frequency of 100 Hz (\(\theta\) = 1 \({\text{ms}}^{ - 1}\)). Under these conditions, each neuron fired spikes independently of the other, although spike times were occasionally simultaneous. Moreover, \(\Delta \phi \left( {\text{t}} \right)\) increased gradually with time (Fig. 4b) and included several short plateaus that were maintained for shorter periods. Figure 4c shows a low peak at around \(\Delta_{c} \phi = 0\). \(\Delta_{c} \phi\) was not limited around 0 and the skirts of probability densities were apparent around the peak, indicating that, opportunities for phase synchronization were reduced.

Fig. 4
figure 4

Spikes induced by the common random pulse with \(k = 5\); a the mean input frequency of the random pulse was 100 Hz (\(\theta\) = 1.0 \({\text{ms}}^{ - 1}\)); vector strength \(\uprho\) = 0.62; b phase differences of spikes; c probability density of cyclic phase differences \(\Delta_{c} \phi\)

Full size image

Figure 5 shows the spike frequency as a function of the mean input frequency for the shape parameter \(k\) = 1 or 5. The spiking frequency of the neurons increased monotonically with the input frequency in both cases. Moreover, when \(k\) = 1, the mean spiking frequency of neuron #1 overlapped with that of neuron #2, indicating that the neurons behave as identical oscillators. Under the conditions of \(k\) = 5, differences in spiking frequencies were found in the range of 50–150 Hz, and these differences led to low degrees of synchronization.

Fig. 5
figure 5

Mean spiking frequency of neurons as a function of the mean input frequency of the random pulse; a\(k\) = 1 and b\(k\) = 5

Full size image

Random pulse-induced synchronized periodic responses

In these experiments, the periodic pulse was applied with the random pulse at \(k = 5\). The resulting vector strength \(\uprho\) is shown in Fig. 6b as a function of the mean frequency of the random pulse, and the synthesized pulse induced a high \(\uprho\) value. Moreover, \(\uprho\) was improved throughout the frequency range. Figure 6a shows membrane potentials of neurons after stimulation with periodic (40 Hz) and random pulses (mean = 33 Hz). Spikes emerged simultaneously in the two neurons under these conditions and phase differences were maintained at \(2\uppi\) or multiples of \(2\pi\) (data not shown). The vector strength ρ at a mean random frequency of 100 Hz was plotted as a function of the potassium channel conductance \(\bar{g}_{{{\text{K}},2}}\) (Fig. 6c), and ρ was approximately 0.9 when \(\bar{g}_{{{\text{K}},2}}\) was between 10 and 11.5 mS/\({\text{cm}}^{2}\). The slope of the vector strength became nonsymmetrical in these simulations. Specifically, when \(\bar{g}_{{{\text{K}},2}} > \bar{g}_{{{\text{K}},1}}\), the slope was shallower than that of the other side. Yet, the common random pulse with the common periodic pulse improved the degree of synchronization, especially when \(\bar{g}_{{{\text{K}},2}} > \bar{g}_{{{\text{K}},1}}\).

Fig. 6
figure 6

Periodic responses were improved by the common random pulse with \(k = 5\). a Responses of the neurons following mixed inputs of periodic (40 Hz) and random pulses (mean = 33 Hz); \(\uprho\) = 0.88. b Vector strengths of the output spikes (mean ± S.E.); synchronization was facilitated by random synaptic inputs in the entire frequency range. c Vector strength \(\uprho\) with random pulses at 100 Hz are plotted as a function of \(\bar{g}_{{{\text{K}},2}}\); \(k\) = 5; periodic pulse frequency = 40 Hz

Full size image

The histogram in Fig. 7 shows the interspike interval of output spikes in neuron #1 following periodic stimulation with the random pulse at 40 Hz (\(k = 5\)). The random pulse with applied with mean frequencies of 33 (\(\theta\) = 0.2 \({\text{ms}}^{ - 1}\)), 67 (\(\theta\) = 0.5 \({\text{ms}}^{ - 1}\)), and 182 Hz (\(\theta\) = 10 \({\text{ms}}^{ - 1}\)). At 33 Hz, peaks of the interval histogram appeared at 25, 50, and 75 ms (Fig. 7a), corresponding with the interval of the periodic input pulse and its multiples. When the random pulse was applied at 67 Hz, a peak of the interval histogram appeared at 25 ms (Fig. 7b) and \(\uprho\) was 0.95. Under conditions of 182 Hz random pulses, the peak of the interval histogram appeared below 25 ms (Fig. 7c). The mean periodic event rate is presented in Fig. 7d, which shows that simulation with a weak periodic pulse alone does not elicit an action potential in the low frequency range of the random pulse. Peaks in histograms of interspike intervals appeared at 25 ms when the frequency range of the random pulses was adequate, indicating that periodic responses were uncovered by random pulse stimulation. In addition, corresponding spikes occurred simultaneously in the two neurons. In Fig. 7d, we present the periodic event rate obtained with periodic pulses of 67 (15 ms) and 22 Hz (45 ms). At 22 Hz, the periodic event rate peaked with the random pulse at 67 Hz. In contrast, the periodic pulse of 67 Hz led to two peaks of periodic event rates. The first peak was induced by stochastic detection of periodic events, whereas the second peak was induced by the high frequency of the random pulse, which also caused short interspike intervals (ISIs) of around 10 ms, as shown in Fig. 7c. These ISIs prevented detection of periodic events.

Fig. 7
figure 7

Histograms of interspike intervals of neuron #1 after stimulation with periodic and random pulses; the input frequency of the periodic pulse train was 40 Hz. Mean input frequencies of the random pulses were a 33 (\(\theta\) = 0.2 \({\text{ms}}^{ - 1}\)), b 67 (\(\theta\) = 0.5 \({\text{ms}}^{ - 1}\)), and c 182 Hz (\(\theta\) = 10 \({\text{ms}}^{ - 1}\)). With random input pulses at 33 and 67 Hz, peaks appeared at of 25 ms (indicated by filled inverted triangle) and its multiples when frequencies of random pulses were adequate; d mean periodic event rates (mean ± S.E.). Periodic pulses were applied at frequencies of 67 (15 ms), 40 (25 ms), or 22 Hz (45 ms)

Full size image

Discussion

In this study, we examined stochastic phase synchronization of uncoupled non-identical neuron models. Phase synchronization was induced using a common random input pulse that was generated by the gamma distribution with the shape parameter \(k = 1\). Bursting patterns in the random input pulse forced synchronized excitation even in non-identical neurons. In addition, noise-induced synchronization in the two uncoupled non-identical canonical neuron models was the product of frequency locking (Neiman and Russell 2002). As shown in Fig. 5a, the common random input pulse caused convergence of the mean interspike intervals of the two neurons, and frequency locking occurred at a wide frequency range of input pulses.

The shape parameter of the common random input pulse changed the degree of synchronization between output spikes. In particular, the common random input pulse that was selected from the gamma distribution with \(k = 5\) reduced the chance of synchronization in the pair of uncoupled neurons. Gamma distributions with \(k = 5\) generated relatively regular pulse patterns and mean spiking frequencies did not converge, especially in the low frequency range. We suggest that this difference in spiking frequency prevents random pulse-induced synchronization. In accordance, the common periodic input pulse induced few pulses and was accompanied by a low degree of synchronization. In subthreshold stimulations, the common periodic input pulse caused independent entrainment in non-identical neuron models, reflecting different thresholds. Hence, these regular input pulses fail to induce synchronized excitation.

When the common periodic pulse was applied with the common random input pulse that was selected from the gamma distribution with a high shape parameter, phase synchronization was facilitated and output spikes were synchronized with incoming periodic input pulses. Because common periodic and random pulses were simultaneously applied to neurons, the dense parts of common input patterns tended to increase periodically. These conditions augmented the opportunities for periodic firing, which did not occur without the common random input pulse. These results further imply that random input pulses can uncover periodic responses of uncoupled non-identical neuron models.

In a small-world network connected with central pattern generators, synchronization depended on random synaptic connections (Liu and Tian 2014). This network showed SR in response to signals from central pattern generators, but noise-induced synchronization was not investigated. In a similar study, however, noise-induced synchronization was shown in a small-world network of identical phase oscillators (Esfahani et al. 2012). Hence, SR and noise-induced synchronization can be induced in small-network models under certain conditions.

When a set neurons start to fire in peripheral nervous systems, they excite neurons in the next layer and firing of these leads to propagation of signals from layer to layer of the central nervous system. However, sets of neurons are connected by diverging and converging pathways, and signal transmission between divergent sets of neurons is difficult. According to the synfire chain theory (Abeles 1991), synchronized volleys of spikes cause synchronous firing in the next layer in a synchronous mode. Hence, SR and noise-induced synchronization in neural networks may contribute to propagation of weak periodic neural activity. Under noiseless conditions, it is difficult to propagate spikes into deeper layers of neural networks (van Rossum et al. 2002). Internal noise from fluctuations of membrane potential supports stable propagation of synchronized spikes and spiking rates from layer to layer (Diesmann et al. 1999; van Rossum et al. 2002). This noise boosts neurons to the spike-ready condition, allowing rapid responses to an input signals.

In the central nervous system, spatiotemporal patterns of neural spikes represent environmental and internal conditions, and regular and irregular spiking patterns were reportedly observed in the cortex (Shinomoto et al. 2009; Mochizuki et al. 2016). In a dynamic neural model with stochastic parameters for feeling of understanding (FU), a process of gathering evidence to understand an event was represented and an initial growth was followed by a quasi-stable regime and then possible decay of FU (Mizraji and Lin 2017). The present pair of HH-type neuron models shows rhythmically or randomly synchronized spiking, or asynchronous spiking. Thus, differences in input patterns can switch spatiotemporal patterns of output spikes and change the synchronous mode. These results indicate that random neural activity contributes to signal transfer and signal processing in neural networks.