The feeling of understanding: an exploration with neural models

Abstract

There exists a dynamic interaction between the world of information and the world of concepts, which is seen as a quintessential byproduct of the cultural evolution of individuals as well as of human communities. The feeling of understanding (FU) is that subjective experience that encompasses all the emotional and intellectual processes we undergo in the process of gathering evidence to achieve an understanding of an event. This experience is part of every person that has dedicated substantial efforts in scientific areas under constant research progress. The FU may have an initial growth followed by a quasi-stable regime and a possible decay when accumulated data exceeds the capacity of an individual to integrate them into an appropriate conceptual scheme. We propose a neural representation of FU based on the postulate that all cognitive activities are mapped onto dynamic neural vectors. Two models are presented that incorporate the mutual interactions among data and concepts. The first one shows how in the short time scale, FU can rise, reach a temporary steady state and subsequently decline. The second model, operating over longer scales of time, shows how a reorganization and compactification of data into global categories initiated by conceptual syntheses can yield random cycles of growth, decline and recovery of FU.

Introduction

We have been witnessing an incredible expansion of information processing and delivery in all domains of life since the arrival of the World Wide Web around 1990. This sustained growth has escalated to amazing levels with the development of very fast and extensive networks of communication. In the sciences, investigators must constantly prepare themselves to review and bring up to date their technical information in briefer intervals of time. This reality confers a dramatic importance on the urgent need to analyze the impact of this expansion of information on the individual’s sense of understanding, which include, among other things, the emotions, insights and knowledge that each conscious intelligence associates with this experience. One of the reasons for this urgency is the desire to understand in what sense the nature of individual actions may be conditioned by the information flow that surrounds us. It is necessary at this point to emphasize that the feeling of understanding does not in any way validate that which it pretends to understand. Peter Lipton has clearly expressed some of the notable differences between “feeling of understanding”, “understanding” and “knowledge”: “To understand why a phenomenon occurs is a cognitive achievement, and it is a greater cognitive achievement than simply knowing that the phenomenon occurs—we all know that the sky is blue, but most of us do not understand why.” and “I will go on to consider a fifth and rather different consequence that consumers of good explanations enjoy. This is the distinctive and satisfying feeling of understanding, the “aha” feeling. I will suggest that although the “aha” feeling is not itself a kind of understanding, it may play an important role in the way understanding is acquired.” (Lipton 2009). In fact, this “feeling of understanding” or FU from now on, can be characterized as the intellectual and emotional process we submit to while attempting to assemble the pieces of evidence that would let us obtain an understanding of an event. As such, it depends as much on the extraordinary variety of cultural and ideological contexts imbedded in science and ethics, as on the most irrational superstitions transmitted through generations of believers.

Let us take as an example, a biochemist in 1950’s, who is an expert in enzymology. He holds a clear understanding of the experimental and theoretical methods of classical enzyme kinetics. This knowledge has allowed him to keep abreast of scientific progress in the field while, at the same time, publish original research. However, in a few years’ time the biochemist notices that current efforts to understand enzyme function and dynamics require, as indispensable tools, the techniques of molecular biology and structural X-ray analyses that he has not been trained for. By noticing that the traditional views of enzyme kinetics are no longer the focus of research in this rapidly advancing field, his FU of what constitutes a meaningful research path to follow is dramatically reduced in the new context. If the biochemist does not embrace and learn the new ideas and techniques, the focus of research becomes muddled and the absence of understanding creates an emotional block, thus hindering efforts to create new knowledge in the field. This would not be a major problem if the shifting basis of knowledge occurs once in the lifetime of a scientific career. But this is no longer true in the XXI century, when the accelerated rate of scientific progress brings about a paradigm shift in each field of knowledge within few years’ time. The assertion ‘adapt or fall behind’ reminds us of the necessity to constantly update our knowledge. This learning process forces us to challenge all previous levels of conceptual comprehension against the current feeling of understanding caused by the inflow of new information.

The FU is a subjective cognitive process that poses a great deal of challenge when we try to examine it from a scientific point of view. Fortunately, after several decades of building theoretical models of cognitive activities, researchers are beginning to develop scenarios that would make possible translating the “subjective into objective”. As an example, the elusive concept of consciousness has been the focus of theoretical models (Edelman 1989; Reeke and Edelman 1987; beim Graben 2014). In addition, some of these models are potentially useful to make contact with brain activities revealed by modern imaging techniques (Damasio 1999; Friston 1995, 2011; Sporns 2010).

The purpose of this work is to support recent research by experts in the field (de Regt et al. 2009). We propose a simple mathematical model that provides a kind of formalized representation of this “feeling of understanding”, one that evolves with the growth of personal knowledge or community-based information. Our first objective is to define a measure for FU that would be consistent with current ideas on neural codification of cognitive events. Once defined, we will develop a basic model that will show how this measure evolves in time with an individual’s acquisition and subsequent conceptualization of information.

Modeling knowledge

Knowledge networks

Let us represent a knowledge system (KS) by means of a network consisting of objects of knowledge (nodes) and directional connections that establish interactions among these objects (edges). This is an extremely simple representation. It does not convey the importance of each node, how strong or essential is an edge in the overall functional pattern of the network or the influence of an ‘outside environment’. Nonetheless we propose this model as a preliminary approach, one that would allow us to frame the problem more precisely, with the later objective of achieving some insight into the dynamic behavior of the system.

In Fig. 1 we represent a cluster of KS’s that can be generated by three objects. In the upper panel we illustrate a situation where all possible connections among the three objects are known. In the lower panel we outline a series of diagrams showing different degrees of partial knowledge. One way to measure the size of KS on graphs of this type is by using the simple but nontrivial concept of “variety” or V(x), as proposed by Ashby (1956). In this approach, all relevant elements x-defined according to a set of criteria—in each category of network G, in a partial or total KS are enumerated as follows,

$${\text{V}}({\text{KS}},{\text{G}}) = {\text{V}}({\text{nodes}}) + {\text{V}}({\text{arrows}})$$

(1)

Fig. 1

A variety of knowledge systems generated from three virtual objects and their potential links

As an example, the three partial graphs T1, T2 and T3 of Fig. 1 have varieties

$$\begin{aligned} {\text{V}}({\text{KS}},{\text{T}}1) = 1 + 1 = 2 \hfill \\ {\text{V}}({\text{KS}},{\text{T}}2) = 3 + 2 = 5 \hfill \\ {\text{V}}({\text{KS}},{\text{T}}3) = 3 + 5 = 8 \hfill \\ \end{aligned}$$

and the global pattern of three nodes has variety

$${\text{V}}({\text{KS}},3) = 3 + 9 = 12$$

In general, the global variety of a KS with N nodes will be

$${\text{V}}({\text{KS}},{\text{N}}) = {\text{N}} + \left[ {{\text{N}}\left( {{\text{N}} - 1} \right) + {\text{N}}} \right] = {\text{N}}\left( {{\text{N}} + 1} \right).$$

(2)

We clarify that in this approach “knowledge” and “information” are taken as having comparable meanings. Ashby (1956) associated this measure of variety with the subset of distinct elements in a set of possibilities as perceived by an observer able to discriminate among these choices. Variety is only one measure of complexity. It will be used later as an example on how to quantify the modulus of a neural vector when we discuss the cognitive aspects of FU. Relational structures represented by graphs are especially well-adapted elements to be implemented in neurocomputational models (for a discussion refer to Kohonen 1988, Section 8.2.3).

It is fair to say that a KS network increases in complexity when new objects appear that are able to interact with the elements of the previous network. One such occurrence is by means of technical advances in instrumentation that open the door to the detection of previously inaccessible events. An example is the Hubble Space Telescope, which has achieved a resolving power 10–20 times better than ground-based telescopes. With this instrument, scientists have been able to study the evolution of irregularly shaped galaxies in the early epochs of our universe and provide evidence for an expanding universe that is currently accelerating, reveal the existence of supermassive black holes and analyze the atmosphere of newly discovered exoplanets (Hubblesite.org).

The emergence of new objects creates a KS with increasing number of edges in the network. Let us take as an example, the upper panel of Fig. 1 and bifurcate an object into two distinct objects. The diagram of the new KS system is shown in Fig. 2.

Fig. 2

Emergence of new links after the division of one of the objects

The global complexity of the new network can be easily calculated to be V(KS, 4) = 20. In general, the change in variety from N to N + 1 nodes is,

$$\Delta {\text{V}}\left( {{\text{KS}},\,\,{\text{N}} \to {\text{N}} + 1} \right) = {\text{V}}\left( {{\text{KS}},{\text{N}} + 1} \right) - {\text{V}}\left( {{\text{KS}},{\text{N}}} \right).$$

(3)

or

$$\Delta {\text{V}}\left( {{\text{KS}},\,\,{\text{N}} \to {\text{N}} + 1} \right) = 2\left( {{\text{N}} + 1} \right).$$

(4)

When the number of nodes increases from N to N + k, the increment in complexity could reach (in the case of maximal connectivity),

$$\Delta {\text{V}}\left( {{\text{KS}},\,\,{\text{N}} \to {\text{N}} + {\text{k}}} \right) = {\text{k}}\left( {2{\text{N}} + {\text{k}} + 1} \right).$$

(5)

In naturally complex systems with large N, when new objects appear either through novel instrumentation, experimental techniques, theoretical or computational ideas, the complexity of KS can increase dramatically.

Cognitive reorganization of knowledge

The human brain may be able to store one or several KS’s, some of them in steady state while other ones in states of continuous expansion or decay. Technical and cultural evolution has brought us to the level where we can codify and save knowledge in non-biological media, usually in books and digital storage devices. All this information can be accessed and decodified by the brain and then reprocessed and synthesized to produce new knowledge. The human brain sustains many types of memories; each memory is codified according to a specific category of knowledge or information content. A fundamental type of knowledge is one that depends on the conceptual edifice that the cognitive brain processes at each instant of time. This type of codification can be dramatically reconfigured and compacted during epochs of great creativity.

A known example is the quadratic equation ${\text{ax}}^{2} + {\text{bx}} + {\text{c}} = 0$. The real roots of this equation initially were found by a graphical method, that is, by looking at the intersection of the parabola ${\text{ax}}^{2}$ with the straight line $- {\text{bx}} - {\text{c}}$. We can imagine that the roots ${\text{x}}_{\text{i}}$ were given as a list including the coefficients $({\text{a}}_{\text{i}} ,{\text{b}}_{\text{i}}, {\text{c}}_{\text{i}} )\,\,\,,\,\,\,{\text{i}} = 1, \ldots,{\text{Q}}$, and thereafter stored in large tables of data. With the progress of mathematical knowledge in the area of algebra, all previous information can be easily reduced to a single formula, ${\text{x}}_{1,2} = - \left( {{\text{b}}/2{\text{a}}} \right) \pm \sqrt {\left( {\text{b}/2{\text{a}}} \right)^{2} - \left( {{\text{c}}/{\text{a}}} \right)}$, that not only include the real solutions obtained by graphical methods but also the previously inaccessible complex solutions. This and other examples eloquently demonstrate that conceptual models created during periods of scientific progress lead to reconfigurations and reductions of previously stored information.

Neural codes for knowledge and understanding

Transforming the subjective into objective

The cognitive performance of individuals can be compared to the performance of models of Artificial Intelligence (AI) (Newell and Simon 1972) and neurocomputational models (Arbib 2003; Brown 2013; Érdi 2015). These performance comparisons provide ways to channel subjective experiences into objects that can be tested by scientific methods. Classical AI behavior reproduces with surprising efficiency symbolic strategies (e.g. reasoning) that are very similar to the behavior displayed by humans. On the other hand, neurocomputational models achieve competent performances during complex pattern recognitions and at information processing in uncertain environments. These approximations establish a kind of correspondence between unobserved (subjective experiences) and measurable events—formally represented by computational or mathematical models. The rite of passage for these representations are other observables: direct comparison of the behaviors of a formal system with human actions as can be seen in strategies for simple (tic-tac-toe) to complex games (chess), or in the interpretation and generation of texts written in the natural language, etc. Even more dramatic are efforts aimed at understanding the neurological basis of such subjective phenomena as consciousness (Edelman 1989; Dehaene 2014).

Models of neural networks are especially interesting because they have the capacity to build approximate linkages between model predictions and the biophysical, biochemical and physiological interactions of the human brain in action. The parallel processing of information, one of the trademarks of distributed and modular network models, find a similar correspondence in the behavior of real brains (McClelland et al. 1986; Kohonen 1988). The techniques of functional magnetic resonance imaging (fMRI), coupled with traditional tools of exploration, are opening new avenues for the objective analysis of subjective experiences (Friston 1995, 2011). The triad pattern of interactions {subjective events, neurocomputation, neuroimaging} promises to unlock fruitful avenues for research and discovery (Valle-Lisboa et al. 2014).

In neurocomputational models, “neural vectors” in a high dimensional vector space represent groups of neurons, and matrix operators acting on these vectors describe the interactions among groups of neurons during cognition. Therefore, the response dynamics of neural vectors (e.g. the time dependence of large sets of firing rates) can be seen as processes operating within a specific time window (Anderson 1972, 1995; Kohonen 1972, 1988). The spatial and temporal dynamics of neural vectors can also be analyzed by means of extended neural fields (Cowan 2014; beim Graben and Rodrigues 2014; Wright and Bourke 2014). These fields are intimately connected to actual data of neural images.

We want to mention that one of the targets of research is the establishment of relations between the brain and the semantic web of any individual. This is important to our argument because a semantic web is an information network that is structured around categories (concepts) with verbs as categorized actions. The work by Huth et al. (2012), shows the existence of continuous representations of semantic webs on the cortical surface. This topographic map also shows the existence of word clusters associated to topics (e.g. a web may display in the same cluster the words, “vehicle”, “boat” and “car”, among others). The neural process that generates this structure is a fascinating open problem and may be the outcome of a dynamic neural field. As is well explored in many formal theories, the cortical neurons have the capacity to produce a territorial organization of neuronal networks (Kohonen 1988; Coombes et al. 2014).

In the theory of associative memories, large matrices with elements proportional to synaptic weights represent memory modules that store information in the brain. The versatility of this approach together with the plausibility of anatomical and physiological counterparts (Mizraji and Lin 2011, 2015), are the main advantages of this vector representation. Hence, the actions of a neural module can always be encoded in a neural vector and sequences of neural vectors can represent sensory perceptions—inputs transported by the optical nerve—or cognitive processes associated with the elaboration of conceptual entities.

It is important to highlight that the degree of similarity between two patterns represented by neural vectors can be measured by their scalar product (Anderson 1995; Kohonen 1988). Pattern identification is not dependent on the length of a vector but on its direction, which is defined by the structure of its components. In these models, it is common but in no way necessary to assume neural vectors as normalized. Figure 3 shows two digitalized images of a well-known face.

Fig. 3

The two images of Winston Churchill are correctly identified even though their intensities are very different

These images can be coded into vectors. Each component of a vector is represented by a pixel with gray tones between 0 (white) and 1 (black). The length of the vector on the left is smaller than the one on the right, but we identify the same person in the two faces. The pattern we identify depends on the direction of the neural vector. We remark that this is not a general characteristic of neural functions. Many important processes of self-organization or feature detection are dependent on vectors with dominant lengths (Kohonen 1988).

We proceed by assuming that it is possible to compare patterns by comparing angles between multidimensional neural vectors. We review some basic definitions. A column vector of dimension r,

$${\text{U}} = \left[ {{\text{U}}_{1} \,\,{\text{U}}_{2} \, \cdots \,\,{\text{U}}_{\text{r}} } \right]^{{{\text{T}}}},\,\,{\text{T}} = {\text{Transpose}}$$

has length

$$\left\| {\,{\text{U}}\,} \right\| = \sqrt {{\text{U}}_{1}^{2} + {\text{U}}_{2}^{2} + \cdots + {\text{U}}_{r}^{2} }$$

A measure of the angle between two real vectors U and V is the scalar product,

$${ \cos }\left( {\widehat{{{\text{U}},{\text{V}}}}} \right) = \frac{{\left\langle {\text{U,V}} \right\rangle }}{{\left\| {\text{U}} \right\| \cdot \left\| {\text{V}} \right\|}},\quad \left\langle {\text{U,V}} \right\rangle = \sum\limits_{{{\text{i}} = 1}}^{\text{r}} {{\text{U}}_{\text{i}} {\text{V}}_{\text{i}} }$$

(6)

The Euclidean distance d(u, v) between the normalized vectors ${{{\text{u}} = {\text{U}}} \mathord{\left/ {\vphantom {{{\text{u}} = {\text{U}}} {\left\| {\text{U}} \right\|}}} \right. \kern-0pt} {\left\| {\text{U}} \right\|}}$ and ${{{\text{v}} = {\text{V}}} \mathord{\left/ {\vphantom {{{\text{v}} = {\text{V}}} {\left\| {\text{V}} \right\|}}} \right. \kern-0pt} {\left\| {\text{V}} \right\|}}$ would then be

$${\text{d}}({\text{u}},{\text{v}}) = \sqrt {2\left( {1 - \,\,\left\langle {{\text{u}}\,,\,{\text{v}}} \right\rangle } \right)}$$

(7)

For parallel vectors we have ${\text{d}}({\text{u}},{\text{v}}) = 0$, and for orthogonal vectors, ${\text{d}}({\text{u}},{\text{v}}) = \sqrt 2$ (this is the maximum distance for u and v with non-negative components). This simple example shows that the angle between two normalized vectors may be an appropriate measure that quantifies the distance between patterns encoded in vectors.

Managing knowledge and understanding by the brain

Our intention is to establish a very simple model that partially captures the feeling of understanding (FU) by associating knowledge as a form of data and understanding as an acquisition of concepts. This is an extreme oversimplification, but it is a first step towards the solution of a difficult problem that aims at capturing the cognitive foundations of FU. Lipton (2009) has analyzed in detail the differences between explanation and understanding and in de Regt (2009) there is an epistemological analysis of FU. As discussed before, many cognitive abilities in neural modules emerge from activities of extensive networks of neurons and codified in neural vectors. We will assume that FU results from the confrontation of two types of neural vectors, vectors that encode data with vectors that encode conceptual categories.

Data vectors evolve dynamically in at least two modalities. In one of these modalities, data vectors ${\text{V}}_{\text{D}}^{\text{S}}$ are refreshed according to the evolution of themes a person is interested in learning and theses updates rest on information stored in the memory or on information stored outside the person (books, data in computer memories, the World Wide Web, etc.). In the other modality, vectors ${\text{V}}_{\text{D}}^{\text{S}}$ map onto other vectors ${\text{V}}_{\text{D}}$ that encode singular topics. It is possible to update ${\text{V}}_{\text{D}}$ by advances in conceptual understanding that compact information into broader categories. Examples would be, 1) reuniting in Newton’s law of gravitation diverse phenomena such as free fall, projectile motion and planetary motion, etc. or 2) using quantum concepts to explain the photoelectric effect, discrete spectral lines of atoms and molecules and electron diffraction in crystals, etc.

Vectors ${\text{V}}_{\text{D}}^{\text{S}}$ may contain huge number of components. We simplify our argument by taking information about certain points of knowledge (topics) codified in ${\text{V}}_{\text{D}}^{\text{S}}$ that are packaged into clusters, each cluster of data—graphs in Fig. 1—forming a subspace that is locally dense but with enough spacing between clusters to make the total vector sparse. Let the elements in each cluster map onto a reduced data vector ${\text{V}}_{\text{D}}$. This is a projection of ${\text{V}}_{\text{D}}^{\text{S}}$ over an abstract space, which collapses all relevant data from a cluster into a single binary topic marker. In this simplified representation we envision a point of knowledge to be defined by 1 at the specific position of a cluster and by 0 when data is absent (the 0 may indicate that a knowledge point exists but it is unknown to the individual or it is inexistent). As an example, a 1 in position 7 of a vector ${\text{V}}_{\text{D}}$ may indicate that a person has partial information about engines and brands of sports cars even though he/she may not be knowledgeable about formula one racing scores, e.g. a 0 in another location of the neural vector.

In a way similar to what happens to data vectors, the conceptual vectors ${\text{V}}_{\text{C}}^{\text{S}}$ are mapped onto binary processed topic vectors ${\text{V}}_{\text{C}}$. In the example mentioned above, a 1 in position 7 indicates that the individual have accumulated the necessary concepts to partially understand the workings of the engine of a sports car—including items such as driving conditions, the functioning of thermal combustion engines and design aerodynamics, etc. The same individual may have a 1 in position 243 of ${\text{V}}_{\text{D}}$ in relation to data related to polymeric materials used in the chassis, but having a 0 in the same position in ${\text{V}}_{\text{C}}$ may indicate a total ignorance concerning the nature of the chemical composition, synthesis and strength properties of these materials. In this context, we may say that a person understands how a car works but does not understand the properties of polymeric materials used in the chassis. On account of the intense processing of factual information it is natural to assume that in general, vectors ${\text{V}}_{\text{D}}$ will have many more 1’s than vectors ${\text{V}}_{\text{C}}$. We remark in passing that the simple codification scheme outlined above is similar to methods of data mining (Berry and Browne 2005). An interesting example with cognitive implications is the Latent Semantic Analysis (LSA), which detects thematic clusters in several documents and codifies them in components of a vector (Deerwester et al. 1990; Landauer and Dumais 1997; Valle-Lisboa and Mizraji 2007). The vectors ${\text{V}}_{\text{D}}$ and ${\text{V}}_{\text{C}}$ are deliberate simplifications to help us represent the complex neurophysiological events at the root of the correlations between vectors ${\text{V}}_{\text{D}}^{\text{S}}$ and ${\text{V}}_{\text{C}}^{\text{S}}$.

The anatomical connectivity of neural networks in the human brain constrains neural vectors to have finite but very large dimensions. We will assume that both simplified vectors, ${\text{V}}_{\text{D}}$ and ${\text{V}}_{\text{C}}$, have equal dimensions as information in ${\text{V}}_{\text{D}}$ contain only data that specifically matches the conceptual content of ${\text{V}}_{\text{C}}$. We can consider that the short-term dynamics of ${\text{V}}_{\text{D}}^{\text{S}}$ allow for rapid modifications of its components, the result of exploratory activities of a brain that continuously searches for data stored in its own memories or in external databases. The time scales of short-term dynamics are the typical turnover times of knowledge acquisition in the natural sciences. The detection of data is like a moving window, selecting finite-dimensional vector components that build, at every moment in time, vectors ${\text{V}}_{\text{D}}^{\text{S}}$. Note that the screening or projection on databases—belonging to the brain or to external sources as in Wikipedia—are constantly refreshed from one instant to another by a working memory. In the medium time scale, data vectors are mapped on topic vectors ${\text{V}}_{\text{D}}$. The evolution of the binary nature of ${\text{V}}_{\text{D}}$ may transform 0 into 1 as the subject acquires information on a topic it did not know. Conversely, the existence of unifying concepts that compresses information of several categories into one (e.g. examples in “Cognitive reorganization of knowledge” section) may substantially reduce the quantity of 1’s in ${\text{V}}_{\text{D}}$ by reorganizing data.

An analysis of the mutual influence among data and concepts in simple models require a definition of these conceptual and data vectors. Since antiquity it has been known that conceptualizing has to do with condensing data from the external world into patterns. In James (1911) we find a clear description of this process and Cooper (1974) outlines a neural network interpretation of data condensation. Along these lines, we shall assume that quantities of topics in data vectors ${\text{V}}_{\text{D}}$ are larger than quantities of topics in conceptual vectors ${\text{V}}_{\text{C}}$. One way to express this difference is to assume that the moduli of vectors ${\text{V}}_{\text{D}}$ are usually greater than the moduli of vectors ${\text{V}}_{\text{C}}$,

$$||{\text{V}}_{\text{D}} | |= {\text{m}}_{\text{d}} ,\;||{\text{V}}_{\text{C}} | |= {\text{m}}_{\text{c}} ,\;{\text{m}}_{\text{d}} \,\geq\ {\text{m}}_{\text{c}} .$$

(8)

The feeling of understanding (FU)

Finding a measure of feeling

Humans possess a wide repertoire of neural structures, especially those related to the limbic system, that are associated with the detection of pleasure or displeasure (Kandel and Schwartz 1985, Ch. 47). A significant part of our behavioral patterns are guided by these subjective perceptions. As an example, the software behind robots trying to emulate human behavior attempts to simulate by means of artificial neural networks, sensations associated with presence or absence of pleasure by training them to act autonomously (Edelman 1989).

Following the previous discussion, we shall assume that FU is a cognitive event, including emotional reactions, which we associate to pleasurable sensations. The brain has well defined structures that establish the functional links between the cortical cognitive processes, the limbic system and the hypothalamus, thus explaining the almost continuous “translation” of cognitive activities into emotional reactions, including pleasure and displeasure sensations (for a classical description, see Kandel and Schwartz 1985, Chap. 46). We attempt here to develop a theory of pattern detection, where interacting neural vectors ${\text{V}}_{\text{D}}$ and ${\text{V}}_{\text{C}}$ are capable of measuring quantitatively FU. Once recorded, this parameter will be transmitted to other neural modules that process pleasurable sensations.

A measure of FU would be the angle between neural vectors ${\text{V}}_{\text{D}}$ and ${\text{V}}_{\text{C}}$. If the angle were small FU would be large and if the angle were close to 90° FU would be small. The association between data and concepts will be of paramount importance. Therefore, we measure FU by means of a correlation coefficient K between two un-normalized vectors,

$${\text{K}} = \frac{{\left\langle {{\text{V}}_{\text{D}} \,,\,{\text{V}}_{\text{C}} } \right\rangle }}{{{\text{m}}_{\text{d}} \,.\,\,{\text{m}}_{\text{c}} }} \le 1$$

(9)

There are different pairs of vectors ${\text{V}}_{\text{D}}$ and ${\text{V}}_{\text{C}}$ in different neural modules and each pair may store information with a different value of K. A historian may have K = 0.87 when the subject refers to the history of Renaissance and K = 0.05 when the subject is differential topology.

In the simplest case, we will assume that every conceptual category corresponds to some well-defined data category. There may be cases where valid data may support false, misguided scientific theories or unsupported beliefs. We will analyze not only cases supported by logic and truth values but also cases based on beliefs, rational or otherwise (de Regt et al. 2009). We will leave aside the philosophical debate about a priori categories. Even if they exist (e.g. in linguistics) they may still require data vectors to process them as categories.

The connection between a sense of well-being when understanding ensues and the percolation of the correlation coefficient K in Eq. (9) along neural structures, can be expressed as a matrix operator that joins patterns

$${\text{E}} = {\text{z}}\,{\text{V}}_{\text{C}}^{\text{T}}$$

(10)

The operator E evaluates how well a conceptual vector ${\text{V}}_{\text{C}}$ matches a neural vector ${\text{V}}_{\text{D}}$, z being a neural vector that channels conceptual information to the limbic system. This is a simple Anderson—Kohonen memory matrix. When applied to a data vector it registers

$${\text{E}}\,{\text{V}}_{\text{D}} = {\text{z}}\,\left\langle {{\text{V}}_{\text{C}} \,,\,{\text{V}}_{\text{D}} } \right\rangle = {\text{z}}\,\upgamma\,{\text{K}} ,$$

(11)

with $\upgamma = {\text{m}}_{\text{c}} {\text{m}}_{\text{d}}$.

In general, FU will be proportional to ${\text{E}}\,{\text{V}}_{\text{D}}$ and therefore to K. A conceptual category reduces the factual information by an amount that scales as

$$\left\langle {{\text{V}}_{\text{D}} \,,\,{\text{V}}_{\text{C}} } \right\rangle \approx \left[ {\sum {\left( {1 ' {\text{s}}\,\,\,{\text{in}}\,\,{\text{vector}}\,\,\,{\text{V}}_{\text{C}} } \right)} } \right] = \left\langle {{\text{V}}_{\text{C}} \,,\,{\text{V}}_{\text{C}} } \right\rangle = \left( {{\text{m}}_{\text{c}} } \right)^{2}$$

There may be cases where the data encoded in ${\text{V}}_{\text{D}}$ do not match certain concepts, but in almost all cases the concepts that are encoded in vectors ${\text{V}}_{\text{C}}$ have their corresponding data stored in ${\text{V}}_{\text{D}}$. Data are not restricted only to facts but may also be data derived from scientific theories.

The correlation coefficient, ${\text{K}} \approx {{({\text{m}}_{\text{c}} )^{2} } \mathord{\left/ {\vphantom {{({\text{m}}_{\text{c}} )^{2} } {({\text{m}}_{\text{d}} \,{\text{m}}_{\text{c}} )}}} \right. \kern-0pt} {({\text{m}}_{\text{d}} \,{\text{m}}_{\text{c}} )}},$ and the measure of FU will thus be approximately equal to

$${\text{FU}}\, \approx {\text{K}} = \frac{{{\text{m}}_{\text{c}} }}{{{\text{m}}_{\text{d}} }}.$$

(12)

Dynamics of the feeling of understanding

We would like to study the time evolution of the interaction between neural vectors ${\text{V}}_{\text{D}}$ and ${\text{V}}_{\text{C}}$. The dynamics is emergent and very complex. We only hope to capture some of the essential features of this interaction by means of simple models. One of the major difficulties in modeling this interaction is the absence of empirical data in support of the neural events involved in this process. Consequently, we interpret our models as heuristic estimates of the growth, structure and interaction of data volumes and their associated concepts. We will describe two models, each one on their own scale of time. In the first, short-time scale, the process may last weeks to years and it is associated with the acquisition of information and the growth of conceptual understanding leading to rapid growth in FU. This is followed by an approximate steady state followed by a decay of FU. The second, long-time scale refers to processes occurring after FU decays to a level requiring new conceptual reorganizations of data that give rise to rapid upswings and downswings of FU. In both models, we evaluate the correlation coefficient K—a measure of FU in the correlation of patterns—as defined in Eq. (12). To measure the quantity of data and the diversity of concepts we use modules ${\text{m}}_{\text{d}}$ and ${\text{m}}_{\text{c}}$. These measures can also be interpreted as measures of ‘variety’, e.g. graphs in “Knowledge networks” section. Our models operate on discrete time and take the form of dynamical systems with the two modules interacting with each other,

$${\text{m}}_{\text{d}} \left( {{\text{t}} + 1} \right) = {\text{F}}\left[ {{\text{m}}_{\text{d}} \left( {\text{t}} \right)\,,\,{\text{m}}_{\text{c}} \left( {\text{t}} \right)\,} \right]$$

(13)

$${\text{m}}_{\text{c}} \left( {{\text{t}} + 1} \right) = {\text{G}}\left[ {{\text{m}}_{\text{d}} \left( {\text{t}} \right)\,,\,{\text{m}}_{\text{c}} \left( {\text{t}} \right)\,} \right]$$

(14)

The functions F[…] and G[…] determine the dynamical interactions between data and concepts. As we show in what follows, the shape of these functions are dependent on the time scale considered.

Vector dimensions

The physical dimensions of vectors ${\text{V}}_{\text{D}}$ and ${\text{V}}_{\text{C}}$ are necessarily identical by the way relevant data are matched to concepts and the correlation coefficient K is defined in this subspace. However, the amount of information coded by ${\text{V}}_{\text{D}}$ and ${\text{V}}_{\text{C}}$ ought to be extremely different. This is due to the fact, previously mentioned, that large amounts of data are condensed onto the conceptual vectors ${\text{V}}_{\text{C}}$. Consequently, we shall consider the existence, aside of real physical dimensions, of a maximum amount of information encoded in each type of neural vector, e.g. the maximum variety in the knowledge networks discussed in “Modeling knowledge” section. For vectors ${\text{V}}_{\text{D}}$ and ${\text{V}}_{\text{C}}$ these numbers correspond to the maximum values S and M of moduli ${\text{m}}_{\text{d}}$ and ${\text{m}}_{\text{c}}$, respectively. In the case of vectors ${\text{V}}_{\text{D}}$ we shall assume that S coincides with their physical dimension. In the case of ${\text{V}}_{\text{C}}$ we shall assume that M ≪ S. Hence, concept vectors ${\text{V}}_{\text{C}}$ are restricted to ${\text{m}}_{\text{c}} \le {\text{M}}$. We are going to assume that inside the time window in the evaluation of the model, M does not change, even if it is not a strict invariant and can suffer changes at different moments always satisfying M ≪ S. The plausibility of this inequality between dimensions can be illustrated by the relationship among semantic webs installed in an individual human brain and real data accessible to this individual. Imagine the relation between names and the variety of information covered by single names. In a geographical context, the word “country” refers to a large and variable number of countries defined by past and present political divisions of the planet. The word “France” labels a huge variety of information found in the cultural, social or political histories of that country. We illustrate some of these ideas by means of a minimalist example in “Appendix”.

Short-term dynamics

The model is based on the following assumptions:

A1::

At time t = 0, modulus ${\text{m}}_{\text{d}}$ has a non-vanishing value but ${\text{m}}_{\text{c}}$ can be zero.

A2::

The value of ${\text{m}}_{\text{c}}$ is bounded and increases monotonically with ${\text{m}}_{\text{d}}$.

A3::

The value of ${\text{m}}_{\text{d}}$ increases with time and in the short-time scale may reach a large but undefined finite value ${\text{m}}_{\text{d}} \gg {\text{m}}_{\text{c}}$ (for neurobiological reasons).

There is a correspondent mutual influence between data and conceptual vectors; only the rapid saturation of ${\text{m}}_{\text{c}}$ makes a qualitative difference. The following model captures the spirit of these assumptions (there may be many other models that satisfy the same assumptions),

$${\text{m}}_{\text{d}} \left( {{\text{t}} + 1} \right) = { \hbox{min} }\left[ {{\text{S}},\,\,{\text{m}}_{\text{d}} \left( {\text{t}} \right)\,\left[ {1\,\, + \,\,{\text{a}}\,{\text{m}}_{\text{c}} \left( {\text{t}} \right)} \right]} \right]$$

(15)

$${\text{m}}_{\text{c}} \left( {{\text{t}} + 1} \right) = { \hbox{min} }\left[ {{\text{M}},\,\,{\text{m}}_{\text{d}} \left( {\text{t}} \right)} \right]\,\,\,\,\frac{{{\text{m}}_{\text{d}} \left( {\text{t}} \right)^{\text{b}} }}{{{\text{R}} + {\text{m}}_{\text{d}} \left( {\text{t}} \right)^{\text{b}} }}$$

(16)

As explained before, the dimension M of conceptual vectors is significantly smaller than the dimension S of data vectors. The other parameters of the model are arbitrarily chosen and positive. The growth of ${\text{m}}_{\text{d}}$ depends on both, ${\text{m}}_{\text{d}}$ and ${\text{m}}_{\text{c}}$. On the contrary, ${\text{m}}_{\text{c}}$ explicitly depends only on ${\text{m}}_{\text{d}}$ but implicitly on itself after a certain delay. Its growth and saturation is modulated by a Hill curve. The parameter R is the constant that ensures saturation.

Figure 4 displays the logarithmic growth of ${\text{m}}_{\text{d}}$ and ${\text{m}}_{\text{c}}$ as functions of time for ${\text{S}} = 10^{8}$, ${\text{M}} = 10^{3}$, a = 0.002, b = 1, R = 1, ${\text{m}}_{\text{d}} \left( 0 \right) = 20$ and ${\text{m}}_{\text{c}} \left( 0 \right) = 0$.

Fig. 4

Logarithmic growth of $m_{d}$ and $m_{c}$

Figure 5 shows the evolution of the correlation coefficient in this model.

Fig. 5

Growth, stabilization and decay of the correlation coefficient K (or FU) as a function of time

Placing upper bounds on ${\text{m}}_{\text{d}}$ and ${\text{m}}_{\text{c}}$, and limiting their growth causes a precipitous decay of FU in Fig. 5. We must be aware that in many cases data keep on accumulating at a dizzying pace and after a collapse, FU recovers on a longer time scale.

Long-term dynamics

The “long-term dynamics” refer to a scale of time involving a succession of several cycles of conceptual reconfigurations. Here we pretend to capture the idea that cultural and scientific advances, by accumulating new concepts, reorganize and compact information in novel ways. The reorganization is a consequence of a crisis promoted by the addition of excess data and catalyzed by the conceptual structures already in place. We have discussed some examples of constructive crises giving rise to emergent, theoretical or practical insights. Although the reconstruction efforts and the compactification of data are in general collective efforts, in the final outcome, this progress is incorporated in the cognitive system of individuals. In our model we will assume that crises occur when the volume of data in ${\text{m}}_{\text{d}}$ reaches certain random threshold U that may exceed by far the bound M of the conceptual vector ${\text{V}}_{\text{C}}$. To address this issue let us add another assumption:

A4::

Each time ${\text{m}}_{\text{d}} \left( {\text{t}} \right)$ exceeds a threshold U, the conceptual structures included in ${\text{m}}_{\text{c}} \left( {\text{t}} \right)$ induce a reorganization of data in expanded classes, drastically reducing the size of ${\text{m}}_{\text{d}} \left( {\text{t}} \right).$

In the following model, the threshold is stochastic with lower bound M added to a random number RND (t) between $\left[ {0\,\,,\,\,\upalpha\,{\text{M}}} \right]$ where α is a relatively large adjustable coefficient, U = M + RND (t). We modify the previous model as follows,

$${\text{m}}_{\text{d}} \left( {{\text{t}} + 1} \right) = \left\{ \begin{array}{ll} { \hbox{min} }\left[ {{\text{S}},\,\,{\text{m}}_{\text{d}} \left( {\text{t}} \right)\,\left[ { 1\,\, + \,\,{\text{a}}\,{\text{m}}_{\text{c}} \left( {\text{t}} \right)} \right]} \right] & {\text{if}}\quad {\text{m}}_{\text{d}} \left( {\text{t}} \right) \le {\text{U}} \hfill \\ {\text{M}}& {\text{if}}\quad {\text{m}}_{\text{d}} \left( {\text{t}} \right) > {\text{U}}\, \hfill \\ \end{array} \right.$$

(17)

$${\text{m}}_{\text{c}} \left( {{\text{t}} + 1} \right) = { \hbox{min} }\left[ {{\text{M}},\,\,{\text{m}}_{\text{d}} \left( {\text{t}} \right)} \right]\,\,\,\,\frac{{{\text{m}}_{\text{d}} \left( {\text{t}} \right)^{\text{b}} }}{{{\text{R}} + {\text{m}}_{\text{d}} \left( {\text{t}} \right)^{\text{b}} }}$$

(18)

As formulated, the model assumes that ${\text{m}}_{\text{d}} \left( {\text{t}} \right)$ never reaches a value below M, implying that there are no conceptual categories without background information. Included in these categories are abstract mathematical concepts based on other formal structures that are able to transfer information from concepts to data.

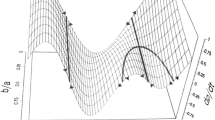
Figure 6 illustrates the temporal evolution of ${\text{m}}_{\text{d}}$ and ${\text{m}}_{\text{c}}$ using the same parameter values as the previous simulation with α = 100. Figure 7 displays the correlation coefficient K.

Fig. 6

Graphs of the logarithms of $m_{d}$ and $m_{c}$ as functions of time in model (17)–(18)

Fig. 7

Evolution of the correlation coefficient K. Please notice the rapid oscillations developing after the initial decay of K. The reason for these rapid cycles is that each new cycle reinitiates with an elevated conceptual volume near M

We mention that while ${\text{m}}_{\text{c}}$ remains bounded, $m_{d}$ oscillates wildly around the lower bound M. For parameter values other than the ones we have chosen ${\text{m}}_{\text{c}}$ may also oscillate close to M. This apparent reduction of information is not inconsistent with the sustained growth of information in the community. Individual cognition may undergo a substantial ‘decongestion’ every time a new synthesis collapses information into new classes.

For high values of U we observe oscillations with longer periods. Figure 8 depicts two examples: $\upalpha = 10^{4}$ and $\upalpha = 10^{6}$.

Fig. 8

The correlation K as a function of time t for $\alpha = 10^{4}$ and $\alpha = 10^{6}$

Discussion

Our civilization has built a magnificent body of knowledge during the last few millennia at an approximate steady rate only to see this rate accelerated to an incredible level over the last few decades as new scientific discoveries and technological innovations shape the landscape of information flow in our culture. More than ever individuals are challenged to keep up with this knowledge and to understand its role in the world we inhabit. In this work we have assumed that understanding is not necessarily connected to rational discourse or finding the appropriate information. We suggest it is more about correlating streaming data to categories of conceptual patterns. However, the correlation as described in Eq. (12) operates as an important measure that facilitates the acquisition of a rational image of the world. Consequently, it has influence on all forms of inquiry, e.g. the creation of novel and effective medical procedures, the design and implementation of useful and usable technologies, or the understanding of global threats to the fabric of our society.

The models proposed in “Dynamics of the feeling of understanding” section pretend to capture two categories of phenomena. First, the growth, stabilization and subsequent weakening of FU caused by the incessant growth of the amount of data that an individual experiences (Fig. 5). Second, the reconstruction and renewed growth of FU that follows a compression of factual information in synthetic categories induced by conceptual innovations (Figs. 6 and 7). These models are heuristic in nature and may take many other mathematical forms, but most of them will probably exhibit similar qualitative behaviors. One common characteristic of these models is the existence of close interactions between accessible empirical data and the conceptual interpretations induced by these data. It may also include the reconfiguration of information generated by novel conceptual creations. The correlation described in our dynamic model by the dot product between data and concepts vectors, Eq. (9), can be produced by transitory memories maintained by information coming from different neural fields: one related to concepts and the other—less structured and more transient-related to data. It is necessary to point out that these vectors can have noisy components (0’s in the binary representation) and bursts of action potentials (1’s in the binary representation). Bursts can be the result of synchronized responses of a neuron cluster in the assembly (Robinson et al. 1998). The activity of these neural fields may come from associative memories operating on longer scales of time, which recreate conceptual vectors.

One may wonder at the origin of the bound M of the conceptual vector. As we explained before, the human cognitive process has a natural tendency to extract common characteristics of different objects or events, group them into patterns and then represent these patterns as unitary concepts. The processing of patterns may be achieved through associative memories that project them onto neural vectors that encode an average representation (Cooper 1974, 1980). The propensity to conceptualize will depend on each individual history; consequently, the size of the bound M is a reflection of that history. An innate or trained conceptualizer will likely try to minimize the value of M without missing on the power of organization that these concepts provide on the surrounding world. From the literary viewpoint, Jorge Luis Borges famously explored in “Funes the Memorious” (Borges 1964) the fundamental importance of conceptualization in generating reenactment thoughts by examining accurately what would happen if these conceptualizations were absent.

We may also consider the interesting possibility of an expansion of the physical dimensions of vectors ${\text{V}}_{\text{D}}$ and ${\text{V}}_{\text{C}}$. In this case, the operator ${\text{E}} = {\text{z}}\,{\text{V}}_{\text{C}}^{\text{T}}$ in Eq. (10) would represent a structure sustained by short-term memories that on successive instants of time replenish the vector ${\text{V}}_{\text{C}}$ with new sources of information by integrating ${\text{V}}_{\text{D}}$, which is updated in the previous step with other concepts. This way of looking at knowledge expansion would generate at each step new correlation coefficients K. The final result would be the creation of a sequence of correlations K that forms a vector generalization of the scalar FU:

$$\overrightarrow {\text{FU}} = \left[ {{\text{K}}_{{{\text{T}}1}} \,,\,\,{\text{K}}_{{{\text{T}}2}} , \ldots ,\,\,{\text{K}}_{\text{Tn}} } \right]$$

Once generated, this vector may be processed by another neural module and the physical dimensions of vectors ${\text{V}}_{\text{D}}$ and ${\text{V}}_{\text{C}}$ will expand by incorporating new information in each cycle, after being computed by transitory memories. Consequently, in each cycle the size of processed information may attain effective bounds, nS for data vectors and nM for concept vectors.

Perhaps in the initial coding of data and conceptual vectors ${\text{V}}_{\text{D}}^{\text{S}}$ and ${\text{V}}_{\text{C}}^{\text{S}}$, their respective dimensions are quite dissimilar. Is there any neurobiological mechanism that couples data vectors ${\text{V}}_{\text{D}}^{\text{S}}$ (of very large dimensions) to concept vectors ${\text{V}}_{\text{C}}^{\text{S}}$ (of smaller dimensions)? A suggestion inspired by Kohonen (1988, p. 54) is to project ${\text{V}}_{\text{D}}^{\text{S}}$ onto one of the many subspaces of the same dimension as ${\text{V}}_{\text{C}}^{\text{S}}$, ${\text{V}}_{\text{D}}^{\text{S}}$ = ${\text{V}}_{\text{C}}^{\text{S}} + {\text{v}}$, where v is orthogonal to the subspace ${\text{V}}_{\text{C}}^{\text{S}}$ and then choose the subspace that gives the minimum $||{\text{v||}}$. This process can be naturally implemented with associative memories acting as projection operators. We may think of these memories as installed temporarily in working memories, not permanent ones.

One may also ask, why is ${\text{m}}_{\text{d}}$ in Eq. (17) set to M after it reaches the threshold? Our model assumes that crises occur when the volume of data in ${\text{m}}_{\text{d}}$ reaches a random threshold U that may far exceed the bound M of the conceptual vector ${\text{V}}_{\text{C}}^{\text{S}}$. To address this issue we have added assumption A4, that each time ${\text{m}}_{\text{d}} \left( {\text{t}} \right)$ exceeds threshold U, the conceptual structures included in ${\text{m}}_{\text{c}} \left( {\text{t}} \right)$ induce a reorganization of data in expanded classes, drastically reducing the subsequent size of ${\text{m}}_{\text{d}}$.

Darwin’s theory of evolution is a dramatic example of a conceptual reinterpretation of available evidence that is capable of reuniting in a logical structure the extraordinary diversity of life on this earth. Another recent and interesting example of information reconfiguration can be found in the theory of networks with the notions of “small-world” (Watts and Strogatz 1998) or “scale-free” interactions (Barabási and Alberts 1999). These new theories, originally applied to the Internet and the World Wide Web, have developed a set of measures (clustering indexes, web sizes, shortest pathways, controllability, etc.) that are progressively applied to a variety of other fields such as neural networks, biochemical cycles, ecological food webs, infectious diseases, semantic webs and social media. All these explorations have uncovered universal features of certain patterns of connectivity and topological behaviors that are common to all networks. These new contributions are revealing surprising conceptual unifications to many areas that previously were thought to be unrelated (Newman et al. 2006).

Human beings inhabit a physical world rigorously constrained by physical laws and another world populated by data streams that conscious brains process along several modes according to their cultural inheritance and their beliefs. Our central purpose has been to show the linkage between the information flow we experience and the neural processing that transforms available data into cognitively processed and subjectively evaluated information. These subjective evaluations are in large part responsible for our psychological well-being and have been studied by many people, from Aristotle to Saint Augustine, and from William James to Sigmund Freud, to name a few. In the last decades, research on the human brain has provided significant insights into the biochemistry, biophysics and behavioral responses from single neurons to clusters of hundred of thousands of them. New functional neuroimaging techniques are beginning to discriminate and select distinct neurocomputational models for specific cognitive activities. We believe that the neural modeling of FU, although still an exploration without definite paradigms, deserves our close attention.

Appendix

Let us illustrate how FU evolves with a minimalist example.

• 1. In the first step we have a large data vector ${\text{V}}_{\text{D}}^{\text{S}}$ = (…, A, …, B, …, C, …), where A, B and C are clusters of data associated with singular topics. This data vector induces a concept vector ${\text{V}}_{\text{C}}^{\text{S}}$ = (…, Ca, …, Cb, …, Cc, …) with clusters of concepts Ca, Cb and Cc. In the binary model, clusters A, B, C, Ca, Cb and Cc are mapped onto 1’s and the inter-cluster spaces are mapped onto 0’s, giving vectors ${\text{V}}_{\text{D}}$ and ${\text{V}}_{\text{C}}$. Let us then imagine a miniature 12-dimensional space where ${\text{V}}_{\text{D}}$ = (001000100100) and ${\text{V}}_{\text{C}}$ = (001000100100). In this ideal situation the initial correlation coefficient K is equal to 1.

• 2. The subsequent accumulation of data increases the number of 1’s in ${\text{V}}_{\text{D}}$ = (011101100111) but leaves ${\text{V}}_{\text{C}}$ temporarily unchanged. This activity is similar to the process of augmenting the number of nodes in the knowledge graphs illustrated in “Knowledge networks” section and Fig. 2. Therefore, the value of K decreases (K < 1). The dynamics of this scenario for high-dimensional vectors are modeled by Eqs. (15)–(16) and their behavior are depicted in Figs. 4 and 5.

• 3. To simplify to the maximum the complex interactions between data and concepts, let us imagine that concepts are enriched and data are reconstituted. Then we may have, ${\text{V}}_{\text{D}}$ = (001101100110) and ${\text{V}}_{\text{C}}$ = (001101100110). In this stage, the correlation K will reach again a maximum value of 1. After this process, we follow a new path to the first step (1) with reconfigured vectors. The evolution of high-dimensional vectors follow Eqs. (17)–(18) and their behavior are sketched in Figs. 6 and 7.

In real situations the sparseness of data and concept vectors create new filling niches of 1’s while maintaining the clusters distant from each other.