Abstract
We systematically investigate the response of neurons to oscillatory currents and synaptic-like inputs and we extend our investigation to non-structured synaptic-like spiking inputs with more realistic distributions of presynaptic spike times. We use two types of chirp-like inputs consisting of (i) a sequence of cycles with discretely increasing frequencies over time, and (ii) a sequence having the same cycles arranged in an arbitrary order. We develop and use a number of frequency-dependent voltage response metrics to capture the different aspects of the voltage response, including the standard impedance (Z) and the peak-to-trough amplitude envelope (\(V_{\text {ENV}}\)) profiles. We show that Z-resonant cells (cells that exhibit subthreshold resonance in response to sinusoidal inputs) also show \( V_{\text {ENV}} \)-resonance in response to sinusoidal inputs, but generally do not (or do it very mildly) in response to square-wave and synaptic-like inputs. In the latter cases the resonant response using Z is not predictive of the preferred frequencies at which the neurons spike when the input amplitude is increased above subthreshold levels. We also show that responses to conductance-based synaptic-like inputs are attenuated as compared to the response to current-based synaptic-like inputs, thus providing an explanation to previous experimental results. These response patterns were strongly dependent on the intrinsic properties of the participating neurons, in particular whether the unperturbed Z-resonant cells had a stable node or a focus. In addition, we show that variability emerges in response to chirp-like inputs with arbitrarily ordered patterns where all signals (trials) in a given protocol have the same frequency content and the only source of uncertainty is the subset of all possible permutations of cycles chosen for a given protocol. This variability is the result of the multiple different ways in which the autonomous transient dynamics is activated across cycles in each signal (different cycle orderings) and across trials. We extend our results to include high-rate Poisson distributed current- and conductance-based synaptic inputs and compare them with similar results using additive Gaussian white noise. We show that the responses to both Poisson-distributed synaptic inputs are attenuated with respect to the responses to Gaussian white noise. For cells that exhibit oscillatory responses to Gaussian white noise (band-pass filters), the response to conductance-based synaptic inputs are low-pass filters, while the response to current-based synaptic inputs may remain band-pass filters, consistent with experimental findings. Our results shed light on the mechanisms of communication of oscillatory activity among neurons in a network via subthreshold oscillations and resonance and the generation of network resonance.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Subthreshold (membrane potential) oscillations (STOs) in a variety of frequency ranges have been observed in many neuron types (Alonso and Llinás 1989; Klink and Alonso 1993; Dickson et al. 2000a; White et al. 1995; Dickson et al. 2000b; Lampl and Yarom 1993, 1997; Gutfreund et al. 1995; Llinás and Yarom 1986; Llinás et al. 1991; Wang 2010; Yoshida and Alonso 2007; Yoshida et al. 2011; Morin et al. 2010; Schmitz et al. 1998; Reboreda et al. 2003; Wu et al. 2001; Amir et al. 1999; Fernandez and White 2008; Chorev et al. 2007; Zhuchkova et al. 2014; Remme et al. 2014; Boehmer et al. 2000; Pedroarena et al. 1999; Bourdeau et al. 2007; Desmaisons et al. 1999; Balu et al. 2004; Giocomo et al. 2007; Stiefel et al. 2010; Baroni et al. 2014; Khosrovani et al. 2007; Bilkey and Heinemann 1999; Manis et al. 1999; Chapman and Lacaille 1999; Bracci et al. 2003; Golomb et al. 2007; Surmeier et al. 2005; Wilson and Callaway 2000; Einstein et al. 2017; Amir et al. 2002). In brain areas such as the entorhinal cortex, the hippocampus and the olfactory bulb, the frequency of the STOs is correlated with the frequency of the networks of which they are part (Alonso and Llinás 1989; Klink and Alonso 1993; Giocomo et al. 2007; Cobb et al. 1995; Colgin 2013; Chapman and Lacaille 1999; Desmaisons et al. 1999; Balu et al. 2004; Kay et al. 2008; Li and Cleland 2017), thus suggesting STOs play a role in the generation of network rhythms (Desmaisons et al. 1999; Brea et al. 2009; Wang 2010), the communication of information across neurons in a network via timing mechanisms (Izhikevich 2002; Stiefel et al. 2010; Dwyer et al. 2012; Lampl and Yarom 1993), cross-frequency coupling in neurons where STOs are interspersed with spikes (mixed-mode oscillations; MMOs) (Bragin et al. 1995; Chrobak and Buzsáki 1998; Colgin et al. 2009; Gireesh and Plenz 2008; Axmacher et al. 2006; Jensen and Colgin 2007; Gloveli et al. 2005; Belluscio et al. 2012), and the encoding of information (Hinzer and Longtin 1996; Burgess et al. 2011) and sensory processing (Einstein et al. 2017). STOs can be generated by cellular intrinsic or network mechanisms. In the first case, STOs result from the interplay of ionic currents that provide positive and slower negative effects (e.g., (Dickson et al. 2000a, b; Rotstein et al. 2006; Rotstein 2017)). (Examples of the former are the persistent sodium and calcium activation and examples of the latter are h-type hyperpolarization-activated mixed sodium-potassium, M-type slow potassium and calcium inactivation.) In the second case, STOs are generated in networks, but the individual cells cannot robustly oscillate when isolated (e.g., (Manor et al. 1997; Chorev et al. 2007; Loewenstein et al. 2001)).
The communication of oscillatory information among neurons in a network and across brain areas requires the generation of spiking patterns that are correlated with the underlying STOs (e.g., MMOs where spikes occur at the peak of the STO or at a consistent phase referred to this peak). It also requires the system to be able to respond to external inputs in such a way as to preserve the oscillatory information. Studies on the latter are typically carried out by using sinusoidal inputs. Subthreshold (membrane potential) resonance (MPR) refers to the ability of a system to exhibit a peak in their voltage amplitude response to oscillatory inputs currents at a preferred (resonant) frequency (Hutcheon and Yarom 2000; Richardson et al. 2003; Rotstein and Nadim 2014; Rotstein 2015) (in voltage-clamp, the input is voltage and the output is current). MPR has been investigated in many neuron types both experimentally and theoretically (Pena et al. 2018; Hutcheon and Yarom 2000; Richardson et al. 2003; Lampl and Yarom 1997; Llinás and Yarom 1986; Gutfreund et al. 1995; Erchova et al. 2004; Schreiber et al. 2004; Hutcheon et al. 1996a; Gastrein et al. 2011; Hu et al. 2002, 2009; Narayanan and Johnston 2007, 2008; Marcelin et al. 2009; D’Angelo et al. 2009; Pike et al. 2000; Tseng and Nadim 2010; Tohidi and Nadim 2009; Solinas et al. 2007; Wu et al. 2001; Muresan and Savin 2007; Heys et al. 2010, 2012; Zemankovics et al. 2010; Nolan et al. 2007; Engel et al. 2008; Boehlen et al. 2010, 2013; Rathour and Narayanan 2012, 2014; Fox et al. 2017; Chen et al. 2016; Beatty et al. 2015; Song et al. 2016; Art et al. 1986; Remme et al. 2014; Higgs and Spain 2009; Yang et al. 2009; Mikiel-Hunter et al. 2016; Rau et al. 2015; Sciamanna and Wilson 2011; D’angelo et al. 2001; Lau and Zochowski 2011; van Brederode and Berger 2008; Rotstein and Nadim 2014; Rotstein 2014, 2015, 2017; Szucs et al. 2017) and it has been shown to have functional implications for the generation of network oscillations (Chen et al. 2016; Bel and Rotstein 2019).
The choice of sinusoidal inputs is based on the fact that for linear systems they can be used to reconstruct the response to arbitrary time-dependent inputs, and relatively good approximations can be obtained for mildly nonlinear systems. However, although neurons may be subject to oscillatory modulated inputs, the communication between neurons in a network occurs via synaptic connections whose waveforms are significantly different from pure sinusoidal functions. Synaptic inputs such as these associated with AMPA or GABA\(_A\) synaptic currents rise very fast (almost instantaneously) and then decay exponentially on a slower time scale. In contrast to sinusoidal inputs, the rise and decay of the periodic synaptic inputs occur over a small portion of the input periods for the smaller input frequencies. The gradual variation of the sinusoidal inputs causes the voltage response to reach the stationary regime after a very small number of cycles, while the abrupt changes in the synaptic inputs over a small time interval sequentially activate the autonomous transient dynamics at every cycle, and therefore is expected to produce different response patterns than these for sinusoidal inputs (Pena and Rotstein 2021).
The main goal of this paper is to understand whether and under what conditions the presence of MPR in a neuron is predictive of the preferred frequency at which the neuron will spike in response to periodic presynaptic inputs when the input amplitude is increased above subthreshold levels.
From a dynamical systems perspective, single-cell sustained STOs can be in the limit cycle regime (robust to noise, driven by DC inputs) or in the fluctuation-driven regime (vanishing or decaying to an equilibrium in the absence of noise). Noisy STOs in the limit cycle regime reflect the stationary dynamics of the system in the absence of noise. In contrast, fluctuation-driven STOs reflect the autonomous transient dynamics (the transient dynamics of the underlying unperturbed system) (Pena and Rotstein 2021). The effects of the autonomous transient dynamics are captured by the system’s response to abrupt changes in constant inputs (Pena and Rotstein 2021). There, the values of the voltage and other variables at the end of a constant input regime become the initial conditions for the new one. By repeated activation of the autonomous transient dynamics, piecewise constant inputs with short-duration pieces and arbitrarily distributed amplitudes (not necessarily randomly distributed) are able to produce oscillatory responses (Pena and Rotstein 2021). Noise-driven oscillations are a limiting case of this mechanism where the input’s constant pieces have randomly distributed amplitudes and their durations approach zero. If the amplitudes are normally distributed, these piecewise constant inputs provide an approximation to Gaussian white noise (Allen et al. 1998). Roughly speaking, each “kick” to the system by the noisy input operates effectively as an abrupt change of initial conditions to which the system responds by activating the transient time scales, and the voltage and other state variables evolve according to the vector field away from equilibrium (or stationary state). For example, noise-driven STOs (White et al. 1998; Rotstein et al. 2006; Chow and White 1996; Pena and Rotstein 2021) can be generated when damped oscillations are amplified by noise, and this may extend to situations where the noiseless system exhibits overdamped oscillations (overshoots) (Pena and Rotstein 2021).
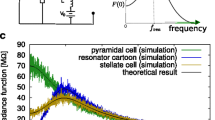
Along these lines of the previous discussion, a series of dynamic clamp experiments (Fernandez and White 2008) using artificially generated synaptic conductances and currents driven by high-rate presynaptic Poisson spike trains showed that medial entorhinal cortex layer II stellate cells (SCs) are able to generate STOs in response to current-based synapses, but not in response to conductance-based synaptic currents. SCs are a prototypical example of an intrinsic fluctuation-driven STO neuron (Dickson et al. 2000a, b; Dorval and White 2005; Rotstein et al. 2006) and resonator (Schreiber et al. 2004). In the response to current-based synaptic inputs, the STOs have similar frequencies and amplitudes as the spontaneous STOs (Dickson et al. 2000a, b) and the resonant responses to sinusoidal inputs (Schreiber et al. 2004). In response to conductance-based synaptic currents, STOs may still be present, but highly attenuated as compared to current-based synaptic inputs. Similar results were found in Kispersky et al. (2012) for hippocampal CA1 OLM (oriens lacunosum-moleculare) cells and in Farries and Wilson (2012a, 2012b) for phase-response curves in subthalamic neurons.
This raises a seeming contradiction between the ability of the impedance (Z-) profile (curve of the voltage V-response normalized by the amplitude of the oscillatory inputs as a function of the input frequency) to predict the existence of STOs for arbitrary time-dependent inputs, in particular Gaussian white noise, and the absence of STOs for conductance-based synaptic inputs in response to Poisson-distributed spike trains whose effect on the target cells have been approximated by Gaussian white noise (Brunel 2000; Amit and Tsodyks 1991; Tuckwell 1989, 1988; Amit and Brunel 1997; Brunel et al. 2001). This can be partially explained by the fact that synaptic currents “add linearity” to the system, but fluctuation-driven STOs can be generated in linear systems and therefore one could expect only changes in amplitude and frequency. Another possible explanation is that while the Z-profile is independent of the input waveform, the voltage response power spectral density (PSD) is not and depends on the current input waveform. The expectation that the PSD be similar for current-based Gaussian white noise and Poisson-driven current-/conductance-based synaptic inputs would assume similarity between the different input types.
In this paper, we systematically address these issues in a broader context. Our results shed light on the mechanisms of communication of oscillatory activity among neurons in a network via subthreshold oscillations and resonance and the generation of suprathreshold and network resonance.
2 Methods
2.1 Models
In this paper, we use relatively simple biophysically plausible models describing the subthreshold dynamics of individual neurons subject to both additive and multiplicative inputs.
2.1.1 Linear model: additive input current
For the individual neurons we use the following linearized biophysical (conductance-based) model
where v (mV) is the membrane potential relative to the voltage coordinate of the fixed-point (equilibrium potential) of the original model, w (mV) is the recovery (gating) variable relative to the gating variable coordinate of the fixed-point of the original model normalized by the derivative of the corresponding activation curve, C ( \(\mu \)F/cm\(^2\)) is the specific membrane capacitance, \( g_L \) (mS/cm\(^2\)) is the linearized leak conductance, \( g_1 \) (mS/cm\(^2\)) is the linearized ionic conductance, \( \tau _1 \) (ms) is the linearized gating variable time constant and \( I_{in}(t) \) (\(\mu \)A/cm\(^2\)) is the time-dependent input current. In this paper we consider resonant gating variables (\( g_1 > 0 \); providing a negative feedback effect). We refer the reader to Richardson et al. (2003); Rotstein and Nadim (2014) for details of the description of the linearization process for conductance-based models.
2.1.2 Conductance-based synaptic input model: multiplicative input
To account for the effects of conductance-based synaptic inputs we extend the model (1)–(2) to include a synaptic current
where
and \( G_{\text {syn}} \) (mS/cm\(^2\)) is the maximal synaptic conductance, \( E_{\text {syn}} \) (mV) is the synaptic reversal potential (\( E_{\text {ex}} \) for excitatory inputs and \( E_{\text {in}} \) for inhibitory inputs) and \( S_{in}(t) \) is the time-dependent synaptic input.
2.1.3 \(I_\mathrm{Nap}\) + \(I_\mathrm{h}\) conductance-based model
To test our ideas in a more realistic model we will use the following conductance-based model combining a fast amplifying gating variable associated to the persistent sodium current \( I_{Nap} \) and a slower resonant gating variable associated to the hyperpolarization-activated mixed cation (h-) current \( I_h \). The model equations for the subthreshold dynamics read
where
and
This model describes the onset of spikes, but not the spiking dynamics (Rotstein et al. 2006). Spikes are added by including a voltage threshold (indicating the occurrence of a spike after its onset) and reset values \( V_{rst} \) and \( r_{rst} \) for the participating variables.
Unless stated otherwise, we use the following parameter values: \(v_{p, 1 / 2}=-38\) mV, \(v_{p,slp}= 6.5\) mV, \(v_{r, 1 / 2}=-79.2\) mV, \(v_{r,slp}=9.78\) mV, \(C=1\) \(\mu \)F/\(\hbox {cm}^2\), \(E_\mathrm{L}=-65\) mV, \(E_\mathrm{Na}=55\) mV, \(E_\mathrm{h}=-20\) mV, \(g_\mathrm{L}=0.5\) mS/\(\hbox {cm}^2\), \(g_p=0.5\) mS/\(\hbox {cm}^2\), \(g_\mathrm{h}=1.5\) mS/\(\hbox {cm}^2\), \(I_\mathrm{app}=-2.5\) \(\mu \)A/\(\hbox {cm}^2\), and \(\tau _r=80\) ms.
2.2 Input functions: periodic inputs and realistic waveforms
The input functions \( I_{\text {in}}(t)\) and \( S_{\text {in}} \) we use in this paper have the general form
2.2.1 Chirp-like input functions: increasingly ordered frequencies
We will use the three chirp-like input functions F(t) shown in Fig. 1-a. The sinusoidal chirp-like function (Fig. 1-a1) consists of a sequence of input cycles with discretely increasing frequencies over time (Fig. 1-a4). We use integer frequencies in the range \( 1-100 \) Hz. These chirp-like functions are a modification of the standard chirp function (Hutcheon et al. 1996a) where the frequency of the sinusoidal input increases (or decreases) continuously with time (Hutcheon et al. 1996a). Sinusoidal inputs of a single frequency and sinusoidal chirps with monotonically and continuously increasing (or decreasing) frequencies with time have been widely used to investigate the resonant properties of neurons both in vitro and in vivo (Hutcheon et al. 1996a; Stark et al. 2013; Tseng and Nadim 2010).
Chirp-like input functions. (a1) Sinusoidal chirp-like input. (a2) Square-wave chirp-like input. (a3) Synaptic-like chirp input. (b) Same input functions as in (a) but with arbitrarily ordered frequencies. (a4) Increasingly ordered frequencies used to construct (a). (b4) Arbitrarily ordered frequencies used to construct (b). All panels show frequencies in the range 1–100 Hz
The square-wave (Fig. 1-a2) and synaptic-like (Fig. 1-a3) chirp-like functions are constructed in the same manner as the sinusoidal one by substituting the sinusoidal functions by square waves (duty cycle = 0.5) and exponentially decreasing functions with a characteristic decay time \( \tau _\mathrm{Dec} \), respectively. We refer to them as sinusoidal, square-wave, and synaptic-like inputs or chirps, respectively (and we drop the “chirp-like”).
The discretely changing chirp-like functions we use here are a compromise between tractability and the ability to incorporate multiple frequencies in the same input signal. They combine the notion of input frequency with the notion of transition between different frequencies in the same signal. Also, note that the square-wave inputs are an intermediate between sinusoidal and synaptic-like inputs in the sense that square-wave inputs have abrupt transitions as synaptic-like inputs but are closer in shape to the sinusoidal input that is changed gradually.
2.2.2 Chirp-like input functions: arbitrarily ordered frequencies
To examine the variability of the cell’s response to the chirp signals described above and to capture the fact that information does not necessarily arrive in a regularly ordered manner, we will use modified versions of these chirp inputs where the cycles are rearranged in an arbitrary order (Fig. 1-b). The regularly (Fig. 1-a4) and arbitrarily (Fig. 1-b4) ordered input signals have exactly the same cycles (one cycle for each frequency value within the considered range) and therefore the same frequency content.
2.2.3 Poisson distributed spikes and white Gaussian noise
To test the oscillatory responses to more realistic inputs we use spike-trains with distributed spikes following a homogeneous Poisson process with rate \(\nu \). Each input spike evokes a synaptic-like input function as described above. In addition, we use an additive Gaussian noise current \( I_{\text {noise}} = \sqrt{2 D} \eta (t) \) where \( \eta (t) \) is a Gaussian white noise input with zero mean and unit variance (\(I_{\text {in}}(t) \) has zero mean and variance 2D). Unless stated otherwise, \(\nu =1000\) Hz and \(D=1\) (additional information is provided in the figure captions).
2.3 Output metrics
2.3.1 Impedance (amplitude) profile
The impedance (amplitude) profile is defined as the magnitude of the ratio of the output (voltage) and input (current) Fourier transforms
where \({\mathfrak {F}}\{x(t)\}=\int _0^T dt e^{-2\pi i f t} x(t)\). In practice, we use the Fast Fourier Transform algorithm (FFT) to compute \({\mathfrak {F}}\{x(t)\}\). Note that Z(f) is typically used as the complex impedance, a quantity that has amplitude and phase. For simplicity, here we used the notation Z(f) for the impedance amplitude.
2.3.2 Voltage and impedance (amplitude) envelope profiles
The upper and lower envelope profiles \( V_{ENV}^{+/-}\) are curves joining the peaks and troughs of the steady state voltage response as a function of the input frequency f. The envelope impedance profile is defined as Rotstein (2014, 2015)
where \(A_\mathrm{in}\) is the input amplitude. For linear systems, \( Z_\mathrm{ENV}(f) \) coincides with Z(f) .
2.3.3 Voltage power spectral density
In the frequency-domain, we compute the power spectral density (PSD) of the voltage as the absolute value of its Fourier transform \({\mathfrak {F}}\{v(t)\}\). We will refer to this measure as PSD or \(V_\mathrm{PSD}\).
2.3.4 Firing rate (suprathreshold) response
We compute the firing rate response of a neuron by counting the number of spikes fired within an interval of length T and normalizing by T
where the neural function x is given by
and \( t_i \) are the spike times within the considered interval.
2.4 Numerical simulations
We used the modified Euler method (Runge-Kutta, order 2) (Burden and Faires 1980) with step size \(\Delta t=0.01\) ms. All neural models and metrics, including phase-plane analysis, were implemented by self-developed MATLAB routines (The Mathworks, Natick, MA) and are available in https://github.com/BioDatanamics-Lab/impedance_input_dependent.
3 Results
3.1 Transient and steady-state neuronal responses to abrupt versus gradual input changes
The properties of the transient responses of dynamical systems to external inputs depend on the intrinsic properties of the target cells, the initial conditions of the participating variables and the nature of the attractors (assumed to exist). The complexity of the autonomous transient dynamics, defined as the transient response to abrupt changes in constant inputs, increases with the model complexity. For example, for the simplest, passive neuron (a one-dimensional system), the voltage V evolves monotonically towards the new equilibrium value determined by a constant input.
Two-dimensional neurons having a restorative current with slow dynamics (e.g., \( I_h \), \( I_M \), \( I_{CaT} \) inactivation) may display overshoots and damped oscillations (Fig. 2), which can be amplified by fast regenerative currents (e.g., \( I_{Nap} \), \( I_{Kir} \), \(I_{CaT} \) activation), and are more pronounced the further away the initial conditions are from the equilibrium (not shown) and the more abrupt is the input change. Here we review the dependence of the transient response properties of relatively simple models with the properties of the input and discuss some of the implications for the steady-state responses of the same systems to periodic inputs.
Transient response to input decreases as the input changes from abrupt to gradual. Input current increases from 0 to 1 (black solid line) but the strength of the transient decreases in every column. Top: Example with overshoot, parameters are \(g_\mathrm{L}=0.2\) and \(g_\mathrm{1}=0.4\). Bottom: Example with subthreshold oscillations, parameters are \(g_\mathrm{L}=0.00025\) and \(g_\mathrm{1}=0.25\). The insets show a zoom-in on the transients
3.1.1 The strength of the transient responses to input changes decreases as the input changes transition from abrupt to gradual
An abrupt change in the input current (e.g., step DC input) can be interpreted as causing a sudden translation of the equilibria (for the voltage and other state variables) in the phase-space diagram from its baseline location (e.g., Fig. 3-a, \( I = 0 \), intersection between the V- and w-nullclines, solid-red and green, respectively) to the to a new location determined by the DC value (e.g., Fig. 3-a, \( I = 1 \), intersection between the displaced V- and w-nullclines, dashed-red and green, respectively). The values of these state variables prior to the transition become the initial conditions with respect to this new equilibrium. Therefore, the voltage responses to abrupt changes in the input currents are expected to exhibit overshoots and damped oscillations ( Fig. 3, insets, and Fig. 2, left ), which are more pronounced the stronger the input (not shown). As the change in input current becomes more gradual, the transient effects become more attenuated (Fig. 2, middle) and eventually the voltage response becomes almost monotonic (Fig. 2, right).
Nonlinear transient response amplifications and attenuations in current- vs. conductance-based inputs. Phase-plane diagrams for \( I = 1 \). The solid-red curve represents the V-nullcline (\(dv/dt=0\)) for \( I = 0\), the dashed-red curve represents the V-nullcline (\(dv/dt=0\)) for \( I = 1\), the solid-green curve represents the w-nullcline (\(dw/dt=0\)) for \( I = 0\), the solid-blue curve represents the trajectory, and the dashed-gray lines are marking the point where the trajectory initially starts at (0, 0) (the fixed-point for \( I = 0 \)), converging to the fixed-point for \( I = 1 \). The insets show the V traces. The 2D linear system exhibits an overshoot in response to step-constant inputs and resonance in response to oscillatory inputs (Richardson et al. 2003; Rotstein and Nadim 2014; Rotstein 2014). a. Linear (LIN) model described by eqs. (1)-(2). b. Current-based piecewise linear (PWL) model described by \(C \frac{dv}{dt} = -g_L\, F_{PWL}(v) - g_1 w - I(t)\) and \(\tau _1 \frac{dw}{dt} = v - w\) where \(F_{PWL}(v) = v\) for \(v < v_c\) and \(F_{PWL}(v) = v_c + g_c / g_L (v-v_c)\) for \(v > v_c\). c. Conductance-based piecewise linear (PWL) model described by \(C \frac{dv}{dt} = -g_L\, F_{PWL}(v) - g_1 w - G_{syn} S(t) (v - E_{syn})\) and \(\tau _1 \frac{dw}{dt} = v - w\) where \(F_{PWL}(v) = v\) for \(v < v_c\) and \(F_{PWL}(v) = v_c + g_c / g_L (v-v_c)\) for \(v > v_c\) (with S substituted by I). We used the following parameter values: \( C = 1\), \( g_L = 0.25 \), \( g_1 = 0.25 \), \( \tau _1 = 100 \) (same as in Fig. 4), \( v_c = 1 \) and \( g_c = 0.1\)
This transition in the strength of the transient responses is expected since a monotonic input change can be approximated by a sequence of smaller step input changes of increasing (constant) magnitude, each one producing a transient response, which becomes smaller the larger the number of steps (the smaller the step size) since the initial conditions for each step in the partition are very close to the corresponding (new) steady state. Therefore, for input transitions between the same constant values, but with different slopes, the amplitude of the transient response becomes more attenuated the more gradual the transition since a larger partition is required in order to keep the step size constant.
3.1.2 Nonlinear amplification of the transient and steady-state response to constant inputs
Certain types of nonlinearities have been shown to amplify the response of neuronal systems (and dynamical systems in general) to the same input. This is reflected in both the responses to constant and oscillatory inputs. For illustrative purposes, in Figs. 3-b and -c we use a piecewise linear (PWL) model obtained from the linear model (1)-(2) by making the v-nullcline a continuous PWL function. It was shown in Rotstein (2014) that this type of model displays nonlinear amplification of the voltage response to sinusoidal inputs and captures similar phenomena observed in nonlinear models, in particular these having parabolic-like V-nullclines describing the subthreshold voltage dynamics (Rotstein 2015).
Figures 3-a and -b show the superimposed phase-plane diagrams for the PWL model (b) and the linear (LIN) model (a) from which it originates for a constant input amplitude \( I = 0 \) (solid-red, baseline) and \( I= 1\) (dashed-red). The w-nullcline is unaffected by changes in I. The trajectory (blue), initially at the fixed-point for \( I= 0 \), converges towards the fixed-point for \( I= 1 \). For low enough values of I (lower than in Fig. 3-a and -b) the trajectory remains within the linear region (the trajectory does not reach the V-nullcline’s “breaking point” value of V) and therefore the dynamics are not affected by the nonlinearity. In both cases (panels a and b), the response exhibits an overshoot. The peak occurs when the trajectory is able to cross the V-nullcline. Because the V-nullcline’s “right piece” has a smaller slope than the “left piece”, the trajectory is able to reach larger values of V before turning around. This amplification is particularly stronger for the transient dynamics (initial upstroke) than for the steady-state response. Nonlinear response amplifications in this type of system are dependent on the time scale separation between the participating variables. For smaller values of \( \tau _1 \) this nonlinear amplification is reduced and although the system is nonlinear, it behaves quasi-linearly (Rotstein 2014, 2015).
3.1.3 Attenuation of the transient and steady-state response of conductance-based versus current-based (constant) synaptic inputs
From the phase-plane diagram in Fig. 3-c we see that increasing values of I (here we have a conductance and a driving-force in the model) reduces the nonlinearity of the V-nullcline (dashed-red) and increases (in absolute value) its slope. Both phenomena oppose the response amplification (blue) and the overshoot becomes much less prominent. The triangular region (bounded by the V-axis, the displaced V-nullcline (dashed-red) and the w-nullcline (green)) is reduced in size as compared to the current-based inputs (panel b) and therefore the response is reduced in amplitude. Moreover, because the displaced V-nullcline in panel c is more vertical than the baseline V-nullcline, the size of the overshoot in response to constant inputs is reduced and, in this sense, the responses become quasi-1D. As a consequence, the initial portion of the transient responses to abrupt changes in input is reduced in size and the oscillatory response to PWC inputs is also attenuated and the resonant peak disappears (Pena and Rotstein 2021).
3.1.4 Implications for the neuronal responses to structured (periodic) and non-structured inputs: hypotheses and questions
An immediate consequence of these observations is the prediction that a system’s responses to square-wave and sinusoidal inputs of the same frequency (and duty cycle) will be qualitatively different, and these differences will depend on the stability properties of the unperturbed cells (e.g., stable nodes versus foci, overshoots versus damped oscillations). The steady-state response to periodic inputs can be interpreted as a sequence of transient responses to input changes. These transient effects (autonomous transient dynamics) are expected to be prominent in the steady-state responses to square-wave inputs, but not in the steady-state responses to sinusoidal inputs. Sinusoidal and square-wave inputs are representative of gradually and abruptly changing signals, respectively, and are amenable for comparison. The result of these comparisons sheds light on more realistic signals such as synaptic-like ones. To test these ideas we will use the chirp-like input currents shown in Fig. 1 (see Section 2.2.1).
A second immediate consequence of the observations referred to above is the finding that a system’s amplitude response to piecewise constant (PWC) inputs having the same set of constant pieces arranged in different order is variable with respect to each other (Pena and Rotstein 2021). At the population level (same cell receiving a number of input signals consisting of permutations of the order of the same constant pieces of the same baseline signal), the properties of this variability crucially depend on the cell’s autonomous transient dynamics. These reflect the multiple ways in which the cell responds to a given constant piece input from the values determined by the responses to the previous piece in the inputs signal, which change across trials. Interestingly, this phenomenon does not require the constant piece amplitudes to be randomly distributed, but they can be generated by a deterministic rule consisting of a baseline input pattern (e.g., increasing order of amplitudes) and a subset of all possible permutations of the constant piece amplitude order. We analyzed this in detail in the companion paper (Pena and Rotstein 2021).
The issues discussed above raise a number of questions. First, whether and under what conditions the frequency-preference properties of a system’s response to sinusoidal inputs are predictive of the response properties of the same system to other types of inputs. While the Fourier theorem guarantees that the latter can be reconstructed from the former if properly normalized, it does not guarantee that the two will have the same waveform and the same frequency-dependence properties using metrics that depend on these waveforms since the normalization factors (related to the input) may have different frequency dependencies. Second, whether and under what conditions the differences between the preferred frequency-band response of sinusoidal and non-sinusoidal inputs, if they exist, persist in the spiking regime. Given that the communication between neurons occurs via synaptic interactions, the failure of the responses to synaptic-like inputs to replicate the frequency-preference properties in response to sinusoidal inputs would indicate that the latter, although useful for the reconstruction of signals, does not have direct implications for the spiking dynamics. Third, whether and under what conditions the frequency-preference properties of a system’s response to structured (deterministic) inputs are predictive of the responses of the same system to unstructured (noisy) inputs. Fourth, whether and under what conditions the oscillatory (intrinsic) and resonant properties of cells result from the very brief initial transients of their autonomous dynamics. Fifth, how does the variability of a cell’s response to different input trials is processed by the feedback effects operating at the cell level. We address these issues in the next sections.
3.2 Subthreshold resonance in response to sinusoidal inputs is captured by the impedance and voltage envelope profiles
3.2.1 Subthreshold resonance
A cell is said to exhibit subthreshold resonance if its voltage amplitude response to subthreshold oscillatory inputs peaks at a preferred (resonant) frequency (Figs. 4-a and 5-a). These responses are typically measured by computing the impedance Z, defined as the quotient of the power spectra of the output and input (see Methods). In current clamp, the input is current and the output is voltage. In controlled experiments and simulations, the unperturbed cells are in equilibrium in the absence of the oscillatory inputs. In response to constant inputs, resonant cells may be non-oscillators, typically exhibiting an overshoot, or exhibit oscillatory behavior (e.g., damped oscillations) (e.g., see Figs. 4-b1 and 5-b1, respectively, where the behavior can be observed in the first cycle). Therefore, resonance is not uncovering an oscillatory property of the unperturbed cell, but rather it is a property of the interaction between the cell and the oscillatory inputs (Rotstein 2014). Hence, it is not clear whether and under what conditions subthreshold resonance persists in the presence of other types of periodic inputs with non-sinusoidal waveforms.
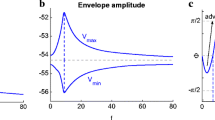
Neuronal response upon application of three different inputs (linear model, overshoot). a Sinusoidal chirp. b Square-wave chirp. c Synaptic-like chirp. (a1,b1, and c1) voltage traces. (a2, b2, and c2) Voltage-response envelopes in the frequency-domain. (a3, b3, and c3) Z(f) (frequency-content) and \(Z_{ENV}(f)\) (envelope) impedance. We used the following parameter values: \(C=1\), \(g_\mathrm{L}=0.25\), \(g_1=0.25\), \(\tau _1=100\) ms, and \(A_\mathrm{in}=1\) (same model as in Fig. 3a)
Neuronal response upon application of three different inputs (linear model, subthreshold oscillations). a Sinusoidal chirp. b Square-wave chirp. c Synaptic-like chirp. (a1,b1, and c1) voltage traces. (a2, b2, and c2) Voltage-response envelopes in the frequency-domain. (a3, b3, and c3) Z(f) (frequency-content) and \(Z_{ENV}(f)\) (envelope) impedance. We used the following parameter values: \(C=1\), \(g_\mathrm{L}=0.05\), \(g_1=0.3\), \(\tau _1=100\) ms, and \(A_\mathrm{in}=1\)
In principle, there are various metrics one could use to characterize the frequency response profiles of neurons (and dynamical systems in general). The impedance Z-profile (curve of the impedance amplitude as a function of the input amplitude) measures the signal frequency content (Fig. 4-a3, green). The upper and lower envelope profiles \( V_{ENV}^{+/-}\) (Fig. 4-a2) capture the stationary peaks and troughs of the voltage response, respectively as a function of the input frequency. The peak profiles, in particular, are a relevant quantity since spikes are expected to occur at the response peaks as the input amplitude crosses threshold (the voltage response to this amplitude crosses the voltage threshold). The envelope impedance \(Z_{ENV}\) profiles (Fig. 4-a3, blue), consisting of the stationary peak-to-trough amplitude normalized by the input amplitude as a function of the input frequency and serves to connect and compare between the two previous profiles.
For sinusoidal inputs, the Z-profile in response to chirp inputs typically coincides with the \(Z_{ENV}\)-profile computed by using sinusoidal inputs of a constant frequency (over a range of input frequencies). This remains true for the sinusoidal chirp-like input we use here (Fig 4-a). It is always true for linear systems (Richardson et al. 2003; Rotstein and Nadim 2014) and certain nonlinear systems (e.g., (Rotstein and Nadim 2019)). In other words, the frequency content of the voltage response (green) is reflected by the voltage upper and lower envelope response profiles and the response to non-stationary chirp-like inputs coincides with the stationary response to sinusoidal inputs of a single frequency. This is a direct consequence of the fact that the input changes are gradual.
3.2.2 Communication of the preferred frequency responses from the sub- to the supra-threshold regimes
The frequency-dependent suprathreshold response patterns to periodic inputs result from the interplay of the frequency-dependent subthreshold voltage responses to the same inputs and the spiking mechanisms. The subthreshold resonant frequency is communicated to the suprathreshold regime when neurons selectively fire action potentials in response to oscillatory inputs only at frequencies within a small enough range around the subthreshold resonant frequency. This type of evoking resonance can be obtained for input amplitudes sightly above these producing only subthreshold responses, for example for neurons for which the spiking response to oscillatory inputs can be thought of as spikes mounted on the corresponding subthreshold responses. Evoked spiking resonance captures a selective coupling between the oscillatory input and firing, and it has been observed experimentally and theoretically (Hutcheon et al. 1996a, b) and the underlying dynamic mechanisms have been investigated in detail (Rotstein 2017). A related measure of the communication of the subthreshold resonant frequency to the suprathreshold regime is that of firing rate resonance (Richardson et al. 2003) where the firing rate in response to oscillatory inputs peaks at or within a small range around the subthreshold resonance frequency. We note that subthreshold resonance does not necessarily imply evoked spiking resonance (Hutcheon et al. 1996a), evoked spiking resonance may be observed as the input amplitude crosses threshold, but lost for higher input amplitudes (Rotstein 2017), the firing rate (or spiking frequency) at the firing rate (evoked) resonant frequency band is not necessarily the same as that frequency band (Hutcheon et al. 1996b; Richardson et al. 2003; Rotstein 2017), and evoked spiking resonance may be occluded in the presence of spontaneous firing, a situation likely to occur in vivo. When the spontaneous (or intrinsic) firing frequency is relatively regular, the associated time scale may dominate over the subthreshold resonant time scale and determine the firing rate resonant frequency (Richardson et al. 2003). A third form of preferred frequency response to oscillatory inputs is the so-called output spiking resonance (Rotstein 2017) where the spiking frequency response to oscillatory inputs remains within a relatively narrow range independently of the input frequency range. The output spiking resonant frequency and the subthreshold resonant frequency are not necessarily the same, but the mechanisms that give rise to both are dynamically related (Rotstein 2017).
While there is no guarantee that subthreshold resonance implies any of the various types of supra-threshold resonance, the communication of the resonant frequency to the suprathreshold regime is favored when the neuron’s upper envelope profile \( V_{ENV}^+\) exhibits a peak at the subthreshold resonant frequency (\(V_{ENV}^+\) resonance). For the examples in Figs. 4-a and 5-a, the models, supplemented with a voltage threshold for spike generation and a reset mechanism, will exhibit evoked spiking resonance in response to sinusoidal inputs at the subthreshold resonant frequency band, and this is well captured by both the Z and \( Z_{ENV} \) profiles. However, while this remains true for a larger class of systems, we note that this is not necessarily the case for nonlinear systems exhibiting, for instance if the \(V_{ENV}^+\) and \(V_{ENV}^-\) are asymmetric with respect to the equilibrium voltage (Pena et al. 2019). For example, a cell that is an upper envelope low-pass filter (\(V_{ENV}^+\) is a decreasing function of the input frequency), but a lower envelope band-pass filter (\(V_{ENV}^-\) has a trough at an intermediate input frequency) will show a peak in the impedance profile Z and therefore will be considered resonant, but this will not necessarily be reflected in the spiking response since the lower frequencies will be communicated better to the spiking regime than the intermediate frequencies as the input amplitude increases above threshold, in particular, these within the subthreshold resonant frequency band.
This together with our discussion in the previous section raises the question of whether the responses of resonant cells to non-sinusoidal periodic inputs will also show a preferred frequency response in the resonant frequency band and whether the Z- and \(V_{ENV}\)- profiles exhibit the same filtering properties. This has implications for the frequency-dependent supra-threshold response patterns to periodic inputs since the communication between neurons occurs via synaptic interactions, which exhibit abrupt changes as compared to the sinusoidal inputs, raising in turn the possibility of a competition between Z- and \(V_{ENV}\)- profiles in determining the spiking frequency filtering properties.
3.3 Resonant cells do not necessarily show \(V_{ENV}^+\) resonance in response to chirp-like square-wave inputs
Figures 4-b1 and -b2 illustrate that (Z) resonant cells (see Fig. 4-a) may not exhibit envelope band-pass filter in responses to square-wave inputs. The \(V_{ENV}^+\) resonant response for sinusoidal inputs (Figs. 4-a1 and -a2) is lost for square-wave inputs and, consequently, these inputs would produce spiking activity preferentially at the lowest frequencies (no evoked spiking resonance) for input current amplitudes above threshold. The absence of \(V_{ENV}^+\)-resonance does not imply the absence of Z-resonant frequency content. In fact, the power spectra for the responses to sinusoidal and square-wave inputs (Fig. 4-b3, green) are very similar to the power spectra for sinusoidal inputs (Fig. 4-a3, green) and all show Z-resonance (see schematic explanation in Fig. S1). However, this Z-resonance is not reflected in the V response and therefore it does not have a direct effect on the communication of the subthreshold frequency content to the spiking regime.
Figure 5-b1 and -b2 shows a representative case where \(V_{ENV}^+\) resonance is still present for square-wave inputs, but the resonance amplitude \( Q_{ENV}^+\) (defined as the quotient of the values of \(V_{ENV}^+\) at the peak and at \(f = 0\)) is very small as compared to \( Q_{ENV}^+\) in response to sinusoidal inputs (Fig. 5-a2). In these cases, the subthreshold resonant frequency will be communicated to the spiking regime, but only for a small range of input amplitudes as compared to the responses to sinusoidal inputs (Fig. 5-a), above which spiking would occur for the lowest frequencies. The frequency content of the voltage response (Fig. 5-b3, green) is not reflected by the \( V_{ENV}^+\) and \( V_{ENV}^-\) response profiles (Fig. 5-b2) and consequently by the \( Z_{ENV} \) profiles (Fig. 5-b3, blue).
The main difference between the two cases presented in Figs. 4 and 5 is the type of autonomous transient dynamics of the two cells. For the parameter values used in Fig. 4 the equilibrium for the isolated cell is a stable node (real eigenvalues, no intrinsic damped oscillations) and the cell displays overshoot transient responses to input changes (e.g., Fig. 2-a), while for the parameter values used in Fig. 5, the equilibrium for the isolated cell is a stable focus and the cell displays damped oscillations in response to input changes (e.g., Fig. 2-b). Biophysically, the transition from stable nodes to stable foci is associated with an increase in the levels of the amplifying currents. In Fig. 5, this is reflected as a decrease in the linearized conductance \(g_L \), which contains information about fast amplifying currents such as \( I_{Nap} \) present in the original biophysical models (Richardson et al. 2003; Rotstein and Nadim 2014).
The persistence of \(V_{ENV}^+\) resonance in cells having stable foci is due to a combination of the (damped) oscillatory response after the abrupt input increase/decrease and summation. More specifically, the response to the abrupt input changes (square-wave or synaptic) has two regimes: a relatively large amplitude response, reflecting the biophysical amplification levels, and a smaller amplitude response reflecting the stability properties of the equilibrium \( V_{\text {eq}}\). The location of the voltage response V right before the arrival of the input from the next cycle determines the response amplitude to this input and this location depends on the stability properties of \( V_{\text {eq}} \). When \( V_{\text {eq}} \) is a node, the voltage response V decreases below \( V_{\text {eq}} \) immediately after the abrupt input change, and then returns to \( V_{\text {eq}} \). When the input from the next cycle arrives, V is below \( V_{\text {eq}} \). In contrast, when \( V_{\text {eq}} \) is a focus, the oscillatory voltage response may be above \( V_{\text {eq}} \) when the input from the next cycle arrives, and therefore, because it starts at a higher value, V reaches higher values. This depends on the frequency of the damped oscillations and the input frequency. If the input frequency is too low, then the damped oscillations die out before the next input arrives, while if the input frequency is high enough, then the damped oscillations are close to their first peak. If the input frequency is higher, then the value that V has when the next input arrives is lower because is further away from the first peak. For still higher input frequencies, the standard summation takes over.
Figures S2 and S3 show similar results for the nonlinear conductance-based \( I_h \) + \( I_{Nap} \) model (the linear models used for Figs. 4 and 5 can be considered as linearized versions of this \( I_h \) + \( I_{Nap} \) model). For the lower levels of the \( I_{Nap} \) conductance \( G_p \) the \( I_h \) + \( I_{Nap} \) shows no \(V_{ENV}^+\) resonance, while \(V_{ENV}^+\) resonance persists for the higher levels of \( G_p \), consistent with the transition of the equilibrium from a stable node to a stable focus.
3.4 Dependence of \(V_{ENV}^+\) resonance in response to synaptic-like input currents on the current sign and the cell’s intrinsic properties
3.4.1 Z-resonant cells do not necessarily show \(V_{ENV}^+\) resonance in response to excitatory synaptic-like inputs currents
As for the square-wave inputs described above, \(V_{ENV}^+\) is absent when \( V_{\text {eq}} \) is a node (Figs. 4-b1 and -b2) and present when \( V_{\text {eq}} \) is a focus (Figs. 5-b1 and -b2), but with a smaller \( Q_{ENV}^+\) than the response to sinusoidal inputs (Fig. 5a). Also similarly to square-wave inputs, the absence of \(V_{ENV}^+\)-resonance does not imply the absence of Z-resonant frequency content; The power spectra of the responses to sinusoidal, square-wave and synaptic-like inputs are very similar and all show Z-resonance (compare Figs. 4-b3 and -5-b3, green, with Figs. 4-a3 and -5-a3, green), and therefore this (Z-) resonance may have no direct effect on the communication of the subthreshold frequency content to the spiking regime (since the frequency-dependent properties that govern the generation of spikes are captured by \( V_{ENV}^+\) profiles and not on the frequency content captured by the Z-profiles).
In contrast to the responses to square-wave inputs, both the \(V_{ENV}^+\) and \(V_{ENV}^-\) responses to excitatory synaptic-like inputs exhibit a trough before increasing due to summation, which is more pronounced in Fig. 4c (\( V_{eq} \) is a node) than in Fig. 5c (\(V_{eq} \) is a focus). The generation of these troughs are the result of the interplay of the accumulation of synaptic inputs and the intrinsic properties of the cell reflected by the transient responses to individual inputs (overshoots, damped oscillations), and occur at a different frequency than the Z-resonant frequency. More specifically, for the lower frequencies in Fig. 4-c, V exhibits a sag before returning to a vicinity of \( V_{eq} \). The value V reaches before the arrival of the next input serves as the initial condition for the next cycle. As the input frequency increases, these initial conditions are lower than for the previous cycles since the periods decrease, and therefore V returns to an even lower value after the synaptic input wears off. As the input frequency increases further, standard summation takes over and the combination of summation and the higher frequency input creates the high-pass filter \( V_{ENV} \) patterns with an amplitude that decreases with frequency. This phenomenon is watered down when \( V_{eq} \) is a focus because the amplification associated to the presence of damped oscillations as compared to overshoots causes the voltage response troughs at every cycle to reach lower values when \( V_{eq} \) (Fig. 5c) is a focus than when \( V_{eq} \) is a node (Fig. 4c).
Figures S2 and S3 show similar results for the nonlinear conductance-based \( I_h \) + \( I_{\text {Nap}} \) model.
3.4.2 Z-resonant cells show \(V_{\text {ENV}}^+\) resonance in response to inhibitory synaptic-like inputs currents in a \( V_{\text {eq}} \)-stability-dependent manner
For inhibitory synaptic-like input, the \(V_{\text {ENV}}^+\) and \(V_{\text {ENV}}^-\) responses are qualitatively inverted images of the ones described above. For linear cells, in particular, the responses for excitatory and inhibitory synaptic-like inputs are symmetric with respect to \( V_{\text {eq}} \) (\(= 0 \)). The most salient feature is the presence of a peak in both \(V_{\text {ENV}}^+\) and in \(V_{\text {ENV}}^-\) (Figs. S4- a1 and -b1 and Figs. S4-a2 and -b2), indicating the occurrence of \(V_{\text {ENV}}^+\) resonance at a frequency, which is different from the Z-resonant frequency (Figs. S4 c1 and c2). The mechanism of generation of this \(V_{\text {ENV}}^+\) band-pass filters is similar to the one described for the troughs in excitatory synaptic-like inputs and involves a combination of summation and intrinsic properties of the cell, reflected in the properties of the transient response of the cells to individual inputs. More specifically, the summation acts as a low-pass filter and the effects of the transient responses to individual neurons, associated with the presence of Z resonance, act as a high-pass filter. We emphasize that the \(V_{\text {ENV}}^+\) and Z resonances are significantly different. We also emphasize that \(V_{\text {ENV}}^+\) resonance is not significant when \( V_{\text {eq}} \) is a focus (Fig. S4–b2) since the amplification associated to the presence of damped oscillations referred to above obstructs the envelope high-pass filtering component.
Figures S5 and S6 show similar results for the nonlinear conductance-based \( I_h \) + \( I_{Nap} \) model.
3.4.3 \(V_{ENV}^+\) low- and high-pass filtering properties of synaptic-like currents
The responses to synaptic-like inputs are affected by the summation effect, which depends on the synaptic decay time \( \tau _\mathrm{Dec} \). Figs. S7 and S8 illustrate the transition of the response (middle and right panels) to excitatory synaptic-like inputs (left panels) for representative values of \( \tau _\mathrm{Dec} \) (including these used in Figs. 4–c and 5-c). In all cases, the frequency content measured by the impedance Z (Figs. S7 and S8, green) remains almost the same. The summation effects, which increases as \( \tau _\mathrm{Dec} \) increases, strengthens the low-pass filter properties of the \( Z_{ENV} \) response. The results for inhibitory synaptic-like inputs are symmetric to these in Figs. S7 and S8 with respect to \( V_{eq} \) (\(=0\)) (not shown), and therefore, increasing values of \( \tau _\mathrm{Dec} \) strengthens the low-pass filter properties of \( Z_{\text {ENV}} \).
3.5 The autonomous transient dynamic properties are responsible for the poor upper envelope (\(V_{ENV}^+\)) resonance (or lack of thereof) exhibited by (Z-) resonant cells in response to non-sinusoidal chirp-like input currents
As discussed above, the differences between the \(V_{ENV}^+\) response patterns to square-wave/synaptic-like and sinusoidal inputs and the differences between the \(V_{\text {ENV}}^+\) response patterns to different types of synaptic-like inputs (excitatory, inhibitory) are due to the different ways in which individual cells transiently respond to abrupt and gradual input changes, which operate at every cycle. Both and the corresponding sinusoidal inputs share the primary frequency component determined by the period (see Fig. S1). However, the sinusoidal input is gradual and causes a gradual response without the prominent transients (overshoots and damped oscillations) observed for the square-wave input, which together with the summation phenomenon produces \( V_{\text {ENV}} \) peaks. The responses to square wave inputs, in particular for the lower frequencies, reach a steady-state value as the responses to sinusoidal inputs do, but in contrast to the latter, the voltage envelope for the former is determined by the transient peaks. These transients appear to be “getting in the way” of the voltage response to produce \( V_{\text {ENV}} \) resonance. However, they are not avoidable. In fact, overshoots in non-oscillatory systems are an important component of the mechanism of generation of resonance in response to sinusoidal inputs (Rotstein 2014, 2015) as are damped oscillations.
For comparison, Fig. S9 shows the responses of a passive cell (\(g_1 = 0 \)) to the three types of inputs. Passive cells exhibit neither overshoot nor damped oscillatory transient responses to abrupt input changes, but monotonic behavior. As expected, this cell does not exhibit resonance in response to oscillatory inputs, but a low-pass filter response in both Z and \( V_{\text {ENV}} \) (Figs. S9-a). The envelope response to square-wave inputs is also a low-pass filter (Fig. S9-b), though it decays slower with increasing values of the input frequency since, because of the waveform, the square-wave input stays longer at its maximum value than the sinusoidal input at each cycle. In contrast to Figs. 4 and 5, the cell’s response to synaptic-like inputs is a \( V_{ENV} \) high-pass filter (Fig. S9-c) due to summation and the lack of interference by the transient effects. Fig. S10 shows similar results for a two-dimensional linear model with a reduced value of the negative feedback conductance \( g_1 \) where overshoots and damped oscillations are not possible. The analogous results for inhibitory synaptic-like inputs are presented in Figs. S4 (rows 3 and 4).
3.6 Current- and conductance-based synaptic-like inputs produce qualitatively different voltage responses and synaptic currents
The synaptic-like inputs considered so far are additive current inputs. However, realistic synaptic currents involve the interaction between the synaptic activity and the postsynaptic voltage response. In biophysical models, the synaptic currents terms consist of the product of synaptic conductances and the voltage-dependent driving force (Eq. 3). Because the voltage response contributes to the current that produces this response, the frequency-dependent response profiles for current- and conductance-based inputs may be qualitatively different.
3.6.1 Z-resonant cells do not show \(V_{\text {ENV}}^+\) resonance in response to conductance-based excitatory synaptic-like inputs, but they do show troughs in the \(V_{\text {ENV}}^-\) response
Figures 6 and 7 show representative comparative examples for the two Z-resonant cells (in response to sinusoidal inputs) discussed in Figs. 4 (stable node) and 5 (stable focus), respectively. For the parameter values corresponding to Fig. 4 (no \(V_{ENV}^+\) resonance in response to current-based synaptic-like inputs, Fig. 6-b, blue), the conductance-based synaptic current shows a peak in the upper envelope (Fig. 6-a2), but not in the voltage response (Fig. 6-b, red), which, instead, shows a trough as for the current-based synaptic input (Fig. 6-b, blue). In spite of the similarities between the two profiles, the \( Z_{\text {ENV}} \) profile for the conductance-based input shows a peak (Fig. 7-c1, red), but this peak does not reflect a true \( Z_{\text {ENV}} \) preferred frequency response.
Comparison between conductance-based and current-based inputs (linear model, overshoot). a Input currents (see Eqs. 1 and 3). (a1) Current-based input. (a2) Conductance based input. b Voltage traces (same colors as in a1 and a2). (c1) \(Z_{ENV}(f)\) (envelope) impedance. (c2) Z(f) (frequency-content). We used the following parameter values: \(C=1\), \(g_\mathrm{L}=0.25\), \(g_1=0.25\), \(\tau _1=100\) ms, and \(A_\mathrm{in}=1\), same model as in Fig. 4
Comparison between conductance-based and current-based inputs (linear model, subthreshold oscillations). a Input currents (see Eqs. 1 and 3). (a1) Current-based input. (a2) Conductance based input. b Voltage traces (same colors as in a1 and a2). (c1) \(Z_{ENV}(f)\) (envelope) impedance. (c2) Z(f) (frequency-content). We used the following parameter values: \(C=1\), \(g_\mathrm{L}=0.05\), \(g_1=0.3\), \(\tau _1=100\) ms, and \(A_\mathrm{in}=1\), same model as in Fig. 5
For the parameter values corresponding to Fig. 5 (mild \(V_{ENV}^+\) resonance in response to current-based synaptic-like inputs, Fig. 7-b, blue), the response to conductance-based synaptic inputs is similar to that in Fig. 6, but more amplified. In particular, there is no \(V_{\text {ENV}}^+\) resonance in response to conductance-based synaptic-like input (Fig. 7-b, red). In both cases, the cells show Z resonance (Figs. 6 -c2 and 7-c2).
For comparison, Fig. S11 shows the result of repeating the protocols used above for a passive cell (\(g_1=0\), same as Fig. S9). The frequency response patterns are the standard Z- and \( Z_{ENV}\) low-pass filters and the expected \( V_{\text {ENV}}^+\) high-pass filter.
3.6.2 Z-resonant cells show \(V_{\text {ENV}}^+\) resonance in response to conductance-based inhibitory synaptic-like inputs
Figures S12, S13, and S14 shows the result of repeating the protocols described above (Figs. 6, 7 and S11, respectively) using synaptic-like inhibitory conductance-based inputs. The Z- and \( Z_{\text {ENV}} \)-profiles are qualitatively similar, except for the relative magnitudes of the synaptic- and conductance-based \( Z_{\text {ENV}} \) that are inverted. The \( V_{\text {ENV}}^+\) profile shows a significant (resonant) peak when the cell has a node (Fig. S12-b), which is almost absent when the cell has a focus (Fig. S13-b), but \( Z_{ENV} \) has a peak when the cell is a focus (Fig. S13-c1), while it is a low-pass filter when the cell has a node (Fig. S12-c1).
Together, these results and the result from the previous section shows that the frequency content (in terms of Z) of resonant cells persists in response to synaptic-like current- and conductance-based inputs, but the \( V_{\text {ENV}}^+\) responses are different between synaptic-like current- and conductance-based inputs, and these differences depend on whether the cell has a node or a focus and whether the synaptic-like input is excitatory or inhibitory. Of particular interest are the peaks in the conductance-based synaptic inputs (Figs. 6-a2 and 7-a2, red).
3.7 Amplitude variability in response to chirp-like inputs with arbitrarily distributed cycles results from the transient response properties of the autonomous system
In the previous sections we used discretely changing frequencies (chirp-like or, simply, chirps, see Sect. 2.2.1) as a compromise between tractability and the ability to incorporate multiple frequencies in the same input signal, and we extended this type of inputs to waveforms with more realistic time-dependent properties. In all the cases considered so far, the chirp-like input cycles were “regularly” ordered in the sense that the input frequency monotonically increases with the cycle number (and with time). In this section, we move one step forward and consider chirp-like inputs where the cycles are arbitrarily ordered (see Sect. 2.2.2 and, Fig. 1-b) in an attempt to capture the fact that information does not necessarily arrive in a regularly ordered manner while keeping some structure properties (sequence of oscillatory cycles), which ultimately allows for a conceptual understanding of the responses.
Each trial consists of a permutation of the order of the cycles using the regularly ordered cycles as a reference. The regularly and arbitrarily ordered input signals have exactly the same cycles (one cycle for each frequency value within some range) and therefore the same frequency content. The corresponding responses are expected to have roughly the same frequency content as captured by the Z-profiles within the range of inputs considered. However, we expect the voltage responses to have different frequency-dependent V responses, captured by the peak-and-trough envelopes \( V_{\text {ENV}}^{+/-} \). The differences between the V responses for two different inputs (different cycle orders) are due to the different ways in which the autonomous transient dynamics are activated across cycles for these inputs as the result of the transition between cycles. The values of the participating variables at the end of one cycle become the initial conditions for the subsequent cycle.
3.7.1 Emergence of the amplitude variability
In Sect. 3.2.1 (Figs. 4-a and 5-a) we showed that (Z-) subthreshold resonance is well captured by the \( V_{ENV}^{+/-}\) profiles in response to chirp-like sinusoidal inputs via the \( Z_{ENV} \)-profiles (difference between the \( V_{ENV}^+ \) and \( V_{ENV}^- \) profiles). In Sect. 3.5 we argued that the transient response properties of the autonomous (unforced) cells (overshoots, damped oscillations, passive monotonic increase/decrease) are responsible for the (frequency-dependent) differences between the \( V_{\text {ENV}}^{+/-}\) profiles and the Z-profiles in response to both square-wave and synaptic-like chirp-like inputs, and for the (frequency-dependent) differences among the \( V_{\text {ENV}}^{+/-}\) profiles in response to the three types of chirp-like inputs.
The ordered chirp-like input signals produced \( V_{\text {ENV}}^{+/-}\) profiles with gradual amplitude variations along with the input frequency range (and a very small number of increasing and decreasing portions). The peaks and troughs for each frequency are determined by two parameters: the values of the variables at the beginning of the corresponding cycle and the duration of the cycle (the intrinsic properties of the cell are the same for all input frequencies), which in turn determines the initial values of the variables in the next cycle. The monotonic increase of the input frequency causes a gradual change in these parameters along the frequency axis, which in turn causes gradual changes in the \( V_{\text {ENV}}^{+/-} \) profiles.
Because of this dependence of the values of the variables at the beginning of each cycle with the values of these variables at the end of the previous cycle, we reasoned that the voltage response to chirp with arbitrarily distributed cycles in time will exhibit non-regularly distributed peak and troughs, leading to amplitude variability in the \( V_{\text {ENV}}^{+/-} \) profiles, while producing at most minimal changes in the Z profiles (as compared to the responses to input signals with order cycles) within the frequency range considered. Moreover, this variability will depend on the type and properties of the autonomous transient dynamics of the participating cells. The arbitrary distribution in the order of the cycles in the input signal is achieved by considering one permutation of the regularly ordered signal (signal with regularly ordered cycles). The randomness in the input signals lies in the choice of a subset of all possible permutations for the considered trials.
Comparison of neuronal response between ordered and random input (linear model, overshoot). a Sinusoidal chirp. b Square-wave chirp. c Excitatory synaptic-like chirp. (a1, b1, and c1) voltage traces with peaks and troughs marked by red circles. (a2, b2, and c2) Voltage-response envelopes in the frequency domain (blue is ordered input; red is random input as in Fig. 1b). (a3, b3, and c3) Z(f) (frequency-content) for ordered and shuffled inputs. In this 2D linear model, we used the following parameter values: \(C=1\), \(g_\mathrm{L}=0.25\), \(g_1=0.25\), \(\tau _1=100\) ms, and \(A_\mathrm{in}=1\). Same model as in Fig. 4
Our results are presented in Figs. 8 and 9 for a cell exhibiting an overshoot (Fig. 8; stable node; same parameter values as in Fig. 4) and damped oscillations (Fig. 9; stable focus; same parameter values as in Fig. 5) in response to step-constant inputs. For sinusoidal and square-wave chirp-like inputs, the output \( V_{\text {ENV}}^{+} \) and \( V_{\text {ENV}}^{-} \) frequencies were computed as the differences between two consecutive troughs and two consecutive peaks, respectively, normalized so that the resulting frequencies have units of Hz. The \( V_{\text {ENV}}^{+} \) and \( V_{\text {ENV}}^{-} \) profiles consist of the sequence of maxima and minima for each frequency (dots superimposed to the v time courses in the left columns) and include the damped oscillations for the lower frequencies (e.g., Fig. 9-b1). For the synaptic-like chirp inputs, we used the \( V_{\text {ENV}}^{+} \) and \( V_{\text {ENV}}^{-} \) profiles consisting of the sequence of maxima and minima for each input frequency and do not include the damped oscillations for the lower frequencies (e.g., shown in Fig. 9-c1, but not present in Fig. 9-c2).
Comparison of neuronal response between ordered and random input (linear model, subthreshold oscillations). a Sinusoidal chirp. b Square-wave chirp. c Excitatory synaptic-like chirp. (a1, b1, and c1) voltage traces with peaks and troughs marked by red circles. (a2, b2, and c2) Voltage-response envelopes in the frequency domain (blue is ordered input; red is random input as in Fig. 1b). (a3, b3, and c3) Z(f) (frequency-content) for ordered and shuffled inputs. In this 2D linear model, we used the following parameter values: \(C=1\), \(g_\mathrm{L}=0.05\), \(g_1=0.3\), \(\tau _1=100\) ms, and \(A_\mathrm{in}=1\). Same model as in Fig. 5
We use the (regularly changing) responses to inputs with regularly ordered cycles (blue) as a reference for the variability of the responses to arbitrarily ordered cycles (red). In both Figs. 8 and 9 the responses to the input with randomly ordered cycles (red) have random amplitudes organized around (sinusoidal and square-wave; panels a and b) or in a vicinity (synaptic-like panel c) of the responses to regularly ordered cycles. The amplitude response variability is stronger for higher frequencies than for the lower frequencies, since the responses for the former are more affected by changes in the initial conditions at the corresponding cycles. Importantly, the variability is stronger for cells having stable foci (exhibiting transient damped oscillations; Fig. 9) than for cells having stable nodes (exhibiting transient overshoots; Fig. 8), reflecting the higher complexity of the latter cells’ autonomous part. In all cases considered, the Z profiles remain almost unaffected by the order of cycles within the input frequency range. For comparison and completeness, Figs. S15 and S16 show similar graphs for a passive cell and synaptic-like inhibition, respectively. An important observation common to the responses of the three types of cells to synaptic-like inputs is the identification of the summation effects in the generation of \( V_{\text {ENV}}^{+/-} \) resonances. For example, Fig. S15-c2 (passive cell) shows that the summation effect in response to regularly ordered cycles (blue) disappears in the responses to randomly ordered cycles (red). Furthermore, the \( V_{\text {ENV}}^{+} \) resonance in response to regularly ordered synaptic-like inhibitory inputs (Fig. S16-a2, blue) also disappears in the responses to randomly ordered synaptic-like inhibitory inputs (Fig. S16-a2, red).
Together these results show that the disruption of the regular order of a set of basic input signals, while the basic signals and their shapes remain unchanged, is translated into the amplitude variability of the response as compared to the responses to the regularly ordered sequence of signals, and this variability results from the properties of the transient dynamics of the (unforced) cells receiving the input.
3.7.2 Dependence of the amplitude response distribution variance with the cycle frequency and the properties of the receiving cell
Here we focus on synaptic-like inputs since they are the most realistic signals cells receive and we considered both current- and conductance-based synaptic-like inputs. We used the model (1)–(2) for current-based inputs and the model (3)–(4) for conductance-based inputs. We use the same input signal for both (\( I(t) = S(t) \)).
In order to quantify the variability of the voltage response envelopes (\( V_{\text {ENV}}^+\) and \( V_{\text {ENV}}^-\)) to arbitrarily ordered chirp-like inputs we considered a number of trials (\(N_{trials} = 100\)) and computed the cycle-by-cycle variance for the corresponding peaks (\( V_{\text {ENV}}^+\)) and troughs (\( V_{\text {ENV}}^-\)). Our results for some representative cases are presented in Fig. 10. In all cases, Var(\( V_{\text {ENV}}^+\)) (blue) is less variable across frequencies than Var(\( V_{\text {ENV}}^-\)) (red). The latter significantly increases for the higher frequencies. This high variability is associated with the phenomenon of summation observed in the regularly ordered cell. In other words, while summation is not observed in the responses to arbitrarily distributed cycles (e.g., Figs. 8-c, 9-c, and S15-c), it is translated into a high response variability. In Fig. 10-a, the transition from the P-cell (passive cell) to the N-cell (node cell) is due to a small increase in \( g_1 \) and therefore the Var patterns are similar. The transition from the N-cell to the F-cell (focus cell) involves changes in both \( g_L \) and \( g_1 \) in order to maintain \( f_{res} \) within the same (small) range. Both \( V_{ENV}^+\) and \( V_{ENV}^-\) are significantly larger for the F-cell than for the N-cell, consistent with Figs. 8 and 9. The amplification of the initial portion of the transient response to constant inputs caused by differences in cell type is translated into a higher response variability. In Fig. 10-b, the transition from the P-cell to the N-cell to the F-cell is due to an increase only in \( g_1 \) (at the expense of having values of \( f_{res} \) distributed on a longer range than in panels a). The Var magnitudes are similar among the different cases. Together, these results reflect the fact that changes in the levels of the positive feedback effects (captured by the parameter \( g_L\) in linear models) have stronger effects on the response variability than changes in the negative feedback effect (captured by the parameter \( g_1\)).
Peak and trough envelope (\(V_{\text {ENV}}^+\) and \( V_{\text {ENV}}^-\)) variability in response to synaptic-like chirp-like inputs with arbitrarily distributed cycles for current- and conductance-based models. We used the linear model (1)–(2). Each trial (\( N_{trials} = 100\)) consists of a permutation of the cycle orders using as reference the ordered input patterns in Figs. 8-c to S15-c. The blue and red curves represent the variances across trials for \(V_{\text {ENV}}^+\) and \( V_{\text {ENV}}^-\) in response to synaptic-like current-based inputs. The light-blue and light-coral curves represent the variances across trials for \(V_{ENV}^+\) and \( V_{\text {ENV}}^-\) in response to synaptic-like conductance-based inputs. Column 1. Passive cells. Column 2. Node (N-) cells. Column 3. Focus (F-) cells. a1. \( g_L = 0.25 \) and \( g_1 = 0 \) (\(f_{nat} = f_{res} = 0 \)). a2. \( g_L = 0.25 \) and \( g_1 = 0.25 \) (\(f_{nat} = 0 \) and \(f_{res} = 9 \)). a3. \( g_L = 0.05 \) and \( g_1 = 0.3 \) (\(f_{nat} = 8.1 \) and \(f_{res} = 8 \)). b1. \( g_L = 0.1 \) and \( g_1 = 0 \) (\(f_{nat} = f_{res} = 0 \)). b2. \( g_L = 0.1 \) and \( g_1 = 0.2 \) (\(f_{nat} = 0 \) and \( f_{res} = 7 \)). b3. \( g_L = 0.1 \) and \( g_1 = 0.8 \) (\(f_{nat} = 12.3 \) and \( f_{res} = 14 \)). We used the additional parameter values: \( C = 1 \), \( \tau _1 = 100 \), \( A_{in} = 1 \), \( G_{syn} = 1 \), \( E_{syn} = 1 \)
3.7.3 The envelope response variabilities are stronger for current- than for conductance-based synaptic-like inputs
The Var(\( V_{\text {ENV}}^+\)) and Var(\( V_{\text {ENV}}^-\)) for the conductance-based synaptic-like inputs follow a similar pattern as these for the current-based inputs (Fig. 10, light-blue and light-coral), but the magnitudes for the former are lower than these for the latter inputs, consistent with the attenuation of the initial portion of the transient response to conductance-based constant synaptic inputs as compared to current-based constant synaptic inputs discussed in Section 3.1.2. These relationships persist when the Var(\( V_{\text {ENV}}^+\)) and Var(\( V_{\text {ENV}}^-\)) patterns are normalized by the amplitude of the response of the first synaptic-like input in the ordered patterns (a metric that takes into account the effects of the differences in parameter values by the relative magnitude of their responses to the same input pattern).
Average PSD for the V response to synaptic-like chirp-like inputs with arbitrarily distributed cycles for current- and conductance-based models. For current-based synaptic-like inputs we used Eqs. (1)–(2). For conductance-based synaptic-like inputs we used the linear component of eqs. (3)-(4). The parameter values are as in Fig. 10. Each trial (\( N_{trials} = 100\)) consists of a permutation of the cycle orders using as reference the ordered input patterns in Figs. 8-c to S15-c. The blue and red curves represent the \( <PSD>\) for the responses to synaptic-like current- and conductance-based inputs, respectively. Column 1. Passive cells. Column 2. Node (N-) cells. Column 3. Focus (F-) cells. a1. \( g_L = 0.25 \) and \( g_1 = 0 \) (\(f_{nat} = f_{res} = 0 \)). a2. \( g_L = 0.25 \) and \( g_1 = 0.25 \) (\(f_{nat} = 0 \) and \(f_{res} = 9 \)). a3. \( g_L = 0.05 \) and \( g_1 = 0.3 \) (\(f_{nat} = 8.1 \) and \(f_{res} = 8 \)). b1. \( g_L = 0.1 \) and \( g_1 = 0 \) (\(f_{nat} = f_{res} = 0 \)). b2. \( g_L = 0.1 \) and \( g_1 = 0.2 \) (\(f_{nat} = 0 \) and \( f_{res} = 7 \)). b3. \( g_L = 0.1 \) and \( g_1 = 0.8 \) (\(f_{nat} = 12.3 \) and \( f_{res} = 14 \)). We used the additional parameter values: \( C = 1 \), \( \tau _1 = 100 \), \( A_{in} = 1 \), \( G_{syn} = 1 \), \( E_{syn} = 1 \)
3.8 Intrinsic oscillations evoked by Gaussian white noise may be lost or attenuated in response to synaptic-like inputs with arbitrarily ordered frequencies
3.8.1 Oscillations (and lack of thereof) in response to synaptic-like chirp inputs
Figure 11-a (blue) corresponds to the same parameter values as Figs. 8-c, 9-c, and S15-c. The most salient feature is the low-pass filter in the middle panel (a2), while the corresponding Z-profile shows a band-pass filter (Figs. 8-c). For the parameter values in Fig. 11-b2 both the PSD-profile and Z-profile (not shown) display a band-pass filter, but the resonant peak in the Z-profile is more pronounced than in the PSD-profile and relatively bigger in comparison to the values of the same quantities at \( f = 0 \). This reflects the different ways in which the autonomous transient dynamics can be evoked by different types of input patterns, leading to significantly different results. This is not unexpected from the sets of parameter values in this graphs (panels a2 and b2) since the autonomous cell has resonance (in response to oscillatory inputs, \( f_{res} > 0 \)) but not intrinsic damped oscillations (\(f_{nat} = 0 \)). For the other panels in Fig. 11 the Z-profile is a relatively good predictor of the PSD-profiles. These correspond to low-pass filters (panels a1 and b1) and strong band-pass filters (panels a3 and b3; \(f_{res} > 0 \) and \( f_{nat} > 0 \)).
3.8.2 The oscillatory voltage responses are stronger for current- than for conductance-based synaptic-like inputs
This is readily seen by comparing the blue and red curves in Fig. 11. These results are inherited from the responses of linear systems to synaptic current- and conductance-based constant inputs discussed in Section 3.1.2, and they can be understood in terms of our phase-plane diagrams discussion (compare Figs. 3-a and -c). Importantly, while in Fig. 11-a2 both responses show a low-pass filter, in Fig. 11-b2, the response to conductance-based synaptic inputs is close to a low-pass filter, while the response to current-based synaptic inputs is a well developed band-pass filter. In both cases, the autonomous cells have a stable node, exhibiting resonance, but not intrinsic (damped) oscillations.
PSD for the V response to Poisson synaptic inputs trains (excitatory rate = 1000 Hz) for current- and conductance-based models. For current-based synaptic-like inputs we used Eqs. (1)–(2). For conductance-based synaptic-like inputs we used the linear component of eqs. (3)–(4). The parameter values are as in Figs. 10 and 11. Poisson inputs (refractory time = 0.2 ms) were generated for a total duration of 1,000,000 ms. White noise had a variance 2D with \( D = 1 \). Blue dots and solid curves represent the PSD in response to current-based synaptic-like inputs. Red dots and solid curves represent the PSD in response to conductance-based synaptic-like inputs. Green dots and solid curves represent the PSD in response to white noise. The solid curves are a smoothed version (“moving”, 13 points) of the corresponding dots. The dashed curves are rescaled versions of the dots/solid curves to Column 1. Passive cells. Column 2. Node (N-) cells. Column 3. Focus (F-) cells. a1. \( g_L = 0.25 \) and \( g_1 = 0 \) (\(f_{nat} = f_{res} = 0 \)). a2. \( g_L = 0.25 \) and \( g_1 = 0.25 \) (\(f_{nat} = 0 \) and \(f_{res} = 9 \)). a3. \( g_L = 0.05 \) and \( g_1 = 0.3 \) (\(f_{nat} = 8.1 \) and \(f_{res} = 8 \)). b1. \( g_L = 0.1 \) and \( g_1 = 0 \) (\(f_{nat} = f_{res} = 0 \)). b2. \( g_L = 0.1 \) and \( g_1 = 0.2 \) (\(f_{nat} = 0 \) and \( f_{res} = 7 \)). b3. \( g_L = 0.1 \) and \( g_1 = 0.8 \) (\(f_{nat} = 12.3 \) and \( f_{res} = 14 \)). We used the additional parameter values: \( C = 1 \), \( \tau _1 = 100 \), \( A_{in} = 1 \), \( G_{syn,ex} = 1 \), \( E_{syn,ex} = 1 \), \( \tau _\mathrm{Dec} = 25 \)
3.8.3 Oscillations (and lack of thereof) in response to Poisson distributed synaptic-like inputs
Poisson distributed inputs have in principle a very different structure than the synaptic-like chirp inputs we discussed above. However, there is a natural transition between the two types of patterns. Roughly speaking, synaptic-like chirp patterns can be first extended to include a larger number of frequencies (not necessarily integer), and more than one cycle for each input frequency according to some distribution. Therefore one expects the results discussed above to extend to Poisson distributed inputs. This is supported by the fact that for high enough Poisson input rates \( \nu \), synaptic-like inputs approximate constant inputs (this is true for Poisson distributed pulses with amplitude \( g \rightarrow 0 \) and rate \( \nu \rightarrow \infty \)), and therefore one should expect the voltage response PSD to approach these for constant inputs reflecting overshoots (low-pass filters) and damped oscillations (band-pass filters). However, for cells exhibiting overshoots there is a conflict between the response pattern “dictated” by the Z-profile (band-pass filter) and the low-pass filter pattern in response to constant inputs. For these cases, we expect the response pattern to be highly sensitive to the interplay of the Poisson rate \( \nu \) and model parameters. For other rates we expect a departure from the overall behavior described above, but less pronounced.
Our results are presented in Fig. 12 (see also Figs. S17 to S20). The blue and red curves correspond to the V responses to synaptic-like current- and conductance-based inputs respectively. The solid curves are smoothed versions of the dotted ones (to which they are superimposed). The green dots/solid curves correspond to the V responses to white noise and are used as a reference for comparison. The blue and red dashed curves are rescaled versions of the corresponding dot/solid curves so that they match the values of the green curves at \( f = 1 \). In all cases, the responses to synaptic-like inputs are attenuated as compared to the responses to white noise. The level of attenuation increases with increasing values of the input Poisson rate (\(\nu \)) as we discussed below. Low-pass filters (panels a1 and b1) and strong band-pass filters (panels a3 and b3, F-cell) remain so with some variations. The responses of N-cells (panels a2 and b2) vary according to the input rate \( \nu \). Consistent with our results discussed above, for the cells that have resonance but not intrinsic (damped) oscillations (panels a2 and b2) and \( \nu = 1000 \) (Fig. S19), the response can be either a low-pass filter or a band-pass filter depending on the model parameters, in particular the level of the (amplifying) positive feedback effect that increases with decreasing values of \( g_L \) (compare panels a2, for \( g_L = 0.25 \), and b2, for \( g_L = 0.1 \)). This remains the case for \( \nu = 500 \) (Fig. S18) for the conductance-based response, but not for the current-based response (a band-pass filter emerges in panel a2). For \( \nu = 100 \) and \( \nu = 10 \) (Figs. S17 and S20), both the current- and conductance-based responses show a band-pass filter.
The results described above persist when the input synaptic train consist of both excitatory and inhibitory synaptic-like inputs (e.g., Fig. S21).
The emergence of band-pass filters in response to synaptic-like inputs is strongly dependent on the synaptic input decay time \( \tau _\mathrm{Dec} \). For values of \( \tau _\mathrm{Dec} \) (\(=25 \) ms) larger than in Figs. S17 to S21 and not realistic for fast synapses the band-pass filters are attenuated for F-cells (compare Figs. 12-a3 and -b3 with Figs. S19-a3 and -b3) and the N-cells show low-pass filters (compare Figs. 12-a2 and -b2 with Figs. S19-a2 and -b2).
3.8.4 The oscillatory voltage responses are stronger for current- than for conductance-based synaptic-like inputs and biophysically plausible in vivo input rates
This is readily seen in Figs. 12 and S19 for the realistic values of in vivo input rates (\(\nu = 1000 \)) also used in controlled experiments (Fernandez and White 2008). For lower values of \( \nu \) (Fig. S17 for \( \nu = 100 \), Fig. S18 for \( \nu = 500 \), Fig. S20 for \( \nu = 10 \)) and when synaptic inhibition is incorporated (Figs. S21 for excitatory \( \nu = 1000 \) and inhibitory \( \nu = 500 \)) the relative magnitudes of the current- and conductance-based responses depends on the input frequency regardless of whether the response has a low- or a band-pass filter. For even lower values of \( \nu \) (Figs. S17 for \( \nu = 10 \)), the conductance-based response is stronger than the current-based response).
Together these results and the results from the previous Sections shed some light on the implications of the experimental findings in (Fernandez and White 2008) where the intrinsically generated subthreshold oscillations observed in medial entorhinal cortex layer II stellate cells (SCs) have been shown to be strongly attenuated by current-based synaptic-like inputs and absent (or almost absent) in response to conductance-based synaptic-like inputs. Our findings suggest that STOs in SCs are generated by noise-dependent mechanisms in the presence of subthreshold resonance with at most strongly damped intrinsic oscillations (Rotstein et al. 2006), but not sustained limit cycle oscillations (Remme et al. 2012) in the presence of noise variability.
4 Discussion
Subthreshold (membrane potential) oscillations (STOs) have been observed in many neuron types in a variety of brain areas and have been argued to be functionally important for the generation of brain rhythms, sensory processing, encoding of information, communication of information via timing mechanisms and cross-frequency coupling (see more details and references in the Introduction).
Intrinsically generated STOs in single neurons require the presence of relatively slow restorative currents providing a negative feedback effect (currents having a resonant gating variable) and are amplified by fast regenerative currents providing a positive feedback effect (currents having an amplifying gating variable) (see Sect. 3.1 for more details). From a dynamical systems perspective, sustained STOs can be generated by limit cycle mechanisms or be noise-driven. In the latter case, the noiseless system may exhibit either damped oscillations (F-cells; the equilibrium has complex eigenvalues) or even overshoots (N-cells; the equilibrium has real eigenvalues) in response to abrupt changes in constant inputs. The interaction between Gaussian white noise and these autonomous transient dynamics may create sustained STOs (Rotstein et al. 2006; Pena and Rotstein 2021).
Neurons are subject to fluctuating inputs from a large number of synaptic currents generated by action potentials whose collective dynamics can be modeled as a high-rate Poisson process. Due to its high-rate, this synaptic noise has been approximated by Gaussian white noise or Ornstein-Uhlenbeck processes (Uhlenbeck and Ornstein 1930) (low-pass filtered versions of Gaussian white noise) (Brunel 2000; Amit and Tsodyks 1991; Tuckwell 1989, 1988; Amit and Brunel 1997; Brunel et al. 2001). Recent experimental results (Fernandez and White 2008) on medial entorhinal cortex SCs, a prototypical intrinsic STO neuron (Dickson et al. 2000a, b) and resonator (Schreiber et al. 2004), using artificially generated current- and conductance-based synaptic inputs driven by high-rate presynaptic Poisson spike trains, showed that STOs are still present in response to current-based synaptic inputs, but absent or strongly attenuated in response to conductance-based synaptic inputs. This would suggest that in realistic conditions the STO properties of SCs are not communicated to the network regime via synaptic mechanisms. On the other hand, in SCs and other cell types exhibiting STOs, the frequency of the STOs has been found to be correlated with the frequency of the networks in which they are embedded (Alonso and Llinás 1989; Klink and Alonso 1993; Giocomo et al. 2007; Cobb et al. 1995; Colgin 2013; Chapman and Lacaille 1999; Desmaisons et al. 1999; Balu et al. 2004; Kay et al. 2008; Li and Cleland 2017), suggesting intrinsic STOs in individual neurons may play, at least, an indirect role in the generation of network oscillations.
These issues are part of the more general question of how the response of neurons to periodic inputs (and to external inputs in general) depends on the interplay of the neuronal intrinsic properties and the properties of the input. Typical experiments on subthreshold and suprathreshold resonance use sinusoidal inputs, which change gradually with time. These studies are motivated by the fact that the resulting patterns can be used for the reconstruction of the system’s response to arbitrary time-dependent inputs under certain assumptions on both the input and the system (e.g., quasi-linearity). However, systems are not necessarily close to linearity and neuronal communication occurs via relatively fast synapses (e.g., AMPA and GABA\(_A\)), which change more abruptly. These abrupt input changes evoke the autonomous intrinsic dynamics (damped oscillations or overshoots), which are occluded in response to gradual input changes. As a result, periodic (and also non-periodic) sequences of sinusoidal and synaptic inputs are expected to produce different patterns and therefore the impedance profile will not be a good predictor of the voltage response to trains of synaptic inputs under general assumptions.
We set out to clarify these issues in a broader context. To develop the main set of ideas, we used a relatively simple neuronal model, the linearization of conductance-based models subject to additive current-based inputs and multiplicative conductance-based synaptic inputs. We then tested these ideas using a conductance-based model. We used three representative waveforms over a range of frequencies: sinusoidal, synaptic-like and square-wave (duty cycle equal to 0.5). Sinusoidal inputs are typically used to uncover the preferred oscillatory responses to external inputs as discussed above. Synaptic-like inputs represent the realistic ways in which communication between neurons occurs. Square-wave inputs can be considered as an intermediate between the first two. Sinusoidal and square-wave inputs share the waveform skeleton (they have the same frequency content except for the high frequency associated with the abrupt changes between phases), but sinusoidal inputs change gradually. Square-wave and synaptic inputs involve abrupt changes between minima and maxima, but the active part of the synaptic-like waveforms is independent of the period for a relatively large range of input frequencies. In addition, we used chirp-like (sinusoidal) inputs with discretely changing frequencies in order to be able to incorporate multiple frequencies in the same signal and we extended these chirps to include square- and synaptic-like waveforms.
We developed the notion of the peak/trough voltage envelope profiles \(V_{\text {ENV}}^\pm (f)\) and the peak-to-trough impedance profiles \( Z_{\text {ENV}}(f) \) as metrics to investigate the frequency-dependent voltage responses to periodic inputs in addition to the (standard) impedance amplitude profiles Z(f) and the corresponding voltage PSD (computed using Fourier transforms of the whole signal). Because the upper (peak) envelope is the most important quantity regarding the communication of information to the suprathreshold regime, we often refer to it indistinctly as \( V_{\text {ENV}} \) or \( V_{\text {ENV}}^+\). The differences between \( V_{\text {ENV}} \) (or \( V_{\text {ENV}}^+ - V_{\text {ENV}}^-\)) and the voltage PSD are due to the signal structure (\( V_{\text {ENV}} \) captures only the envelope of the voltage response). The differences between \( Z_{\text {ENV}} \) and Z capture the effect of the input signal (\( Z_{\text {ENV}} \) is normalized by the input signal’s amplitude \( A_{\text {in}} \), while Z is normalized by the amplitude of its PSD). The differences between the \( V_{\text {ENV}} \) and \( Z_{\text {ENV}} \) profiles are due to the asymmetries in the voltage responses.
We showed that cells that exhibit resonance in response to sinusoidal inputs (Z-resonant cells) also show resonance in the \( V_{\text {ENV}}\)- and \( Z_{\text {ENV}}\)-responses to sinusoidal chirp inputs independently of whether they were N-cells or F-cells. This was expected given the gradual increase of the sinusoidal waveforms, but it served as a baseline for comparison with the other input types. For suprathreshold input amplitudes within some range, the frequency properties of Z-resonant cells in response to sinusoidal inputs are communicated to the suprathreshold regime in the form of evoked spiking resonance (Rotstein 2017) or firing-rate resonance (Richardson et al. 2003). In contrast, Z-resonant N-cells are \( V_{\text {ENV}}\) and \( Z_{\text {ENV}} \) low-pass filters and Z-resonant F-cells have mild \( V_{\text {ENV}} \) and \( Z_{\text {ENV}}\) resonant properties. In other words, the cells’ subthreshold frequency-dependent properties, are not necessarily communicated to the spiking regime in response to non-sinusoidal inputs. The \( V_{\text {ENV}}^\pm \) patterns in response to these two types of inputs are dominated by the autonomous intrinsic dynamics and this is particularly strong for the lower frequencies (longer periods) where the overshoots and damped oscillations can be prominent. In response to sinusoidal inputs, the autonomous transient dynamics develops gradually and their contribution to the \( V_{\text {ENV}}^\pm \) patterns remains occluded.
We used these protocols to compare the response of these neuron types to current- vs. conductance-based synaptic-like inputs. In all cases, the response to conductance-based inputs was attenuated as compared to the response to current-based inputs. Each one of the metrics produced different results, capturing different aspects of the voltage responses to these two types of inputs and their relationship with the input signals. For N-cells the responses to both current- and conductance-based inputs are \( V_{\text {ENV}} \) low-pass filters. In contrast, for F-cells the \( V_{\text {ENV}} \) responses to current-based inputs were band-pass filters, while the responses to conductance-based inputs were low-pass filters. These band-pass filters were generated as the result of the interplay of the autonomous transient dynamics (damped oscillations) and summation.
The \( Z_{\text {ENV}} \) profiles tell a different story. For N-cells, the \( Z_{\text {ENV}} \) responses to current-based inputs are low-pass filters, while they are band-pass filters for conductance-based inputs. For F-cells, the \( Z_{\text {ENV}} \) responses to both current- and conductance-based inputs are band-pass filters. In both cases, the \( Z_{\text {ENV}} \) band-pass filters in response to conductance-based inputs reflect troughs in the \( V_{\text {ENV}}^-\) profiles rather than a real preferred voltage response. The Z profiles tell yet a different story. In all cases considered (N- and F-cells, current- and conductance-based inputs), the Z profiles are band-pass filters. For passive cells, where the autonomous transient dynamics are relatively simple (monotonic increase or decrease), the response patterns are dominated by summation and, while \( Z_{\text {ENV}} \) and Z are low-pass filters, \( V_{\text {ENV}} \) are high-pass filters.
In order to understand the contribution of the autonomous intrinsic dynamics to the generation of variability in the neuronal response patterns to external inputs, we used the three types of chirp-like inputs with arbitrarily ordered cycles. These inputs are an intermediate step between the regularly ordered and the fully irregular chirp-like inputs. The prototypical example of the latter (and the one we had in mind) are the synaptic-like inputs generated in response to spike-trains with Poisson-distributed spike times. The inputs have the same cycles for all trials, and hence the same frequency content, but each trial corresponded to a different permutation of the order of the cycles. The only source of uncertainty was the subset of all possible permutations of the cycle period. The differences in the voltage responses for cycles with the same period across trials were due to the differences in the initial conditions across trials for the same period. More specifically, for a given period (\(T_k\)) the previous cycle has different periods across trials and therefore different voltage values at the end of these periods, which become the initial conditions for period \( T_k \). The variability of these initial conditions across trials involves not only the voltage but the (hidden) recovery variables. Our results demonstrated the emergence of variability of the voltage responses across trials for all input waveforms inherited from this mechanism. This variability was stronger for the F-cells than for the N-cells considered and, again, it did not require stochastic input fluctuations, but it was the result of the multiple different ways in which the inputs evoked the autonomous intrinsic dynamics.
The average voltage PSD (\(<PSD>\)) responses for F-cells were band-pass filters for both current- and conductance-based synaptic-like inputs with arbitrarily order periods. For N-cells, in contrast, the \(<PSD>\) responses to current-based input were low-pass filters, while the \(<PSD>\) responses to conductance-based inputs were low-pass filters or mild band-pass filters. This is consistent with the results in Fernandez and White (2008) and previous results showing that STOs in SCs are noise-driven (Dorval and White 2005; Rotstein et al. 2006) (but see (Remme et al. 2012)). Our protocols consisted of the response of one cell type to variable inputs. More research is needed to understand the effects of variability across cells using some baseline attribute to all of them (e.g., same resonant properties or the same noise-driven oscillation properties).
Armed with these results, we compared the voltage responses (\(V_{\text {PSD}}\)) of these cell types to high-rate Poisson distributed current- and conductance-based synaptic inputs and additive Gaussian white noise (noise-driven oscillations). The \(V_{\text {PSD}}\)-profiles in response to both current- and conductance-based synaptic inputs were attenuated with respect to the response to white noise. The \(V_{PSD}\)-profiles in response to current-based synaptic inputs were low-pass filters for F-cells and low-pass filters (or mild band-pass filters) for N-cells. The \(V_{\text {PSD}}\)-profiles in response to conductance-based synaptic inputs were low-pass filters for all cell types. This is, again, consistent with the results in Fernandez and White (2008) and suggests that in contrast to the noise-driven oscillations that emerge in both F- and N-cells, the current-based synaptic-like Poisson-driven oscillation requires a stronger intrinsic oscillatory structure. These results also show that the responses to synaptic-like high-rate Poisson-driven inputs are not necessarily captured by the response to additive Gaussian white noise in contrast to standard assumptions. More research is needed to establish the conditions under which oscillations emerge in response to synaptic-like inputs. Representative examples show that oscillatory responses for current- and conductance-based synaptic-like inputs emerge for both F- and N-cells for lower Poisson rates. More research is also needed to establish the conditions under which the Gaussian white noise approximation provides good approximations to high-rate synaptic inputs.
The question arises whether the lack of oscillatory responses to synaptic-like inputs (almost complete for conductance-based and partial for current-based) implies the lack of communication of the intrinsic (noise-driven) oscillatory and resonant properties to the suprathreshold regime. While this requires a detailed analysis and is beyond the scope of this paper, we conducted a number of simulations to explore a few representative cases. We used the biophysical (conductance-based) \( I_h \) + \( I_{Nap} \) model (6)–(7) having two-dimensional subthreshold dynamics (Figs. S22 to S25) and compared them with the results using an integrate-and-fire model (Fig. S26) for which the subthreshold dynamics is one-dimensional. The results are mixed, but an important common theme is that the responses show output firing rate resonance (the response firing remains within a relatively small bounded range) even when the subthreshold resonance is not present. The most salient cases are shown in Fig. S22-a and -b. This phenomenon is absent in the absence of the intrinsic oscillatory dynamics for the leaky integrate-and-fire model (Fig. S22-d, Fig. S26). These results strongly depend on the input amplitude (Fig. S23 to S26). These results suggest that the oscillatory properties of individual neurons may be occluded at the subthreshold level, but they are still communicated to the suprathreshold regime. One may potentially contrast these observations against the cancellation of frequency-dependent redundant sensory stimuli in electric fish (Mejias et al. 2013; Benda et al. 2005; Bol et al. 2011, 2013). In such experiments, chirps create responses that are significantly enhanced compared with slower beats. This type of experimentation would certainly benefit from future discussions that derive from our work given the nature of their oscillatory inputs.
Our study is focused on a specific type of resonance in response to deterministic periodic inputs (in the form of chirps) and leaves out the response of systems to stochastic inputs that may lead to stochastic and coherence resonance (Benzi et al. 1982, Gammaitoni et al. 1998; McNamara and Wiesenfeld 1989; Mato 1989; McDonnell and Abboott 2009; Douglass et al. 1993; Wiesenfeld and Moss 1995; Collins et al. 1996; Muratov et al. 2005; Pikovsky and Kurths 1997; Lindner et al. 2004; Neiman et al. 1997; Lee et al. 1998; Pradines et al. 1999; Tateno and Pakdaman 2004; DeVille et al. 2005; Baspinar et al. 2021) (and references therein). These are related, but different phenomena, which may be affected by the use of non-sinusoidal inputs of the form we use here. More research is required to understand these issues.
The synaptic-like inputs we use in this paper have constant amplitude across cycles. Previous work showed that synaptic short-term plasticity (STP, depression and facilitation) can lead to the emergence of temporal filters (Fortune and Rose 2001; Mondal 2021; Mondal et al. 2021) and synaptic resonance (Drover et al. 2007; Mondal 2021). Additionally, STP has been shown to play a role in modulated intrinsic subthreshold oscillations (Flores et al. 2016; Torres et al. 2011; Uzuntarla et al. 2017). Future work should consider the effects of adding STP to the protocols we used here. However, this may require the use of full periodic signals instead of chirps to capture phenomena mentioned above. A step in this direction has been done in Mondal et al. (2021).
Simply put, under rather general circumstances, neurons that exhibit subthreshold resonance in response to sinusoidal inputs would exhibit spiking resonance in response to the same inputs (for small enough values of the input amplitude), but would not exhibit spiking resonance for other types of inputs, in particular for synaptic-like waveforms, which are the ones that operate in networks. This includes the difference between the responses to current- and conductance-based inputs. These issues have been overlooked in the literature and, often, claims are made about the implications of resonance in response to sinusoidal inputs for spiking activity in realistic setups. Our results generate a number of predictions that can be tested experimentally in vitro using the dynamic clamp technique (Sharp et al. 1993; Prinz et al. 2003) or in vivo using optogenetic tools (Zhang et al. 2007; Deisseroth 2011; Bernstein and Boyden 2012; Stark et al. 2013).
References
Allen EJ, Novosel SJ, Zhang Z (1998) Finite element and difference approximation of some linear stochastic partial differential equations. Stoch Stoch Rep 64:117–142
Alonso AA, Llinás RR (1989) Subthreshold Na\(^{+} \)-dependent theta like rhythmicity in stellate cells of entorhinal cortex layer II. Nature 342:175–177
Amir R, Michaelis M, Devor M (1999) Membrane potential oscillations in dorsal root ganglion neurons: role in normal electrogenesis and neuropathic pain. J Neurosci 19:8589–8596
Amir R, Liu C-N, Kocsis J, Devor M (2002) Oscillatory mechanism in primary sensory neurons. Brain 125:421–435
Amit DJ, Brunel N (1997) Dynamics of a recurrent network of spiking neurons before and following learning. Cereb Cortex 7:237–252
Amit DJ, Tsodyks MV (1991) Quantitative study of attractor neural network retrieving at low spike rates I: substrate spikes, rates and neuronal gain. Network 2:259–274
Art JJ, Crawford AC, Fettiplace R (1986) Electrical resonance and membrane currents in turtle cochlear hair cells. Hear Res 22:31–36
Axmacher N, Mormann F, Fernandez G, Elger CE, Fell J (2006) Memory formation by neuronal synchronization. Brain Res Rev, 170–1802
Balu R, Larimer P, Strowbridge BW (2004) Phasic stimuli evoke precisely timed spikes in intermittently discharging mitral cells. J Neurophysiol 92:743–753
Baroni F, Burkitt AN, Grayden DB (2014) Interplay of intrinsic and synaptic conductances in the generation of high-frequency oscillations in interneuronal networks with irregular spiking. PLoS Comp Biol 10:e1003574
Baspinar E, Schulen L, Olmi S, Zakharova A (2021) Coherence resonance in neuronal populations: mean-field versus network model. Phys Rev E 103:032308
Beatty J, Song SC, Wilson CJ (2015) Cell-type-specific resonances shape the response of striatal neurons to synaptic inputs. J Neurophysiol 113:688–700
Benzi R, Parisi G, Sutera A, Vulpiani A (1982) Stochastic resonance in climatic change. Tellus 34:10–16
Bel A, Rotstein HG (2019) Membrane potential resonance in non-oscillatory neurons interacts with synaptic connectivity to produce network oscillations. J Comp Neurosci 46:169–195
Belluscio MA, Mizuseki K, Schmidt R, Kemper R, Buzsáki G (2012) Cross-frequency phase-phase coupling between theta and gamma oscillations in the hippocampus. J Neurosci 32:423–435
Benda J, Longtin A, Maler L (2005) Spike-frequency adaptation separates transient communication signals from background oscillations. J Neurosci 25:2312–2321
Bernstein JG, Boyden ES (2012) Optogenetic tools for analyzing the neural circuits of behavior. Curr Opin Neurobiol 22:61–71
Bilkey DK, Heinemann U (1999) Intrinsic theta-frequency membrane potential oscillations in layer III/V perirhinal cortex neurons of the rat. Hippocampus 9:510–518
Boehlen A, Heinemann U, Erchova I (2010) The range of intrinsic frequencies represented by medial entorhinal cortex stellate cells extends with age. J Neurosci 30:4585–4589
Boehlen A, Henneberger C, Heinemann U, Erchova I (2013) Contribution of near-threshold currents to intrinsic oscillatory activity in rat medial entorhinal cortex layer II stellate cells. J Neurophysiol 109:445–463
Boehmer G, Greffrath W, Martin E, Hermann S (2000) Subthreshold oscillation of the membrane potential in magnocellular neurones of the rat supraoptic nucleus. J Physiol 526:115–128
Bol K, Marsat G, Harvey-Girard E, Longtin A, Maler L (2011) Frequency-tuned cerebellar channels and burst-induced LTD lead to the cancellation of redundant sensory inputs. J Neurosci 31:11028–11038
Bol K, Marsat G, Mejías JF, Maler L, Longtin A (2013) Modeling cancelation of periodic inputs with burst-stdp and feedback. Neural Netw 47:120–133
Bourdeau M, Morin F, Laurent C, Azzi M, Lacaille J (2007) Kv4.3-mediated A-type K\(^+\) currentes underlie rhythmic activity in hippocampal interneurons. J Neurosci 27:1942–1953
Bracci E, Centonze D, Bernardi G, Calabresi P (2003) Voltage-dependent membrane potential oscillations in rat striatal fast-spiking interneurons. J Physiol 15:121–130
Bragin A, Jando G, Nadasdy Z, Hetke J, Wise K, Buzsáki G (1995) Gamma (40–100 hz) oscillation in the hippocampus of the behaving rat. J Neurosci 15:47–60
Brea JN, Kay LM, Kopell NJ (2009) Biophysical model for gamma rhythms in the olfactory bulb via subthreshold oscillations. Proc Natl Acad Sci USA 106:21954–21959
Brunel N (2000) Dynamics of sparsely connected networks of excitatory and inhibitory spiking neurons. J Comp Neurosci 8:183–208
Brunel N, Chance FS, Fourcaud N, Abbott LF (2001) Effects of synaptic noise and filtering on the frequency response of spiking neurons. Phys Rev Lett 86:2186–2189
Burden RL, Faires JD (1980) Numerical analysis. PWS Publishing Company, Boston
Burgess C, Schuck NW, Burgess N (2011) Temporal neuronal oscillations can produce spatial phase codes. In: Space, Time and Number in the Brain (S. Dehaene & E. M. Brannon, eds.), pp. 59–69
Chapman CA, Lacaille JC (1999) Intrinsic theta-frequency membrane potential oscillations in hippocampal CA1 interneurons of stratum lacunosum-moleculare. J Neurophysiol 81:1296–1307
Chen Y, Li X, Rotstein HG, Nadim F (2016) Membrane potential resonance frequency directly influences network frequency through gap junctions. J Neurophysiol 116:1554–1563
Chorev E, Yarom Y, Lampl I (2007) Rhythmic episodes of subthreshold membrane potential oscillations in the rat inferior olive nuclei in vivo. J Neurosci 27:5043–5052
Chow CC, White JA (1996) Spontaneous action potentials due to channel fluctuation. Biophys J 71:3013–3021
Chrobak JJ, Buzsáki G (1998) Gamma oscillations in the entorhinal cortex of the freely behaving rat. J Neurosci 18:388–398
Cobb SR, Buhl EH, Halasy K, Paulsen O, Somogyi P (1995) Synchronization of neuronal activity in the hippocampus by individual GABAergic interneurons. Nature 378:75–78
Colgin LL (2013) Mechanisms and functions of theta rhythms. Annu Rev Neurosci 36:295–312
Colgin LL, Denninger T, Fyhn M, Hafting T, Bonnevie T, Jensen O, Moser M-B, Moser EI (2009) Frequency of gamma oscillations routes flow of information in the hippocampus. Nature 462:353–358
Collins JJ, Imhoff TT, Grigg P (1996) Noise-enhanced information transmission in rat SA1 cutaneous mechanoreceptors via aperiodic stochastic resonance. J Neurophysiol 76:642–645
D’angelo E, Nieus T, Maffei A, Armano S, Rossi P, Taglietti V, Fontana A, Naldi G (2001) Theta-frequency bursting and resonance in cerebellar granule cells: experimental evidence and modeling of a slow K\(^{+} \) - dependent mechanism. J Neurosci 21:759–770
D’Angelo E, Koekkoek SKE, Lombardo P, Solinas S, Ros E, Garrido J, Schonewille M, De Zeeuw CI (2009) Timing in the cerebellum: oscillations and resonance in the granular layer. Neuroscience 162:805–815
Deisseroth K (2011) Optogenetics. Nat Methods 8:26–29
Desmaisons D, Vincent J-D, Lledo P-M (1999) Control of action potential timing by intrinsic subthreshold oscillations in olfactory bulb output neurons. J Neurosci 19:10727–10737
DeVille E, Vanden-Eijnden REL, Muratov CB (2005) Two distinct mechanisms of coherence in randomly perturbed dynamical systems. Phys Rev E 72:031105
Dickson CT, Magistretti J, Shalinsky MH, Fransén E, Hasselmo M, Alonso AA (2000) Properties and role of I\(_{h} \) in the pacing of subthreshold oscillation in entorhinal cortex layer II neurons. J Neurophysiol 83:2562–2579
Dickson CT, Magistretti J, Shalinsky M, Hamam B, Alonso AA (2000) Oscillatory activity in entorhinal neurons and circuits. Ann Y Acad Sci 911:127–150
Dorval AD Jr, White JA (2005) Channel noise is essential for perithreshold oscillations in entorhinal stellate neurons. J Neurosci 25:10025–10028
Douglass JK, Wilkens L, Pantazelou E, Moss F (1993) Noise enhancement of information transfer in crayfish mechanoreceptors by stochastic resonance. Nature 365:337–340
Drover JD, Tohidi V, Bose A, Nadim F (2007) Combining synaptic and cellular resonance in a feedforward neuronal network. Neurocomputing 70:2041–2045
Dwyer J, Lee H, Martell A, van Drongelen W (2012) Resonance in neocortical neurons and networks. Eur J Neurosci 36:3698–3708
Einstein MC, Pollack P-O, Tran DT, Golshani P (2017) Visually evoked 35 Hz membrane potential oscillations reduce the responsiveness of visual cortex neurons in awake behaving mice. J Neurosci 37:5084–5098
Engel TA, Schimansky-Geier L, Herz AV, Schreiber S, Erchova I (2008) Subthreshold membrane-potential resonances shape spike-train patterns in the entorhinal cortex. J Neurophysiol 100:1576–1588
Erchova I, Kreck G, Heinemann U, Herz AVM (2004) Dynamics of rat entorhinal cortex layer II and III cells: Characteristics of membrane potential resonance at rest predict oscillation properties near threshold. J Physiol 560:89–110
Farries MA, Wilson CJ (2012) Phase response curves of subthalamic neurons measured with synaptic input and current injection. J Neurophysiol 108:1822–1837
Farries MA, Wilson CJ (2012) Biophysical basis of the phase response curve of subthalamic neurons with generalization to other cell types. J Neurophysiol 108:1838–1855
Fernandez R, White JA (2008) Artificial synaptic conductances reduce subthreshold oscillations and periodic firing in stellate cells of the entorhinal cortex. J Neurosci 28:3790–3803
Flores A, Manilla S, Huidobro N, De la Torre-Valdovinos B, Kristeva R, Mendez-Balbuena I, Galindo F, Treviño M, Manjarrez E (2016) Stochastic resonance in the synaptic transmission between hair cells and vestibular primary afferents in development. Neuroscience 322:416–429
Fortune E, Rose G (2001) Short-term plasticity as a temporal filter. Trends Neurosci 24:381–385
Fox DM, Tseng H, Smolinsky T, Rotstein HG, Nadim F (2017) Mechanisms of generation of membrane potential resonance in a neuron with multiple resonant ionic currents. PLoS Comp Biol 13:e1005565
Gammaitoni L, Hanggi P, Jung P, Marchesoni F (1998) Stochastic resonance. Rev Mod Phys 70:223–287
Gastrein P, Campanac E, Gasselin C, Cudmore RH, Bialowas A, Carlier E, Fronzaroli-Molinieres L, Ankri N, Debanne D (2011) The role of hyperpolarization-activated cationic current in spike-time precision and intrinsic resonance in cortical neurons in vitro. J Physiol 589:3753–3773
Giocomo LM, Zilli EA, Fransén E, Hasselmo ME (2007) Temporal frequency of subthreshold oscillations scales with entorhinal grid cell field spacing. Science 315:1719–1722
Gireesh E, Plenz D (2008) Neuronal avalanches organize as nested theta- and beta/gamma-oscillations during development of cortical layer 2/3. Proc Natl Acad Sci USA 105:7576–7581
Gloveli T, Dugladze T, Rotstein HG, Traub R, Monyer H, Heinemann U, Whittington MA, Kopell N (2005) Orthogonal arrangement of rhythm-generating microcircuits in the hippocampus. Proc Natl Acad Sci USA 102:13295–13300
Golomb D, Donner K, Shacham L, Shlosberg D, Amitai Y, Hansel D (2007) Mechanisms of firing patterns in fast-spiking cortical interneurons. PLoS Comp Biol 3:e156
Gutfreund Y, Yarom Y, Segev I (1995) Subthreshold oscillations and resonant frequency in guinea pig cortical neurons: physiology and modeling. J Physiol 483:621–640
Heys JG, Giacomo LM, Hasselmo ME (2010) Cholinergic modulation of the resonance properties of stellate cells in layer II of the medial entorhinal. J Neurophysiol 104:258–270
Heys JG, Schultheiss NW, Shay CF, Tsuno Y, Hasselmo ME (2012) Effects of acetylcholine on neuronal properties in entorhinal cortex. Front Behav Neurosci 6:32
Higgs MH, Spain WJ (2009) Conditional bursting enhances resonant firing in neocortical layer 2–3 pyramidal neurons. J Neurosci 29:1285–1299
Hinzer K, Longtin A (1996) Encoding with bursting, subthreshold oscillations, and noise in mammalian cold receptors. Neural Comput 8:215–255
Hu H, Vervaeke K, Storm JF (2002) Two forms of electrical resonance at theta frequencies generated by M-current, h-current and persistent Na\(^{+}\) current in rat hippocampal pyramidal cells. J Physiol 545(3):783–805
Hu H, Vervaeke K, Graham LJ, Storm JF (2009) Complementary theta resonance filtering by two spatially segregated mechanisms in CA1 hippocampal pyramidal neurons. J Neurosci 29:14472–14483
Hutcheon B, Yarom Y (2000) Resonance, oscillations and the intrinsic frequency preferences in neurons. Trends Neurosci 23:216–222
Hutcheon B, Miura RM, Puil E (1996) Models of subthreshold membrane resonance in neocortical neurons. J Neurophysiol 76:698–714
Hutcheon B, Miura RM, Puil E (1996) Subthreshold membrane resonance in neocortical neurons. J Neurophysiol 76:683–697
Izhikevich EM (2002) Resonance and selective communication via bursts in neurons having subthreshold oscillations. Biosystems 67:95–102
Jensen O, Colgin LL (2007) Cross-frequency coupling between neuronal oscillations. Trends Cogn Sci 11:267–269
Kay LM, Beshel J, Brea J, Martin C, Rojas-Líbano D, Kopell N (2008) Olfactory oscillations: the what, how and what for. Trends Neurosci 32:207–214
Khosrovani S, Van Der Giessen RS, De Zeeuw CI, De Jeu MTG (2007) In vivo mouse inferior olive neurons exhibit heterogeneous subthreshold oscillations and spiking patterns. Proc Natl Acad Sci USA 104:15911–15916
Kispersky TJ, Fernandez FR, Economo MN, White JA (2012) Spike resonance properties in hippocampal O-LM cells are dependent on refractory dynamics. J Neurosci 32:3637–3651
Klink RM, Alonso A (1993) Ionic mechanisms for the subthreshold oscillations and differential electroresponsiveness of medial entorhinal cortex layer II neurons. J Neurophysiol 70:128–143
Lampl I, Yarom Y (1993) Subthreshold oscillations of the membrane potential: a functional synchronizing and timing device. J Neurophysiol 70:2181–2186
Lampl I, Yarom Y (1997) Subthreshold oscillations and resonant behaviour: two manifestations of the same mechanism. Neuroscience 78:325–341
Lau T, Zochowski M (2011) The resonance frequency shift, pattern formation, and dynamical network reorganization via sub-threshold input. PLoS ONE 6:e18983
Lee S-G, Neiman A, Kim S (1998) Coherence resonance in a hodgkin-huxley neuron. Phys Rev E 57:3292–3297
Li G, Cleland T (2017) A coupled-oscillator model of olfactory bulb gamma oscillations. PLoS Comp Biol 13:e1005760
Lindner B, García-Ojalvo J, Neiman A, Schimansky-Geier L (2004) Effects of noise in excitable systems. Phys Rep 392:321–424
Llinás RR, Yarom Y (1986) Oscillatory properties of guinea pig olivary neurons and their pharmachological modulation: an in vitro study. J Physiol 376:163–182
Llinás RR, Grace AA, Yarom Y (1991) In vitro neurons in mammalian cortical layer 4 exhibit intrinsic oscillatory activity in the 10- to 50-hz frequency range. Proc Natl Acad Sci USA 88:897–901
Loewenstein Y, Yarom Y, Sompolinsky H (2001) The generation of oscillations in networks of electrically coupled cells. Proc Natl Acad Sci USA 98:8095–8100
Manis PB, Molitor SC, Wu H (1999) Subthreshold oscillations generated by TTX-sensitive sodium currents in dorsal cochlear nucleus pyramidal cells. Exp Brain Res 153:443–451
Manor Y, Rinzel J, Segev I, Yarom Y (1997) Low-amplitude oscillations in the inferior olive: a model based on electrical coupling of neurons with heterogeneous channel densities. J Neurophysiol 77:2736–2752
Marcelin B, Becker A, Migliore M, Esclapez M, Bernard C (2009) h channel-dependent deficit of theta oscillation resonance and phase shift in temporal lobe epilepsy. Neurobiol Dis 33:436–447
Mato G (1989) Stochastic resonance using noise generated by a neural network. Phys Rev E 59:3339–3343
McDonnell MD, Abboott D (2009) What is stochastic resonance? Definitions, misconceptions, debates, and its relevance to biology. PLoS Comp Biol 5:e1000348
McNamara B, Wiesenfeld K (1989) Theory of stochastic resonance. Phys Rev A 39:4854–4869
Mejias JF, Marsat G, Bol K, Maler L, Longtin A (2013) Learning contrast-invariant cancellation of redundant signals in neural systems. PLoS Comp Biol 9:e1003180
Mikiel-Hunter J, Kotak V, Rinzel J (2016) High-frequency resonance in the gerbil medial superior olive. PLoS Comp Biol 12:1005166
Mondal Y (2021) Effects of heterogeneity in oscillatory network dynamics. PhD Thesis, Stony Brook University, Stony Brook, NY
Mondal Y, Pena RFO, Rotsten HG (2021) Temporal filters in response to presynaptic spike trains: Interplay of cellular, synaptic and short-term plasticity time scales. bioRxiv, p. 460719
Morin F, Haufler D, Skinner FK, Lacaille J-C (2010) Characterization of voltage-gated K\(^+\) currents contributing to subthreshold membrane potential oscillations in hippocampal CA1 interneurons. J Neurophysiol 103:3472–3489
Muratov CB, Vanden-Eijnden E, WE (2005) Self-induced stochastic resonance in excitable systems. Physica D, 210: 227–240
Muresan R, Savin C (2007) Resonance or integration? Self-sustained dynamics and excitability of neural microcircuits. J Neurophysiol 97:1911–1930
Narayanan R, Johnston D (2007) Long-term potentiation in rat hippocampal neurons is accompanied by spatially widespread changes in intrinsic oscillatory dynamics and excitability. Neuron 56:1061–1075
Narayanan R, Johnston D (2008) The h channel mediates location dependence and plasticity of intrinsic phase response in rat hippocampal neurons. J Neurosci 28:5846–5850
Neiman A, Saparin PI, Stone L (1997) Coherence resonance at noisy precursors of bifurcations in nonlinear dynamical systems. Phys Rev E 56:270–273
Nolan MF, Dudman JT, Dodson PD, Santoro B (2007) HCN1 channels control resting and active integrative properties of stellate cells from layer II of the entorhinal cortex. J Neurosci 27:12440–12551
Pedroarena CM, Pose IE, Yamuy J, Chase MH, Morales FR (1999) Oscillatory membrane potential activity in the soma of a primary afferent neuron. J Neurophysiol 82:1465–1476
Pena RFO, Rotstein HG (2021) Oscillations and variability in neuronal systems: the role of autonomous transient dynamics in the presence of fast deterministic fluctuations. bioRxiv, p. 448371
Pena RFO, Ceballos CC, Lima V, Roque AC (2018) Interplay of activation kinetics and the derivative conductance determines resonance properties of neurons. Phys Rev E 97:042408
Pena RFO, Lima V, Shimoura RO, Ceballos CC, Rotstein HG, Roque AC (2019) Asymmetrical voltage response in resonant neurons shaped by nonlinearities. Chaos 29:103135
Pike FG, Goddard RS, Suckling JM, Ganter P, Kasthuri N, Paulsen O (2000) Distinct frequency preferences of different types of rat hippocampal neurons in response to oscillatory input currents. J Physiol 529:205–213
Pikovsky AS, Kurths J (1997) Coherence resonance in a noise-driven excitable system. Phys Rev Lett 78:775–778
Pradines JR, Osipov GV, Collins JJ (1999) Coherence resonance in excitable and oscillatory systems: the essential role of slow and fast dynamics. Phys Rev E 60:6407–6410
Prinz AA, Thirumalai V, Marder E (2003) The functional consequences of changes in the strength and duration of synaptic inputs to oscillatory neurons. J Neurosci 23:943–954
Rathour RK, Narayanan R (2012) Inactivating ion channels augment robustness of subthreshold intrinsic response dynamics to parametric variability in hippocampal model neurons. J Physiol 590:5629–5652
Rathour RK, Narayanan R (2014) Homeostasis of functional maps in inactive dendrites emerges in the absence of individual channelostasis. Proc Natl Acad Sci USA 111:E1787–E1796
Rau F, Clemens J, Naumov V, Hennig RM, Schreiber S (2015) Firing-rate resonances in the peripheral auditory system of the cricket, gryllus bimaculatus. J Comp Physiol 201:1075–1090
Reboreda A, Sanchez E, Romero M, Lamas JA (2003) Intrinsic spontaneous activity and subthreshold oscillations in neurones of the rat dorsal column nuclei in culture. J Physiol 551:191–205
Remme MWH, Lengyel M, Gutkin BS (2012) A theoretical framework for the dynamics of multiple intrinsic oscillators in single neurons. In: Phase Response Curves in Neuroscience: Theory, Experiments and Analysis. N. W. Schultheiss, A. A. Prinz and R. A. Butera, Eds. (Springer), pp. 53–72
Remme MWH, Lengyel M, Gutkin BS (2014) A trade-off between dendritic democracy and independence in neurons with intrinsic subthreshold membrane potential oscillations. In: Cuntz H, Remme MWH, Torben-Nielsen B (eds) The Computing Dendrite. Springer, New York
Remme WH, Donato R, Mikiel-Hunter J, Ballestero JA, Foster S, Rinzel J, McAlpine D (2014) Subthreshold resonance properties contribute to the efficient coding of auditory spatial cues. Proc Natl Acad Sci USA 111:E2339–E2348
Richardson MJE, Brunel N, Hakim V (2003) From subthreshold to firing-rate resonance. J Neurophysiol 89:2538–2554
Rotstein HG (2014) Frequency preference response to oscillatory inputs in two-dimensional neural models: a geometric approach to subthreshold amplitude and phase resonance. J Math Neurosci 4:11
Rotstein HG (2015) Subthreshold amplitude and phase resonance in models of quadratic type: nonlinear effects generated by the interplay of resonant and amplifying currents. J Comp Neurosci 38:325–354
Rotstein HG (2017) Resonance modulation, annihilation and generation of antiresonance and antiphasonance in 3d neuronal systems: interplay of resonant and amplifying currents with slow dynamics. J Comp Neurosci 43:35–63
Rotstein HG (2017) Spiking resonances in models with the same slow resonant and fast amplifying currents but different subthreshold dynamic properties. J Comp Neurosci 43:243–271
Rotstein HG (2017) The shaping of intrinsic membrane potential oscillations: positive/negative feedback, ionic resonance/amplification, nonlinearities and time scales. J Comp Neurosci 42:133–166
Rotstein HG, Nadim F (2014) Frequency preference in two-dimensional neural models: a linear analysis of the interaction between resonant and amplifying currents. J Comp Neurosci 37:9–28
Rotstein HG, Nadim F (2019) Frequency dependent responses of neuronal models to oscillatory inputs in current versus voltage clamp. Biol Cybern 113:373–395
Rotstein HG, Oppermann T, White JA, Kopell N (2006) The dynamic structure underlying subthreshold oscillatory activity and the onset of spikes in a model of medial entorhinal cortex stellate cells. J Comp Neurosci 21:271–292
Schmitz D, Gloveli T, Behr J, Dugladze T, Heinemann U (1998) Subthreshold membrane potential oscillations in neurons of deep layers of the entorhinal cortex. Neuron 85:999–1004
Schreiber S, Erchova I, Heinemann U, Herz AV (2004) Subthreshold resonance explains the frequency-dependent integration of periodic as well as random stimuli in the entorhinal cortex. J Neurophysiol 92:408–415
Sciamanna G, Wilson CJ (2011) The ionic mechanism of gamma resonance in rat striatal fast-spiking neurons. J Neurophysiol 106:2936–2949
Sharp AA, O’Neil MB, Abbott LF, Marder E (1993) The dynamic clamp: artificial conductances in biological neurons. Trends Neurosci 16:389–394
Solinas S, Forti L, Cesana E, Mapelli J, De Schutter E, D’Angelo E (2007) Fast-reset of pacemaking and theta-frequency resonance in cerebellar Golgi cells: simulations of their impact in vivo. Front Cell Neurosci 1:4
Song SC, Beatty JA, Wilson CJ (2016) The ionic mechanism of membrane potential oscillations and membrane resonance in striatal lts interneurons. J Neurophysiol 116:1752–1764
Stark E, Eichler R, Roux L, Fujisawa S, Rotstein HG, Buzsáki G (2013) Inhibition-induced theta resonance in cortical circuits. Neuron 80:1263–1276
Stiefel KM, Fellous J-M, Thomas PJ, Sejnowski TJ (2010) Intrinsic subthreshold oscillations extend the influence of inhibitory synaptic inputs on cortical pyramidal neurons. Eur J Neurosci 31:1019–1026
Surmeier DJ, Mercer JN, Chan CS (2005) Autonomous pacemakers in the basal ganglia: Who needs excitatory synapses anyway? Curr Opin Neurobiol 15:312–318
Szucs A, Ráktak A, Schlett K, Huerta R (2017) Frequency-dependent regulation of intrinsic excitability by voltage-activated membrane conductances, computational modeling and dynamic clamp. Eur J Neurosci 46:2429–2444
Tateno T, Pakdaman K (2004) Random dynamics of the morris-lecar neural model. Chaos 14:511–530
Tohidi V, Nadim F (2009) Membrane resonance in bursting pacemaker neurons of an oscillatory network is correlated with network frequency. J Neurosci 29:6427–6435
Torres JJ, Marro J, Mejias JF (2011) Can intrinsic noise induce various resonant peaks? New J Phys 13:053014
Tseng H, Nadim F (2010) The membrane potential waveform on bursting pacemaker neurons is a predictor of their preferred frequency and the network cycle frequency. J Neurosci 30:10809–10819
Tuckwell HC (1989) Stochastic processes in the neurosciences. The Society for Industrial and Applied Mathematics
Tuckwell HC (1988) Introduction to Theoretical Neurobiology, vol 2. Cambridge University Press, Cambridge
Uhlenbeck GE, Ornstein LS (1930) On the theory of brownian motion. Phys Rev 36:823–841
Uzuntarla M, Barreto E, Torres J (2017) Inverse stochastic resonance in networks of spiking neurons. PLoS Comp Biol 13:e1005646
van Brederode JFM, Berger AJ (2008) Spike-firing resonance in hypoglossal motoneurons. J Neurophysiol 99:2916–2928
Wang XJ (2010) Neurophysiological and computational principles of cortical rhythms in cognition. Physiol Rev 90:1195–1268
White JA, Budde T, Kay AR (1995) A bifurcation analysis of neuronal subthreshold oscillations. Biophys J 69:1203–1217
White JA, Klink R, Alonso A, Kay AR (1998) Noise from voltage-gated ion channels may influence neuronal dynamics in the entorhinal cortex. J Neurophysiol 80:262–269
Wiesenfeld K, Moss F (1995) Stochastic resonance and the benefits of noise: from ice ages to crayfish and SQUIDs. Nature 373:33–36
Wilson CJ, Callaway JC (2000) A coupled oscillator model of the dopaminergic neurons of the substantia Nigra. J Neurophysiol 83:3084–3100
Wu N, Hsiao C-F, Chandler SH (2001) Membrane resonance and subthreshold membrane oscillations in mesencephalic V neurons: Participants in burst generation. J Neurosci 21:3729–3739
Yang S, Lin W, Feng AA (2009) Wide-ranging frequency preferences of auditory midbrain neurons: roles of membrane time constant and synaptic properties. Eur J Neurosci 30:76–90
Yoshida M, Alonso A (2007) Cell-type-specific modulation of intrinsic firing properties and subthreshold membrane oscillations by the M(Kv7)-currents in neurons of the entorhinal cortex. J Neurophysiol 98:2779–2994
Yoshida M, Giocomo LM, Boardman I, Hasselmo ME (2011) Frequency of subthreshold oscillations at different membrane potential voltages in neurons at different anatomical positions on the dorsoventral axis in the rat medial entorhinal cortex. J Neurosci 31:12683–12694
Zemankovics R, Káli S, Paulsen O, Freund TF, Hájos N (2010) Differences in subthreshold resonance of hippocampal pyramidal cells and interneurons: The role of h-current and passive membrane characteristics. J Physiol 588:2109–2132
Zhang F, Wang L-P, Brauner M, Lewwald JF, Kay K, Watzke N, Wookd PG, Bamberg E, Nagel G, Gottschalk A, Deisseroth K (2007) Multimodal fast optical interrogation of neural circuitry. Nature 446:633–641
Zhuchkova E, Remme MWH, Schreiber S (2014) Subthreshold resonance and membrane potential oscillations in a neuron with nonuniform active dendrite properties. In: Cuntz H, Remme MWH, Torben-Nielsen B (eds) The Computing Dendrite. Springer, New York
Acknowledgements
This work was partially supported by the National Science Foundation grant DMS-1608077 (HGR).
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Antonio C. Roque.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This article belongs to Special Issue: Stochastic Oscillators.
Supplementary Information
Below is the link to the electronic supplementary material.
Appendix: Intrinsic and resonant oscillatory properties of 2D linear systems
Appendix: Intrinsic and resonant oscillatory properties of 2D linear systems
Consider
where a, b, c and d are constants, \( \omega = 2 \pi f / 1000 > 0 \) is the input frequency and \( A_{in} \ge 0 \) is the input amplitude. The prime sign represents the derivative with respect to t. The units of t are ms and the units of f are Hz.
1.1 Intrinsic oscillations
The characteristic polynomial for the corresponding homogeneous system (\(A_{in} = 0 \)) is given by
The eigenvalues are given by
and the natural (intrinsic) frequency of the (damped) oscillations (in Hz if t has units of ms) is given by
assuming \( (a-d)^2+4 b c < 0 \).
1.2 Resonance and the impedance amplitude profile
The impedance amplitude profile \( Z(\omega ) \) for system (15)–(16) is the magnitude
of the complex valued coefficient of the particular solution to the system
For 1D system, these quantities are given, respectively, by
and
The resonance frequency \( f_{\text {res}} \) (in Hz if t has units of ms) is the frequency at which Z reaches its maximum
Rights and permissions
About this article
Cite this article
Pena, R.F.O., Rotstein, H.G. The voltage and spiking responses of subthreshold resonant neurons to structured and fluctuating inputs: persistence and loss of resonance and variability. Biol Cybern 116, 163–190 (2022). https://doi.org/10.1007/s00422-021-00919-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00422-021-00919-0