Modeling the Potential Role of Engineered Symbiotic Bacteria in Malaria Control

Abstract

Recent experimental study suggests that the engineered symbiotic bacteria Serratia AS1 may provide a novel, effective and sustainable biocontrol of malaria. These recombinant bacteria have been shown to be able to rapidly disseminate throughout mosquito populations and to efficiently inhibit development of malaria parasites in mosquitoes in controlled laboratory experiments. In this paper, we develop a climate-based malaria model which involves both vertical and horizontal transmissions of the engineered Serratia AS1 bacteria in mosquito population. We show that the dynamics of the model system is totally determined by the vector reproduction ratio $R_\mathrm{v}$, and the basic reproduction ratio $R_0$. If $R_\mathrm{v}\le 1$, then the mosquito-free state is globally attractive. If $R_\mathrm{v}>1$ and $R_0\le 1$, then the disease-free periodic solution is globally attractive. If $R_\mathrm{v}>1$ and $R_0>1$, then the positive periodic solution is globally attractive. Numerically, we verify the obtained analytic result and evaluate the effects of releasing the engineered Serratia AS1 bacteria in field by conducting a case study for Douala, Cameroon. We find that ideally, by using Serratia AS1 alone, it takes at least 25 years to eliminate malaria from Douala. This implies that continued long-term investment is needed in the fight against malaria and confirms the necessity of integrating multiple control measures.

1 Introduction

Malaria is a mosquito-borne infectious disease caused by Plasmodium protozoan parasites, which is accountable for a substantial public health and economic burden across tropics and subtropics. According to the estimates of World Health Organization, about 216 million cases and 445,000 deaths due to malaria occurred globally in 2016, mostly in WHO African region. Malaria is transmitted among humans by the bites of female Anopheles mosquitoes. If a mosquito carrying the malaria parasites bites a susceptible human, then the parasites may enter the blood stream of the human body and undergo several developmental stages, infecting human liver cells and red blood cells. Eventually, the parasites evolve into gametocytes which may be ingested by another mosquito, leading to the infection of malaria for that mosquito. Inside the mosquito, malaria parasites also need to complete a few stages to make the mosquito become infectious. Once the parasites enter the salivary glands of the mosquito in the form of sporozoites, the mosquito can inject them into another person during another blood meal (https://www.cdc.gov/malaria/about/biology/index.html).

The use of insecticide-treated bed nets (ITNs), indoor residual spraying and other vector control strategies have made a great contribution in malaria control, resulting in a dramatic reduction in infection prevalence and clinical incidence between 2000 and 2015 (Bhatt et al. 2006). However, in recent years, the benefits of these control measures are greatly compromised by the frequent emergence of insecticide resistance and drug resistance driven by the selective pressures of insecticides and antimalarial drugs (Hemingway and Ranson 2000; Trape 2001). In addition, there is no safe and effective vaccine for use in humans at the current moment (World Health Organization 2018). Climate change also poses a vast challenge for malaria control. It has been shown that both mosquitoes and malaria parasites are highly sensitive to temperature (Shapiro et al. 2017). Global warming may worsen the malaria transmission case in current endemic regions and cause malaria to establish in new areas or re-emerge in some malaria-eliminated regions (Rogers and Randolph 2000). Facing these challenges, new sustainable strategies are urgently needed to control this deadly disease. With the fast development of bio-technology, some artificial control methods such as the use of symbiotic bacteria have appeared in fighting against mosquito-borne diseases. For example, it is very promising to control dengue fever, chikungunya and Zika disease by releasing A. aegypti mosquitoes infected by the bacterium Wolbachia since the bacteria can limit the vectorial competence of A. aegypti (Bliman et al. 2018; Ruang-Areerate and Kittayapong 2006).

The Johns Hopkins group led by Marcelo Jacobs-Lorena, where Sibao Wang is a member, earlier found that the engineered bacteria Pantoea agglomerans can inhibit the development of malaria parasites by up to $98\%$ and reduce the proportion of infected mosquitoes by $84\%$ in lab setting (Wang et al. 2012). The challenge then was to introduce and propagate recombinant bacteria in mosquito populations in the field. Recently, Sibao Wang came up with his own engineered bacterium, tagged Serratia AS1, that can do so (Wang et al. 2017). Serratia AS1 is a strain of nonpathogenic bacteria which are able to stably colonize and persist in several mosquito organs including midguts, hemolymphs, ovaries and accessory glands. In fact, the AS1 bacteria carry the same anti-Plasmodium genes that the Jacobs-Lorena team added into Pantoea agglomerans; and, unlike other bacteria, AS1 is known to spread like “wild fire.” AS1 bacteria can be transferred from male mosquitoes to virgin females during mating. They observed that AS1 bacteria attached to the laid eggs, floated and propagated in the water and were ingested by the larvae that hatched from these eggs, and that AS1 continued to rapidly proliferate in the midguts of adults that emerged from these larvae. To investigate the efficiencies of AS1 bacteria dissemination through a life cycle and transmission from one generation to another, they mixed 10 AS1-infected virgin female mosquitoes and 10 AS1-infected virgin male mosquitoes with 190 uninfected virgin female mosquitoes and 190 uninfected virgin male mosquitoes in a laboratory cage. They found that AS1 were present in all larvae and adults for three generations. This suggests that Serratia AS1 bacteria can be transmitted both vertically and horizontally and are likely to exhibit long-term persistence in wild mosquito populations. Moreover, Serratia AS1 bacteria showed no obvious negative effect on mosquito lifespan, fecundity, fertility or blood feeding behaviors. These results indicate that the engineered Serratia AS1 bacteria have the potential to become a promising biocontrol of malaria with almost no bad effect on mosquito life cycle or environment. How well can the engineered Serratia AS1 bacteria be engaged in combating malaria in field? How will the AS1 bacteria impact malaria transmission dynamics? Is it possible to eliminate malaria from some areas by releasing AS1 bacteria or AS1-infected mosquitoes? We intend to seek answers to these questions by mathematical modeling.

The first malaria model was proposed by Ross (1911) and later modified by Macdonald (1957). Since then an increasing number of mathematical models have been developed to study malaria transmission dynamics including different factors such as seasonality, stage structure of mosquitoes, immunity, different parasite species, extrinsic incubation period, the spatial effects, the effects of various control strategies and so on (see, e.g., Ai et al. 2012; Arino et al. 2012; Ngonghala et al. 2016; Wang and Zhao 2017; Xiao and Zou 2013a, b, 2014 and the references therein). In the analysis of these models, the basic reproduction ratio is a key parameter in determining the disease transmission threshold dynamics. It is also one of the foremost and most valuable ideas that mathematical thinking has brought to epidemiology. Following the pioneering works on $R_0$ by Diekmann et al. (1990) and van den Driessche and Watmough (2002), there are several papers about the theory and applications of $R_0$ for various types of models (see, e.g., Bacaër and Ait Dads 2012; Bacaër and Guernaoui 2006; Inaba 2012; Thieme 2009; Wang and Zhao 2008; Zhao 2017 and the references therein). In this paper, we will develop and analyze a climate-based malaria transmission model taking into account the transmission of Serratia AS1 bacteria among the mosquito population. To analyze our model, we will identify two threshold parameters: one is related to the threshold dynamics of the mosquito population, whereas the other determines the disease transmission dynamics. We hope that our work can help gain insights into the potential role of the engineered Serratia AS1 bacteria can play in malaria control and hopefully provide some guidance for future field release trials.

The rest of this paper is organized as follows. In the next section, we formulate the model. In Sect. 3, we derive two critical parameters: the vector reproduction ratio $R_\mathrm{v}$, and the basic reproduction ratio $R_0$. Then, we show the threshold dynamics of the model system in terms of $R_\mathrm{v}$ and $R_0$. In Sect. 4, we carry out a case study for a Sub-Saharan African country to investigate the potential role of engineered Serratia AS1 bacteria in malaria control. We give a brief discussion is Sect. 5.

2 Model Formulation

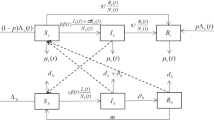
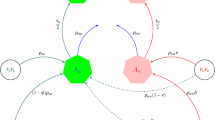
Motivated by the models in Ai et al. (2012), Lou and Zhao (2011), Wang and Zhao (2018), we divide the female mosquito population into the larval and the adult groups. We use $L_\mathrm{v}(t)$ to denote the number of female larval mosquitoes at time t. The advantages of considering the larval stage mosquitoes mainly include the following three points: (i) The dynamics of the larval stage of mosquitoes influences that of the adult mosquito population, and hence, affects the disease transmission dynamics; (ii) it would be helpful for investigating larval control strategies based on a model having the larval stage; (iii) since the experiment in Wang et al. (2017) involves the transmission of Serratia AS1 bacteria from larvae to adults, the larval stage should be included in order to model this vertical transmission phenomenon. We divide the adult group into malaria-susceptible mosquitoes and malaria-infective ones. Let $S_\mathrm{v}(t)$ and $I_\mathrm{v}(t)$ be the numbers of adult female malaria-susceptible and malaria-infective mosquitoes at time t, respectively. We assume that the total number of human population stabilizes at a constant value $N_\mathrm{h}$. Let $I_\mathrm{h}(t)$ be the number of malaria-infected humans at time t. It follows that the number of susceptible humans at time t is $N_\mathrm{h}-I_\mathrm{h}(t)$. With the above preparation we arrive at the following climate-based malaria transmission model without Serratia AS1 bacteria-infected mosquitoes:

$$\begin{aligned} \begin{aligned} \frac{\mathrm{d}L_\mathrm{v}(t)}{\mathrm{d}t}&=\lambda (t)(S_\mathrm{v}(t)+I_\mathrm{v}(t))-\mu _l(t)L_\mathrm{v}(t)-\alpha L_\mathrm{v}(t)^2-\delta (t)L_\mathrm{v}(t), \\ \frac{\mathrm{d}S_\mathrm{v}(t)}{\mathrm{d}t}&=\delta (t)L_\mathrm{v}(t)-\mu _\mathrm{v}(t)S_\mathrm{v}(t)-b\beta (t)\frac{I_\mathrm{h}(t)}{N_\mathrm{h}}S_\mathrm{v}(t), \\ \frac{\mathrm{d}I_\mathrm{v}(t)}{\mathrm{d}t}&=b\beta (t)\frac{I_\mathrm{h}(t)}{N_\mathrm{h}}S_\mathrm{v}(t)-\mu _\mathrm{v}(t)I_\mathrm{v}(t),\\ \frac{\mathrm{d}I_\mathrm{h}(t)}{\mathrm{d}t}&=c\beta (t)\frac{N_\mathrm{h}-I_\mathrm{h}(t)}{N_\mathrm{h}}I_\mathrm{v}(t)-(d_\mathrm{h}+\rho )I_\mathrm{h}(t). \end{aligned} \end{aligned}$$

(1)

Here, $\lambda (t)$ is the recruitment rate of larval mosquitoes, $\mu _l(t)$ is the natural death rate of larval mosquitoes, $\alpha$ is the mortality rate of larval mosquitoes due to intraspecies competition, $\delta (t)$ is the maturation rate of mosquitoes, and $\mu _\mathrm{v}(t)$ is the mortality rate of adult mosquitoes. The term $b\beta (t)\frac{I_\mathrm{h}(t)}{N_\mathrm{h}}S_\mathrm{v}(t)$ represents the number of newly occurred malaria-infected mosquitoes per unit time at time t, where b is the transmission probability of malaria from infectious humans to susceptible mosquitoes and $\beta (t)$ is the biting rate of mosquitoes. Similarly, $c\beta (t)\frac{N_\mathrm{h}-I_\mathrm{h}(t)}{N_\mathrm{h}}I_\mathrm{v}(t)$ is the number of newly occurred infected humans per unit time at time t, where c is the transmission probability from infected mosquitoes to susceptible humans. Compared with mosquitoes, humans are much less likely affected by climate factors. Thus, we incorporate seasonality into the model by considering that only the parameters related to mosquitoes are positive, continuous and $\omega$-periodic functions and assuming that for humans the natural death rate $d_\mathrm{h}$, and the recovery rate $\rho$ are positive constants.

The idea of using engineered Serratia AS1 bacteria to control malaria is to make mosquitoes incapable of transmitting malaria. Thus, we need to introduce a new variable to represent the number of vectors infected with AS1 bacteria in our model. We denote such a variable as $B_\mathrm{v}(t)$, that is the number of AS1 bacteria-infected adult female mosquitoes at time t. Based on the findings in the experimental study, we pose the following assumptions.

• (i) Among all the adult mosquitoes infected with the bacteria, we assume that the sex ratio is 1 : 1.

• (ii) Both malaria-susceptible and malaria-infected wild mosquitoes can be infected with Serratia AS1 bacteria through mating with AS1-infected mosquitoes.

• (iii) Malaria-susceptible mosquitoes will not be infected with malaria once they are infected with Serratia AS1 bacteria (suggested by Wang et al. (2017)).

• (iv) Malaria-infected mosquitoes will not be able to transmit malaria once they are infected with Serratia AS1 bacteria.

In the experimental study reported in Wang et al. (2017), newly emerged larvae and adult mosquitoes are all infected with AS1 bacteria. However, this may not be the case if we release AS1 bacteria in some mosquito breeding water in field. For example, if we release the bacteria in some location whose surface area may be so large that we cannot guarantee every newly born mosquito get infected with the bacteria. To model the vertical transmission of AS1 bacteria, we assume that a proportion p of larvae are infected with AS1 and the remaining proportion $1-p$ grow into adults with no infection of AS1. From assumption (i), we know that the number of AS1-infected adult male mosquitoes at time t is also $B_\mathrm{v}(t)$. We describe the horizontal transmission of AS1 bacteria by the terms $q\gamma \frac{S_\mathrm{v}(t)}{S_\mathrm{v}(t)+I_\mathrm{v}(t)+B_\mathrm{v}(t)}B_\mathrm{v}(t)$ and $q\gamma \frac{I_\mathrm{v}(t)}{S_\mathrm{v}(t)+I_\mathrm{v}(t)+B_\mathrm{v}(t)}B_\mathrm{v}(t)$ where q is the transmission probability of Serratia AS1 bacteria from a male mosquito to a female during a sexual contact and $\gamma$ is the sexual contact rate of mosquitoes [see Heffernan et al. (2014) for more details about modeling of sexual transmitted diseases]. Incorporating the variable $B_\mathrm{v}(t)$ into (1) based on the above discussion, we obtain our model described by the following non-autonomous system of ordinary differential equations:

$$\begin{aligned} \begin{aligned} \frac{\mathrm{d}L_\mathrm{v}(t)}{\mathrm{d}t}&=\lambda (t)(S_\mathrm{v}(t)+I_\mathrm{v}(t)+B_\mathrm{v}(t))-\mu _l(t)L_\mathrm{v}(t)-\alpha L_\mathrm{v}(t)^2-\delta (t)L_\mathrm{v}(t), \\ \frac{\mathrm{d}S_\mathrm{v}(t)}{\mathrm{d}t}&=(1-p)\delta (t)L_\mathrm{v}(t)-\mu _\mathrm{v}(t)S_\mathrm{v}(t)-q\gamma \frac{S_\mathrm{v}(t)}{S_\mathrm{v}(t)+I_\mathrm{v}(t)+B_\mathrm{v}(t)}B_\mathrm{v}(t)\\&\quad -\,b\beta (t)\frac{I_\mathrm{h}(t)}{N_\mathrm{h}}S_\mathrm{v}(t), \\ \frac{\mathrm{d}I_\mathrm{v}(t)}{\mathrm{d}t}&=b\beta (t)\frac{I_\mathrm{h}(t)}{N_\mathrm{h}}S_\mathrm{v}(t)-\mu _\mathrm{v}(t)I_\mathrm{v}(t)-q\gamma \frac{I_\mathrm{v}(t)}{S_\mathrm{v}(t)+I_\mathrm{v}(t)+B_\mathrm{v}(t)}B_\mathrm{v}(t),\\ \frac{\mathrm{d}B_\mathrm{v}(t)}{\mathrm{d}t}&=p\delta (t)L_\mathrm{v}(t)-\mu _\mathrm{v}(t)B_\mathrm{v}(t)+q\gamma \frac{S_\mathrm{v}(t)+I_\mathrm{v}(t)}{S_\mathrm{v}(t)+I_\mathrm{v}(t)+B_\mathrm{v}(t)}B_\mathrm{v}(t), \\ \frac{\mathrm{d}I_\mathrm{h}(t)}{\mathrm{d}t}&=c\beta (t)\frac{N_\mathrm{h}-I_\mathrm{h}(t)}{N_\mathrm{h}}I_\mathrm{v}(t)-(d_\mathrm{h}+\rho )I_\mathrm{h}(t). \end{aligned} \end{aligned}$$

(2)

For readers’ convenience, we give the interpretation of all variables and parameters in Table 1.

Table 1 Biological interpretations for variables and parameters of model (2)

3 Threshold Dynamics

If $p=1$, then the dynamics of the model system is trivial. From the second equation of system (2), we have $\lim _{t\rightarrow \infty }S_\mathrm{v}(t)=0$. Then from the third equation of (2), it is easy to see that $\lim _{t\rightarrow \infty }I_\mathrm{v}(t)=0$, and hence, from the last equation of (2) we obtain $\lim _{t\rightarrow \infty }I_\mathrm{h}(t)=0$. Considering that in reality, it is impossible to guarantee $p=1$, we assume that $0\le p<1$ in the rest of this section.

Let $N_\mathrm{v}(t)=S_\mathrm{v}(t)+I_\mathrm{v}(t)+B_\mathrm{v}(t)$. Then, system (2) is equivalent to the following system:

$$\begin{aligned} \begin{aligned} \frac{\mathrm{d}L_\mathrm{v}(t)}{\mathrm{d}t}&=\lambda (t)N_\mathrm{v}(t)-\mu _l(t)L_\mathrm{v}(t)-\alpha L_\mathrm{v}(t)^2-\delta (t)L_\mathrm{v}(t), \\ \frac{\mathrm{d}N_\mathrm{v}(t)}{\mathrm{d}t}&=\delta (t)L_\mathrm{v}(t)-\mu _\mathrm{v}(t)N_\mathrm{v}(t), \\ \frac{\mathrm{d}B_\mathrm{v}(t)}{\mathrm{d}t}&=p\delta (t)L_\mathrm{v}(t)-\mu _\mathrm{v}(t)B_\mathrm{v}(t)+q\gamma \frac{N_\mathrm{v}(t)-B_\mathrm{v}(t)}{N_\mathrm{v}(t)}B_\mathrm{v}(t) \\ \frac{\mathrm{d}I_\mathrm{v}(t)}{\mathrm{d}t}&=b\beta (t)\frac{I_\mathrm{h}(t)}{N_\mathrm{h}}(N_\mathrm{v}(t)-B_\mathrm{v}(t)-I_\mathrm{v}(t))-\mu _\mathrm{v}(t)I_\mathrm{v}(t)-q\gamma \frac{I_\mathrm{v}(t)}{N_\mathrm{v}(t)}B_\mathrm{v}(t),\\ \frac{\mathrm{d}I_\mathrm{h}(t)}{\mathrm{d}t}&=c\beta (t)\frac{N_\mathrm{h}-I_\mathrm{h}(t)}{N_\mathrm{h}}I_\mathrm{v}(t)-(d_\mathrm{h}+\rho )I_\mathrm{h}(t). \end{aligned} \end{aligned}$$

(3)

Note that the first two equations of system (3) is decoupled from the other three equations. Thus, we first study the following system:

$$\begin{aligned} \begin{aligned} \frac{\mathrm{d}L_\mathrm{v}(t)}{\mathrm{d}t}&=\lambda (t)N_\mathrm{v}(t)-\mu _l(t)L_\mathrm{v}(t)-\alpha L_\mathrm{v}(t)^2-\delta (t)L_\mathrm{v}(t), \\ \frac{\mathrm{d}N_\mathrm{v}(t)}{\mathrm{d}t}&=\delta (t)L_\mathrm{v}(t)-\mu _\mathrm{v}(t)N_\mathrm{v}(t). \end{aligned} \end{aligned}$$

(4)

Linearizing system (4) at (0, 0), we obtain the following linear cooperative system:

$$\begin{aligned} \begin{aligned} \frac{\mathrm{d}L_\mathrm{v}(t)}{\mathrm{d}t}&= \lambda (t)N_\mathrm{v}(t)-(\mu _l(t)+\delta (t))L_\mathrm{v}(t), \\ \frac{\mathrm{d}N_\mathrm{v}(t)}{\mathrm{d}t}&= \delta (t)L_\mathrm{v}(t) -\mu _\mathrm{v}(t)N_\mathrm{v}(t). \end{aligned} \end{aligned}$$

(5)

We rewrite system (5) as $\frac{\mathrm{d}v}{\mathrm{d}t}=({\tilde{F}}(t)-{\tilde{V}}(t))v$, where

$$\begin{aligned} {\tilde{F}}(t)=\begin{bmatrix} 0&\lambda (t)\\ 0&0 \end{bmatrix},\quad {\tilde{V}}(t)=\begin{bmatrix} \mu _l(t)+\delta (t)&0\\ -\delta (t)&\mu _\mathrm{v}(t)\end{bmatrix}. \end{aligned}$$

Let ${\tilde{Y}}(t,s), t\ge s$, be the evolution operator of the linear periodic system

$$\begin{aligned} \frac{\mathrm{d}y}{\mathrm{d}t}=-{\tilde{V}}(t)y, \end{aligned}$$

which is represented as a $2\times 2$ matrix. That is, for each $s\in {\mathbb {R}}$, the $2\times 2$ matrix ${\tilde{Y}}(t,s)$ satisfies

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}{\tilde{Y}}(t,s)=-{\tilde{V}}(t){\tilde{Y}}(t,s),\quad \forall t\ge s,\quad {\tilde{Y}}(s,s)=I, \end{aligned}$$

where I is the $2\times 2$ identity matrix.

Let $C_\omega$ be the ordered Banach space of all $\omega$-periodic functions from ${\mathbb {R}}$ to ${\mathbb {R}}^2$, equipped with the maximum norm and the positive cone $C_\omega ^+:=\{\phi \in C_\omega : \phi (t)\ge 0, \forall t\in {\mathbb {R}}\}$. According to Wang and Zhao (2008, Sect. 2), we assume that $\phi (s)\in C_\omega$ is the initial distribution of mosquitoes. Then, ${\tilde{F}}(s)\phi (s)$ is the distribution of new larval mosquitoes produced by the adults introduced at time s. Given $t\ge s$, then ${\tilde{Y}}(t,s){\tilde{F}}(s)\phi (s)$ gives the distribution of those mosquitoes who were newly born into the larval mosquito compartment at time s and remain alive (either as larval mosquitoes or as adult ones) at time t. It follows that

$$\begin{aligned} \psi (t):=\int _{-\infty }^t{\tilde{Y}}(t,s){\tilde{F}}(s)\phi (s)\mathrm{d}s=\int _0^{\infty }{\tilde{Y}}(t,t-a){\tilde{F}}(t-a)\phi (t-a)\mathrm{d}a \end{aligned}$$

is the distribution of accumulative new larval and adult mosquitoes at time t produced by all those adult mosquitoes $\phi (s)$ introduced before the time t.

We define a linear operator ${\tilde{L}}: C_\omega \rightarrow C_\omega$ by

$$\begin{aligned} ({\tilde{L}}\phi )(t)=\int _0^{\infty }{\tilde{Y}}(t,t-a){\tilde{F}}(t-a)\phi (t-a)\mathrm{d}a,\quad \forall t\in {\mathbb {R}},\quad \phi \in C_\omega . \end{aligned}$$

It then follows from Wang and Zhao (2008) that the vector reproduction ratio is $R_\mathrm{v}:=\rho ({\tilde{L}})$, the spectral radius of ${\tilde{L}}$. Let $r_1$ be the principal Floquét multiplier of system (5), that is, the spectral radius of the Poincaré map associated with system (5). By Wang and Zhao (2008, Theorem 2.2), $R_\mathrm{v}-1$ has the same sign as $r_1-1$. As a straightforward consequence of Zhao (2003, Theorem 3.1.2), we have the following result.

Lemma 1

The following statements are valid:

• (i) If $R_\mathrm{v}\le 1$, then (0, 0) is globally attractive for system (4) in ${\mathbb {R}}_+^2$;

• (ii) If $R_\mathrm{v}>1,$ then system (4) admits a unique positive $\omega$-periodic solution $(L_\mathrm{v}^*(t), N_\mathrm{v}^*(t))$, which is globally attractive for system (4) in ${\mathbb {R}}_+^2\setminus \{(0,0)\}$.

Let $W=\{(\varphi _1, \varphi _2, \varphi _3, \varphi _4, \varphi _5)\in {\mathbb {R}}_+^5: \varphi _2>0, \varphi _2\ge \varphi _3, \varphi _2\ge \varphi _4, \varphi _5\le N_\mathrm{h}\}$. We have the following preliminary result for system (3) on the invariance of W.

Lemma 2

For any $\varphi \in W$, system (3) has a unique nonnegative bounded solution $u(t,\varphi )$ on $[0,\infty )$ with $u(0)=\varphi$, and $u(t,\varphi )\in W$ for all $t\ge 0$.

Proof

For any $\varphi =(\varphi _1, \varphi _2, \varphi _3, \varphi _4, \varphi _5)\in W$, we define

$$\begin{aligned} {\hat{f}}(t,\varphi )= \left( \begin{array}{c} \lambda (t)\varphi _2-\mu _l(t)\varphi _1 -\alpha \varphi _1^2-\delta (t)\varphi _1\\ \delta (t)\varphi _1-\mu _\mathrm{v}(t)\varphi _2\\ p\delta (t)\varphi _1-\mu _\mathrm{v}(t)\varphi _3+q\gamma \frac{\varphi _2-\varphi _3}{\varphi _2}\varphi _3\\ b\beta (t)\frac{\varphi _5}{N_\mathrm{h}}(\varphi _2-\varphi _3-\varphi _4)-\mu _\mathrm{v}(t)\varphi _4-q\gamma \frac{\varphi _4}{\varphi _2}\varphi _3\\ c\beta (t)\frac{N_\mathrm{h}-\varphi _5}{N_\mathrm{h}}\varphi _4-(d_\mathrm{h}+\rho )\varphi _5 \end{array} \right) . \end{aligned}$$

Since ${\hat{f}}(t,\varphi )$ is continuous in $(t,\varphi )\in {\mathbb {R}}\times W$, and ${\hat{f}}(t,\varphi )$ is Lipschitz in $\varphi$ on each compact subset of W, it follows that system (3) has a unique solution $u(t,\varphi )$ on its maximal interval $[0,\sigma _\varphi )$ of existence with $u(0)=\varphi$ [see, e.g., Hale and Verduyn Lunel (1993, Theorems 2.2.1 and 2.2.3)].

Let $\varphi =(\varphi _1, \varphi _2, \varphi _3, \varphi _4, \varphi _5)\in {\mathbb {R}}_+^4\times [0,N_\mathrm{h}]$ with $\varphi _2\ge \varphi _3$ and $\varphi _2\ge \varphi _4$ be given. If $\varphi _i=0$ for some $i\in \{1,2,3,4,5\}$, then ${\hat{f}}_i(t,\varphi )\ge 0$. If $\varphi _5=N_\mathrm{h}$, then ${\hat{f}}_5(t,\varphi )\le 0$. By Smith (1995, Theorem 5.2.1 and Remark 5.2.1), it follows that for any $\varphi \in {\mathbb {R}}_+^4\times [0,N_\mathrm{h}]$, the unique solution $u(t,\varphi )$ of system (3) with $u(0)=\varphi$ satisfies $u(t,\varphi )\in {\mathbb {R}}_+^4\times [0,N_\mathrm{h}]$ for all $t\in [0,\sigma _\varphi )$. It is easy to see that $u_2(t,\varphi )\ge u_3(t,\varphi )$ and $u_2(t,\varphi )\ge u_4(t,\varphi )$ for all $t\in [0,\sigma _\varphi )$. Clearly, $0\le u_5(t,\varphi )\le N_\mathrm{h}$ for all $t\in [0,\sigma _\varphi )$. It follows from Lemma 1 that there exists $M_1>0$ and $M_2>0$ such that $u_1(t,\varphi )\le M_1$ and $u_2(t,\varphi )\le M_2$ for all $t\in [0,\sigma _\varphi )$. Then, Hale and Verduyn Lunel (1993, Theorem 2.3.1) implies that $\sigma _\varphi =\infty$.

From the second equation of system (3), we have

$$\begin{aligned} \frac{\mathrm{d}N_\mathrm{v}(t)}{\mathrm{d}t}\ge -\mu _\mathrm{v}(t)N_\mathrm{v}(t). \end{aligned}$$

It then easily follows that $u_2(t,\varphi )>0$ for all $t\ge 0$. This proves Lemma 2. $\square$

If $R_\mathrm{v}\le 1$, by Lemma 1(i), we have

$$\begin{aligned} \lim _{t\rightarrow \infty }L_\mathrm{v}(t)=\lim _{t\rightarrow \infty }S_\mathrm{v}(t)=\lim _{t\rightarrow \infty }B_\mathrm{v}(t)=\lim _{t\rightarrow \infty }I_\mathrm{v}(t)=0. \end{aligned}$$

Then, the last equation of system (2) gives rise to the following limiting equation for $I_\mathrm{h}(t)$:

$$\begin{aligned} \frac{\mathrm{d}I_\mathrm{h}(t)}{\mathrm{d}t}=-(d_\mathrm{h}+\rho )I_\mathrm{h}(t). \end{aligned}$$

It follows that $\lim _{t\rightarrow \infty }I_\mathrm{h}(t)=0$.

If $R_\mathrm{v}>1$, we consider the following system

$$\begin{aligned} \begin{aligned} \frac{\mathrm{d}L_\mathrm{v}(t)}{\mathrm{d}t}&=\lambda (t)N_\mathrm{v}(t)-\mu _l(t)L_\mathrm{v}(t)-\alpha L_\mathrm{v}(t)^2-\delta (t)L_\mathrm{v}(t), \\ \frac{\mathrm{d}N_\mathrm{v}(t)}{\mathrm{d}t}&=\delta (t)L_\mathrm{v}(t)-\mu _\mathrm{v}(t)N_\mathrm{v}(t), \\ \frac{\mathrm{d}B_\mathrm{v}(t)}{\mathrm{d}t}&=p\delta (t)L_\mathrm{v}(t)-\mu _\mathrm{v}(t)B_\mathrm{v}(t)+q\gamma \frac{N_\mathrm{v}^*(t)-B_\mathrm{v}(t)}{N_\mathrm{v}^*(t)}B_\mathrm{v}(t). \end{aligned} \end{aligned}$$

(6)

Linearizing system (6) at (0, 0, 0), we get the following linear cooperative system:

$$\begin{aligned} \begin{aligned} \frac{\mathrm{d}L_\mathrm{v}(t)}{\mathrm{d}t}&=\lambda (t)N_\mathrm{v}(t)-\mu _l(t)L_\mathrm{v}(t)-\delta (t)L_\mathrm{v}(t), \\ \frac{\mathrm{d}N_\mathrm{v}(t)}{\mathrm{d}t}&=\delta (t)L_\mathrm{v}(t)-\mu _\mathrm{v}(t)N_\mathrm{v}(t), \\ \frac{\mathrm{d}B_\mathrm{v}(t)}{\mathrm{d}t}&=p\delta (t)L_\mathrm{v}(t)-(\mu _\mathrm{v}(t)-q\gamma )B_\mathrm{v}(t). \end{aligned} \end{aligned}$$

(7)

Let $r_2$ be the principal Floquét multiplier of system (7), that is, the spectral radius of the Poincaré map associated with system (7). Note that system (6) is obtained by adding an equation about $B_\mathrm{v}(t)$ to system (4) and the equation about $B_\mathrm{v}(t)$ is decoupled from the other two equations of system (6). By Wang and Zhao (2008, Theorem 2.2), $R_\mathrm{v}-1$ has the same sign as $r_2-1$. As a straightforward consequence of Zhao (2003, Theorem 3.1.2), we have the following result.

Lemma 3

If $R_\mathrm{v}>1,$ then system (6) admits a unique positive $\omega$-periodic solution $({\bar{L}}_\mathrm{v}^*(t), {\bar{N}}_\mathrm{v}^*(t), B_\mathrm{v}^*(t))$, which is globally attractive for system (6) in ${\mathbb {R}}_+^3\setminus \{(0,0,0)\}$.

By the uniqueness of the positive $\omega$-periodic solution in Lemma 1(ii), it follows that $L_\mathrm{v}^*(t)={\bar{L}}_\mathrm{v}^*(t)$ and $N_\mathrm{v}^*(t)={\bar{N}}_\mathrm{v}^*(t)$. Suppose ${\tilde{B}}_\mathrm{v}(t)$ is any solution of the following system.

$$\begin{aligned} \begin{aligned} \frac{\mathrm{d}B_\mathrm{v}(t)}{\mathrm{d}t}&=p\delta (t)L_\mathrm{v}^*(t)-\mu _\mathrm{v}(t)B_\mathrm{v}(t)+q\gamma \frac{N_\mathrm{v}^*(t)-B_\mathrm{v}(t)}{N_\mathrm{v}^*(t)}B_\mathrm{v}(t). \end{aligned} \end{aligned}$$

(8)

Then, $(L_\mathrm{v}^*(t), N_\mathrm{v}^*(t), {\tilde{B}}_\mathrm{v}(t))=({\bar{L}}_\mathrm{v}^*(t), {\bar{N}}_\mathrm{v}^*(t), {\tilde{B}}_\mathrm{v}(t))$ is a solution of system (6). According to Lemma 3, we have $\lim _{t\rightarrow \infty }({\tilde{B}}_\mathrm{v}(t)-B_\mathrm{v}^*(t))=0$. Thus, $B_\mathrm{v}^*(t)$ is globally attractive for system (8).

Consider the following system:

$$\begin{aligned} \begin{aligned} \frac{\mathrm{d}L_\mathrm{v}(t)}{\mathrm{d}t}&=\lambda (t)N_\mathrm{v}(t)-\mu _l(t)L_\mathrm{v}(t)-\alpha L_\mathrm{v}(t)^2-\delta (t)L_\mathrm{v}(t), \\ \frac{\mathrm{d}N_\mathrm{v}(t)}{\mathrm{d}t}&=\delta (t)L_\mathrm{v}(t)-\mu _\mathrm{v}(t)N_\mathrm{v}(t), \\ \frac{\mathrm{d}B_\mathrm{v}(t)}{\mathrm{d}t}&=p\delta (t)L_\mathrm{v}(t)-\mu _\mathrm{v}(t)B_\mathrm{v}(t)+q\gamma \frac{N_\mathrm{v}(t)-B_\mathrm{v}(t)}{N_\mathrm{v}(t)}B_\mathrm{v}(t). \end{aligned} \end{aligned}$$

(9)

By the theory of chain transitive set, we have

Lemma 4

If $R_\mathrm{v}>1,$ then system (9) admits a unique positive $\omega$-periodic solution $(L_\mathrm{v}^*(t), N_\mathrm{v}^*(t), B_\mathrm{v}^*(t))$, which is globally attractive for system (9) in $Y:=\{(\varphi _1, \varphi _2, \varphi _3)\in {\mathbb {R}}_+^3: \varphi _2>0, \varphi _2\ge \varphi _3\}$.

Proof

By similar arguments as in Lemma 2, it follows that for any $\varphi \in Y$, system (9) has a unique nonnegative bounded solution $w(t,\varphi )$ on $[0,\infty )$ with $w(0)=\varphi$, and $w(t,\varphi )\in Y$ for all $t\ge 0$. Let $\{\varPhi (t)\}_{t\ge 0}$ be the positive periodic semiflow associated with system (9) on Y, that is, $\varPhi (t)(\varphi ):=(L_\mathrm{v}(t,\varphi ), N_\mathrm{v}(t,\varphi ), B_\mathrm{v}(t,\varphi ))$ is the unique solution of system (9) with initial value $\varphi \in Y$. Then, $\varPhi :=\varPhi (\omega )$ is the Poincaré map of system (9), and $\{\varPhi ^n\}_{n\ge 0}$ defines a discrete-time dynamical system on Y. For any $\varphi \in Y$, let ${\mathcal {M}}$ be the omega limit set of the discrete-time orbit $\{\varPhi ^n(\varphi )\}_{n\ge 0}$. It follows from Hirsch et al. (2001, Lemma 2.1) [see also Zhao (2003, Lemma 1.2.1)] that ${\mathcal {M}}$ is an internally chain transitive set for $\{\varPhi ^n\}$ on Y.

Since $R_\mathrm{v}>1$, by Lemma 1(ii) we have

$$\begin{aligned} \lim _{n\rightarrow \infty }((\varPhi ^n(\varphi ))_1,(\varPhi ^n(\varphi ))_2)=(L_\mathrm{v}^*(0),N_\mathrm{v}^*(0)). \end{aligned}$$

Then, there exists a subset ${\mathcal {M}}_1$ of ${\mathbb {R}}$ such that ${\mathcal {M}}=\{(L_\mathrm{v}^*(0),N_\mathrm{v}^*(0))\}\times {\mathcal {M}}_1$. For any given $z=(z_1,z_2,z_3)\in {\mathcal {M}}$,

$$\begin{aligned} \varPhi ^n|_{{\mathcal {M}}}(L_\mathrm{v}^*(0),N_\mathrm{v}^*(0),z_3)=\{(L_\mathrm{v}^*(0),N_\mathrm{v}^*(0))\}\times Q^n|_{{\mathcal {M}}_1}(z_3) \end{aligned}$$

where $\{Q(t)\}_{t\ge 0}$ is the solution semiflow associated with system (8).

Since M is an internally chain transitive set for $\varPhi ^n$, if follows that ${\mathcal {M}}_1$ is an internally chain transitive set for $Q^n$.

Since $B_\mathrm{v}^*(t)$ is a globally attractive positive periodic solution of system (8), it follows from Hirsch et al. (2001, Theorem 3.1) [see also Zhao (2003, Theorem 1.2.1)] that ${\mathcal {M}}_1=\{B_\mathrm{v}^*(0)\}$ and hence, ${\mathcal {M}}=\{(L_\mathrm{v}^*(0),N_\mathrm{v}^*(0),B_\mathrm{v}^*(0))\}$. This implies that the statement is true. $\square$

If $\lim _{t\rightarrow \infty }(L_\mathrm{v}(t)-L_\mathrm{v}^*(t))= \lim _{t\rightarrow \infty }(N_\mathrm{v}(t)-N_\mathrm{v}^*(t))=\lim _{t\rightarrow \infty }(B_\mathrm{v}(t)-B_\mathrm{v}^*(t))=0$, then the last two equations in system (3) form an asymptotically periodic system with the following limiting system:

$$\begin{aligned} \begin{aligned} \frac{\mathrm{d}I_\mathrm{v}(t)}{\mathrm{d}t}&=b\beta (t)\frac{I_\mathrm{h}(t)}{N_\mathrm{h}}(N_\mathrm{v}^*(t)-B_\mathrm{v}^*(t)-I_\mathrm{v}(t))-\mu _\mathrm{v}(t)I_\mathrm{v}(t)-q\gamma \frac{I_\mathrm{v}(t)}{N_\mathrm{v}^*(t)}B_\mathrm{v}^*(t),\\ \frac{\mathrm{d}I_\mathrm{h}(t)}{\mathrm{d}t}&=c\beta (t)\frac{N_\mathrm{h}-I_\mathrm{h}(t)}{N_\mathrm{h}}I_\mathrm{v}(t)-(d_\mathrm{h}+\rho )I_\mathrm{h}(t). \end{aligned} \end{aligned}$$

(10)

The following result implies that the domain $G(t):=[0,N_\mathrm{v}^*(t)-B_\mathrm{v}^*(t)]\times [0,N_\mathrm{h}]$ is positively invariant for system (10).

Lemma 5

For any $\varphi =(\varphi _1,\varphi _2)\in G(0)$, system (10) has a unique solution $v(t,\varphi )$ with $v(0)=\varphi$ and $v(t,\varphi )=(I_\mathrm{v}(t,\varphi ),I_\mathrm{h}(t,\varphi ))\in G(t)$ for all $t\ge 0$.

Proof

For any $\varphi \in G(0)$, define

$$\begin{aligned} \tilde{f}(t,\varphi )= \left( \begin{array}{c} b\beta (t)\frac{\varphi _2}{N_\mathrm{h}}(N_\mathrm{v}^*(t)-B_\mathrm{v}^*(t)-\varphi _1)-(\mu _\mathrm{v}(t)+q\gamma \frac{B_\mathrm{v}^*(t)}{N_\mathrm{v}^*(t)})\varphi _1 \\ c\beta (t)\frac{N_\mathrm{h}-\varphi _2}{N_\mathrm{h}}\varphi _1-(d_\mathrm{h}+\rho )\varphi _2 \end{array} \right) . \end{aligned}$$

Since ${\tilde{f}}$ is continuous in $(t,\varphi )\in {\mathbb {R}}\times G(0)$ and ${\tilde{f}}$ is Lipschitz in $\varphi$ on each compact subset of G(0), it follows that system (10) has a unique solution $v(t,\varphi )$ with $v(0)=\varphi$ on its maximal interval $[0,\sigma _\varphi )$ of existence.

Let $\varphi =(\varphi _1,\varphi _2)\in G(0)$ be given. If $\varphi _1=0$, then ${\tilde{f}}_1(t,\varphi )\ge 0$. If $\varphi _2=0$, then ${\tilde{f}}_2(t,\varphi )\ge 0$. If $\varphi _2=N_\mathrm{h}$, then ${\tilde{f}}_2(t,\varphi )\le 0$. By Smith (1995, Theorem 5.2.1 and Remark 5.2.1), it follows that the unique solution $v(t,\varphi )$ of system (10) with $v(0)=\varphi$ satisfies $v(t,\varphi )\in {\mathbb {R}}_+\times [0,N_\mathrm{h}]$.

It remains to prove that $v_1(t)\le N_\mathrm{v}^*(t)-B_\mathrm{v}^*(t)$ for all $t\in [0,\sigma _\varphi )$. Suppose this does not hold. Then, there exists $t_0\in [0,\sigma _\varphi )$ and $\epsilon _0>0$ such that

$$\begin{aligned} v_1(t_0)=N_\mathrm{v}^*(t_0)-B_\mathrm{v}^*(t_0)\quad \text {and}\quad v_1(t)>N_\mathrm{v}^*(t)-B_\mathrm{v}^*(t),\quad \forall t\in (t_0,t_0+\epsilon _0). \end{aligned}$$

Since

$$\begin{aligned} \begin{aligned} \frac{\mathrm{d}v_1(t_0)}{\mathrm{d}t}&=-\left( \mu _\mathrm{v}(t_0)+q\gamma \frac{B_\mathrm{v}^*(t_0)}{N_\mathrm{v}^*(t_0)}\right) v_1(t_0)\\&= -\left( \mu _\mathrm{v}(t_0)+q\gamma \frac{B_\mathrm{v}^*(t_0)}{N_\mathrm{v}^*(t_0)}\right) (N_\mathrm{v}^*(t_0)-B_\mathrm{v}^*(t_0))\\&<(1-p)\delta (t_0)L_\mathrm{v}^*(t_0)-\mu _\mathrm{v}(t_0)(N_\mathrm{v}^*(t_0)-B_\mathrm{v}^*(t_0))\\&\quad -\,q\gamma \frac{N_\mathrm{v}^*(t_0)-B_\mathrm{v}^*(t_0)}{N_\mathrm{v}^*(t_0)}B_\mathrm{v}^*(t_0)\\&=\frac{\mathrm{d}(N_\mathrm{v}^*(t)-B_\mathrm{v}^*(t))}{\mathrm{d}t}\bigg \arrowvert _{t=t_0}, \end{aligned} \end{aligned}$$

there exists $\epsilon _1\in (0,\epsilon _0)$ such that $v_1(t)\le N_\mathrm{v}^*(t)-B_\mathrm{v}^*(t)$ for all $t\in (t_0,t_0+\epsilon _1)$, which is a contradiction. This proves that $v(t,\varphi )\in G(t)$ for all $t\in [0,\sigma _\varphi )$. Clearly, $v(t,\varphi )$ is bounded on $[0,\sigma _\varphi )$, and hence, Hale and Verduyn Lunel (1993, Theorem 2.3.1) implies that $\sigma _\varphi =\infty$. $\square$

Linearizing system (10) at (0, 0) gives the following linear system

$$\begin{aligned} \begin{aligned} \frac{\mathrm{d}I_\mathrm{v}(t)}{\mathrm{d}t}&=b\beta (t)\frac{I_\mathrm{h}(t)}{N_\mathrm{h}}(N_\mathrm{v}^*(t)-B_\mathrm{v}^*(t))-\left( \mu _\mathrm{v}(t)+q\gamma \frac{B_\mathrm{v}^*(t)}{N_\mathrm{v}^*(t)}\right) I_\mathrm{v}(t),\\ \frac{\mathrm{d}I_\mathrm{h}(t)}{\mathrm{d}t}&=c\beta (t)I_\mathrm{v}(t)-(d_\mathrm{h}+\rho )I_\mathrm{h}(t). \end{aligned} \end{aligned}$$

(11)

We rewrite system (11) as $\frac{\mathrm{d}u}{\mathrm{d}t}=(F(t)-V(t))u$, where

$$\begin{aligned} F(t)=\begin{bmatrix} 0&\frac{b\beta (t)(N_\mathrm{v}^*(t)-B_\mathrm{v}^*(t))}{N_\mathrm{h}}\\ c\beta (t)&0 \end{bmatrix},\quad V(t)=\begin{bmatrix} \mu _\mathrm{v}(t)+\frac{q\gamma B_\mathrm{v}^*(t)}{N_\mathrm{v}^*(t)}&0\\ 0&d_\mathrm{h}+\rho \end{bmatrix}. \end{aligned}$$

Let $Y(t,s), t\ge s$, be the evolution operator of the linear periodic system

$$\begin{aligned} \frac{\mathrm{d}y}{\mathrm{d}t}=-V(t)y. \end{aligned}$$

That is, for each $s\in {\mathbb {R}}$, the $2\times 2$ matrix Y(t, s) satisfies

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}Y(t,s)=-V(t)Y(t,s),\quad \forall t\ge s,\quad Y(s,s)=I, \end{aligned}$$

where I is the $2\times 2$ identity matrix.

We assume that $\varphi (s)\in C_\omega$ is the initial distribution of infectious mosquitoes and infectious humans. Then, $F(s)\varphi (s)$ is the distribution of new infections produced by the infectious mosquitoes and infectious humans who were introduced at time s. Given $t\ge s$, $Y(t,s)F(s)\varphi (s)$ gives the distribution of those infectious mosquitoes and infectious humans who were newly infected at time s and remain in the infected compartments at time t. It follows that

$$\begin{aligned} \int _{-\infty }^tY(t,s) F(s)\varphi (s)\mathrm{d}s=\int _0^{\infty }Y(t,t-a) F(t-a)\varphi (t-a)\mathrm{d}a \end{aligned}$$

is the distribution of accumulative new infections at time t produced by all those infectious mosquitoes and infectious humans $\varphi (s)$ introduced at previous time to t.

We define a linear operator $L: C_\omega \rightarrow C_\omega$ by

$$\begin{aligned} (L\varphi )(t)=\int _0^{\infty }Y(t,t-a) F(t-a)\varphi (t-a)\mathrm{d}a,\quad \forall t\in {\mathbb {R}},\quad \varphi \in C_\omega . \end{aligned}$$

It then follows from Wang and Zhao (2008) that the basic reproduction ratio is $R_0:=\rho (L)$, the spectral radius of L.

Lemma 6

Assume $R_\mathrm{v}>1$, then the following statements are valid:

• (i) If $R_0\le 1$, then (0, 0) is globally attractive for system (10) in G(0);

• (ii) If $R_0>1$, then system (10) admits a unique positive $\omega$-periodic solution $(I_\mathrm{v}^*(t),I_\mathrm{h}^*(t))$, which is globally attractive for system (10) in $G(0)\setminus \{(0,0)\}$.

Proof

Let S(t) be the solution maps of system (10), that is, $S(t)(I_\mathrm{v}(0), I_\mathrm{h}(0))=(I_\mathrm{v}(t), I_\mathrm{h}(t)), t\ge 0$, where $(I_\mathrm{v}(t), I_\mathrm{h}(t))$ is the unique solution of system (10) with $(I_\mathrm{v}(0), I_\mathrm{h}(0))\in G(0).$ It follows from Lemma 5 that S(t) maps G(0) into G(t), and $S:=S(\omega ): G(0)\rightarrow G(\omega )=G(0)$ is the Poincaré map associated with system (10).

Let $({\bar{y}}_1(0), {\bar{y}}_2(0))\ge (y_1(0), y_2(0))$. Let $({\bar{y}}_1(t), {\bar{y}}_2(t))$ and $(y_1(t), y_2(t))$ be the solutions of system (10) with initial values $({\bar{y}}_1(0), {\bar{y}}_2(0))$ and $(y_1(0), y_2(0))$, respectively. Then, the comparison theorem for cooperative ordinary differential systems implies that $({\bar{y}}_1(t),{\bar{y}}_2(t))\ge (y_1(t),y_2(t)), \forall t\ge 0,$ that is, $S(t): G(0)\rightarrow G(t)$ is monotone for each $t\ge 0$.

Next, we show that $S(t): G(0)\rightarrow G(t)$ is strongly monotone for each $t>0$. Suppose $({\bar{y}}_1(0), {\bar{y}}_2(0))>(y_1(0), y_2(0))$. Then, the comparison theorem for cooperative ordinary differential systems implies that

$$\begin{aligned} ({\bar{y}}_1(t), {\bar{y}}_2(t))>(y_1(t), y_2(t)), \quad \forall t\ge 0. \end{aligned}$$

We proceed with two cases.

Case 1 ${\bar{y}}_1(0)>y_1(0).$

Let

$$\begin{aligned} g_1(y):=b\beta (t)\frac{y_2(t)}{N_\mathrm{h}}(N_\mathrm{v}^*(t)-B_\mathrm{v}^*(t)-y) -\left( \mu _\mathrm{v}(t)+q\gamma \frac{B_\mathrm{v}^*(t)}{N_\mathrm{v}^*(t)}\right) y. \end{aligned}$$

Since

$$\begin{aligned} \begin{aligned} \frac{\mathrm{d}{\bar{y}}_1(t)}{\mathrm{d}t}&= b\beta (t)\frac{{\bar{y}}_2(t)}{N_\mathrm{h}}(N_\mathrm{v}^*(t)-B_\mathrm{v}^*(t)-{\bar{y}}_1(t))-\left( \mu _\mathrm{v}(t)+q\gamma \frac{B_\mathrm{v}^*(t)}{N_\mathrm{v}^*(t)}\right) {\bar{y}}_1(t)\\&\ge b\beta (t)\frac{y_2(t)}{N_\mathrm{h}}(N_\mathrm{v}^*(t)-B_\mathrm{v}^*(t)-{\bar{y}}_1(t))-\left( \mu _\mathrm{v}(t)+q\gamma \frac{B_\mathrm{v}^*(t)}{N_\mathrm{v}^*(t)}\right) {\bar{y}}_1(t)\\&= g_1({\bar{y}}_1(t)), \end{aligned} \end{aligned}$$

we have

$$\begin{aligned} \frac{\mathrm{d}{\bar{y}}_1(t)}{\mathrm{d}t}-g_1({\bar{y}}_1(t))\ge 0=\frac{\mathrm{d}y_1(t)}{\mathrm{d}t}-g_1(y_1(t)), \quad \forall t\ge 0. \end{aligned}$$

Since ${\bar{y}}_1(0)>y_1(0)$, Walter (1997, Theorem 4) implies that ${\bar{y}}_1(t)>y_1(t)$ for all $t\ge 0$.

To prove ${\bar{y}}_2(t)>y_2(t)$ for all $t>0$, we first prove that for any $\epsilon >0$, there exists an open interval $(a_1,b_1)\subset [0,\epsilon ]$ such that $N_\mathrm{h}>{\bar{y}}_2(t)$ for all $t\in (a_1,b_1)$. Otherwise, there exists $\epsilon _0>0$ such that $N_\mathrm{h}={\bar{y}}_2(t)$ for all $t\in (0,\epsilon _0)$. It then follows from the second equation of system (10) that $0=-(d_\mathrm{h}+\rho )N_\mathrm{h}$, which is a contradiction. Let

$$\begin{aligned} f_1(y):=c\beta (t)\frac{N_\mathrm{h}-y}{N_\mathrm{h}}y_1(t) -(d_\mathrm{h}+\rho )y. \end{aligned}$$

Then, we have

$$\begin{aligned} \begin{aligned} \frac{\mathrm{d}{\bar{y}}_2(t)}{\mathrm{d}t}&= c\beta (t)\frac{N_\mathrm{h}-{\bar{y}}_2(t)}{N_\mathrm{h}}{\bar{y}}_1(t)-(d_\mathrm{h}+\rho ){\bar{y}}_2(t)\\&> c\beta (t)\frac{N_\mathrm{h}-{\bar{y}}_2(t)}{N_\mathrm{h}}y_1(t)-(d_\mathrm{h}+\rho ){\bar{y}}_2(t)\\&= f_1({\bar{y}}_2(t)),\quad \forall t\in (a_1,b_1), \end{aligned} \end{aligned}$$

and hence,

$$\begin{aligned} \frac{\mathrm{d}{\bar{y}}_2(t)}{\mathrm{d}t}-f_1({\bar{y}}_2(t))>0= \frac{\mathrm{d}y_2(t)}{\mathrm{d}t}-f_1(y_2(t)), \quad \forall t\in (a_1,b_1). \end{aligned}$$

Since ${\bar{y}}_2(0)\ge y_2(0)$, it follows from Walter (1997, Theorem 4) that ${\bar{y}}_2(t)>y_2(t)$ for all $t>0$.

Case 2 ${\bar{y}}_1(0)=y_1(0).$

Since

$$\begin{aligned} \begin{aligned} \frac{\mathrm{d}{\bar{y}}_2(t)}{\mathrm{d}t}&= c\beta (t)\frac{N_\mathrm{h}-{\bar{y}}_2(t)}{N_\mathrm{h}}{\bar{y}}_1(t)-(d_\mathrm{h}+\rho ){\bar{y}}_2(t)\\&\ge c\beta (t)\frac{N_\mathrm{h}-{\bar{y}}_2(t)}{N_\mathrm{h}}y_1(t)-(d_\mathrm{h}+\rho ){\bar{y}}_2(t)\\&= f_1({\bar{y}}_2(t)),\quad \forall t\ge 0, \end{aligned} \end{aligned}$$

we have

$$\begin{aligned} \frac{\mathrm{d}{\bar{y}}_2(t)}{\mathrm{d}t}-f_1({\bar{y}}_2(t))\ge 0= \frac{\mathrm{d}y_2(t)}{\mathrm{d}t}-f_1(y_2(t)), \quad \forall t\ge 0. \end{aligned}$$

Since $({\bar{y}}_1(0),{\bar{y}}_2(0))>(y_1(0),y_2(0))$ and ${\bar{y}}_1(0)=y_1(0)$, we have ${\bar{y}}_2(0)>y_2(0)$. It follows from Walter (1997, Theorem 4) that ${\bar{y}}_2(t)>y_2(t)$ for all $t>0.$

To prove ${\bar{y}}_1(t)>y_1(t)$ for all $t>0$, we first show that for any $\epsilon >0$, there exists $(a_2,b_2)\subset [0,\epsilon ]$ such that ${\bar{y}}_1(t)<N^*_\mathrm{v}(t)-B_\mathrm{v}^*(t)$ for all $t\in (a_2,b_2)$. Otherwise, there exists $\epsilon _1>0$ such that ${\bar{y}}_1(t)=N_\mathrm{v}^*(t)-B_\mathrm{v}^*(t)$ for all $t\in (0,\epsilon _1)$. By the first equation of system (10), we have

$$\begin{aligned} \begin{aligned}&\frac{\mathrm{d}(N_\mathrm{v}^*(t)-B_\mathrm{v}^*(t))}{\mathrm{d}t}\\&\quad =\frac{\mathrm{d}{\bar{y}}_1(t)}{\mathrm{d}t} \\&\quad = -\mu _\mathrm{v}(t)(N_\mathrm{v}^*(t)-B_\mathrm{v}^*(t))-q\gamma \frac{N_\mathrm{v}^*(t)-B_\mathrm{v}^*(t)}{N_\mathrm{v}^*(t)}B_\mathrm{v}^*(t),\quad t\in (0,\epsilon _1), \end{aligned} \end{aligned}$$

which contradicts the fact that

$$\begin{aligned} \begin{aligned}&\frac{\mathrm{d}(N_\mathrm{v}^*(t)-B_\mathrm{v}^*(t))}{\mathrm{d}t}\\&\quad =(1-p)\delta L_\mathrm{v}^*(t)-\mu _\mathrm{v}(t)(N_\mathrm{v}^*(t)-B_\mathrm{v}^*(t))-q\gamma \frac{N_\mathrm{v}^*(t)-B_\mathrm{v}^*(t)}{N_\mathrm{v}^*(t)}B_\mathrm{v}^*(t). \end{aligned} \end{aligned}$$

Since

$$\begin{aligned} \begin{aligned} \frac{\mathrm{d}{\bar{y}}_1(t)}{\mathrm{d}t}&= b\beta (t)\frac{{\bar{y}}_2(t)}{N_\mathrm{h}}(N_\mathrm{v}^*(t)-B_\mathrm{v}^*(t)-{\bar{y}}_1(t))-\mu _\mathrm{v}(t){\bar{y}}_1(t)-q\gamma \frac{B_\mathrm{v}^*(t)}{N_\mathrm{v}^*(t)}{\bar{y}}_1(t)\\&> b\beta (t)\frac{y_2(t)}{N_\mathrm{h}}(N_\mathrm{v}^*(t)-B_\mathrm{v}^*(t)-{\bar{y}}_1(t))-\mu _\mathrm{v}(t){\bar{y}}_1(t)-q\gamma \frac{B_\mathrm{v}^*(t)}{N_\mathrm{v}^*(t)}{\bar{y}}_1(t)\\&= g_1({\bar{y}}_1(t)),\quad \forall t\in (a_2,b_2), \end{aligned} \end{aligned}$$

we have

$$\begin{aligned} \frac{{\bar{y}}_1(t)}{dt}-g_1({\bar{y}}_1(t))>0=\frac{\mathrm{d}y_1(t)}{\mathrm{d}t}-g_1(y_1(t)), \quad \forall t\in (a_2,b_2). \end{aligned}$$

Since ${\bar{y}}_1(0)=y_1(0)$, Walter (1997, Theorem 4) implies that ${\bar{y}}_1(t)>y_1(t)$ for all $\forall t>0$. Consequently, $S(t): G(0)\rightarrow G(t)$ is strongly monotone for each $t>0$.

For any given $x=(x_1, x_2)\in G(0), \lambda \in [0,1]$, let v(t, x) and $v(t,\lambda x)$ be the solutions of system (10) satisfying $v(0)=x$ and $v(0)=\lambda x$, respectively. Denote $u(t)=\lambda v(t,x)$ and $z(t)=v(t,\lambda x)$. Define f by

$$\begin{aligned} f(t,x)=\begin{bmatrix} b\beta (t)\frac{x_2}{N_\mathrm{h}}(N_\mathrm{v}^*(t)-B_\mathrm{v}^*(t)-x_1)-\mu _\mathrm{v}(t)x_1-q\gamma \frac{x_1}{N_\mathrm{v}^*(t)}B_\mathrm{v}^*(t) \\ c\beta (t)\frac{N_\mathrm{h}-x_2}{N_\mathrm{h}}x_1-(d_\mathrm{h}+\rho )x_2 \end{bmatrix}. \end{aligned}$$

Note that for any $\psi \in G(t)$ and $\lambda \in [0,1]$, we have $f(t,\lambda \psi )\ge \lambda f(t,\psi )$. Then,

$$\begin{aligned} \frac{\mathrm{d}u(t)}{\mathrm{d}t}=\lambda \frac{\mathrm{d}v(t,x)}{\mathrm{d}t}=\lambda f(t,v(t,x))\le f(t,\lambda v(t,x))=f(t,u(t)). \end{aligned}$$

Clearly, $\frac{\mathrm{d}z(t)}{\mathrm{d}t}=f(t,z(t))$ and $u(0)=\lambda v(0,x)=\lambda x=z(0)$. By the comparison principle, we have $u(t)\le z(t)$ for all $t\ge 0$, that is, $\lambda v(t,x)\le v(t,\lambda x)$ for all $t\ge 0$. This shows that the solution map $S(t): G(0)\rightarrow G(t)$ is subhomogeneous.

Next, we prove that for any $t>0$, $S(t): G(0)\rightarrow G(t)$ is strictly subhomogeneous. For any given $x\in G(0)$ with $x\gg 0$ and $\lambda \in (0,1)$, let

$$\begin{aligned} \begin{aligned} f_2(r)&:= c\beta (t)\frac{N_\mathrm{h}-r}{N_\mathrm{h}}z_1(t)-(d_\mathrm{h}+\rho )r,\\ g_2(r)&:= c\beta (t)\frac{N_\mathrm{h}-r}{N_\mathrm{h}}. \end{aligned} \end{aligned}$$

Since $g_2(r)$ is strictly decreasing in r and $\lambda v_1(t,x)\le v_1(t,\lambda x)=z_1(t), v_2(t,x)>\lambda v_2(t,x)=u_2(t), \forall \lambda \in (0,1), \forall t>0$, it follows that

$$\begin{aligned} \begin{aligned} \frac{\mathrm{d}u_2(t)}{\mathrm{d}t}&= \lambda \frac{\mathrm{d}v_2(t,x)}{\mathrm{d}t}\\&= \lambda c\beta (t)\frac{N_\mathrm{h}-v_2(t,x)}{N_\mathrm{h}}v_1(t,x)-(d_\mathrm{h}+\rho )\lambda v_2(t,x)\\&<c\beta (t)\frac{N_\mathrm{h}-u_2(t)}{N_\mathrm{h}}z_1(t)-(d_\mathrm{h}+\rho )u_2(t)\\&= g_2(u_2(t))z_1(t)-(d_\mathrm{h}+\rho )u_2(t)\\&= f_2(u_2(t)), \end{aligned} \end{aligned}$$

and hence,

$$\begin{aligned} \frac{\mathrm{d}u_2(t)}{\mathrm{d}t}-f_2(u_2(t))<0=\frac{\mathrm{d}z_2(t)}{\mathrm{d}t}-f_2(z_2(t)), \quad \forall t>0. \end{aligned}$$

Note that $u_2(0)=\lambda v_2(0,x)=\lambda x=v_2(0,\lambda x)=z_2(0)$. By Walter (1997, Theorem 4), we obtain $u_2(t)<z_2(t), \forall t>0.$ Thus, $\lambda v(t,x)<v(t,\lambda x), \forall t>0$.

Let P be the Poincaré map associated with system (11) on ${\mathbb {R}}^2$ and r(P) be its spectral radius. By the continuity and differentiability of solutions with respect to initial values, it follows that S is differentiable at zero and the Frechét derivative $DS(0)=P.$ By Zhao (2003, Theorem 2.3.4), as applied to S, we have the following result:

• (a) If $r(P)\le 1$, then (0, 0) is globally attractive for system (10) in G(0);

• (b) If $r(P)>1,$ then system (10) admits a unique positive $\omega$-periodic solution $(I_\mathrm{v}^*(t), I_\mathrm{h}^*(t))$, which is globally attractive for system (10) in $G(0)\setminus \{(0,0)\}$.

By Wang and Zhao (2008, Theorem 2.2), $R_0-1$ has the same sign as $r(P)-1$. Therefore, we have the desired threshold type result in terms of $R_0$. $\square$

Next, we use the theory of chain transitive sets [see Hirsch et al. (2001 and Zhao 2003, Chapter 1)] to lift the threshold type result for system (10) to system (3).

Theorem 1

The following statements are valid:

• (i) If $R_\mathrm{v}>1$ and $R_0\le 1$, then $(L_\mathrm{v}^*(t), N_\mathrm{v}^*(t), B_\mathrm{v}^*(t), 0, 0)$ is globally attractive for system (3) in W;

• (ii) If $R_\mathrm{v}>1$ and $R_0>1$, then $(L_\mathrm{v}^*(t), N_\mathrm{v}^*(t), B_\mathrm{v}^*(t), I_\mathrm{v}^*(t), I_\mathrm{h}^*(t))$ is globally attractive for system (3) in $W \setminus ({\mathbb {R}}_+^3\times \{(0,0)\})$.

Proof

Let $\{\varPsi (t)\}_{t\ge 0}$ be the periodic semiflow associated with system (3) on W, that is,

$$\begin{aligned} \varPsi (t)(x):= (L_\mathrm{v}(t,x), N_\mathrm{v}(t,x), B_\mathrm{v}(t,x), I_\mathrm{v}(t,x), I_\mathrm{h}(t,x)) \end{aligned}$$

is the unique solution of system (3) with initial value $x\in W$. Then, $\varPsi :=\varPsi (\omega )$ is the Poincaré map of system (3), and $\{\varPsi ^n\}_{n\ge 0}$ defines a discrete-time dynamical system on W. For any given $x\in W$, let ${\mathcal {L}}$ be the omega limit set of the discrete-time orbit $\{\varPsi ^n(x)\}_{n\ge 0}$. It follows from Hirsch et al. (2001, Lemma 2.1) [see also Zhao (2003, Lemma 1.2.1)] that ${\mathcal {L}}$ is an internally chain transitive set for $\varPsi ^n$ on W.

Since $R_\mathrm{v}>1$, by Lemma 4, we have

$$\begin{aligned} \lim _{n\rightarrow \infty }((\varPsi ^n(x))_1, (\varPsi ^n(x))_2, (\varPsi ^n(x))_3)=(L_\mathrm{v}^*(0), N_\mathrm{v}^*(0), B_\mathrm{v}^*(0)). \end{aligned}$$

Then, there exists a subset ${\mathcal {L}}_1$ of ${\mathbb {R}}^2$ such that

$$\begin{aligned} {\mathcal {L}}=\{(L_\mathrm{v}^*(0), N_\mathrm{v}^*(0), B_\mathrm{v}^*(0))\}\times {\mathcal {L}}_1. \end{aligned}$$

For any given $z=(z_1,z_2,z_3,z_4,z_5)\in {\mathcal {L}}$, there exists a sequence $n_k\rightarrow \infty$ such that $\varPsi ^{n_k}(x)\rightarrow z$ as $k\rightarrow \infty$. Since $0\le (\varPsi ^{n_k}(x))_4=I_\mathrm{v}(n_k\omega ,x)\le N_\mathrm{v}(n_k\omega ,x)-B_\mathrm{v}(n_k\omega ,x)$ and $0\le (\varPsi ^{n_k}(x))_5=I_\mathrm{h}(n_k\omega ,x)\le N_\mathrm{h}$ for all $x\in W$, letting $n_k\rightarrow \infty$, we obtain $0\le z_4\le N_\mathrm{v}^*(0)-B_\mathrm{v}^*(0)$, $0\le z_5\le N_\mathrm{h}$. It then follows that ${\mathcal {L}}_1\subset [0,N_\mathrm{v}^*(0)-B_\mathrm{v}^*(0)]\times [0,N_\mathrm{h}]=G(0)$. It is easy to see that

$$\begin{aligned} \varPsi ^n|_{{\mathcal {L}}}(L_\mathrm{v}^*(0), N_\mathrm{v}^*(0), B_\mathrm{v}^*(0), z_4, z_5)=\{(L_\mathrm{v}^*(0), N_\mathrm{v}^*(0), B_\mathrm{v}^*(0))\}\times S^n|_{{\mathcal {L}}_1}(z_4,z_5), \end{aligned}$$

where S is the Poincaré map associated with system (10). Since ${\mathcal {L}}$ is an internally chain transitive set for $\varPsi ^n$, it follows that ${\mathcal {L}}_1$ is an internally chain transitive set for $S^n$.

In the case $R_0\le 1$, by Lemma 6(i) and Hirsch et al. (2001, Theorem 3.1) [see also Zhao (2003, Theorem 1.2.1)], it follows that ${\mathcal {L}}_1=\{(0,0)\}$, and hence, ${\mathcal {L}}=\{(L_\mathrm{v}^*(0), N_\mathrm{v}^*(0)$, $B_\mathrm{v}^*(0)$, $0, 0)\}$. This implies that statement (i) is valid.

In the case $R_0>1$, by Lemma 6(ii) and Hirsch et al. (2001, Theorem 3.2) [see also Zhao (2003, Theorem 1.2.2)], it follows that

$$\begin{aligned} \text {either}\quad {\mathcal {L}}_1=\{(0,0)\}\quad \text {or}\quad {\mathcal {L}}_1=\{(I_\mathrm{v}^*(0),I_\mathrm{h}^*(0))\}. \end{aligned}$$

We further claim that ${\mathcal {L}}_1\ne \{(0,0)\}$. Suppose, by contradiction, that ${\mathcal {L}}_1=\{(0,0)\}$. Then, we have ${\mathcal {L}}=\{(L_\mathrm{v}^*(0), N_\mathrm{v}^*(0), B_\mathrm{v}^*(0), 0, 0)\}$. Thus, $\lim _{t\rightarrow \infty }(I_\mathrm{v}(t,x)$, $I_\mathrm{h}(t,x))=(0,0)$ uniformly for $x\in W$, and for any $\epsilon >0$, there exists $T=T(\epsilon )>0$ such that

$$\begin{aligned} |(L_\mathrm{v}(t,x), N_\mathrm{v}(t,x), B_\mathrm{v}(t,x))-(L_\mathrm{v}^*(t), N_\mathrm{v}^*(t), B_\mathrm{v}^*(t))|<\epsilon \end{aligned}$$

for all $t\ge T$ and $x\in W$. Then for any $t\ge T$, we have

$$\begin{aligned} \begin{aligned} \frac{\mathrm{d}I_\mathrm{v}(t)}{\mathrm{d}t}\ge \,&b\beta (t)\frac{I_\mathrm{h}(t)}{N_\mathrm{h}} (N_\mathrm{v}^*(t)-B_\mathrm{v}^*(t)-2\epsilon -I_\mathrm{v}(t))-\mu _\mathrm{v}(t)I_\mathrm{v}(t)\\&-q\gamma \frac{I_\mathrm{v}(t)}{N_\mathrm{v}^*(t)-\epsilon }(B_\mathrm{v}^*(t)+\epsilon ), \\ \frac{\mathrm{d}I_\mathrm{h}(t)}{\mathrm{d}t}&= c\beta (t)\frac{N_\mathrm{h}-I_\mathrm{h}(t)}{N_\mathrm{h}} I_\mathrm{v}(t)-(d_\mathrm{h}+\rho )I_\mathrm{h}(t). \end{aligned} \end{aligned}$$

(12)

Let $r_\epsilon$ be the spectral radius of the Poincaré map associated with the following linear system:

$$\begin{aligned} \begin{aligned} \frac{\mathrm{d}{\bar{I}}_\mathrm{v}(t)}{\mathrm{d}t}&= b\beta (t)\frac{{\bar{I}}_\mathrm{h}(t)}{N_\mathrm{h}} (N_\mathrm{v}^*(t)-B_\mathrm{v}^*(t)-2\epsilon )-\mu _\mathrm{v}(t){\bar{I}}_\mathrm{v}(t)\\&\quad -\,q\gamma \frac{{\bar{I}}_\mathrm{v}(t)}{N_\mathrm{v}^*(t)-\epsilon }(B_\mathrm{v}^*(t)+\epsilon ), \\ \frac{\mathrm{d}{\bar{I}}_\mathrm{h}(t)}{\mathrm{d}t}&= c\beta (t){\bar{I}}_\mathrm{v}(t)-(d_\mathrm{h}+\rho ){\bar{I}}_\mathrm{h}(t). \end{aligned} \end{aligned}$$

Since $\lim _{\epsilon \rightarrow 0^+}r_\epsilon =r(P)>1$, we can fix $\epsilon$ small enough such that $r_\epsilon >1$ and $\epsilon <\frac{1}{2}\min _{t\in [0,\omega ]}(N_\mathrm{v}^*(t)-B_\mathrm{v}^*(t))$. By a result similar to Lemma 3, we see that the Poincaré map of the following system

$$\begin{aligned} \begin{aligned} \frac{\mathrm{d}{\bar{I}}_\mathrm{v}(t)}{\mathrm{d}t}&= b\beta (t)\frac{{\bar{I}}_\mathrm{h}(t)}{N_\mathrm{h}} (N_\mathrm{v}^*(t)-B_\mathrm{v}^*(t)-2\epsilon -{\bar{I}}_\mathrm{v}(t))-\mu _\mathrm{v}(t){\bar{I}}_\mathrm{v}(t)\\&\quad -\,q\gamma \frac{{\bar{I}}_\mathrm{v}(t)}{N_\mathrm{v}^*(t)-\epsilon }(B_\mathrm{v}^*(t)+\epsilon ), \\ \frac{\mathrm{d}{\bar{I}}_\mathrm{h}(t)}{\mathrm{d}t}&= c\beta (t)\frac{N_\mathrm{h}-{\bar{I}}_\mathrm{h}(t)}{N_\mathrm{h}} {\bar{I}}_\mathrm{v}(t)-(d_\mathrm{h}+\rho ){\bar{I}}_\mathrm{h}(t) \end{aligned} \end{aligned}$$

(13)

admits a globally attractive fixed point $({\bar{I}}_\mathrm{v}^*(0), {\bar{I}}_\mathrm{h}^*(0))\gg 0$. In view of (12) and (13), the comparison principle implies that

$$\begin{aligned} \liminf _{n\rightarrow \infty }(I_\mathrm{v}(n\omega ,x), I_\mathrm{h}(n\omega ,x))\ge ({\bar{I}}_\mathrm{v}^*(0),{\bar{I}}_\mathrm{h}^*(0))\gg 0, \end{aligned}$$

which contradicts $\lim _{t\rightarrow \infty }(I_\mathrm{v}(t,x), I_\mathrm{h}(t,x))=(0,0)$. It then follows that ${\mathcal {L}}_1=\{(I_\mathrm{v}^*(0),I_\mathrm{h}^*(0))\}$, and hence, ${\mathcal {L}}=\{(L_\mathrm{v}^*(0),N_\mathrm{v}^*(0),B_\mathrm{v}^*(0),I_\mathrm{v}^*(0),I_\mathrm{h}^*(0))\}$. This implies that statement (ii) is valid. $\square$

Since system (2) is equivalent to (3), we have the following result on the global dynamics of the model system.

Theorem 2

The following statements are valid:

• (i) If $R_\mathrm{v}\le 1$, then $\lim _{t\rightarrow \infty }(L_\mathrm{v}(t), S_\mathrm{v}(t), I_\mathrm{v}(t), B_\mathrm{v}(t), I_\mathrm{h}(t))=(0, 0, 0, 0, 0)$, that is, the mosquito-free state (0, 0, 0, 0, 0) is globally attractive for system (2) in $U:=\{(\varphi _1, \varphi _2, \varphi _3, \varphi _4, \varphi _5)\in {\mathbb {R}}_+^5: \varphi _2+\varphi _3+\varphi _4>0, \varphi _5\le N_\mathrm{h}\}$.

• (ii) If $R_\mathrm{v}>1$ and $R_0\le 1$, then the disease-free periodic solution $(L_\mathrm{v}^*(t), N_\mathrm{v}^*(t)-B_\mathrm{v}^*(t), 0, B_\mathrm{v}^*(t), 0)$ is globally attractive for system (2) in U;

• (iii) If $R_\mathrm{v}>1$ and $R_0> 1$, then the positive periodic solution $(L_\mathrm{v}^*(t), N_\mathrm{v}^*(t)-I_\mathrm{v}^*(t)-B_\mathrm{v}^*(t), I_\mathrm{v}^*(t), B_\mathrm{v}^*(t), I_\mathrm{h}^*(t))$ is globally attractive for system (2) in $U\setminus ({\mathbb {R}}_+^2\times \{0\}\times {\mathbb {R}}_+\times \{0\})$.

Note that in our model we do not consider disease-induced human death rate. If we incorporate disease-induced death rate and still assume that the total human population size stabilizes at a constant $N_\mathrm{h}$, then there is no impact on the theoretical result since the disease-induced death rate is a constant parameter just like the human recovery rate. Then, the model with disease-induced mortality will have the same form as the model system (2) if we combine the recovery rate and the disease-induced death rate. However, if we allows the total human population size to vary with time t, then we need to explicitly write down the equation for susceptible human population or the total human population. In that case, the model with disease-induced human death rate may have different dynamical behaviors.

4 A Case Study

In this section, we study the effect of Serratia AS1 on the malaria transmission dynamics in Douala, Cameroon by using the available data in Douala and applying our theoretical results obtained in Sect. 3. According to the records from the Cameroon Ministry of Health, malaria accounts for $30\%$ to $35\%$ of the total deaths in Cameroon every year (Ndo et al. 2011). Malaria species in Cameroon consist of P. falciparum ($>85\%$), P. ovale ($5{-}10\%$), P. vivax (rare) (https://www.cdc.gov/malaria/about/biology/index.html). Douala locates on the estuary of Wouri River and has tropical climate, which is favorable for mosquito breeding and growth. Malaria transmission in Douala is endemic and seasonal with Anopheles gambiae being the main vector (Craig et al. 1999).

We carry out the numerical simulations by using ode45 and the Curve Fitting Toolbox in MATLAB. First, we need to estimate the parameter values. Douala has a population of 1,338,082 (see http://worldpopulationreview.com/countries/cameroon-population/cities/), which can be chosen as the value of $N_\mathrm{h}$. The life expectancy of Cameroon is 59 years (see https://www.who.int/countries/cmr/en/). Using this number, we estimate the human natural death rate as $d_\mathrm{h}$$=$$\frac{1}{59\times 12}$$=0.0014$$\hbox {month}^{-1}$. The values of all the constant parameters are listed in Table 2.

Table 2 Parameter values

Since temperature plays a major role in mosquito life cycle and activities, we evaluate the periodic parameters by using the monthly mean temperatures of Douala from 1991 to 2015 (obtained from Climate Change Knowledge Portal website: http://sdwebx.worldbank.org/climateportal), as shown in Table 3.

Table 3 Monthly mean temperature for Douala, Cameroon (in $^{\circ }$C)

According to Paaijmans et al. (2009), the temperature-dependent mosquito biting rate can be expressed as

$$\begin{aligned} \begin{aligned} \beta (T)&=30.4\times 0.000203T(T-11.7)\sqrt{42.3-T}\ \text { month}^{-1}, \end{aligned} \end{aligned}$$

(14)

where and hereinafter T is the temperature in $^{\circ }C$. Considering T as a function of the time variable t (in month) and using (14) and the data set in Table 3, the biting rate of mosquitoes in Douala can then be fitted by

$$\begin{aligned} \begin{aligned} \beta (t)&=\beta (T(t))\\&=0.4504\cos (2\pi t/12)+0.8635\sin (2\pi t/12)-0.09128\cos (4\pi t/12)\\&\quad -\,0.2758\sin (4\pi t/12) -0.0354\cos (6\pi t/12)-0.009206\sin (6\pi t/12)\\&\quad +\,0.03871\cos (8\pi t/12)-0.06943\sin (8\pi t/12)+0.04601\cos (10\pi t/12)\\&\quad -\,0.05516\sin (10\pi t/12)+9.907\ \text {month}^{-1}. \end{aligned} \end{aligned}$$

(15)

It follows from Rubel et al. (2008) that the birth rates of larval mosquitoes, the maturation rate of mosquitoes and the death rate of larval mosquitoes can be, respectively, given by

$$\begin{aligned} \lambda (T)= & {} 2.325\beta (T), \end{aligned}$$

(16)

$$\begin{aligned} \delta (T)= & {} \frac{\lambda (T)}{10}, \end{aligned}$$

(17)

and

$$\begin{aligned} \begin{aligned} \mu _l(T)&= 30.4\times (0.0025T^2-0.094T+1.0257)\ \text {month}^{-1}. \end{aligned} \end{aligned}$$

(18)

Equations (16) and (17) together with (14) and (15) directly give approximations of $\lambda$ and $\delta$ as functions of t. For $\mu _l$, again by (18) and the data set in Table 3, it can be fitted by

$$\begin{aligned} \begin{aligned} \mu _l(t)&=0.7474\cos (2\pi t/12) +1.529\sin (2\pi t/12)-0.2234\cos (4\pi t/12)\\&\quad -\,0.4017\sin (4\pi t/12) -0.0348\cos (6\pi t/12)-0.0671\sin (6\pi t/12)\\&\quad +\,0.0568\cos (8\pi t/12)-0.1369\sin (8\pi t/12) +0.09603\cos (10\pi t/12)\\&\quad -\,0.1006\sin (10\pi t/12) +9.423\ \text {month}^{-1}. \end{aligned} \end{aligned}$$

(19)

According to Martens et al. (1995), Ngarakana-Gwasira et al. (2014), the death rate of adult mosquitoes is evaluated as

$$\begin{aligned} \begin{aligned} \mu _\mathrm{v}(T)&= \frac{30.4}{-0.03T^2+1.31T-4.4}\ \text {month}^{-1}. \end{aligned} \end{aligned}$$

(20)

Then by (20) and the data set in Table 3, $\mu _\mathrm{v}$ can be approximated, as a function of t, by

$$\begin{aligned} \begin{aligned} \mu _\mathrm{v}(t)&= 0.06434\cos (2\pi t/12) +0.1396 \sin (2\pi t/12)-0.02537\cos (4\pi t/12)\\&\quad -\,0.03013\sin (4\pi t/12)-0.001558\cos (6\pi t/12)-0.01003\sin (6\pi t/12)\\&\quad +\, 0.0046\cos (8\pi t/12) -0.01353\sin (8\pi t/12) +0.009855\cos (10\pi t/12)\\&\quad -\,0.009518\sin (10\pi t/12) +3.348\ \text {month}^{-1}. \end{aligned} \end{aligned}$$

(21)

First, we verify the obtained analytic result in the last section by investigating the long-term behaviors of the solutions. To numerically calculate $R_0$, we use Theorem 2.2 in Zhao (2017), Lemma 2.5 in Liang et al. (2007) and the bisection method. Considering that mosquitoes with greater q may have smaller $\gamma$ and those with greater $\gamma$ may have smaller q, we set $\eta =q\gamma$. Thus, we can focus on how the dynamics varies with $\eta$ instead of q and $\gamma$ in order to investigate the effect of horizontal transmission of the bacteria. Note that another parameter we are interested in is p which is related to vertical transmission of the bacteria. In Fig. 1a, we set $p=0.3, \eta =3$. In this case, $R_\mathrm{v}=1.3544>1$ and $R_0=1.5067>1$. We see that all the variables approach positive periodic states. Biologically, this means that malaria persists and exhibits seasonal fluctuation. In Fig. 1b, we increase the values of p and $\eta$ to 0.5 and 6, respectively. We get $R_\mathrm{v}=1.3544>1$ and $R_0=0.7876<1$, and we observe that both the population sizes of malaria-infected mosquitoes and -infective humans approach zero eventually. In this case, malaria is eliminated from this area although the mosquito population persists.

Next, we explore the effects of vertical and horizontal transmissions of the bacteria in reducing $R_0$. Figure 2 gives the graph of $R_0$ as a function of the parameters p and $\eta$. We see that increasing the values of p and $\eta$ is helpful for reducing $R_0$. In Fig. 3, we consider the situation in which the vertical or the horizontal transmission of the bacteria is relatively weak. In Fig. 3a, we let $\eta =2$. We find that the higher value of p is, the lower level $I_\mathrm{h}(t)$ can be reduced to and p needs to be high enough to make $I_\mathrm{h}(t)$ approach 0. In Fig. 3b, we set $p=0.1$ to represent a weak vertical transmission of the bacteria. We observe that the greater value of $\eta$ is, the lower level $I_\mathrm{h}(t)$ can be decreased to and $\eta$ also needs to be large enough to reduce $I_\mathrm{h}(t)$ to 0. These results imply that both vertical and horizontal transmissions of the bacteria play important roles in malaria control. Besides, it is possible to reduce $R_0$ to be less than 1 even if one of these two transmission modes is weak.

In the above, we have discussed the impact of p and $\eta$ on the threshold parameter $R_0$. We now numerically explore the effects of these two parameters on the population dynamics, particularly short time dynamics which can help us predict the malaria dynamics in Douala in the near future. To this end, we set $B_\mathrm{v}(0)=100{,}000$. The numerical results for infected human population are presented in Fig. 4 for various combinations of p and $\eta$. When $p=0.4, \eta =4$, $I_\mathrm{h}(t)$ can be reduced to a lower level but $R_0=1.1490>1$. When $p=0.5, \eta =5$, $I_\mathrm{h}(t)$ can be reduced to 0 eventually, and in this case, $R_0=0.8855<1$. When $p=0.9, \eta =10$, $I_\mathrm{h}(t)$ can be reduced to 0 much faster and $R_0=0.2609$ in this case. If we further increase the values of p and $\eta$, say, $p=1, \eta =100$ or $p=1, \eta =200$, we find that the dynamics of $I_\mathrm{h}(t)$ is almost the same with the case where $p=0.9, \eta =10$. Note that the maximum possible value of p is 1; Fig. 4 tells us that when p is large enough, increasing the value of $\eta$ will not make big difference for the dynamics of malaria-infected human population. In addition, after we change the initial values, say, $B_\mathrm{v}(0)=0$ or $B_\mathrm{v}(0)=500{,}000$, we get the same result. From Fig. 4, we also see that if we use the engineered Serratia AS1 bacteria alone to control malaria in Douala, it takes at least about 300 months (i.e., 25 years) to eliminate malaria from this area.

Fig. 1

Long-term behavior of the solution. a$p=0.3, \eta =3$, here $R_0=1.5067$; b$p=0.5, \eta =6$, here $R_0=0.7876$ (Color figure online)

Fig. 2

The graph of $R_0$ as a function of p and $\eta$ (Color figure online)

Fig. 3

The effects of horizontal and vertical transmissions of bacteria in controlling the infected human population size. a$\eta =2$, p varies. b$p=0.1$, $\eta$ varies (Color figure online)

Fig. 4

The effects of vertical and horizontal bacteria transmission in malaria elimination (Color figure online)

5 Discussion

The engineered Serratia AS1 bacteria can efficiently reduce vector competence and rapidly disseminate through mosquito population via horizontal and vertical transmissions with no obvious fitness cost to mosquitoes and therefore offers the potential to become an effective tool in malaria control. Based on the experiment results obtained by Wang et al. (2017), we developed a malaria transmission model incorporating the transmission of AS1 bacteria among the mosquito population. To analyze the model, we defined two threshold parameters: the vector reproduction ratio, $R_\mathrm{v}$, and the basic reproduction ratio, $R_0$. First, we obtained the threshold dynamics for the mosquito population, that is, the mosquito population will go to extinction if $R_\mathrm{v}<1$ and persist if $R_\mathrm{v}>1$. In the case $R_\mathrm{v}>1$, we are led to a limiting system of the sub-system which governs the dynamics of the malaria-infective compartments (both infected humans and infected mosquitoes). Fortunately, this limiting system is monotone so that we can obtain the threshold dynamics in terms of $R_0$ for the limiting system by using the theory of monotone and subhomogeneous systems, that is, the infective compartments approach zero eventually if $R_0<1$, and approach positive periodic fluctuations if $R_0>1$. Finally, we lift the threshold dynamics for the limiting system to the full model system by using the theory of chain transitive sets. Numerically, we carried out a case study for Douala, Cameroon. We verified the obtained analytic results by simulating the long-term behaviors of the solutions. By a graph showing how the value of $R_0$ varies with the parameters related to vertical and horizontal transmissions of AS1 bacteria, we found that it is possible to eliminate malaria from Douala when both vertical and horizontal transmissions are strong. Furthermore, even if one of these two transmission ways is weak it is still possible to eliminate malaria as long as the other AS1 transmission route is extremely strong. By simulating the long-term values of the infected human compartment, we estimated that it takes at least 25 years to eliminate malaria from Douala.

By similar method and with more sufficient and accurate parameter values, researchers are expected to give a better evaluation of the effects of the engineered AS1 bacteria in malaria control in future field release trials. A suitable Monte-Carlo sampling method (e.g., Latin Hypercube sampling approach) can be used to explain the effect of uncertainties in the estimate of these values on the overall outcome of the simulations. In addition, we used mean monthly temperature data to fit the temperature-dependent parameters of the model. A more accurate estimation can be made by incorporating daily temperature fluctuations [see Beck-Johnson et al. (2017); Paaijmans et al. (2010) for the effect of daily temperature variation on malaria transmission].

Mathematical models can be developed in future based on modified assumptions according to new findings in the research of malaria control with AS1 bacteria. For instance, AS1-infected malaria-susceptible mosquitoes may still acquire malaria infection but at a reduced rate in comparison with wild mosquitoes. It is also possible that AS1-infected malaria-infected mosquitoes are also able to transmit malaria but at a reduced rate compared to malaria-infected wild mosquitoes. Besides, there may be some heterogeneity in the AS1 infection of malaria-infected mosquitoes and that of malaria-susceptible mosquitoes. Since the role of AS1 bacteria is to inhibit malaria parasite development in the vector, it is interesting to develop a model which includes exposed class for the vector or to construct a delay differential equations model with the delay representing the extrinsic incubation period.

One of the advantages of the control measure with AS1 bacteria is that they can self-propagate among wild mosquito populations. Thus, less labor is needed to continuously release AS1 bacteria or AS1-infected mosquitoes in field. Recently, Koosha et al. (2018) carried out experiments examining delivery of genetically engineered Serratia AS1 bacteria to arthropods that are vectors for malaria, West Nile, Zika virus and several other diseases. They found that bacteria can be introduced at different points of the vector lifetime through host skin, water sipping, vertical, transstadial and venereal acquisition. They suggested to use these routes singularly or in combination to introduce engineered bacteria to mosquitoes in field. It is instructive to determine conditions for the AS1-infected mosquitoes to invade the wild population and to figure out how long this is likely to take if such an invasion could occur.

Integrated management is highly recommended in malaria control (Koenraadt and Takken 2018; Yakob and Yan 2009). It is interesting to study the comprehensive effect of releasing AS1 bacteria in conjunction with other control measures. For example, if we combine the use of insecticide-treated bed nets (ITNs) with AS1 bacteria, then hopefully, in order to eliminate malaria locally, a smaller proportion of the humans would be needed to use ITNs. This may bring new hope for malaria eradication especially for those poor areas with limited resources where people usually use bed nets for fishing. We leave this for future investigation.