Dynamical Analysis for a Malaria Transmission Model

Abstract

In this paper, we present a malaria transmission model with climatic factors to study the climatic transmission dynamics of malaria with the effect of the Serratia AS1 bacterium. It has been shown in controlled laboratory experiments that Serratia AS1 bacterium can rapidly disseminate throughout mosquito populations and efficiently inhibit development of malaria parasites in mosquitoes. We derive the basic reproduction ratio $R_{0}$. We introduce the basic reproduction ratio $R_{0}$ which can be used as a threshold parameter in the global dynamical model. When $R_{0}\le 1$, the disease-free periodic solution of this model is globally asymptotically stable; and when $R_{0}>1$, the disease remains persistent. We analyze the sensitivity of $R_{0}$ in terms of the vertical and horizontal transmission rates of Serratia AS1, and find that $R_{0}$ can be small when the vertical transmission rate of Serratia AS1 tends to 1 and the influence of the horizontal transmission rate performs inversely proportional to $R_{0}$ when the vertical transmission rate is less than 1. Based on the data of Luanda, we perform numerical simulations to illustrate our theoretical results, which indicate that treatment of Serratia AS1 provides us an effective measure in controlling malaria.

1 Introduction

Malaria is a life-threatening disease caused by Plasmodium parasites that are transmitted to people through the bites of infected female Anopheles mosquitoes. It is preventable and curable. According to the Global Malaria Report 2020 released by World Health Organization (WHO), there are about 229 million malaria cases and 409,000 deaths worldwide in 2019, and nearly half of the world’s population is at risk of malaria [37]. The African region, which is home to 94$\%$ of malaria cases and deaths in 2019, carries a disproportionately high share of the global malaria burden. The primary vulnerable group affected by malaria is children aged under 5 years, accounting for 67$\%$ (274,000) of all malaria deaths worldwide [37, 38].

Preventing and controlling malaria infection research has been highly concerned for a long time. As early as 1955, the World Health Assembly introduced the Global Malaria Eradication Project. However, the situation in many malaria-endemic areas remains dire. There are three main interventions to control malaria infection, namely malaria vector control, chemoprophylaxis and case treatment. Malaria vector control hampers malaria parasites from mosquitoes to humans and vice versa, such as insecticide-treated mosquito nets and indoor residual spraying. Chemoprophylaxis suppresses the blood stage of malaria infections, such as sulfadoxine-pyrimethamine (SP). IPTp (intermittent preventive treatment in pregnancy) with SP is used to protect pregnant women, and SMC (seasonal malaria chemoprevention) and IPTc (intermittent preventive treatment in children) are used to protect children. The best available treatment is artemisinin-based combination therapy (ACT). Antimalarial medicines can also be used to prevent malaria [38]. Although these methods reduce incidence of malaria to some extent, the benefits of these methods are limited. Due to a lack of funding, millions of pregnant women and children could not benefit from chemoprevention. With the use of repellents, resistance to at least 1 of the 4 commonly-used insecticide classes is widespread in all major malaria vectors across the WHO regions [6, 17, 38]. In addition, resistance to antimalarial medicines is also increasing, and the benefits of drugs for malaria treatment are compromised [10, 16]. Hence, WHO continues to highlight the urgent need for new and improved tools in the global response to malaria.

With the rapid development of biotechnology, genetic technology is used to control the malaria infection such as sterile mosquitoes technology [12, 45] and symbiotic bacteria technology [9]. Sterile mosquito technology reduces the population number of mosquitoes by releasing a large number of sterile male mosquitoes. Symbiotic bacteria technology prevents mosquito-borne diseases by changing mosquito symbiotic bacteria. For example, Dengue fever and Zika disease was effectively controlled by releasing Aedes aegypti mosquitoes infected with the bacterium Wolbachia [11, 24].

As we know, Serratia-AS1 is a bacterium found in mosquitoes and is genetically modified for expression of antimalaria effector molecules that repress development of malaria parasites in mosquitoes. As described in [18, 34], Serratia AS1 is a strain of nonpathogenic bacteria and can isolate from Anopheles ovaries. In fact, Serratia-AS1 can stably colonize the mosquito midgut, female ovaries, male accessory glands and spread rapidly throughout mosquito populations through horizontal and vertical transmission. Sarreia AS1 is genetically engineered for secretion of anti-Plasmodium effector proteins, which can inhibit development of Plasmodium falciparum in mosquitoes. Horizontal transmission of AS1 bacteria is mainly transmitted from male to virgin female through mating. Vertical transmission means that AS1 bacteria attach to laid eggs, float and propagates in the water and are ingested by the larvae that hatched from these eggs. Thus, Sarreia AS1 bacteria are likely to exhibit long-term persistence in wild mosquito populations and have little or no effect on the life span, fecundity, fertility and blood feeding behaviors of adult mosquitoes. These results indicate that the AS1 bacteria could be a good vector for treating malaria.

In the field of mathematical epidemiology, one of the foundational malaria models was introduced by Ross [29] and developed by Macdonald [22], where the concept of the basic reproduction ratio was put forward. Since then a great number of mathematical models have been proposed to study malaria transmission. With the continuous in-depth investigation of mathematical models, an increasing number of factors have been considered to study malaria transmission dynamics such as seasonality, stage structure of mosquitoes, effect of time delay, nonlinear infection rate, and effects of various control strategies (see, e.g. [1, 3, 7, 13, 25,26,27, 30, 32, 40, 41, 43] and the references therein). Some others consider the impact of genetic technology on the spread of disease [4, 20]. In terms of model analyses on infectious diseases, the basic reproduction ratio $R_{0}$, one of the most important concepts in infectious disease dynamics, is the average number of secondary infections caused by a single infectious individual during his/her entire infectious lifetime. There are tremendous theoretical studies on $R_{0}$ for various types of biological models (see, e.g. [31, 35]).

Recently, Wang and Zou [36] formulated a climate-based malaria transmission model by taking into account the transmission of Serratia AS1 among the mosquito population. They counted two threshold parameters: one is for the threshold dynamics of the mosquito population $R_V$, whereas the other determines the disease transmission dynamics $R_0$. If $R_V < 1$, it means that the entire mosquito population will die out. Meanwhile, $R_0$ makes no sense when $R_V < 1$. Hence, $R_V > 1$ is always assumed in [36] when the effects of Serratia AS1 bacteria was considered on $R_0$. Main purpose of this paper is to develop a climate-based malaria transmission model by incorporating the transmission of Serratia AS1 bacteria and the time-dependent human population size. We calculate the basic reproduction ratio and analyze the dynamical behaviors. Numerically, we use this model to simulate the malaria transmission in Luanda and Angola. Moreover, we perform sensitivity analysis of $R_0$ in terms of the vertical and horizontal transmission parameters of Serratia AS1.

The paper is organized as follows. In Sect. 2, we formulate a climate-based malaria transmission model. In Sect. 3, we discuss the basic reproduction number $R_{0}$ of the malaria model and analyze the threshold dynamics in terms of $R_{0}$. In Sect. 4, we numerically demonstrate the long-term transmission behavior of malaria in Luanda. A discussion is given in Sect. 5.

2 Model Formulation

In this section we propose a new malaria transmission model with climatic factors to study the climatic transmission dynamics of malaria with the effect of the Serratia AS1. The total human population at time t, denoted by $N_{h}(t)$, is subdivided into three subclasses: susceptible $S_{h}(t)$, infectious $I_{h}(t)$ and recovered $R_{h}(t)$. Here, $R_{h}(t)$ means those who recover because of treatments or are immune to malaria at time t. This immunity is due to the exposure of recovered individuals to mosquito bites, thus recovered individuals may lose immunity and become susceptible humans again. The total number of adult mosquitoes is denoted by $N_{V}(t)$, which is classified into three subclasses, namely susceptible mosquito $S_{V}(t)$, infectious mosquito $I_{V}(t)$ (those who are infected by infectious humans $I_{h}(t)$ or recovered humans $R_{h}(t)$) and Serratia AS1-infected mosquito $B_{V}(t)$. That is,

$$\begin{aligned}&N_{V}(t)=S_{V}(t)+I_{V}(t)+B_{V}(t), \end{aligned}$$

(1)

$$\begin{aligned}&N_{h}(t)=S_{h}(t)+I_{h}(t)+R_{h}(t). \end{aligned}$$

(2)

The mathematical model is constructed based on the conventional assumptions [21, 34, 36]:

• (A1): Mosquito bites are the only means of malaria transmission.

• (A2): Both susceptible and infected wild mosquitoes can be infected with Serratia AS1 through mating with AS1-infected mosquitoes.

• (A3): If mosquitoes are infected with Serratia AS1, malaria-susceptible mosquitoes will not be infected with malaria and malaria-infected mosquitoes will not transmit malaria [18, 34].

The flow diagram for malaria transmission among humans and mosquitoes is illustrated in Fig. 1. Since the life activities of mosquitoes are closely related to climatic factors, we assume the parameters to be $\omega$-periodic functions (the period $\omega = 12$-month) in our model. Then the recruitment rate of mosquitoes $\Lambda _v(t)$, the natural death rate of all mosquitoes subclasses $\mu _{v}(t)$ and the biting rate of mosquitoes $\beta (t)$ (the average number of bites per mosquito per unit time at time t) are positive, continuous and periodic functions. The infection rates per susceptible mosquito at time t is $b\beta (t)\frac{I_{h}(t)+\sigma R_{h}(t)}{N_{h}(t)}$, where b represents the probability of infection transmission from humans to mosquitoes and $\sigma$ is the probability of recoverers who are still infectious. Similarly, the term $c\beta (t)\frac{I_{V}(t)}{N_{h}(t)}$ represents the infection rate per susceptible human at time t, where c is the probability of infection transmission from mosquitoes to humans.

Fig. 1

Transmission diagram of malaria among different categories: dashed arrows indicate the direction of the infection and solid arrows represent the transition from one class to another

Serratia AS1 can infect larvae by mosquito breeding water and adult mosquitoes by mating [34, 36], so Serratia AS1 infects mosquitoes through vertical and horizontal transmission. We assume that the proportion of mosquitoes infected by Serratia AS1 is p. Then the recruitment rate of mosquitoes with Serratia AS1 is $p{\Lambda _v(t)}$ and the proportion $(1-p){\Lambda _v(t)}$ is susceptible. Meanwhile, the mating rate of mosquitoes with Serratia AS1 can be expressed by $\gamma \frac{B_{V}(t)}{N_{V}(t)}$, where $\gamma$ is the natural mating rate of mosquitoes, so the horizontal transmission rate of Serratia AS1 is expressed by $q\gamma \frac{B_{V}(t)}{N_{V}(t)}$, where q is the transmission proportion of Serratia AS1 from a male mosquito to a female by mating. Let $\Lambda _h$ represent the recruitment (birth or immigration) rate of human population, m be the rate of recoverers who lose their natural immunity against infection and $\rho _h$ denote the treated and spontaneous immune recovery rate of humans. Malaria mortality rate for humans is $\delta _{h}$ and the nature death rate for all human subclasses is denoted by $d_h$.

Arising from the above details, our mathematical model is described by the following system of ordinary differential equations:

$$\begin{aligned} \left\{ \begin{aligned}&\frac{dS_{V}(t)}{dt}=(1-p)\Lambda _v(t)-\mu _{v}(t)S_{V}(t)-b\beta (t)\frac{I_{h}(t)+\sigma R_{h}(t)}{N_{h}(t)}{S_{V}(t)}-q\gamma \frac{B_{V}(t)}{N_{V}(t)}S_{V}(t),\\&\frac{dI_{V}(t)}{dt}=b\beta (t)\frac{I_{h}(t)+\sigma R_{h}(t)}{N_{h}(t)}{S_{V}(t)}-\mu _{v}(t)I_{V}(t)-q\gamma \frac{B_{V}(t)}{N_{V}(t)}I_{V}(t),\\&\frac{dB_{V}(t)}{dt}=p{\Lambda _v(t)}+q\gamma \frac{B_{V}(t)}{N_{V}(t)}S_{V}(t)+q\gamma \frac{B_{V}(t)}{N_{V}(t)}I_{V}(t)-\mu _{v}(t)B_{V}(t)\\&\frac{dS_{h}(t)}{dt}=\Lambda _{h}+m{R_{h}}(t)-d_{h}S_{h}(t)-c\beta (t)\frac{I_{V}(t)}{N_{h}(t)}{S_{h}(t)},\\&\frac{dI_{h}(t)}{dt}=c\beta (t)\frac{I_{V}(t)}{N_{h}(t)}{S_{h}(t)}-d_{h}I_{h}(t)-\delta _{h}I_{h}(t)-\rho _{h}I_{h}(t)\\&\frac{dR_{h}(t)}{dt}=\rho _{h}I_{h}(t)-d_{h}R_{h}(t)-m{R_{h}(t)}.\\ \end{aligned} \right. \end{aligned}$$

(3)

Explicit description of the parameters of system (3) is given in Table 1.

Table 1 Biological description of the parameters in system (3)

3 Threshold Dynamics

In this section, we shall analyze the global behavior of periodic solutions of system (3) and the threshold effect of the basic reproduction ratio $R_{0}$. According to the biological background of system (3), the initial values of system (3) starting at $t=0$ are given as follows:

$$\begin{aligned} \begin{aligned} S_{V}(0)>0,\ \, I_{V}(0)\ge 0,\,\ B_{V}(0)\ge 0,\,\ S_{h}(0)>0,\,\ I_{h}(0)\ge 0,\,\ R_{h}(0)\ge 0. \end{aligned} \end{aligned}$$

If $p = 1$, from system (3) it follows that

$$\begin{aligned} \begin{aligned} \lim _{t\rightarrow \infty }S_{V}(t)=\lim _{t\rightarrow \infty }I_{V}(t)=\lim _{t\rightarrow \infty }I_{h}(t) =\lim _{t\rightarrow \infty }R_{V}(t)=0, \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} \frac{\mathrm {d}B_{V}(t)}{\mathrm {d}t}=\Lambda _v(t)-\mu _{v}(t){B_{V}(t)}, \ \ \ \frac{\mathrm {d}S_{h}(t)}{\mathrm {d}t}=\Lambda _{h}-d_{h}S_{h}(t). \end{aligned} \end{aligned}$$

System (3) has a unique trivial periodic solution $(0, 0, B^{*}_{V}(t), S^{*}_{h}(t), 0, 0)$ in this case. Biologically, p is usually not equal to one. Therefore, we just consider $0 \le p < 1$ in the rest of this section.

3.1 Positivity and Boundedness of Solutions

Let ${\mathbb {R}}^{n}_{+}$ be the standard ordered n-dimensional Euclidean space. For $u,v\in {\mathbb {R}}^{n}$, we denote

$$\begin{aligned} \begin{aligned}&u\ge v,\quad \mathrm {if}\ u-v\in {\mathbb {R}}^{n}_{+};\\&u>v,\quad \mathrm {if}\ u-v\in {\mathbb {R}}^{n}_{+}/ \{\mathbf{0}\};\ and\\&u\gg v,\quad \mathrm {if}\ u-v\in \mathrm {int}({\mathbb {R}}^{n}_{+}). \end{aligned} \end{aligned}$$

Let $W =\{u=(N_V, I_V, B_V, S_h, I_h, R_h)\in {\mathbb {R}}^{6}_{+}\}$. Upon the positivity and boundedness of solutions of system (3), we have the following result.

Lemma 3.1

For any $\varphi \in W$, system (3) has a unique nonnegative solution $u(t,\varphi )$ on $[0,\infty )$ with $u(0)=u(0,\varphi )=\varphi$, $u(t,\varphi ) \in W$ for all $t > 0$ and all solutions are ultimately bounded. If $\varphi \gg 0$, then $u(t,\varphi )\gg 0$ for $t>0$.

Proof

For any $\varphi =(\varphi _{1},\varphi _{2},\varphi _{3},\varphi _{4},\varphi _{5},\varphi _{6})\in W$, system (3) can be written as

$$\begin{aligned} \left\{ \begin{aligned}&{\dot{u}}={\tilde{f}}(t,u),\\&u(0,\varphi )=\varphi , \end{aligned} \right. \end{aligned}$$

(4)

where the vector field ${\tilde{f}}(t,u)$ is generated by the right side of system (3). Since ${\tilde{f}}(t,u)$ is continuous in $(t,u)\in \mathbbm {R}_{+}\times W$ and is Lipschitz in u on each compact subset of W, system (4) has a unique solution $u(t, \varphi )$ on its maximal interval $[0, t_{\varphi })$ (see [15,  Theorems 2.2.1 and 2.2.3]). Note that ${\widetilde{f}}_i(t,u)\ge 0$ whenever $\varphi _i=0$ for $i=1,2,3,4,5$, then $u(t, \varphi )\ge 0$ for all $t\in [0, t_{\varphi })$.

By (1), we find

$$\begin{aligned} \begin{aligned} \frac{\mathrm {d}N_{V}(t)}{\mathrm {d}t}=\Lambda _v(t)-\mu _{v}(t)N_V(t), \end{aligned} \end{aligned}$$

(5)

which implies $N_{V}(t)=N_{V}(0)e^{-{\int ^{t}_{0}}\mu _{V}(s)\mathrm {d}s}+\int _{0}^{t} b(s)e^{-{\int ^{t}_{s}\mu _{V}(u)}\mathrm {d}u}\mathrm {d}s.$ Since $\int ^{t}_{0}\mu _{V}(s)\mathrm {d}s=\theta t+\phi (t)$, where $\theta =\frac{1}{\omega }\int ^{\omega }_0 \mu _{V}(s)\mathrm {d}s$ and $\phi (s)$ is an $\omega$-periodic function, we have

$$\begin{aligned} \begin{aligned} \limsup _{t\rightarrow \infty }(N_{V}(t)-N^{*}_{V}(t))\le 0, \end{aligned} \end{aligned}$$

where $N^{*}_{V}(t)= \int _{0}^{t} b(s)e^{-{\int ^{t}_{s}\mu _{V}(u)}\mathrm {d}u}\mathrm {d}s$ is the $\omega$-periodic solution of Eq. (5) and $N_{V}(t)$ is bounded. This indicates that $S_V(t)$, $I_V(t)$ and $B_V(t)$ are bounded for $t\ge 0$. It follows from (2) that

$$\begin{aligned} \frac{\mathrm {d}N_{h}(t)}{\mathrm {d}t}=\Lambda _{h}-d_{h}N_{h}(t)-\delta _{h}I_{h}(t) \le \Lambda _{h}-d_{h}N_{h}(t) \end{aligned}$$

for $t \ge 0$. By the comparison principle, we have

$$\begin{aligned} \begin{aligned} {\limsup _{t\rightarrow \infty }}N_{h}(t)\le \frac{\Lambda _{h}}{d_{h}}. \end{aligned} \end{aligned}$$

So $S_h(t)$, $I_h(t)$ and $R_h(t)$ are ultimately bounded. It then follows that $t_{\varphi }=+\infty$.

For any $\varphi \gg 0$, by solving the first equation of system (3), for $t>0$ we have

$$\begin{aligned} \begin{aligned} S_V(t)=\mathrm {exp}\left( -\int ^t_0H_1(\tau )\mathrm {d}\tau \right) \left[ S_V(0)+\int ^t_0(1-p)b(\tau )\mathrm {exp}\left( \int ^\tau _0H_1(s) \mathrm {d}s\right) \mathrm {d}\tau \right] >0, \end{aligned} \end{aligned}$$

where $H_1(t)=-\left( \mu _{v}(t)+b\beta (t)\frac{I_{h}(t)+\sigma R_{h}(t)}{N_{h}(t)}+q\gamma \frac{B_{V}(t)}{N_{V}(t)}\right)$. Similarly, we can obtain $u(t,\varphi )\gg 0$ for $t>0$. $\square$

3.2 Basic Reproduction Ratio

In this subsection, we deduce the basic reproduction ratio $R_{0}$ of system (3) by the theory recently developed in [35].

When $I_{V}({t})=I_{h}({t})=R_{h}({t})=0$, the disease-free state of system (3) is given by

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\mathrm {d}S_{V}(t)}{\mathrm {d}t}=(1-p)\Lambda _v(t)-\mu _{v}(t)S_{V}(t)-q\gamma \frac{B_{V}(t)}{N_{V}(t)}S_{V}(t),\\&\frac{\mathrm {d}B_{V}(t)}{\mathrm {d}t}=p{\Lambda _v(t)}+q\gamma \frac{B_{V}(t)}{N_{V}(t)}S_{V}(t)-\mu _{v}(t)B_{V}(t),\\&\frac{\mathrm {d}S_{h}(t)}{\mathrm {d}t}=\Lambda _{h}-d_{h}S_{h}(t). \end{aligned} \right. \end{aligned}$$

(6)

As we discussed in the proof of Lemma 3.1, for any $\varphi =(\varphi _1, \varphi _2, \varphi _3)\in {\mathbb {R}}_+^3$, system (6) has a unique nonnegative bounded solution $w(t, \varphi )$ on $[0, \infty )$ with $w_0=\varphi$ and $w(t, \varphi )\in {\mathbb {R}}^+_3$.

Lemma 3.2

System (6) admits a unique globally attractive positive $\omega$-periodic solution $(S^*_{V}(t)$, $B^*_{V}(t), S^{*}_{h})$.

Proof

When $I_{V}({t})=0$, $N_V(t)=S_V(t)+B_V(t)$, system (6) is equivalent to

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\mathrm {d}N_{V}(t)}{\mathrm {d}t}=\Lambda _v(t)-\mu _{v}(t)N_{V}(t),\\&\frac{\mathrm {d}B_{V}(t)}{\mathrm {d}t}=p{\Lambda _v(t)}+q\gamma B_{V}(t)-q\gamma \frac{B_{V}^{2}(t)}{N_{V}(t)}-\mu _{v}(t)B_{V}(t),\\&\frac{\mathrm {d}S_{h}(t)}{\mathrm {d}t}=\Lambda _{h}-d_{h}S_{h}(t). \end{aligned} \right. \end{aligned}$$

(7)

It is easy to see that the first equation of system (7) has a unique continuous globally attractive positive $\omega$-periodic solution $N_V^*(t)$ and the third equation of system (7) has a unique globally attractive positive equilibrium $S_h^*$, where $S_h^*=N_h^*=\frac{\Lambda _{h}}{d_{h}}$. Rewrite the second equation in system (7) as

$$\begin{aligned} \begin{aligned} \frac{\mathrm {d}B_{V}(t)}{\mathrm {d}t}=p{\Lambda _v(t)}+(q\gamma -\mu _{v}(t)) B_{V}(t)-q\gamma \frac{B_{V}^{2}(t)}{N_{V}^{*}(t)}. \end{aligned} \end{aligned}$$

(8)

Note that the coefficients $p{\Lambda _v(t)}$, $q\gamma -\mu _{v}(t)$ and $-\frac{q\gamma }{N_{V}^{*}(t)}$ are continuous $\omega$-periodic functions, Eq. (8) is a Riccati equation and has a unique nonnegative bounded solution $B_{V}(t, \varphi )$ on $[0, \infty )$ with $B_V(0)=\varphi \in {\mathbb {R}}^+$. Moreover, according to [28,  Theorem 3.2], Eq. (8) has a continuous positive $\omega$-periodic solution ${\tilde{B}}_V(t)$. Let $B_V(t)={\tilde{B}}_V(t)+\frac{1}{u(t)}$. Then u(t) satisfies the scalar linear periodic equation

$$\begin{aligned} \begin{aligned} \frac{\mathrm {d}u}{\mathrm {d}t}=\frac{q\gamma }{N_{V}^{*}(t)}-A(t)u, \end{aligned} \end{aligned}$$

(9)

where $A(t)=\left( 1-2\frac{{\tilde{B}}_V(t)}{N_V^*(t)}\right) q\gamma -\mu _V(t)$ is a continuous $\omega$-periodic function. The general solution of Eq. (9) is

$$\begin{aligned} \begin{aligned} u(t)=e^{-\int ^t_0A(t)\mathrm {d}t} \left[ \int ^t_0\frac{q\gamma }{N_V^*(s)}e^{\int ^s_0A(\tau )\mathrm {d}\tau }\mathrm {d}s +u(0)\right] . \end{aligned} \end{aligned}$$

Thus, the general solution of Eq. (8) is

$$\begin{aligned} \begin{aligned} B_V(t)={\tilde{B}}_V(t)+\frac{\left( \varphi -{\tilde{B}}_V(0)\right) e^{\int ^t_0A(t)dt}}{1+ (\varphi -{\tilde{B}}_V(0))\left[ \int ^t_0\frac{q\gamma }{N_V^*(s)}e^{\int ^s_0A(\tau ) \mathrm {d}\tau }\mathrm {d}s \right] }. \end{aligned} \end{aligned}$$

If $\int ^\omega _0A(t)\mathrm {d}t\le 0$, it is easy to see that Eq. (8) has a unique globally attractive positive $\omega$-periodic solution ${\tilde{B}}_V(t)$. If $\int ^\omega _0A(t)\mathrm {d}t>0$, Eq. (9) has a unique globally attractive positive $\omega$-periodic solution $u^*(t)$. Then Eq. (8) has a unique globally attractive positive periodic solution ${\tilde{B}}_V(t)+\frac{1}{u^*(t)}$. Therefore, the Riccati Eq. (8) admits a unique globally attractive positive periodic solution $B_V^*(t)$.

Since the third equation of system (7) is relatively independent, we consider the first two equations of system (7), i.e.

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\mathrm {d}N_{V}(t)}{\mathrm {d}t}=\Lambda _v(t)-\mu _{v}(t)N_{V}(t),\\&\frac{\mathrm {d}B_{V}(t)}{\mathrm {d}t}=p{\Lambda _v(t)}+q\gamma B_{V}(t)-q\gamma \frac{B_{V}^{2}(t)}{N_{V}(t)}-\mu _{v}(t)B_{V}(t). \end{aligned} \right. \end{aligned}$$

(10)

Let ${\bar{\Phi }}(t)$ be the periodic semiflow of system (10) on ${\mathbb {R}}_{+}^{2}$, that is, ${\bar{\Phi }}(t)\varphi := (N_V(t, \varphi ), B_V(t, \varphi ))$ is the unique solution of system (10) with the initial value $\varphi \in {\mathbb {R}}_{+}^{2}$. Then $\Phi := {\bar{\Phi }}(\omega )$ is the Poincaré map associated with system (10):

$$\begin{aligned} \begin{aligned}&\Phi (\varphi )={\bar{\Phi }}(\omega )\varphi =(N_V(\omega ,\varphi ),B_V(\omega ,\varphi )),\quad \varphi \in {\mathbb {R}}_{+}^{2}, \\&\Phi ^n(\varphi )={\bar{\Phi }}(n\omega )\varphi =(N_V(n\omega ,\varphi ),B_V(n\omega ,\varphi )),\quad n\ge 0.\\ \end{aligned} \end{aligned}$$

Hence, we reduce system (10) to a discrete-time dynamical system $\{\Phi ^{n}\}_{n\ge 0}$ on ${\mathbb {R}}_{+}^{2}$. For any $\varphi \in {\mathbb {R}}_{+}^{2}$, let M be the omega limit set of the discrete-time orbit $\{\Phi ^{n}\}_{n\ge 0}$. It follows from [44,  Lemma 1.2.1] that M is an internally chain transitive set for $\{\Phi ^{n}\}$ on ${\mathbb {R}}_{+}^{2}$. Thus, we have

$$\begin{aligned} \begin{aligned} \limsup _{t\rightarrow \infty }\left( \Phi ^n(\varphi )\right) _1=N_V^*(0). \end{aligned} \end{aligned}$$

There exists a subset $M_1\subset {\mathbb {R}}$ such that $M =N_V^*(0)\times M_1$ . For any given $z = (z_1, z_2)\in M$ there holds

$$\begin{aligned} \begin{aligned} \Phi ^n|_M(N_V^*(0),z_2)={N_V^*(0)}\times Q^n|_{M_1}(z_2), \end{aligned} \end{aligned}$$

where $\{Q(t)\}_{t\ge 0}$ is the solution semiflow associated with system (8).

Since M is an internally chain transitive set for $\Phi ^n$, if follows that $M_1$ is an internally chain transitive set for $Q^n$. Since $B_V^*(t)$ is a globally attractive positive periodic solution of Eq. (8), according to [44,  Theorem 1.2.1], we have $M_1 = \{B_V^*(t)\}$ and hence $M = \{N_V^*(0), B_V^*(0)\}$. This implies that system (10) has a globally attractive positive $\omega$-periodic solution $(N_V^*(t), B_V^*(t))$.

Thus, system (7) has a unique globally attractive positive $\omega$-periodic solution $(N^*_{V}(t)$, $B^*_{V}(t)$, $S^{*}_{h})$. In other words, system (6) has a unique globally attractive positive $\omega$-periodic solution $(S^*_{V}(t)$, $B^*_{V}(t)$, $S^{*}_{h})$, where $S^*_{V}(t)=N^*_{V}(t)- B^*_{V}(t)$. $\square$

Base on Lemma 3.2, we find that system (3) has a unique disease-free periodic solution $E_0=( S^*_{V}(t),\ 0, B^*_{V}(t), S^{*}_{h}$, 0, 0). In what follows, we introduce the basic reproduction ratio for the malaria transmission system following the general calculation procedure described in [35]. Linearizing system (3) at the disease-free periodic solution $(S^*_{V}(t), 0, B^*_{V}(t), S^{*}_{h}, 0, 0)$, we obtain a periodic linear system:

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\mathrm {d}I_{V}(t)}{\mathrm {d}t}=b\beta (t)\frac{S_{V}^{*}(t)}{N_{h}^{*}}\left( I_{h}(t)+\sigma R_{h}(t)\right) -\left( \mu _{v}(t)+q\gamma \frac{B_{V}^{*}(t)}{N_{V}^{*}(t)}\right) I_{V}(t),\\&\frac{\mathrm {d}I_{h}(t)}{\mathrm {d}t}=c\beta (t){I_{V}(t)}-\left( d_{h}+\delta _{h}+\rho _{h}\right) I_{h}(t),\\&\frac{\mathrm {d}R_{h}(t)}{\mathrm {d}t}=\rho _{h}I_{h}(t)-\left( d_{h}+m\right) {R_{h}(t)}.\\ \end{aligned} \right. \end{aligned}$$

We denote

$$\begin{aligned} \begin{aligned} F(t)=\left( \begin{array}{lll} 0 &{}\quad b\beta (t)\frac{S_{V}^{*}(t)}{N_{h}^{*}} &{}\quad b\sigma \beta (t)\frac{S_{V}^{*}(t)}{N_{h}^{*}} \\ c\beta (t) &{}\quad 0 &{} \quad 0 \\ 0 &{}\quad 0 &{}\quad 0 \\ \end{array} \right) \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} V(t)=\left( \begin{array}{lll} \mu _{v}(t)+q\gamma \frac{B_{V}^{*}(t)}{N_{V}^{*}(t)}&{}\quad 0 &{}\quad 0 \\ 0 &{}\quad d_{h}+\delta _{h}+\rho _{h}&{}\quad 0\\ 0 &{}\quad -\rho _{h}&{}\quad d_{h}+ m \\ \end{array} \right) . \end{aligned} \end{aligned}$$

Assume that Y(t, s), $t\ge s$ is the $3\times 3$ matrix evolution operator of the of above periodic linear system. That is,

$$\begin{aligned} \frac{d}{dt}Y(t,s)=-V(t)Y(t,s), \,\ s\in {\mathbb {R}},\,\ t \ge s \,\ \mathrm {and} \,\ Y(s,s)=I, \end{aligned}$$

where I is the $3\times 3$ identity matrix.

Let $C_{\omega }$ be the ordered Banach space of all $\omega$-periodic continuous functions from ${\mathbb {R}}$ to ${\mathbb {R}}^{3}$, equipped with the maximum norm $\parallel .\parallel$ and the positive cone $\{C^{+}_{\omega }:= {\phi \in C_{\omega }:\phi (t)\ge 0,\, t\in {\mathbb {R}}}\}.$ According to [35], we suppose that $\phi (s)\in C_{\omega }$ is the initial distribution of infectious individuals in this periodic environment, then F(s)v(s) is the rate of new infections produced by the infected individuals who were introduced at time s, and Y(t, s)F(s)v(s) represents the distribution of those infected individuals who were newly infected at time s and remain in the infected compartments at time t for $t\ge s$. Naturally,

$$\begin{aligned} \begin{aligned} \int _{-\infty }^{t}Y(t,s)F(s)v(s)\mathrm {d}s=\int _{0}^{+\infty }Y(t,t-a)F(t-a)v(t-a)\mathrm {d}a \end{aligned} \end{aligned}$$

is the distribution of accumulative new infections at time t produced by all those infected individuals v(s) introduced at the previous time to t. We define a linear operator $L: C_{\omega }\rightarrow C_{\omega }$ as follows

$$\begin{aligned} \begin{aligned} (L\phi )(t)=\int _{0}^{+\infty }Y(t,t-a)F(t-a)\phi (t-a)\mathrm {d}a, \,\ t\in {\mathbb {R}},\ \phi \in C_{\omega }, \end{aligned} \end{aligned}$$

where L is called the next infection operator. It follows from [35] that the basic reproduction ratio $R_{0}$ for system (11) is defined by the spectral radius of the operator L, i.e. $R_{0} =\rho (L)$.

3.3 Global Stability of Disease-Free Equilibrium

As a straightforward consequence of [35], we have the following result.

Lemma 3.3

For the basic reproduction number $R_0$, we have

• (i) $R_{0}<1$ if and only if $\rho (\Phi _{F-V}(\omega ))<1$;

• (ii) $R_{0}=1$ if and only if $\rho (\Phi _{F-V}(\omega ))=1$; and

• (iii) $R_{0}>1$ if and only if $\rho (\Phi _{F-V}(\omega ))>1$.

Then $E_0$ is locally asymptotically stable if $R_0 < 1$ and unstable if $R_0 > 1$, where $\Phi _{F-V}(t)$ is the monodromy matrix of the linear $\omega$-periodic system $\frac{dv(t)}{dt}=(F(t)-V(t))v(t)$.

Theorem 3.4

If $R_0 < 1$ and $\delta _h = 0$, the disease-free equilibrium $E_0$ is globally asymptotically stable.

Proof

If $\delta _h = 0$, the total number of adult mosquito $N_V(t)$ and human $N_h(t)$ admit the following two equations:

$$\begin{aligned} \begin{aligned} \frac{\mathrm {d}N_V(t)}{\mathrm {d}t}=\Lambda _v(t)-\mu _{v}(t)N_V(t),\quad \frac{\mathrm {d}N_{h}(t)}{\mathrm {d}t}=\Lambda _{h}-d_{h}N_{h}(t). \end{aligned} \end{aligned}$$

(11)

Let $B_V(t, \phi )$ be the solution of the third equation of system (3) with the initial value $\phi$ and ${\tilde{B}}_V(t, \phi )$ be the solution of the second equation of system (7) with the same initial value $\phi$. Using Lemma 3.2, we have $\lim \limits _{t\rightarrow \infty }({\tilde{B}}_V(t, \phi )-B^*_V(t))=0$.

Therefore, for any given $\epsilon$, there exists $T (\epsilon ) > 0$ such that for $t\ge T(\epsilon )$ there holds

$$\begin{aligned} \begin{aligned} N_V(t)\le N_V^*(t)+\epsilon ,\quad N_h(t)\ge N_h^*-\epsilon =S_h^*-\epsilon \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} B_V(t):= B_V(t, \phi )\ge {\tilde{B}}_V(t, \phi )\ge B^*_V(t)-\epsilon \end{aligned} \end{aligned}$$

(12)

by using the comparison principle. In view of $S_V(t)=N_V(t)-B_V(t)-I_V(t)$ and $S^*_V(t)=N^*_V(t)-B^*_V(t)$, it follows from (11) and (12) that

$$\begin{aligned} S_V(t)\le N^*_V(t)-B^*_V(t)+2\epsilon =S^*_V(t)+2\epsilon . \end{aligned}$$

Thus, for all $t\ge T(\epsilon )$, from system (3) we have

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\mathrm {d}I_{V}(t)}{\mathrm {d}t}\le b\beta (t)\frac{S_{V}^{*}(t)+2\epsilon }{N_{h}^*-\epsilon }{(I_{h}(t)+\sigma R_{h}(t))}-\left( \mu _{v}(t) +q\gamma \frac{B_{V}^{*}(t)-\epsilon }{N_{V}^{*}(t)+\epsilon }\right) I_{V}(t),\\&\frac{\mathrm {d}I_{h}(t)}{\mathrm {d}t}\le c\beta (t){I_{V}(t)}-(d_{h}+\rho _{h})I_{h}(t),\\&\frac{\mathrm {d}R_{h}(t)}{\mathrm {d}t}= \rho _{h}I_{h}(t)-(d_{h}+m){R_{h}(t)}.\\ \end{aligned} \right. \end{aligned}$$

(13)

Consider the associated auxiliary system:

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\mathrm {d}{\bar{I}}_{V}(t)}{\mathrm {d}t}= b\beta (t)\frac{S_{V}^{*}(t)+2\epsilon }{N_{h}^*-\epsilon }{({\bar{I}}_{h}(t)+\sigma {\bar{R}}_{h}(t))}-\left( \mu _{v}(t) +q\gamma \frac{B_{V}^{*}(t)-\epsilon }{N_{V}^{*}(t)+\epsilon }\right) {\bar{I}}_{V}(t),\\&\frac{\mathrm {d}{\bar{I}}_{h}(t)}{\mathrm {d}t}= c\beta (t){{\bar{I}}_{V}(t)}-(d_{h}+\rho _{h}){\bar{I}}_{h}(t),\\&\frac{\mathrm {d}{\bar{R}}_{h}(t)}{\mathrm {d}t}= \rho _{h}{\bar{I}}_{h}(t)-(d_{h}+m){{\bar{R}}_{h}(t)}.\\ \end{aligned} \right. \end{aligned}$$

We have

$$\begin{aligned} \begin{aligned}&\frac{\mathrm {d}h(t)}{\mathrm {d}t}= M_\epsilon (t)h(t), \end{aligned} \end{aligned}$$

(14)

where

$$\begin{aligned} \begin{aligned} M_\epsilon (t)=\left( \begin{array}{lll} -\left( \mu _{v}(t)+q\gamma \frac{B_{V}^{*}(t)-\epsilon }{N_{V}^{*}(t)+\epsilon }\right) &{}\quad b\beta (t)\frac{S_{V}^{*}(t)+2\epsilon }{N_{h}^{*}-\epsilon }&{}\quad b\sigma \beta (t)\frac{S _{V}^{*}(t)+2\epsilon }{N_{h}^{*}-\epsilon } \\ c\beta (t) &{}\quad -(d_{h}+\rho _{h})&{} \quad 0\\ 0 &{} \quad \rho _{h}&{}\quad -(d_{h}+ m) \\ \end{array} \right) \end{aligned} \end{aligned}$$

and $h(t)=({\bar{I}}_{V}(t),{\bar{I}}_{h}(t),{\bar{R}}_{h}(t))^T$. By [42,  Lemma 2.1], there exists a positive $\omega$-periodic function $\phi (t)=(\phi _1(t),\phi _2(t),\phi _3(t))^T$ such that $h(t)=e^{\mu t}\phi (t)$ is a solution of system (14), where $\mu =\frac{1}{\omega }\ln \rho (\Phi _{M_\epsilon }(\omega ))$. In addition, from $\lim \nolimits _{\epsilon \rightarrow 0^+}\rho (\Phi _{M_\epsilon }(\omega ))=\rho (\Phi _{F-V}(\omega ))$ and Lemma 3.3, we obtain $\lim \nolimits _{\epsilon \rightarrow 0^+}\rho (\Phi _{M_\epsilon }(\omega ))<1$ for $R_0<1$. It follows that there exists $\epsilon _1 > 0$ such that $\rho (\Phi _{M_\epsilon }(\omega ))<1$ for $\epsilon \in [0,\epsilon _1]$. Thus, $\mu <0$. Since the positive $\omega$-periodic function $\phi (t)$ is bounded, we deduce that $h(t)\rightarrow 0$ as $t\rightarrow \infty$. It follows from the comparison principle and (13) that

$$\begin{aligned} \begin{aligned} \lim \limits _{t\rightarrow \infty }(I_{V}(t),I_{h}(t),R_{h}(t))=(0,0,0). \end{aligned} \end{aligned}$$

Moreover, by Lemma 3.2 we can get

$$\begin{aligned} \begin{aligned} \lim \limits _{t\rightarrow \infty }S_{V}(t)=S_V^*(t),\quad \lim \limits _{t\rightarrow \infty }B_{V}(t)=B_V^*(t),\quad \lim \limits _{t\rightarrow \infty }S_{h}(t)=S_h^*. \end{aligned} \end{aligned}$$

Therefore, $E_0$ is globally attractive when $R_0 < 1$. By virtue of Lemma 3.3, we see that the disease-free equilibrium $E_0$ is globally asymptotically stable. $\square$

To reduce system (3) to an autonomous one, we set all coefficients of system (3) to constants and let $\Lambda _v(t)\equiv {\bar{b}}$. Using the method described in [33], we obtain the corresponding basic reproduction ratio

$$\begin{aligned} \begin{aligned} R_0=\rho (FV^{-1})=\beta \sqrt{\frac{bcS_V^*(d_h+m+\sigma \rho _h)}{N_h^*(d_h+\delta _h+\rho _h)(d_h+m)(\mu _V+q\gamma \frac{B_V^*}{N_V^*})}}, \end{aligned} \end{aligned}$$

where $N_h^*=S_h^*=\frac{\Lambda _h}{d_h}$. By the second equation of system (6), we know that $S_V^*=N_V^*-B_V^*$ and $B_V^*$ only has one positive solution

$$\begin{aligned} \begin{aligned} B_V^*=\frac{\mu _V-q\gamma +\sqrt{(q\gamma -\mu _V)^2+4\frac{q\gamma }{N_V^*} pb}}{2\frac{q\gamma }{N_V^*}}, \end{aligned} \end{aligned}$$

where $N_V^*=\frac{{\bar{b}}}{\mu _V}$. As a consequence of Theorem 3.4, we have the following corollary.

Corollary 3.5

If $R_0 < 1$ and $\delta _h = 0$, then for the autonomous system (3), the disease-free equilibrium $(S_v^*, 0, B_v^*, S_h^*, 0, 0)$ is globally asymptotically stable.

3.4 Persistence of Malaria Transmission

For the sake of convenience, we let

$$\begin{aligned} \begin{aligned} X&=\{(S_{V},I_{V},B_{V},S_{h},I_{h},R_{h}):S_{V}>0,I_{V}\ge 0,B_{V}> 0, S_{h}>0,I_{h}\ge 0,R_{h}\ge 0 \},\\ X_0&=\{(S_{V},I_{V},B_{V},S_{h},I_{h},R_{h})\in X : I_{V}>0,I_{h}> 0, R_{h}>0\},\\ \partial X_0&=X\backslash X_0=\{(S_{V},I_{V},B_{V},S_{h},I_{h},R_{h})\in X : I_{V}I_{h}R_{h}=0\}. \end{aligned} \end{aligned}$$

According to Lemma 3.3, X and $X_0$ are positively invariant, and $\partial X_0$ is a relatively closed set in X.

Let $\Phi (t)$ be the periodic semiflow generated by the periodic system (3) on X, that is, $\Phi (t)\varphi$ = $u(t,\varphi )$, $t\ge 0$ is the unique solution of system (3) with the initial condition $\varphi$ = $(S_V(0)$, $I_V(0)$, $B_V(0)$, $S_h(0)$, $I_h(0)$, $R_h(0))$ $\in$ W. Let $P : X\rightarrow X$ be the Poincaré map associated with system (3). Then

$$\begin{aligned} P(\varphi )= & {} \Phi (\omega )\varphi =u(\omega , \varphi ),\ \ \varphi \in X,\\ P^n(\varphi )= & {} \Phi (n\omega )\varphi =u(n\omega , \varphi ),\ \ n\ge 0. \end{aligned}$$

It is easy to see that $\Phi (t)(X_0)\subset X_0$ for $t\ge 0$. By Lemma 3.1, the Poincaré map P is compact and point dissipative on X. It follows from [44,  Theorem 1.1.3] that P admits a global attractor A in X. Therefore, the assumption $(C_1)$ in [44,  Theorem 1.3.1] holds.

Lemma 3.6

The Poincaré map P has a global attractor $M=(S^*_{V}(t), 0, B^*_{V}(t), S^{*}_{h}, 0, 0)$ on $\partial X_0$.

Proof

Let

$$\begin{aligned} \begin{aligned} M_\partial =\{\varphi \in \partial X_0:P^n(\varphi )\in \partial X_0,n>0\ and \ n\in Z^+\}. \end{aligned} \end{aligned}$$

We now verify that

$$\begin{aligned} \begin{aligned} M_\partial =\{(S_{V}, 0, B_{V}, S_{h}, 0, 0):S_{V}> 0, B_{V}>0, S_{h}>0 \}. \end{aligned} \end{aligned}$$

(15)

If the initial condition $(S_V(0), I_V(0), B_V(0), S_h(0), I_h(0), R_h(0))= (S_V(0), 0, B_V(0), S_h(0), 0, 0)$ with $S_V(0)>0$, $B_V(0)>0$ and $S_h(0)>0$, then the solution $(S_V(t), I_V(t), B_V(t), S_h(t), I_h(t), R_h(t)) \equiv (S_V(t), 0, B_V(t), S_h(t), 0, 0)$ with $S_V(t)>0, B_V(t)>0$ and $S_h(t)>0$. It is not difficult to see that $M_\partial \supseteq \{(S_{V}, 0, B_{V}, S_{h}, 0, 0):S_{V}> 0, B_{V}>0, S_{h}>0) \}$.

On the other hand, if

$$\begin{aligned} \begin{aligned} M_\partial \subseteq \{(S_{V}, 0, B_{V}, S_{h}, 0, 0):S_{V}> 0, B_{V}>0, S_{h}>0) \} \end{aligned} \end{aligned}$$

does not hold, there exists at least a point $\varphi _1=(S_V(0), I_V(0), B_V(0), S_h(0), I_h(0), R_h(0))$ $\in M_\partial$ satisfying $I_V(0)>0$ or $I_h(0)>0$ or $R_h(0)>0$.

Since $\varphi _1\in M_\partial$, $(S_{V}(0), B_{V}(0), S_{h}(0))\gg (0,0,0)$, from the first, third and forth equations of system (3) we get $(S_{V}(t), B_{V}(t), S_{h}(t))\gg (0,0,0)$ for $t>0$ . If $I_V(0)>0$, from the second equation of system (3), we have

$$\begin{aligned} \begin{aligned} I_V(t)\ge I_V(0)e^{-\left( \mu _{v}(t)+q\gamma \frac{B_{V}(t)}{N_{V}(t)}\right) }>0, \ \ t>0. \end{aligned} \end{aligned}$$

(16)

Using the fifth equation of system (3), for $t>0$ we derive

$$\begin{aligned} \begin{aligned} I_h(t)= e^{-(d_{h}+\delta _{h}+\rho _{h})t}\left[ I_h(0)+\int ^t_0 c\beta (\tau ) \frac{I_{V}(\tau )}{N_{h}(\tau )}{S_{h}(\tau )}e^{(d_{h}+\delta _{h}+\rho _{h})\tau } \mathrm {d}\tau \right] >0. \end{aligned}\qquad \end{aligned}$$

(17)

By the sixth equation of system (3), we further obtain

$$\begin{aligned} \begin{aligned} R_h(t)= e^{-(d_{h}+m)t}\left[ R_h(0)+\int ^t_0\rho _{h}I_{h}(\tau )e^{(d_{h}+m)\tau }\mathrm {d}\tau \right]>0, \ \ t>0. \end{aligned} \end{aligned}$$

(18)

Combining (16–18) yields

$$\begin{aligned} \begin{aligned} (S_V(t), I_V(t), B_V(t), S_h(t), I_h(t), R_h(t))\gg (0,0,0,0,0,0),\ \ t>0. \end{aligned} \end{aligned}$$

This shows that $(S_V(t), I_V(t), B_V(t), S_h(t), I_h(t), R_h(t))\notin M_\partial$, which leads to a contradiction. Similarly, when $I_h(0)>0$ or $R_h(0)>0$, by discussing in an analogous manner there yields another contradiction to $(S_V(t), I_V(t), B_V(t), S_h(t), I_h(t), R_h(t))\notin M_\partial$. Therefore, we have $M_\partial$ $\subseteq$ $\{(S_{V}, 0, B_{V}, S_{h}, 0, 0):S_{V}> 0, B_{V}>0, S_{h}>0) \}$. This indicates that (15) is true.

In view of system (6) on $\partial X_0$, by virtue of Lemma 3.2 we see that the Poincaré map P has a global attractor $M=(S^*_{V}(t), 0, B^*_{V}(t), S^{*}_{h}, 0, 0)$ on $\partial X_0$. $\square$

Let $\varphi _2=(S_V(0), I_V(0), B_V(0), S_h(0), I_h(0), R_h(0))\in X_0$, $M=(S_V^*(0), 0, B_V^*(0), S_h^*, 0, 0)$. Due to the continuity of solutions with respect to the initial values, for any small enough $\varepsilon > 0$, there is a $\delta > 0$ such that whenever $\parallel \varphi _2-M\parallel \le \delta$, we have

$$\begin{aligned} \begin{aligned} \parallel \Phi (t)\varphi _2-\Phi (t)M\parallel <\varepsilon ,\ \ t\in [0,\omega ]. \end{aligned} \end{aligned}$$

(19)

Lemma 3.7

If $R_0 > 1$ and $\parallel \varphi _2-M \parallel \le \delta$ for any $\varphi _2\in X_0$, then $\limsup \nolimits _{n\rightarrow \infty }\parallel P^n(\varphi _2)-M\parallel \ge \delta$.

Proof

Suppose that is not true. Then $\limsup \nolimits _{n\rightarrow \infty }\parallel P^n(\varphi _2)-M\parallel <\delta$ for some $\varphi _2\in X_0$. So there exists an integer $N\ge 1$ such that

$$\begin{aligned} \begin{aligned} \parallel P^n(\varphi _2)-M\parallel <\delta ,\,\ n\ge N. \end{aligned} \end{aligned}$$

(20)

From (19), we have $\parallel \Phi (t)(P^n(\varphi _2))-\Phi (t)(M)\parallel <\varepsilon$ for all $n\ge N$ and $t\in [0,\omega ]$. Then, for any $t\ge N\omega$, let $t=n\omega +{\tilde{t}}$, where ${\tilde{t}}\in [0,\omega )$ and $n=[\frac{t}{\omega }]$ is the greatest integer less than or equal to $\frac{t}{\omega }$. By (20), we have $\parallel \Phi (t)(\varphi _2)-\Phi (t)(M)\parallel =\parallel \Phi ({\tilde{t}})(P^n(\varphi _2))-\Phi ({\tilde{t}})(M)\parallel <\varepsilon$. For all $t\ge N\omega$ it follows that

$$\begin{aligned} S_V^*(t)-\varepsilon\le & {} S_V(t)\le S_V^*(t)+\varepsilon , B_V^*(t)-\varepsilon \le B_V(t)\\\le & {} B_V^*(t)+\varepsilon , S_h^*-\varepsilon \le S_h\le S_h^*(t)+\varepsilon . \end{aligned}$$

Thus, we have

$$\begin{aligned} \frac{B_V(t)}{N_V(t)}\le \frac{B_V^*(t)}{N_V^*(t)}+\kappa _1(\varepsilon ),\ \ \frac{S_V(t)}{N_h(t)}\ge \frac{S_V^*(t)}{N_h^*}-\kappa _2(\varepsilon )\ \ \mathrm {and}\ \ \frac{S_h(t)}{N_h(t)}\ge 1-\kappa _3(\varepsilon ) \end{aligned}$$

for all $t\ge N\omega$, where $\kappa _i(\varepsilon )$ $(i=1, 2, 3)$ are infinitesimals of the same order of $\varepsilon$. Then for all $t\ge N\omega$, from system (3) we obtain

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\mathrm {d}I_{V}(t)}{\mathrm {d}t}\ge b\beta (t)\left( \frac{S_V^*(t)}{N_h^*}-\kappa _2(\varepsilon )\right) (I_{h}(t)+\sigma R_{h}(t))-\left( \mu _{v}(t) +q\gamma \left( \frac{B_V^*(t)}{N_V^*(t)}+\kappa _1(\varepsilon )\right) \right) I_{V}(t),\\&\frac{\mathrm {d}I_{h}(t)}{\mathrm {d}t}\ge c\beta (t)(1-\kappa _3(\varepsilon ))I_{V}(t)-(d_{h}+\rho _{h})I_{h}(t),\\&\frac{\mathrm {d}R_{h}(t)}{\mathrm {d}t}= \rho _{h}I_{h}(t)-(d_{h}+m){R_{h}(t)}. \end{aligned} \right. \end{aligned}$$

(21)

Consider the auxiliary system:

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\mathrm {d}{\tilde{I}}_{V}(t)}{\mathrm {d}t}= b\beta (t)\left( \frac{S_V^*(t)}{N_h^*}-\kappa _2(\varepsilon )\right) ({\tilde{I}}_{h}(t)+\sigma {\tilde{R}}_{h}(t))-\left( \mu _{v}(t) +q\gamma \left( \frac{B_V^*(t)}{N_V^*(t)}+\kappa _1(\varepsilon )\right) \right) {\tilde{I}}_{V}(t),\\&\frac{\mathrm {d}{\tilde{I}}_{h}(t)}{\mathrm {d}t}= c\beta (t)(1-\kappa _3(\varepsilon )){\tilde{I}}_{V}(t)-(d_{h}+\rho _{h}){\tilde{I}}_{h}(t),\\&\frac{\mathrm {d}{\tilde{R}}_{h}(t)}{\mathrm {d}t}= \rho _{h}{\tilde{I}}_{h}(t)-(d_{h}+m){{\tilde{R}}_{h}(t)}. \end{aligned} \right. \end{aligned}$$

That is,

$$\begin{aligned} \begin{aligned} \frac{d h}{d t}=\widetilde{M_\varepsilon }(t)h(t),\quad h(t)=({\tilde{I}}_V(t),{\tilde{I}}_h(t),{\tilde{R}}_h(t))^T, \end{aligned} \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} {\widetilde{M}}_\epsilon (t)=\left( \begin{array}{lll} -\left( \mu _{v}(t) +q\gamma \left( \frac{B_V^*(t)}{N_V^*(t)}+\kappa _1(\varepsilon )\right) \right) &{}\quad b\beta (t)\left( \frac{S_V^*(t)}{N_h^*}-\kappa _2(\varepsilon )\right) &{}\quad b\sigma \beta (t)\left( \frac{S_V^*(t)}{N_h^*}-\kappa _2(\varepsilon )\right) \\ c\beta (t)(1-\kappa _3(\varepsilon )) &{}\quad -(d_{h}+\delta _{h}+\rho _{h})&{} \quad 0\\ 0 &{}\quad \rho _{h}&{}\quad -(d_{h}+ m) \\ \end{array} \right) . \end{aligned} \end{aligned}$$

According to [42,  Lemma 2.1], there exists a positive $\omega$-periodic function $\psi (t)=(\psi _1(t),\psi _2(t),\psi _3(t))^T$ such that $h(t)=e^{\mu t}\psi (t)$ is a solution of system (14), where $\mu =\frac{1}{\omega }\ln \rho (\Phi _{\widetilde{M_\epsilon }}(\omega ))$. In view of $\rho \left( \Phi _{{\widetilde{M}}_\varepsilon (\omega )}\right) >1$ and $\mu$ is a positive constant, we have $h(t)\rightarrow +\infty$ as $t\rightarrow \infty$. From (21), the comparison principle implies that $\lim \nolimits _{t\rightarrow \infty }(I_V(t),I_h(t),R_h(t))=(\infty ,\infty ,\infty )$, which yields a contradiction with (20). $\square$

By Lemma 3.6, it is clear that on $\partial X_0$, M is isolated, invariant, and does not form a cycle. Therefore, conditions (a)-(c) in [44,  Theorem 1.3.1] are satisfied. Lemma 3.7 implies that $W^s(M)\cap X_0 =\varnothing$. By the acyclicity theorem on uniform persistence for maps [44,  Theorem 1.3.1, Remark 1.3.1 and Theorem 3.1.1], we obtain

Theorem 3.8

If $R_0 > 1$, system (3) is uniformly persistent. That is, there exists a positive constant $\epsilon$ such that any solution $(S_v(t), I_v(t), B_v(t), S_h(t), I_h(t), R_h(t))$ of system (3) with the initial conditions $(S_v(0), I_v(0), B_v(0), S_v(0), I_h(0), R_h(0))\gg (0,0,0,0,0,0)$ satisfies

$$\begin{aligned} \liminf \limits _{t\rightarrow \infty }(S_v(t), I_v(t), B_v(t), S_h(t), I_h(t), R_h(t)) \ge (\epsilon ,\epsilon ,\epsilon ,\epsilon ,\epsilon ,\epsilon ). \end{aligned}$$

Therefore, system (3) has at least one positive periodic solution.

4 Numerical Simulations

In this section, with the help of optimization toolbox-ODE45 and CFTOOL in MATLAB, we analyze the parameters in system (3), and present a series of numerical simulations to verify our theoretical results. We also discuss the impact of vertical and horizontal Serratia AS1 transmission parameters on the threshold $R_{0}$ by using the climate and population data in Luanda, where is the capital of Angola.

4.1 Estimation of the Parameters

According to demographic data, the total population of Luanda was $N_{h}=2{,}776{,}168$ [39] and the life expectancy was 61.71 years in 2021 [5]. Thus, the human natural death rate $d_{h}$ can be calculated as follows:

$$\begin{aligned} d_{h}=\frac{1}{61.71\times 12} \approx 0.00135 \quad \mathrm {Month}^{-1}. \end{aligned}$$

The recruitment rate $\Lambda _{h}$ for Luanda is determined by:

$$\begin{aligned} \Lambda _{h}= d_{h}\times 2776168 \approx 3748 \quad \mathrm {Humans} \times \mathrm {Month}^{-1}. \end{aligned}$$

In addition, the values of some constant parameters for malaria transmission system (3) are listed in Table 2 with the references therein. Next, we use the monthly mean temperatures to estimate the periodic coefficients of system (3) and the relationship among temperature, death rate, and biting rate to determine the periodic parameters $\Lambda _v(t)$, $\mu (t)$ and $\beta (t)$, respectively. The monthly mean temperatures of Luanda from 1991 to 2020 [2] are shown in Table 3.

Moreover, according to [23, 36], the temperature-dependent mosquito biting rate can be expressed by

$$\begin{aligned} \begin{aligned} \beta (C)=30.4\times 0.000203C(C-11.7)\sqrt{42.3-C} \quad \mathrm {Month^{-1}}, \end{aligned} \end{aligned}$$

(22)

where C represents temperature. Assuming that C is a function of the time t (in month), we use (22) and the data set in Table 3 to get the biting rate of mosquitoes in Luanda as

$$\begin{aligned} \begin{aligned} \beta (t)=\beta (C(t)) =&\, 8.707+0.9975\cos (2\pi t/12) +1.768 \sin (2\pi t/12)\\&+0.03659 \cos (4\pi t/12)-0.7502\sin (4\pi t/12)-0.1156 \cos (6\pi t/12)\\ {}&+0.08462\sin (6\pi t/12)-0.03714\cos (8\pi t/12)+0.0413\sin (8\pi t/12)\\ {}&+0.005464\cos (10\pi t/12) -0.01912\sin (10\pi t/12) \quad \mathrm {Month^{-1}}. \end{aligned} \end{aligned}$$

Table 2 Parameter values

Table 3 Monthly mean temperature of Luanda (in $^{^{\circ }}$C)

Similarly, according to [14, 36], the temperature-dependent death rate of adult mosquitoes is given by

$$\begin{aligned} \mu _{v}(C)=\frac{30.4}{-0.03C^{2}+1.31C-4.4} \quad \mathrm {Month^{-1}}. \end{aligned}$$

(23)

Then by (23) and the data set in Table 3, $\mu _{v}(t)$ can be approximated by

$$\begin{aligned} \begin{aligned} \mu _{v}(t)=\mu _{v}(C) =&\,3.234 + 0.06796\cos (2\pi t/12) + 0.1561\sin (2\pi t/12)\\&-0.02152\cos (4\pi t/12)-0.03058\sin (4\pi t/12)+0.01739\cos (6\pi t/12)\\ {}&-0.004319\sin (6\pi t/12) -0.01406\cos (8\pi t/12)+ 0.002268\sin (8\pi t/12)\\ {}&-0.001653\cos (10\pi t/12) -0.001919\sin (10\pi t/12) \quad \mathrm {Month^{-1}}. \end{aligned} \end{aligned}$$

To estimate the maturation function of the mosquito, we suppose that the egg deposition rate is a linear function of the biting rate [21], that is

$$\begin{aligned} \Lambda _v(t)=l\times \beta (t) \quad \mathrm {Mosquitoes} \times \mathrm {Month}^{-1}, \end{aligned}$$

where $l=5\times 2{,}776{,}168$ is a positive number.

4.2 Numerical Results

Based on these parametric values, we verify the obtained theoretical results in Theorems 3.4 and 3.8 by investigating the long-term behaviors of the solutions of system (3). The initial values are given by $S_{v}(0)=6.15\times 10^6$, $I_{v}(0)=2\times 10^5$, $B_{v}(0)=2\times 10^7$, $S_{h}(0)=1.7\times 10^6$, $I_{h}(0)=4\times 10^5$, and $R_{h}(0)=5\times 10^5$. Following [36], we can take the horizontal transmission probability q and the sexual contact rate $\gamma$ of mosquitoes as a whole. Let $\eta =q\gamma$, which represents the number of mosquitoes transmitted by males with AS1 to females through mating.

We compute the basic reproduction ratios $R_{0}$ numerically with the different parameters p and $\eta$ by using the bisection method and [35,  Theorem 2.2]. In Fig. 2, we set $p=0.2$ and $\eta =2$, then $R_{0}=2.8034>1$. We observe that all the variables tend to a stable positive periodic state $(S^{*}_{v}(t), B^{*}_{v}(t), I_{v}^{*}(t), S^{*}_{h}(t), I_{h}^{*}(t), R_{h}^{*}(t))$ which agree well with Theorem 3.8. Furthermore, malaria persists and exhibits seasonal fluctuation in this case. When increasing the parameters values of p and $\eta$ to 0.6 and 7, respectively, we get $R_{0}=0.8590<1$. We note that the disease-related variables approach zero and others approach positive periodic states. This means that system (3) converges to the disease-free periodic solution $(S^{*}_{v}(t), 0, B^{*}_{v}(t), S^{*}_{h}, 0, 0)$, which is globally asymptotically stable reflected by Theorem 3.4. Biologically, it can be interpreted that malaria is eliminated from the area under this substance, see Fig. 3.

Fig. 2

Long-term behavior of the solution with $R_{0} =2.8034$, where $p = 0.2$ and $\eta = 2$

4.3 Sensitivity Analysis of $R_{0}$

In order to explore the effect of Serratia AS1 on malaria transmissions, it is necessary to investigate the impact of the vertical and horizontal transmissions of Serratia AS1 on $R_{0}$.

Fig. 3

Long-term behavior of the solution with $R_{0} =0.8590$, where $p = 0.6$ and $\eta = 7$

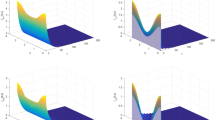
Fixing the transmission probability, we study the impact of the other form of transmission on the infected population and $R_{0}$. In Fig. 4a, by setting $\eta =5$ to represent a weak horizontal transmission probability of the bacteria, we find that the level of $I_{h}$ decreases by increasing the vertical transmission probability p. At least when $p =0.6450$, $I_{h}$ can approach 0 and achieve the goal of eliminating malaria. In Fig. 4b, setting $p=0.5$, we observe that the level of $I_{h}$ is decreased with respect to the large value of $\eta$, and $\eta$ also needs to be large enough to reduce $I_{h}$ to 0. When $\eta =7$, $I_{h}$ is close 0. Figure 4c shows the relationship between $R_{0}$ and p at $\eta =5$. Figure 4d shows the graph of $R_{0}$ as a function of $\eta$ with $p=0.5$. Through observation and comparative analysis, we can find that the vertical and horizontal transmissions of Serratia AS1 play important roles in malaria control, even though its two transmission levels are weak. When one form of transmission probability is low, the other transmission probability can still make $R_{0}$ less than 1.

Let us briefly analyze the impact of p and $\eta$ on the population dynamics numerically. The numerical result for infected human population is presented in Fig. 5 for various combinations of p and $\eta$. When $p=0.5$ and $\eta =5$, $I_{h}(t)$ can be reduced to a lower level but the basic reproduction ratio $R_{0}=1.2625>1$. When $p=0.6$ and $\eta =6$, $I_{h}(t)$ can be reduced to 0 eventually. Namely, malaria can be completely eliminated in this area with $R_{0}=0.9687<1$. When $p=0.9$ and $\eta =9$, $I_{h}(t)$ can be reduced to 0 much faster with $R_{0} = 0.3434$. If we increase the vertical propagation rate to the limit, i.e. $p=1$ and the horizontal transmission rate $\eta$ varies, we find that the dynamical behavior of $I_{h}(t)$ is almost the same. This means, when p is large enough, $\eta$ will not make big difference for the transmission of malaria. In addition, we can get similar results with the different initial value $B_v(0)$. From Fig. 5, we also see that if we use the engineered Serratia AS1 alone to control malaria, it will take at least about 100 months to completely eliminate malaria in Luanda.

Fig. 4

The effects of horizontal and vertical transmissions of bacteria in controlling the infected human population size: (a) $\eta = 5$, p varies; (b) $p = 0.5$, $\eta$ varies; (c) the graph of $R_{0}$ as a function of p with $\eta =5$; and (d) the graph of $R_{0}$ as a function of $\eta$ with $p=0.5$

5 Conclusion

Establishing mathematical models and analyzing the dynamics of disease transmission can provide us useful information to formulate disease prevention and make effective control plans. By studying the model, we can identify which biological factors are important and crucial for infectious diseases.

Considering the impact of seasons on the growth and development of mosquitoes based on [34], we have formulated a periodic mathematical malaria model by incorporating the transmission characteristics of Serratia AS1 into the mosquito population and the time-dependent human population size. For the sake of simplicity and convenience, we divided the mosquito population into susceptible, infectious and Serratia AS1-infected. The parameters related to mosquitoes are assumed to be periodic functions such as the recruitment rate, natural death rate and biting rate. Furthermore, a human growth rate $\Lambda _{h}$ is allowed. We derived the basic reproduction ratio $R_{0}$ and analyzed the dynamics of system (3). That is, the disease will die out if $R_{0} < 1$ and will eventually stabilize at a positive periodic state if $R_{0}> 1$. Numerically, using the monthly mean temperature data of Luanda, we estimated the periodic parameters in our model. Then we verified our theoretical results by numerical simulations on the long-term behaviors of the solutions. Our numerical results show that even if one of vertical and horizontal transmission parameters of Serratia AS1 becomes weak, it is still possible to make the basic reproduction ratio $R_{0}<1$ as long as the other transmission parameter is very strong. By using the maximum vertical transmission level, we find that it would take at least nine years for the elimination of malaria through Serratia AS1 in Luanda. Furthermore, only a small amount of Serratia AS1-infected mosquitoes released into wild mosquito population can still inhibit the spread of malaria. This indicates that using Serratia AS1 engineered bacteria to control malaria is likely to be an effective control method in the realistic life.

Fig. 5

The effects of different combinations of vertical and horizontal transmissions on the number of people infected with malaria

At this stage we only consider using Serratia AS1 alone to inhibit malaria parasite. It will take at least nine years for the elimination of malaria through Serratia AS1 in Luanda under ideal conditions. It is also interesting to consider releasing Serratia AS1 in combination with other control measures to jointly control malaria. On the other hand, time delay is a common phenomenon in nature [19, 43]. Hence, it is worthwhile to develop a delay model with Serratia AS1 and other different control measures. We leave these challenging problems for future consideration and study.