Reconstruction of Certain Phylogenetic Networks from Their Tree-Average Distances

Abstract

Trees are commonly utilized to describe the evolutionary history of a collection of biological species, in which case the trees are called phylogenetic trees. Often these are reconstructed from data by making use of distances between extant species corresponding to the leaves of the tree. Because of increased recognition of the possibility of hybridization events, more attention is being given to the use of phylogenetic networks that are not necessarily trees. This paper describes the reconstruction of certain such networks from the tree-average distances between the leaves. For a certain class of phylogenetic networks, a polynomial-time method is presented to reconstruct the network from the tree-average distances. The method is proved to work if there is a single reticulation cycle.

1 Introduction

The evolution of a collection of species is commonly modeled via a directed graph with no directed cycles. The vertices correspond to species and the arcs correspond to direct descent, usually with modification under mutation. Most commonly these networks are directed trees. Recently, the importance of reticulation events have been recognized, such as hybridization of species or lateral gene transfer (Doolittle et al. 2003; Boc and Makarenkov 2003). General frameworks for phylogenetic networks are discussed in Bandelt and Dress (1992), Baroni et al. (2004, 2006), Moret et al. (2004), Nakhleh et al. (2004). See also the recent book (Huson et al. 2010). An example of a published nontree network published by a biologist is in Marcussen et al. (2012).

Suppose X denotes the set of extant species, including an outgroup, which is used to locate the root. The DNA information may be summarized via the computation of distances between members of X. If x,y∈X, then d(x,y) summarizes the amount of genetic difference between the DNA strings of x and y. A number of different distances are in use, based on different models of mutation (Jukes and Cantor 1969; Kimura 1980; Hasegawa et al. 1985; Lake 1994; Steel 1994).

There exist fast methods for reconstruction of phylogenetic trees from distances. The most commonly used method is Neighbor-joining (Saitou and Nei 1987). Another more recent method FastME Desper and Gascuel (2002, 2004) is based on the principle of balanced minimum evolution, in which one assumes that the correct tree is the one that exhibits the minimal total amount of evolution, suitably measured. In fact, it has been shown that Neighbor-joining is a greedy algorithm for balanced minimum evolution (Gascuel and Steel 2006).

The subject of this paper is a distance method to construct phylogenetic networks that are not necessarily trees. Prior methods for constructing phylogenetic networks that are not necessarily trees from distances include Neighbor-Net (Bryant and Moulton 2004) and MC-Net (Eslahchi et al. 2010). In particular, Neighbor-Net is conveniently available in the software package SplitsTree4 (Huson and Bryant 2006).

This paper is an extension of the author’s earlier paper (Willson 2012). The earlier paper defined the “tree-average distance” on a phylogenetic network. Suppose a phylogenetic network N is weighted so that each arc has an arc-length or weight corresponding to the amount of mutation along the arc. At each reticulation vertex, there is a certain probability that inheritance of a character comes from each parent. Roughly, the tree-average distance d(u,v) between two vertices u and v of a phylogenetic network is the expected value of the distance between u and v in each possible tree displayed by N. See Sect. 2 for a more formal review of the tree-average distance.

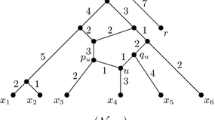
For example, Fig. 1 displays a phylogenetic network N. The set of tips is X={r,x ₁,x ₂,x ₃,y}. These vertices correspond to extant species with known DNA. The root r usually is identified with an outgroup species. Vertex h is a reticulation or hybrid node with two parents q ₁ and q ₂. The probability that a character is inherited at h from q ₁ is α ₁ and the probability that a character is inherited at h from q ₂ is α ₂=1−α ₁. With probability α ₁ the gene tree T ₁ will look like N with arc (q ₂,h) removed because the inheritance at h will be along arc (q ₁,h). Similarly, with probability α ₂, the gene tree T ₂ will look like N with arc (q ₁,h) removed. Each arc has a weight. The distance d(u,v;T ₁) between two vertices u and v on T ₁ will be found by adding the weights on the unique path joining the vertices in T ₁. The distance d(u,v;T ₂) between the same two vertices on T ₂ will be found by adding the weights on the path joining them in T ₂. The tree-average distance d(u,v;N) will then be the expected value

$$d(u,v;N) = \alpha_1 d(u,v;T_1) + \alpha_2 d(u,v;T_2). $$

Fig. 1

A phylogenetic network N with tips X={r,x ₁,x ₂,x ₃,y}

Assume that the tree-average distance is known on the network N and that the underlying directed graph is known. In Willson (2012), various formulas were derived that permitted the calculation of the weight of each arc. The formulas required knowledge of the directed graph as well as the tree-average distances d(x,y). Thus, Willson (2012) showed that if the network N is known as well as the tree-average distance d(x,y) for all x,y∈X, then the weights of each arc could be computed uniquely.

But Willson (2012) did not describe how the directed graph itself could be reconstructed given the tree-average distances d(x,y). One needed to assume that the topology of the directed graph was given as well as the tree-average distances, and then one could compute the weights.

This current paper shows in certain circumstances how, from the tree-average distances d(x,y), the directed graph itself can be reconstructed. Thus, the entire input is the collection of exact distances d(x,y) for all x,y∈X and the method outputs the network as well as the weights on each arc and the probabilities of inheritance at each reticulation vertex. Rather than assuming that the underlying directed graph is known, this paper shows how to derive the directed graph from the distances d(x,y), under certain assumptions. The methods of Willson (2012) let us then find the uniquely-determined weights for each arc. Moreover, the probabilities of inheritance at each hybrid vertex are uniquely determined and can be computed by explicit formulas. For Fig. 1, the entire input consists of the 10 numbers d(x,y) for x,y∈X. Since from this input, the network, its weights, and its probabilities are uniquely reconstructed, the current results show that, under the given assumptions, the method of tree-average distances is consistent.

The reconstruction described in this paper is possible only because the formulas in Willson (2012) have simple forms which can be used recursively when only part of the network is yet known.

Particular kinds of acyclic networks have been studied in various papers. Wang et al. (2001) and Gusfield et al. (2004) study “galled trees” in which all recombination events are associated with node-disjoint recombination cycles; the idea occurs also earlier in Wang et al. (2000). Choy et al. (2005) and Van Iersel et al. (2009) generalized galled trees to “level-k” networks. Baroni et al. (2004) introduced the idea of a “regular” network, which coincides with its cover digraph. Cardona et al. (2009) discussed “tree-child” networks, in which every vertex that is not a leaf has a child that is not a reticulation vertex. An arc (a,b) is redundant if there is a directed path from a to b that does not utilize this arc.

A network is normal if it is tree-child and it contains no redundant arc. Most results in this paper assume that the network is normal. These networks include trees, but have only limited complexity, and hence are more easily interpreted than general networks. For example, (Willson 2010) if there are n tips, then a normal network has at most (n ²−n+2)/2 vertices. By contrast, a regular network with n tips might have 2ⁿ⁻¹ vertices, making the biological interpretation difficult and requiring exponential time for reconstruction.

It is interesting to contrast this paper with Neighbor-Net (Bryant and Moulton 2004). Both methods use distances to produce a network that need not be a tree. Both methods recursively combine nodes in an agglomerative manner generally resembling Neighbor-Joining. Neighbor-Net identifies circular collections of splits which are generally represented by systems of parallel edges rather than single edges. As such, Neighbor-Net produces networks which exhibit ambiguity among various trees, or allow “visualizing a space of feasible trees” (Bryant and Moulton 2004, p. 255), “rather than an explicit history of which reticulations took place” (Bryant and Moulton 2004, p. 259). By contrast, the current paper seeks to produce a single phylogeny in which each arc can be interpreted in the same manner as in a tree. Neighbor-Net constructs a network, which is simple in the sense that it is a circular split system, and hence representable in the plane. The authors concede (Bryant and Moulton 2004, p. 263) that “the definition of circular splits and circular distances is not biologically motivated.” By contrast, the current paper constructs a phylogenetic network, which is simple in the sense that it is normal. In Willson (2010), there are biological motivations for considering normal networks. As a final comparison, the splits graph representation of Neighbor-Net is not necessarily unique (Bryant and Moulton 2004, p. 258), forcing extra care in the interpretation of the output. The current reconstruction, under the given hypotheses, is unique.

Here is an outline of the current paper. Theorem 3.2 shows that a recursive reconstruction of N will be possible provided that one can correctly recognize two situations using the tree-average distance d. These two situations are a cherry {x,y} and a hybrid h with parents q ₁ and q ₂ such that h has a leaf-child y, q ₁ has a leaf-child x ₁, and q ₂ has a leaf-child x ₂ as in Fig. 1. For each of these situations, one can use the formulas of Willson (2012) to find the weights and probabilities needed to simplify the problem to a smaller problem. In the case of a cherry, one can reduce to a simpler problem in which both x and y have been removed; in the case of a hybrid one can reduce to a simpler problem in which h, y, x ₁, and x ₂ have been removed.

Section 4 deals with the problem of recognizing a cherry {x,y}. The main result is Theorem 4.5, which gives a necessary and sufficient condition that {x,y} be a cherry, given in terms of the tree-average distance. As a result of Theorem 4.5, there remains only the problem of correctly recognizing the hybrid situation.

The recognition of a hybrid is studied in Sect. 5. Several necessary conditions in terms of the tree-average distance are described. The main Theorem 6.1 asserts that these conditions are sufficient when there is a single reticulation cycle. A proof is given in Sect. 6. Section 7 gives a more complicated example with two reticulation cycles in which the conditions are also sufficient.

Some extensions of the current results and problems are discussed in the concluding Sect. 8.

2 Fundamental Concepts

A directed graph or digraph N=(V,A) consists of a finite set V of vertices and a finite set A of arcs, each consisting of an ordered pair (u,v) where u∈V, v∈V, u≠v. We interpret (u,v) as an arrow from u to v and say that the arc starts at u and ends at v. There are no multiple arcs and no loops. If (u,v)∈A, say that u is a parent of v and v is a child of u. A directed path is a sequence u ₀,u ₁,…,u _k of vertices such that for i=1,…,k, (u _i−1,u _i )∈A. The path is trivial if k=0. Write u≤v if there is a directed path starting at u and ending at v. We may refer to such any such path in context as P(u,v) or P(u,v;N). Write u<v if u≤v and u≠v. The digraph is acyclic if there is no nontrivial directed path starting and ending at the same point. If the digraph is acyclic, it is easy to see that ≤ is a partial order on V.

The indegree of vertex u is the number of v∈V such that (v,u)∈A. The outdegree of u is the number of v∈V such that (u,v)∈A. A leaf is a vertex of outdegree 0. A normal vertex (or tree vertex) is a vertex of indegree 1. A child c of a vertex v is called a tree-child of v if c has indegree 1. A hybrid vertex (or reticulation vertex) is a vertex of indegree at least 2. An arc (u,v) is a normal arc if v is a normal vertex.

A digraph (V,A) is rooted if it has a unique vertex r∈V with indegree 0 such that, for all v∈V, r≤v. This vertex r is called the root.

Let X denote a finite set. Typically in phylogeny, X is a collection of species. Measurements are assumed to be possible among members of X, so that we may assume that, for example, their DNA is known for each x∈X.

A phylogenetic X-network N=(V,A,r,X) is a rooted acyclic digraph G=(V,A) with root r such that there is a one-to-one map ϕ:X→V whose image contains all vertices v such that either

• (i) v is a leaf; or

• (ii) v=r; or

• (iii) v has indegree 1 and outdegree 1.

There may be additional vertices in X. We will identify each x∈X with its image ϕ(x). The set X will be called the base-set for N.

An example of a phylogenetic network N is given in Fig. 1.

In biology, the network gives a hypothesized relationship among the members of X. It is quite common also that a certain extant outgroup species r′ is assumed to have evolved separately from the rest of the species in question. When this happens, we identify the species r′ with the root r. Thus, extant species (the leaves) are in X by (i) since measurements can be made on them. The outgroup r′, which is identified with the root, is in X by (ii). If a vertex has indegree 1 and outdegree 1, then nothing uniquely determines it unless, for fortuitous reasons, it is possible to make measurements on its DNA, in which case it lies in the base-set X.

An X-tree is a phylogenetic X-network such that the underlying digraph is a tree.

An arc (u,v)∈A is redundant if there exists w∈V such that u, v, and w are distinct and u<w<v. The removal of a redundant arc (u,v) still leaves u≤v in the network.

A phylogenetic X-network N=(V,A,r,X) with base-set X is normal provided (1) whenever v∈V and v∉X, then v has a tree-child (a child with indegree 1); and (2) there are no redundant arcs. The network in Fig. 1 is normal.

A normal path in N from v to x is a directed path v=v ₀,v ₁,…,v _k =x such that for i=1,…,k, v _i is normal. A normal path from v to X is a normal path starting at v and ending at some x∈X. For example, in Fig. 1, the path v, q ₃, q ₂, x ₂ is normal and is a normal path from v to X. The path q ₁, h, y is not normal since h is hybrid. The trivial path x ₁ is normal.

If N=(V,A,r,X) is a phylogenetic X-network, then a parent map p for N consists of a map p:V−{r}→V such that, for all v∈V−{r}, p(v) is a parent of v. Note that r has no parent. If v is normal, then there is only one possibility for p(v), while if v is hybrid, there are at least two possibilities for p(v). In Fig. 1, an example of a parent map p satisfies p(h)=q ₂, and for all other vertices w besides r, p(w) is the unique parent of w.

Write Par(N) for the set of all parent maps for N. In general, if there are k distinct hybrid vertices and they have indegrees, respectively, i ₁,i ₂,…,i _k , then the number of distinct parent maps p is |Par(N)|=∏[i _j :j=1,…,k]. If N is a network with k distinct hybrid vertices, each of indegree 2, then |Par(N)|=2^k.

Given p∈Par(N) the set A _p of p-arcs is A _p ={(p(v),v):v∈V−{r}}. The induced tree N _p is the directed graph (V,A _p ) with root r. In Fig. 1, if p(h)=q ₁, then N _p consists of N with arc (q ₂,h) deleted. Note that each vertex in V−{r} has a unique parent in N _p . Thus, N _p is a tree with vertex set V. The set X, however, need not be a base-set of N _p . For example, in Fig. 1, if p(h)=q ₁, then N _p contains the vertex h with indegree 1 and outdegree 1, yet h∉X.

Several of the proofs will require the notion of “complementary parents”. Suppose p∈Par(N) and h is a particular hybrid vertex with exactly two parents q ₁ and q ₂. Assume p(h)=q ₁. The complementary parent map p′ of p with respect to h is defined by

Thus, p′ agrees with p except at h, where p′ chooses the other parent from that chosen by p. Of occasional use will be the network G _p =N _p ∪N _p′.

A phylogenetic X-network is weighted provided that for each arc (a,b)∈A there is a non-negative number ω(a,b) called the weight of (a,b) such that

• (1) if b is hybrid, then ω(a,b)=0;

• (2) if b is normal, then ω(a,b)≥0.

We call the function ω from the set of arcs to the reals the weight function of N. We interpret ω(a,b) as a measure of the amount of genetic change from species a to species b. If h is hybrid with parents q ₁ and q ₂ and unique child c, then the hybridization event is essentially assumed to be instantaneous between q ₁ and q ₂ with no genetic change in those character states inherited by h from q ₁ or q ₂ respectively. Further mutation then occurs from h to c, as measured by ω(h,c).

If N=(V,A,r,X) is a phylogenetic X-network and S⊂X, then the restriction of N to S, denoted N|S, consists of that part of N, which includes all possible ancestors of members of S. More formally, N|S=(V′,A′,r,S), where V′={v∈V: there exists s∈S such that v≤s}, A′={(u,v)∈A:u∈V′,v∈V′}. It is easy to see that N|S is a phylogenetic S-network. If N is weighted, then N|S is also weighted, using the same weight function but restricted to A′.

In any rooted network N=(V,A,r,X), a most recent common ancestor of two vertices u and v is a vertex w such that (1) w≤u and w≤v, and (2) there is no vertex w′ such that w′≤u, w′≤v, w<w′. In general, a most recent common ancestor of u and v exists, but it need not be uniquely determined. In any rooted tree, however, there is a unique most recent common ancestor of u and v.

Suppose that N=(V,A,r,X) is a weighted phylogenetic X-network with weight function ω. For each p∈Par(N) and for each u,v∈V, define the distance d(u,v;N _p ) as follows: In N _p there is a unique undirected path P(u,v) between u and v; define d(u,v;N _p ) to be the sum of the weights of arcs along P(u,v). More precisely, since N _p is a tree, there exists a most recent common ancestor m=mrca(u,v;N _p ), a directed path P ₁ given by m=u ₀,u ₁,…,u _k =u from m to u, and a directed path P ₂ given by m=v ₀,v ₁,…,v _j =v from m to v. Define

$$\begin{aligned} d(u,v; N_p) &= \sum \bigl[\omega(u_i,u_{i+1}): i = 0, \ldots, k-1 \bigr] \\ & \quad {}+ \sum \bigl[\omega(v_i,v_{i+1}): i = 0, \ldots, j-1 \bigr]. \end{aligned} $$

We shall refer to d(u,v;N _p ) as the distance between u and v in N _p .

Let H denote the set of hybrid vertices of N. For each h∈H, let P(h) denote the set of parents of h, i.e. the set of vertices u such that (u,h)∈A. Since h∈H, |P(h)|≥2. For each u∈P(h), let α(u,h) denote the probability that a character is inherited by h from u. As an approximation, α(u,h) measures the fraction of the genome that h inherits from u. Note for all h∈H, ∑[α(u,h):u∈P(h)]=1.

In Fig. 1, P(h)={q ₁,q ₂}, and Par(N) consists of two maps. The first map p has p(h)=q ₁, p(y)=h, p(x ₁)=q ₁, p(q ₁)=v, p(v)=r, p(x ₂)=q ₂, p(q ₂)=q ₃, p(x ₃)=q ₃, p(q ₃)=v, p(v)=r. The complementary map p′ agrees with p except that p′(h)=q ₂.

If h and h′ are distinct members of H, we will assume that the inheritances at h and h′ are independent. More generally, suppose for every h∈H that q _h is a parent of h. Then we assume that the events that a character at h is inherited from q _h are independent. It is then easy to see that for each p∈Par(N) the probability that inheritance follows the parent map p is Pr(p)=∏[α(p(h),h):h∈H].

Following Willson (2012) we define the tree-average distance d(u,v;N) between u and v in N by

$$d(u,v; N) = \sum \bigl[ \Pr(p) d(u,v; N_p): p \in \mathit{Par}(N) \bigr]. $$

It is thus the expected value of the distances between u and v in the various displayed trees N _p .

The simplest situation has each parent of h equally likely, so α(p(h),h)=1/|P(h)| for each p∈Par(N). If this situation occurs, we call the network equiprobable at h.

In this paper as in Willson (2012), we will assume that the weight of an arc into a hybrid vertex is 0. Thus, in Fig. 1, the weights of arcs (q ₁,h) and (q ₂,h) will be zero. The reason for this assumption is that vertex h corresponds to the immediate offspring of a hybridization event, in which some characters came intact from q ₁ and the remainder intact from q ₂. For those characters inherited from q ₁, there is no change between q ₁ and h; the inheritance is exactly 0 as measured by the weight of (q ₁,h), and similarly for characters inherited from q ₂. Alternatively, in the tree on which the character was inherited from q ₁ there was no mutational change between q ₁ and h. Further mutation occurred before species y evolved from h, as measured by the weight of arc (h,y).

An additional explanation for why in Fig. 1 we assume that the weights of arcs (q ₁,h) and (q ₂,h) will be zero is as follows: Suppose that the weights of (q ₁,h), (q ₂,h), and (h,y) were all positive. Then we could subtract the same arbitrary number ϵ from the weights of (q ₁,h) and (q ₂,h) while adding the same ϵ to the weight of (h,y) without changing any distances between leaves of the network. Hence, the true weights could not be uniquely determined from the data.

Further details and examples are in Willson (2012).

If T=(V,A,,X) is a undirected phylogenetic tree with leaf set X, a 4-set {x ₁,x ₂,x ₃,x ₄} from X is a quartet. When T is restricted to a quartet, the result is called a quartet tree. The only possible quartet trees are denoted x ₁ x ₂|x ₃ x ₄, x ₁ x ₃|x ₂ x ₄, x ₁ x ₄|x ₂ x ₃, and x ₁ x ₂ x ₃ x ₄. In x ₁ x ₂|x ₃ x ₄ removal of the internal edge disconnects T so that one component contains x ₁ and x ₂ while the other component contains x ₃ and x ₄. The star is denoted x ₁ x ₂ x ₃ x ₄. For additive distances on trees, it is well known (Semple and Steel 2003) that x ₁ x ₂|x ₃ x ₄ if and only if d(x ₁,x ₂)+d(x ₃,x ₄)<d(x ₁,x ₃)+d(x ₂,x ₄)=d(x ₁,x ₄)+d(x ₂,x ₃).

Let N=(V,A) be an acyclic digraph. A pseudocycle in N is a sequence of vertices x ₀,x ₁,x ₂,…,x _n from V with n>0 such that x _n =x ₀ and for each i (taken mod n) either

• (1) (x _i ,x _i+1) is an arc; or

• (2) x _i is hybrid with distinct parents x _i−1 and x _i+1 and (x _i+1,x _i ) is an arc.

A pseudocycle is not a cycle since it is not a directed path. Nevertheless, it is very similar to a cycle since time is moving forward on most parts of the sequence. The existence of a pseudocycle indicates a lack of “time consistency.” For example, if there is a temporal representation on the network (Baroni et al. 2006), then each vertex v has a “time” f(v) such that when v has parents p and q, then f(p)=f(q); and when c is a child of u, then f(u)<f(c). Following a pseudocycle, we see that the successive hybrid parents must exist later in time and yet loop back to the original hybrid node, an impossibility. Hence, the network can have no pseudocycle.

3 Overview of the Reconstruction

Throughout the reconstruction, we will make the following assumptions:

Assumptions 3.1

Let N=(V,A,r,X) be a rooted directed network. Assume

• (0) N is normal.

• (1) All hybrids have indegree 2 and outdegree 1, and the child is a tree-child.

• (2) Every weight of an arc to a hybrid vertex is 0.

• (3) The weight of every arc to a normal vertex is positive.

• (4) All normal vertices have outdegree 0 or 2.

• (5) N has no pseudocycles.

• (6) X consists of the set of leaves of N together with r.

A cherry {x,y} is a set of two vertices x and y in X such that

• (1) both x and y are leaves which are normal vertices;

• (2) both x and y have the same parent q;

• (3) q is normal;

• (4) q has outdegree 2.

Suppose that the tree-average distance d is known between all members of X. We wish to see how to reconstruct N. The first key result, Theorem 3.2, asserts that either there is a cherry or else there is a hybrid vertex of a particularly simple kind.

Theorem 3.2

Let N satisfy Assumptions 3.1. Suppose N has no cherry and at least 4 vertices in X. Then there exists a hybrid vertex h with parents q ₁ and q ₂ such that each of these has a tree-child which is a leaf.

The conclusion of Theorem 3.2 is illustrated in Fig. 1. In the figure, there is no cherry but h is hybrid with parents q ₁ and q ₂. Then h has tree-child y, which is a leaf, q ₁ has tree-child x ₁ which is a leaf, and q ₂ has tree-child x ₂ which is a leaf. If these conditions occur, we will say that (y;x ₁,x ₂) is a hybrid triple.

Proof

Choose a maximal path (with the most arcs) from r ending at v ₁ with parent w ₁. Then v ₁ is a leaf, hence normal. If w ₁ has another child c, then c cannot be hybrid, since then c would have a child and a longer path from r could have been obtained. Hence, c is normal. Moreover, if c had a child then a longer path could have been obtained; hence, c is a normal leaf. Since v ₁ is normal then {c,v ₁} is a cherry, a contradiction. Hence, v ₁ has no sibling whence w ₁ is hybrid with two parents q ₁₁ and q ₁₂. We choose the labeling so that q ₁₁ is on the given maximal path from r to w ₁. Note there are two arcs on the path after q ₁₁. By normality, q ₁₁ has a normal child z. If z is not a leaf, it has at least two children c ₁ and c ₂. By maximality, each child c _i is a leaf. But no leaf is hybrid, whence both are normal, so {c ₁,c ₂} is a cherry, a contradiction. Hence, z is a normal leaf.

By normality, q ₁₂ has a normal child u ₁. If u ₁ is a leaf then, we are done with h=w ₁, q ₁=q ₁₁, q ₂=q ₁₂, y=v ₁, x ₁=z, x ₂=u ₁. Otherwise, choose a maximal directed path starting at u ₁. Repeat the argument. Since the vertex set is finite there is ultimately a repetition leading to a pseudocycle. This is impossible, so the procedure terminates. □

We may now present the general idea of the reconstruction of N. Suppose that N=(V,A,r,X) is a phylogenetic X-network satisfying Assumptions 3.1. Suppose we are given all the tree-average distances d(x,y;N) for x and y in X. Initially a network R=(W,B) has vertex set W=X and arc set B=∅. We recursively simplify the network N to a new network N′ as follows:

(1) For each distinct x and y in X we check, using Theorem 4.5 (in the next section), whether {x,y} is a cherry.

(2) If a cherry {x,y} is recognized, then we proceed as follows:

By Willson (2012) Lemma 4.3(2), the parent q of both x and y satisfies that ω(q,x)=[d(x,y;N)+d(x,r;N)−d(r,y;N)]/2 and ω(q,y)=[d(y,x;N)+d(y,r;N)−d(r,x;N)]/2. Moreover, by additivity of the distances, for every z∈X, z other than x or y, d(z,q;N)=d(q,x;N)−ω(q,x)=d(q,y;N)−ω(q,y).

We construct a new phylogenetic network N′=(V′,A′,r,X′) with distance d′ and a network R′=(W′,B′) as follows: Since {x,y} is recognized as a cherry, there exists in N a vertex q which is the parent of x and y. Let V′=V−{x,y}, X′=X−{x,y}∪{q}, A′=A−{(q,x),(q,y)}. Moreover, for z∈X′, d(z,q;N′)=d(z,x;N)−ω(q,x) is known. Finally, d′(u,v;N′)=d(u,v;N) for {u,v}⊂X′ if neither u nor v is q; and d′(z,q;N′)=d(q,x;N)−ω(q,x).

There is a new vertex q (identified with the q in N) such that W′=W∪{q} and B′=B∪{(q,x),(q,y)} where ω(q,x) and ω(q,y) are given as above.

(3) Suppose no cherry {x,y} is recognized. Then by Theorem 4.5, no cherry exists in N, and by Theorem 3.2 there exists a hybrid triple (y ₀;x ₁₀,x ₂₀). For each possible choice of (y;x ₁,x ₂), we use Sect. 5 to determine whether (y;x ₁,x ₂) is a hybrid triple. By Theorem 3.2, this will succeed for some choice. By Theorem 6.1, no triple that is not a hybrid triple will be falsely identified, under certain additional assumptions. There are now two possibilities:

(3a) Suppose (y;x ₁,x ₂) is identified as an equiprobable hybrid triple. By Willson (2012), we know ω(h,y), ω(q ₁,x ₁), and ω(q ₂,x ₂). We modify N to N′=(V′,A′,r,X′) where V′=V−{h,y,x ₁,x ₂}, A′=A−{(h,y),(q ₁,x ₁),(q ₂,x ₂)}, X′=X−{y,x ₁,x ₂}∪{q ₁,q ₂}. We know for v∈V′, v other than q ₁, q ₂ by Willson (2012) d(v,q ₁;N)=d(v,x ₁;N)−ω(q ₁,x ₁) d(v,q ₂;N)=d(v,x ₂;N)−ω(q ₂,x ₂). Moreover, d(q ₁,q ₂;N)=d(x ₁,x ₂;N)−ω(q ₁,x ₁)−ω(q ₂,x ₂).

We modify R=(W,B) to R′=(W′,B′) where W′=W∪{q ₁,q ₂,h}, B′=B∪{(h,y),(q ₁,x ₁),(q ₂,x ₂),(q ₁,h),(q ₂,h)}, α(q ₁,h)=1/2, α(q ₂,h)=1/2, ω(q ₁,h)=ω(q ₂,h)=0. Moreover, by Willson (2012), ω(h,y), ω(q ₁,x ₁), and ω(q ₂,x ₂) are given by the formulas a _rv =(d(r,x ₁)+d(r,x ₂)−d(x ₁,x ₂))/2, ω(q ₁,x ₁)=d(x ₁,y)−d(r,y)+a _rv , ω(q ₂,x ₂)=d(x ₂,y)−d(r,y)+a _rv , ω(h,y)=(d(y,x ₁)+d(y,x ₂)−d(x ₁,x ₂))/2.

(3b) Suppose (y;x ₁,x ₂) is identified as a hybrid triple such that x ₃ is identified as a normal descendant of an appropriate ancestor of x ₂. Then Lemma 4.9 of Willson (2012) gives formulas in this situation for ω(h,y), ω(q ₁,x ₁), ω(q ₂,x ₂) as well as α(q ₁,h) and α(q ₂,h). Then we proceed as in (3a) except that we use these alternative formulas for these quantities.

4 Recognition of a Cherry

In this section, we prove necessary and sufficient conditions to recognize whether {x,y} is a cherry.

Suppose w and z in X satisfy that w, x, y, z are distinct in X. For any network M with base-set X, let W _x (M)=d(w,x;M)+d(z,y;M), W _y (M)=d(w,y;M)+d(x,z;M), W _z (M)=d(w,z;M)+d(x,y;M), using the tree-average distance d on M.

Lemma 4.1

Suppose x and y are leaves that form a cherry in the network N. Suppose w and z in X satisfy that w, x, y, z are distinct in X. Then W _z (N)<W _x (N)=W _y (N).

Proof

For every parent map p, we have wz|xy in N _p , so

$$d(w,z;N_p)+d(x,y;N_p) < d(w,x;N_p)+d(z,y;N_p) = d(w,y;N_p)+d(z,x;N_p) $$

with the strict inequality since the common parent q of x and y is normal so the arc into q has positive weight. Hence, W _z (N _p )<W _x (N _p )=W _y (N _p ). Taking averages over p weighted by Pr(p), we see that W _z (N)<W _x (N)=W _y (N). □

Theorem 4.2 is the converse of Lemma 4.1. Together these two results give a necessary and sufficient condition for {x,y} to be a cherry.

Theorem 4.2

Assume Assumptions 3.1. Suppose x and y are in X. Suppose that for all choices of w and z in X such that w, x, y, z are distinct, we have that W _z (N)<W _x (N)=W _y (N). Then {x,y} is a cherry.

The proof of Theorem 4.2 will require a lemma. The lemma shows that if for various parent maps of N we have exactly two of the possibilities among W _z <W _x =W _y , W _x <W _z =W _y , W _y <W _z =W _x , then for the tree-average distance we cannot have the condition W _z (N)<W _x (N)=W _y (N) in Theorem 4.2.

Lemma 4.3

Suppose x and y are in X. Pick w and z in X so that w, x, y, z are distinct.

(1) Assume for a nonempty collection of parent maps p we have W _z (N _p )<W _x (N _p )=W _y (N _p ) and for a nonempty collection of parent maps p we have W _x (N _p )<W _z (N _p )=W _y (N _p ) but we never have a parent map p for which W _y (N _p )<W _z (N _p )=W _x (N _p ). Then we cannot have W _z (N)<W _x (N)=W _y (N).

(2) Assume for a nonempty collection of parent maps p we have W _y (N _p )<W _z (N _p )=W _x (N _p ) and for a nonempty collection of parent maps p we have W _x (N _p )<W _z (N _p )=W _y (N _p ), but we never have a parent map p for which W _z (N _p )<W _x (N _p )=W _y (N _p ). Then we cannot have W _z (N)<W _x (N)=W _y (N).

(3) Assume for a nonempty collection of parent maps p we have W _z (N _p )<W _x (N _p )=W _y (N _p ) and for a nonempty collection of parent maps p we have W _y (N _p )<W _z (N _p )=W _x (N _p ) but we never have a parent map p for which W _x (N _p )<W _z (N _p )=W _y (N _p ). Then we cannot have W _z (N)<W _x (N)=W _y (N).

Here is a geometric interpretation of Lemma 4.3: Suppose w,x,y,z are distinct members of X. Suppose there exist parent maps p such that N _p displays the quartet wz|xy and parent maps p such that N _p displays the quartet wx|yz but no N _p displays the quartet wy|xz. Then the tree average distance cannot appear to have quartet wz|xy via d(w,z)+d(x,y)<d(w,x)+d(y,z)=d(w,y)+d(x,z). Nor can it appear to have quartet wy|xz via d(w,y)+d(x,z)<d(w,x)+d(y,z)=d(w,z)+d(x,y).

Proof

(1) Write A _z for the sum of the W _z (N _p ) for p such that W _z (N _p )<W _x (N _p )=W _y (N _p ) weighted by the probability of p; thus

$$A_z = \sum\bigl[\Pr(p) W_z(N_p): W_z(N_p) < W_x(N_p) = W_y(N_p) \bigr]. $$

Similarly let B _z =∑[Pr(p)W _z (N _p ):W _x (N _p )<W _z (N _p )=W _y (N _p )]. Then W _z (N)=A _z +B _z since these exhaust all the parent maps p under the assumptions of (1). Similarly, define

$$\begin{aligned} & A_x = \sum\bigl[\Pr(p) W_x(N_p): W_z(N_p) < W_x(N_p) = W_y(N_p) \bigr] \\ & B_x = \sum\bigl[\Pr(p) W_x(N_p): W_x(N_p) < W_z(N_p) = W_y(N_p) \bigr], \\ & A_y = \sum\bigl[\Pr(p) W_y(N_p): W_z(N_p) < W_x(N_p) = W_y(N_p) \bigr] \\ & B_y = \sum\bigl[\Pr(p) W_x(N_p): W_x(N_p) < W_z(N_p) = W_y(N_p) \bigr]. \end{aligned}$$

Thus, W _x (N)=A _x +B _x and W _y (N)=A _y +B _y .

Suppose (1) is false, so A _z +B _z <A _x +B _x =A _y +B _y .

By linearity, A _z <A _x =A _y and B _x <B _z =B _y .

Since A _x +B _x =A _y +B _y and A _x =A _y , it follows that B _x =B _y . This contradicts B _x <B _y , proving (1).

(2) Let

$$\begin{aligned} & A_z =\sum\bigl[\Pr(p) W_z(N_p): W_y(N_p) < W_z(N_p) = W_x(N_p) \bigr] \\ & B_z = \sum\bigl[\Pr(p) W_z(N_p): W_x(N_p) < W_z(N_p) = W_y(N_p) \bigr] \end{aligned}$$

and similarly define A _x ,A _y ,B _x ,B _y . Then A _y <A _z =A _x and B _x <B _z =B _y . Moreover, W _z (N)=A _z +B _z since these exhaust all the parent maps p under the assumptions of (2). If (2) is false and W _z (N)<W _x (N)=W _y (N) then A _z +B _z <A _x +B _x =A _y +B _y .

But A _z =A _x so A _x +B _z <A _x +B _x whence B _z <B _x , a contradiction, proving (2).

(3) follows symmetrically with the proof of (1). □

Corollary 4.4

Suppose N is a phylogenetic network satisfying Assumptions 3.1. Suppose w,x,y,z are distinct leaves. Assume

• (i) there exists a quartet wx|yz or wy|xz or wz|xy such that there is no parent map p for which this quartet occurs in N _p ; and

• (ii) there exists a parent map p for which wx|yz or wy|xz occurs in N _p .

Then it cannot be the case that W _z (N)<W _x (N)=W _y (N).

Proof

If there exist two different quartets that arise in some N _p but not three, then one of (1), (2), or (3) in Lemma 4.3 occurs and the conclusion follows. By (i), we cannot have all three quartets occurring in N _p for various parent maps p. Hence, the only case that remains is that only one quartet occurs in N _p for various p. By (ii), it is either wx|yz or wy|xz. In the former case we have W _x <W _y =W _z and in the latter we have W _y <W _x =W _z . □

We can now prove Theorem 4.2.

Proof

Both x and y are normal leaves. Let q _y be the parent of y and q _x be the parent of x. I claim q _x =q _y .

If q _x ≠q _y , then there exists a most recent common ancestor v of x and y and it must satisfy that either v<q _x or v<q _y or both. Without loss of generality, assume v<q _y . Hence, there is a directed path P(v,q _y ) from v to q _y of positive length such that no vertex of P(v,q _y ) except v is ancestral to x. In particular, we do not have q _y ≤x. There are 5 cases to consider.

Assume first that q _y is normal, hence of indegree 1. Since it has a child and its outdegree cannot be 1, its outdegree is 2. Since the outdegree of q _y is 2, it has another child c, which is either normal or hybrid.

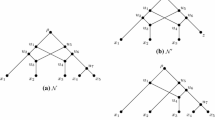
Case 1. Suppose c is normal. By normality of N, we may choose a normal path from c to z∈X. See Fig. 2a.

Fig. 2

(a) Case 1 of Theorem 4.2. (b) Case 2

I claim that for all p, in N _p we have yz|rx. To see this, note that each N _p contains the arcs (q _y ,y) and (q _y ,c) and the normal path P(c,z). Their union forms the undirected path P(y,z) in N _p between y and z. But then P(y,z) is disjoint from the undirected path P(r,x) in N _p . (Otherwise, they would meet in a vertex on P(q _y ,z) and it would follow that q _y ≤x, a contradiction.)

Since N _p is a tree, it follows that for all p, with w=r, W _x (N _p )<W _y (N _p )=W _z (N _p ). If we take the averages weighted by the probabilities, we see W _x (N)<W _y (N)=W _z (N), contradicting the hypotheses. Thus, Case 1 cannot occur.

Case 2. Suppose c is hybrid with other parent q. Since there are no hybrid leaves, choose a nontrivial normal path P(c,z) from c to z∈X. Since q has outdegree 2, we may choose a normal path P(q,w) from q to w∈X. Assume q is not ≤x. See Fig. 2b.

Claim 2a. There is no parent map p such that N _p has wy|xz.

To see Claim 2a, we show that for any p, P(w,y;N _p ) intersects P(x,z;N _p ). First, there exists t such that P(w,y;N _p ) is the union of the directed paths P(t,w;N _p ) and P(t,y;N _p ). And there exists s such that P(x,z;N _p )=P(s,x;N _p )∪P(s,z;N _p ).

First, observe that P(t,y;N _p ) must include q _y since q _y is the unique parent of y. Moreover, since t≤ w in N _p and P(q,w) is normal in N, either t lies on P(q,w) or else t≤q and P(t,y;N _p ) contains P(q,w). But if t lies on P(q,w) then q≤t≤q _y so (q,c) is redundant. Thus, P(t,y;N _p ) contains P(q,w) and in particular q. Hence, P(t,y;N _p ) must contain both q and q _y .

Second, observe that P(x,z;N _p ) must contain either q or q _y . To see this, since s≤z and P(c,z) is normal, either s≤c or else s lies on P(c,z). But if s lies on P(c,z) then q _y ≤c≤s≤x contradicting that q _y is not ≤x. Hence, s≤c in N _p . Since c has only the two parents q and q _y , it follows that P(s,z) contains either q or q _y .

Thus, P(w,y;N _p ) intersects P(x,z;N _p ) as claimed.

Claim 2b. There exists a parent map p such that N _p displays yz|wx.

To see Claim 2b, suppose p satisfies p(c)=q _y . Since y is normal and P(c,z;N) is normal, it follows that P(y,z;N _p ) is the union of (q _y ,y), (q _y ,c), and P(c,z). There exists t such that P(w,x;N _p )=P(t,w;N _p )∪P(t,x;N _p ). I claim that P(w,x) is disjoint from P(y,z). To see this note

• (i) P(t,w;N _p ) cannot contain the leaf y.

• (ii) P(t,w;N _p ) cannot contain q _y . If P(t,w;N _p ) contains q _y then q _y ≤w. Since P(q,w) is normal, either q _y ≤q or else q _y lies on P(q,w). If q _y ≤q then (q _y ,c) is redundant, a contradiction. If q _y lies on P(q,w) then q≤q _y so (q,c) is redundant, a contradiction.

• (iii) P(t,w;N _p ) cannot intersect P(c,z). If they met in u, then c≤u≤ w. Since P(q,w) is normal either c≤q or else c lies on P(q,w). But if c≤q, there is a directed cycle in N. If c lies on P(q,w), then since q≠c the arc (q,c) is redundant.

• (iv) P(t,x;N _p ) cannot contain the leaf y.

• (v) P(t,x;N _p ) cannot contain q _y . Otherwise, q _y ≤x, a contradiction.

• (vi) P(t,x;N _p ) cannot intersect P(c,z). If they met in u, then c≤u≤x whence q _y ≤x, a contradiction.

This proves Claim 2b.

By Corollary 4.4, we cannot have W _z (N)<W _x (N)=W _y (N). Hence, Case 2 cannot occur.

Case 3. Suppose c is hybrid with other parent q. Since there are no hybrid leaves, we may choose a normal path from c to z∈X. Suppose we may also choose a normal path from q to x∈X. Let w=r. See Fig. 3a.

Fig. 3

(a) Case 3 of Theorem 4.2. (b) Case 4. (c) Case 5

Claim 3a. There is no parent map p such that wz|xy in N _p .

To see this, suppose p is a parent map. Recall w=r. We show that the undirected path P(w,z;N _p ) from w to z in N _p always intersects P(x,y;N _p ). In the rooted tree N _p , note that q and q _y have a most recent common ancestor u. N _p must contain either (q,c) or (q _y ,c). Thus, the path P(w,z;N _p ) must contain P(r,u;N _p ), P(c,z;N _p ), and either P(u,q;N _p ) or P(u,q _y ;N _p ). In particular, P(w,z;N _p ) must contain either q or q _y .

On the other hand, P(x,y;N _p ) must contain q _y since it is the unique parent of the leaf y. Moreover, P(x,y;N _p ) must contain q. This is because P(x,y;N _p )=P(s,x)∪P(s,y) for some s. Since P(q,x) is normal and s≤x, either s≤q or s lies on P(q,x) and s≠q. In the latter case, q<s≤y, whence q≤q _y and (q,c) is redundant, a contradiction.

Claim 3b. There exists a parent map p such that wx|yz in N _p .

To see this, choose p such that p(c)=q _y . I claim P(w,x;N _p ) does not intersect P(y,z;N _p ). Note that P(r,x;N _p ) must consist of directed paths P(r,u;N _p ) together with P(r,q;N _p ) and P(q,x;N _p ) since P(q,x) is normal in N. On the other hand, P(y,z;N _p ) consists of (q _y ,y), (q _y ,c) and P(c,z) since P(c,z) is normal in N. It is now clear that P(w,x;N _p ) is disjoint from P(y,z;N _p ).

By Corollary 4.4 we cannot have W _z (N)<W _x (N)=W _y (N), showing that Case 3 cannot occur.

Now instead of assuming that q _y is normal, we assume q _y is hybrid and the leaf y is the unique child of q _y . Let q ₁ and q ₂ be the parents of q _y . Choose normal children c _i of q _i respectively and normal paths from c _i to x _i ∈X, respectively.

Case 4. Assume that we may choose x ₁ and x ₂ so that x, y, x ₁, and x ₂ are all distinct. See Fig. 3b.

Let w=x ₁, z=x ₂.

Claim 4a. There is no parent map p such that in N _p we have wz|xy. To see this, suppose p is a parent map. Suppose wz|xy, so that P(x ₁,x ₂;N _p ) is disjoint from P(x,y;N _p ).

Note that P(x ₁,x ₂;N _p ) is the union of P(s,x ₁;N _p ) and P(s,x ₂;N _p ) for some s. Since s≤x ₁ in N _p , either s≤q ₁ or else s lies on P(q ₁,x ₁;N _p ) and is distinct from q ₁. But in the latter case q ₁<s≤x ₂ in N _p , whence q ₁<s≤q ₂ in N _p and (q ₁,q _y ) is redundant in N, a contradiction. Hence, s≤q ₁ in N _p . A similar argument shows s≤q ₂ in N _p . Hence, P(x ₁,x ₂;N _p ) includes both q ₁ and q ₂.

On the other hand, P(x,y;N _p ) must contain the leaf y, hence its unique child q _y , hence the parent of q _y in N _p , hence either q ₁ or q ₂. This shows that P(x,y;N _p ) cannot be disjoint from P(x ₁,x ₂;N _p ), proving the claim.

For every p, N _p is binary, so in any N _p it follows we must have either wx|yz or wy|xz.

By Corollary 4.4, it follows that we cannot have W _z (N)<W _x (N)=W _y (N), so Case 4 cannot occur.

Since Case 4 cannot occur, it follows that we cannot select x ₁ and x ₂ so that x ₁, x ₂, x, and y are distinct. Hence (possibly by interchanging x ₁ and x ₂), we may assume that the only leaf descendant of q ₁ by a normal path is x. Thus, the only remaining case is the following case 5. See Fig. 3c.

Case 5. The vertex q _y is hybrid with parents q ₁ and q ₂. There is a normal path from q ₁ to x and a normal path from q ₂ to x ₂. Let w=r, z=x ₂.

Claim 5a. There is no parent map p such that ry|xx ₂ in N _p .

To see claim 5a, it suffices to show P(r,y;N _p ) and P(x,x ₂;N _p ) must intersect. Let u denote the most recent common ancestor of x and x ₂ in N _p , so P(x,x ₂;N _p ) is the union of P(u,x;N _p ) and P(u,x ₂;N _p ). But u≤x in N _p , so either u lies on P(q ₁,x) or u≤q ₁ in N _p . If u lies on P(q ₁,x), then in N _p we have q ₁≤u≤x ₂, whence in N _p we have q ₁≤q ₂, whence q ₁≤q ₂ in N, which implies that (q ₁,q _y ) is redundant, a contradiction. Hence, u≤q ₁ in N _p . A similar argument shows u≤q ₂ in N _p . Hence, P(x,x ₂;N _p ) contains both q ₁ and q ₂. On the other hand P(r,y;N _p ) must include y; hence, its unique parent q _y , hence either q ₁ or q ₂, so P(r,y;N _p ) intersects P(x,x ₂;N _p ).

Claim 5b. There exists a parent map p such that rx|yx ₂ in N _p .

To see claim 5b, choose p such that p(q _y )=q ₂. Then in N _p we have that P(y,x ₂;N _p ) is the union of P(q ₂,x ₂;N _p ) and P(q ₂,q _y ,y;N _p ). If u=mrca(q ₁,q ₂;N _p ), then P(r,x) is the union of P(r,u), P(u,q ₁), and P(q ₁,x). Suppose P(r,x) meets P(y,x ₂;N _p ) in s.

• (i) If s∈P(q ₁,x)∩P(q ₂,x ₂), then q ₁≤s≤x ₂, forcing q ₁≤s≤q ₂, making (q ₁,q _y ) redundant.

• (ii) If s=y, there is a contradiction since y has no children, and if s=q _y there is a contradiction since the only proper descendant is y.

• (iii) If s∈P(u,q ₁)∩P(q ₂,x ₂) then q ₂≤s≤q ₁, so (q ₂,q _y ) is redundant.

• (iv) If s∈P(r,u)∩P(q ₂,x ₂) then q ₂≤s≤u≤q ₁ so (q ₂,q _y ) is redundant.

Hence, there can be no intersection of P(r,x) and P(y,x ₂), so rx|yx ₂ in N _p .

By Corollary 4.4, it follows that we cannot have W _z (N)<W _x (N)=W _y (N), so Case 5 cannot occur.

Cases 1 through 5 show that the assumption that q _x ≠q _y is impossible, so q _x =q _y . Since q _x has outdegree at least two, it must have outdegree exactly 2 by the hypotheses, and it must be normal (since a hybrid vertex has outdegree one). Hence {x,y} form a cherry, as asserted. This completes the proof of the theorem. □

We may combine Lemma 4.1 and Theorem 4.2 into the following summary.

Theorem 4.5

(a) If |X|≥4, then {x,y} is a cherry if and only if for all w and z in X such that {w,x,y,z} are distinct, we have W _z (N)<W _x (N)=W _y (N).

(b) If |X|=3, say X={r,x,y}, then {x,y} is a cherry.

Proof

(a) is immediate from Lemma 4.1 and Theorem 4.2. If |X|=3 then there can be no hybrid vertex and (b) is immediate. □

5 Recognition of a Hybrid Vertex

Suppose that we seek to reconstruct N=(V,A,r,X) from the tree-average distances on X. From Sect. 4, we know how to recognize a cherry {x,y}. Hence, we may assume there is no cherry, and by Theorem 3.2 there exists a hybrid vertex h with parents q ₁ and q ₂ such that h has a child y, which is a leaf, q ₁ has a child x ₁ which is a leaf, and q ₂ has a child x ₂ which is a leaf. The essential step is to identify such y, x ₁, and x ₂. To do this, we consider all possibilities for y, x ₁, and x ₂ and find a choice, which satisfies certain necessary criteria.

We present five necessary criteria, labeled B through F.

5.1 Criterion B: Clustering Conditions

This criterion is the most useful for quickly eliminating false candidates for hybrids.

Lemma 5.1

Assume that h is hybrid with parents q ₁ and q ₂ and both α(q ₁,h)>0 and α(q ₂,h)>0. Suppose h has a normal leaf child y, q ₁  has a normal leaf child x ₁, and q ₂ has a normal leaf child x ₂. Suppose w∈X is distinct from y, x ₁, and x ₂. For each network M with the same X let W _y (M)=d(w,y;M)+d(x ₁,x ₂;M), $W_{x_{1}}(M) = d(w,x_{1};M)+d(y,x_{2};M)$, $W_{x_{2}}(M) = d(w,x_{2};M) + d(y,x_{1};M)$.

Then for all such w, $W_{x_{1}}(N) < W_{y} (N)$ and $W_{x_{2}}(N) < W_{y} (N)$.

The geometric content of Lemma 5.1 is seen in Fig. 1. Suppose w∈X is distinct from y, x ₁, and x ₂ somewhere in the network (unspecified in Fig. 1). Note that for a parent map p with p(h)=q ₁, for the 4-set {w,y,x ₁,x ₂} we necessarily have the quartet tree yx ₁|wx ₂. For the complementary parent map p′ with p′(h)=q ₂, we necessarily have the quartet tree yx ₂|wx ₁. Lemma 5.1 essentially says that there is no parent map p such that wy|x ₁ x ₂ in N _p .

The proof will require the following definition. For a given parent map p with p(h)=q ₁, let p′ denote the complementary parent map and G _p =N _p ∪N _p′ be the network N _p with the additional arc (q ₂,h). Let H be the set of hybrid vertices of N. For each p∈Par(N) satisfying p(h)=q ₁, let W(p)=∏[α(p(h′),h′):h′∈H,h′≠h]. Hence, Pr(p)=α(q ₁,h)W(p) and Pr(p′)=α(q ₂,h)W(p).

Proof

Each parent map satisfies either p(h)=q ₁ or p(h)=q ₂. If p(h)=q ₁, then for every w∈X distinct from y, x ₁, x ₂ we have that {y,x ₁} is a cherry in N _p , so $W_{x_{2}}(N_{p}) < W_{x_{1}}(N_{p})=W_{y} (N_{p})$. If p(h)=q ₂, then for all such w we have that {y,x ₂} is a cherry, so $W_{x_{1}}(N_{p}) < W_{x_{2}}(N_{p})=W_{y} (N_{p})$. In particular, if p(h)=q ₁ we have $W_{x_{2}}(N_{p}) < W_{x_{1}}(N_{p})=W_{y} (N_{p})$ and if p′ is the complementary parent map (so p′(h)=q ₂) then $W_{x_{1}}(N_{p'}) < W_{x_{2}}(N_{p'})=W_{y} (N_{p'})$. It follows that

$$\alpha(q_1,h)W_{x_2}(N_p) < \alpha(q_1,h)W_{x_1}(N_p)=\alpha(q_1,h)W_y (N_p) $$

and

$$\alpha(q_2,h)W_{x_1}(N_{p'}) < \alpha(q_2,h)W_{x_2}(N_{p'})=\alpha (q_2,h)W_y (N_{p'}). $$

We combine N _p and N _p′ into the network G _p =N _p ∪N _p′. When we take into account the probabilities at h, we see W _y (G _p )=α(q ₁,h)W _y (N _p )+α(q ₂,h)W _y (N _p′).

Take the sum over all parent maps. Since each p satisfying p(h)=q ₁ has its complementary p′, we see that

$$W_y (N) = \sum\bigl[ W(p) W_y (G_p); p(h) = q_1\bigr]. $$

Similarly,

$$\begin{aligned} & W_{x_1}(G_p) = \alpha(q_1,h) W_{x_1}(N_p) + \alpha(q_2,h) W_{x_1}(N_{p'}), \\ & W_{x_1}(N) = \sum\bigl[ W(p) W_{x_1}(G_p): p(h) = q_1\bigr], \\ & W_{x_2}(G_p) = \alpha(q_1,h) W_{x_2}(N_p) + \alpha(q_2,h) W_{x_2}(N_{p'}), \\ & W_{x_2}(N) = \sum\bigl[ W(p) W_{x_2}(G_p): p(h) = q_1\bigr]. \end{aligned}$$

Hence, $W_{x_{1}}(G_{p}) = \alpha(q_{1},h) W_{x_{1}}(N_{p}) + \alpha(q_{2},h) W_{x_{1}}(N_{p'}) < \alpha(q_{1},h) W_{y} (N_{p}) + \alpha(q_{2},h) W_{y} (N_{p'}) = W_{y} (G_{p})$ and the inequality is strict since the case p′(h)=q ₂ occurs and α(q ₂,h)>0 so $W_{x_{1}}(G_{p}) < W_{y} (G_{p})$. Similarly, $W_{x_{2}}(G_{p}) = \alpha(q_{1},h) W_{x_{2}}(N_{p}) + \alpha(q_{2},h) W_{x_{2}}(N_{p'}) < \alpha(q_{1},h) W_{y} (N_{p}) + \alpha(q_{2},h) W_{y} (N_{p'}) = W_{y} (G_{p})$, but the inequality is strict since p(h)=q ₁ occurs and α(q ₁,h)>0 so $W_{x_{2}}(G_{p}) < W_{y} (G_{p})$.

Now $W_{x_{1}}(N) = \sum[W(p) W_{x_{1}}(G_{p}): p(h) = q_{1}] < \sum[W(p) W_{y} (G_{p}) : p(h) = q_{1}] = W_{y}(N)$ so $W_{x_{1}}(N) < W_{y} (N)$. Similarly, $W_{x_{2}}(N) < W_{y} (N)$. □

We say that (y;x ₁,x ₂) passes Criterion B provided that the conclusion of Lemma 5.1 holds. Alternatively, Lemma 5.1 says that if y, x ₁, and x ₂ have the hypothesized relationship with a hybrid vertex, then (y;x ₁,x ₂) passes Criterion B.

5.2 Criterion C: Exact Relationships Among Distances Relating y, x ₁, and x ₂

The following Lemma 5.2 is useful since it gives an exact relationship that must hold for any z between d(z,y), d(z,x ₁), d(z,x ₂), and α(q ₁,h). Assume that N=(V,A,r,X) has hybrid h with parents q ₁, q ₂, such that q ₁ has a child x ₁ which is a normal leaf, q ₂ has a child x ₂ which is a normal leaf, and h has a child y, which is a normal leaf.

Lemma 5.2

For every z∈X other than y, x ₁, x ₂

• (1) d(z,h)=α(q ₁,h)d(z,q ₁)+α(q ₂,h)d(z,q ₂),

• (2) d(z,y)−ω(h,y)=α(q ₁,h)[d(z,x ₁)−ω(q ₁,x ₁)]+α(q ₂,h)[d(z,x ₂)−ω(q ₂,x ₂)].

In particular, in the equiprobable case,

• (3) d(z,y)−ω(h,y)=(1/2)[d(z,x ₁)−ω(q ₁,x ₁)]+(1/2)[d(z,x ₂)−ω(q ₂,x ₂)].

Proof

For each parent map p such that p(h)=q ₁, let p′ denote the complementary parent map, which agrees with p except that p′(h)=q ₂. Then every parent map has the form either p or p′. For each z∈X, z other than y, x ₁, x ₂, note

$$\begin{aligned} & d(z,h; N_p) = d(z,q_1;N_p) \quad \mbox{since } \omega(q_1,h) = 0\quad \mbox{and}\\ & d(z,h;N_{p'}) = d(z,q_2;N_{p'}) \quad \mbox{since } \omega(q_2,h) = 0. \end{aligned}$$

Hence, if p(h)=q ₁, then

$$d(z,h;G_p) = \alpha(q_1,h) d(z,h;N_p) + \alpha(q_2,h) d(z,h;N_{p'}). $$

By Lemma 4.6 of Willson (2012), for each parent map p with p(h)=q ₁, d(z,h;N)=∑[W(p)d(z,h:G _p );p(h)=q ₁] where W(p)=∏(α(p(h′),h′):h′≠h), whence

$$\begin{aligned} & d(z,h;N) \\ &\quad = \sum\Bigl[\alpha(q_1,h) W(p) d(z,h;N_p) + \sum\alpha(q_2,h) W(p) d(z,h;N_{p'}): p(h) = q_1\Bigr] \\ &\quad = \sum\alpha(q_1,h) W(p) d(z,h;N_p) + \sum\alpha(q_2,h) W(p) d(z,h;N_{p'}) \\ &\quad = \sum\alpha(q_1,h) W(p) d(z,q_1;N_p) + \sum\alpha(q_2,h) W(p) d(z,q_2;N_{p'}) \\ &\quad \bigl(\mbox{since }\omega(q_1,h)=\omega(q_2,h)=0 \bigr) \\ &\quad = \alpha(q_1,h) \sum\bigl[W(p) d(z,q_1;N_p) \bigr] + \alpha(q_2,h) \sum\bigl[W(p) d(z,q_2;N_{p'}) \bigr]. \end{aligned}$$

But d(z,q ₁;N _p )=d(z,q ₁;N _p′) and d(z,q ₂;N _p )=d(z,q ₂;N _p′) since the path connecting z to q ₁ in either case does not pass through h. Hence, by Lemma 4.6 of Willson (2012) d(z,q ₁;N)=∑[W(p)d(z,q ₁;G _p ):p(h)=q ₁] and similarly d(z,q ₂;N)=∑[W(p)d(z,q ₂;G _p ):p(h)=q ₁]. It follows that d(z,h;N)=α(q ₁,h)d(z,q ₁;N)+α(q ₂,h)d(z,q ₂;N) proving (1).

Since d(z,q ₁;N)+ω(q ₁,x ₁)=d(z,x ₁;N) we have d(z,q ₁;N)=d(z,x ₁;N)−ω(q ₁,x ₁). Similarly, d(z,q ₂;N)=d(z,x ₂;N)−ω(q ₂,x ₂) and d(z,h;N)=d(z,y;N)−ω(h,y). If we substitute these into (1), we obtain (2). Finally, we obtain (3) from (2) in the equiprobable case since then α(q ₁,h)=1/2. □

Corollary 5.3

The value d(z,y)−ω(h,y) should lie between the values [d(z,x ₁)−ω(q ₁,x ₁)] and [d(z,x ₂)−ω(q ₂,x ₂)].

We say that the hybrid passes Criterion C2 if (2) from Lemma 5.2 holds, and it passes Criterion C3 if (3) from Lemma 5.2 holds.

5.3 Criterion D. Relationship Among r, x ₁, x ₂, x ₃

In the event of a non-equiprobable hybrid, Lemma 5.4 gives a relationship that most hold among r, x ₁, x ₂, and x ₃.

Lemma 5.4

In the case of a non-equiprobable hybrid (y;x ₁,x ₂,x ₃), we must have that

$$\begin{aligned} d(r,x_1;N)+d(x_2,x_3;N) &< d(r,x_2;N)+d(x_1,x_3;N)\\&= d(r,x_3;N)+d(x_1,x_2;N). \end{aligned} $$

Proof

From Fig. 1, we see that for every parent map p we have that rx ₁|x ₂ x ₃ is a quartet in N _p . Hence,

$$\begin{aligned} d(r,x_1;N_p)+d(x_2,x_3;N_p) &< d(r,x_2;N_p)+d(x_1,x_3;N_p) \\&= d(r,x_3;N_p)+d(x_1,x_2;N_p) \end{aligned} $$

for each p. Taking the weighted sum where N _p is weighted by Pr(p), we obtain the result. □

5.4 Criterion E. Conditions on Signs in the Equiprobable Case

This subsection gives some inequalities that must hold in the equiprobable case.

Let y, x ₁, x ₂ be distinct leaves (and distinct from r). In the equiprobable case for the network M, define

$$\begin{aligned} w_{rv}(M) :=& \bigl(d(r,x_1; M)+d(r,x_2; M)-d(x_1,x_2; M)\bigr)/2 \\ w_{q_1x_1}(M) :=& d(x_1,y; M)-d(r,y; M) +w_{rv}(M) \\ w_{q_2x_2}(M) :=& d(x_2,y; M)-d(r,y; M)+w_{rv}(M) \\ w_{vq_1}(M) :=& d(r,x_1; M)-w_{rv}(M)-w_{q_1x_1}(M) \\ w_{vq_2}(M) :=& d(r,x_2; M)-w_{rv}(M)-w_{q_2x_2}(M) \\ w_{hy}(M) :=& \bigl(d(y,x_1; M)+d(y,x_2; M)-d(x_1,x_2; M)\bigr)/2. \end{aligned}$$

These definitions are made plausible from the diagram of N in Fig. 1. In the diagram from Willson (2012), w _rv (M) is the estimate for the distance between r and v; $w_{q_{1}x_{1}}(N)$ is the estimate for the distance between q ₁ and x ₁; $w_{q_{2}x_{2}}$ is the estimate for d(q ₂,x ₂;N); $w_{vq_{1}}(N)$ estimates d(v,q ₁;N); $w_{vq_{2}}(N)$ estimates d(v,q ₂;N); and w _hy (N) estimates d(h,y;N). We now show that, if the distances are exactly known, then these estimates tell the exact values.

Lemma 5.5

Assume that h is an equiprobable hybrid with parents q ₁ and q ₂. Suppose h has a normal child y which is a leaf. Suppose q ₁ and q ₂ have normal children x ₁ and x ₂ respectively which are leaves. Then the quantities w _rv (N), $w_{q_{1}x_{1}}(N)$, $w_{q_{2}x_{2}}(N)$, $w_{vq_{1}}(N)$, $w_{vq_{2}}(N)$, and w _hy (N) are all positive. Moreover, $d(q_{1},x_{1}) = w_{q_{1}x_{1}}(N)$, $d(q_{2},x_{2}) = w_{q_{2}x_{2}}(N)$, and d(h,y)=w _hy (N).

Proof

Note that for every complementary pair p and p′, if G _p =N _p ∪N _p′ then the network in Fig. 1 depicts part of G _p , where v is the most recent common ancestor of q ₁ and q ₂ in both N _p and N _p′. If w is another vertex distinct from r, y, x ₁, and x ₂, there are three possibilities for the placement of w: it could be attached on the path from r to v, on the path from v to q ₁, or on the path from v to q ₂.

Then in G _p we have the distances determined as follows:

$$\begin{aligned} w_{rv}(G_p) :=& d(r,v;G_p) = \bigl(d(r,x_1;G_p)+d(r,x_2;G_p)-d(x_1,x_2;G_p) \bigr)/2 \\ w_{q_1x_1}(G_p) :=& d(q_1,x_1;G_p) = d(x_1,y;G_p)-d(r,y;G_p) + d(r,v;G_p) \\ w_{q_2x_2}(G_p) :=& d(q_2,x_2;G_p) = d(x_2,y;G_p)-d(r,y;G_p)+d(r,v;G_p) \\ w_{vq_1}(G_p) :=& d(v,q_1;G_p) = d(r,x_1;G_p)-w_{rv}(G_p)-w_{q_1x_1}(G_p) \\ w_{vq_2}(G_p) :=& d(v,q_2;G_p) = d(r,x_2;G_p)-w_{rv}(G_p)-w_{q_2x_2}(G_p) \\ w_{hy}(G_p) :=& d(h,y;G_p) = \bigl(d(y,x_1;G_p)+d(y,x_2;G_p)-d(x_1,x_2;G_p) \bigr)/2 \end{aligned}$$

and all are positive.

By Lemma 4.6 of (Willson 2012) w _rv (N)=∑[W(p)w _rv (G _p ):p∈Par(N),p(h)=q ₁] which is positive since W(p)>0 and w _rv (G _p )>0.

A similar argument proves the other conclusions. The identification of the values for d(q ₁,x ₁), d(q ₂,x ₂), and d(h,y) follows from Willson (2012). □

A choice of (y;x ₁,x ₂) will be said to satisfy Criterion E in the equiprobable case provided that the conclusion of Lemma 5.5 holds.

5.5 Criterion F. Conditions on Signs in the General Case

The material in this subsection is like that for Criterion E, but applies to the general case which is not equiprobable.

For the general case in which the hybrid need not be equiprobable, we assume the existence of x ₃ as in Fig. 1. From Willson (2012), Lemma 4.9, we obtain the following explicit formulas.

Lemma 5.6

Suppose h is hybrid with indegree 2 and parents q ₁ and q ₂. Suppose there is a normal path from q ₁ to x ₁∈X, from q ₂ to x ₂∈X, and from h to y∈X. Assume q ₃ is such that there is a normal path from q ₃ to q ₂, a normal path from q ₃ to x ₃∈X, but no directed path from q ₃ to q ₁. Suppose M is a phylogenetic X-network that is a subnetwork of N. Let

• (a) w _rv (M)=[d(r,x ₁;M)+d(r,x ₃;M)−d(x ₁,x ₃;M)]/2=[d(r,x ₁;M)+d(r,x ₂;M)−d(x ₁,x ₂;M)]/2

• (b) $w_{vq_{3}}(M) = [d(r,x_{3}; M)+d(x_{1},x_{2}; M)-d(r,x_{1}; M)-d(x_{3},x_{2}; M)]/2$

• (c) $w_{q_{3}x_{3}}(M)= [d(r,x_{3}; M)+d(x_{3},x_{2}; M)-d(r,x_{2}; M)]/2$

• (d) w _hy (M)=[d(y,x ₂;M)+d(y,x ₁;M)−d(x ₁,x ₂;M)]/2

• (e) E ₂(M)=d(x ₁,y;M)−d(r,y;M)+w _rv (M)

• (f) E ₄(M)=d(x ₂,y;M)−d(r,y;M)+w _rv (M)

• (g) $\alpha(M) = [2 d(x_{3},y; M) - 2 w_{q_{3}x_{3}}(M) - 2 w_{hy}(M) - d(r,x_{1}; M)+E_{2}(M)+2 w_{rv}(M)+E_{4}(M) - d(r,x_{2}; M) + 2 w_{vq_{3}}(M)] / [4 w_{vq_{3}}(M)]$

• (h) $w_{vq_{1}}(M) = [d(r,x_{1}; M)-E_{2}(M)-w_{rv}(M)] / [2 \alpha(M)]$

• (i) $w_{q_{3}q_{2}}(M) = [ d(x_{3},y; M) - w_{q_{3}x_{3}}(M) - w_{hy}(M) - \alpha(M) (w_{vq_{3}}(M)+ w_{vq_{1}}(M)) ] / (1-\alpha(M))$

• (j) $w_{q_{1}x_{1}}(M) = d(r,x_{1}; M) - w_{rv}(M) - w_{vq_{1}}(M)$

• (k) $w_{q_{2}x_{2}}(M)= d(r,x_{2}; M)-w_{rv}(M)-w_{vq_{3}}(M)-w_{q_{3},q_{2}}(M)$

• (l) $C(M) = 2 d(x_{3},y;M) - 2 w_{q_{3}x_{3}}(M) - 2 w_{hy}(M) -d(r,x_{1};M)+E_{2}(M)+2 w_{rv}(M)+E_{4}(M) - d(r,x_{2}; M) + 2 w_{vq_{3}}(M)$

• (m) $D(M) = 4 w_{vq_{3}}(M)$.

Then

• (i) α(q ₁,h;N)=α(N)=C(N)/D(N).

• (ii) $d(q_{1},x_{1}; N) = w_{q_{1}x_{1}}(N)$.

• (iii) $d(q_{2}, x_{2}; N) = w_{q_{2}x_{2}}(N)$.

Indeed, w _rv (N), $w_{vq_{1}}(N)$, $w_{q_{1}x_{1}}(N)$, w _hy (N), $w_{vq_{3}}(N)$, $w_{q_{3}x_{3}}(N)$, $w_{q_{3}q_{2}}(N)$, $w_{q_{2}x_{2}}(N)$, and α(N) estimate the respective quantities d(r,v;N), d(v,q ₁;N), d(q ₁,x ₁;N), d(h,y;N), d(v,q ₃;N), d(q ₃,x ₃;N), d(q ₃,x ₂;M), α(q ₁,h;N) and give the exact values when the hypotheses are satisfied.

Lemma 5.7

In the general case, the quantities w _rv (N), $w_{vq_{1}}(N)$, $w_{q_{1}x_{1}}(N)$, w _hy (N), avq ₃(N), aq ₃ x ₃(N), aq ₃ q ₂(N), $w_{q_{2}x_{2}}(N)$ of Lemma 5.6 are all positive. Moreover, 0<α(q ₁,h;N)<1.

The proof is similar to that of Lemma 5.5.

A choice of (y;x ₁,x ₂) with x ₃ will be said to satisfy Criterion F provided that the conclusion of Lemma 5.7 holds.

5.6 Summary of the Test for a Hybrid

Suppose we are given the tree-average distances for N. Using Theorem 4.5, we may eliminate all cherries. Hence, we may assume that there are no cherries. By Theorem 3.2, there exists a hybrid vertex h with parents q ₁ and q ₂ such that h has a child y which is a leaf, q ₁ has a child x ₁ which is a leaf, and q ₂ has a child x ₂ which is a leaf. We consider all possibilities for y, x ₁ and x ₂. For each choice of (y,x ₁,x ₂), we perform the following checks:

• (i) equiprobable(y,x ₁,x ₂): The choice passes the test provided it passes Criteria B, C3, and E.

• (ii) general(y,x ₁,x ₂): Consider all possible x ₃∈X distinct from y, x ₁, x ₂. The choice of (y,x ₁,x ₂) with x ₃ passes the test provided that it passes Criteria B, C2, D, and F. In checking Criterion C2, we utilize the formulas of Lemma 5.6 to estimate ω(h,y), ω(q ₁,x ₁), ω(q ₂,x ₂), and α(q ₁,h); note α(q ₂,h)=1−α(q ₁,h).

We accept any (y,x ₁,x ₂) that passes either (i) or (ii).

6 Proof that the Algorithm Works if There Is Only One Reticulation Cycle

The main theorem of this paper is the following result.

Theorem 6.1

Suppose the phylogenetic network N=(V,A,r,X) satisfies Assumptions 3.1. Assume N has a single reticulation cycle and has its exact tree-average distances known. Then N is reconstructed by the algorithm from its tree-average distances.

By Theorem 4.5, we may recognize any cherry that occurs in N and remove it by following the method described in Sect. 3. Hence, we may assume that N has no cherries. Then N appears as in Fig. 4 (possibly with some vertices deleted).

Fig. 4

The reality when there is a single reticulation cycle to hybrid h and there are no cherries. Here the parents of h are q ₁ and q ₂. Moreover, h, q ₁, and q ₂ have respectively normal children y, x ₁, x ₂ in X

Suppose that the hybrid h has normal child y∈X and parents q ₁ and q ₂ with respective normal children x ₁ and x ₂ in X. We say A(v;v ₁,v ₂) is true if v=y, v ₁=x ₁, v ₂=x ₂ passes Criterion B. In other words, for w∈X let W _v (N)=d(w,v;N)+d(v ₁,v ₂;N), $W_{v_{1}}(N) = d(w,v_{1};N)+d(v,v_{2};N)$, $W_{v_{2}}(N) = d(w,v_{2};N) + d(v,v_{1};N)$. Then A(v;v ₁,v ₂) is true iff for all w∈X other than v, v ₁, v ₂ we have both $W_{v_{1}}(N) < W_{v}(N)$ and $W_{v_{2}}(N) < W_{v}(N)$. By Lemma 5.1, A(y;x ₁,x ₂) is true. Note that by symmetry, A(a;b,c) is true if and only if A(a;c,b) is true.

Observe that we are interested only in possibilities for a, b, c in X such that A(a;b,c) is true and also such that a, b, c are all possibilities for being children of a hybrid and the parents of a hybrid. Consequently, none of a, b, c can be the root r. On the other hand, w in the test could possibly equal r.

Lemma 6.2

Suppose A(a;b,c) is true. Then for all e∈X, e∉{a,b,c} both A(a;b,e) and A(a;e,c) are false.

Proof

If A(a;b,e) is true, then choosing w=c we have d(c,b)+d(a,e)<d(a,c)+d(b,e). But since A(a;b,c) is true, then choosing w=e yields d(e,b)+d(a,c)<d(e,a)+d(b,c), a contradiction. Hence, A(a;b,e) is false. A symmetric argument shows A(a;e,c) is false. □

Lemma 6.3

Suppose there is a 4-set {a,b,c,e} such that for all parent maps p, the same quartet tree is in N _p . Then A(a;b,c) is false.

Proof

Suppose that the common quartet tree is uv|xy for a permutation u, v, x, y of a, b, c, e. Then d(u,v)+d(x,y)<d(u,x)+d(v,y)=d(u,y)+d(v,x). But if A(a;b,c) is true then there is a unique strict maximum among the three quantities d(a,b)+d(c,e), d(a,c)+d(b,e), d(a,e)+d(b,c), a contradiction. □

Lemma 6.4

Suppose there is a subset S of X such that |S|≥4 and for all parent maps p, the restriction N _p |S is the same tree. Then for {a,b,c}⊆S, A(a;b,c) is false.

Proof

Since |X|≥4 we may suppose w∈S−{a,b,c}. Then for all p, the trees N _p induce the same quartet on the 4-set {a,b,c,w}. By Lemma 6.3, A(a;b,c) is false. □

Lemma 6.5

Assume that for a nonempty collection of parent maps p, we have wx|yz in N _p and for a nonempty collection of parent maps p we have wy|xz in N _p but there is no parent map p such that in N _p we have wz|xy. Then A(y;x,z), A(y;z,x), A(x;y,z), and A(x;z,y) are false.

Briefly, Lemma 6.5 assumes that for the 4-set {w,x,y,z} exactly two quartet trees appear in the various N _p , including wy|xz. The lemma asserts that A(y;x,z), A(y;z,x), A(x;y,z), and A(x;z,y) are false. This leaves open the possibility that A(z;x,y) is true.

Proof

Let P ₁⊂Par(N) be the set of p such that wx|yz in N _p , and let P ₂ be the set of p such that wy|xz in N _p . Then Par(N)=P ₁∪P ₂ since the other quartet never occurs.

For p∈P ₁,

$$\begin{aligned} d(w,x;N_p) + d(y,z;N_p) &< d(w,y;N_p)+d(x,z;N_p) \\&= d(w,z;N_p)+d(x,y;N_p). \end{aligned} $$

For p∈P ₂,

$$\begin{aligned} d(w,y;N_p) + d(x,z;N_p) & < d(w,x;N_p)+d(y,z;N_p) \\& = d(w,z;N_p)+d(x,y;N_p). \end{aligned} $$

Taking the weighted sums, it follows

$$\begin{aligned} & \sum\bigl[\Pr(p) d(w,y;N_p): p \in P_2\bigr] + \sum \Pr(p) d(x,z;N_p) p \in P_2\bigr] \\ &\quad < \sum\bigl[\Pr(p) d(w,z;N_p): p \in P_2\bigr] + \sum\bigl[\Pr(p) d(x,y;N_p): p \in P_2\bigr]. \end{aligned} $$

Add to each side ∑[Pr(p)d(w,y;N _p ):p∈P ₁]+∑[Pr(p)d(x,z;N _p ):p∈P ₁].

We obtain

$$\begin{aligned} & \sum\bigl[\Pr(p) d(w,y;N_p): p \in P_2\bigr] + \sum \Pr(p) d(x,z;N_p) p \in P_2\bigr] \\ &\qquad {}+ \sum\bigl[\Pr(p) d(w,y;N_p): p \in P_1\bigr] + \sum\bigl[\Pr(p) d(x,z;N_p): p \in P_1\bigr] \\ &\quad < \sum\bigl[\Pr(p) d(w,z;N_p): p \in P_2\bigr] + \sum\bigl[\Pr(p) d(x,y;N_p): p \in P_2\bigr] \\ &\qquad {}+ \sum\bigl[\Pr(p) d(w,y;N_p): p \in P_1\bigr] + \sum\bigl[\Pr(p) d(x,z;N_p): p \in P_1\bigr]. \end{aligned}$$

But the left side

$$\begin{aligned} & = \Bigl[\sum\bigl[\Pr(p) d(w,y;N_p): p \in P_1\bigr] +\sum\bigl[\Pr(p) d(w,y;N_p): p \in P_2\bigr]\Bigr] \\ &\quad {} + \Bigl[\sum\bigl[\Pr(p) d(x,z;N_p): p \in P_1\bigr] + \sum \Pr(p) d(x,z;N_p): p \in P_2\Bigr] \Bigr] \\ &= d(w,y;N)+d(x,z;N) \end{aligned} $$

and the right side

$$\begin{aligned} & = \Bigl[\sum\bigl[\Pr(p) d(w,z;N_p): p \in P_2\bigr] + \sum\bigl[\Pr(p) d(x,y;N_p): p \in P_2\bigr] \Bigr] \\ &\quad {}+\Bigl[ \sum\bigl[\Pr(p) d(w,z;N_p): p \in P_1\bigr] + \sum\bigl[\Pr(p) d(x,y;N_p): p \in P_1\bigr]\Bigr] \\ & = d(w,z;N) + d(x,y;N). \end{aligned} $$

Hence, d(w,y;N)+d(x,z;N)<d(w,z;N)+d(x,y;N). Yet if A(y;x,z) is true then d(w,z;N)+d(x,y;N)<d(w,y;N)+d(x,z;N), a contradiction. Thus, A(y;x,z) is false, and equivalently A(y;z,x) is false.

If we interchange x and y we obtain by symmetry that A(x;y,z) and A(x;z,y) are false. □

Note that Lemma 6.5 may be contrasted with Lemma 5.1, which says that if for all w, wx|yz in some N _p and wz|xy in some N _p but never wy|xz then A(y;x,z) is true.

Lemma 6.6

Suppose that N=(V,A,r,X) satisfies that A(y ₁;x ₁₁,x ₁₂),A(y ₁;x ₁₂,x ₁₁),A(y ₂;x ₂₁,x ₂₂),A(y ₂;x ₂₁,x ₂₁),…,A(y _k ;x _k1,x _k2),A(y _k ;x _k2,x _k1) are the only acceptances that are true. Form N′=(V′,A′,r,X′) by picking a leaf z∈X and replacing it by a cherry {z ₁,z ₂}. (Thus, we add z ₁, z ₂, and arcs (z,z ₁), (z,z ₂), with positive weights, removing z from X but adding z ₁ and z ₂ to make X′.) Then in N′ the following hold:

• (i) If there is no i such that z is y _i or x _i1 or x _i2, then A(y _i ;x _i1,x _i2) and A(y _i ;x _i2,x _i1) remain true in N′.

• (ii) Suppose A(a;b,c) is true in N′. Then {a,b,c}⊂X−{z}, so none of a, b, c is z ₁ or z ₂.

Proof

Note that for each u∈X, d(u,z ₁)=d(u,z)+ω(z,z ₁) and d(u,z ₂)=d(u,z)+ω(z,z ₂) by the construction.

(i) Suppose z is not y _i or x _i1 or x _i2. In N we have A(y _i ;x _i1,x _i2) is true. Hence for every w∈X other than y _i , x _i1, x _i2 we have

$$\begin{aligned} & d(w,x_{i1};N)+d(y_i, x_{i2};N) < d(w,y_i;N)+d(x_{i1},x_{i2};N) \\ & d(w, x_{i2};N) + d(y_i, x_{i1};N) < d(w,y_i;N) + d(x_{i1},x_{i2};N). \end{aligned} $$

In N′, for each w≠z ₁,z ₂ the same inequalities will still hold. I claim the same inequalities also hold for w=z ₁ or z ₂. To see this note that choosing w=z yields

$$\begin{aligned} & d(z,x_{i1};N)+d(y_i, x_{i2};N) < d(z,y_i;N)+d(x_{i1},x_{i2};N)\quad \mbox{and} \\ & d(z, x_{i2};N) + d(y_i, x_{i1};N) < d(z,y_i;N) + d(x_{i1},x_{i2};N). \end{aligned} $$

Hence, when we add ω(z,z ₁) to each side, we obtain

$$\omega(z,z_1) + d(z,x_{i1};N)+d(y_i, x_{i2};N) < \omega(z, z_1) + d(z,y_i;N)+d(x_{i1},x_{i2};N) $$

and

$$\omega(z,z_1) + d(z, x_{i2};N) + d(y_i, x_{i1};N) < \omega(z,z_1) + d(z,y_i;N) + d(x_{i1},x_{i2};N). $$

Hence, d(z ₁,x _i1;N′)+d(y _i ,x _i2;N′)<d(z ₁,y _i ;N′)+d(x _i1,x _i2;N′) and d(z ₁,x _i2;N′)+d(y _i ,x _i1;N′)<d(z ₁,y _i ;N′)+d(x _i1,x _i2;N′) so A(y _i ;x _i1,x _i2) is true in N′. The same argument shows A(y _i ;x _i2,x _i1) is true in N′.

(ii) Suppose A(a;b,c) is true in N′. I claim that {a,b,c}⊂X−{z}, so none of a, b, c is z ₁ or z ₂.

Case 1. Suppose a=z ₁ so A(z ₁;b,c) in N′ and neither b nor c equals z ₂. Then for all w, d(w,b)+d(z ₁,c)<d(w,z ₁)+d(b,c) and d(w,c)+d(z ₁,b)<d(w,z ₁)+d(b,c). In particular, if w=z ₂, then d(z ₂,b)+d(z ₁,c)<d(z ₂,z ₁)+d(b,c) and d(z ₂,c)+d(z ₁,b)<d(z ₂,z ₁)+d(b,c). But relating distances to z ₂ and z ₁ we have ω(z,z ₂)+d(z,b)+ω(z,z ₁)+d(z,c)<ω(z,z ₂)+ω(z,z ₁)+d(z,z)+d(b,c) and ω(z,z ₂)+d(z,c)+ω(z,z ₁)+d(z,b)<ω(z,z ₂)+ω(z,z ₁)+d(z,z)+d(b,c).

Hence, d(z,b)+d(z,c)<d(b,c) which contradicts the triangle inequality, shown to be true in Willson (2012).

Case 2. Suppose a=z ₁ so A(z ₁;b,c) in N′ and b=z ₂, so A(z ₁;z ₂,c) is true in N′. Then for all w∈X−{z}, d(w,z ₂)+d(z ₁,c)<d(w,z ₁)+d(z ₂,c) and d(w,c)+d(z ₁,z ₂)<d(w,z ₁)+d(z ₂,c). Substituting d(w,z ₂)=d(w,z)+ω(z,z ₂) etc. we obtain ω(z,z ₂)+d(w,z)+d(z,c)+ω(z,z ₁)<d(w,z)+ω(z,z ₁)+d(z,c)+ω(z,z ₂) and d(w,c)+d(z,z)+ω(z,z ₁)+ω(z,z ₂)<d(w,z)+ω(z,z ₁)+d(z,c)+ω(z,z ₂). Hence, d(w,z)<d(w,z) contradicting that d is a metric, shown in Willson (2012).

It follows that a cannot be z ₁, and a symmetric argument shows a≠z ₂.

Case 3. Suppose a∉{z ₁,z ₂} but b=z ₁, c≠z ₂ yet A(a;z ₁,c) is true. Then for all w, d(w,z ₁)+d(a,c)<d(w,a)+d(z ₁,c) and d(w,c)+d(z ₁,a)<d(w,a)+d(z ₁,c). In particular, for w=z ₂, d(z ₂,,z ₁)+d(a,c)<d(z ₂,a)+d(z ₁,c) and d(z ₂,c)+d(z ₁,a)<d(z ₂,a)+d(z ₁,c).

Thus, ω(z,z ₂)+ω(z,z ₁)+d(a,c)<d(z,a)+d(z,c)+ω(z,z ₂)+ω(z,z ₁) and ω(z,z ₂)+ω(z,z ₁)+d(z,c)+d(z,a)<d(z,a)+d(z,c)+ω(z,z ₂)+ω(z,z ₁).

This shows that d(a,c)<d(z,a)+d(z,c) and d(z,c)+d(z,a)<d(z,a)+d(z,c) so 0<0, a contradiction.

Case 4. Suppose a∉{z ₁,z ₂} but b=z ₁, c=z ₂ and A(a;z ₁,z ₂) is true. Then for w distinct from z ₁, z ₂, and a, we have d(w,z ₁)+d(z ₂,a)<d(w,a)+d(z ₁,z ₂) and d(w,z ₂)+d(z ₁,a)<d(w,a)+d(z ₁,z ₂).

Since d(w,z ₁)=d(w,z)+ω(q,z ₁), it follows that ω(z,z ₁)+ω(z,z ₂)+d(w,z)+d(z,a)<ω(z,z ₁)+ω(z,z ₂)+d(w,a) and ω(z,z ₁)+ω(z,z ₂)+d(w,z)+d(z,a)<ω(z,z ₁)+ω(z,z ₂)+d(w,a). Hence d(w,z)+d(z,a)<d(w,a) and d(w,z)+d(z,a)<d(w,a) contradicting the triangle inequality. This completes the proof of (ii). □

Lemma 6.7

Assume the hypotheses of Lemma 6.6 and the construction of N′. If z=y _i , then A(z;x _i1,x _i2) is meaningless for N′ since z∉X′. Moreover, A(z ₁;x _i1,x _i2) and A(z ₂;x _i1,x _i2) are false for N′. Similarly, if z=x _i1 so A(y _i ;z,x _i2) is true in N, then A(y _i ;z,x _i2) is meaningless in N′, while A(y;z ₁,x _i2) is false in N′.

Proof

Suppose z=y _i . Since A(z;x _i1,x _i2) is true for every w∈X other than y _i =z, x _i1, x _i2 we have

$$\begin{aligned} & d(w,x_{i1};N)+d(z, x_{i2};N) < d(w,z;N)+d(x_{i1},x_{i2};N)\quad \mbox{and} \\ & d(w, x_{i2};N) + d(z, x_{i1};N) < d(w,z;N) + d(x_{i1},x_{i2};N). \end{aligned} $$

I claim that A(z ₁;x _i1,x _i2) is false. Adding ω(z,z ₁) to the above yields that for w∈X other than z, x _i1, x _i2 we have

$$\begin{aligned} & d(w,x_{i1};N)+\omega(z,z_1)+d(z, x_{i2};N) < d(w,z;N)+\omega (z,z_1)+d(x_{i1},x_{i2};N)\\ & d(w, x_{i2};N) + d(z, x_{i1};N)+\omega(z,z_1) < d(w,z;N)+\omega(z,z_1) + d(x_{i1},x_{i2};N). \end{aligned} $$

Hence,

$$\begin{aligned} & d\bigl(w,x_{i1};N'\bigr)+d \bigl(z_1, x_{i2};N'\bigr) < d \bigl(w,z_1;N'\bigr)+d\bigl(x_{i1},x_{i2};N' \bigr)\quad \mbox{and} \\ & d\bigl(w, x_{i2};N'\bigr) + d\bigl(z_1, x_{i1};N'\bigr) < d\bigl(w,z_1;N' \bigr) + d\bigl(x_{i1},x_{i2};N'\bigr). \end{aligned} $$

The only remaining issue is whether the same is true for w=z ₂. We ask whether

$$\begin{aligned} & d\bigl(z_2,x_{i1};N'\bigr)+d \bigl(z_1, x_{i2};N'\bigr) < d \bigl(z_2,z_1;N'\bigr)+d\bigl(x_{i1},x_{i2};N' \bigr)\quad \mbox{and} \\ & d\bigl(z_2, x_{i2};N'\bigr) + d \bigl(z_1, x_{i1};N'\bigr) < d \bigl(z_2,z_1;N'\bigr) + d \bigl(x_{i1},x_{i2};N'\bigr). \end{aligned} $$

But d(z ₂,z ₁)=ω(z,z ₁)+ω(z,z ₂) and d(z ₂,x _i1;N′)=d(z,x _i1;N′)+ω(z,z ₂). Hence, these inequalities would imply

$$\begin{aligned} & d(z,x_{i1};N)+\omega(z,z_2)+d(z, x_{i2};N) + \omega(z,z_1)\\ &\quad < \omega (z,z_1)+\omega(z,z_2)+d(x_{i1},x_{i2};N)\quad \mbox{and}\\ & \omega(z,z_2)+d(z, x_{i2};N) + \omega(z,z_1)+d(z, x_{i1};N) \\ &\quad < \omega(z,z_1)+\omega(z,z_2) + d(x_{i1},x_{i2};N). \end{aligned} $$

But then we obtain d(z,x _i1;N)+d(z,x _i2;N)<d(x _i1,x _i2;N) and d(z,x _i2;N)+d(z,x _i1;N)<d(x _i1,x _i2;N), which violates the triangle inequality. Hence, A(z ₁;x _i1,x _i2) is false. A symmetric argument shows A(z ₂;x _i1,x _i2) is false.

A similar argument applies if z=x _i1 or x _i2. The lemma follows. □

We now give the proof of Theorem 6.1. We are assuming there are no cherries. See Fig. 4.

Since there is a single reticulation cycle, if h and y are removed, then we obtain a tree T. Consider the path P ₁ in T from the root r to x ₁ and the path P ₂ from r to x ₂. These paths diverge at a point v (possibly v=r). Suppose x is a leaf other than y, x ₁, or x ₂. Then the path from r to x in T must depart from P ₁∪P ₂ at a point w, whence there is a path P _x from w to x disjoint from P ₁∪P ₂ except for w. But a path from w that starts along P _x toward x and has a maximal number of arcs must end at a leaf with parent q; and if this maximal length is greater than one, then the other child of q must also be a leaf by maximality. Since neither can be hybrid (since h is the only hybrid), it follows that if the maximal path from w in that direction has length greater than one, then N has a cherry, a contradiction. It follows that x is a leaf with parent w.

It is possible that h is equiprobable. It is also possible that q ₂ has an ancestor q ₃ such that there is a normal path from q ₃ to q ₂ and there is no path from q ₃ to q ₁, and there is a normal path from q ₃ to x ₃∈X that is disjoint from the normal path to q ₂ except for q ₃. In either situation, if we can correctly identify y, x ₁, x ₂ and α(q ₁,h), then we may remove the correct hybrid. Once this has occurred, there are no more hybrid vertices and successive identification of cherries may take place. Hence, the theorem is true provided we can correctly identify y, x ₁, x ₂, and α(q ₁,h). Of course, in either case the correct choice satisfies the criteria of Sect. 5. Hence, we must show that there is no false signal to accept a different choice.

Write A(v;v ₁,v ₂,α) if the algorithm accepts the hybrid h′ as having child v and parents q ₁ and q ₂ with respective normal children v ₁ and v ₂ in X, with α(q ₁,h′)=α. Clearly, if A(v;v ₁,v ₂) is false, then for all α, A(v;v ₁,v ₂,α) is false.

The proof of Theorem 6.1 will involve a sequence of claims.

Claim 1

Suppose none of v, v ₁, v ₂ is y. Then A(v;v ₁,v ₂) is false.

Proof

Let S=X−{y}. Then Lemma 6.4 applies since {v,v ₁,v ₂}⊆S. □

Hence, if A(v;v ₁,v ₂) is true then one of v, v ₁, v ₂ is y.

Claim 2

Suppose A(y;x ₁,v) is true. Then v=x ₂.

Proof

Since A(y;x ₁,x ₂) is true, then by Lemma 6.2 for v≠x ₂ we must have that A(y;x ₁,v) is false. □

Similarly, we have the following.

Claim 3

Suppose A(y;x ₂,v) is true. Then v=x ₁.

Claim 4

If {u ₁,u ₂} is disjoint from {x ₁,x ₂}, then A(y;u ₁,u ₂) is false.

Proof

Let T=N with h removed as well as all arcs involving h, so T is a directed tree. See Fig. 4. Note that if p(h)=q ₁ then N _p consists of T with x ₁ replaced by a cherry {x ₁,y}, while if p′(h)=q ₂ the N _p′ consists of T with x ₂ replaced by a cherry {x ₂,y}. All leaves other than x ₁ and x ₂ have their parent on the path P ₁ or P ₂. In particular, u ₁ and u ₂ are situated in this manner. The vertex where P ₁ and P ₂ diverge is denoted v.

We analyze 7 cases.

Case 1. Suppose u ₁ and u ₂ both branch off the path from r to v. Then the quartet for {u ₁,u ₂,y,x ₁} in N _p is always u ₁ u ₂|yx ₁. Hence, A(y;u ₁,u ₂) is false by Lemma 6.3.

Case 2. Suppose u ₁ branches off the path from r to v but u ₂ branches off the path from v to x ₂. If p(h)=q ₁ then the quartet for {u ₁,u ₂,y,x ₁} in N _p is u ₁ u ₂|yx ₁, while if p′(h)=q ₂ then the quartet in N _p′ is yu ₂|u ₁ x ₁. Hence, by Lemma 6.5 with w=x ₁, A(y;u ₁,u ₂) is false.

Case 3. Suppose u ₁ branches off the path from r to v but u ₂ branches off the path from v to x ₁. An argument symmetric to that of Case 2 with w=x ₂ yields a contradiction.

Case 4. Suppose u ₂ branches off the path from r to v but u ₁ branches off the path from v to x ₂. An argument symmetric to that of Case 2 yields a contradiction.

Case 5. Suppose u ₂ branches off the path from r to v but u ₁ branches off the path from v to x ₁. An argument symmetric to that of Case 3 yields a contradiction.

Case 6. Suppose u ₁ and u ₂ both branch off the path from v to x ₁. By symmetry we may assume that the branch for u ₁ is closer to r than the branch for u ₂. Let w=x ₁ and consider the quartets for {x ₁,y,u ₁,u ₂}. If p(h)=q ₁ then N _p has the quartet x ₁ y|u ₁ u ₂ while if p′(h)=q ₂ then N _p′ has the quartet x ₁ u ₂|u ₁ y. Hence, by Lemma 6.5, A(y;u ₁,u ₂) is false.

Case 7. Suppose u ₁ and u ₂ both branch off the path from v to x ₂. An argument symmetric to Case 6 yields a contradiction.

This completes the proof of Claim 4. □

It follows from Claims 2, 3, and 4 that if A(v;u ₁,u ₂) is true, then either the correct hybrid is found via v=y; {u ₁,u ₂}={x ₁,x ₂} or else we may assume u ₁=y. We must eliminate the possibility that u ₁=y.

Claim 5

Suppose A(k;y,u) is true. Then k=x ₁ or x ₂.

Proof

As with Claim 4, the proof considers 7 cases.

Case 1. Suppose k and u both branch off the path from r to v. Then for all parent maps p, N _p has the quartet x ₁ y|uk. Hence, A(k;y,u) is false by Lemma 6.3.

Case 2. Suppose k and u both branch off the path from v to x ₁, k≠x ₁, u≠x ₁, k further from r than is u. Let w=x ₁. If p(h)=q ₁ then N _p has the quartet yx ₁|ku and if p′(h)=q ₂ then N _p′ has the quartet x ₁ k|yu. Hence, by Lemma 6.5, A(k;y,u) is false.

Case 3. Suppose k and u both branch off the path from v to x ₁, k≠x ₁, u≠x ₁, k closer to r than is u. Let w=x ₂. If p(h)=q ₁ then N _p has the quartet yu|kx ₂ and if p′(h)=q ₂ then N _p′ has the quartet ku|yx ₂. By Lemma 6.5, A(k;y,u) is false.

Case 4. Suppose k and u both branch off the path from v to x ₂, k≠x ₂, u≠x ₂, k further from r than is u. Then A(k;y,u) is false by an argument symmetric to Case 2.

Case 5. Suppose k and u both branch off the path from v to x ₂, k≠x ₂, u≠x ₂, k closer to r than is u. Then A(k;y,u) is false by an argument symmetric to the proof of Case 3.

Case 6. Suppose k branches off the path from v to x ₁, k≠x ₁, while u branches off the path from v to x ₂, u≠x ₂. Then A(k;y,u) is false. To see this, let w=x ₁. If p(h)=q ₁ then N _p has the quartet yx ₁|ku and if p′(h)=q ₂ then N _p′ has the quartet x ₁ k|yu. By Lemma 6.5, A(k;y,u) is false.

Case 7. Suppose k branches off the path from v to x ₂, k≠x ₂, while u branches off the path from v to x ₁, u≠x ₁. Then A(k;y,u) is false by an argument symmetric to Case 6.

This completes the proof of Claim 5. □

As a result of Claim 5, the only possible accepted false hybrids are A(x ₁;y,u) or A(x ₂;y,u). Since the cases are symmetric, we will study only the possibility of A(x ₂;y,u).

Claim 6

Suppose the attachment point of u lies on the path from v to x ₁. Then A(x ₂;y,u) is false.

Proof

Let w=r. We consider the 4-set {x ₂,y,u,r}. If p(h)=q ₁ then we obtain rx ₂|yu. If p′(h)=q ₂ then we obtain ru|yx ₂. By Lemma 6.5, A(x ₂;y,u) is false. □

Claim 7

Suppose the attachment point of u lies on the path from r to v. Then A(x ₂;y,u) is false.

Proof

Note that u≠r. Consider the quartet {r,x ₂,y,u}. For every parent map p, N _p displays ru|x ₂ y. Hence, A(x ₂;y,u) is false by Lemma 6.3. □

If A(x ₂;y,u) is true, it follows that the attachment point of u lies on the path from v to x ₂. The next claim shows that this attachment point must be the parent of q ₂.

Claim 8

Suppose A(x ₂;y,u) is true. If the parent of x ₂ is q ₂, then the parent q ₃ of q ₂ satisfies that q ₃ is not ≤q ₁, and u=x ₃ is the other child of q ₃ besides q ₂.

Proof

Suppose first that the parent q ₃ of q ₂ satisfies that q ₃ is not ≤q ₁ and that x ₃≠u is the other child of q ₃. Let w=x ₃. We consider the quartet for {x ₂,y,x ₃,u}. If p(h)=q ₁, then the quartet tree is x ₃ x ₂|yu; if p′(h)=q ₂ then the quartet is x ₃ u|yx ₂. Hence, A(x ₂;y,u) is false by Lemma 6.5.

Now suppose that the parent of q ₂ is v≤q ₁ (so no x ₃ exists). Then u must satisfy the hypotheses of either Claim 6 or Claim 7, and then that claim would lead to a contradiction. Thus, this case cannot occur. □

It follows that the only other possibility besides the correct A(y;x ₁,x ₂) is that A(x ₂;y,x ₃) holds (or a symmetric case A(x ₁;y,x ₀) where the parent of x ₀ is the grandparent of x ₁). The proofs above show that Lemma 5.1 (Criterion B) eliminates all other possibilities. In fact, A(x ₂;y,x ₃) is consistent with Lemma 5.1. To see this, if w≠y, x ₂, x ₃, then if p(h)=q ₁ we have wy|x ₂ x ₃ in N _p , while if p′(h)=q ₂ then N _p′ displays wx ₃|yx ₂, the same predictions as A(x ₂;y,x ₃). Hence other criteria besides Criterion B are now needed.

Claim 9

A(x ₂;y,x ₃,1/2) is false. More specifically, the equiprobable case is eliminated by Criterion C.

Proof

Suppose in a network M , x ₂ is the child of a hybrid, while y and x ₃ are the normal children of the parents of the hybrid, yet the tree-average distances are those given for N. See Fig. 5 for two possibilities M ₁ and M ₂ for M.

Fig. 5

Networks M ₁ or M ₂ might suggest that A(x ₂;y,x ₃,α) is true

We test whether M could pass the tests as an equiprobable hybrid. This would require by Criterion C, that for any z,

$$d(z,x_2) - \omega(h,y) = (1/2) \bigl[d(z,y) - \omega(q_1,x_1) \bigr] + (1/2) \bigl[d(z,x_3)-\omega(q_2,x_2) \bigr]. $$

Moreover, by Lemma 5.5 we have

$$\begin{aligned} & w_{rv}(M) = \bigl(d(r,y)+d(r,x_3)-d(y,x_3) \bigr)/2 \\ & \omega(q_1,x_1) = w_{q_1x_1}(M) := d(y,x_2)-d(r,x_2) +w_{rv}(M) \\ & \omega(q_2,x_2) = w_{q_2x_2}(M):= d(x_3,x_2)-d(r,x_2)+w_{rv}(M) \\ & \omega(h,y) = w_{hy}(M):= \bigl(d(x_2,y)+d(x_2,x_3)-d(y,x_3) \bigr)/2. \end{aligned}$$

This simplifies to

$$2 d(z,x_2) +d(r,y) + d(r,x_3) = d(z,y) +2 d(r,x_2) + d(z,x_3) . $$

To check whether this equation holds, we substitute the true values obtained from N.

$$\begin{aligned} & d(r,y) = d(r,v)+\omega(h,y)+(1/2)d(v,q_1)+(1/2)d(v,q_3)+(1/2)\omega(q_3,q_2)\\ & d(r,x_3) = d(r,v)+d(v,q_3)+\omega(q_3,x_3)\\ & d(r,x_2)= d(r,v)+d(v,q_3)+\omega(q_3,q_2)+\omega(q_2,x_2). \end{aligned} $$

This leads to 2d(z,x ₂)+d(r,v)+ω(h,y)+(1/2)d(v,q ₁)+(1/2)d(v,q ₃)+(1/2)ω(q ₃,q ₂)+d(r,v)+d(v,q ₃)+ω(q ₃,x ₃)=d(z,y)+2d(r,v)+2d(v,q ₃)+2ω(q ₃,q ₂)+2ω(q ₂,x ₂)+d(z,x ₃).

This must hold for all z∈X distinct from x ₂, y, x ₃, in particular for z=x ₁. The true values are d(x ₁,x ₂)=ω(q ₁,x ₁)+d(v,q ₁)+d(v,q ₃)+ω(q ₃,q ₂)+ω(q ₂,x ₂), d(x ₁,y)=ω(q ₁,x ₁)+ω(h,y)+(1/2)d(v,q ₁)+(1/2)d(v,q ₃)+(1/2)ω(q ₃,q ₂), d(x ₁,x ₃)=ω(q ₁,x ₁)+d(v,q ₁)+d(v,q ₃)+ω(q ₃,x ₃).

When these values are substituted, the equation simplifies to d(v,q ₁)=0, which contradicts Assumption A(3).

Hence, A(x ₂;y,x ₃,1/2) is false since it fails Criterion C under the assumption that the hybrid is equiprobable. □

There remains only the possibility that A(x ₂;y,x ₃,α) is true, where α≠1/2, and in reality the attachment point of x ₃ is the parent of x ₂.

Claim 10

If α≠1/2, then A(x ₂;y,x ₃,α) is false.

Proof

Suppose that A(x ₂;y,x ₃,α) is true. Since α≠1/2, there must be an ancestor of the hybrid on one side of the reticulation cycle with a normal child u in X. Thus, we assume that one of M ₁ and M ₂ in Fig. 5 passes all the tests for being a hybrid with child x ₂.

If M ₁ is true, then for every p, N _p must display r,x ₃|u,y by Criterion D. Hence, d(r,x ₃)+d(u,y)<d(r,u)+d(x ₃,y)=d(r,y)+d(u,x ₃). If u attaches between v and x ₁, then when p(h)=q ₁ it follows that N _p displays uy|rx ₃ while when p′(h)=q ₂ then N _p′ displays ur|yx ₃ whence by Lemma 4.3 we cannot have d(r,x ₃)+d(u,y)<d(r,u)+d(x ₃,y)=d(r,y)+d(u,x ₃). If u attaches between r and v then for all p, N _p displays ru|yx ₃, whence d(r,u)+d(y,x ₃)<d(r,y)+d(u,x ₃)=d(r,x ₃)+d(u,y), a contradiction. Finally, if u attaches between v and x ₂ then when p(h)=q ₁, N _p displays ux ₃|ry while when p′(h)=q ₂, N _p′ displays yx ₃|ru; hence, by Lemma 4.3, we cannot have d(r,x ₃)+d(u,y)<d(r,u)+d(x ₃,y)=d(r,y)+d(u,x ₃). Hence, in every case, Criterion D fails, so in the event of M ₁, A(x ₂;y,x ₃,α) is false.

Hence, we must assume that M ₂ depicts the assumed situation. In this situation, there is no path from q ₃ to q ₁, but there is a normal path from q ₃ to q ₂. It need not be the case that q ₃ is actually a parent of q ₂.

Note that if M ₂ is true, then for every p, N _p must display ry|ux ₃. Hence, d(r,y)+d(u,x ₃)<d(r,u)+d(y,x ₃)=d(r,x ₃)+d(u,y). But the reality is Fig. 5. If u attaches between r and v, then when p(h)=q ₁ N _p must display ru|yx ₃ while when p′(h)=q ₂ then N _p′ must display ru|yx ₃. Hence, we must have d(r,u)+d(y,x ₃)<d(r,y)+d(u,x ₃)=d(r,x ₃)+d(u,y), a contradiction. If u attaches between v and x ₁, then when p(h)=q ₁ N _p must display uy|rx ₃ while when p′(h)=q ₂, N _p′ must display yx ₃|ru. Since these are different by Lemma 4.3, we cannot have d(r,y)+d(u,x ₃)<d(r,u)+d(y,x ₃)=d(r,x ₃)+d(u,y).

It follows that in reality u must attach between v and x ₂. Since x ₃ attaches to an ancestor of x ₂, it follows that the attachment point q ₄ of u must lie between v and q ₃. If p(h)=q ₁ then for the 4-set {u,y,x ₃,r}, N _p must display ux ₃|ry, so Criterion B does not prevent A(x ₂;yx ₃).

We now show that the value of α computed from Lemma 5.6 cannot satisfy 0<α<1, contradicting Criterion F.

Since we are assuming M ₂, the formulas in Lemma 5.6 must be utilized with x ₁ replaced by y, y replaced by x ₂, x ₂ replaced by x ₃, and x ₃ replaced by u. These become:

• (a) w _rv =[d(r,y)+d(r,u)−d(y,u)]/2=[d(r,y)+d(r,x ₃)−d(y,x ₃)]/2,

• (b) $w_{vq_{3}} = [d(r,u)+d(y,x_{3})-d(r,y)-d(u,x_{3})]/2$,

• (c) $w_{q_{3}u}= [d(r,u)+d(u,x_{3})-d(r,x_{3})]/2$,

• (d) $w_{hx_{2}} = [d(x_{2},x_{3})+d(x_{2},y)-d(y,x_{3})]/2$,

• (e) E ₂=d(y,x ₂)−d(r,x ₂)+w _rv ,

• (f) E ₄=d(x ₃,x ₂)−d(r,x ₂)+w _rv ,

• (g) $\alpha= [2 d(u,x_{2}) - 2 w_{q_{3}u} - 2 w_{hx_{2}} - d(r,y)+E_{2}+2w_{rv}+E_{4} - d(r,x_{3}) + 2 w_{vq_{3}}] / [4 w_{vq_{3}}]$,

• (h) $w_{vq_{1}} = [d(r,y)-E_{2}-w_{rv}] / [2 \alpha]$,

• (i) $w_{q_{3}q_{2}} = [ d(u,x_{2}) - w_{q_{3}u} - w_{hx_{2}} - \alpha(w_{vq_{3}}+w_{vq_{1}}) ] / (1-\alpha)$,

• (j) $w_{q_{1}y} = d(r,y) - w_{rv} - w_{vq_{1}}$,

• (k) $w_{q_{2}x_{3}}= d(r,x_{3})-w_{rv}-w_{vq_{3}}-w_{q_{3}q_{2}}$,

• (l) $C = 2 d(u,x_{2}) - 2 w_{q_{3}u} - 2 w_{hx_{2}} - d(r,y)+E_{2}+2 w_{rv}+E_{4}- d(r,x_{3}) + 2 w_{vq_{3}}$,

• (m) $D = 4 w_{vq_{3}}$.

Then

• (i) α(q ₁,h)=α=C/D.

• (ii) $d(q_{1},y) = w_{q_{1}y}$.

• (iii) $d(q_{2}, x_{3}) = w_{q_{2}x_{3}}$.

We must substitute the true quantities from the true network given in Fig. 5.

$$\begin{aligned} d(r,y) =& d(r,v)+d(h,y) + \alpha d(v, q_1) +d(v,q_4)+d(q_4,q_3)+d(q_3,q_2) \\ &{}-\alpha d(v,q_4) - \alpha d(q_4,q_3) -\alpha d(q_3,q_2)\\ d(u,x_3) =& d(q_4,u)+d(q_4,q_3)+d(q_3,x_3)\\ d(r,u) =& d(r,v)+d(v,q_4)+d(q_4,u)\\ d(y,x_3) =& d(h,y)+d(q_3,x_3) + \alpha d(v,q_1)+ \alpha d(v,q_4) +\alpha d(q_4, q_3)+ d(q_3,q_2) \\ &{} -\alpha d(q_3, q_2)\\ d(r,x_3) =& d(r,v)+d(v,q_4)+d(q_4, q_3) + d(q_3,x_3)\\ d(y,x_2) =& d(h,y)+d(q_2,x_2) + \alpha d(v,q_1)+\alpha d(v,q_4)+\alpha d(q_4, q_3) + \alpha d(q_3, q_2)\\ d(r,x_2) =& d(r,v)+d(v,q_4) + d(q_4, q_3) + d(q_3, q_2)+d(q_2,x_2)\\ d(u,x_2) =& d(q_4,u)+d(q_4,q_3)+d(q_3,q_2)+d(q_2,x_2)\\ d(x_3,x_2) =& d(q_3,x_3)+d(q_3,q_2)+d(q_2,x_2)\\ d(y,u) =& d(h,y) + d(q_4, u) + \alpha d(v,q_1) + \alpha d(v, q_4) + d(q_4, q_3) -\alpha d(q_4, q_3) \\ &{} + d(q_3,q_2) - \alpha d(q_3, q_2). \end{aligned}$$

When we make these substitutions and simplify, we find after considerable algebra:

$$\begin{aligned} & C = -4 d(q_4,q_3) + 4 \alpha d(q_4,q_3)\\ & D = 4 \alpha d(v,q_4) + 4 \alpha d(q_4, q_3) -4 d(q_4,q_3). \end{aligned} $$

Hence α=C/D=[−4d(q ₄,q ₃)+4αd(q ₄,q ₃)]/[4αd(v,q ₄)+4αd(q ₄,q ₃)−4d(q ₄,q ₃)].

We require 0<α<1 by Criterion F.

Case 1. Suppose D>0. Then 0<C/D<1 requires 0<C<D so 0<−4d(q ₄,q ₃)+4αd(q ₄,q ₃)<4αd(v,q ₄)+4αd(q ₄,q ₃)−4d(q ₄,q ₃). In particular, 0<4(α−1)d(q ₄,q ₃), which is impossible since d(q ₄,q ₃)>0 and 1−α>0.

Case 2. Suppose D<0. Then 0<C/D<1 requires 0>C>D, 0>−4d(q ₄,q ₃)+4αd(q ₄,q ₃)>4αd(v,q ₄)+4αd(q ₄,q ₃)−4d(q ₄,q ₃).

In particular, −4d(q ₄,q ₃)+4αd(q ₄,q ₃)>4αd(v,q ₄)+4αd(q ₄,q ₃)−4d(q ₄,q ₃) so 0>4αd(v,q ₄) which is impossible since α>0 and d(v,q ₄)>0.

Case 3. Suppose D=0 so $w_{vq_{3}} = 0$. But then from Willson (2012) it follows that $0 = w_{vq_{3}} = d(v, q_{3})$ whence v=q ₃. This is a contradiction since in Fig. 5 we saw that u must attach strictly between v and q ₃.

This completes the proof of Claim 10, which completes the proof of Theorem 6.1. □

In summary, suppose the truth was that there was a hybrid h with child y and parents q ₁ and q ₂ with respective children x ₁ and x ₂, where y, x ₁, and x ₂ are in X. Then Criterion B eliminates all false possibilities except A(x ₂;y,x ₃) and the symmetric possibility A(x ₁;y,x ₀) (where x ₃ attaches to the parent of q ₂ or x ₀ attaches to the parent of q ₁). The elimination of these two false possibilities makes use of the other criteria.

It is clear that the reconstruction is polynomial. Indeed

Theorem 6.8

Suppose N=(V,A,r,X) is normal and satisfies Assumptions 3.1. Let |X|=n. Given the tree-average distances d(x,y;N) for all x, y, in X, then the procedure reconstructs N in time O(n ⁷).

Proof

By Willson (2010), the number of vertices is O(n ²). For each vertex, the analysis of the possibilities of a hybrid includes for a given y, x ₁, x ₂, x ₃, a check for all w distinct from these, hence time O(n ⁵). The analysis of the possibilities of a cherry involves for a given {x,y} a check for all {w,z} distinct from these, hence time O(n ⁴)≤O(n ⁵). Hence, we need O(n ²) steps, each using at most time O(n ⁵), for a total time of O(n ⁷). □

Neighbor-Net (Bryant and Moulton 2004) takes time O(n ³) in the same situation, comparable to the time taken by Neighbor-Joining (Saitou and Nei 1987). As n grows, it follows that the tree-average distance method will take much more time than Neighbor-Net.

7 A More Complicated Example

The methods of the paper also work for some normal networks that do not contain a single reticulation cycle. It is easy to see, for example, that they work for galled trees (Gusfield et al. 2004) that satisfy Assumptions 3.1. They also work for the normal network N shown in Fig. 6.

Fig. 6

A network N with two reticulation cycles. This network can also be reconstructed from its tree-average distances

Suppose we were given the tree-average distances between members of X={1,2,3,4,5,6,7,8,9,10}, where 1 is the root. We would check all pairs {x,y} for possible cherries by seeing whether the conclusion of Theorem 4.5 holds. We would conclude that the network has no cherry. Checking for hybrids we would locate the hybrid with

• (a) y=5, x ₁=6, x ₂=4, x ₃=3, satisfying all the criteria.

This same hybrid would also be recognized as

• (b) y=5, x ₁=6, x ₂=4, x ₃=2

• (c) y=5, x ₁=4, x ₂=6, x ₃=7.

All of these descriptions will lead to the correct identification, with the correct weights ω(17,6), ω(16,5), ω(15,4) and probability α(17,16). If α(17,16)=1/2, then an equiprobable hybrid

• (d) y=5, x ₁=6, x ₂=4

would also be accepted and would result in the same weights.

The only issue so far is whether an incorrect hybrid might have been identified instead of (a), (b), (c), or (d). If the correct hybrid is identified, then it is removed. The resulting network has only a single reticulation cycle, so Theorem 6.1 applies. Thus, the network N is correctly reconstructed and can be drawn exactly as in Fig. 6 without the labels on internal vertices.

In fact, arguments like those for the proof of Theorem 6.1 show that no incorrect hybrid would be identified in that first step. The arguments are made more complicated by the fact that N has four different trees of form N _p rather than just two, as in Theorem 6.1. The hypotheses of Lemma 6.5 require a bit more checking, since we must avoid the possibility of having all three quartets arise for a certain choice of w. (This is immediate in Theorem 6.1 since there are only two trees N _p .) In addition, there are many more cases. We omit further analysis.

Suppose in Fig. 6 all the weights are 10 and the probabilities at both hybrid vertices are 0.5. When the tree-average distances are input to the current method, the output is precisely the same as Fig. 6 except for the arbitrary labeling of the internal vertices. When the tree-average distances are input to Neighbor-Net (implemented in Splitstree4 (Huson and Bryant 2006)), the output is the network in Fig. 7, rather than Fig. 6. This output illustrates the different type of network constructed by Neighbor-Net. Neighbor-Net does not reconstruct the reality shown in Fig. 6 but instead creates a network displaying certain incompatibilities.

Fig. 7

The output of Neighbor-Net from the tree-average distances in Fig. 6

8 Conclusions and Extensions

In this section, we remark on some related issues.

(a) Dealing with inaccuracies in the distances

The methods in this paper assume that the correct tree-average distances are known exactly. A major difficulty is that some of the criteria for a cherry or a hybrid as stated require some exact equalities. For example, the criterion that {x,y} is a cherry requires that for all w and z such that x,y,w,z are distinct, we must have d(x,y)+d(w,z)<d(x,w)+d(y,z)=d(x,z)+d(w,y). Such a condition is unlikely to hold if the true distances are subject to small errors, since the equality will almost certainly fail. Similarly, the formulas used in Theorem 6.1 for recognition of a hybrid involve an equality.

More generally, if we are to be able to use the results on real data, it would be useful to have a more robust calculation that will work when the data have sufficiently small errors. While the author has a computer program that works well when the exact tree-average distances are input or are input with only very small perturbations, the program does not appear to be reliable yet with real data. Nor is it reliable when simulations, using for example a Kimura process (Kimura 1980) for nucleotide mutation, generate artificial nucleotide data from which a Kimura distance is computed between each pair of leaves. Further research is needed to make the method practical.

The significance of the current paper is theoretical. It shows that, under certain specified general assumptions, distances between taxa uniquely determine a phylogenetic network proposing an evolutionary history that may not be a tree. The algorithm which is used to reconstruct the network from its distances is not intended as a practical method at this time.

(b) Taxon sampling

The results raise the issue of taxon sampling. Suppose that the true network is as in Fig. 1, with the probability α(q ₁,h)≠1/2, say α(q ₁,h)=1/3. Suppose that the taxon x ₃ were not present, so X={r,x ₁,y,x ₂} and the true tree-average distances were still known. Our method could correctly find that there is no cherry and use Criterion B to find that y is child to the hybrid and the parents have children x ₁ and x ₂. But we would be forced to accept the hybrid as equiprobable and we would not reconstruct the correct α(q ₁,h). The tree-average distances in the reconstructed network would not match the input distances.

With real data, of course, we would not expect an exact match in any event. A more serious problem, however, is that unless x ₃ is present, there is no possibility of finding the correct α(q ₁,h). Thus the method needs to be applied only when x ₃ is present. On the other hand, it is not possible in advance to guarantee that all hybrids have a taxon in a position analogous to x ₃.

(c) Hybrids of indegree 3 or higher

It is quite possible that a network could have hybrids with indegree 3 or higher. Suppose that a hybrid has indegree 3. The results of Willson (2012) do not apply to give explicit formulas for the weights even in the equiprobable case when each parent of the lower hybrid has probability 1/3. With inadequate taxon sampling, such a normal network might well be the best description of a system in which several species in tandem experience gene transfer and/or hybridization.