Constructing Tree-Child Networks from Distance Matrices

Abstract

A tree-child network is a phylogenetic network with the property that each non-leaf vertex is the parent of a tree vertex or a leaf. In this paper, we show that a tree-child network on taxa (leaf) set X with an outgroup and a positive real-valued weighting of its edges is essentially determined by the multi-set of all path-length distances between elements in X provided, for each reticulation, the edges directed into it have equal weight. Furthermore, we give a polynomial-time algorithm for reconstructing such a network from this inter-taxa distance information. Such constructions are of central importance in evolutionary biology where phylogenetic networks represent the ancestral history of a collection of present-day taxa.

1 Introduction

A central task in evolutionary biology is inferring the ancestral history of a collection X of present-day (species) taxa based on the inherited characteristics amongst the taxa in X. This inference is usually represented by a phylogenetic (evolutionary) tree whose leaf set is X. One fundamental and widely-used approach for inferring the tree-like ancestral history of a collection of present-day taxa is to utilise a measure of distance between taxa, such as the time since separation from the most recent common ancestor, to infer the structure of ancestral relationships between taxa. Such approaches are called distance-based methods, and include the popular method of Neighbor-Joining [10]. They are often used because they are computationally fast compared to maximum likelihood methods. For a recent survey of distance-based methods for inferring phylogenetic trees see Pardi and Gascuel [7].

Although one typically thinks of evolution as being a tree-like process, it is now well recognised that for many collections of taxa the ancestral history is non-tree-like and is more accurately represented by a phylogenetic network rather than a phylogenetic tree. This is because of reticulate (non-tree-like) processes in evolution such as hybridisation and horizontal gene transfer. To date, most of the focus in inferring phylogenetic networks has been based on topological information [5], but there is now a growing interest in making this inferences based on distance information.

In this paper we establish an algorithm for efficiently (polynomial time in the size of the input) reconstructing an edge-weighted tree-child network from its inter-taxa distances. Reconstruction of edge-weighted phylogenetic networks from distances is significantly more difficult than the analogous task for phylogenetic trees. A crucial feature of this problem is that, for a phylogenetic network ${\mathcal {N}}$, there is no longer a unique distance between every pair of taxa unless ${\mathcal {N}}$ is a phylogenetic tree, so one must work with shortest distances, average distances, sets of distances, or some other variation. As a result, we have more strenuous requirements on the distances as well as the class of phylogenetic networks. To be precise, we shall require the multi-set of distances between each pair of taxa, that the edge-weighted phylogenetic network is tree child with an outgroup, and that the pair of edges directed into a reticulation have equal weight.

In related prior work, Chan et al. [4] take a matrix of inter-taxa distances and reconstruct an ultrametric galled network such that there is a path between each pair of taxa having the length given in the matrix, if such a phylogenetic network exists. Willson [11] studied the problem of determining a phylogenetic network given the average distance between each pair of taxa, where each reticulation assigns a probability to the two edges directed into it. From such distances, one can reconstruct phylogenetic networks having a single reticulation cycle in polynomial time [12]. In earlier work [1], Bordewich and Semple showed that (unweighted) tree-child networks can be reconstructed from the multi-set of distances between taxa and that (unweighted) temporal, tree-child networks can be reconstructed from the set of distances between taxa, each in polynomial time. Furthermore, Bordewich and Tokac [2] have shown that ultrametric, tree-child networks can be reconstructed from the set of distances between taxa in polynomial time.

The originality of our work is in applying a ${\mathcal {Q}}$-score, inspired by the Neighbor-Joining algorithm [10], to determine key local structures in the network. This enables us to establish a polynomial-time algorithm for reconstructing edge-weighted tree-child networks from inter-taxa distances. Although we build upon the prior works mentioned above, it is a significant step to remove the ultrametric condition, which is not realistic in many biological settings, and to allow weighted edges, rather than the topological path lengths used in [1]. The results are rigorously proved, not based upon empirical evidence. The significance of the work is that it is an important step towards developing practical methods for fast reconstruction of phylogenetic networks based upon distance data, and the proper understanding of the phylogenetic history of taxa has major implications in healthcare (see e.g. [6] and [9]) as well as biological understanding of the origins of present-day taxa.

For the rest of the introduction, we formally state the main result, after some necessary definitions, as well as outlining the organisation of the paper. Throughout, X will always denote a non-empty finite set.

Fig. 1

A weighted tree-child network $({\mathcal {N}}, w)$ on $X=\{r, x_1, x_2, x_3, x_4, x_5, x_6\}$ with outgroup r

A phylogenetic network ${\mathcal {N}}$ on X is a rooted acyclic digraph with no parallel edges and the following properties:

• (i) the unique root has out-degree two,

• (ii) the set X is the set of vertices of out-degree zero, each of which has in-degree one, and

• (iii) all other vertices either have in-degree one and out-degree two, or in-degree two and out-degree one.

For technical reasons, if $|X|=1$, we additionally allow the directed graph consisting of the single vertex in X to be a phylogenetic network. The vertices of out-degree zero are called leaves. Furthermore, the vertices of in-degree one and out-degree two are called tree vertices, while the vertices of in-degree two and out-degree one are called reticulations. An edge directed into a reticulation is a reticulation edge; all other edges are tree edges. An element in X is an outgroup if its parent is the root of ${\mathcal {N}}$. A phylogenetic network ${\mathcal {N}}$ is a tree-child network [3] if each non-leaf vertex in ${\mathcal {N}}$ is the parent of either a tree vertex or a leaf.

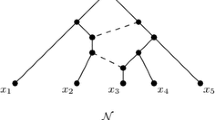
Let ${\mathcal {N}}$ be a phylogenetic network on X. Two distinct reticulation edges $e_1$ and $e_2$ in ${\mathcal {N}}$ is a reticulation pair if $e_1$ and $e_2$ are directed into the same reticulation. We say ${\mathcal {N}}$ has a reticulation-pair weighting, denoted $({\mathcal {N}}, w)$, if the edges of ${\mathcal {N}}$ are assigned a positive real-valued weighting w with the properties that: for each reticulation pair $e_1$ and $e_2$ we have $w(e_1)=w(e_2)$; and internal tree edges have strictly positive weight. (Without this restriction on internal tree edges, it would not be possible to distinguish the internal structure of networks with many zero-weight edges.) To illustrate, a reticulation-pair weighted tree-child network $({\mathcal {N}}, w)$ on X with outgroup r is shown in Fig. 1, where $X=\{r, x_1, x_2, x_3, x_4, x_5, x_6\}$. The vertex u is a reticulation. As with all drawings of phylogenetic networks in this paper, edges are directed down the page.

To ease reading, throughout the paper, a “weighted tree-child network” means a “reticulation-pair weighted tree-child network”. Let $({\mathcal {N}}, w)$ be a weighted phylogenetic network on X, and let v and $v'$ be vertices in $({\mathcal {N}}, w)$. An up-down path from v to $v'$ in ${\mathcal {N}}$ is an underlying path

$$\begin{aligned} v, u_1, u_2, \ldots , u_{k-1}, v', \end{aligned}$$

where, for some $i\le k-1$,

$$\begin{aligned} (u_i, u_{i-1}), (u_{i-1}, u_{i-2}), \ldots , (u_1, v) \end{aligned}$$

and

$$\begin{aligned} (u_i, u_{i+1}), (u_{i+1}, u_{i+2}), \ldots , (u_{k-1}, v') \end{aligned}$$

are edges in ${\mathcal {N}}$. The length of an up-down path is the sum of the weights of the edges along it.

Now let ${\mathcal {P}}_{x, y}$ be the set of up-down paths from x to y in ${\mathcal {N}}$. The multi-set of distances from x to y, denoted ${\mathcal {D}}_{x, y}$, is the multi-set of lengths of paths in ${\mathcal {P}}_{x, y}$. Of course, ${\mathcal {D}}_{x, y}={\mathcal {D}}_{y, x}$ for all $x, y\in X$ and ${\mathcal {D}}_{x, x}=\{0\}$ for all $x\in X$. The multi-set distance matrix ${\mathcal {D}}$ of $({\mathcal {N}}, w)$ is the $|X|\times |X|$ matrix whose (x, y)-th entry is ${\mathcal {D}}_{x, y}$ for all $x, y\in X$, in which case ${\mathcal {D}}$ is realised by $({\mathcal {N}}, w)$. As an example, in Fig. 1, there are two up-down paths connecting $x_1$ and $x_3$, and ${\mathcal {D}}_{x_1, x_3}=\{14, 21\}$.

Let ${\mathcal {D}}$ be a multi-set distance matrix on X. Let $({\mathcal {N}}, w)$ be a weighted phylogenetic network on X with outgroup r, and suppose that $({\mathcal {N}}, w)$ realises ${\mathcal {D}}$. The weighting w is certainly not unique. Let u be the child of the root $\rho$ of ${\mathcal {N}}$ that is not r. Then, provided the sum of the weights $w(\rho , r)+w(\rho , u)$ is fixed, we can change the weights of the edges $(\rho , r)$ and $(\rho , u)$ to construct a different weighting, $w'$ say, such that $({\mathcal {N}}, w')$ also realises ${\mathcal {D}}$ (where w and $w'$ are equal on the other edges). We refer to this scenario as re-weighting the edges at the root of ${\mathcal {N}}$. A similar scenario happens at any reticulation of ${\mathcal {N}}$. In particular, let u be a reticulation in ${\mathcal {N}}$ with parents $p_u$ and $q_u$, and let v be the unique child of u. Then, provided the sum of the weights of $(p_u, u)$ and (u, v) and the sum of the weights of $(q_u, u)$ and (u, v) are equal to $w(p_u, u)+w(u, v)$, we can change the weights of the edges $(p_u, u)$, $(q_u, u)$, and (u, v), again fixing the weights of all other edges, to construct a different weighting, $w''$ say, such that $({\mathcal {N}}, w'')$ realises ${\mathcal {D}}$. We refer to this last scenario as re-weighting the edges at a reticulation of ${\mathcal {N}}$. For example, consider the weighted phylogenetic network show in Fig. 1. If we increase the weights of both $(p_u, u)$ and $(q_u, u)$ to 2, and simultaneously decrease the weight of $(u, x_4)$ to 2, then the resulting weighted phylogenetic network also realises ${\mathcal {D}}$.

Now let $({\mathcal {N}}_1, w_1)$ be another weighted phylogenetic network on X with outgroup r, and suppose, in addition to $({\mathcal {N}}, w)$, that $({\mathcal {N}}_1, w_1)$ realises ${\mathcal {D}}$. We say $({\mathcal {N}}, w)$ and $({\mathcal {N}}_1, w_1)$ are equivalent if ${\mathcal {N}}$ is isomorphic to ${\mathcal {N}}_1$, and $w_1$ can be obtained from w by re-weighting the edges at the root and at each reticulation. Observe that this induces an equivalence relation on the set of weighted phylogenetic networks on X with outgroup r realising ${\mathcal {D}}$. Furthermore, under this relation, there is a unique weighted phylogenetic network, denoted $({\mathcal {N}}_0, w_0)$, in the equivalence class of $({\mathcal {N}}, w)$, where the weight of each reticulation edge is zero, and the weight of the pendent edge incident with the root $\rho$, that is $(\rho , r)$, is zero. The main result of the paper is the following theorem.

Theorem 1

Let ${\mathcal {D}}$ be a multi-set distance matrix on X with distinguished element r. Let $({\mathcal {N}}, w)$ be a weighted tree-child network on X with outgroup r realising ${\mathcal {D}}$. Then, up to equivalence, $({\mathcal {N}}, w)$ is the unique such network realising ${\mathcal {D}}$, in which case $({\mathcal {N}}_0, w_0)$ can be found from ${\mathcal {D}}$ in time quadratic in $|{\mathcal {D}}|$.

The unweighted analogue of Theorem 1 is established in [1]. Furthermore, the analogue of Theorem 1 for when the multi-set distance matrix ${\mathcal {D}}$ is realised by a weighted tree-child network whose weighting satisfies the ultrametric condition is established in [2]. A weighting is ultrametric if the lengths of all paths from the root to a leaf are the same.

To provide some intuition to the proof of Theorem 1 and the content of the paper, the algorithm proceeds iteratively by identifying a pair of taxa that form one of two local structures (a cherry or a reticulated cherry) in the target network. Before recursing, it either deletes one of these taxa or reduces the distance matrix to effectively delete a reticulation edge from the network under construction. We identify an appropriate pair of taxa using a so-called ${\mathcal {Q}}$-score, which is inspired by the ${\mathcal {Q}}$-score used to identify a pair of taxa to agglomerate in the popular Neighbor Joining algorithm [10].

The paper is organised as follows. The next section consists of some additional preliminaries, including the notion of a reticulated cherry. Section 3 introduces the ${\mathcal {Q}}$-score of a pair of elements in X. This score is calculated using values in a distance matrix on X and is the key idea underlying Theorem 1. The uniqueness and computational parts of Theorem 1 are proved in Sects. 4 and 5, respectively. A phylogenetic network ${\mathcal {N}}$ is stack free if each reticulation is the parent of either a tree vertex or a leaf. Also note that if ${\mathcal {N}}$ is a stack-free network on X, where $|X|=1$, then ${\mathcal {N}}$ consists of the single vertex in X. Observe that if ${\mathcal {N}}$ is a tree-child network, then ${\mathcal {N}}$ is a stack-free network, but the converse does not hold. In Sect. 6, we state, as a conjecture, an analogue of Theorem 1 for stack-free networks and establish a lemma supporting the conjecture. Consequently, where appropriate, the results in Sects. 2 and 3 are generalised to stack-free networks.

We end the introduction with two remarks. First, it is natural to ask if all of the inter-taxa distances are necessary in recovering a weighted tree-child network. A separate collaboration is currently investigating this question. Second, for the approach taken in this paper of using the ${\mathcal {Q}}$-score, the assumption in the statement of Theorem 1 that the edges directed into the same reticulation have the same weight is necessary (for details, see Sect. 3). However, whether this assumption is necessary in general, remains an open problem.

2 Preliminaries

Let ${\mathcal {N}}$ be a phylogenetic network on X, and let $\{s, t\}$ be a 2-element subset of X. We say $\{s, t\}$ is a cherry, alternatively a 0-reticulated cherry, if there is an up-down path,

$$\begin{aligned} s, u_1, t \end{aligned}$$

say, between s and t, where $u_1$ is (necessarily) a tree vertex. Furthermore, $\{s, t\}$ is a 1-reticulated cherry if there is an up-down path,

$$\begin{aligned} s, u_1, u_2, t \end{aligned}$$

say, between s and t, where exactly one of $u_1$ and $u_2$ is a tree vertex. If $u_1$ is the tree vertex, then t is the reticulation leaf of the 1-reticulated cherry. Lastly, $\{s, t\}$ is a 2-reticulated cherry if there is an up-down path,

$$\begin{aligned} s, u_1, u_2, u_3, t \end{aligned}$$

say, between s and t, where both $u_1$ and $u_3$ are reticulations, and $u_2$ is a tree vertex. Depending on whether $\{s, t\}$ is a 0- , 1- , or 2-reticulated cherry, we refer to the unique tree vertex in the associated up-down paths as the tree vertex of the 0- , 1- , or 2-reticulated cherry, respectively. For example, in Fig. 1, $\{x_1, x_2\}$ is a cherry, while $\{x_4, x_5\}$ is a 1-reticulated cherry with tree vertex $q_u$. The 2-element set $\{x_3, x_4\}$ is also a 1-reticulated cherry.

The proof of Lemma 1 for when ${\mathcal {N}}$ is tree child is established in [1].

Lemma 1

Let ${\mathcal {N}}$ be a stack-free (resp. tree-child) network on X, where $|X|\ge 2$. Then ${\mathcal {N}}$ has a k-reticulated cherry for some $k\in \{0, 1, 2\}$ (resp. $k\in \{0, 1\}$). Moreover, if ${\mathcal {N}}$ is weighted and u is a tree vertex at maximum distance from the root, then u is the tree vertex of a k-reticulated cherry for some $k\in \{0, 1, 2\}$ (resp. $k\in \{0, 1\}$).

Proof

Let u be a tree vertex at maximum distance from the root of ${\mathcal {N}}$. We prove the lemma for when ${\mathcal {N}}$ is stack free by showing that u is the tree vertex of a k-reticulated cherry for some $k\in \{0, 1, 2\}$.

By maximality, there is no tree vertex in ${\mathcal {N}}$ below u, and so, as ${\mathcal {N}}$ has no parallel edges, there are exactly two elements, x and y say, in X below u. Moreover, as ${\mathcal {N}}$ is stack free, the number of edges on the unique directed path from u to x (respectively, y) is at most two. By a routine check, it now follows, for some $k\in \{0, 1, 2\}$, that u is the tree vertex of the k-reticulated cherry $\{x, y\}$.

In the case that ${\mathcal {N}}$ is tree child, at least one child of u must be a leaf, and hence for some $k\in \{0, 1\}$, that u is the tree vertex of the k-reticulated cherry $\{x, y\}$. $\square$

Let $({\mathcal {N}}, w)$ be a weighted phylogenetic network on X. Let $\{s, t\}$ be a 2-element subset of X that is either a 0- or 1-reticulated cherry of ${\mathcal {N}}$, and denote the parents of s and t by $p_s$ and $p_t$, respectively. First assume that $\{s, t\}$ is a 0-reticulated cherry, and so $p_s=p_t$. Let $g_s$ denote the parent of $p_s$. Then reducing t is the operation of deleting t and its incident edge, suppressing $p_s$, and setting the weight of the resulting edge $(g_s, s)$ to be

$$\begin{aligned} w(g_s, p_s)+w(p_s, s). \end{aligned}$$

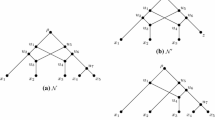
Now assume that $\{s, t\}$ is a 1-reticulated cherry in which t is the reticulation leaf. Let $g_s$ and $g_t$ denote the parents of $p_s$ and $p_t$, respectively, where $g_t\ne p_s$. Then cutting $\{s, t\}$ is the operation of deleting $(p_s, p_t)$, suppressing $p_s$ and $p_t$, and setting the weight of the resulting edge $(g_s, s)$ to $w(g_s, p_s)+w(p_s, s)$ and the weight of the edge $(g_t, t)$ to $w(g_t, p_t)+w(p_t, t)$. To illustrate, consider Fig. 2. The weighted tree-child network $({\mathcal {N}}_1, w_1)$ has been obtained from $({\mathcal {N}}, w)$ in Fig. 1 by reducing $x_2$. Furthermore, the weighted tree-child network $({\mathcal {N}}_2, w_2)$ has been obtained from $({\mathcal {N}}, w)$ by cutting $\{x_4, x_5\}$.

Fig. 2

Two weighted tree-child networks $({\mathcal {N}}_1, w_1)$ and $({\mathcal {N}}_2, w_2)$ obtained from $({\mathcal {N}}, w)$ in Fig. 1 by reducing $x_2$ and by cutting $\{x_4, x_5\}$, respectively

The proof of the next lemma follows from [1, Lemma 4.1].

Lemma 2

Let $({\mathcal {N}}, w)$ be a weighted tree-child network. Suppose $({\mathcal {N}}', w')$ is obtained from $({\mathcal {N}}, w)$ by either reducing a leaf in a cherry, or cutting a 1-reticulated cherry. Then $({\mathcal {N}}', w')$ is also a weighted tree-child network.

Let ${\mathcal {D}}$ be a multi-set distance matrix on X. For all $x, y\in X$, we denote the maximum and minimum values in ${\mathcal {D}}_{x, y}$ by $d_{\max }(x, y)$ and $d_{\min }(x, y)$, respectively. Now, let r be a distinguished element in X. We next describe two reduction operations on ${\mathcal {D}}$ that parallel the above reduction and cutting operations on a weighted phylogenetic network. This is necessary because in the reconstruction algorithm we will be working with the input data ${\mathcal {D}}$, and not with the unknown (as yet) network. We will only need to perform these parallel operations in cases in which we have already identified a pair of taxa $\{s, t\}$ that form a k-reticulated cherry at maximum distance from the outgroup r, in a sense that shall be defined precisely in the next section. In these cases the assumptions made in the definitions below will be shown to hold.

Let $\{s, t\}$ be a 2-element subset of $X-\{r\}$. First assume $|{\mathcal {D}}_{s, t}|=1$. Let ${\mathcal {D}}'$ be the multi-set distance matrix on $X'=X-\{t\}$ obtained from ${\mathcal {D}}$ by setting

$$\begin{aligned} {\mathcal {D}}'_{x, y}={\mathcal {D}}'_{y, x}={\mathcal {D}}_{x, y} \end{aligned}$$

for all $x, y\in X'$. We say that ${\mathcal {D}}'$ has been obtained by reducing t in ${\mathcal {D}}$. Second assume that, for all $x\in X-\{s, t\}$,

$$\begin{aligned} \{d+c: d\in {\mathcal {D}}_{s, x}\}{\subsetneqq } {\mathcal {D}}_{t, x}, \end{aligned}$$

where $c=d_{\max }(r, t)-d_{\max }(r, s)$. Now let ${\mathcal {D}}'$ be the multi-set distance matrix on X obtained from ${\mathcal {D}}$ by setting

$$\begin{aligned} {\mathcal {D}}'_{x, y}={\mathcal {D}}'_{y, x}={\mathcal {D}}_{x, y} \end{aligned}$$

for all $x, y\in X-\{t\}$,

$$\begin{aligned} {\mathcal {D}}'_{t, x}={\mathcal {D}}'_{x, t}={\mathcal {D}}_{t, x}-\{d+c: d\in {\mathcal {D}}_{s, x}\} \end{aligned}$$

for all $x\in X-\{s, t\}$, where $c=d_{\max }(r, t)-d_{\max }(r, s)$, and

$$\begin{aligned} {\mathcal {D}}'_{s, t}={\mathcal {D}}'_{t, s}={\mathcal {D}}_{s, t}-\{d_{\min }(s, t)\}. \end{aligned}$$

We say ${\mathcal {D}}'$ has been obtained by cutting $\{s, t\}$ in ${\mathcal {D}}$.

3 ${\mathcal {Q}}$-Score

We establish Theorem 1 by iteratively determining a 2-element subset $\{s, t\}$ in $X-\{r\}$ that is either a 0- or a 1-reticulated cherry in $({\mathcal {N}}, w)$. The same approach is used in [1] to prove an unweighted analogue of this theorem, but there the determination is straightforward. For example, in the unweighted setting, $|{\mathcal {D}}_{s, t}|=1$ and ${\mathcal {D}}_{s, t}=\{2\}$ is both a necessary and sufficient condition to determine that $\{s, t\}$ is a 0-reticulated cherry of $({\mathcal {N}}, w)$. However, with an arbitrary weighting, the canonical generalisation of this condition is neither necessary nor sufficient. The key to resolving this hurdle is the notion of a ${\mathcal {Q}}$-score.

Let ${\mathcal {D}}$ be a multi-set distance matrix on X. For all $x, y, z\in X$, the ${\mathcal {Q}}$-score of x and y with respect to z, denoted ${\mathcal {Q}}_z(x, y)$, is the value

$$\begin{aligned} {\mathcal {Q}}_z(x, y)={\textstyle \frac{1}{2}}\left( d_{\max }(z, x)+d_{\max }(z, y)-d_{\min }(x, y)\right) . \end{aligned}$$

For example, referring to the multi-set distance matrix realised by $({\mathcal {N}}, w)$ in Fig. 1,

$$\begin{aligned} {\mathcal {Q}}_r(x_4, x_6)&= {\textstyle \frac{1}{2}}\left( d_{\max }(r, x_4)+d_{\max }(r, x_6)-d_{\min }(x_4, x_6)\right) \\&= {\textstyle \frac{1}{2}}\left( 21+14-8\right) = {\textstyle \frac{27}{2}}. \end{aligned}$$

Given the multi-set distance matrix of a weighted tree-child network $({\mathcal {N}}, w)$ with outgroup r, the next lemma shows that maximising the ${\mathcal {Q}}$-score with respect to r identifies a k-reticulated cherry of $({\mathcal {N}}, w)$.

Lemma 3

Let ${\mathcal {D}}$ be a multi-set matrix of distances between elements of a set X with distinguished element r, where $|X|\ge 3$. Let $({\mathcal {N}}, w)$ be a weighted stack-free (resp. tree-child) network on X with outgroup r realising ${\mathcal {D}}$. Let $\{s, t\}$ be a 2-element subset of $X-\{r\}$ such that

$$\begin{aligned} {\mathcal {Q}}_r(s, t)=\max \{{\mathcal {Q}}_r(x, y): x, y\in X-\{r\}\}. \end{aligned}$$

Then

• (i) For some $k\in \{0, 1, 2\}$ (resp. $k\in \{0, 1\}$), the set $\{s, t\}$ is a k-reticulated cherry in $({\mathcal {N}}, w)$.

• (ii) The length of the longest up-down path in $({\mathcal {N}}, w)$ starting at r and ending at a tree vertex is ${\mathcal {Q}}_r(s, t)$.

• (iii) The length of the longest up-down path in $({\mathcal {N}}, w)$ starting at r and ending at the tree vertex u in the k-reticulated cherry $\{s, t\}$ is ${\mathcal {Q}}_r(s, t)$, and $d_{\max }(r, s)$ and $d_{\max }(r, t)$ are realised by paths that include u.

Proof

We begin by establishing a lower bound for

$$\begin{aligned} \max \{{\mathcal {Q}}_r(x, y): x, y\in X-\{r\}\}. \end{aligned}$$

Let l be the length of the longest up-down path in $({\mathcal {N}}, w)$ starting at r and ending at a tree vertex, u say. By Lemma 1, u is a tree vertex of a k-reticulated cherry $\{a, b\}$ for some $k\in \{0,1, 2\}$. Observe that if $({\mathcal {N}}, w)$ is tree child, then $k\in \{0, 1\}$. Using the maximality of l, and the fact that reticulations pairs have equal weight, it is easily checked that ${\mathcal {Q}}_r(a, b)=l$ and so

$$\begin{aligned} l&\le \max \{{\mathcal {Q}}_r(x, y): x, y\in X-\{r\}\}. \end{aligned}$$

(1)

Now let $\{s, t\}$ be a 2-element subset of $X-\{r\}$ such that

$$\begin{aligned} {\mathcal {Q}}_r(s, t)=\max \{{\mathcal {Q}}_r(x, y): x, y\in X-\{r\}\}. \end{aligned}$$

Let $p_s$ and $p_t$ be the parents of s and t in $({\mathcal {N}}, w)$, respectively. The rest of the proof is partitioned into three cases depending on whether $p_s$ and $p_t$ are tree vertices or reticulations. For the first case, suppose that $p_s$ and $p_t$ are both tree vertices. Let $l_s$ and $l_t$ denote the lengths of the longest up-down paths in $({\mathcal {N}}, w)$ from r to $p_s$ and r to $p_t$, respectively. Noting that

$$\begin{aligned} d_{\max }(r, s)=l_s+w(p_s, s) \end{aligned}$$

and

$$\begin{aligned} d_{\max }(r, t)=l_t+w(p_t, t), \end{aligned}$$

and $l_s, l_t\le l$, we have

$$\begin{aligned} {\mathcal {Q}}_r(s, t)&= {\textstyle \frac{1}{2}}\big (d_{\max }(r, s) + d_{\max }(r, t) - d_{\min }(s, t)\big ) \\&= {\textstyle \frac{1}{2}}\big (l_s+w(p_s, s) + l_t+w(p_t, t) \\&\quad - d_{\min }(p_s, p_t)-w(p_s, s)-w(p_t, t)\big ) \\&\le {\textstyle \frac{1}{2}}\big (l_s+l_t\big ) \\&\le l, \end{aligned}$$

where $d_{\min }(p_s, p_t)$ denotes the minimum length of an up-down path in $({\mathcal {N}}, w)$ between $p_s$ and $p_t$. Since ${\mathcal {Q}}_r(s, t)=\max \{{\mathcal {Q}}_r(x, y): x, y\in X-\{r\}\}$, it follows by (1) that equality holds throughout and so $d_{\min }(p_s, p_t)=0$. Since internal tree edges have strictly positive weight, we have $p_s=p_t$, in which case $\{s, t\}$ is a 0-reticulated cherry in $({\mathcal {N}}, w)$.

For the second case, suppose that exactly one of $p_s$ and $p_t$ is a tree vertex. Without loss of generality, we may assume that $p_s$ is a tree vertex. Let $l_s$ and $l_t$ denote the lengths of the longest up-down paths in $({\mathcal {N}}, w)$ from r to $p_s$ and r to a parent, $g_t$ say, of $p_t$. Observe that

$$\begin{aligned} d_{\max }(r, s)=l_s+w(p_s, s) \end{aligned}$$

and, as w is reticulation paired,

$$\begin{aligned} d_{\max }(r, t)=l_t+w(g_t, p_t)+w(p_t, t). \end{aligned}$$

Let $g'_t$ denote the parent of $p_t$ that is on an up-down path in $({\mathcal {N}}, w)$ realising $d_{\min }(s, t)$. Note that $g_t$ and $g'_t$ may or may not be distinct. Since ${\mathcal {N}}$ is stack-free, $g_t$ and $g'_t$ are tree vertices. Therefore, as $w(g_t, p_t)=w(g'_t, p_t)$ and $l_s, l_t\le l$,

$$\begin{aligned} {\mathcal {Q}}_r(s, t)&= {\textstyle \frac{1}{2}}\big (d_{\max }(r, s) + d_{\max }(r, t) - d_{\min }(s, t)\big ) \\&= {\textstyle \frac{1}{2}}\big (l_s+w(p_s, s) + l_t+w(g_t, p_t)+w(p_t, t) \\&\quad - d_{\min }(p_s, g'_t)-w(p_s, s)-w(g_t, p_t)-w(p_t, t)\big ) \\&= {\textstyle \frac{1}{2}}\big (l_s+l_t-d_{\min }(p_s, g'_t)\big ) \\&\le {\textstyle \frac{1}{2}}\big (l_s+l_t\big ) \\&\le l, \end{aligned}$$

where $d_{\min }(p_s, g'_t)$ denotes the minimum length of an up-down path in $({\mathcal {N}}, w)$ between $p_s$ and $g'_t$. By the choice of $\{s, t\}$ and (1), equality holds throughout and so $d_{\min }(p_s, g'_t)=0$, that is $p_s=g'_t$, in which case $\{s, t\}$ is a 1-reticulated cherry.

Lastly, suppose that $p_s$ and $p_t$ are both reticulations. Let $l_s$ and $l_t$ denote the lengths of the longest up-down paths in $({\mathcal {N}}, w)$ from r to a parent, $g_s$ say, of $p_s$ and from r to a parent, $g_t$ say, of $p_t$. Then

$$\begin{aligned} d_{\max }(r, s)=l_s+w(g_s, p_s)+w(p_s, s) \end{aligned}$$

and

$$\begin{aligned} d_{\max }(r, t)=l_t+w(g_t, p_t)+w(p_t, t). \end{aligned}$$

Let $g'_s$ and $g'_t$ denote the parents of $p_s$ and $p_t$, respectively, on an up-down path in $({\mathcal {N}}, w)$ realising $d_{\min }(s, t)$. As ${\mathcal {N}}$ is stack free, each of $g_s$, $g'_s$, $g_t$, and $g'_t$ are tree vertices. Since w is reticulation paired, $w(g_s, p_s)=w(g'_s, p_s)$ and $w(g_t, p_t)=w(g'_t, p_t)$. Therefore, as $l_s, l_t\le l$,

$$\begin{aligned} {\mathcal {Q}}_r(s, t)&= {\textstyle \frac{1}{2}}\big (d_{\max }(r, s) + d_{\max }(r, t) - d_{\min }(s, t)\big ) \\&= {\textstyle \frac{1}{2}}\big (l_s+w(g_s, p_s)+w(p_s, s) + l_t+w(g_t, p_t)+w(p_t, t)\big ) \\&\qquad -d_{\min }(g'_s, g'_t)-w(g_s, p_s)-w(p_s, s)-w(g_t, p_t)-w(p_t, t)\big ) \\&= {\textstyle \frac{1}{2}}\big (l_s+l_t-d_{\min }(g'_s, g'_t)\big ) \\&\le {\textstyle \frac{1}{2}}\big (l_s+l_t\big ) \\&\le l, \end{aligned}$$

where $d_{\min }(g'_s, g'_t)$ denotes the minimum length of an up-down path in $({\mathcal {N}}, w)$ between $g'_s$ and $g'_t$. By the choice of $\{s, t\}$ and (1), equality holds throughout and so $d_{\min }(g'_s, g'_t)=0$, that is $g'_s=g'_t$. If $({\mathcal {N}}, w)$ is not tree child, then $\{s, t\}$ is a 2-reticulated cherry. While if $({\mathcal {N}}, w)$ is tree child, then $({\mathcal {N}}, w)$ has a vertex with two child reticulations; a contradiction.

In each case, it easily follows that ${\mathcal {Q}}_r(s,t)$ is the length of the longest up-down path in $({\mathcal {N}}, w)$ starting at r and ending at the tree vertex of the k-reticulated cherry $\{s,t\}$. In addition, in each case we have the equality $l_s=l_t=l$, from which it follows that $d_{\max }(r, s)$ and $d_{\max }(r, t)$ are each realised by a path via the tree vertex of the k-reticulated cherry. This completes the proof of the lemma. $\square$

Fig. 3

Two weighted tree-child networks for which the maximum ${\mathcal {Q}}_r$-score is not realised by either a 0- or 1-reticulated cherry

Lemma 3 does not necessarily hold if $({\mathcal {N}}, w)$ is not stack free or if the weighting does not have the property that $w(e_1)=w(e_2)$ for each reticulation pair $e_1$ and $e_2$. Consider the two weighted tree-child networks $({\mathcal {N}}_1, w_1)$ on $X_1$ and $({\mathcal {N}}_2, w_2)$ on $X_2$ shown in Fig. 3, where $X_1=\{r, x_1, x_2, x_3\}$ and $X_2=\{r, x_1, x_2, x_3, x_4\}$. Here, b is a positive real and, for clarity, unweighted edges each have weight one. The fact that unweighted edges each have the same weight is simply for convenience. Observe that $({\mathcal {N}}_1, w_1)$ is not stack free and the weighting in $({\mathcal {N}}_2, w_2)$ does not satisfy the reticulation pair property. With regards to (i), it is easy to check that

$$\begin{aligned} {\mathcal {Q}}_r(x_2, x_3)=\max \{{\mathcal {Q}}_r(x_i, x_j): x_i, x_j\in X_1-\{r\}\} \end{aligned}$$

provided b is sufficiently large. But $\{x_2, x_3\}$ is neither a 0- nor 1-reticulated cherry in $({\mathcal {N}}_1, w_1)$. In (ii), provided b is sufficiently large,

$$\begin{aligned} {\mathcal {Q}}_r(x_1, x_3)={\mathcal {Q}}_r(x_2, x_3)=\max \{{\mathcal {Q}}_r(x_i, x_j): x_i, x_j\in X-\{r\}\}, \end{aligned}$$

and $\{x_1, x_3\}$, as well as $\{x_2, x_3\}$, is not a 0- or 1-reticulated cherry.

4 Tree-Child Networks

In this section, we prove the uniqueness part of Theorem 1. We begin with a lemma which will be used again in the next section.

Lemma 4

Let $({\mathcal {N}}, w)$ be a weighted tree-child network on X with outgroup r, where $|X|\ge 3$. Let ${\mathcal {D}}$ be the multi-set distance matrix of $({\mathcal {N}}, w)$. For some $k\in \{0, 1\}$, let $\{s, t\}$ be a k-reticulated cherry in $({\mathcal {N}}, w)$ such that

$$\begin{aligned} {\mathcal {Q}}_r(s, t)=\max \{{\mathcal {Q}}_r(x, y): x, y\in X-\{r\}\}. \end{aligned}$$

Depending on k, let ${\mathcal {D}}'$ be the multi-set distance matrix obtained from ${\mathcal {D}}$ by reducing t if $k=0$ and by cutting $\{s, t\}$ if $k=1$. Then ${\mathcal {D}}'$ is realised by the weighted tree-child network obtained from $({\mathcal {N}}, w)$ by reducing t if $k=0$ and by cutting $\{s, t\}$ if $k=1$.

Proof

If $k=0$, then it is clear that ${\mathcal {D}}'$ is realised by the weighted tree-child network on $X'$ obtained from $({\mathcal {N}}, w)$ by reducing t. Therefore suppose that $k=1$ and t is the reticulation leaf of the 1-reticulated cherry $\{s, t\}$. Let $({\mathcal {N}}', w')$ be the weighted tree-child network on X obtained from $({\mathcal {N}}, w)$ by cutting $\{s, t\}$. We next show that ${\mathcal {D}}'$ is realised by $({\mathcal {N}}', w')$.

Let $p_s$ and $p_t$ be the (unique) parents of s and t in $({\mathcal {N}}, w)$, respectively. Since the only up-down paths in $({\mathcal {N}}, w)$ between elements in X traversing $(p_s, p_t)$ involve t, it follows that ${\mathcal {D}}'_{x, y}={\mathcal {D}}'_{y, x}$ is realised by $({\mathcal {N}}', w')$ for all $x, y\in X-\{s,t\}$. Let $x\in X-\{s, t\}$ and consider the set of up-down paths starting at s and ending at x, and the set of up-down paths starting at t, traversing $(p_s, p_t)$, and ending at x. There is an obvious one-to-one correspondence between the two sets. Under this correspondence, if $d_{s, x}$ is the length of an up-down path starting at s and ending at x, then the length $d_{t, x}$ of the corresponding up-down path starting at t, traversing $(p_s, p_t)$, and ending at x is

$$\begin{aligned} d_{t, x}&= d_{s, x}+w(p_s, p_t)+w(p_t, t)-w(p_s, s) \\&= d_{s, x}+c, \end{aligned}$$

where, by Lemma 3 and the equality of weights on reticulations pairs, $c=d_{\max }(r, t)-d_{\max }(r, s)$. Hence, for each $x\in X-\{s, t\}$,

$$\begin{aligned} {\mathcal {D}}'_{t, x}={\mathcal {D}}'_{x, t}={\mathcal {D}}_{t, x}-\{d+c: d\in {\mathcal {D}}_{s, x}\} \end{aligned}$$

is realised by $({\mathcal {N}}', w')$. Lastly, ${\mathcal {D}}'_{s, t}={\mathcal {D}}'_{t, s}$ is realised by $({\mathcal {N}}', w')$ as there is exactly one up-down path $P=s, p_s, p_t, t$ in $({\mathcal {N}}, w)$ between s and t that traverses $(p_s, p_t)$, and which is therefore the only path removed when cutting $\{s, t\}$ in $({\mathcal {N}}, w)$. Path P must have distance $d_{\min }(s, t)$, since any other up-down path $P'$ from s to t also traverses the edges $(p_s,s)$ and $(p_t,t)$ and must traverse the reticulation edge paired with $(p_s,p_t)$, which has weight equal to $(p_s,p_t)$, and hence $P'$ is at least as long as P.

$\square$

By way of example, consider $({\mathcal {N}}_1, w_1)$ as shown in Fig. 2. The pair that maximise the ${\mathcal {Q}}_r$-score is $\{x_3,x_4\}$ with ${\mathcal {Q}}_r(x_3,x_4)=\tfrac{1}{2} (19+21-6)=17$. Consider the multi-set distance matrix ${\mathcal {D}}$ realised by $({\mathcal {N}}_1, w_1)$, and the multi-set distance matrix ${\mathcal {D}}'$ obtained by cutting $\{x_3,x_4\}$ in ${\mathcal {D}}$. Now ${\mathcal {D}}_{x_1,x_3}=\{14,21\}$ and ${\mathcal {D}}_{x_1,x_4}=\{16,21,23\}$. The latter set can be viewed as

$$\begin{aligned} \{21\}\cup \{d+c: d\in {\mathcal {D}}_{x_1,x_3}, c=2\}, \end{aligned}$$

where 21 is the only distance realised by a path not going via the parent of $x_3$. Observe that ${\mathcal {D}}'_{x_1,x_4}=\{21\}$. Finally, ${\mathcal {D}}_{x_3,x_4}=\{6,14,21\}$, and ${\mathcal {D}}'_{x_3,x_4}=\{14,21\}$, where the length 6 up-down path is the only path removed by cutting $\{x_3,x_4\}$ in $({\mathcal {N}}_1, w_1)$.

The following theorem establishes the uniqueness part of Theorem 1.

Theorem 2

Let ${\mathcal {D}}$ be a multi-set distance matrix on X with distinguished element r. Let $({\mathcal {N}}, w)$ be a weighted tree-child network on X with outgroup r realising ${\mathcal {D}}$. Then, up to equivalence, $({\mathcal {N}}, w)$ is the unique such network realising ${\mathcal {D}}$.

Proof

The proof is by induction on the sum of the number n of leaves and the number k of reticulations in $({\mathcal {N}}, w)$. If this sum is 1, then $({\mathcal {N}}, w)$ consists of the single vertex r and so the theorem holds. If the sum is 2, then $({\mathcal {N}}, w)$ consists of two leaves attached to the root and again the theorem holds. Now suppose that $n+k\ge 3$ and the theorem holds for all weighted tree-child networks with outgroup r, where the sum of the number of leaves and the number of reticulations is at most $n+k-1$.

Let $\{s, t\}$ be a 2-element subset of $X-\{r\}$ such that

$$\begin{aligned} {\mathcal {Q}}_r(s, t)=\max \{{\mathcal {Q}}_r(x, y): x, y\in X-\{r\}\}. \end{aligned}$$

Then, by Lemma 3, $\{s, t\}$ is a k-reticulated cherry for some $k\in \{0, 1\}$. If $k=1$, we may assume without loss of generality that t is the reticulation leaf. Depending on k, let $({\mathcal {N}}', w')$ be the weighted tree-child network obtained from $({\mathcal {N}}, w)$ by reducing t if $k=0$ and cutting $\{s, t\}$ if $k=1$. Furthermore, let ${\mathcal {D}}'$ be the multi-set distance matrix obtained from ${\mathcal {D}}$ by reducing t in ${\mathcal {D}}$ if $k=0$ and by cutting $\{s, t\}$ in ${\mathcal {D}}$ if $k=1$. By Lemmas 2 and 4 respectively, $({\mathcal {N}}', w')$ is tree child and realises ${\mathcal {D}}'$. Since $({\mathcal {N}}', w')$ has $n-1$ leaves if $k=0$ and $k-1$ reticulations if $k=1$, it follows by the induction assumption that, up to equivalence, $({\mathcal {N}}', w')$ is the unique weighted tree-child network with outgroup r realising ${\mathcal {D}}'$.

Let $({\mathcal {N}}_1, w_1)$ be a weighted tree-child network on X with outgroup r realising ${\mathcal {D}}$. Since

$$\begin{aligned} {\mathcal {Q}}_r(s, t)=\max \{{\mathcal {Q}}_r(x, y): x, y\in X-\{r\}\}, \end{aligned}$$

it follows by Lemma 3 that $\{s, t\}$ is a k-reticulated cherry in $({\mathcal {N}}_1, w_1)$ for some $k\in \{0, 1\}$. First assume that $\{s, t\}$ is a 0-reticulated cherry in $({\mathcal {N}}, w)$. Then $|{\mathcal {D}}_{s, t}|=1$, and so $\{s, t\}$ is a 0-reticulated cherry in $({\mathcal {N}}_1, w_1)$. Let $({\mathcal {N}}'_1, w'_1)$ be the weighted tree-child network on $X-\{t\}$ obtained from $({\mathcal {N}}_1, w_1)$ by reducing t. Then, by Lemma 4, $({\mathcal {N}}'_1, w'_1)$ realises ${\mathcal {D}}'$ and so, by the induction assumption, $({\mathcal {N}}'_1, w'_1)$ is equivalent to $({\mathcal {N}}', w')$. Using this equivalence and considering a distance in ${\mathcal {D}}_{r, t}$, it is easily seen that $({\mathcal {N}}_1, w_1)$ is equivalent to $({\mathcal {N}}, w)$.

Now assume that $\{s, t\}$ is a 1-reticulated cherry in $({\mathcal {N}}, w)$. Then $|{\mathcal {D}}_{s, t}|\ne 1$, so $\{s, t\}$ is a 1-reticulation in $({\mathcal {N}}_1, w_1)$. Furthermore, as t is the reticulation leaf of $\{s, t\}$ in $({\mathcal {N}}, w)$,

$$\begin{aligned} \{d+c: d\in {\mathcal {D}}_{s, x}\}{\subsetneqq } {\mathcal {D}}_{t, x}, \end{aligned}$$

where $c=d_{\max }(r, t)-d_{\max }(r, s)$, for all $x\in X-\{s, t\}$, and so t is the reticulation leaf of $\{s, t\}$ in $({\mathcal {N}}_1, w_1)$. Let $({\mathcal {N}}'_1, w'_1)$ be the weighted tree-child network on X obtained from $({\mathcal {N}}_1, w_1)$ by cutting $\{s, t\}$. Then, as $({\mathcal {N}}_1, w_1)$ realises ${\mathcal {D}}$, it follows by Lemma 4 that $({\mathcal {N}}'_1, w'_1)$ realises ${\mathcal {D}}'$. Therefore, by the induction assumption, $({\mathcal {N}}'_1, w'_1)$ is equivalent to $({\mathcal {N}}', w')$. Using $d_{\min }(s, t)$, it is now easily deduced that $({\mathcal {N}}_1, w_1)$ is equivalent to $({\mathcal {N}}, w)$. This completes the proof of the theorem. $\square$

5 The Algorithm

Let $({\mathcal {N}}, w)$ be a weighted tree-child network on X with outgroup r. Let ${\mathcal {D}}$ be the multi-set distance matrix of $({\mathcal {N}}, w)$. In this section, we present the algorithm ${\mathcal {Q}}$-Reduction which takes as input X, ${\mathcal {D}}$, and r, and outputs $({\mathcal {N}}_0, w_0)$. As described at the end of the introduction, this algorithm recursively finds a 2-element subset that maximises the ${\mathcal {Q}}$-score with respect to r and then, depending on whether this subset is a 0- or 1-reticulated cherry, reduces or cuts a 2-element subset of X in the current distance matrix. Once this matrix is small, it recursively reverses these operations to construct $({\mathcal {N}}_0, w_0)$. Formally, ${\mathcal {Q}}$-Reduction works as follows:

• 1. If $|X|=1$, then return the phylogenetic network $({\mathcal {N}}_0, w_0)$ consisting of the single vertex r.

• 2. If $|X|=2$, say $X=\{r, s\}$, then return the phylogenetic network $({\mathcal {N}}_0, w_0)$ consisting of leaves r and s adjoined to the root $\rho$ with $(\rho , r)$ weighted the single value in ${\mathcal {D}}_{r, s}$ and $(\rho , s)$ weighted 0.

• 3. Else, find a 2-element subset $\{s, t\}$ of X such that

  $$\begin{aligned} {\mathcal {Q}}_r(s, t)=\max \{{\mathcal {Q}}_r(x, y): x, y\in X-\{r\}\}. \end{aligned}$$

  • (a) If $|{\mathcal {D}}_{s, t}|=1$ (in which case, $\{s, t\}$ is a 0-reticulated cherry), then

    • (i) Reduce t in ${\mathcal {D}}$ to give the multi-set distance matrix ${\mathcal {D}}'$ on $X'=X-\{t\}$.

    • (ii) Apply ${\mathcal {Q}}$-Reduction to input $X'$, ${\mathcal {D}}'$, and r. Construct $({\mathcal {N}}_0, w_0)$ from the returned network $({\mathcal {N}}'_0, w'_0)$ on $X'$ by reversing the reduction on t. In particular, if u is the parent of s in $({\mathcal {N}}'_0, w'_0)$, then subdivide (u, s) with a new vertex v, add a new leaf t and adjoin it with the new edge (v, t), assign weights $w_0(u, v)$ and $w_0(v, s)$ so that

      $$\begin{aligned} {\mathcal {Q}}_r(s, t)=\max \{{\mathcal {Q}}_r(x, y): x, y\in X-\{r\}\} \end{aligned}$$

      and

      $$\begin{aligned} w_0(u, v)+w_0(v, s)=w'_0(u, s), \end{aligned}$$

      and assign weight $w_0(v, t)$ so that $d_{\min }(s, t)=w_0(v, s)+w_0(v, t)$. Return $({\mathcal {N}}_0, w_0)$.

  • (b) Else ($\{s, t\}$ is a 1-reticulated cherry, in which case it has reticulation leaf t if, for all $x\in X-\{s, t\}$,

    $$\begin{aligned} \{d+c: d\in {\mathcal {D}}_{s, x}\}{\subsetneqq } {\mathcal {D}}_{t, x}, \end{aligned}$$

    where $c=d_{\max }(r, t)-d_{\max }(r, s)$),

    • (i) Cut $\{s, t\}$ in ${\mathcal {D}}$ to give the multi-set distance matrix ${\mathcal {D}}'$ on X.

    • (ii) Apply ${\mathcal {Q}}$-Reduction to input X, ${\mathcal {D}}'$, and r. Construct $({\mathcal {N}}_0, w_0)$ from the returned network $({\mathcal {N}}'_0, w'_0)$ on X by reversing the cutting of $\{s, t\}$. In particular, if $u_1$ and $u_2$ denote the parents of s and t, respectively, in $({\mathcal {N}}'_0, w'_0)$, then subdivide $(u_1, s)$ and $(u_2, t)$ with new vertices $v_1$ and $v_2$, respectively, adjoin $v_1$ and $v_2$ with the new edge $(v_1, v_2)$, assign weight $w_0(u_1, v_1)$ so that

      $$\begin{aligned} {\mathcal {Q}}_r(s, t)=\max \{{\mathcal {Q}}_r(x, y): x, y\in X\}, \end{aligned}$$

      assign weight $w_0(v_1, s)$ so that

      $$\begin{aligned} w_0(u_1, v_1)+w_0(v_1, s)=w'_0(u_1, s), \end{aligned}$$

      and assign weight 0 to $(v_1, v_2)$ and $(u_2, v_2)$, and weight $w'_0(u_2, t)$ to $(v_2, t)$. Return $({\mathcal {N}}_0, w_0)$.

The next theorem shows that ${\mathcal {Q}}$-Reduction does indeed work as expected.

Theorem 3

Let $({\mathcal {N}}, w)$ be a weighted tree-child network on X with outgroup r. Let ${\mathcal {D}}$ be the multi-set distance matrix of $({\mathcal {N}}, w)$. Then ${\mathcal {Q}}$-Reduction applied to X, ${\mathcal {D}}$, and r returns $({\mathcal {N}}_0, w_0)$.

Proof

The proof is by induction on the sum of the number n of leaves and the number k of reticulations in $({\mathcal {N}}, w)$. If this sum is 1, then $({\mathcal {N}}, w)$ consists of the single vertex r and ${\mathcal {Q}}$-Reduction correctly returns $({\mathcal {N}}_0, w_0)$. If the sum is 2, then $({\mathcal {N}}, w)$ consists of two leaves attached to the root and, again, ${\mathcal {Q}}$-Reduction correctly returns $({\mathcal {N}}_0, w_0)$.

Now suppose that $({\mathcal {N}}, w)$ has n leaves and k reticulations, where $n+k\ge 3$, and note that $n\ge 3$. Let ${\mathcal {D}}'$ be a multi-set matrix of distances on a set $X'$, and let r be a distinguished element in $X'$. Suppose that ${\mathcal {D}}'$ is realised by a weighted tree-child network $({\mathcal {N}}', w')$ on $X'$ with outgroup r, and with $n'$ leaves and $k'$ reticulations such that

$$\begin{aligned} 1\le n'+r'< n+r. \end{aligned}$$

The inductive hypothesis is that if ${\mathcal {Q}}$-Reduction is applied to $X'$, ${\mathcal {D}}'$, and r, then $({\mathcal {N}}'_0, w'_0)$ is returned.

Consider the run of the algorithm on input X, ${\mathcal {D}}$, and r. Since $n\ge 3$, at the first iteration it finds a 2-element subset $\{s, t\}$ of $X-\{r\}$ such that

$$\begin{aligned} {\mathcal {Q}}_r(s, t)=\max \{{\mathcal {Q}}_r(x, y): x, y\in X-\{r\}\}. \end{aligned}$$

Furthermore, by Lemma 3, as ${\mathcal {D}}$ is realised by $({\mathcal {N}}, w)$, either (i) we have $|{\mathcal {D}}_{s, t}|=1$ or (ii) without loss of generality we have

$$\begin{aligned} \{d+c: d\in {\mathcal {D}}_{s, x}\}{\subsetneqq } {\mathcal {D}}_{t, x}, \end{aligned}$$

where $c=d_{\max }(r, t)-d_{\max }(r, s)$. First suppose (i) holds. Then the algorithm reduces t in ${\mathcal {D}}$ producing the multi-set distance matrix ${\mathcal {D}}'$ on $X'=X-\{t\}$ given by

$$\begin{aligned} {\mathcal {D}}'_{x, y}={\mathcal {D}}'_{y, x}={\mathcal {D}}_{x, y} \end{aligned}$$

for all $x, y\in X'$. This completes the first iteration and ${\mathcal {Q}}$-Reduction is now recursively applied to $X'$, ${\mathcal {D}}'$, and r. By Lemma 4, ${\mathcal {D}}'$ is realised by a weighted tree-child network, $({\mathcal {N}}', w')$ say, on $X'$ with outgroup r. Since $({\mathcal {N}}', w')$ has $n-1$ leaves and k reticulations, it follows by the induction assumption that ${\mathcal {Q}}$-Reduction applied to $X'$, $D'$, and r returns $({\mathcal {N}}'_0, w'_0)$. It is easily checked that the construction in Step 3(a) (ii) of ${\mathcal {Q}}$-Reduction applied to $({\mathcal {N}}'_0, w'_0)$ returns $({\mathcal {N}}_0, w_0)$. In this construction, observe that there is exactly one choice for the weights of the edges incident with the parent of s and t in the returned network.

Now suppose (ii) holds. Then ${\mathcal {Q}}$-reduction cuts $\{s, t\}$ in ${\mathcal {D}}$ to produce the multi-set distance matrix ${\mathcal {D}}'$ on X. This completes the first iteration and ${\mathcal {Q}}$-Reduction is now recursively applied to X, ${\mathcal {D}}'$, and r. By Lemma 4, ${\mathcal {D}}'$ is realised by a weighted tree-child network $({\mathcal {N}}', w')$ on X with outgroup r. Since $({\mathcal {N}}', w')$ has n leaves and $k-1$ reticulations, it follows by the induction assumption that ${\mathcal {Q}}$-Reduction applied to X, ${\mathcal {D}}'$, and r returns $({\mathcal {N}}'_0, w'_0)$. It is easily checked that the construction in Step 3(b) (ii) of ${\mathcal {Q}}$-Reduction applied to $({\mathcal {N}}'_0, w'_0)$ returns $({\mathcal {N}}_0, w_0)$. Note that the weighting of $(u_1, v_1)$ is unique as is the weighting of $(v_1, s)$ in constructing $({\mathcal {N}}_0, w_0)$. $\square$

We now turn our attention to the running time of ${\mathcal {Q}}$-Reduction. The algorithm takes as input a set X, an $|X|\times |X|$ matrix ${\mathcal {D}}$ whose entries are multi-sets of up-down path distances of a weighted tree-child network $({\mathcal {N}}, w)$ on X, and an element r in X. We will assume that each entry in ${\mathcal {D}}$ is presented as an ascending list of distances. Unless $|X|\in \{1, 2\}$, in which case ${\mathcal {Q}}$-Reduction runs in constant time, each iteration involves finding a 2-element subset $\{s, t\}$ of $X-\{r\}$ such that

$$\begin{aligned} {\mathcal {Q}}_r(s, t)=\max \{{\mathcal {Q}}_r(x, y): x, y\in X-\{r\}\}. \end{aligned}$$

Since each entry is an ascending list of distances, finding such a subset takes $O(|X|^2)$ time, that is $O(|{\mathcal {D}}|)$ time, where |D| is the sum of the cardinalities of the multi-sets that are the elements of ${\mathcal {D}}$.

With a suitable 2-element subset of $X-\{r\}$ found, we compute ${\mathcal {D}}'$. This computation is done in one of two ways depending on whether or not $|{\mathcal {D}}_{s, t}|=1$. If $|{\mathcal {D}}_{s, t}|\ne 1$, we need to additionally check which of

$$\begin{aligned} \{d+c: d\in {\mathcal {D}}_{s, x}\}{\subsetneqq } {\mathcal {D}}_{t, x}\text { and }\{d-c: d\in {\mathcal {D}}_{t, x}\}{\subsetneqq } {\mathcal {D}}_{s, x}, \end{aligned}$$

where $c=d_{\max }(r, t)-d_{\max }(r, s)$ holds, for all $x\in X-\{s, t\}$. Since ${\mathcal {D}}$ is the multi-set distance matrix of $({\mathcal {N}}, w)$, it suffices to do this check for only one element in $X-\{s, t\}$ and this can be done in $O(|{\mathcal {D}}|)$ time. Computing ${\mathcal {D}}'$ takes $O(|{\mathcal {D}}|)$ time and once $({\mathcal {N}}'_0, w'_0)$ is returned, it can be augmented to $({\mathcal {N}}_0, w_0)$ in constant time. Hence the total time of the iteration is linear in $|{\mathcal {D}}|$.

When we recurse, the multi-set distance matrix ${\mathcal {D}}'$ inputted to the recursive call is strictly smaller than ${\mathcal {D}}$ since we either reduce an element, in which case we delete a row and column of ${\mathcal {D}}$, or we cut a 2-element set, in which case we delete elements in entries of ${\mathcal {D}}$. Thus the total number of iterations is at most $|{\mathcal {D}}|$, and so ${\mathcal {Q}}$-Reduction completes in time $O(|{\mathcal {D}}|^2)$. Together with Theorems 2 and 3, this establishes Theorem 1.

6 Stack-Free Networks

In this section, we consider an analogue of Theorem 1 for stack-free networks. Let $({\mathcal {N}}, w)$ be a weighted phylogenetic network on X. If F is a subset of edges of $({\mathcal {N}},w)$, we denote by w(F) the sum of the weights of the edges in F. Without loss of generality, let $E'$ be a subset of the edges of $({\mathcal {N}},w)$ consisting of all the tree edges of $({\mathcal {N}},w)$ and exactly one edge from each reticulation pair of $({\mathcal {N}},w)$. We say w is generic if $w(F)\ne w(G)$ for all distinct non-empty subsets F and G of $E'$. Up to the restriction that reticulation pairs have equal weights, if a weighting of each edge of ${\mathcal {N}}$ is selected independently from any continuous probability distribution on the positive reals, then the probability of the weighting being generic is one. Note that our requirement for a generic weighting is very close to the no-equally-long-paths (NELP) property of Pardi and Scornavacca [8], and is introduced for similar reasons.

In writing this paper, we felt we were tantalisingly close to establishing an analogue of Theorem 1 for stack-free networks with a generic weighting. In particular, the following which we state as a conjecture:

Conjecture 1

Let ${\mathcal {D}}$ be a multi-set distance matrix on X with a distinguished element r. Let $({\mathcal {N}}, w)$ be a generically-weighted stack-free network on X with outgroup r realising ${\mathcal {D}}$. Then, up to equivalence, $({\mathcal {N}}, w)$ is the unique such network realising ${\mathcal {D}}$.

Note that a reticulation-pair weighting is not sufficient for the conjecture to hold. Figure 4 gives an example of two reticulation-pair weighted, stack-free networks that share the same multiset-matrix of inter-taxa distances but are non-isomorphic.

Fig. 4

In this figure all edges have weight 1. ${\mathcal {N}}_1$ and ${\mathcal {N}}_2$ are two non-isomorphic stack-free phylogenetic networks on $\{x_1, x_2, x_3, x_4, y, r\}$ with the same multiset-matrix of inter-taxa distances

The following lemma supports Conjecture 1, in that it proves a partial result that could potentially be used in a proof of Conjecture 1. Given a distance matrix ${\mathcal {D}}$ on X with distinguished element r that is realised by a weighted stack-free network $({\mathcal {N}}, w)$ on X with outgroup r, this lemma not only allows us to find a 2-element subset of $X-\{r\}$ that is a 0- , 1- , or 2-reticulated cherry of $({\mathcal {N}}, w)$ using just ${\mathcal {D}}$, but also to determine its type. The notion of a generic weighting is crucially used in the proof of this lemma. Whether one can relax this condition remains an open problem.

Lemma 5

Let ${\mathcal {D}}$ be a multi-set distance matrix on X with a distinguished element r, where $|X|\ge 3$. Let $({\mathcal {N}}, w)$ be a generically-weight stack-free network on X with outgroup r realising ${\mathcal {D}}$. Let $\{s, t\}$ be a 2-element subset of $X-\{r\}$ such that

$$\begin{aligned} {\mathcal {Q}}_r(s, t)=\max \{{\mathcal {Q}}_r(x, y): x, y\in X\}. \end{aligned}$$

Then

• (i) $\{s, t\}$ is a 0-reticulated cherry in $({\mathcal {N}}, w)$ if $|{\mathcal {D}}_{s, t}|=1$;

• (ii) $\{s, t\}$ is a 1-reticulated cherry in $({\mathcal {N}}, w)$ with reticulation leaf t if, for all $x\in X-\{s, t\}$,

  $$\begin{aligned} \{d+c: d\in {\mathcal {D}}_{s, x}\}{\subsetneqq } {\mathcal {D}}_{t, x}, \end{aligned}$$

  where $c=d_{\max }(r, t)-d_{\max }(r,s)$; and

• (iii) $\{s, t\}$ is a 2-reticulated cherry in $({\mathcal {N}}, w)$ otherwise.

Proof

By Lemma 3, $\{s, t\}$ is a k-reticulated cherry for some $k\in \{0, 1, 2\}$. If $|{\mathcal {D}}_{s, t}|=1$, then it is clear that $\{s, t\}$ is a 0-reticulated cherry in $({\mathcal {N}}, w)$. Suppose that, for all $x\in X-\{s, t\}$,

$$\begin{aligned} \{d+c: d\in {\mathcal {D}}_{s, x}\}{\subsetneqq } {\mathcal {D}}_{t, x}, \end{aligned}$$

where $c=d_{\max }(r, t)-d_{\max }(r, s)$. We next show that, under this assumption, $\{s, t\}$ is a 1-reticulated cherry in $({\mathcal {N}}, w)$ with reticulation leaf t.

If $\{s, t\}$ is a 1-reticulated cherry in $({\mathcal {N}}, w)$, then, because of the strict subset assumption, t is the reticulation leaf. Assume, to the contrary, that $\{s, t\}$ is a 2-reticulated cherry in $({\mathcal {N}}, w)$. Let $p_s$ and $p_t$ be the parents of s and t in $({\mathcal {N}}, w)$, respectively. Let $g_{st}$ be a common parent of $p_s$ and $p_t$. Since $\{s, t\}$ is a 2-reticulated cherry in $({\mathcal {N}}, w)$, it follows that $p_s$ and $p_t$ have at least one such parent. If $p_s$ and $p_t$ have both parents in common, then $|{\mathcal {D}}_{s, x}|=|{\mathcal {D}}_{t, x}|$ for all $x\in X-\{s, t\}$; a contradiction. So $g_{st}$ is the only such parent. Let $g_s$ and $g_t$ be the parents of $p_s$ and $p_t$ in $({\mathcal {N}}, w)$, respectively, that is not $g_{st}$.

Let $z\in X-\{s, t\}$ such that z can be reached by an up-down path, $P_s$ say, starting at s, traversing $(g_s, p_s)$ in $({\mathcal {N}}, w)$. Since $\{d+c: d\in {\mathcal {D}}_{s, z}\}{\subsetneqq } {\mathcal {D}}_{t, z}$, there is an injection from the set of up-down paths from s to z to the set of up-down paths from t to z, where each path is mapped onto a path whose length differs by exactly c. Moreover, we may create this injection by extending the canonical bijection between the set of up-down paths starting at s, traversing $(g_{st}, p_s)$, and ending at z and the set of up-down paths starting at t, traversing $(g_{st}, p_t)$, and ending at z. Thus we may assume that under the injection each path traversing $(g_{s},p_s)$ maps to a path traversing $(g_t,p_t)$. Hence there is an up-down path $P_t$ starting at t and ending at z such that

$$\begin{aligned} w(P_s)+c&= w(P_t), \end{aligned}$$

(2)

where $w(P_s)$ and $w(P_t)$ are the sums of the weights of the edges in $P_s$ and $P_t$, respectively, and $P_t$ traverses $(g_t, p_t)$. By Lemma 3, $d_{\max }(r, t)$ and $d_{\max }(r,s)$ are realised by paths via $g_{st}$, hence we can express c as

$$\begin{aligned} c=w(g_{st}, p_t)+w(p_t, t)-w(g_{st}, p_s)-w(p_s, s), \end{aligned}$$

and so (2) implies

$$\begin{aligned} w(P_s)+w(g_{st}, p_t)+w(p_t, t)=w(P_t)+w(g_{st}, p_s)+w(p_s, s). \end{aligned}$$

(3)

Let $P'_s$ consist of the edges of $P_s$ starting at $g_s$ and ending at z, and let $P'_t$ consist of the edges of $P_t$ starting at $g_t$ and ending at z. So $w(P_s)=w(P'_s)+w(g_{s}, p_s)+w(p_s, s)$ and $w(P_t)=w(P'_t)+w(g_{t}, p_t)+w(p_t, t)$. Then, by (3)

$$\begin{aligned} w(P'_s)+w(g_{s}, p_s)+w(g_{st}, p_t)=w(P'_t)+w(g_{t}, p_t)+w(g_{st}, p_s). \end{aligned}$$

But as w is reticulation paired $w(g_{s}, p_s)=w(g_{st}, p_s)$ and $w(g_{t}, p_t)=w(g_{st}, p_t)$, so $w(P'_s)=w(P'_t)$, contradicting that w is generic. Thus $\{s, t\}$ is a 1-reticulated cherry with reticulation leaf t, and the lemma follows. $\square$

Unfortunately, although we are able to determine a 0- , 1- , or 2-reticulated cherry of $({\mathcal {N}}, w)$ using just ${\mathcal {D}}$, in the case that we find a pair $\{s, t\}$ that form a 2-reticulated cherry, it is not clear how to obtain a multi-set distance matrix ${\mathcal {D}}'$ from ${\mathcal {D}}$ such that ${\mathcal {D}}'$ is displayed by the network obtained from $({\mathcal {N}}, w)$ by cutting one of the reticulation edges in $\{s, t\}$. In particular it is not clear which elements of ${\mathcal {D}}_{s, t}$ should be in ${\mathcal {D}}'_{s, t}$.