Determining phylogenetic networks from inter-taxa distances

Abstract

We consider the problem of determining the topological structure of a phylogenetic network given only information about the path-length distances between taxa. In particular, one of the main results of the paper shows that binary tree-child networks are essentially determined by such information.

1 Introduction

A core component in the development and analysis of algorithms for reconstructing phylogenetic (evolutionary) trees has been the mathematical properties relating the input data to the desired output structure. For example the Build algorithm of Aho et al. (1981) and its various generalisations (e.g. Berry et al. 2013; Bordewich et al. 2006; Huber et al. 2011) rely on the property that the collection of rooted triples of a rooted phylogenetic tree ${\mathcal {T}}$ determine the topological structure of ${\mathcal {T}}$. Another example is the classical clustering algorithm UPGMA (Sokal and Michener 1958), which relies on the property that the closest pair of leaves in an ultrametric tree (a rooted phylogenetic tree with branch lengths satisfying a “molecular clock”) must share a common parent vertex. Understanding these properties, and under what circumstances they hold, is vital to developing and selecting accurate algorithms. For example, recognizing the reliance on the ultrametric assumption and that it is too strong for many situations has led to the widespread use of Neighbor Joining (Saitou and Nei 1987) instead of UPGMA to reconstruct phylogenetic trees from inter-taxa distances. Indeed, Neighbor Joining is one of numerous distanced-based methods for reconstructing phylogenetic trees that have been developed and refined. Other methods include least squares (Fitch and Margoliash 1967), BioNJ (Gascuel 1997), minimum evolution (Rzhetsky and Nei 1993), and balanced minimum evolution (Desper and Gascuel 2004).

In this paper, we consider the task of reconstructing phylogenetic networks, rather than phylogenetic trees, from information about inter-taxa distances, and what underlying mathematical properties of the data are required to determine the topological structure of such networks. This turns out to be a much more challenging and richer problem than that of reconstructing phylogenetic trees: a phylogenetic tree is determined uniquely by its inter-taxa distances, whereas this is not necessarily the case for phylogenetic networks (see Fig. 4). The rest of the introduction highlights three main results and ends with a description of the organisation of the paper.

Throughout the paper, X denotes a non-empty finite set. A rooted phylogenetic X-tree ${\mathcal {T}}$ is a rooted tree with no degree-two vertices, except possibly the root which has degree at least two, and whose leaf set is X. If $|X|=1$, then ${\mathcal {T}}$ consists of the single vertex in X. In addition, ${\mathcal {T}}$ is binary if either $|X|=1$ or the root has degree two and every other interior vertex has degree three. In evolutionary biology, rooted phylogenetic X-trees are used to represent the ancestral history of a collection X of present-day species. Here, one assumes that all evolutionary events are tree-like. However, it is now well-known that, for certain collections, phylogenetic networks rather than rooted phylogenetic trees provide a more accurate representation of the ancestral history as they allow for non-tree-like events. Collectively known as reticulation events, these events include recombination and hybridisation.

A phylogenetic network ${\mathcal {N}}$ on X is directed acyclic graph with the following properties:

• (i) a unique vertex of in-degree zero called the root, which has out-degree at least two (except in the case $|X|=1$),

• (ii) the set X is the set of vertices of out-degree zero, each of which has in-degree one, and

• (iii) every other vertex either has in-degree one and out-degree at least two, or in-degree at least two and out-degree one.

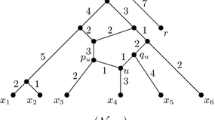
The vertices of out-degree zero are called leaves, while the vertices of in-degree one and out-degree at least two are called tree vertices and the vertices of in-degree at least two and out-degree one are called reticulations. The arcs directed into a reticulation are called reticulation arcs; all other arcs are called tree arcs. If $|X|=1$, then we also allow ${\mathcal {N}}$ to be the single vertex in X. In addition, ${\mathcal {N}}$ is binary if either ${\mathcal {N}}$ is a single vertex or the root has degree two and every other non-leaf vertex has degree three. To illustrate, Fig. 1a shows a binary phylogenetic network ${\mathcal {N}}$ on $X=\{x_1, x_2, x_3, x_4, x_5\}$, where $u_3$ and $u_4$ are the reticulations of ${\mathcal {N}}$. Observe that a rooted binary phylogenetic X-tree is a binary phylogenetic network on X with no reticulations and, more generally, a rooted phylogenetic X-tree is a phylogenetic network on X with no reticulations.

Fig. 1

a A binary phylogenetic network ${\mathcal {N}}$ on $X=\{x_1, x_2, x_3, x_4, x_5\}$, b the binary phylogenetic network ${\mathcal {N}}'$ on $X'=\{x_1, x_2, x_3, z\}$ obtained from ${\mathcal {N}}$ by reducing the cherry $\{x_4, x_5\}$ and replacing it with a new leaf z, and c the phylogenetic network ${\mathcal {N}}''$ on X obtained from ${\mathcal {N}}$ by reducing the reticulated cherry $\{x_1, x_2\}$

Let ${\mathcal {N}}$ be a phylogenetic network on X. For any two vertices u and v in ${\mathcal {N}}$ that are joined by an arc (u, v), we say u is a parent (or parent vertex) of v and, conversely, v is a child (or child vertex) of u. We say ${\mathcal {N}}$ is a tree-child network if every non-leaf vertex has a child which is either a tree vertex or a leaf. The phylogenetic network in Fig. 1a is a tree-child network. An underlying path (respectively, cycle) of ${\mathcal {N}}$ is a path (respectively, cycle) of the undirected graph containing as undirected edges all arcs of ${\mathcal {N}}$.

Given a phylogenetic network ${\mathcal {N}}$ on X, we define the multiset-matrix ${\mathcal {D}}$ of inter-taxa distances as follows. For any two elements $x,y\in X$, an up-down path from x to y is an underlying path $x,v_1,v_2,\ldots ,v_{k-1},y$ in ${\mathcal {N}}$ such that, for some $i\le k-1$, ${\mathcal {N}}$ contains the arcs

$$\begin{aligned} (v_i, v_{i-1}), (v_{i-1}, v_{i-2}), \ldots , (v_1, x) \end{aligned}$$

and

$$\begin{aligned} (v_i, v_{i+1}), (v_{i+1}, v_{i+2}), \ldots , (v_{k-1}, y). \end{aligned}$$

The length of an up-down path is the number of arcs it contains, here k. For example, in Fig. 1a, $x_1, u_2, u_1, u_4, x_3$ is an up-down path in ${\mathcal {N}}$ from $x_1$ to $x_3$.

Now let ${\mathcal {P}}_{x,y}$ be the set of distinct up-down paths from x to y in ${\mathcal {N}}$. The multiset of distances between x and y, denoted ${\mathcal {D}}_{x,y}$, is the multiset of path lengths in ${\mathcal {P}}_{x,y}$. Observe that ${\mathcal {D}}_{x,y}={\mathcal {D}}_{y,x}$ for all $x, y\in X$, and ${\mathcal {D}}_{x,x}=\{0\}$ for all $x\in X$. As an example, in Fig. 1a, it is easily checked that the multiset of distances between $x_2$ and $x_3$ is $\{5, 5, 6, 8\}$. The multiset-matrix ${\mathcal {D}}$ of ${\mathcal {N}}$ is the |X| by |X| matrix whose (x, y)-th entry is ${\mathcal {D}}_{x,y}$. Note that, when we restrict ${\mathcal {N}}$ to be a rooted phylogenetic X-tree, each ${\mathcal {P}}_{x,y}$ has a single element and thus ${\mathcal {D}}$ naturally corresponds to the standard matrix of inter-taxa distances, though technically each entry in our matrix ${\mathcal {D}}$ would be a set containing a single integer, rather than simply an integer. If ${\mathcal {D}}$ is the multiset-matrix of ${\mathcal {N}}$, we say ${\mathcal {N}}$ realises ${\mathcal {D}}$.

The first two results we highlight are the next two theorems. The first theorem concerns tree-child networks, while the second theorem concerns a subclass of temporal networks.

Theorem 1.1

Let ${\mathcal {D}}$ be a multiset-matrix of distances between elements of a set X. If there is a binary tree-child network ${\mathcal {N}}$ on X realising ${\mathcal {D}}$, with no arc joining the two children of the root then, up to isomorphism, ${\mathcal {N}}$ is the unique binary phylogenetic network on X realising ${\mathcal {D}}$, in which case ${\mathcal {N}}$ can be found in time quadratic in $|{\mathcal {D}}|$.

Note that we have specifically disallowed an arc between the children of the root. If the children of the root are u and v and there is an arc (u, v) in ${\mathcal {N}}$, then the multiset-matrix of distances realised by ${\mathcal {N}}$ is also realised by the network ${\mathcal {N}}'$ in which the arc (u, v) is deleted and replaced by the arc (v, u). In this case, ${\mathcal {N}}$ and ${\mathcal {N}}'$ are the only two binary phylogenetic networks on X realising ${\mathcal {D}}$, and the algorithm presented may easily be adapted to return both these networks.

To state the second theorem, let ${\mathcal {N}}$ be a binary phylogenetic network on X. An underlying cycle of ${\mathcal {N}}$ is a crown if it consists entirely of reticulation arcs. Further, a temporal labelling of ${\mathcal {N}}$ is a labelling $t:V({\mathcal {N}})\rightarrow \mathbb Z^+$ of the vertices of ${\mathcal {N}}$ with positive integers such that if (u, v) is a tree arc, then $t(u)<t(v)$, and if (u, v) is a reticulation arc, then $t(u)=t(v)$. We say ${\mathcal {N}}$ is temporal if it admits a temporal labelling. Biologically, the motivation for this definition is that if a phylogenetic network is temporal, then it is guaranteed to satisfy two natural timing constraints. The first constraint is successively occurring speciation events, and the second constraint is contemporaneously occurring reticulation events so that such events are realised by coexisting ancestral species. Note that not every binary phylogenetic network is temporal. More particularly, binary tree-child networks are not necessarily temporal as the binary phylogenetic network in Fig. 1a illustrates, and not all temporal binary phylogenetic networks are binary tree-child networks. A reticulation v is visible if there is a leaf $\ell$ such that every directed path from the root of ${\mathcal {N}}$ to $\ell$ passes through v.

Theorem 1.2

Let ${\mathcal {D}}$ be a multiset-matrix of distances between elements of a set X, and let ${\mathcal {N}}$ be a temporal binary phylogenetic network on X with no crowns and in which every reticulation is visible. If ${\mathcal {N}}$ realises ${\mathcal {D}}$, then, unless the children of the root are joined by an arc, up to isomorphism, ${\mathcal {N}}$ is the unique binary phylogenetic network on X realising ${\mathcal {D}}$, in which case ${\mathcal {N}}$ can be found in time quadratic in $|{\mathcal {D}}|$.

Theorem 1.1 shows that, given a multiset-matrix ${\mathcal {D}}$ of distances between elements of a set X, if there is a binary tree-child network on X realising ${\mathcal {D}}$, then ${\mathcal {N}}$ is the unique binary phylogenetic network realising ${\mathcal {D}}$. What if, instead, we are only given the set, rather than the multiset, of distances between elements of X? Does the analogous result hold? The third result we highlight says the answer is yes for temporal binary tree-child networks.

Let ${\mathcal {N}}$ be a phylogenetic network on X and let $x,y\in X$. The set of distances between x and y, denoted $\overline{{\mathcal {D}}_{x,y}}$, is the set of lengths of distinct up-down paths from x to y in ${\mathcal {N}}$. The set-matrix $\overline{{\mathcal {D}}}$ of ${\mathcal {N}}$ is the |X| by |X| matrix whose (x, y)-th entry is $\overline{{\mathcal {D}}_{x,y}}$. If $\overline{{\mathcal {D}}}$ is the set-matrix of ${\mathcal {N}}$, we say ${\mathcal {N}}$ realises $\overline{{\mathcal {D}}}$.

Theorem 1.3

Let $\overline{{\mathcal {D}}}$ be a set-matrix of distances between elements of a set X. If there is a temporal binary tree-child network ${\mathcal {N}}$ on X realising $\overline{{\mathcal {D}}}$, then, up to isomorphism, ${\mathcal {N}}$ is the unique binary phylogenetic network on X realising $\overline{{\mathcal {D}}}$, in which case ${\mathcal {N}}$ can be found in time quartic in |X|.

Tree-child networks were introduced by Cardona et al. (2009). By way of comparison with Theorems 1.1 and 1.3, let u be a vertex of a phylogenetic network ${\mathcal {N}}$ on $X=\{x_1, x_2, \ldots , x_n\}$. For each $i\in \{1, 2, \ldots , n\}$, let $p_i(u)$ denote the number of distinct directed paths from u to $x_i$ in ${\mathcal {N}}$. Further, let p(u) denote the n-tuple $(p_1(u), p_2(u), \ldots , p_n(u))$. The multiset $\mathcal P$ of path n-tuples of ${\mathcal {N}}$ is the multiset $\{p(u): u\in V({\mathcal {N}})\}$. If $\mathcal P$ is the multiset of path n-tuples of ${\mathcal {N}}$, we say ${\mathcal {N}}$ realises $\mathcal P$. The following theorem is established in Cardona et al. (2009).

Theorem 1.4

(Cardona et al. 2009, Theorem 1) Let X be a set of size n and let $\mathcal P$ be a multiset of path n-tuples. If ${\mathcal {N}}$ is a tree-child network on X realising ${\mathcal {P}}$, then, up to isomorphism, ${\mathcal {N}}$ is the unique tree-child network on X realising ${\mathcal {P}}$, in which case ${\mathcal {N}}$ can be found in polynomial time.

Note that, in the statement of Theorem 1.4, ${\mathcal {N}}$ is not necessarily binary. However, if ${\mathcal {N}}$ realises ${\mathcal {P}}$, then it is only guaranteed to be unique within the class of tree-child networks. For further details, see Cardona et al. (2009).

Related work on reconstructing phylogenetic networks from inter-taxa distances has been done by Willson (2012, 2013). An arc (u, v) in a rooted phylogenetic network ${\mathcal {N}}$ is redundant if there is a directed path from u to v in ${\mathcal {N}}$ which does not use the arc (u, v). A network in normal, if it is a tree-child network with no redundant arcs. In Willson (2012) it is shown that given both the network topology and average inter-taxa genetic distances for a normal network, then individual arc lengths and probabilities at each reticulation vertex can be inferred, which realize these average distances. In Willson (2013) sufficient conditions are given for when the network topology itself may be inferred from the average inter-taxa genetic distances, and these conditions are shown to be satisfied whenever the distances arise from a normal network with a single reticulation cycle. Hence Willson deals with a more complex and general case (average genetic distances rather than sets of path lengths) and so achieves more restricted results (handling a single reticulation, rather than all tree-child networks). For further details, including the definition of average genetic distance, see Willson (2013).

Throughout the paper, notation and terminology follows (Semple and Steel 2003). The paper is organised as follows. The next section contains some preliminaries, in particular, the concepts of cherries and reticulated cherries. In Sect. 3, we describe an algorithm that is central to the paper. This algorithm takes as input a multiset-matrix ${\mathcal {D}}$ of distances between elements in a set X and constructs, if possible, a binary phylogenetic network on X by recursively looking for values in ${\mathcal {D}}$ yielding cherries and reticulated cherries. The main result of this section shows that if a binary phylogenetic network ${\mathcal {N}}$ on X is returned by the algorithm, then ${\mathcal {N}}$ is the unique binary phylogenetic network on X realising ${\mathcal {D}}$. In Sect. 4, we make use of the results in Sect. 3 to prove the uniqueness parts of Theorems 1.1 and 1.2. Section 5 consists of the proof of the uniqueness part of Theorem 1.3. The running-time parts of Theorems 1.1–1.3 are established in Sect. 6. The paper ends with a brief discussion based around several open problems.

2 Preliminaries

Let ${\mathcal {N}}$ be a binary phylogenetic network on X. A 2-element subset $\{x, y\}$ of X is a cherry in ${\mathcal {N}}$ if there is an up-down path of length two between x and y. Equivalently, $\{x, y\}$ is a cherry if the parents of x and y are the same. Note that if there is an up-down path of length two between x and y, then this is the unique up-down path between x and y. As an example, $\{x_4, x_5\}$ is a cherry in the phylogenetic network shown in Fig. 1a. Reducing a cherry $\{x, y\}$ is the operation of deleting x and y, and their incident arcs, and labelling their common parent (now itself a leaf) with an element not in X. Observe that, by reducing a cherry, the number of leaves in the resulting binary phylogenetic network is reduced by one, but the number of reticulations is unchanged. In Fig. 1, the binary phylogenetic network ${\mathcal {N}}'$ on $X'=\{x_1, x_2, x_3, z\}$ shown in Fig. 1b has been obtained from the binary phylogenetic network ${\mathcal {N}}$ on X shown in Fig. 1a by reducing the cherry $\{x_4, x_5\}$ and replacing it with a new leaf z.

A two-element subset $\{x, y\}$ of X is a reticulated cherry in ${\mathcal {N}}$ if there is an up-down path of length three, say $x, v_1, v_2, y$, between x and y with one of $v_1$ and $v_2$ a tree vertex and the other a reticulation vertex. Necessarily, the arc joining $v_1$ and $v_2$ is directed from the tree vertex to the reticulation. This arc is referred to as the reticulation arc of the reticulated cherry. The leaf adjacent to the tree vertex is called the tree leaf of the reticulated cherry, and the leaf adjacent to the reticulation is the reticulation leaf of the reticulated cherry. Again note that if there is an up-down path of length three as above between x and y, then it is the unique up-down path of length 3 between x and y. In Fig. 1a, $\{x_1, x_2\}$ is a reticulated cherry in the phylogenetic network ${\mathcal {N}}$. Reducing a reticulated cherry $\{x, y\}$ is the operation of deleting the reticulation arc of the reticulated cherry and suppressing the degree-two vertices resulting from the deletion. Observe that, by reducing a reticulated cherry, the number of reticulations in the resulting binary phylogenetic network is reduced by one, but the number of leaves and, in particular, the leaf set, is unchanged. To illustrate, the binary phylogenetic network ${\mathcal {N}}''$ on X shown in Fig. 1c has been obtained from the binary phylogenetic network ${\mathcal {N}}$ on X shown in Fig. 1a by reducing the reticulated cherry $\{x_1, x_2\}$.

3 Reconstructing a network from the multiset-matrix of inter-taxa distances

In this section, we present the algorithm Multiset Cherry Reduction for reconstructing a binary phylogenetic network from a multiset-matrix of inter-taxa distances. We also show that, when the algorithm completes, it correctly constructs the unique binary phylogenetic network realising those distances. In the next section, we show that it always completes on binary tree-child networks with no arc joining the children of the root and a certain subclass of temporal binary phylogenetic networks.

For a set X and a multiset-matrix ${\mathcal {D}}$ of distances on X, Multiset Cherry Reduction applied to input X and ${\mathcal {D}}$ informally works by recursively finding a pair of elements $x, y\in X$ that yields a cherry or a reticulated cherry. After finding such a pair x, y, the algorithm reduces $\{x, y\}$, updates X and ${\mathcal {D}}$, and repeats. Eventually, Multiset Cherry Reduction either reduces X to a singleton or determines that there is no pair of leaves yielding a cherry or a reticulated cherry. If the former holds, then the algorithm works backwards and constructs a binary phylogenetic network on X, in which case, as we shall show, the constructed network is the unique binary phylogenetic network on X realising ${\mathcal {D}}$. Formally, Multiset Cherry Reduction works as follows:

• 1. If $|X|=1$, say $X=\{x\}$, then return the unique binary phylogenetic tree on one leaf x.

• 2. Else,

  • (a) If there is a pair $x, y\in X$ such that $2\in {\mathcal {D}}_{x,y}$ (thereby $\{x, y\}$ forms a cherry), then

    • (i) Reduce the cherry $\{x, y\}$ by adjusting ${\mathcal {D}}$ as follows. Let $z\not \in X$, and set $X'=(X-\{x,y\})\cup \{z\}$ and ${\mathcal {D}}'$ to be the multiset-matrix of inter-taxa distances on $X'$ given by ${\mathcal {D}}'_{v,w}={\mathcal {D}}_{v,w}$ if $v, w\in X-\{x, y\}$, and

      $$\begin{aligned} {\mathcal {D}}'_{z,v}={\mathcal {D}}'_{v,z}=\{d-1:d\in {\mathcal {D}}_{x,v}\} \end{aligned}$$

      if $v\in X-\{x, y\}$.

    • (ii) Reapply Multiset Cherry Reduction to input $X'$ and ${\mathcal {D}}'$. If a binary phylogenetic network ${\mathcal {N}}'$ on $X'$ is returned, form ${\mathcal {N}}$ by reversing the cherry reduction, replacing leaf z with a cherry $\{x, y\}$ by attaching pendant children x and y to z. Return the binary phylogenetic network ${\mathcal {N}}$ on X.

  • (b) Else,

    • (i) If there is a pair $x, y\in X$ such that $3\in {\mathcal {D}}_{x,y}, |X|\ge 3$, and

      $$\begin{aligned} \{d+1:d\in {\mathcal {D}}_{y,v}\}\subset {\mathcal {D}}_{x,v} \end{aligned}$$

      for all $v\in X-\{x, y\}$ (thereby $\{x, y\}$ forms a reticulated cherry with x the reticulation leaf), then

      • (I) For all $v\in X-\{x,y\}$, let ${\mathcal {D}}_{y,v}=\{d_1,d_2,\ldots ,d_k\}$ and ${\mathcal {D}}_{x,v}=\{d_1+1,d_2+1,\ldots ,d_k+1\}\cup \{d'_1,d'_2,\ldots ,d'_l\}$. Set ${\mathcal {D}}'$ to be the multiset-matrix of inter-taxa distances on X given by

        $$\begin{aligned} {\mathcal {D}}'_{x,v}= & {} {\mathcal {D}}'_{v,x}=\{d'_1-1,d'_2-1,\ldots ,d'_l-1\},\\ {\mathcal {D}}'_{y,v}= & {} {\mathcal {D}}'_{v,y}=\{d_1-1,d_2-1,\ldots ,d_k-1\},\\ {\mathcal {D}}'_{x,y}= & {} {\mathcal {D}}'_{y,x}=\{d-2:d\in {\mathcal {D}}_{x,y}-\{3\}\}, \end{aligned}$$

        and

        $$\begin{aligned} {\mathcal {D}}'_{v,w}={\mathcal {D}}_{v,w} \end{aligned}$$

        if $v, w\in X-\{x, y\}$.

      • (II) Reapply Multiset Cherry Reduction to input X and ${\mathcal {D}}'$. If a binary phylogenetic network ${\mathcal {N}}'$ on X is returned, form ${\mathcal {N}}$ by reversing the reticulated cherry reduction, subdividing the arcs to x and y, and adding an arc from the parent of y to the parent of x. Return the binary phylogenetic network ${\mathcal {N}}$ on X.

    • (ii) Else, there is no such pair of elements in X and return “Network not found”.

Note that, in the description of Multiset Cherry Reduction, we explicitly assume that any network returned by the algorithm applied to a set X and a multiset-matrix ${\mathcal {D}}$ of distances on X is a binary phylogenetic network on X. It follows by construction that this is indeed the case.

The next three lemmas establish that the various steps in the algorithm work. We then combine them to show that, up to isomorphism, when the algorithm returns a binary phylogenetic network on X, it is the unique binary phylogenetic network on X that realises the input X and ${\mathcal {D}}$.

Lemma 3.1

Let ${\mathcal {N}}$ be a binary phylogenetic network on X, and let $\{x,y\}$ be a cherry of ${\mathcal {N}}$. Let ${\mathcal {D}}$ be the multiset-matrix of inter-taxa distances of ${\mathcal {N}}$. Let $z\not \in X$, and let $X'=(X-\{x,y\})\cup \{z\}$ and ${\mathcal {D}}'$ be the multiset-matrix of inter-taxa distances on $X'$ given by ${\mathcal {D}}'_{v,w}={\mathcal {D}}_{v,w}$ if $v, w\in X-\{x, y\}$, and

$$\begin{aligned} {\mathcal {D}}'_{z,v}={\mathcal {D}}'_{v,z}=\{d-1:d\in {\mathcal {D}}_{x,v}\} \end{aligned}$$

if $v\in X-\{x, y\}$. Then ${\mathcal {D}}'$ is realised by the binary phylogenetic network ${\mathcal {N}}'$ on $X'$ obtained from ${\mathcal {N}}$ by reducing the cherry $\{x, y\}$, where the new leaf is labelled z. Moreover, up to isomorphism, if ${\mathcal {N}}'$ is the unique binary phylogenetic network on $X'$ realising ${\mathcal {D}}'$, then, up to isomorphism, ${\mathcal {N}}$ is the unique binary phylogenetic network on X realising ${\mathcal {D}}$.

Proof

We begin by first noting that, if we label the parent of x and y in ${\mathcal {N}}$ by z, and then delete x and y, and their incident arcs, we obtain ${\mathcal {N}}'$. Thus, for all $v,w\in X-\{x,y\}$, any up-down path in ${\mathcal {N}}'$ between v and w does not pass through z, and so the up-down paths between v and w in ${\mathcal {N}}$ are exactly the up-down paths between v and w in ${\mathcal {N}}'$. Further, for all $v\in X-\{x,y\}$, each up-down path between x (respectively, y) and v passes through the common parent of x and y in ${\mathcal {N}}$, and corresponds to precisely one up-down path between z and v in ${\mathcal {N}}'$, namely the same up-down path but with (z, x) [respectively, (z, y)] omitted. Hence the set of up-down paths between x (respectively, y) and v in ${\mathcal {N}}$ induces a bijection with the set of up-down paths between z and v in ${\mathcal {N}}'$, where each path maps onto a path that is exactly one arc shorter. Hence ${\mathcal {D}}'$ is realised by the binary phylogenetic network ${\mathcal {N}}'$ on $X'$.

Finally, suppose that, up to isomorphism, ${\mathcal {N}}'$ is the unique binary phylogenetic network on $X'$ realising ${\mathcal {D}}'$. Let ${\mathcal {N}}_1$ be a binary phylogenetic network on X that realises ${\mathcal {D}}$. Since $\{x,y\}$ is a cherry in ${\mathcal {N}}$, we have $2 \in {\mathcal {D}}_{x,y}$, so $\{x,y\}$ is a cherry in ${\mathcal {N}}_1$. By the first part of the lemma, the network ${\mathcal {N}}'_1$, obtained from ${\mathcal {N}}_1$ by reducing the cherry $\{x,y\}$, also realises ${\mathcal {D}}'$, and so, by assumption, ${\mathcal {N}}'_1$ must be isomorphic to ${\mathcal {N}}'$. It now follows that ${\mathcal {N}}_1$ is isomorphic to ${\mathcal {N}}$, completing the proof of the lemma. $\square$

Lemma 3.2

Let ${\mathcal {D}}$ be the multiset-matrix of inter-taxa distances on X with $|X|\ge 3$. Suppose there is a pair of elements $x, y\in X$ such that $3\in {\mathcal {D}}_{x,y}$ and $\{d+1:d\in {\mathcal {D}}_{y,v}\}\subset {\mathcal {D}}_{x,v}$ for all $v\in X-\{x, y\}$. If ${\mathcal {N}}$ is a binary phylogenetic network on X realising ${\mathcal {D}}$, then $\{x, y\}$ is a reticulated cherry of ${\mathcal {N}}$ with x the reticulation leaf.

Proof

Suppose ${\mathcal {N}}$ is a binary phylogenetic network on X realising ${\mathcal {D}}$. Then there is an up-down path P of length 3 between x and y in ${\mathcal {N}}$. Let p and q be the parents of x and y, respectively, in ${\mathcal {N}}$. Now P contains the arcs (q, y) and (p, x), and an arc between q and p. Due to the condition relating ${\mathcal {D}}_{x,v}$ and ${\mathcal {D}}_{y,v}$ for all $v\in X-\{x, y\}$ in the statement of the lemma, it can only be that the third arc is (q, p). Since q has two child vertices, it must be a tree vertex. Suppose, for a contradiction, that p is also a tree vertex. Then, for all $v\in X-\{x,y\}$, there is a bijection between the set of up-down paths from y to v and those from x to v. In particular, $|{\mathcal {D}}_{x,v}|=|{\mathcal {D}}_{y,v}|$ for all $v\in X-\{x, y\}$, contradicting the assumption that $\{d+1:d\in {\mathcal {D}}_{y,v}\}$ is a proper subset of ${\mathcal {D}}_{x,v}$ for all $v\in X-\{x, y\}$. Hence p is a reticulation, and the lemma immediately follows. $\square$

Lemma 3.3

Let ${\mathcal {N}}$ be a binary phylogenetic network on X with $|X|\ge 3$, and let $\{x,y\}$ be a reticulated cherry of ${\mathcal {N}}$ with x the reticulation leaf. Let ${\mathcal {D}}$ be the multiset-matrix of inter-taxa distances of ${\mathcal {N}}$. Then the following hold:

• (i) Let $v\in X-\{x,y\}$. If ${\mathcal {D}}_{y,v}=\{d_1,d_2,\ldots ,d_k\}$, then

  $$\begin{aligned} {\mathcal {D}}_{x,v}=\{d_1+1,d_2+1,\ldots ,d_k+1\}\cup \{d'_1,d'_2,\ldots ,d'_l\}, \end{aligned}$$

  where the elements in the first set correspond to the lengths of up-down paths between x and v that make use of the reticulation arc of the reticulated cherry $\{x, y\}$, and the elements in the second set correspond to the lengths of up-down paths between x and v that make use of the arc incident with the parent of x that is not the reticulation arc of $\{x, y\}$.

• (ii) Let ${\mathcal {D}}'$ be the multiset-matrix of inter-taxa distances on X given by

  $$\begin{aligned} {\mathcal {D}}'_{x,v}={\mathcal {D}}'_{v,x}=\{d'_1-1,d'_2-1,\ldots ,d'_l-1\} \end{aligned}$$

  and

  $$\begin{aligned} {\mathcal {D}}'_{y,v}={\mathcal {D}}'_{v,y}=\{d_1-1,d_2-1,\ldots ,d_k-1\} \end{aligned}$$

  if $v\in X-\{x, y\}$,

  $$\begin{aligned} {\mathcal {D}}'_{x,y}={\mathcal {D}}'_{y, x}=\{d-2:d\in {\mathcal {D}}_{x,y}-\{3\}\}, \end{aligned}$$

  and ${\mathcal {D}}'_{v,w}={\mathcal {D}}_{v,w}$ if $v,w\in X-\{x, y\}$. Then ${\mathcal {D}}'$ is realised by the binary phylogenetic network ${\mathcal {N}}'$ on X obtained from ${\mathcal {N}}$ by reducing the reticulated cherry $\{x, y\}$.

• (iii) If, up to isomorphism, ${\mathcal {N}}'$ is the unique binary phylogenetic network on X realising ${\mathcal {D}}'$, then, up to isomorphism, ${\mathcal {N}}$ is the unique binary phylogenetic network on X realising ${\mathcal {D}}$.

Proof

Let p and q be the parents of x and y, respectively, in ${\mathcal {N}}$. Since q is a tree vertex, it has a unique parent $q'$ and, since p is a reticulation vertex, it has a parent $p'$ additional to q. The reduction of the reticulated cherry $\{x, y\}$ involves removing the arc (q, p) and suppressing the resulting degree-two vertices q and p. Intuitively, we delete q and p, and their incident arcs, and introduce arcs $(q',y)$ and $(p',x)$. Part (i) of the lemma follows easily from the definitions by noting that every up-down path P from x to a leaf $v\in X-\{x,y\}$ does exactly one of the following: either passes through q, in which case we could remove the two arcs (q, p) and (p, x) from P, and replace them with the arc (q, y) to obtain an up-down path from y to v that is one arc shorter than P, or it does not pass through q, in which case it uses the arc $(p',p)$.

For (ii), first note that any up-down path between a pair of vertices in ${\mathcal {N}}$ that uses the reticulation arc of the reticulated cherry $\{x, y\}$ is a path between x and some other leaf. Consider first the up-down paths between x and y in ${\mathcal {N}}$. The only up-down path between x and y that uses the reticulation arc of the reticulated cherry $\{x, y\}$ is the unique up-down path of length 3 between x and y. All other up-down paths between x and y are preserved in the reduction of the reticulated cherry $\{x, y\}$, although their lengths are shortened by 2 as the vertices q and p are suppressed.

Now consider the up-down paths between x and v in ${\mathcal {N}}$, where $v\in X-\{x,y\}$. The up-down paths present in ${\mathcal {N}}$ but not ${\mathcal {N}}'$ between x and v are precisely those that use (q, p). All remaining up-down paths between x and v each have their length reduced by 1 following the reduction of the reticulated cherry $\{x, y\}$ as the vertex p is suppressed. It is now easily checked that ${\mathcal {D}}'$ is realised by ${\mathcal {N}}'$.

Finally, for (iii), suppose ${\mathcal {N}}'$ is the unique binary phylogenetic network on X realising ${\mathcal {D}}'$, and let ${\mathcal {N}}_1$ be a binary phylogenetic network on X realising ${\mathcal {D}}$. By Lemma 3.2, $\{x,y\}$ is a reticulated cherry in ${\mathcal {N}}_1$. Furthermore, by (ii), the binary phylogenetic network ${\mathcal {N}}'_1$ on X obtained from ${\mathcal {N}}_1$ by reducing the reticulated cherry $\{x,y\}$ also realises ${\mathcal {D}}'$. Therefore, by the assumption in the statement, ${\mathcal {N}}'_1$ is isomorphic to ${\mathcal {N}}'$. It is now easily seen that ${\mathcal {N}}_1$ is isomorphic to ${\mathcal {N}}$. $\square$

Theorem 3.4

Let ${\mathcal {D}}$ be a multiset-matrix of inter-taxa distances on X. If Multiset Cherry Reduction applied to X and ${\mathcal {D}}$ returns a binary phylogenetic network ${\mathcal {N}}$ on X, then, up to isomorphism, ${\mathcal {N}}$ is the unique binary phylogenetic network on X that realises ${\mathcal {D}}$.

Proof

Suppose that Multiset Cherry-Reduction applied to X and ${\mathcal {D}}$ returns a binary phylogenetic network ${\mathcal {N}}$ on X. The proof is by induction on the sum of the number n of leaves and the number r of reticulations in ${\mathcal {N}}$. The base case is when this sum is 1, in which case ${\mathcal {N}}$ has one leaf and zero reticulations. Up to isomorphism, there is only one binary phylogenetic network on X with these parameters, which is the unique rooted binary phylogenetic tree on one leaf, and it is correctly returned by the algorithm. Now suppose that ${\mathcal {N}}$ has n leaves and r reticulations, where $n+r\ge 2$. The inductive hypothesis is that, for any multiset-matrix ${\mathcal {D}}'$ of inter-taxa distances on a set $X'$, if Multiset Cherry Reduction applied to $X'$ and ${\mathcal {D}}'$ returns a binary phylogenetic network ${\mathcal {N}}'$ on $X'$ with $n'$ leaves and $r'$ reticulations such that $1\le n'+r'< n+r$, then, up to isomorphism, ${\mathcal {N}}'$ is the unique binary phylogenetic network on $X'$ that realises ${\mathcal {D}}'$.

Consider the run of the algorithm on input X and ${\mathcal {D}}$. Since it returns a binary phylogenetic network on X, the first iteration finds either (i) a pair of elements $x,y\in X$ at distance 2 in ${\mathcal {D}}$, or (ii) no pair of elements in X at distance 2 in ${\mathcal {D}}$, but a pair $x,y\in X$ such that $3\in {\mathcal {D}}_{x,y}, |X|\ge 3$, and $\{d+1:d\in {\mathcal {D}}_{y,v}\}\subset {\mathcal {D}}_{x,v}$ for all $v\in X-\{x, y\}$. If (i) occurs in the first iteration, let $X'=(X-\{x,y\})\cup \{z\}$, where $z\not \in X$ is the new element replacing the cherry $\{x, y\}$, and set ${\mathcal {D}}'$ to be the multiset-matrix of inter-taxa distances on $X'$ given by ${\mathcal {D}}'_{v,w}={\mathcal {D}}_{v,w}$ if $v, w\in X-\{x, y\}$, and

$$\begin{aligned} {\mathcal {D}}'_{z,v}={\mathcal {D}}'_{v,z}=\{d-1:d\in {\mathcal {D}}_{x,v}\} \end{aligned}$$

if $v\in X-\{x, y\}$. After the first iteration, Multiset Cherry Reduction is recursively applied to $X'$ and ${\mathcal {D}}'$, and eventually constructs a binary phylogenetic network ${\mathcal {N}}'$ on $X'$. Since $n'<n$ and, by construction, $r'=r$, it follows by the inductive hypothesis that, up to isomorphism, ${\mathcal {N}}'$ is the unique binary phylogenetic network on $X'$ realising ${\mathcal {D}}'$. By Lemma 3.1, ${\mathcal {N}}$, which the algorithm constructs from ${\mathcal {N}}'$ by replacing the leaf z with the cherry $\{x,y\}$, is the unique binary phylogenetic network on X realising ${\mathcal {D}}$ up to isomorphism.

We may now assume that (ii) occurs. Let ${\mathcal {D}}'$ be the multiset-matrix of inter-taxa distances on X as given in the statement of Lemma 3.3(ii). After the first iteration, Multiset Cherry Reduction is recursively applied to X and ${\mathcal {D}}'$, and constructs a binary phylogenetic network ${\mathcal {N}}'$ on X with $r'$ reticulations. Finally, the algorithm constructs ${\mathcal {N}}$ from ${\mathcal {N}}'$ by subdividing the pendant arcs incident with the leaves x and y, and adding an arc from the parent of y to the parent of x. Since this creates a new reticulation, $r'<r$. As $n'=n$, it follows by the inductive hypothesis that, up to isomorphism, ${\mathcal {N}}'$ is the unique binary phylogenetic network on X realising ${\mathcal {D}}'$. By Lemmas 3.2 and 3.3, up to isomorphism, ${\mathcal {N}}$ is the unique binary phylogenetic network on X realising ${\mathcal {D}}$. This completes the proof of the theorem. $\square$

4 Tree-child networks

In this section, we prove the uniqueness parts of Theorems 1.1 and 1.2. For an arbitrary phylogenetic network on X, a non-leaf vertex u has the tree-child property if it has a child that is either a tree vertex or a leaf. With this definition, a phylogenetic network on X is a tree-child network if each non-leaf vertex has the tree-child property. We begin with the following lemma.

Lemma 4.1

Let ${\mathcal {N}}$ be a binary tree-child network on X. Then the following hold:

• (i) If $|X|\ge 2$, then ${\mathcal {N}}$ contains either a cherry or a reticulated cherry.

• (ii) If ${\mathcal {N}}'$ is obtained from ${\mathcal {N}}$ by reducing either a cherry or a reticulated cherry, then ${\mathcal {N}}'$ is a binary tree-child network.

Proof

To prove (i), suppose that $|X|\ge 2$ and ${\mathcal {N}}$ does not contain a cherry. Since all rooted binary phylogenetic X-trees with $|X|\ge 2$ contain a cherry, it follows that ${\mathcal {N}}$ has a reticulation. Let v be a reticulation in ${\mathcal {N}}$ such that amongst all reticulations it is at maximum distance from the root; thus a longest directed path P from the root to v is a maximum length directed path from the root to any reticulation in ${\mathcal {N}}$. Let $u_1$ and $u_2$ denote the parent vertices of v. If $u_i$ is a reticulation for some $i\in \{1, 2\}$, then, as v is a reticulation and the only child of $u_i$ (since ${\mathcal {N}}$ is binary), it follows that $u_i$ does not have the tree-child property; a contradiction. Thus both $u_1$ and $u_2$ are tree vertices. Now P passes through either $u_1$ or $u_2$. Without loss of generality, we may assume it passes through $u_1$. Let the child vertex of $u_1$ that is not v be w. Note that w is a tree vertex or a leaf; otherwise, $u_1$ does not have the tree-child property. By the maximality of P, no reticulations can be reached by a directed path from either v or w. Intuitively, this implies that the structures below v and below w are tree-like. If two or more leaves are reachable from v via a directed path, then ${\mathcal {N}}$ contains a cherry; a contradiction. So the only vertex reachable from v is a single leaf, x say. A similar argument shows that w itself is a leaf. Thus $\{x, w\}$ is a reticulated cherry in ${\mathcal {N}}$ with x the reticulation leaf. This establishes (i).

For the proof of (ii), let ${\mathcal {N}}'$ be obtained from ${\mathcal {N}}$ by reducing either a cherry or a reticulated cherry. Consider some non-leaf vertex $u'$ in ${\mathcal {N}}'$, and let u denote the corresponding non-leaf vertex in ${\mathcal {N}}$. Since ${\mathcal {N}}$ is a tree-child network, u has a child vertex w in ${\mathcal {N}}$ which is either a tree vertex or a leaf. First assume we reduced a cherry $\{x, y\}$ to create ${\mathcal {N}}'$. Let $z\not \in X$ denote the leaf in ${\mathcal {N}}'$ that replaces the cherry $\{x, y\}$. Then either $u'$ is the parent of z in ${\mathcal {N}}'$ and the vertex corresponding to w in ${\mathcal {N}}'$ is z (hence a leaf) or the vertex corresponding to w in ${\mathcal {N}}'$ is unchanged and therefore still a tree-vertex or a leaf in ${\mathcal {N}}'$ after the reduction. In both cases, ${\mathcal {N}}'$ is a binary tree-child network. Now assume we reduced a reticulated cherry $\{x, y\}$ with x the reticulation leaf to create ${\mathcal {N}}'$. Then either $u'$ is the parent of x or y in ${\mathcal {N}}'$, or the vertex corresponding to w in ${\mathcal {N}}'$ is unchanged and still a tree-vertex or a leaf after the reduction. Regardless, ${\mathcal {N}}'$ is a binary tree-child network, thereby establishing (ii). $\square$

Proposition 4.2

Let ${\mathcal {N}}$ be a binary tree-child network on X with no arc joining the children of the root, and let ${\mathcal {D}}$ be the multiset-matrix of inter-taxa distances of ${\mathcal {N}}$. Then Multiset Cherry Reduction applied to X and ${\mathcal {D}}$ returns ${\mathcal {N}}$, up to isomorphism.

Proof

If $|X|=1$, then there is only one possible binary tree-child network on X, and this is the unique binary phylogenetic network consisting of the vertex in X, in which case it is correctly returned by the algorithm. Using this as the base case, a simple induction argument in combination with Lemmas 3.1, 3.3, and 4.1 proves the proposition. $\square$

Combining Theorem 3.4 and Proposition 4.2 establishes the uniqueness part of Theorem 1.1. We next prove the uniqueness part of Theorem 1.2.

Lemma 4.3

Let ${\mathcal {N}}$ be a temporal binary phylogenetic network on X with no crowns and in which every reticulation is visible. Then the following hold:

• (i) If $|X|\ge 2$, ${\mathcal {N}}$ contains either a cherry or a reticulate cherry.

• (ii) If ${\mathcal {N}}'$ is obtained from ${\mathcal {N}}$ by reducing either a cherry or a reticulated cherry, then ${\mathcal {N}}'$ is a temporal binary phylogenetic network with no crowns and in which every reticulation is visible.

Proof

Let t be a temporal labelling of ${\mathcal {N}}$. For the proof of (i), let v be a reticulation of ${\mathcal {N}}$ that maximises t(v). Starting at v construct a maximal underlying path P consisting entirely of reticulation arcs. Since each reticulation is visible, the child vertex of every reticulation in ${\mathcal {N}}$ is a tree vertex or a leaf, and so P alternates between following arcs against the direction and with the direction. Furthermore, as ${\mathcal {N}}$ has no crowns, this path eventually terminates at each end at a tree vertex, u say, with one child $u_1$ of u a tree vertex or a leaf and the other child $u_2$ a reticulation in P. Since $t(u_1)>t(u)=t(v)$, it follows by the maximality of t(v) that no reticulation can be reached from $u_1$, that is there is no directed path starting at $u_1$ and ending at a reticulation. Moreover, as $t(u_2)=t(u)=t(v)$, no reticulation can be reached from $u_2$ except for $u_2$ itself. If two or more leaves can be reached from $u_1$, or two or more leaves can be reached from $u_2$, then ${\mathcal {N}}$ contains a cherry. Therefore we may assume that $u_1$ itself is a leaf and the child vertex of $u_2$, say x, is a leaf. But then $\{x, u_1\}$ is a reticulated cherry of ${\mathcal {N}}$ with x the reticulation leaf, completing the proof of (i).

To prove (ii), let ${\mathcal {N}}'$ be a binary phylogenetic network obtained from ${\mathcal {N}}$ by reducing either a cherry or a reticulated cherry, $\{x, y\}$ say. First assume that $\{x, y\}$ is a cherry, and ${\mathcal {N}}'$ is obtained by reducing $\{x, y\}$ and replacing it with a leaf $z\not \in X$. Let $t':V({\mathcal {N}}')\rightarrow {\mathbb Z}^+$ be the labelling obtained from t by setting $t'(u')=t(u)$, where u is the vertex of ${\mathcal {N}}$ corresponding to $u'$ if $u'\ne z$, and $t'(z)=t(p)$, where p is the parent of x and y in ${\mathcal {N}}$. Since t is a temporal labelling of ${\mathcal {N}}$, it follows that $t'$ is a temporal labelling of ${\mathcal {N}}$. Furthermore, it is easily checked that, as ${\mathcal {N}}$ has no crowns and each reticulation is visible, ${\mathcal {N}}'$ has no crowns and each reticulation is visible.

Now assume that $\{x, y\}$ is a reticulated cherry with x the reticulation leaf. Let $t':V({\mathcal {N}}')\rightarrow {\mathbb Z}^+$ be the labelling obtained from t by setting $t'(u')=t(u)$, where u is the vertex of ${\mathcal {N}}$ corresponding to $u'$. Noting that $t(x)>t(p)$ and $t(y)>t(q)$, where p and q are the unique parents of x and y in ${\mathcal {N}}$, respectively, it follows that $t'$ is a temporal labelling of ${\mathcal {N}}'$. Also, since deleting a reticulation arc keeps the property of having no crowns and each reticulation being visible, ${\mathcal {N}}'$ has no crowns and each reticulation is visible. This completes the proof of (ii). $\square$

A simple induction argument in combination with Lemmas 3.1, 3.3, and 4.3 establishes the following proposition.

Proposition 4.4

Let ${\mathcal {N}}$ be a temporal binary phylogenetic network on X with no crowns and in which every reticulation is visible. Then Multiset Cherry Reduction applied to X and ${\mathcal {D}}$ returns ${\mathcal {N}}$ up to isomorphism.

The uniqueness part of Theorem 1.2 now follows from Theorem 3.4 and Proposition 4.4.

5 Temporal tree-child networks

This section consists of the proof of the uniqueness part of Theorem 1.3. The overall approach is similar to that used to prove the analogous parts of Theorems 1.1 and 1.2 but, instead of working with multisets, we are working with sets. We begin with three lemmas.

Let ${\mathcal {N}}$ be a binary phylogenetic network on X. A triple (x, y, z) of distinct elements of X is a double-reticulated cherry if both $\{x, y\}$ and $\{x, z\}$ are reticulated cherries of ${\mathcal {N}}$, in which case, necessarily, x is the reticulation leaf for both $\{x, y\}$ and $\{x, z\}$. To illustrate, $(x_3, x_2, x_4)$ is a double-reticulated cherry of the binary phylogenetic network ${\mathcal {N}}$ on $\{x_1, x_2, x_3, x_4, x_5\}$ shown in Fig. 2.

Fig. 2

A binary phylogenetic network ${\mathcal {N}}$ on $\{x_1, x_2, x_3, x_4, x_5\}$ with a double-reticulated cherry $(x_3, x_2, x_4)$

Lemma 5.1

Let ${\mathcal {N}}$ be a temporal binary tree-child network on X. Then the following hold:

• (i) If $|X|\ge 2$, then ${\mathcal {N}}$ contains either a cherry or a double-reticulated cherry.

• (ii) If ${\mathcal {N}}'$ is obtained from ${\mathcal {N}}$ by reducing either a cherry or a reticulated cherry, then ${\mathcal {N}}'$ is a temporal binary tree-child network.

Proof

To prove (i), let t be a temporal labelling of ${\mathcal {N}}$, and suppose that $|X|\ge 2$ and ${\mathcal {N}}$ has no cherries. Then ${\mathcal {N}}$ has a reticulation. Let v be a reticulation in ${\mathcal {N}}$ that maximises t(v). Let $u_1$ and $u_2$ be the parents of v. Furthermore, let y and z be the child of $u_1$ and $u_2$, respectively, that is not v. Since each of $u_1$ and $u_2$ has the tree-child property, y and z exist. Now $t(y)>t(u_1)=t(v)$ and $t(z)>t(u_2)=t(v)$. Therefore, as ${\mathcal {N}}$ has no cherries, it follows by the maximality of t(v) that both y and z are leaves. A similar argument shows that the unique child of v, say x, is also a leaf. Hence (x, y, z) is a double-reticulated cherry, completing the proof of (i).

For the proof of (ii), first note that, as each non-leaf vertex in ${\mathcal {N}}$ has the tree-child property, ${\mathcal {N}}$ has no crowns and every reticulation is visible. Thus, by combining Lemmas 4.1(ii) and 4.3(ii), we deduce (ii). $\square$

Lemma 5.2

Let $\overline{{\mathcal {D}}}$ be the set-matrix of inter-taxa distances on X. Suppose that there are distinct elements $x, y, z\in X$ with the following properties:

• (i) $3\in \overline{{\mathcal {D}}_{x,y}}$ and $3\in \overline{{\mathcal {D}}_{x,z}}$,

• (ii) $\{d+1:d\in \overline{{\mathcal {D}}_{y,v}}\}\subseteq \overline{{\mathcal {D}}_{x,v}}$ for all $v\in X-\{x, y\}$, and

• (iii) $\{d+1:d\in \overline{{\mathcal {D}}_{z,v}}\}\subseteq \overline{{\mathcal {D}}_{x,v}}$ for all $v\in X-\{x, z\}$.

If ${\mathcal {N}}$ is a binary phylogenetic network on X realising $\overline{{\mathcal {D}}}$, then (x, y, z) is a double-reticulated cherry of ${\mathcal {N}}$.

Proof

Suppose ${\mathcal {N}}$ is a binary phylogenetic network on X realising $\overline{{\mathcal {D}}}$. Then there are up-down paths $P_1$ and $P_2$ of length 3 between x and y, and between x and z, respectively. If p denotes the parent of x, and $q_1$ and $q_2$ denote the parents of y and z, respectively, then $P_1$ contains $(q_1, y)$ and (p, x), and $P_2$ contains $(q_2, z)$ and (p, x). As x, y, z satisfy (ii) and (iii) in the statement of the lemma, $P_1$ must contain $(q_1, p)$ and $P_2$ must contain $(q_2, p)$. Thus p is a reticulation, and it follows that (x, y, z) is a double-reticulated cherry of ${\mathcal {N}}$. $\square$

The proof of the next lemma is similar to the proofs of Lemmas 3.1 and 3.3, and omitted. However, we note that Lemma 5.2 is used to prove Lemma 5.3(ii) in the analogous way that Lemma 3.2 was used to prove Lemma 3.3.

Lemma 5.3

Let ${\mathcal {N}}$ be a binary phylogenetic network on X, and let $\overline{{\mathcal {D}}}$ be the set-matrix of inter-taxa distances of ${\mathcal {N}}$. Then the following hold:

• (i) Let $\{x, y\}$ be a cherry of ${\mathcal {N}}$ and let $z\not \in X$. Let $X'=(X-\{x, y\})\cup \{z\}$, and let $\overline{{\mathcal {D}}}'$ be the set-matrix of inter-taxa distances on $X'$ given by $\overline{{\mathcal {D}}_{v,w}}'=\overline{{\mathcal {D}}_{v,w}}$ if $v, w\in X-\{x, y\}$, and

  $$\begin{aligned} \overline{{\mathcal {D}}_{z,v}}'=\overline{{\mathcal {D}}_{v,z}}'=\{d-1:d\in \overline{{\mathcal {D}}_{x,v}}\} \end{aligned}$$

  if $v\in X-\{x, y\}$. Then $\overline{{\mathcal {D}}}'$ is realised by the binary phylogenetic network ${\mathcal {N}}'$ on $X'$ obtained from ${\mathcal {N}}$ by reducing the cherry $\{x, y\}$, where the new leaf is labelled z. Moreover, if, up to isomorphism, ${\mathcal {N}}'$ is the unique binary phylogenetic network on $X'$ realising $\overline{{\mathcal {D}}}'$, then, up to isomorphism, ${\mathcal {N}}$ is the unique binary phylogenetic network on X realising $\overline{{\mathcal {D}}}$.

• (ii) Let (x, y, z) be a double-reticulated cherry of ${\mathcal {N}}$. Let $\overline{{\mathcal {D}}}'$ be the set-matrix of inter-taxa distances on X given by

  $$\begin{aligned} \overline{{\mathcal {D}}_{x,v}}'=\overline{{\mathcal {D}}_{v,x}}'=\{d:d\in \overline{{\mathcal {D}}_{z,v}}\} \end{aligned}$$

  and

  $$\begin{aligned} \overline{{\mathcal {D}}_{y,v}}'=\overline{{\mathcal {D}}_{v,y}}'=\{d-1:d\in \overline{{\mathcal {D}}_{y,v}}\} \end{aligned}$$

  if $v\in X-\{x, y,z\}$,

  $$\begin{aligned} \overline{{\mathcal {D}}_{x,y}}'= & {} \overline{{\mathcal {D}}_{y,x}}'=\{d-2:d\in \overline{{\mathcal {D}}_{x,y}}-\{3\}\},\\ \overline{{\mathcal {D}}_{y,z}}'= & {} \overline{{\mathcal {D}}_{z,y}}'=\{d-1:d\in \overline{{\mathcal {D}}_{y,z}}\},\\ \overline{{\mathcal {D}}_{x,z}}'= & {} \overline{{\mathcal {D}}_{z,x}}'=\{2\} \end{aligned}$$

  and $\overline{{\mathcal {D}}_{v,w}}'=\overline{{\mathcal {D}}_{v,w}}$ if $v,w\in X-\{x, y,z\}$. Then $\overline{{\mathcal {D}}}'$ is realised by the binary phylogenetic network ${\mathcal {N}}'$ on X obtained from ${\mathcal {N}}$ by reducing the reticulated cherry $\{x, y\}$. Moreover, if, up to isomorphism, ${\mathcal {N}}'$ is the unique binary phylogenetic network on X realising $\overline{{\mathcal {D}}}'$, then, up to isomorphism, ${\mathcal {N}}$ is the unique binary phylogenetic network on X realising $\overline{{\mathcal {D}}}$.

We next present an algorithm, called Set Cherry Reduction, that plays the role of Multiset Cherry Reduction for the results in the previous two sections. The input to Set Cherry Reduction is a set-matrix $\overline{{\mathcal {D}}}$ of inter-taxa distances on a set X. Furthermore, its description is the same as that for Multiset Cherry Reduction except that any multiset is replaced by its set counterpart, and Step 2.(b) is replaced with the following:

• 2.(b) Else,

  • (i) If there are distinct elements $x, y, z\in X$ such that $3\in \overline{{\mathcal {D}}_{x,y}}$, $3\in \overline{{\mathcal {D}}_{x,z}}$,

    $$\begin{aligned} \{d+1:d\in \overline{{\mathcal {D}}_{y,v}}\}\subseteq \overline{{\mathcal {D}}_{x,v}} \end{aligned}$$

    for all $v\in X-\{x, y\}$, and

    $$\begin{aligned} \{d+1:d\in \overline{{\mathcal {D}}_{z,v}}\}\subseteq \overline{{\mathcal {D}}_{x,v}} \end{aligned}$$

    for all $v\in X-\{x, z\}$, thereby (x, y, z) forms a double-reticulated cherry, then

    • (I) Set $\overline{{\mathcal {D}}}'$ to be the set-matrix of inter-taxa distances on X given by

      $$\begin{aligned} \overline{{\mathcal {D}}_{x,v}}'=\overline{{\mathcal {D}}_{v,x}}'=\{d:d\in \overline{{\mathcal {D}}_{z,v}}\} \end{aligned}$$

      and

      $$\begin{aligned} \overline{{\mathcal {D}}_{y,v}}'=\overline{{\mathcal {D}}_{v,y}}'=\{d-1:d\in \overline{{\mathcal {D}}_{y,v}}'\} \end{aligned}$$

      if $v\in X-\{x, y,z\}$,

      $$\begin{aligned} \overline{{\mathcal {D}}_{x,y}}'= & {} \overline{{\mathcal {D}}_{y,x}}'=\{d-2:d\in \overline{{\mathcal {D}}_{x,y}}-\{3\}\},\\ \overline{{\mathcal {D}}_{y,z}}'= & {} \overline{{\mathcal {D}}_{z,y}}'=\{d-1:d\in \overline{{\mathcal {D}}_{y,z}}\},\\ \overline{{\mathcal {D}}_{x,z}}'= & {} \overline{{\mathcal {D}}_{z,x}}'=\{2\}, \end{aligned}$$

      and

      $$\begin{aligned} \overline{{\mathcal {D}}_{v,w}}'=\overline{{\mathcal {D}}_{v,w}} \end{aligned}$$

      if $v,w\in X-\{x, y,z\}$.

    • (II) Reapply Set Cherry Reduction to input X and $\overline{{\mathcal {D}}}'$. If a binary phylogenetic network ${\mathcal {N}}'$ on X is returned, form ${\mathcal {N}}$ by reversing the reticulated cherry reduction, subdividing the arcs to x and y, and adding an arc from the parent of y to the parent of x. Return the binary phylogenetic network ${\mathcal {N}}$ on X.

  • (ii) Else, there is no such three elements in X and return “Network not found”.

The proof of the next theorem is similar to that of Theorem 3.4 but, instead of using Lemmas 3.1–3.3, it uses Lemmas 5.2 and 5.3. It is worth noting that the crucial point here is that when we reduce a cherry, or reduce a reticulated cherry that is part of a double-reticulated cherry in a binary phylogenetic network ${\mathcal {N}}$, the set-matrix $\overline{{\mathcal {D}}}'$ of inter-taxa distances of the resulting binary phylogenetic network ${\mathcal {N}}'$ is recoverable from $\overline{{\mathcal {D}}}$, the set-matrix of inter-taxa distances of ${\mathcal {N}}$.

Theorem 5.4

Let $\overline{{\mathcal {D}}}$ be a set-matrix of inter-taxa distances on a set X. If Set Cherry Reduction applied to X and $\overline{{\mathcal {D}}}$ returns a network ${\mathcal {N}}$, then, up to isomorphism, ${\mathcal {N}}$ is the unique binary phylogenetic network on X that realises $\overline{{\mathcal {D}}}$.

A simple induction together with Lemmas 5.1 and 5.3 establishes the following proposition.

Proposition 5.5

Let ${\mathcal {N}}$ be a temporal binary tree-child network on X and let $\overline{{\mathcal {D}}}$ be the set-matrix of inter-taxa distances of ${\mathcal {N}}$. Then Set Cherry Reduction applied to X and $\overline{{\mathcal {D}}}$ returns ${\mathcal {N}}$, up to isomorphism.

The proof of Theorem 1.3 now follows by combining Theorem 5.4 and Proposition 5.5.

6 Running times

In this section, we analyse the running times of Multiset Cherry Reduction and Set Cherry Reduction, thereby establishing the running-time parts of Theorems 1.1–1.3. The input is a set X and a multiset-matrix ${\mathcal {D}}$ (respectively, set-matrix $\overline{{\mathcal {D}}}$) of inter-taxa distances on X. We iteratively search through the input for a cherry or reticulated cherry (respectively, double-reticulated cherry), and then either recurse or end the algorithm. We will show that there are at most $|{\mathcal {D}}|$ (respectively, $|\overline{{\mathcal {D}}}|$) iterations with each iteration taking at most $O(|{\mathcal {D}}|)$ [respectively, $O(|\overline{{\mathcal {D}}}|)$] steps. Hence both algorithms run in time quadratic in their input size. Moreover, we will show that if Set Cherry Reduction is applied to an input realised by a temporal binary tree-child network ${\mathcal {N}}$ on X, then, up to isomorphism, ${\mathcal {N}}$ is found in time $O(|X|^4)$.

6.1 Multiset Cherry Reduction

The algorithm Multiset Cherry Reduction takes as input a set X, and a |X| by |X| multiset-matrix ${\mathcal {D}}$ of inter-taxa distances on X. For all $x, y\in X$, we will assume that each entry ${\mathcal {D}}_{x,y}$ is presented as a sorted list of distances. Each step involves searching the entries in ${\mathcal {D}}$ for an element 2, or an element 3 with additional conditions. Since any 2 will be the smallest element in its entry, and any 3 will be the smallest element in its entry if there is no 2, we can find every 2 or candidate 3 in $O(|X|^2)$ steps. Checking the additional conditions on a 3 involves comparing the multisets in two columns of ${\mathcal {D}}$, which may be done in time $O(|{\mathcal {D}}|)$. Therefore identifying any cherries or reticulated cherries, or deciding there are none can be done in time $O(|X|^2|{\mathcal {D}}|)=O(|{\mathcal {D}}|^2)$. However, if X and ${\mathcal {D}}$ arises from a binary phylogenetic network ${\mathcal {N}}$ on X, then, as any leaf x in ${\mathcal {N}}$ can be at distance 3 from at most two other leaves, any column of ${\mathcal {D}}$ has at most two entries containing a 3, and thus each column will be compared with at most two other columns. Using this knowledge, we can find and check all candidate 3’s, or reject the input as not being realised by a binary phylogenetic network on X in time $O(|X|^2+|{\mathcal {D}}|)=O(|{\mathcal {D}}|)$.

If a 2 or suitable 3 is found in some entry, we compute ${\mathcal {D}}'$, as in the description of Multiset Cherry Reduction, and this can be done in $O(|{\mathcal {D}}|)$ time. Furthermore, if a binary phylogenetic network ${\mathcal {N}}'$ is returned, then it can augmented to ${\mathcal {N}}$ in constant time. Thus the whole iteration takes time linear in $|{\mathcal {D}}|$. If we recurse, then the multiset-matrix ${\mathcal {D}}'$ passed to the recursive call is strictly smaller than the current input since we have either reduced a cherry, and thereby ${\mathcal {D}}'$ has one less row and column, or reduced a reticulated cherry, and thereby removed at least one element, namely 3, from an entry in ${\mathcal {D}}$. Thus the total number of iterations is at most $|{\mathcal {D}}|$, and so the algorithm completes in time $O(|{\mathcal {D}}|^2)$. This establishes the running-time parts of Theorems 1.1 and 1.2.

Lastly, we note that ${\mathcal {D}}$ can be very much larger than X. The number of distinct up-down paths between two leaves in a binary phylogenetic network on X, or even a binary tree-child network on X, can be exponential in the number of vertices in the network. Although we might locate a pair of elements at distance 2, or a pair of elements at distance 3 in time polynomial in $|X|^2$, checking whether a pair of elements at distance 3 form a reticulated cherry may involve a number of individual checks that is exponential in |X|.

6.2 Set Cherry Reduction

The algorithm Set Cherry Reduction takes as input a set X, and a |X| by |X| set-matrix $\overline{{\mathcal {D}}}$ of inter-taxa distances on X, and its analysis is almost the same as that for Multiset Cherry Reduction. The only step that is significantly different is that we must check for a double-reticulated cherry in $\overline{{\mathcal {D}}}$. However, we can again use the observation above. In particular, if we find more than two entries containing a 3 in a single column of $\overline{{\mathcal {D}}}$, we can reject the input as not being realised by a binary phylogenetic network on X. Therefore, each column of $\overline{{\mathcal {D}}}$ is involved in a constant number of checks for being part of a double-reticulated cherry, and so we can find a cherry or double-reticulated cherry in time $O(|\overline{{\mathcal {D}}}|)$.

As for Multiset Cherry Reduction, the reduction and augmentation steps are easily implemented in time linear in $|\overline{{\mathcal {D}}}|$, and the number of iterations is again bounded by $|\overline{{\mathcal {D}}}|$, so the whole algorithm completes in time $O(|\overline{{\mathcal {D}}}|^2)$. However, since we are dealing now with sets, rather than multi-sets, of distances, we are also able to bound $\overline{{\mathcal {D}}}$ in terms of the size of the outputted binary phylogenetic network on X if that is what is finally returned by the algorithm. Suppose Set Cherry Reduction applied to X and $\overline{{\mathcal {D}}}$ returns such a network ${\mathcal {N}}$. Let $|{\mathcal {N}}|$ denote the number of edges in ${\mathcal {N}}$. Then the maximum distance between any two leaves is bounded by $|{\mathcal {N}}|$, and so each entry in $\overline{{\mathcal {D}}}$ is a set of size at most ${\mathcal {N}}$. Thus

$$\begin{aligned} |\overline{{\mathcal {D}}}|\le |X|^2|{\mathcal {N}}|\le |{\mathcal {N}}|^3. \end{aligned}$$

This gives a running-time bound for Set Cherry Reduction of $O(|{\mathcal {N}}|^4)$ since, in each iteration, we effectively reduce the number of edges in ${\mathcal {N}}$ by at least one, and so there are no more than ${\mathcal {N}}$ iterations, each taking time $O(|\overline{{\mathcal {D}}}|)$. Lastly, if ${\mathcal {N}}$ is a binary tree-child network on X, then ${\mathcal {N}}$ has O(|X|) edges (Cardona et al. 2009, Proposition 1) in which case the running time of Set Cherry Reduction applied to X and $\overline{{\mathcal {D}}}$ is $O(|X|^4)$. This establishes the running-time part of Theorem 1.3.

7 Open problems

In this section, we raise several questions relating to the work presented in the paper.

Question 1

What is the class $\mathcal M$ of binary phylogenetic networks that, up to isomorphism, are uniquely determined by their multiset-matrix of inter-taxa distances?

Theorems 1.1 and 1.2 show that $\mathcal M$ contains all binary tree-child networks, and all temporal binary phylogenetic networks with no crowns and in which every reticulation is visible. However, $\mathcal M$ is strictly bigger than the union of these two classes. For example, consider the binary phylogenetic network ${\mathcal {N}}_1$ on $\{x_1, x_2, x_3\}$ shown in Fig. 3. Let ${\mathcal {D}}_1$ be the multiset-matrix of inter-taxa distances of ${\mathcal {N}}_1$. It is easily checked that when Multiset Cherry Reduction is applied to $\{x_1, x_2, x_3\}$ and ${\mathcal {D}}_1$, the algorithm completes and so, by Theorem 3.4, ${\mathcal {N}}_1$ is in $\mathcal M$. But ${\mathcal {N}}_1$ is neither a tree-child network nor has the property that every reticulation is visible.

Fig. 3

A binary phylogenetic network ${\mathcal {N}}_1$ on $\{x_1, x_2, x_3\}$ that is neither tree-child nor has the property that every reticulation is visible

We also note that $\mathcal M$ is not the class of all binary phylogenetic networks as the following example illustrates. Let ${\mathcal {N}}_2$ and ${\mathcal {N}}_3$ denote the binary phylogenetic networks on $\{x_1, x_2, x_3, x_4, y\}$ shown in Fig. 4a, b, respectively. The multiset-matrices ${\mathcal {D}}_2$ and ${\mathcal {D}}_3$ of inter-taxa distances of ${\mathcal {N}}_2$ and ${\mathcal {N}}_3$ have exactly the same entries, namely

$$\begin{aligned} D_{x_1,x_2}&= \{4, 6, 9, 9\}, \\ D_{x_1,x_3}&= \{6, 6, 9, 9\}, \\ D_{x_1,x_4}&= \{4, 6, 9, 9\}, \\ D_{x_1,y}&= \{5, 6\}, \\ D_{x_2,x_3}&= \{4, 6, 9, 9\}, \\ D_{x_2,x_4}&= \{6, 6, 9, 9\}, \\ D_{x_2,y}&=\{5, 6\}, \\ D_{x_3,x_4}&= \{4, 6, 9, 9\}, \\ D_{x_3,y}&= \{5, 6\}, \\ D_{x_4,y}&= \{5, 6\}. \\ \end{aligned}$$

But ${\mathcal {N}}_2$ is not isomorphic to ${\mathcal {N}}_3$.

Fig. 4

Two non-isomorphic binary phylogenetic networks ${\mathcal {N}}_2$ and ${\mathcal {N}}_3$ on $\{x_1, x_2, x_3, x_4, y\}$ with the same multiset-matrix of inter-taxa distances on $\{x_1, x_2, x_3, x_4, y\}$

Question 2

What is the class of binary phylogenetic networks that, up to isomorphism, are correctly reconstructed when Multiset Cherry Reduction is applied to their multiset-matrix of inter-taxa distances?

Again, as the binary phylogenetic network ${\mathcal {N}}_1$ in Fig. 3 shows, this class is strictly bigger than the union of the class of binary tree-child networks and the class of temporal binary phylogenetic networks with no crowns and in which every reticulation is visible. This prompts the next question.

Question 3

Can Multiset Cherry Reduction applied to a set X and a multiset-matrix ${\mathcal {D}}$ of inter-taxa distances on X be extended to allow networks which exhibit neither a cherry nor a reticulated cherry, i.e. with a minimum distance of 4 between elements of X?

Of course, one also wants the property that if the extended algorithm returns a binary phylogenetic network ${\mathcal {N}}$ on X, then, up to isomorphism, ${\mathcal {N}}$ is the unique binary phylogenetic network on X that realises ${\mathcal {D}}$.

Questions 1–3 are posed in the context of multiset-matrices. However, given the results in Sect. 5, the analogous questions in the context of set-matrices can also be asked.

Question 4

What is the class of binary phylogenetic networks that, up to isomorphism, are uniquely determined by their set-matrix of inter-taxa distances?

Question 5

What is the class of binary phylogenetic networks that, up to isomorphism, are correctly reconstructed when Set Cherry Reduction is applied to their set-matrix of inter-taxa distances?

Question 6

Can Set Cherry Reduction applied to a set X and a set-matrix ${\mathcal {D}}$ of inter-taxa distances on X be extended to allow for networks exhibiting neither a cherry nor a double-reticulated cherry?

In this paper, we have measured the distance between taxa as the graph-theoretic path length. However, practical methods for phylogenetic reconstruction will need to be based on distance estimates of the amount of genetic mutation along a path, and not simply the number of speciation and reticulation events along a path. This motivates our final question.

Question 7

Given a binary phylogenetic network ${\mathcal {N}}$ on X with positively-weighted edge lengths, when does the information of up-down path lengths between elements in X, as measured by the sum of edge lengths in the path and not the number of edges, determine ${\mathcal {N}}$ up to isomorphism?