A double-yield-surface plasticity theory for transversely isotropic rocks

Abstract

We present a double-yield-surface plasticity theory for transversely isotropic rocks that distinguishes between plastic deformation through the solid matrix and localized plasticity along the weak bedding planes. A recently developed anisotropic modified Cam-Clay model is adopted to model the plastic response of the solid matrix, while the Mohr–Coulomb friction law is used to represent the sliding mechanism along the weak bedding planes. For its numerical implementation, we derive an implicit return mapping algorithm for both the semi-plastic and fully plastic loading processes, as well as the corresponding algorithmic tangent operator for finite element problems. We validate the model with triaxial compression test data for three different transversely isotropic rocks and reproduce the undulatory variation of rock strength with bedding plane orientation. We also implement the proposed model in a finite element setting and investigate the deformation of rock surrounding a borehole subjected to fluid injection. We compare the results of simulations using the proposed double-yield-surface model with those generated using each single yield criterion to highlight the features of the proposed theory.

1 Introduction

Anisotropy is a ubiquitous property of natural rocks [108]. Typical anisotropic rocks include sedimentary rocks that possess marked depositional layers such as shale, and foliated metamorphic rocks such as slates, gneisses, phyllites, and schists. The most common type of anisotropy is that of transverse isotropy characterized by parallel or nearly parallel sets of depositional layers or foliations forming a simple laminated structure. Such a laminated internal structure plays a critical role in determining the geophysical [27, 35, 110], hydrologic [44, 45, 103, 104, 106, 107], and mechanical [25, 50, 68, 69, 81, 85, 100] properties of transversely isotropic rocks.

In recent years, numerous investigators have conducted laboratory experiments to quantify and analyze the influence of material anisotropy on the mechanical behaviors of transversely isotropic rocks [2, 10, 19, 27, 54, 56, 60, 73, 98]. Unlike isotropic materials, both the stiffness and the strength of transversely isotropic rocks are dependent on the bedding plane orientation $\theta$ in the test specimens, varying in a highly nonlinear fashion. In terms of rock stiffness, the apparent Young’s modulus of transversely isotropic rocks often varies with bedding plane orientation as a U-shaped curve [93] or an S-shaped curve [1]. When it comes to rock strength, Ramamurthy [70] classified the variation curves into three groups, namely (a) U-type, (b) shoulder type, and (c) undulatory type of variation [83], as demonstrated in Fig. 1. Among them, the undulatory type exhibits the most complicated characteristics that could be regarded either as a U-type or a shoulder type curve with an additional concave portion within the range $45^\circ<\theta <90^\circ$, which is the range of bedding plane orientations in rock specimens under which condition of failure along the bedding plane is likely to occur [33, 64, 84, 95].

Fig. 1

Variation of rock strength with bedding plane orientation for transversely isotropic rocks. Modified from [70]

To describe the variation of rock strength with bedding plane orientation, one common approach is to regard transversely isotropic rocks as a continuum and develop the corresponding anisotropic elastoplastic constitutive model illustrating their mechanical responses [28, 47, 78, 87, 88, 96]. For anisotropic materials, Gol’denblat and Kopnov [34] proposed a general formulation expressing the yield criterion as a polynomial of stress components for glass-reinforced plastics. Tsai and Wu [86] proposed a yield criterion for filamentary composites as a polynomial that only contains the linear and quadratic terms of stress components.

Alternatively, instead of developing a general expression of the yield criterion for anisotropic materials, a vast majority of the models in the literature extend existing isotropic yield criteria to account for material anisotropy. Hill [40] extended the von Mises yield criterion for metals using six material parameters that scale the second-order stress terms in the yield criterion. Wang et al. [92] extended Hill’s criterion by considering the impact of the hydrostatic stress on the yield function, which resulted in an anisotropic version of Drucker–Prager model for transversely isotropic rocks. Boehler and Sawczuk [11] introduced a general method that takes advantage of isotropic plasticity models by substituting a fictitious stress state projected with a rank-four tensor into the yield criterion. Based on this concept, Bennett et al. [9] developed a generalized capped Drucker–Prager model for anisotropic geomaterials with finite deformation. Nova [65] extended the Cam-Clay model for transversely isotropic rocks. Crook et al. [24] extended the modified Cam-clay model using a projection tensor similar to that adopted by Hashagen and de Borst [38]. Semnani et al. [74] and Zhao et al. [108] also enhanced the modified Cam-Clay model with a projection tensor that only has three parameters for transversely isotropic rocks. Borja et al. [17] further enriched this model to consider material heterogeneity and viscoplasticity for shale rocks. Bryant and Sun [18] also refined this model with micromorphic regularization to accommodate size-dependent anisotropy of geomaterials.

Another approach to modeling the behavior of transversely isotropic rocks is to represent the laminated structure or the matrix-foliation system of the rock explicitly. Representative works include the microplane model [6,7,8] and the multi-laminate model [66, 111], both of which are based on the concept of angular discretization of space in which the overall material behavior is quantified as the aggregated response on several so-called integration planes where plasticity models are applied. By assigning different plastic parameters to the integration planes according to their spatial angle, this class of models can be used for materials with inherent anisotropy [26, 51, 52]. Crystal plasticity [4, 13, 15, 16, 39, 48, 49, 63, 71] is another common technique to handle materials with inherent microstructures, which adopts multiplane slip systems determined by the crystalline microstructures to describe the plastic responses of single crystals. Semnani and White [72] introduced an inelastic homogenization framework for layered materials. They assumed a laminated microstructure with weak planes where the layers and the interfaces are modeled with various isotropic plasticity models. Through homogenization over such a microstructure, the macroscopic anisotropic responses of transversely isotropic rocks can then be calculated. Choo et al. [23] extended this framework to consider time-dependent responses in the constituent layers and proposed an anisotropic viscoplastic model for shale.

In addition to micromechanical modeling and computational homogenization, the foliations can also be modeled explicitly at the macroscopic level. Tang et al. [82] conducted finite element simulations of uniaxial compression tests on stratified geomaterials in which the foliations were explicitly modeled as bands with a finite width in the simulated specimen with weaker materials. Their simulation can capture different failure modes either through the rock matrix or along the weak planes for specimens with different bedding plane orientation. Various authors have also attempted to explicitly model the matrix-foliation system with discrete element method [32, 55, 61, 67, 75, 94, 99], where the foliation is idealized as bonds between discrete solid particles at the weak planes governed by discrete constitutive laws that allows for shear or tensile failure, with which macroscopic failure of the specimens along the weak planes can be captured.

Focusing on the strength instead of the constitutive responses, various investigators have also proposed discontinuous failure criteria for transversely isotropic rocks that can account for different failure modes. Pioneering works in this category include the single plane of weakness theory of Jaeger [46], which generalized the Coulomb-Navier criterion for laminated rocks by considering two failure modes, namely failure along the weak planes or through the rock matrix. Based on this idea, Walsh and Brace [89] proposed a failure criterion where the failure of the schistosity planes is governed by a modified Griffith theory. Hoek [41] extended Jaeger’s theory through the application of the Hoek-Brown failure criterion [42] to both the weak planes and the rock matrix. Tien and Kuo [83] extended Jaeger’s theory and proposed a more elaborate criterion for failure through the solid matrix, which adopted the Hoek-Brown failure criterion to distinguish rock strength at $\theta =0^\circ$ and $\theta =90^\circ$. A maximum axial strain criterion was then introduced to calibrate the strength of specimens with inclined bedding planes. Jaeger’s theory has also been extended to model rocks with multiple groups of weak planes or joints (see [37, 62, 90]).

Each of the three types of models for the description of the strength of transversely isotropic rocks has its own pros and cons. With the first two types of models, one can reproduce the stress-strain curve of transversely isotropic rocks measured in laboratory tests and capture rock strength naturally [74, 108]. However, for continuum models, the rock is treated as an anisotropic continuum, and the plastic sliding failure mode along the weak planes is seldom considered, making them incapable of reproducing the undulatory type strength variation curve with bedding planes. For models that consider the weak planes explicitly, in theory, they can capture all three types of strength variation curves, but it comes with the disadvantage that many more microscale parameters are needed to calibrate them, accompanied with significant computational costs. For the discontinuous failure criteria, different failure modes are considered and the plastic sliding failure mode along the weak planes is properly captured, and thus the additional concave portion in the undulatory type strength variation curve governed by failure along the weak planes can be modeled. However, the disadvantage of this method is that the failure criterion for the rock matrix has been over-simplified, and it is hard to capture the nonlinearity in the strength variation curve governed by this failure mode. For example, in Jaeger’s theory where the isotropic Coulomb-Navier criterion is adopted for the rock matrix, rock strength is a constant when the failure mode is through the matrix, which is insufficient to reflect experimental observations demonstrated in Fig. 1. Efforts such as the work of Tien and Kuo [83] tried to make up for this disadvantage by using a more complicated criterion for the rock matrix. Such an enhancement, however, is highly empirical and lacks mathematical foundations.

In this paper, we introduce a double-yield-surface plasticity model for transversely isotropic rocks that combines the advantages of the continuum constitutive model formulation and the discontinuous failure criteria. In the proposed model, we make a clear distinction between bulk plasticity in the rock matrix and sliding mechanism along the weak bedding planes. A recently developed anisotropic modified Cam-Clay model is adopted to model the plastic response of the rock matrix, while the Mohr–Coulomb friction law is used to represent sliding deformation along the weak bedding planes. For the numerical implementation of the proposed model, we derive an implicit return mapping algorithm for different loading processes along with the corresponding algorithmic tangent operator for the solution of finite element problems. We then validate the model by reproducing the undulatory variation of rock strength with bedding plane orientation observed in triaxial compression tests for three different transversely isotropic rocks. Lastly, we implement the model in a finite element framework and conduct boundary value problem simulations to investigate the deformation of surrounding rocks around a borehole subjected to fluid injection.

As for notations and symbols, we use boldfaced characters (e.g., $\varvec{a}$) to represent vectors and rank-two tensors, and blackboard bold letters (e.g., ${\mathbb{I}}$) to represent rank-four tensors. $\mathbf{1}$ and ${\mathbb{I}}$ stand for rank-two and rank-four symmetric identity tensors, respectively, and ${\mathbb{O}}$ is the rank-four zero tensor. Dot product and double dot product are defined with symbols $\cdot$ and :, respectively. Tensorial operators $\otimes , \oplus$ and $\ominus$ are defined such that $(\bullet \otimes \circ )_{ijkl}=(\bullet )_{ij}(\circ )_{kl}$, $(\bullet \oplus \circ )_{ijkl}=(\bullet )_{jl}(\circ )_{ik}$, and $(\bullet \ominus \circ )_{ijkl} =(\bullet )_{il}(\circ )_{jk}$.

2 Theoretical formulation

In this section, we introduce the theoretical formulation of the proposed double-yield-surface plasticity model for transversely isotropic rocks. We first introduce the underlying assumptions and the constitutive laws of the proposed model. Next, we present a formulation for double-yield-surface plasticity model, adapted from [12, 43], with explicit definitions of different loading and unloading processes.

2.1 Double-yield-surface formulation

In this model, we assume that a rock can be regarded as a homogenized elastoplastic transversely isotropic continuum. The laminated structure would result in the anisotropic continuous response of the rock matrix, and besides that, the bedding direction of the laminated structure would serve as a weak direction along which plastic sliding could occur. Based on this assumption, the plastic deformation in transversely isotropic rocks can be decomposed into two mechanisms: yielding in the rock matrix and/or yielding along the weak bedding planes. The total strain can thus be expressed as

$$\begin{aligned} \varvec{\epsilon } = \varvec{\epsilon }^e + \varvec{\epsilon }^p_m + \varvec{\epsilon }^p_w\,. \end{aligned}$$

(1)

In this expression, the superscripts e and p refer to the elastic and plastic parts of the strain tensor, respectively; the subscripts m and w indicate plastic strain in the rock matrix and along the weak planes, respectively.

To reflect the influence of the laminated structure on the mechanical response of transversely isotropic rocks, we first introduce a rank-two microstructure tensor $\varvec{m}$ defined as

$$\begin{aligned} \varvec{m}=\varvec{n}\otimes \varvec{n}\,, \end{aligned}$$

(2)

where $\varvec{n}$ stands for the unit normal vector to the bedding planes.

Assuming a linearly elastic material response,

$$\begin{aligned} \varvec{\sigma } = {\mathbb{C}}^e:\varvec{\epsilon }^e\,, \end{aligned}$$

(3)

where $\varvec{\sigma }$ is the Cauchy stress tensor and ${\mathbb{C}}^e$ is the elastic tangent operator. For transversely isotropic rocks, the expression for ${\mathbb{C}}^e$ is given by [79]

$$\begin{aligned} {\mathbb{C}}^e&=\lambda \mathbf{1}\otimes \mathbf{1} + 2\mu _T{\mathbb{I}} +a(\mathbf{1}\otimes \varvec{m} + \varvec{m}\otimes \mathbf{1}) + b\varvec{m} \otimes \varvec{m}\nonumber \\&\quad +(\mu _L - \mu _T)(\mathbf{1}\oplus \varvec{m} + \varvec{m} \oplus \mathbf{1} +\mathbf{1}\ominus \varvec{m} + \varvec{m}\ominus \mathbf{1})\,, \end{aligned}$$

(4)

where $\lambda , a, b, \mu _L, \mu _T$ are five material constants.

As for the plastic response, we use two different yield criteria to model ductile deformation mechanisms in the rock matrix and sliding along the weak planes. For the first part, we adopt an anisotropic modified Cam-Clay model introduced by Semnani et al. [74] and Zhao et al. [105, 108] to represent the anisotropic response of the rock matrix. To this end, we introduce a fictitious stress state $\varvec{\sigma }^*$ as

$$\begin{aligned} \varvec{\sigma }^* = {\mathbb{P}}:\varvec{\sigma }\,, \end{aligned}$$

(5)

where ${\mathbb{P}}$ is a rank-four projection tensor defined as

$$\begin{aligned} {\mathbb{P}}&=c_1{\mathbb{I}}+\frac{c_2}{2}(\varvec{m}\oplus {\varvec{m}} + \varvec{m}\ominus {\varvec{m}})\nonumber \\&\quad +\frac{c_3}{4}(\mathbf{1}\oplus {\varvec{m}} + \varvec{m}\oplus {\mathbf{1}} + \mathbf{1}\ominus {\varvec{m}} + \varvec{m}\ominus {\mathbf{1}})\,, \end{aligned}$$

(6)

in which $c_1,c_2,c_3$ are parameters that control the degree of anisotropy of the yield surface. The projection tensor ${\mathbb{P}}$ contains the anisotropy information through the microstructure tensor $\varvec{m}$. Inserting $\varvec{\sigma }^*$ into the isotropic modified Cam-Clay yield surface yields the anisotropic yield function for the rock matrix as

$$\begin{aligned} f_m(\varvec{\sigma }^*,p_c) = \frac{q^{*2}}{M^2} + p^*(p^*-p_c)\le 0, \end{aligned}$$

(7)

where $p^* = \mathrm{tr}(\varvec{\sigma }^*)$, $q^*=\sqrt{3/2}\Vert \varvec{s}^*\Vert$, $\varvec{s}^* =\varvec{\sigma }^*-p^*\mathbf{1}$, and $p_c<0$ is the preconsolidation stress. In terms of the Cauchy stress tensor $\varvec{\sigma }$, we have

$$\begin{aligned} f_m(\varvec{\sigma },p_c) = \frac{\varvec{\sigma }:{\mathbb{A}}^*: \varvec{\sigma }}{2M^2}+(\varvec{a}^*:\varvec{\sigma })(\varvec{a}^*: \varvec{\sigma }-p_c)\le 0\,, \end{aligned}$$

(8)

where

$$\begin{aligned} \varvec{a}^* = \frac{1}{3}{\mathbb{P}}:\mathbf{1} \,,\qquad {\mathbb{A}}^*=3{\mathbb{P}}:\left( {\mathbb{I}} -\frac{1}{3}\mathbf{1}\otimes \mathbf{1}\right) :{\mathbb{P}}\,. \end{aligned}$$

(9)

Assuming an associative flow rule, we can derive the rate of plastic deformation in the rock matrix as

$$\begin{aligned} \dot{\varvec{\epsilon }}^p_m = \dot{\lambda }_m\frac{\partial f_m}{\partial \varvec{\sigma }} = \dot{\lambda }_m\frac{\partial f_m}{\partial \varvec{\sigma }^*}:\frac{\partial \varvec{\sigma }^*}{\partial \varvec{\sigma }} = \dot{\lambda }_m{\mathbb{P}}: \frac{\partial f_m}{\partial \varvec{\sigma }^*}\,, \end{aligned}$$

(10)

where $\dot{\lambda }_m\ge 0$ is a plastic multiplier for the rock matrix. As for the hardening law, we correlate the preconsolidation stress $p_c$ to the volumetric part of the plastic strain $\epsilon ^p_v$ as

$$\begin{aligned} p_c = p_{c0}\mathrm{exp}\left( -\frac{\epsilon ^p_v}{\lambda ^p}\right) , \end{aligned}$$

(11)

where $\lambda ^p$ is a plastic compressibility index and $\epsilon ^p_v=\mathbf{1}:\varvec{\epsilon }^p_m$. Plastic dilation is characterized by $\epsilon ^p_v>0$ while plastic compression is defined by $\epsilon ^p_v<0$.

For sliding mechanism along the weak bedding planes, we adopt the Mohr–Coulomb failure criterion

$$\begin{aligned} f_w(\tau ,\sigma _n) = |\tau |-(c_w-\sigma _n\mathrm{tan}\,\phi _w)\le 0\,, \end{aligned}$$

(12)

where $c_w$ and $\phi _w$ are the cohesion and friction angle, and $\tau$ and $\sigma _n$ are the shear and normal stresses on the weak planes, which can be calculated as

$$\begin{aligned} \sigma _n=\varvec{n}\cdot \varvec{\sigma }\cdot \varvec{n} = \varvec{\sigma }: \varvec{m}\,,\qquad |\tau |=\sqrt{|\varvec{\sigma }\cdot \varvec{n}|^2-\sigma _n^2}\,. \end{aligned}$$

(13)

To prescribe the plastic flow direction, we define the plastic potential function as

$$\begin{aligned} g_w(\tau ,\sigma _n) = |\tau | + \sigma _n\mathrm{tan}\,\psi _w\,, \end{aligned}$$

(14)

where $\psi _w\le \phi _w$ is the dilatancy angle on the weak planes. The rate of plastic deformation can then be expressed as

$$\begin{aligned} \dot{\varvec{\epsilon }}_w^p = \dot{\lambda }_w \frac{\partial g_w}{\partial \varvec{\sigma }} = \dot{\lambda }_w\frac{\partial g_w}{\partial \tau } \frac{\partial \tau }{\partial \varvec{\sigma }} +\dot{\lambda }_w\frac{\partial g_w}{\partial \sigma _n} \frac{\partial \sigma _n}{\partial \varvec{\sigma }}\,, \end{aligned}$$

(15)

where $\dot{\lambda }_w\ge 0$ is a plastic multiplier for sliding along the weak planes [14].

Fig. 2

Sketch of the yield surfaces in the proposed plasticity model for transversely isotropic rocks given a biaxial compression stress state shown in the right figure. The shaded area represents the elastic regime of the proposed plasticity model

Figure 2 depicts the yield surfaces under a biaxial compression stress state. The rotated ellipse is the anisotropic modified Cam-Clay yield surface $f_m$ for the solid matrix, while the two rays are the projections of the yield surface $f_w$ for the weak planes. The shaded area represents the elastic region, which is now bounded by the two yield surfaces. For a stress state within the elastic region, both yield functions $f_m$ and $f_w$ are less than zero.

2.2 Definitions of various processes

To illustrate the plastic deformation of transversely isotropic rocks modeled with two distinct yield surfaces $f_m$ and $f_w$, we first define all possible cases of loading and unloading. Let $\delta \varvec{\sigma }$ be the variation of stress state, i.e., the stress probe. Various processes can be defined as follows:

(a) Elastic process:

$$\begin{aligned}&f_m< 0\quad \mathrm{or} \quad \left( f_m = 0 \quad \mathrm{and} \quad \frac{\partial f_m}{\partial \varvec{\sigma }}: \delta \varvec{\sigma }<0\right) \,, \end{aligned}$$

(16a)

$$\begin{aligned}&\quad \mathrm{and} \quad f_w< 0\quad \mathrm{or} \quad \left( f_w = 0 \quad \mathrm{and} \quad \frac{\partial f_w}{\partial \varvec{\sigma }}:\delta \varvec{\sigma }<0\right) \,. \end{aligned}$$

(16b)

The two equations in (16) refer to the process in which the stress state is either inside the yield surface or on the yield surface but unloading.

(b) Semi-plastic loading process on $f_m$:

$$\begin{aligned}&f_m = 0 \quad \mathrm{and} \quad \frac{\partial f_m}{\partial \varvec{\sigma }}:\delta \varvec{\sigma }>0\,, \end{aligned}$$

(17a)

$$\begin{aligned}&\quad \mathrm{and} \quad f_w < 0\quad \mathrm{or} \quad \left( f_w = 0 \quad \mathrm{and} \quad \frac{\partial f_w}{\partial \varvec{\sigma }}:\delta \varvec{\sigma }\le 0\right) \,. \end{aligned}$$

(17b)

For this process, the material yields according to the yield criterion $f_m$ alone.

(c) Semi-plastic loading process on $f_w$:

$$\begin{aligned}&f_m < 0\quad \mathrm{or} \quad \left( f_m = 0 \quad \mathrm{and} \quad \frac{\partial f_m}{\partial \varvec{\sigma }}:\delta \varvec{\sigma }\le 0\right) \,, \end{aligned}$$

(18a)

$$\begin{aligned}&\quad \mathrm{and} \quad f_w = 0 \quad \mathrm{and} \quad \frac{\partial f_w}{\partial \varvec{\sigma }}:\delta \varvec{\sigma }>0\,. \end{aligned}$$

(18b)

For this process, the material yields according to the yield criterion $f_w$ alone.

(d) Fully plastic loading process:

$$\begin{aligned}&f_m = 0 \quad \mathrm{and} \quad \frac{\partial f_m}{\partial \varvec{\sigma }}: \delta \varvec{\sigma }>0\,, \end{aligned}$$

(19a)

$$\begin{aligned}&\quad \mathrm{and} \quad f_w = 0 \quad \mathrm{and} \quad \frac{\partial f_w}{\partial \varvec{\sigma }}:\delta \varvec{\sigma }>0\,. \end{aligned}$$

(19b)

For this process, the material yields according to the combined yield criteria $f_m$ and $f_w$.

(e) Semi-neutral process on $f_m$:

$$\begin{aligned}&f_m = 0 \quad \mathrm{and} \quad \frac{\partial f_m}{\partial \varvec{\sigma }}:\delta \varvec{\sigma }=0\,, \end{aligned}$$

(20a)

$$\begin{aligned}&\quad \mathrm{and}\quad f_w< 0\quad \mathrm{or} \quad \left( f_w = 0 \quad \mathrm{and} \quad \frac{\partial f_w}{\partial \varvec{\sigma }}:\delta \varvec{\sigma }<0\right) \,. \end{aligned}$$

(20b)

For this process, the stress state moves tangentially to the yield surface $f_m$.

(f) Semi-neutral process on $f_w$:

$$\begin{aligned}&f_m< 0\quad \mathrm{or} \quad \left( f_m = 0 \quad \mathrm{and} \quad \frac{\partial f_m}{\partial \varvec{\sigma }}: \delta \varvec{\sigma }<0\right) \,, \end{aligned}$$

(21a)

$$\begin{aligned}&\quad \mathrm{and} \quad f_w = 0 \quad \mathrm{and} \quad \frac{\partial f_w}{\partial \varvec{\sigma }}: \delta \varvec{\sigma }=0\,. \end{aligned}$$

(21b)

For this process, the stress state moves tangentially to the yield surface $f_w$.

(g) Fully neutral process:

$$\begin{aligned}&f_m = 0 \quad \mathrm{and} \quad \frac{\partial f_m}{\partial \varvec{\sigma }}:\delta \varvec{\sigma }=0\,, \end{aligned}$$

(22a)

$$\begin{aligned}&\quad \mathrm{and} \quad f_w = 0 \quad \mathrm{and} \quad \frac{\partial f_w}{\partial \varvec{\sigma }}:\delta \varvec{\sigma }=0\,. \end{aligned}$$

(22b)

For this process, the stress state moves tangentially to both yield surfaces.

2.3 Continuum formulation

In what follows, we consider the continuum formulations for all possible loading/unloading scenarios.

(a) Fully plastic loading process:

The consistency conditions for the two yield surfaces are given by

$$\begin{aligned} \dot{f}_m&= \frac{\partial f_m}{\partial \varvec{\sigma }}: \dot{\varvec{\sigma }} + \frac{\partial f_m}{\partial p_c} \dot{p_c} = 0\,, \end{aligned}$$

(23a)

$$\begin{aligned} \dot{f}_w&= \frac{\partial f_w}{\partial \varvec{\sigma }}: \dot{\varvec{\sigma }} = 0\,. \end{aligned}$$

(23b)

Combining Eqs. (10) and (15), together with the rate form of the elastic constitutive response $\dot{\varvec{\sigma }} = {\mathbb{C}}^e:(\dot{\varvec{\epsilon }} -\dot{\varvec{\epsilon }}^p_m-\dot{\varvec{\epsilon }}^p_w)$, we can rewrite the consistency conditions as

$$\begin{aligned}&\frac{\partial f_m}{\partial \varvec{\sigma }}:{\mathbb{C}}^e: \left( \dot{\varvec{\epsilon }}-\dot{\lambda }_m \frac{\partial f_m}{\partial \varvec{\sigma }} -\dot{\lambda }_w\frac{\partial g_w}{\partial \varvec{\sigma }}\right) \nonumber \\&\qquad +\frac{\partial f_m}{\partial p_c} \frac{\partial p_c}{\partial \epsilon ^p_v} \dot{\lambda }_m\mathbf{1}: \frac{\partial f_m}{\partial \varvec{\sigma }}=0\,, \end{aligned}$$

(24a)

$$\begin{aligned}&\frac{\partial f_w}{\partial \varvec{\sigma }}:{\mathbb{C}}^e: \left( \dot{\varvec{\epsilon }}-\dot{\lambda }_m \frac{\partial f_m}{\partial \varvec{\sigma }}-\dot{\lambda }_w \frac{\partial g_w}{\partial \varvec{\sigma }}\right) =0\,. \end{aligned}$$

(24b)

We can then solve for $\dot{\lambda }_m$ and $\dot{\lambda }_w$ using the equations above. By collecting terms and rearranging the expressions, we can reorganize the two equations into matrix form,

$$ \left[ \begin{array}{cc} \alpha _{11} &{} \alpha _{12}\\ \alpha _{21} &{} \alpha _{22} \end{array}\right] \left\{ \begin{array}{c} \dot{\lambda }_m\\ \dot{\lambda }_w \end{array}\right\} =\left\{ \begin{array}{c} b_1\\ b_2 \end{array}\right\} $$

(25)

where

$$\begin{aligned} \alpha _{11}&= \frac{\partial f_m}{\partial \varvec{\sigma }}:{\mathbb{C}}^e: \frac{\partial f_m}{\partial \varvec{\sigma }} -\frac{\partial f_m}{\partial p_c}\frac{\partial p_c}{\partial \epsilon _v^p}\mathbf{1}:\frac{\partial f_m}{\partial \varvec{\sigma }}\,, \end{aligned}$$

(26a)

$$\begin{aligned} \alpha _{12}&= \alpha _{21} = \frac{\partial f_m}{\partial \varvec{\sigma }}: {\mathbb{C}}^e:\frac{\partial g_w}{\partial \varvec{\sigma }}\,, \end{aligned}$$

(26b)

$$\begin{aligned} \alpha _{22}&= \frac{\partial f_w}{\partial \varvec{\sigma }}:{\mathbb{C}}^e: \frac{\partial g_w}{\partial \varvec{\sigma }}\,. \end{aligned}$$

(26c)

and

$$\begin{aligned} b_1&= \frac{\partial f_m}{\partial \varvec{\sigma }}:{\mathbb{C}}^e: \dot{\varvec{\epsilon }}\,, \end{aligned}$$

(27a)

$$\begin{aligned} b_2&= \frac{\partial f_w}{\partial \varvec{\sigma }}:{\mathbb{C}}^e: \dot{\varvec{\epsilon }}\,. \end{aligned}$$

(27b)

From Eq. (25), we can see that $\dot{\lambda }_m$ and $\dot{\lambda }_w$ can be solved when the parameter matrix is invertible, and

$$\begin{aligned} \left\{ \begin{array}{c} \dot{\lambda }_m\\ \dot{\lambda }_w \end{array}\right\} =\left[ \begin{array}{cc} \alpha _{11}' &{} \alpha _{12}'\\ \alpha _{21}' &{} \alpha _{22}' \end{array}\right] \left\{ \begin{array}{c} b_1\\ b_2 \end{array}\right\} \end{aligned}$$

(28)

where

$$\begin{aligned} \left[ \begin{array}{cc} \alpha _{11}' &{} \alpha _{12}'\\ \alpha _{21}' &{} \alpha _{22}' \end{array}\right] =\left[ \begin{array}{cc} \alpha _{11} &{} \alpha _{12}\\ \alpha _{21} &{} \alpha _{22} \end{array}\right] ^{-1} \end{aligned}$$

(29)

is the inverse of the parameter matrix.

Inserting Eq. (28) into the rate form of the elastic constitutive response gives

$$\begin{aligned} \dot{\varvec{\sigma }}&= {\mathbb{C}}^e:(\dot{\varvec{\epsilon }} -\dot{\varvec{\epsilon }}^p_m-\dot{\varvec{\epsilon }}^p_w),\nonumber \\&=\left( {\mathbb{C}}^e-\alpha _{11}'{\mathbb{C}}^e: \frac{\partial f_m}{\partial \varvec{\sigma }} \otimes \frac{\partial f_m}{\partial \varvec{\sigma }}:{\mathbb{C}}^e -\alpha _{12}'{\mathbb{C}}^e:\frac{\partial f_m}{\partial \varvec{\sigma }} \otimes \frac{\partial f_w}{\partial \varvec{\sigma }}: {\mathbb{C}}^e\right. \nonumber \\&\quad \left. -\alpha _{21}'{\mathbb{C}}^e: \frac{\partial g_w}{\partial \varvec{\sigma }} \otimes \frac{\partial f_m}{\partial \varvec{\sigma }}:{\mathbb{C}}^e -\alpha _{22}'{\mathbb{C}}^e:\frac{\partial g_w}{\partial \varvec{\sigma }} \otimes \frac{\partial f_w}{\partial \varvec{\sigma }}:{\mathbb{C}}^e\right) : \dot{\varvec{\epsilon }}\nonumber \\&={\mathbb{C}}^{ep}:\dot{\varvec{\epsilon }}\,, \end{aligned}$$

(30)

From the expression above, we see that the elastoplastic tangent operator of the material is given as

$$\begin{aligned} {\mathbb{C}}^{ep}&= {\mathbb{C}}^e-\alpha _{11}'{\mathbb{C}}^e: \frac{\partial f_m}{\partial \varvec{\sigma }} \otimes \frac{\partial f_m}{\partial \varvec{\sigma }}: {\mathbb{C}}^e-\alpha _{12}'{\mathbb{C}}^e: \frac{\partial f_m}{\partial \varvec{\sigma }} \otimes \frac{\partial f_w}{\partial \varvec{\sigma }}:{\mathbb{C}}^e\nonumber \\&\quad -\alpha _{21}'{\mathbb{C}}^e:\frac{\partial g_w}{\partial \varvec{\sigma }} \otimes \frac{\partial f_m}{\partial \varvec{\sigma }}:{\mathbb{C}}^e -\alpha _{22}'{\mathbb{C}}^e:\frac{\partial g_w}{\partial \varvec{\sigma }} \otimes \frac{\partial f_w}{\partial \varvec{\sigma }}:{\mathbb{C}}^e\,. \end{aligned}$$

(31)

(b) Semi-plastic loading process on $f_m$:

For this case, the plastic deformation of the material is governed by the yield surface $f_m$ while the yield surface $f_w$ is inactive. We can write the elastic constitutive response as

$$\begin{aligned} \dot{\varvec{\sigma }} = {\mathbb{C}}^e:(\dot{\varvec{\epsilon }} -\dot{\varvec{\epsilon }}^p_m)={\mathbb{C}}^{ep}:\dot{\varvec{\epsilon }}\,, \end{aligned}$$

(32)

and the simplified consistency condition shown in Eq. (24a) as

$$\begin{aligned} \frac{\partial f_m}{\partial \varvec{\sigma }}:{\mathbb{C}}^e: \left( \dot{\varvec{\epsilon }}-\dot{\lambda }_m \frac{\partial f_m}{\partial \varvec{\sigma }}\right) +\frac{\partial f_m}{\partial p_c} \frac{\partial p_c}{\partial \epsilon ^p_v} \dot{\lambda }_m\mathbf{1}:\frac{\partial f_m}{\partial \varvec{\sigma }}=0\,, \end{aligned}$$

(33)

from which we can solve for the plastic multiplier $\dot{\lambda }_m$:

$$ \alpha _{11}\dot{\lambda }_m=b_1, $$

(34)

where

$$ \alpha _{11} = \frac{\partial f_m}{\partial \varvec{\sigma }}: {\mathbb{C}}^e:\frac{\partial f_m}{\partial \varvec{\sigma }} -\frac{\partial f_m}{\partial p_c} \frac{\partial p_c}{\partial \epsilon _v^p}\mathbf{1}: \frac{\partial f_m}{\partial \varvec{\sigma }}, $$

(35)

and

$$ b_1 = \frac{\partial f_m}{\partial \varvec{\sigma }}:{\mathbb{C}}^e: \dot{\varvec{\epsilon }}. $$

(36)

The elastoplastic tangent operator for this process can be expressed as

$$ {\mathbb{C}}^{ep} = {\mathbb{C}}^e - \alpha _{11}^{-1}{\mathbb{C}}^e: \frac{\partial f_m}{\partial \varvec{\sigma }} \otimes \frac{\partial f_m}{\partial \varvec{\sigma }}:{\mathbb{C}}^e. $$

(37)

(c) Semi-plastic loading process on $f_w$:

For this case, the plastic deformation of the material is governed by the yield surface $f_w$ while the yield surface $f_m$ is inactive. Again, we can write the elastic constitutive response as

$$ \dot{\varvec{\sigma }} = {\mathbb{C}}^e:(\dot{\varvec{\epsilon }} -\dot{\varvec{\epsilon }}^p_w)={\mathbb{C}}^{ep}:\dot{\varvec{\epsilon }}, $$

(38)

and for this case, the simplified consistency condition shown in Eq. (24b) as

$$ \frac{\partial f_w}{\partial \varvec{\sigma }}:{\mathbb{C}}^e: \left( \dot{\varvec{\epsilon }}-\dot{\lambda }_w \frac{\partial g_w}{\partial \varvec{\sigma }}\right) =0\,, $$

(39)

from which we can solve for the plastic multiplier $\dot{\lambda }_w$:

$$ \alpha _{22}\dot{\lambda }_w=b_2\,, $$

(40)

where

$$\begin{aligned} \alpha _{22} = \frac{\partial f_w}{\partial \varvec{\sigma }}: {\mathbb{C}}^e:\frac{\partial g_w}{\partial \varvec{\sigma }}\,, \end{aligned}$$

(41)

and

$$\begin{aligned} b_2 = \frac{\partial f_w}{\partial \varvec{\sigma }}:{\mathbb{C}}^e: \dot{\varvec{\epsilon }}\,. \end{aligned}$$

(42)

The elastoplastic tangent operator for this process can be expressed as

$$\begin{aligned} {\mathbb{C}}^{ep} = {\mathbb{C}}^e - \alpha _{22}^{-1}{\mathbb{C}}^e: \frac{\partial g_w}{\partial \varvec{\sigma }} \otimes \frac{\partial f_w}{\partial \varvec{\sigma }}:{\mathbb{C}}^e\,. \end{aligned}$$

(43)

The relevant partial derivatives are summarized in Appendix A.

3 Numerical implementation

This section presents the numerical implementation of the double-yield-surface plasticity model at the stress point level, covering both an implicit return mapping algorithm and the derivation of the algorithmic tangent operator.

From loading step n to loading step $n+1$, the return mapping algorithm iteratively calculates the state variables $\varvec{\epsilon }^e_{n+1}$, $\varvec{\epsilon }^p_{m,n+1}$, $\varvec{\epsilon }^p_{w,n+1}$, $\varvec{\sigma }_{n+1}$, and $p_{c,n+1}$ from given incremental strain tensor $\varDelta \varvec{\epsilon }$ and starting values of the state variables at loading step n. The iteration is based on a predictor-corrector scheme. First, a trial elastic stress predictor $\varvec{\sigma }_{n+1}^{\rm tr}$ is calculated as

$$\begin{aligned} \varvec{\sigma }^{\rm tr}_{n+1} = \varvec{\sigma }_{n} + {\mathbb{C}}^e: \varDelta \varvec{\epsilon }\,, \end{aligned}$$

(44)

which is then used to identify the active constraint(s).

In single yield surface plasticity theory, a trial elastic stress predictor $\varvec{\sigma }_{n+1}^{\rm tr}$ that lies outside the yield surface automatically implies that the yield surface is active. However, this is not necessarily the case for double-yield-surface plasticity theory. Figure 3 portrays three possible regions outside the two yield surfaces where the elastic stress predictor $\varvec{\sigma }_{n+1}^{\rm tr}$ could land. When $\varvec{\sigma }_{n+1}^{\rm tr}$ lands in Region I, the process is semi-plastic on $f_m$ even though $f_w(\varvec{\sigma }_{n+1}^{\rm tr})>0$. In Region II, the process is semi-plastic on $f_w$ for the same reason. The process is fully plastic only when $\varvec{\sigma }_{n+1}^{\rm tr}$ lands in Region III, requiring that the predictor stress be corrected and mapped back to the intersection of the two yield surfaces. In addition, the hardening or softening of $f_m$ can also impact the final process as well as the final position of the stress point $\varvec{\sigma }_{n+1}$.

Simo et al. [76] introduced a general return mapping algorithm for multi-surface plasticity model in which the potentially active yield surfaces are first identified based on the value of the trial elastic stress predictor. A first sweep is conducted to calculate the preliminary values of the plastic multipliers for the potentially active constraints. Yield surfaces for which the incremental plastic multipliers are negative are eliminated. The iteration is considered to have converged when all yield criteria are satisfied and all plastic multipliers are nonnegative, i.e., when the discrete Kuhn–Tucker conditions are satisfied on all yield constraints. However, Borja and Wren [13] noted that this algorithm can fail to identify some active constraints, particularly when they are redundant constraints, which led them to develop an ‘ultimate algorithm’ for identifying active constraints in crystals.

We adopt a slightly different approach in the present work. Instead, we first assume that the process is semi-plastic on either $f_w$ or $f_m$. Then, we assume a fully plastic process if the corrected stress state does not satisfy the yield criterion for the other yield surface. A final correction is made if it was the other yield surface that was active. Figure 4 summarizes the return mapping algorithm adopted in this paper. Details of the formulations are given below.

Fig. 3

Possible locations of the trial stress state $\varvec{\sigma }^{\rm tr}_{n+1}$ outside the two yield surfaces. Arrows represent the normal vectors to the yield surfaces

Fig. 4

Return mapping algorithm for the double-yield-surface plasticity model

(a) Fully plastic loading process:

For the fully plastic loading process, both yield surfaces $f_m$ and $f_w$ are active and the stress state is mapped back to the intersection of the two yield surfaces. In this case, we impose the discrete consistency conditions for both yield surfaces

$$\begin{aligned} f_m(\varvec{\sigma }_{n+1},p_{c,n+1})&=0\,, \end{aligned}$$

(45a)

$$\begin{aligned} f_w(\varvec{\sigma }_{n+1})&=0\,, \end{aligned}$$

(45b)

and the discrete versions of the flow rules

$$\begin{aligned} \varvec{\epsilon }^p_{m,n+1}-\varvec{\epsilon }^p_{m,n}&= \varDelta \lambda _m\frac{\partial f_m}{\partial \varvec{\sigma }}\,, \end{aligned}$$

(46a)

$$\begin{aligned} \varvec{\epsilon }^p_{w,n+1}-\varvec{\epsilon }^p_{w,n}&= \varDelta \lambda _w \frac{\partial g_w}{\partial \varvec{\sigma }}\,. \end{aligned}$$

(46b)

The aim is to update the state variables $\varvec{\epsilon }^p_{m,n+1},\varvec{\epsilon }^p_{w,n+1}$ and the two plastic multipliers $\varDelta \lambda _m$ and $\varDelta \lambda _w$. To this end, we employ the Newton-Raphson scheme and define the residuals as

$$\begin{aligned} \varvec{{\mathcal {R}}}_1&= f_m(\varvec{\sigma }_{n+1},p_{c,n+1})\,, \end{aligned}$$

(47a)

$$\begin{aligned} \ \varvec{{\mathcal {R}}}_2&= -\varvec{\epsilon }^p_{m,n+1} +\varvec{\epsilon }^p_{m,n} + \varDelta \lambda _m \frac{\partial f_m}{\partial \varvec{\sigma }}\,, \end{aligned}$$

(47b)

$$\begin{aligned} \varvec{{\mathcal {R}}}_3&= f_w(\varvec{\sigma }_{n+1})\,, \end{aligned}$$

(47c)

$$\begin{aligned} \varvec{{\mathcal {R}}}_4&= -\varvec{\epsilon }^p_{w,n+1} +\varvec{\epsilon }^p_{w,n} + \varDelta \lambda _w \frac{\partial g_w}{\partial \varvec{\sigma }}\,, \end{aligned}$$

(47d)

where $\varvec{{\mathcal {R}}}_1$ and $\varvec{{\mathcal {R}}}_3$ are scalars, while $\varvec{{\mathcal {R}}}_2$ and $\varvec{{\mathcal {R}}}_4$ are $6\times 1$ vectors converted from rank-two tensors in Voigt notation. We define the total residual vector $\varvec{{\mathcal {R}}}$ as

$$\begin{aligned} \varvec{{\mathcal {R}}} = \left[ \begin{array}{cccc} \varvec{{\mathcal {R}}}_1&\varvec{{\mathcal {R}}}_2&\varvec{{\mathcal {R}}}_3&\varvec{{\mathcal {R}}}_4 \end{array}\right] ^{\mathsf {T}} \end{aligned}$$

(48)

and the total unknown vector $\varvec{x}$ as

$$\begin{aligned} \varvec{x} = \left[ \begin{array}{cccc} \varDelta \lambda _m&\varvec{\epsilon }^p_{m,n+1}&\varDelta \lambda _w&\varvec{\epsilon }^p_{w,n+1} \end{array}\right] ^{\mathsf {T}}\,. \end{aligned}$$

(49)

Both $\varvec{{\mathcal {R}}}$ and $\varvec{x}$ are of size $14\times 1$ in 3D.

The linearized system takes the form

$$\begin{aligned} \varvec{{\mathcal {J}}}\delta \varvec{x} = -\varvec{{\mathcal {R}}}\,, \end{aligned}$$

(50)

where $\varvec{{\mathcal {J}}} = \partial \varvec{{\mathcal {R}}}/\partial \varvec{x}$ is the Jacobian matrix and $\delta \varvec{x}$ is the search direction [14]. To be more specific, the equation above can be expanded as

$$\begin{aligned} \left[ \begin{array}{cccc} \varvec{{\mathcal {J}}}_{11} &{} \varvec{{\mathcal {J}}}_{12} &{} \varvec{{\mathcal {J}}}_{13} &{} \varvec{{\mathcal {J}}}_{14} \\ \varvec{{\mathcal {J}}}_{21} &{} \varvec{{\mathcal {J}}}_{22} &{} \varvec{{\mathcal {J}}}_{23} &{} \varvec{{\mathcal {J}}}_{24} \\ \varvec{{\mathcal {J}}}_{31} &{} \varvec{{\mathcal {J}}}_{32} &{} \varvec{{\mathcal {J}}}_{33} &{} \varvec{{\mathcal {J}}}_{34} \\ \varvec{{\mathcal {J}}}_{41} &{} \varvec{{\mathcal {J}}}_{42} &{} \varvec{{\mathcal {J}}}_{43} &{} \varvec{{\mathcal {J}}}_{44} \end{array}\right] \left\{ \begin{array}{c} \delta \varDelta \lambda _m \\ \delta \varvec{\epsilon }^p_{m,n+1} \\ \delta \varDelta \lambda _w \\ \delta \varvec{\epsilon }^p_{w,n+1} \end{array}\right\} =-\left\{ \begin{array}{c} \varvec{{\mathcal {R}}}_1 \\ \varvec{{\mathcal {R}}}_2 \\ \varvec{{\mathcal {R}}}_3 \\ \varvec{{\mathcal {R}}}_4 \end{array}\right\} \,, \end{aligned}$$

(51)

where the components of $\varvec{{\mathcal {J}}}$ are derived in Appendix B. We note that the following state variables vary with the unknown vector $\varvec{x}$:

$$\begin{aligned} \varvec{\epsilon }^e_{n+1}&= \varvec{\epsilon }_{n+1} - \varvec{\epsilon }^p_{m,n+1} -\varvec{\epsilon }^p_{w,n+1}\,, \end{aligned}$$

(52a)

$$\begin{aligned} \varvec{\sigma }_{n+1}&= {\mathbb{C}}^e:\varvec{\epsilon }^e_{n+1}\,, \end{aligned}$$

(52b)

$$\begin{aligned} p_{c,n+1}&= p_{c0}\mathrm{exp}\left( -\frac{\mathbf{1}: \varvec{\epsilon }^p_{m,n+1}}{\lambda _p}\right) \,. \end{aligned}$$

(52c)

In evaluating the algorithmic tangent operator ${\mathbb{C}}$, we regard $\varDelta \varvec{\epsilon }$ and $\varvec{x}$ as functions of the prescribed total strain $\varvec{\epsilon }_{n+1}$. Thus, we have

$$\begin{aligned} {\mathbb{C}} ={\mathbb{C}}^e:\left( {\mathbb{I}}-\frac{\partial \varvec{\epsilon }_{m,n+1}^p}{\partial \varvec{\epsilon }_{n+1}} -\frac{\partial \varvec{\epsilon }_{w,n+1}^p}{\partial \varvec{\epsilon }_{n+1}}\right) \,. \end{aligned}$$

(53)

To derive the expression ${\partial \varvec{\epsilon }_{m,n+1}^p}/{\partial \varvec{\epsilon }_{n+1}}$ and ${\partial \varvec{\epsilon }_{w,n+1}^p}/{\partial \varvec{\epsilon }_{n+1}}$, we make use of the fact that at the locally converged state,

$$\begin{aligned} \frac{\partial \varvec{{\mathcal {R}}}}{\partial \varvec{\epsilon }_{n+1}} =\frac{\partial \varvec{{\mathcal {R}}}}{\partial \varvec{x}} \biggr |_{\varDelta \varvec{\epsilon }} \frac{\partial \varvec{x}}{\partial \varvec{\epsilon }_{n+1}} +\frac{\partial \varvec{{\mathcal {R}}}}{\partial \varDelta \varvec{\epsilon }}\biggr |_{\varvec{x}} \frac{\partial \varDelta \varvec{\epsilon }}{\partial \varvec{\epsilon }_{n+1}}=\mathbf{0}\,, \end{aligned}$$

(54)

where

$$\begin{aligned} \frac{\partial \varvec{{\mathcal {R}}}}{\partial \varvec{x}} \biggr |_{\varDelta \varvec{\epsilon }}&=\varvec{{\mathcal {J}}}\,, \end{aligned}$$

(55a)

$$\begin{aligned} \frac{\partial \varDelta \varvec{\epsilon }}{\partial \varvec{\epsilon }_{n+1}}&={\mathbb{I}}\,. \end{aligned}$$

(55b)

Thus, we have

$$\begin{aligned} \frac{\partial \varvec{x}}{\partial \varvec{\epsilon }_{n+1}} =\varvec{{\mathcal {J}}}^{-1} \frac{\partial \varvec{{\mathcal {R}}}}{\partial \varDelta \varvec{\epsilon }} \biggr |_{\varvec{x}}\,, \end{aligned}$$

(56)

and the remaining term is derived as

$$\begin{aligned} \frac{\partial \varvec{{\mathcal {R}}}}{\partial \varDelta \varvec{\epsilon }}\biggr |_{\varvec{x}} =\left[ \begin{array}{c} \frac{\partial f_m}{\partial \varvec{\sigma }}:{\mathbb{C}}^e \\ \varDelta \lambda _m\frac{\partial ^2 f_m}{\partial \varvec{\sigma }^2}:{\mathbb{C}}^e \\ \frac{\partial f_w}{\partial \varvec{\sigma }}:{\mathbb{C}}^e \\ \varDelta \lambda _w\frac{\partial ^2 g_w}{\partial \varvec{\sigma }^2}:{\mathbb{C}}^e \end{array}\right] _{14\times 6}\,, \end{aligned}$$

(57)

The components are expressed in tensorial form for brevity, but one should note that the rank-two and rank-four tensors in 3D should be converted to $1\times 6$ vectors and $6\times 6$ matrices in Voigt form, respectively.

By combining Eqs. (56) and (57), we can evaluate ${\partial \varvec{x}}/{\partial \varvec{\epsilon }_{n+1}}$ at the converged configuration. We note that

$$\begin{aligned} \frac{\partial \varvec{x}}{\partial \varvec{\epsilon }_{n+1}} = \left[ \begin{array}{c} \frac{\partial \varDelta \lambda _m}{\partial \varvec{\epsilon }_{n+1}} \\ \frac{\partial \varvec{\epsilon }^p_{m,n+1}}{\partial \varvec{\epsilon }_{n+1}} \\ \frac{\partial \varDelta \lambda _w}{\partial \varvec{\epsilon }_{n+1}} \\ \frac{\partial \varvec{\epsilon }^p_{w,n+1}}{\partial \varvec{\epsilon }_{n+1}} \end{array}\right] _{14\times 6}\,, \end{aligned}$$

(58)

and thus, we can evaluate $\partial \varvec{\epsilon }^p_{m,n+1}/\partial \varvec{\epsilon }_{n+1}$ and $\partial \varvec{\epsilon }^p_{w,n+1}/ \partial \varvec{\epsilon }_{n+1}$.

The partial derivatives appearing in Eqs. (47) and (57) are elaborated further in Appendix A.

(b) Semi-plastic loading process on $f_m$:

For the semi-plastic loading process on $f_m$, only the yield surface $f_m$ is active, and the plastic strain for $f_w$ remains unchanged, i.e., $\varvec{\epsilon }^p_{w,n+1} = \varvec{\epsilon }^p_{w,n}$ and $\varDelta \lambda _w = 0$. The return mapping algorithm reduces to that for the anisotropic modified Cam-Clay model reported in [74, 108]. For this case, we just need to solve the discrete consistency condition and incremental flow rule for $f_m$ (Eqs. (45a) and (46a)) for $\varvec{\epsilon }^p_{m,n+1}$ and $\varDelta \lambda _m$.

The residual vector and the unknown vector reduces to

$$\begin{aligned} \varvec{{\mathcal {R}}} = \left[ \begin{array}{cc} \varvec{{\mathcal {R}}}_1&\varvec{{\mathcal {R}}}_2 \end{array}\right] ^{\mathsf {T}}\,, \end{aligned}$$

(59)

and

$$\begin{aligned} \varvec{x} = \left[ \begin{array}{cc} \varDelta \lambda _m&\varvec{\epsilon }^p_{m,n+1} \end{array}\right] ^{\mathsf {T}}\,. \end{aligned}$$

(60)

The linearized system for the Newton-Raphson scheme then takes the form

$$\begin{aligned} \left[ \begin{array}{cc} \varvec{{\mathcal {J}}}_{11} &{} \varvec{{\mathcal {J}}}_{12} \\ \varvec{{\mathcal {J}}}_{21} &{} \varvec{{\mathcal {J}}}_{22} \end{array}\right] \left[ \begin{array}{c} \delta \varDelta \lambda _m \\ \delta \varvec{\epsilon }^p_{m,n+1} \end{array}\right] =-\left[ \begin{array}{c} \varvec{{\mathcal {R}}}_1 \\ \varvec{{\mathcal {R}}}_2 \end{array}\right] \,, \end{aligned}$$

(61)

For the semi-plastic process on $f_m$, the Jacobian matrix $\varvec{{\mathcal {J}}}$ becomes a $7\times 7$ matrix. To calculate the algorithmic tangent operator ${\mathbb{C}}$, we follow the same step for the fully plastic process shown in Eqs. (53–58), which yields

$$\begin{aligned} {\mathbb{C}} ={\mathbb{C}}^e:\left( {\mathbb{I}}-\frac{\partial \varvec{\epsilon }_{m,n+1}^p}{\partial \varvec{\epsilon }_{n+1}}\right) \,. \end{aligned}$$

(62)

We solve Eq. (56) again for $\partial \varvec{x}/\partial \varvec{\epsilon }_{n+1}$ with

$$\begin{aligned} \frac{\partial \varvec{{\mathcal {R}}}}{\partial \varDelta \varvec{\epsilon }}\biggr |_{\varvec{x}} =\left[ \begin{array}{c} \frac{\partial f_m}{\partial \varvec{\sigma }}:{\mathbb{C}}^e \\ \varDelta \lambda _m\frac{\partial ^2 f_m}{\partial \varvec{\sigma }^2}:{\mathbb{C}}^e \end{array}\right] _{7\times 6}\,. \end{aligned}$$

(63)

Thus, we can evaluate ${\partial \varvec{\epsilon }_{m,n+1}^p}/{\partial \varvec{\epsilon }_{n+1}}$ from the submatrix of the expression

$$\begin{aligned} \frac{\partial \varvec{x}}{\partial \varvec{\epsilon }_{n+1}} = \left[ \begin{array}{c} \frac{\partial \varDelta \lambda _m}{\partial \varvec{\epsilon }_{n+1}} \\ \frac{\partial \varvec{\epsilon }^p_{m,n+1}}{\partial \varvec{\epsilon }_{n+1}} \end{array}\right] _{7\times 6}\,. \end{aligned}$$

(64)

(c) Semi-plastic loading process on $f_w$:

The only difference here is that $f_w$ is the active yield surface. Plastic strain for $f_m$ remains unchanged, and $\varvec{\epsilon }^p_{m,n+1} = \varvec{\epsilon }^p_{m,n}$, $p_{c,n+1} = p_{c,n}$, and $\varDelta \lambda _m = 0$. For the return mapping algorithm, we only need to solve the discrete consistency condition and incremental flow rule for $f_w$ (Eqs. (45b) and (46b)) for $\varvec{\epsilon }^p_{w,n+1}$ and $\varDelta \lambda _w$.

The residual vector and the unknown vector now reduce to

$$\begin{aligned} \varvec{{\mathcal {R}}} = \left[ \begin{array}{cc} \varvec{{\mathcal {R}}}_3&\varvec{{\mathcal {R}}}_4 \end{array}\right] ^{\mathsf {T}}\,, \end{aligned}$$

(65)

and

$$\begin{aligned} \varvec{x} = \left[ \begin{array}{cc} \varDelta \lambda _w&\varvec{\epsilon }^p_{w,n+1} \end{array}\right] ^{\mathsf {T}}\,. \end{aligned}$$

(66)

The linearized system for the Newton-Raphson scheme is

$$\begin{aligned} \left[ \begin{array}{cc} \varvec{{\mathcal {J}}}_{33} &{} \varvec{{\mathcal {J}}}_{34} \\ \varvec{{\mathcal {J}}}_{43} &{} \varvec{{\mathcal {J}}}_{44} \end{array}\right] \left[ \begin{array}{c} \delta \varDelta \lambda _w \\ \delta \varvec{\epsilon }^p_{w,n+1} \end{array}\right] =-\left[ \begin{array}{c} \varvec{{\mathcal {R}}}_3 \\ \varvec{{\mathcal {R}}}_4 \end{array}\right] \,, \end{aligned}$$

(67)

while the Jacobian $\varvec{{\mathcal {J}}}$ is now a $7\times 7$ matrix. To calculate the algorithmic tangent operator ${\mathbb{C}}$, we again follow the same step for the fully plastic process shown in Eqs. (53–58) and obtain

$$\begin{aligned} {\mathbb{C}} ={\mathbb{C}}^e:\left( {\mathbb{I}} -\frac{\partial \varvec{\epsilon }_{w,n+1}^p}{\partial \varvec{\epsilon }_{n+1}}\right) \,. \end{aligned}$$

(68)

We solve Eq. (56) again for $\partial \varvec{x}/\partial \varvec{\epsilon }_{n+1}$ with

$$\begin{aligned} \frac{\partial \varvec{{\mathcal {R}}}}{\partial \varDelta \varvec{\epsilon }}\biggr |_{\varvec{x}} = \left[ \begin{array}{c} \frac{\partial f_w}{\partial \varvec{\sigma }}:{\mathbb{C}}^e \\ \varDelta \lambda _w\frac{\partial ^2 g_w}{\partial \varvec{\sigma }^2}:{\mathbb{C}}^e \end{array}\right] _{7\times 6}\,. \end{aligned}$$

(69)

Again, we can evaluate ${\partial \varvec{\epsilon }_{w, n+1}^p}/{\partial \varvec{\epsilon }_{n+1}}$ as a submatrix in

$$\begin{aligned} \frac{\partial \varvec{x}}{\partial \varvec{\epsilon }_{n+1}} = \left[ \begin{array}{c} \frac{\partial \varDelta \lambda _w}{\partial \varvec{\epsilon }_{n+1}} \\ \frac{\partial \varvec{\epsilon }^p_{w,n+1}}{\partial \varvec{\epsilon }_{n+1}} \end{array}\right] _{7\times 6}\,. \end{aligned}$$

(70)

4 Model validation

In this section, we validate the double-yield-surface plasticity theory using triaxial compression experimental data from three different types of transversely isotropic rocks, namely NW-Spain slate [1], Longmaxi shale [93], and a synthetic transversely isotropic rock [84]. The aim of the validation is to reproduce the experimentally observed undulatory variation of rock strength with bedding orientation observed for these rocks.

4.1 Synthetic transversely isotropic rock

Synthetic rock is an artificially simulated material that has similar properties to those of natural rocks. It is a common man-made material for physical modeling produced by mixing water and rock-like components including sand, kaolinite, cement, resin, and curing for a certain period of time. Tien et al. [84] prepared two synthetic rocks with different weight ratios of water, cement, and kaolinite to result in different strength and stiffness for the two materials. They then layered the two materials in an alternating fashion to generate a synthetic transversely isotropic rock. The joints of the layers then represent the weak bedding planes of the rock.

Zhao et al. [108] used the anisotropic modified Cam-Clay model described in this paper to model plastic deformation in the solid matrix and reproduce the variation of rock strength with bedding orientation for the synthetic transversely isotropic rock measured in triaxial compression under a confining pressure of 14 MPa. Their result is shown by the dashed curve in Fig. 5 and reveals some deviation of an experimental data point at bedding plane orientation of $60^\circ$. Tien et al. [84] reported that the observed failure modes in the tested rock included sliding along the weak planes. Such discrepancy highlights the need for additional modeling of the failure mechanism along the weak planes on top of the plastic deformation predicted by the anisotropic modified Cam-Clay model.

Table 1 Parameters for synthetic transversely isotropic rocks

We use the proposed double-yield-surface plasticity theory to better fit the experimental data of Tien et al. [84]. The parameters in the model are reported in Table 1. The elastic parameters are determined through homogenization of the parameters of the two constituent materials of the synthetic transversely isotropic rocks based on Backus average [5], while the plastic parameters are calibrated to fit the experimental data. As one can see in Fig. 5, the calibrated model reproduces the undulatory variation of rock strength with bedding orientation quite well. The portion of the curve that protrudes downward is the result of the activation of yield surface $f_w$. Besides, we also observe two clear transition points on the curve that differentiates the failure modes through the solid matrix and along the weak planes. The range of bedding plane orientation for the sliding failure mode along the weak planes is from 41 to $79^\circ$, which perfectly matches the observed range of 45 to $75^\circ$ reported by Tien et al. [84].

Lastly, we also conduct a parametric study to investigate how the parameters in the yield function $f_w$ for sliding along the weak planes, the cohesion $c_w$ and the friction angle $\phi _w$, influence the shape of the variation curve between rock strength and bedding orientation. As reported in Fig. 6, a decrease in both $\phi _w$ and $c_w$ expands the range of bedding plane orientation in which the failure mode is governed by sliding along the weak planes, as well as reduces the minimum rock strength. The difference is that decreasing $\phi _w$ leads to a lower bedding plane orientation that corresponds to the minimum rock strength, while $c_w$ does not have any impact on it. This is because the minimum rock strength is achieved when the bedding plane orientation is equal to $45^\circ +\phi _w/2$. We note that this critical bedding orientation depends solely on the friction angle $\phi _w$ and not on the dilatancy angle $\psi _w$, since the weak planes are prescribed in this case, as opposed to a continuum problem where the dilatancy angle plays a role in the inception of a shear band (see [29, 30]).

Fig. 5

Variation of rock strength with bedding orientation for synthetic transversely isotropic rocks. Experimental data are from Tien et al. [84]

Fig. 6

Impact of mechanical parameters of the weak planes on the variation of rock strength with bedding orientation. Left: Influence of $\phi _w$, Right: Influence of $c_w$

4.2 Longmaxi shale

Longmaxi shale is a black organic-rich shale from the Lower Silurian Longmaxi formation in South China. The Lower Silurian shale formation was deposited in a restricted marine basin environment and were formed under bottom water anoxic conditions [80]. In terms of the lithological composition, laminated and nonlaminated siliceous shale predominate in the Silurian Longmaxi formation [93]. To analyze the mineral composition of Longmaxi shale, Liang et al. [57] conducted X-ray diffraction analysis on 192 Longmaxi shale specimens. Their study revealed that the major components in Longmaxi shale are quartz and clay, with an average weight content of 43.2% and 39.6%, respectively. Other minor mineral components include plagioclase, potassium feldspar, calcite, dolomite, and pyrite. They also reported that the Longmaxi shale has a total organic carbon (TOC) content ranging up to 8.6%, with an average of 3.2%. The Lower Silurian Longmaxi formation has long been known as the principal source rock for conventional petroleum reservoirs [102]. In recent years, attempts have been made to exploit unconventional shale gas in this formation. Wu et al. [93] conducted triaxial compression tests on Longmaxi shale specimens extracted from the outcrops in the formation that constitutes the Chongqing Jiaoshiba shale gas block reservoirs to investigate their mechanical properties and failure modes. In this study, we will use the proposed model to reproduce the triaxial compression test response of Longmaxi shale at a confining pressure of 40 MPa.

Table 2 Parameters for Longmaxi Shale

Wu et al. [93] reported the apparent Young’s modulus and Poisson’s ratio of Longmaxi shale as functions of bedding orientation in the test specimens. We used these data to calibrate the elasticity parameters for the model as shown in Table 2 and Fig. 7. In Fig. 7, we see that the calibrated model can capture the U-shaped variation of the apparent Young’s modulus and the reverse U-shaped variation of Poisson’s ratio with bedding orientation in the specimens. We note that there exists a 10% error between the calibrated Poisson’s ratio against the measured data when the bedding orientation in the test specimen is 45$^\circ$. This could be due to some adjoint plastic deformation along the weak bedding planes that was not accounted for in the model calibration.

Fig. 7

Variation of elasticity parameters with bedding orientation. Left: Young’s modulus, Right: Poisson’s ratio

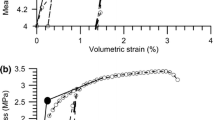
We next calibrate the plasticity parameters for the model shown in Table 2 by reproducing the stress-strain relationship in triaxial compression on specimens with bedding orientations of $\theta =0$, 45, and $90^\circ$. For $\theta =0$ and $90^\circ$, the yield surface $f_w$ remains inactive throughout the simulation, and the stress-strain response is governed solely by yielding in the rock matrix. As a result, the stress gradually approaches the peak strength defined by the critical-state line of the anisotropic modified Cam-Clay model. For $\theta =45^\circ$, the material response is initially governed by $f_m$, but the stress state no longer hits the critical-state line since the peak stress bounded by $f_w$ is lower. Once the stress activates $f_w$, it stops changing with strain increments.

Fig. 8

Calibrated stress-strain curve for Longmaxi Shale with various bedding orientations

With the calibrated parameters, Fig. 9 shows the predicted variation of rock strength with bedding orientation for Longmaxi shale. It is evident that the simulation result fits the experimental data well. In addition, the model predicts that the failure mode is sliding along the weak planes for specimens with bedding orientations ranging from 27 to $76^\circ$. Incidentally, the failure modes reported by Wu et al. [93] indicate that specimens with $\theta =45$, 60, and $75^\circ$ orientations tended to break down along the weak planes, in agreement with the model prediction. For $\theta =30^\circ$, however, the specimen fractured along the diagonal direction across the rock matrix. The deviation in failure modes between the experimental observation and model prediction may be due to end constraints on the specimen. Besides, the orientation $\theta =30^\circ$ is also near the lower limit of the predicted range, so small perturbations in the experiment may lead to an opposite result.

Fig. 9

Variation of rock strength with bedding orientation for Longmaxi Shale

4.3 NW-Spain slate

In this last example, we use the proposed model to reproduce the variation of rock strength with bedding orientation for a NW-Spain slate reported by Alejano et al. [1]. The rock specimens were acquired from a quarry site located in O Barco de Valdeorras in the northwest of Spain. The slate has a black to very dark blue color and exhibits a high fissility. It possesses significant foliation patterns and is easy to fracture along the weak planes, layers of which were quarried to produce roofing slate tiles. Alejano et al. [1] conducted a series of triaxial compression tests and wave velocity tests on this slate, and showed that its mechanical behavior and failure modes are heavily dependent on the orientation of the bedding structures.

Table 3 Parameters for NW-Spain slate

We now conduct numerical simulations of triaxial compression tests on NW-Spain slate at a confining pressure of 10 MPa. The calibrated model parameters are shown in Table 3. Here, the elasticity parameters were converted from those reported by Alejano et al. [1] measured from wave velocity tests, while the plasticity parameters were calibrated from the experimental variation of rock strength with bedding orientation in triaxial compression. As shown in Fig. 10, the model prediction fits the experimental data quite well, and also indicates that the threshold for failure along the weak planes ranges from 27 to 84$^\circ$. This range matches the experimental observations where specimens with bedding orientations of 30, 45, 60, and $75^\circ$ followed such a failure mode.

Fig. 10

Variation of rock strength with bedding orientation for NW-Spain slate

Alejano et al. [1] also proposed several models to capture the relationship between rock strength and bedding plane orientation for the NW-Spain slate. Their prediction with the best performance is also shown in Fig. 10. Their model consisted of two failure criteria, one for the solid matrix and the other for the weak bedding planes. For the weak planes, their failure criterion was the same as the one used in our model. Since we used the same parameter $\phi _w$ and $c_w$ for the weak planes, there is an overlap of predictions with our model for cases where the failure of the slate is along the weak planes. For the rock matrix, however, they assumed that the rock strength was a linear function of the bedding plane orientation. They calibrated the model with Hoek-Brown failure criterion for specimens with bedding orientations of 0 and $90^\circ$, and interpolated the strength linearly in between. However, it has been reported by several investigators that in transversely isotropic rocks the dependence of strength with bedding orientation follows a nonlinear U-shaped variation when the sliding mechanism along the weak planes is not apparent. Thus, their linear relationship was insufficient to describe the response of the rock matrix. By comparing our prediction with that by Alejano et al. [1], it is evident that our model more realistically captures the nonlinear variation of rock strength with bedding orientation when the material fails through the rock matrix. Our model prediction also exhibits a more natural transition of the responses governed by the two failure modes.

5 Cylindrical cavity expansion in NW-Spain slate

We implement the proposed double-yield-surface plasticity model in a finite element framework built upon an open source library Deal.II [3]. We use this code to simulate the expansion of a cylindrical cavity in a transversely isotropic rock. The problem of cylindrical cavity expansion in geomaterials is widely encountered in numerous practical applications in geotechnical and petroleum engineering [21, 31, 36, 97, 101]. Applications include pressuremeter testing in shale formation [59], tunnel excavation [101], pile driving [77], and horizontal wellbore drilling [109]. Research on this topic has been extensively carried out with the surrounding geomaterials modeled by different constitutive laws. For instance, Wang et al. [91] developed an analytical solution to cylindrical cavity expansion in Mohr–Coulomb soils. Carter et al. [20] analyzed the problem with the surrounding geomaterials modeled by the Cam-Clay model. Chen and Abousleiman [22] introduced a semi-analytical method for the problem with the modified Cam-Clay soils. Li et al. [53] and Liu and Chen [58] investigated the problem considering the anisotropic mechanical properties of the surrounding soils. In this paper, we investigate the cylindrical cavity expansion problem in transversely isotropic rocks containing a borehole subjected to fluid injection.

Fig. 11

Setup for the cylindrical cavity expansion problem and finite element mesh

The setup for the problem is shown on the left side of Fig. 11. The simulation domain is a 10 m$\times$10 m square with a bedding orientation of $\theta =45^\circ$ and deforming in plane strain. The outer boundaries of the domain are constrained with roller supports. In the middle of the domain is a cylindrical cavity of radius 0.5 m. The surrounding rock is modeled with the parameters calibrated from the NW-Spain slate, as summarized in Table 3. We assume that the surrounding rock is normally consolidated with an initial isotropic in-situ stress of $p_{c0}$. An injection pressure of $\sigma _i$ is then prescribed on the wall of the borehole, which starts from 10 MPa and linearly increases with the loading steps to reach the target value of 100 MPa. The right side of Fig. 11 shows the finite element mesh with 1064 four-node quadrilaterial elements. We conduct three sets of numerical simulations, one with the proposed double-yield-surface theory and the other two with each yield criterion $f_w$ or $f_m$, and investigate the distributions of stress and plastic deformation in the surrounding rock as well as the deformed shape of the borehole.

The distributions of the mean normal stress p and deviatoric stress q are shown in Fig. 12 for the three aforementioned scenarios. The injection pressure is taken as $\sigma _i=100$ MPa. For a clearer display, the contours were zoomed within the 6 m$\times$6 m region in the vicinity of the borehole. Fig. 12a shows that when the surrounding rock is modeled with $f_m$, no significant difference in the stress field develops along the bed-parallel direction or along the bed-normal direction. In contrast, when the surrounding rock is modeled with $f_w$, lower values are noted for both p and q at four corners around the borehole along the bed-parallel direction, as shown in Fig. 12b. This can attribute to the activation of the yield function $f_w$ in these places where the stress state are bounded. Lastly, for simulations where the surrounding rocks are modeled with the double-yield-surface (DYS) plasticity model, the stress distribution in the domain is affected by both yield surfaces. The overall patterns of p and q follow those for simulation with only $f_m$ active. At the four corners around the borehole, a lower value in the contour of q can be observed as the case with only $f_w$ being active. Interestingly, we see that the stress components now have higher values along the bed-normal direction than along the bed-parallel direction around the borehole, compared with Fig. 12a. This is due to the plastic sliding mechanism along the bedding planes that releases the stress along the bed-parallel direction in the vicinity the borehole.

Fig. 12

Stress distribution for simulations with a only fm, b only $f_w$, c the proposed double-yield-surface plasticity model. Left: hydrostatic component of stress, p; Right: deviatoric component of stress, q. Color bars are stresses in MPa

Figure 13 shows the contours of plastic strain in the simulation domain for the three aforementioned loading scenarios. We see that when only $f_w$ is active, the plastic strain component $\varvec{\epsilon }_w^p$ develops and propagates from the four corners around the borehole into the surrounding rock, while for the case with the proposed double-yield-surface plasticity model, $\varvec{\epsilon }_w^p$ concentrates more prominently around the borehole. This is due to the fact that the stress state around the borehole is also capped by $f_m$, which limits the region where plastic sliding governed by $f_w$ can occur. Comparing Fig. 13a, c, we conclude that the activation of $f_w$ also perturbs the distribution of $\varvec{\epsilon }_m^p$.

Fig. 13

Distribution of norm of plastic strain in the domain($\times 1000$). Left: Norm of plastic strain in the solid matrix $\Vert \varvec{\epsilon }_m^p\Vert$; Right: Norm of plastic strain along the weak bedding planes $\Vert \varvec{\epsilon }_w^p\Vert$

Lastly, Fig. 14 compares the deformed shapes of the borehole for the three loading scenarios. The borehole wall in the simulation with only $f_w$ active has the least deformation. In this case, the only places that undergo plastic deformation are the four corners around the borehole, while most region surrounding the borehole still deforms elastically, as shown in Fig. 13b. Deformation along the bed-normal direction of the borehole is larger than along the bed-parallel direction due to the anisotropic elastic property of the rock where the stiffness along the bed-normal direction is lower. The borehole experiences significantly larger deformation when $f_m$ is active. In this case, the rock surrounding the borehole undergoes volumetric plastic compaction as the material hardens to bear the injection pressure. The response predicted by the proposed double-yield-surface plasticity model is similar to that predicted when only $f_m$ is active, but the deformation is larger at the four corners where plastic sliding mechanism occurs.

Fig. 14

Comparison of deformed shapes of the borehole. Displacement scaled by a factor of 200 for display

6 Closure

We introduced a double-yield-surface plasticity model for transversely isotropic rocks that explicitly quantifies the bulk plasticity in the rock matrix and plastic sliding along the weak planes. A recently developed anisotropic modified Cam-Clay model was used to describe the plastic response of the rock matrix, while the Mohr–Coulomb friction law was used to represent plastic sliding along the weak planes. An implicit return mapping algorithm that systematically identifies the active yield constraint(s) was developed for the numerical implementation of the constitutive model.

We validated the proposed model with triaxial compression test data for three transversely isotropic rocks, including the NW-Spain slate, the Longmaxi shale, and a synthetic transversely isotropic rock. We showed that the proposed model can reproduce the complex undulatory variation of rock strength with bedding orientation for all three rocks. By using two distinctive mechanisms of plastic responses in the rock, the threshold of the bedding plane orientation can be identified for the two failure modes.

We used the new model to analyze the problem of cylindrical cavity expansion in a transversely isotropic rock assuming three scenarios, one in which the elastoplastic property of the rock is described by the double-yield-surface plasticity theory and the other two in which either only bulk plasticity or plastic sliding is considered. The numerical results suggest that combining bulk plasticity and plastic sliding can result in rock responses that differ significantly from those obtained by considering the two plastic mechanisms separately.

Appendices

Appendix A. Relevant partial derivatives

This Appendix derives the partial derivatives of $f_w$ and $f_m$. For partial derivatives associated with $f_m$, we have

$$\begin{aligned}&\frac{\partial f_m}{\partial \varvec{\sigma }} =\frac{{\mathbb{A}}^*:\varvec{\sigma }}{M^2} +(2\varvec{a}^*:\varvec{\sigma }-p_c)\varvec{a}^*\,, \end{aligned}$$

(71)

$$\begin{aligned}&\frac{\partial ^2 f_m}{\partial \varvec{\sigma }^2} =\frac{{\mathbb{A}}^*}{M^2} + 2\varvec{a}^*\otimes \varvec{a}^*\,, \end{aligned}$$

(72)

$$\begin{aligned}&\frac{\partial f_m}{\partial p_c} =\varvec{a}^*:\varvec{\sigma }\,, \end{aligned}$$

(73)

$$\begin{aligned}&\frac{\partial p_c}{\partial \epsilon ^p_v} =-\frac{p_c}{\lambda _p}\,. \end{aligned}$$

(74)

For partial derivatives associated with $f_w$ and $g_w$, we limit the discussion to 2D plane strain problem and define $\varvec{l}$ as the tangential direction of the weak plane. The traction vector $\varvec{t}$ on the weak plane is

$$\begin{aligned} \varvec{t} = \varvec{\sigma }\cdot {\varvec{n}}\,. \end{aligned}$$

(75)

We can evaluate the shear stress $\tau$ and normal stress $\sigma _n$ on the weak plane as

$$\begin{aligned} \sigma _n&= \varvec{n}\cdot \varvec{t} = \varvec{\sigma }:\varvec{m}\,, \end{aligned}$$

(76a)

$$\begin{aligned} \tau&=\varvec{l}\cdot \varvec{t} = \varvec{\sigma }:\varvec{\alpha }\,, \end{aligned}$$

(76b)

where

$$\begin{aligned} \varvec{\alpha } = \frac{1}{2}\left( \varvec{l}\otimes \varvec{n} +\varvec{n}\otimes \varvec{l}\right) \,. \end{aligned}$$

(77)

Thus,

$$\begin{aligned}&\frac{\partial f_w}{\partial \varvec{\sigma }} =\mathrm{sgn}(\tau )\varvec{\alpha }+\mathrm{tan}\phi _w\varvec{m}\,, \end{aligned}$$

(78)

$$\begin{aligned}&\frac{\partial ^2 f_w}{\partial \varvec{\sigma }^2} = {\mathbb{O}}\,, \end{aligned}$$

(79)

$$\begin{aligned}&\frac{\partial g_w}{\partial \varvec{\sigma }} = \mathrm{sgn}(\tau ) \varvec{\alpha }+\mathrm{tan}\psi _w\varvec{m}\,, \end{aligned}$$

(80)

$$\begin{aligned}&\frac{\partial ^2 g_w}{\partial \varvec{\sigma }^2} = {\mathbb{O}}\,, \end{aligned}$$

(81)

where sgn($\tau$) is the sign of $\tau$.

Appendix B. Jacobian matrix

The submatrices $\varvec{{\mathcal {J}}}_{ij}$ in the Jacobian matrix $\varvec{{\mathcal {J}}}$ for the fully plastic process are given as follows:

$$\begin{aligned}&\varvec{{\mathcal {J}}}_{11} = 0\,, \end{aligned}$$

(82)

$$\begin{aligned}&\varvec{{\mathcal {J}}}_{12} = -\frac{\partial f_m}{\partial \varvec{\sigma }}: {\mathbb{C}}^e+\varvec{a}^*:\varvec{\sigma }_{n+1} \frac{p_c}{\lambda _p}\mathbf{1}\,, \end{aligned}$$

(83)

$$\begin{aligned}&\varvec{{\mathcal {J}}}_{13} = 0\,, \end{aligned}$$

(84)

$$\begin{aligned}&\varvec{{\mathcal {J}}}_{14} = -\frac{\partial f_m}{\partial \varvec{\sigma }}:{\mathbb{C}}^e\,, \end{aligned}$$

(85)

$$\begin{aligned}&\varvec{{\mathcal {J}}}_{21} =\frac{\partial f_m}{\partial \varvec{\sigma }}\,, \end{aligned}$$

(86)

$$\begin{aligned}&\varvec{{\mathcal {J}}}_{22} = -{\mathbb{I}}-\varDelta \lambda _m\nonumber \\&\qquad \qquad \left[ \left( \frac{{\mathbb{A}}^*}{M^2} +2\varvec{a}^*\otimes \varvec{a}^*\right) :{\mathbb{C}}^e -\frac{p_{c,n+1}}{\lambda _p}\varvec{a}^*\otimes \mathbf{1}\right] \,, \end{aligned}$$

(87)

$$\begin{aligned}&\varvec{{\mathcal {J}}}_{23} = \mathbf{0}\,, \end{aligned}$$

(88)

$$\begin{aligned}&\varvec{{\mathcal {J}}}_{24} = -\varDelta \lambda _m \left( \frac{{\mathbb{A}}^*}{M^2}+2\varvec{a}^* \otimes \varvec{a}^*\right) :{\mathbb{C}}^e\,, \end{aligned}$$

(89)

$$\begin{aligned}&\varvec{{\mathcal {J}}}_{31} = 0\,, \end{aligned}$$

(90)

$$\begin{aligned}&\varvec{{\mathcal {J}}}_{32} = -\frac{\partial f_w}{\partial \varvec{\sigma }}:{\mathbb{C}}^e\,, \end{aligned}$$

(91)

$$\begin{aligned}&\varvec{{\mathcal {J}}}_{33} = 0\,, \end{aligned}$$

(92)

$$\begin{aligned}&\varvec{{\mathcal {J}}}_{34} = -\frac{\partial f_w}{\partial \varvec{\sigma }}:{\mathbb{C}}^e\,, \end{aligned}$$

(93)

$$\begin{aligned}&\varvec{{\mathcal {J}}}_{41} = \mathbf{0}\,, \end{aligned}$$

(94)

$$\begin{aligned}&\varvec{{\mathcal {J}}}_{42} = {\mathbb{O}}\,, \end{aligned}$$

(95)

$$\begin{aligned}&\varvec{{\mathcal {J}}}_{43} =\frac{\partial g_w}{\partial \varvec{\sigma }}\,, \end{aligned}$$

(96)

$$\begin{aligned}&\varvec{{\mathcal {J}}}_{44} = - {\mathbb{I}}\,. \end{aligned}$$

(97)

The expressions above are given in tensorial expression for brevity, but they should be converted to matrix form for numerical implementation. Rank-two and rank-four tensors transform to $1\times 6$ vectors and $6\times 6$ matrices in 3D, respectively.