1 Introduction

Geomaterials such as soils and rocks often exhibit strong anisotropy in their strength and deformation properties, which is mostly due to bedding planes and preferred particle contact arrangements that arise from various depositional mechanisms during geologic history.

The consideration of anisotropy in the mechanical behaviour of materials was invoked as early as in the 1950s in the pioneering work of Hill [8] where an orthotropic failure criterion was formulated using modified stress invariants written in axes of principal anisotropy. Ever since, advances in laboratory experimental studies as well as in the constitutive and numerical modelling of anisotopic materials have developed methods for providing a better understanding of structured-oriented media, including layered and fractured rocks. A comprehensive summary together with a systematic comparison of the various approaches for describing anisotropic rock strength can be found in [6]. More modern incarnations of the so-called critical plane approach to anisotropy of geomaterials can be found in the works of Mroz and Pietruszczak [11, 14] which incorporate the effect of fabric into material strength variation, resulting into an anisotropic failure criterion.

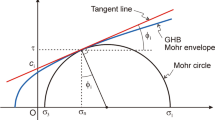
However, a closer look into the rock mechanics literature reveals some inconsistencies when applying anisotropic failure criteria in boundary value problems, especially during the interpretation of laboratory experimental results; see [1, 7, 13], for instance. A common mistake is often repeated in these cases, where a tangent line (or curve) to the Mohr stress circle is used as a failure envelope, and as a result, the direction dependency of the strength parameters is incorporated in failure functions that are written in terms of stress invariants. However, the tangency of the Mohr stress circle with the failure envelope that emerges from the critical plane approach with constant friction angle can be shown to be no longer valid when the strength parameters such as internal friction depends on spatial direction.

The current paper addresses the above-mentioned issue by proposing an appropriate numerical technique based on perturbation theory along with a new graphical method for describing the anisotropic strength of rocks. The visualization method and analytical calculations proposed herein provide useful tools to interpret experimental results on anisotropic rock strength data in a coherent manner which is yet practical.

2 Equations of failure in isotropic case

Material failure analysis within the critical plane framework requires finding the first stress state during loading history that satisfies the failure condition on a potential plane. This procedure can be recast mathematically into an optimization problem, whereby the failure function is being maximized with respect to the orientation of a potential sliding plane. For an isotropic material, failure in a potential plane—with normal and tangent vectors \(\varvec{n}\) and \(\varvec{s}\), respectively—can be written in its most general form as a function of both normal and tangential tractions, \({{\varvec{t}}}^n\) and \({{\varvec{t}}}^s\) [11] as:

$$\begin{aligned} &F(\varvec{t}^n,\varvec{t}^s,K,c)=0 \,\,\, {\text { such}}\,{\text {that}} \,\,\, \forall \varvec{n}:F(\varvec{t}^n,\varvec{t}^s,K,c)\le 0\\&\varvec{t}^n=(\varvec{n}\, {\varvec{\sigma }}\,\varvec{n})\,\varvec{n}\,{\text { or }}\,t^n_i=(\sigma _{jk} n_j n_k) n_i \\&\varvec{t}^s=(\varvec{\delta }-\varvec{n}\otimes \varvec{n})\, {\varvec{\sigma }}\,\varvec{n}\,{\text { or }}\,t^s_i=(\delta _{ij}-n_i n_j) \sigma _{jk} n_k \end{aligned}$$
(1)

where K and c are friction- and cohesion-like material parameters, \(\varvec{\sigma }\) is the second-order stress tensor, \(\varvec{\delta }\) is the Kronecker Delta, and the operator \(\otimes\) denotes a dyadic product such that \(\varvec{a}\otimes \varvec{b}=a_i b_j\).

The unknowns to the system of failure equations are identified as the failure plane orientation, \(\varvec{n}_\mathrm{f}\), and the state of stress at failure, \(\varvec{\sigma }_\mathrm{f}\). In relation to applications in saturated and partially saturated conditions, it should be mentioned that all the stresses and material properties discussed in this study are “effective” and as such the common “ \('\) ” notation has been omitted.

The condition \(F\le 0\) signifies that the failure function F is bounded by \(F=0\) referring to failure conditions. Hence, F is maximized whenever the failure state is reached, i.e.

$$\begin{aligned} \frac{\partial F}{\partial \varvec{n}}\varvec{s}&=\frac{\partial F}{\partial \varvec{t}^n}\frac{\partial \varvec{t}^n}{\partial \varvec{n}}\varvec{s}+\frac{\partial F}{\partial \varvec{t}^s}\frac{\partial \varvec{t}^s}{\partial \varvec{n}}\varvec{s}=0\,{\text { or }}\\ \frac{\partial F}{\partial n_i}s_i&=\frac{\partial F}{\partial t^n_j}\frac{\partial t^n_j}{\partial n_i}s_i+\frac{\partial F}{\partial t^s_j}\frac{\partial t^s_j}{\partial n_i}s_i=0 \end{aligned}$$
(2)

Furthermore, considering the so-called conventional triaxial stress condition where two of the principal stresses are equal \((\sigma _2=\sigma _3)\), the solution of Eqs. 1 and 2 reduces the problem to finding the major principal stress, \(\sigma _\mathrm{1f}\), at failure and the failure plane orientation, \(\varvec{n}_\mathrm{f}\). As an aside, it is argued in [5, 15] that in continuously deforming materials, the failure does not take place along the orientation where the failure function, F, is maximized, and instead, slip-lines form along the orientation of zero extension. The two criteria can be shown to be the same when the plastic deformations follow an associated flow rule where stress and kinematic characteristics coincide [15].

For the simple case of isotropic materials with direction-independent strength parameters, K and c, and linearity of the failure envelope, the failure function reduces to the conventional Mohr–Coulomb criterion which is expressed as:

$$\begin{aligned} F=\tau -\sigma _n\,\tan \varphi -c=0 \end{aligned}$$
(3)

where \({\tau }=\left\| \varvec{t}^s\right\|\) and \({{\sigma }_{n}=\left\| \varvec{t}^n\right\| }\) are the shear and normal stresses, and \(\varphi\) is the internal friction angle. In this case, the maximization following \(\partial F / \partial \varvec{n} = 0\) can be conducted independently of the failure condition \(F=0\) since the failure envelope is linear. As such, this maximization procedure is graphically represented in the Mohr stress space by the tangency condition between the Mohr stress circle and the failure envelope. The failure plane orientation in this case can be easily shown to be at \(\theta _\mathrm{f}=(\pi /4 + \varphi /2)\) with respect to the major principal stress direction. This result, in turn, can be substituted into Eq. 3, reducing it to a relation between stress components only, which, assuming that stress tensor is expressed in its principal direction, takes the following form:

$$\begin{aligned} \frac{({{\sigma }_{1}}-{{\sigma }_{2}})}{2}=\frac{({{\sigma }_{1}}+{{\sigma }_{2}})}{2}\sin \varphi +c\cos \varphi \end{aligned}$$
(4)

This form of the failure equation is convenient since it is expressed in terms of stress invariants and the optimization procedure is no longer required as the critical plane angle is embedded into Eq. 4.

Turning to the anisotropic case, it is tempting to introduce a directional dependency on the material parameters as an extension of the invariant form similar to that in Eq. 4. However, the directional dependency of material parameters prevents the maximization equation (Eq. 2) from being solved independently of stresses, and hence, the invariant form as expressed in Eq. 4 is no longer valid as will be discussed next.

3 Equations of failure in anisotropic case

Extending the isotropic case formulation, the failure criterion for an anisotropic material can be expressed by introducing the directional dependency into the material parameter, i.e.

$$\begin{aligned} F(\varvec{t}^n,\varvec{t}^s,K(\varvec{n}),c(\varvec{n}))=0 \end{aligned}$$
(5)

whose maximization takes the following form:

$$\begin{aligned} \frac{\partial F}{\partial \varvec{n}}\varvec{s}&=\frac{\partial F}{\partial \varvec{t}^n}\frac{\partial \varvec{t}^n}{\partial \varvec{n}}\varvec{s}+\frac{\partial F}{\partial \varvec{t}^s}\frac{\partial \varvec{t}^s}{\partial \varvec{n}}\varvec{s}+\frac{\partial F}{\partial K}\frac{\partial K}{\partial \varvec{n}}\varvec{s}+\frac{\partial F}{\partial c}\frac{\partial c}{\partial \varvec{n}}\varvec{s}=0\\&{\text {or}}\\ \frac{\partial F}{\partial n_i}s_i&=\frac{\partial F}{\partial t^n_j}\frac{\partial t^n_j}{\partial n_i}s_i+\frac{\partial F}{\partial t^s_j}\frac{\partial t^s_j}{\partial n_i}s_i+\frac{\partial F}{\partial K}\frac{\partial K}{\partial n_i}s_i+\frac{\partial F}{\partial c}\frac{\partial c}{\partial n_i}s_i=0 \end{aligned}$$
(6)

The analysis herein has been carried out for the simpler case where the dependency on direction, \(\varvec{n}\), can be reduced to one variable, \(\theta\), as shown for a 2D case in Fig. 1. Assuming a conventional Mohr–Coulomb criterion, the system of equations describing failure in this case can be written as:

$$\begin{aligned} {{F}}&=\tau -{{\sigma }_{n}} K_{(\theta )} -c_{(\theta )}=0 \\ \frac{\partial F}{\partial \theta }&= \frac{\partial \tau }{\partial \theta } -\frac{\partial {{\sigma }_{n}}}{\partial \theta }K_{(\theta )}- {{\sigma }_{n}}\frac{\partial K_{(\theta )}}{\partial \theta } -\frac{\partial c_{(\theta )}}{\partial \theta }=0 \end{aligned}$$
(7)

where \(\theta\) is the orientation of the normal to a given plane in space.

Also, depending on the form of the functions \(K_{(\theta )}\) and \(c_{(\theta )}\), it is usually not possible to solve the system of equations analytically. However, we immediately see that the appearance of strength dependency terms with \(\theta\) in Eq. 7 prevents us from solving the maximization equation independently of stresses, and hence destroys the conventional tangency condition in the Mohr stress space which, in the isotropic Mohr–Coulomb case, follows from the requirement that:

$$\begin{aligned} \frac{\partial \tau }{\partial \theta } =\frac{\partial {{\sigma }_{n}}}{\partial \theta }\tan (\varphi ) \end{aligned}$$
(8)

since \(K_{\theta }=\tan (\varphi )=\) const. Thus, the dependence of strength parameters on spatial direction \(\theta\) in the anisotropic case leads to a departure in the failure plane orientation from the usual \((\pi /4 + \varphi /2)\) in the isotropic case. Also, we note that the critical plane orientation may change with the relative angle, \(\beta\) shown in Fig. 1, between principal directions of \(K_{(\theta )}\) and stress.

Fig. 1
figure 1

a Schematic representation of bedding plane orientation with respect to principal stress directions and \(\varvec{n}\) as the normal vector defining orientation in the space. b General form of strength directional distribution as described by Eq. 18

Full size image

The above issue compromises the convenient expression of the failure criterion in its invariant form, like Eq. 4, as mentioned earlier. Nonetheless, a representation of mixed invariants taking into account the dependence \(\beta\) and material anisotropy axes can be used in addition to stress invariants to formulate anisotropic failure criteria as developed in [17] and [3] with the only difference that the complexity of directional dependency is removed for material parameters (internal friction and cohesion) and transferred to new invariants.

4 Graphical method

The failure conditions computed for an anisotropic material from Eq. 7, if illustrated in the conventional Mohr stress space (\(\tau\) vs. \(\sigma _n\)), would result in failure lines with slope of \(K_{\theta _\mathrm{f}}\) cutting through the stress Mohr’s circle at failure angle, \(\theta _\mathrm{f}\), clearly showing that tangency condition cannot be illustrated in such a graph. The sole reason for this shortcoming is that the direction \(\theta\) is not being illustrated explicitly as one of the bases of the space, but it merely is used as the parametric descriptor of the two bases, \(\sigma _n\) and \(\tau\). Herein, we use a polar representation by assigning a separate dimension to orientation which is inspired by rearranging the Mohr–Coulomb criterion into the following form:

$$\begin{aligned} \frac{\tau -{{c}_{\theta }}}{{{\sigma }_{n}}}={{K}_{\theta }} \end{aligned}$$
(9)

The two sides of the equation are functions of directions, \(\theta\), prescribing closed curves in a polar plot. As such, the optimization procedure leads to the tangency between these two curves in polar coordinates [16]. Figure 2 shows how both isotropic and anisotropic failures would look like in this space. The reference of the polar plot is translated by a certain value to represent a circle so as to avoid plotting negative values.

Fig. 2
figure 2

Polar plot visualization of shear failure condition: a isotropic case, b anisotropic case, and c bifurcation condition with two equally admissible solutions

Full size image

An interesting feature that emerges from such a graphical representation is the occurrence of two admissible solutions for some forms of strength distribution, see Fig. 2c where the failure plane can occur either near the plane of weakness or along the maximum stress ratio direction. Such dual solutions are also suggested in [4] as the intersection of two failure criteria: one describing the failure along the plane of weakness and the other along the maximum stress ratio, resulting in a kink in the failure stress evolution as the bedding orientation is varied with respect to the major stress direction. This phenomenon and its consequences are further investigated in the next sections.

5 Perturbation analysis

Evidently, no-closed-form solution exists for the system of Eqs. 5 and 6 in its general form, even though a numerical solution can always be envisaged. However, approximated closed-form solutions can be obtained from perturbation analysis which renders the calibration procedure objective. Otherwise, in the absence of a closed-form solution, calibrating such anisotropic models through experimental results requires back-calculating the parameters from numerical solutions of the boundary value problem, and can be potentially sensitive to the procedure chosen.

However, if deviations from the isotropic case are small enough, approximate closed-form solution can be obtained using a perturbation method in which the whole system of equations is expanded into polynomials about the isotropic case.

Depending on how significant the directional dependency of strength parameters is, a first, or second, or theoretically higher-order polynomial can be considered. Herein, we carry out the general calculation for the first-order, and a specific case of second-order perturbations. The need for higher-order analysis can be best assessed by examining the extent to which the experimental data of strength depends on direction. In particular, a preliminary comparison of the trends in experimental results and the characteristics of first and second-order perturbations (presented later in Fig. 3) can be an accurate indicator of the proper level of perturbation.

The outcome of such an approach is that it facilitates the interpretation of experimental results for anisotropic materials by providing a systematic calibration procedure.

5.1 First-order perturbation

It is assumed that anisotropic failure parameters deviate from isotropic ones as a first-order perturbation of the anisotropy parameters, i.e.

$$\begin{aligned} &{\varvec{n}_\mathrm{f}}={\varvec{n}_\mathrm{f0}}+\varvec{A_1} {{\omega }_{K}}+ \varvec{A_2} {{\omega }_{c}}+O_\theta ({{\omega }_{K}}^2,{{\omega }_{c}}^2)\\&{ {\varvec{\sigma }}_\mathrm{f}}={ {\varvec{\sigma }}_\mathrm{f0}}+\varvec{B_1} {{\omega }_{K}}+ \varvec{B_2} {{\omega }_{c}}+O_\sigma ({{\omega }_{K}}^2,{{\omega }_{c}}^2) \end{aligned}$$
(10)

with \(\omega _K\) and \(\omega _c\) being parameters smaller than 1 that describe the anisotropy of internal friction, \(K_\theta\) and cohesion \(c_\theta\) respectively. The terms \(\varvec{n}_\mathrm{f0}\) and \({\varvec{\sigma }}_\mathrm{f0}\) are the solutions for the isotropic case assuming \(\omega _K=\omega _c=0\). Notice that for more complex functions describing directional variations in material characteristics, there would be more than two parameters.

The system of failure equations can now be linearized by substituting Eq. 10 into Eqs. 5 and 6, and truncating the Taylor’s series expansion up to the first order of anisotropy parameters, i.e.

$$\begin{aligned}(F)_\mathrm{aniso}&=F_0+\frac{\partial F}{\partial \varvec{X}^\alpha }\frac{\partial \varvec{X}^\alpha }{\partial {\varvec{\sigma }}} \delta {\varvec{\sigma }}+\frac{\partial F}{\partial \varvec{X}^\alpha }\frac{\partial \varvec{X}^\alpha }{\partial \varvec{n}} \delta \varvec{n}\\&{\text {or}}\\ (F)_\mathrm{aniso}&=F_0+\frac{\partial F}{\partial X^\alpha _i}\frac{\partial X^\alpha _i}{\partial {\sigma _{jk}}} \delta {\sigma _{jk}}+\frac{\partial F}{\partial X^\alpha _i}\frac{\partial X^\alpha _i}{\partial n_j} \delta n_j \end{aligned}$$
(11)
$$\begin{aligned}\frac{\partial F}{\partial \varvec{n}}\varvec{s}=&\left( \frac{\partial F}{\partial \varvec{n}}\varvec{s}\right) _0+\left( \frac{\partial ^2 F}{\partial \varvec{X}^\alpha \partial \varvec{X}^\beta }\frac{\partial \varvec{X}^\beta }{\partial \varvec{n}}\frac{\partial \varvec{X}^\alpha }{\partial {\varvec{\sigma }}}+\frac{\partial F}{\partial \varvec{X}^\alpha }\frac{\partial ^2 \varvec{X}^\alpha }{\partial \varvec{n} \partial {\varvec{\sigma }}}\right) \delta {\varvec{\sigma }} \, \varvec{s}\\&+\left( \frac{\partial ^2 F}{\partial \varvec{X}^\alpha \partial \varvec{X}^\beta }\frac{\partial \varvec{X}^\beta }{\partial \varvec{n}}\frac{\partial \varvec{X}^\alpha }{\partial {\varvec{\sigma }}}+\frac{\partial F}{\partial \varvec{X}^\alpha }\frac{\partial ^2 \varvec{X}^\alpha }{\partial \varvec{n} \partial \varvec{n}}\right) \delta \varvec{n}\, \varvec{s}\\&{\text {or}}\\ \frac{\partial F}{\partial n_i}s_i=&\left( \frac{\partial F}{\partial n_i}s_i\right) _0+\left( \frac{\partial ^2 F}{\partial X^\alpha _j \partial X^\beta _k}\frac{\partial X^\beta _k}{\partial n_i}\frac{\partial X^\alpha _j}{\partial \sigma _{lm}}+\frac{\partial F}{\partial X^\alpha _j}\frac{\partial ^2 X^\alpha _j}{\partial n_i \partial \sigma _{lm}}\right) \delta \sigma _{lm}\,s_i\\&+\left( \frac{\partial ^2 F}{\partial X^\alpha _j \partial X^\beta _k}\frac{\partial X^\beta _k}{\partial n_i}\frac{\partial X^\alpha _j}{\partial n_l}+\frac{\partial F}{\partial X^\alpha _j}\frac{\partial ^2 X^\alpha _j}{\partial n_i \partial n_l}\right) \delta n_l\,s_i \end{aligned}$$
(12)

where \(F_0\) and \(({\partial F}/{\partial \varvec{n}})_0\) are the zero-th-order terms which are the same as for isotropic failure Eqs. 1 and 2 assuming that \({{\omega }_{k}}={{\omega }_{c}}=0\). \(\varvec{X}^\alpha\) represents the variables in the failure criterion (in our case, \(\varvec{t}^n\), \(\varvec{t}^s\), K and c), whereas \(\delta {\varvec{\sigma }}\) and \(\delta \varvec{n}\) are first-order functions of the anisotropy variables:

$$\begin{aligned} &\delta \varvec{n}=\varvec{A_1} {{\omega }_{K}}+ \varvec{A_2} {{\omega }_{c}}\\&\delta {\varvec{\sigma }}=\varvec{B_1} {{\omega }_{K}}+ \varvec{B_2} {{\omega }_{c}} \end{aligned}$$
(13)

We herein present calculations for a cohesive-frictional case where it is considered that approximations of both friction and cohesion through first-order harmonic series are accurate enough, i.e.

$$\begin{aligned} &{{K}_{\theta }}={{K}_{0}}\left( 1+{{\omega }_{K}}\cos 2(\theta -\beta )\right) \\&{{c}_{\theta }}={{c}_{0}}\left( 1+{{\omega }_{c}}\cos 2(\theta -\beta )\right) \end{aligned}$$
(14)

where \(K_0\) and \(c_0\) are constants defining the mean internal friction and cohesion. Substituting Eqs. 14 and 10 into 7 would change the original problem into one where coefficients A’s and B’s are to be sought since the values of \({{\theta }_\mathrm{f0}}\) and \({{\sigma }_\mathrm{1f0}}\) are known from the isotropic solution. Following the perturbation analysis procedure, and ignoring second and higher-order terms of \(\omega\)’s for consistency, a Taylor’s expansion can be now applied so as to linearize the initially nonlinear system of equations into the following form:

$$\begin{aligned} &F({{\omega }_{K}},{{\omega }_{c}})=F_{0}+D_{1k} {{\omega }_{K}}+D_{1c}{{\omega }_{c}}=0\\&\frac{\partial F({{\omega }_{K}},{{\omega }_{c}})}{\partial \theta }=\frac{\partial F_{0}}{\partial \theta }+D_{2k} {{\omega }_{K}}+D_{2c} {{\omega }_{c}}=0 \end{aligned}$$
(15)

with the coefficients defined below:

$$\begin{aligned} F_{0}=\,&\frac{1}{2} \left[ 2 {c_0}+{K_0} ({\sigma }_\mathrm{1f0}+{\sigma _3})+({\sigma }_\mathrm{1f0}-{\sigma _3}) ({K_0} {\cos }{2 {\theta }_\mathrm{f0}}-{\sin }{2 {\theta }_\mathrm{f0}})\right] \\ D_{1k}=\,&{B_1} {K_0}+({B_1} {K_0}-2 {A_1} {\sigma }_\mathrm{1f0}+2 {A_1} {\sigma _3})\, {\cos }{2 {\theta }_\mathrm{f0}}\\&+{K_0}\, {\cos }(2 \beta -2{\theta }_\mathrm{f0})\, \left[ {\sigma }_\mathrm{1f0}+{\sigma _3}+({\sigma }_\mathrm{1f0}-{\sigma _3})\, {\cos }{2 {\theta }_\mathrm{f0}}\right] \\&-\left[ {B_1}+2 {A_1} {K_0} ({\sigma }_\mathrm{1f0}-{\sigma _3})\right] \, {\sin }{2 {\theta }_\mathrm{f0}}\\ D_{1c}=\,&{B_2} {K_0}+({B_2} {K_0}-2 {A_2} {\sigma }_\mathrm{1f0}+2 {A_2} {\sigma _3}+2 {c_0} {\cos }{2 \beta })\, {\cos }{2 {\theta }_\mathrm{f0}}\\&-\left[ {B_2}+2 {A_2} {K_0} ({\sigma }_\mathrm{1f0}-{\sigma _3})-2 {c_0}\, {\sin }{2 \beta }\right] \,{\sin }{2 {\theta }_\mathrm{f0}}\\ \frac{\partial F_{0}}{\partial \theta }=&-({\sigma }_\mathrm{1f0}-{\sigma _3}) ({\cos }{2 {\theta }_\mathrm{f0}}+{K_0} \, {\sin }{2 {\theta }_\mathrm{f0}})\\ D_{2k}=&-\left[ {B_1}+2 {A_1} {K_0} ({\sigma }_\mathrm{1f0}-{\sigma _3})\right] \,{\cos }{2 {\theta }_\mathrm{f0}}+{K_0}\, ({\sigma }_\mathrm{1f0}-{\sigma _3})\,{\sin }(2 \beta -4 {\theta }_\mathrm{f0})\\&+{K_0}\, ({\sigma }_\mathrm{1f0}+{\sigma _3})\, {\sin }(2 \beta -2{\theta }_\mathrm{f0})-({B_1} {K_0}-2 {A_1} {\sigma }_\mathrm{1f0}+2 {A_1} {\sigma _3})\, {\sin }{2 {\theta }_\mathrm{f0}}\\ D_{2c}=&-\left[ {B_2}+2 {A_2} {K_0} ({\sigma }_\mathrm{1f0}-{\sigma _3})\right] \, {\cos }{2 {\theta }_\mathrm{f0}}+2 {c_0}\, {\sin }(2 \beta -2{\theta }_\mathrm{f0})\\&-({B_2} {K_0}-2 {A_2} \,{\sigma }_\mathrm{1f0}+2 {A_2}\, {\sigma _3}) \,{\sin }{2 {\theta }_\mathrm{f0}} \end{aligned}$$
(16)

Recalling the perturbation procedure, each term on the right-hand-side of the system of Eqs. 15 should satisfy the problem conditions individually which, in this case, means that they should each be equal to zero leading to six different equations with six unknowns: \({{\theta }_\mathrm{f0}}\), \({{\sigma }_\mathrm{1f0}}\), \(A_1\), \(A_2\), \(B_1\), and \(B_2\). Such equations should be solved successively with respect to their order in perturbation. The zero-th-order equations, \(F_{0}=0\) and \(\frac{\partial F_{0}}{\partial \theta }=0\), are the same as the isotropic failure equations, i.e., Eqs. 1 and 2, which can be solved separately to calculate \({{\theta }_\mathrm{f0}}\), \({{\sigma }_\mathrm{1f0}}\). The other four relations form a first-order system of equations that determines the unknown coefficients as follows. For better readability, it is assumed here that \(K_0=\tan \varphi\). Thus,

$$\begin{aligned} &A_1 \, =\frac{\left( \sigma _3\cos (2 \beta -2\varphi )+c_0 \left( \cos (2 \beta -\varphi )+\sin(2 \beta -2 \varphi )\right) \right) }{2 ({c_0}+{\sigma_3} \tan \varphi )}\\ &\,\,\times \sin \varphi \\ &A_2 \,=-\frac{{c_0} {\cos }(2 \beta -\varphi) (-1+{\sin }\varphi )}{2 ({c_0}+{\sigma _3} {\tan }\varphi)}\\&B_1 \,=\frac{2 \sin (2 \beta -\varphi ) (\sigma _3+c_0 \cos\varphi +\sigma _3 \sin\varphi ) \tan \varphi }{\sec \varphi -\tan\varphi }\\&B_2 \,=\frac{2 c_0 \sin (2 \beta -\varphi )}{\sec\varphi -\tan \varphi } \end{aligned}$$
(17)

Figures 3a and b show a comparison between the “exact” solution obtained from numerical methods and the first-order perturbation analysis presented here for a given set of parameters. Herein, the exact solution has been found by numerically solving the system of equations given by Eqs. 5, 6, and 14 to find the failure direction and stresses that maximize the failure function. The accuracy of the perturbation results in Fig. 3 is acceptable for both failure stress and failure plane orientation, especially at the far left and right sides of the curve.

5.2 Second-order perturbation

A higher-order perturbation can be invoked in order to deal with more sophisticated \(K_\theta\) and \(c_\theta\) functions in a hierarchical manner by considering the previous step outcome as the basis for the next approximation. For instance, we have previously proposed proper expressions that describe the directional dependency of material parameters [16], a general functional form of which is given as follows:

$$\begin{aligned} {{\varGamma }_{\theta }}={{\varGamma }_{0}}\left( 1+{{\omega }_{\varGamma }}\cos 2(\theta -\beta )+\frac{{{\omega }_{\varGamma }}{{\lambda }_{\varGamma }}{{\sin }^{2}}2(\theta -\beta )}{1+{{\lambda }_{\varGamma }}\cos 2(\theta -\beta )} \right) \end{aligned}$$
(18)

where \(\varGamma\) represents an arbitrary material parameter with \({\omega }_{\varGamma }\) describing the degree of anisotropy, \({\lambda }_{\varGamma }\) refers to an additional parameter to control the smoothness of variation, and \(\beta\) defines the non-coaxiality between stress and strength.

A schematic plot of such expression is shown in Fig. 1. The functional form has been chosen such that when \({\lambda }_{\varGamma }=0\), we revert to the first-order harmonic distribution used in many studies like [9] and [10] among others, while the singularity point at \({\lambda }_{\varGamma }\rightarrow 1\) resembles the discontinuous-plane-of-weakness model put forward by [9]. A special numerical method has been worked out to solve the system of failure equations, Eq. 7, assuming that both internal friction and cohesion follow the functional form introduced in Eq. 18.

Knowing that the value of \(\lambda _{\varGamma }\) varies between 0 and 1, the additional term can be assumed to be of orders higher than the first due to the term \(\omega _\varGamma \, \lambda _\varGamma\) in the numerator, and as such the perturbation method can be applied to parameter \(\lambda _\varGamma\) by assuming the results of Eqs. 10 and 17 being the zero-th-order term (with respect to \(\lambda _\varGamma\)). The failure unknown parameters in this case can be written as follows:

$$\begin{aligned} &{{\theta }_\mathrm{f}}={{\theta }_\mathrm{f0}}+A_1 {{\omega }_{K}}+ A_2 {{\omega }_{c}}+A_3(\omega _K,\omega _c) \lambda _K + A_4(\omega _K,\omega _c) \lambda _c +O_\theta (\lambda _K^2,\lambda _c^2)=0\\&{{\sigma }_\mathrm{1f}}={{\sigma }_\mathrm{1f0}}+B_1 {{\omega }_{K}}+ B_2 {{\omega }_{c}}+ B_3(\omega _K,\omega _c) \lambda _K + B_4(\omega _K,\omega _c) \lambda _c +O_\sigma (\lambda _K^2,\lambda _c^2)=0 \end{aligned}$$
(19)

The coefficients describing the effect of parameters \(\lambda\)’s are a function of \(\omega\)’s to be consistent with the functional form in Eq. 18. The coefficients \(A_1\), \(A_2\), \(B_1\) and \(B_2\) determine the zero-th-order results with respect to \(\lambda\)’s and are the same as those in Eq. 17. Details of the perturbation procedure are lengthy and have not been included here. However, the rationale stays the same; the system of failure equations (Eq. 7) is expanded with respect to \(\lambda\)’s up to the first order, and the consecutive terms are assumed to be equal to zero individually. The zero-th term will be the same as Eq. 10, while the first-order term can be used to calculate coefficients \(A_3\), \(A_4\), \(B_3\) and \(B_4\), the values of which are also truncated to the first order of \(\omega\)’s. The final result emerges as:

$$\begin{aligned} &A_3= -\frac{\omega_k\cos(2\beta -\varphi ) \cos \varphi }{4 (c_0+\sigma _3 \tan\varphi)}\\ & \,\,\left[ \sigma _3 \left( \sin 2\beta +3 \sin(2\beta-2\varphi )\right)\right.\\ &\,\,\left.+c_0 \left( \cos 2\beta -3 \cos (2\beta-2\varphi )+4 \sin (2 \beta -\varphi )\right) \right]\\A_4 &\,\, =-\frac{\omega _c\, \cos ^3\varphi .\sin (4 \beta -2\varphi )}{2(1+\sin \varphi ) \,(c_0 \cos \varphi +\sigma _3 \sin\varphi )}\\& B_3 \,= -\frac{2 \omega _k \,\cos ^2(2 \beta-\varphi ) \,(1+\sin\varphi ) }{-1+\sin\varphi }\\&\,\,\times (c_0+\sigma _3 \cos \varphi -c_0\sin \varphi )\\& B_4 \,= 2 \omega _c\, \cos ^2(2\beta -\varphi )\,(\sec \varphi +\tan \varphi) \end{aligned}$$
(20)

Figure 3c and d also include a comparison between such second-order approximation and the ‘exact’ numerical solution for the system of equations in Eq. 7. Evidently, the accuracy of the stress predictions is much better than the failure angle. Moreover, such curves can be used in order to estimate the ranges over which the approximation is more accurate for calibration purposes.

Fig. 3
figure 3

Comparisons between exact solutions obtained numerically and the perturbation method: a and b failure stress and failure angle from Eq. 14 with first-order perturbation; c and d failure stress and failure angle from Eq. 18 with second-order perturbation. Input parameters are \(\sigma _3=100\), \(K_0=\tan \pi /6\), \(c_0=50\), \(\omega _K=0.2\), \(\omega _c=0.4\), \(\lambda _K=\lambda _c=0.8\)

Full size image

6 Interpreting experimental results

The intrinsic parameters of anisotropic rocks are classically evaluated through conventional triaxial testing although direct shear testing is also used. However, when it comes to interpreting experimental results, a common mistake is repeatedly found in the literature where a failure envelope is drawn tangent to the failure Mohr’s circle determined for every bedding plane orientation in order to evaluate cohesion and friction angle, see [1, 7, 13] for instance. The mathematical argument in the previous sections, on the other hand, shows clearly that there is a potentially non-negligible error associated with this procedure and a correction is needed to maintain consistency between interpreting experimental results and the mathematical modelling.

Figure 4 shows the error associated with calculating the failure friction parameter, K, and cohesion, c, by drawing a tangent to Mohr’s circle when analysing anisotropic rocks with similar characteristics as in Fig. 3c and d. For a given value of \(\beta\), the tangent solution has been found by first obtaining the exact numerical solution for at least two confining stresses, and next, finding the line tangent to the two Mohr’s circle at failure. The slope and the intercept of this tangent line give the internal friction and cohesion in the tangent method. The corresponding percentage error in estimating internal friction and cohesion by drawing a tangent to the Mohr’s circle is also presented in Fig. 5 for more clarifications. The relative error for internal friction at failure is calculated here as follows:

$$\begin{aligned} {\text {Relative error for }}K={\frac{K_{\text {exact}} - K_{\text {tangent}}}{K_{\text {exact}}}} \end{aligned}$$
(21)

where \(K_{\text {exact}}\) is the exact internal friction parameter at the failure plane calculated numerically, and \(K_{\text {tangent}}\) is the same value calculated by drawing a tangent to Mohr’s circle. A similar method is used to calculate the error for cohesion.

It is important to notice that, in this case, the error due to the tangent method can reach values as large as \(18\%\), and more importantly, the error overestimates the strength of the material for both internal friction and cohesion, which can lead to non-conservative choices for strength parameters.

Fig. 4
figure 4

Comparisons between a internal friction, and b cohesion obtained by exact numerical solution and by drawing tangent to the Mohr’s circle at failure. Input parameters are \(\sigma _3=100\), \(K_0=\tan \pi /6\), \(c_0=50\), \(\omega _K=0.2\), \(\omega _c=0.4\), \(\lambda _K=\lambda _c=0.8\)

Full size image
Fig. 5
figure 5

Relative percentage of error in estimating internal friction and cohesion by drawing tangent envelopes to Mohr’s circle at failure

Full size image

It goes without saying that the aforementioned perturbation analysis can be ideally used in order to calibrate anisotropic strength models. For a set of experimental results that follow the first-order harmonic trend shown in Fig. 3a, the directional dependencies can be assumed to be well described by functions presented in Eq. 14, and as such, the main objective of the calibration procedure would be to evaluate strength parameters \(K_0\), \(c_0\), \(\omega _K\), and \(\omega _c\) through experimental results.

The higher accuracy of the perturbed solution at \(\beta =0\) and \(\beta =\pi /2\), as shown in Fig. 3, together with the fact that sample coring is easier along these orientations, make these two points suitable for calibrating experimental results. Moreover, a closer look at perturbation results reveals that there is a simple relation between failure stresses at these two points and the isotropic parameters as:

$$\begin{aligned} {{\sigma }_\mathrm{1f0}}=\frac{1}{2} \left[ ({{\sigma }_\mathrm{1f}})^{\beta =0}+({{\sigma }_\mathrm{1f}})^{\beta =\pi /2}\right] \end{aligned}$$
(22)

Ideally, if the material parameters were known to closely follow a first-order harmonic function, a total number of four non-redundant triaxial tests would be enough to evaluate four calibration parameters. According to Fig. 3, an appropriate set of experiments would include performing tests on samples with bedding plane inclinations at \(\beta =0\) and \(\beta =\pi /2\), with each test repeated for two different confining pressures. The isotropic parameters, \(K_0\) and \(c_0\), can be computed using Eq. 22 and zero-th-order equations in the perturbation analysis. Furthermore, the same values of failure stress at \(\beta =0\) and \(\beta =\pi /2\) can be substituted in Eq. 10, with A’s and B’s values already known from Eq. 17, in order to find the anisotropy parameters, \(\omega _K\) and \(\omega _c\), through a two-equation, two-unknown system of equations. More tests, however, are suggested to be conducted together with a regression analysis in order to further confirm the appropriateness of the perturbation order considered. For instance, given that the second-order distributions involve two more variables (\(\lambda\)’s originating in Eq. 18), it is suggested that two more tests with different bedding orientations, \(\beta\), be performed to confirm/rule out the second-order effects.

For more comprehensive experimental results, as the one presented in Fig. 6, the second-order perturbation method can be used together with more sophisticated functions for \(K_\theta\) and \(c_\theta\). For instance, Fig. 6 illustrates results obtained using such a procedure and assuming that material parameters follow the functional form in Eq. 18. Knowing the failure stress for different \(\beta\)’s and \(\sigma _2\)’s, a least square regression analysis has been performed in order to estimate material parameters \(K_0\), \(c_0\), \(\omega\)’s and \(\lambda\)’s.

It is worth mentioning that the accuracy of the assumed material parameter function in matching the experimental results is not the purpose of the current study. Instead, we are more concerned with the systematic calibration process and its consistency. It goes without saying that different forms of directional variation of material parameter can lead to different trends in failure stress.

Moreover, caution needs to be exercised on the non-coaxiality of strength and stress, \(\beta\), when applying the current calculation procedure to experimental data. According to Eq. 18, the angle \(\beta\) measures the deviation between the direction of \(\sigma _1\) and the major principal direction of strength (which is orthogonal to bedding plane orientation).

Fig. 6
figure 6

A comparison between experimental results from Donath (1961) and numerical modelling assuming Eq. 18

Full size image

It is interesting to note that a rather characteristic feature emerges from the continuous function expressed in Eq. 18 within the consistent critical plane approach framework. It can be shown that the kink point at the two shoulders of the curve is related to having two non-conjugate solutions one near the plane of weakness and the other one close to maximum normal-to-shear stress ratio, as shown in Fig. 7. The two solutions are both admissible at the kink after and before which the solution jumps from the former to latter just like in the classic case of bifurcation in solutions. It goes without saying that the solution with the smaller deviatoric stress, when failure first occurs, is to be chosen. The trend of these two admissible solutions is also shown in Fig. 7 with the bifurcation point corresponding to the intersection of the two. Such a phenomenon has been previously investigated in [4] by explicitly incorporating two piecewise-defined failure criteria corresponding to the two above-mentioned failure modes, parallel and across, with respect to bedding laminates. Judging from the failure conditions illustrated back in Fig. 2, it is plausible that the presence of such kink and shoulder is related to the curvature of the failure function with respect to direction, i.e., \({\partial ^2 F}/{\partial \theta ^2}\).

Fig. 7
figure 7

Evolution of the two possible solutions for the system of Eq. 7

Full size image

It should also be acknowledged that the failure characteristics of geomaterials is also affected by their deformational characteristics. As demonstrated in [15], the failure can be aptly interpreted in terms of dilatancy of geomaterials with the failure function used to redistribute the stress. In such cases, the failure should be explained in conjunction with irreversible deformations and their characteristics. While such correlations can further complicate the interpretation of failure in anisotropic materials, they can also be useful in that they can potentially provide additional information about the directional dependency of material parameters. In particular, if the anisotropy of the strength parameters is shown to correlate with the anisotropy of stiffness variables such as elastic modulus, then small strain experiments such as wave propagation techniques can be used to estimate the directional dependency of strength parameters with only a few experiments.

Finally, the perturbation analysis provided in this study could be applied to the modelling of deformations in anisotropic elasto-plastic materials. Starting from yield functions and plastic potentials along different orientations [2, 12], similar perturbation analysis could be carried out to estimate the deviation of deformations in anisotropic materials compared to the ones in the isotropic case.

7 Conclusions

The current study outlines a mathematical procedure for the proper interpretation of the strength of anisotropic materials within the framework of the critical plane approach. The underlying mathematical equations of failure are appropriately formulated by introducing direction dependent parameters for a potential plane of failure. We show that the conventional Mohr’s circle approach is inadequate and even misleading when used to describe the stress conditions at failure for anisotropic materials, and will lead to overestimation of the strength parameters. Hence, a new graphical method is developed based on polar representation of stress projection rule juxtaposed on the strength rosette plot. Furthermore, a perturbation analysis has been conducted to obtain an approximated closed-form solution for the system of equations describing anisotropic failure in a triaxial test. In this context, this perturbation method allows for a practical, but yet theoretically sound procedure to interpret experimental results on anisotropic strength of rocks.