Introduction

Predictive modeling has now been considered as an inherent component of research in science and engineering. Models are frequently used to perform calculations, generally of extrapolation type, which prediction is made to regions where there are no experimental data. The success of prediction depends both on the proper form of the model and values of the model parameters, which are usually estimated from the experimental data (Ngo et al. 2004). Among various predictive modeling approaches, the regression techniques have become very popular and several multivariate linear modeling methods, such as multiple linear regression (MLR), ridge regression (RR), principal component regression (PCR), and partial least squares regression (PLSR), have widely been used to construct a mathematical model that relates the response(s) to the set of independent variables (Cao et al. 2011; Ekinci et al. 2011). However, the multivariate experimental or the field monitoring data in general exhibit nonlinear relationships among the variables and the linear methods may not be appropriate for capturing the underlying nonlinear data structure (Cao et al. 2011; Singh et al. 2009). Therefore, it is very much desirable to have nonlinear modeling methods which could capture the complex nonlinearities in the data to make precise predictions. Since the mathematical form of the nonlinear relationship between the measured variables in a system is usually unknown, modeling the nonlinear systems is a difficult task. However, several nonlinear modeling methods, such as multivariate polynomial regression (MPR), artificial neural networks (ANNs), kernel ridge regression (KRR), kernel principal component regression (KPCR), kernel partial least squares regression (KPLSR), and support vector regression (SVR) methods are now available for the regression problems (Singh et al. 2004, 2006, 2009, 2011; Li et al. 2009; Zhang and Ma 2011). The kernel method is a nonparametric technique where, differently from classical parametric approach, no assumptions are made on statistics of the underlying data (Pagnini 2009). MPR is a low-order nonlinear method which maximizes covariance between response and independent data sets (Singh et al. 2010). ANNs, although widely used, have some problems inherent to its architecture, such as overtraining, over-fitting, network optimization, and non-reproducibility of the results, due to random initialization of the networks and variation of stopping criteria (Li et al. 2009). On the other hand, kernel-based modeling techniques (KRR, KPCR, KPLSR, and SVR) are becoming more popular because they allow interpretation of the calibration models. In these methods, the calibration is carried out in space of nonlinearly transformed input data, so-called feature space, without actually carrying out the transformation. The feature space is defined by the kernel function (Cozzolino et al. 2011). From all points of view, computational, statistical, and conceptual, the kernel-based nonlinear methods are very efficient. The problems of local minima and over fitting that were typical of ANNs have been overcome. However, due to the fact that the kernel-based methods employ kernel transformation, they lose the correlation between the obtained kernel model and the original input space (Li et al. 2009). During past few decades, the kernel-based regression methods have been used in various research areas (Zhang et al. 2007; Woo et al. 2009; Zhang and Teng 2010; Chu et al. 2011). However, most studies report application of these methods to synthetic data (Rosipal and Trejo 2001; Rosipal et al. 2001; Jade et al. 2003). Singh et al. (2011) have recently applied SVMs to water quality problems; however, to our knowledge, kernel regression methods (KRR, KPCR, KPLS) have not been applied to water quality prediction problems.

Here, we have considered a hydro-chemical dataset pertaining to the surface water (Northern India) monitored for 20 different variables each month over a period of 10 years (2002–2011) at 10 different sites in the northern part of India (Singh et al. 2011). Dissolved oxygen (DO) levels in surface water were predicted using the kernel-based regression modeling approaches. DO is an important water quality parameter determining the health of a water body (Basant et al. 2010). It plays an important role in the aquatic eco-system affecting the flora and fauna (Wang et al. 2003). DO levels lower than 5 mg L−1 may cause detrimental effects on aquatic life (Thomann and Mueller 1987; Chapra 1997). Hence, great importance is attached to maintain the DO at desirable level. The DO in an aquatic system is used by aquatic plants and animals for respiration and by the aerobic bacteria which consume oxygen during the process of decomposition of organic matter (Shaghaghian 2010). However, oxygen enters the water by direct absorption from the atmosphere or by plant photosynthesis. Generally, a single point measurement of DO by the traditional method is not reliable, and sometimes may be misleading in assessing the state of the water body. This is due to the fact that it does not reflect the effect of biological activity and also do not reveal extremes in DO concentrations (Naik and Manjapp 2010). In recent years, numerous computational and statistical approaches have successfully been applied to predict the DO levels in various aquatic systems using different sets of input variables (Chen and Liu 2013; Wen et al. 2013; Evrendilek and Karakaya 2013; Heddam 2013).

Present research focuses on construction of different kernel-based regression models, such as KRR, KPCR, KPLSR, and SVR for predicting the DO levels in surface water using a hydro-chemical data set (2002–2011) exhibiting nonlinear structure. Accordingly, the kernel-based regression models were developed, validated and used to predict the DO levels in surface water using a set of independent water quality parameters. Performances of these models were evaluated in terms of several statistical criteria parameters. This study has shown that the application of kernel methods can be useful in predicting the water quality successfully for the water resource management.

Materials and methods

Dataset

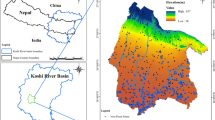
Here, we have considered a hydro-chemical data set pertaining to the surface water quality of the Gomti River, India (Singh et al. 2011). The water quality was monitored each month at 10 different sites on the river (Fig. 1) over a period of 10 years (2002–2011) representing large spatial and temporal coordinates and thus, covering all possible sources of variation in the region. The first three sites (S1–S3) are located in the area of relatively low river pollution. Other three sites (S4–S6) are in the region of gross pollution, and the last four sites (S7–S10) are in the region of moderate pollution as the river considerably recovers in the course (Singh et al. 2009). Hydro-chemical parameters (20 numbers) measured include the water temperature (T, °C), pH, electrical conductivity (EC, microsiemens per centimeter), total solids (TS, in milligram per liter), total dissolved solids (TDS, in milligram per liter), total suspended solids (TSS, in milligram per liter), total alkalinity (T-Alk, in milligram per liter), total hardness (T-Hard, in milligram per liter), calcium hardness (Ca-Hard, in milligram per liter), sulphate (SO4, in milligram per liter), nitrate (NO3, in milligram per liter), ammonical nitrogen (NH4–N, in milligram per liter), chloride (Cl, in milligram per liter), phosphate (PO4, in milligram per liter), fluoride (F, in milligram per liter), potassium (K, in milligram per liter), sodium (Na, in milligram per liter), dissolved oxygen (DO, in milligram per liter), chemical oxygen demand (COD, in milligram per liter), and biochemical oxygen demand (BOD, in milligram per liter). Detailed analytical procedures are available elsewhere (Singh et al. 2004).

Fig. 1
figure 1

Map showing the network of sampling sites on the Gomti River, India

Full size image

Initial feature selection and data processing

Since the hydro-chemical data considered here represented all possible sources of variations, it may be contaminated by human and measurement errors. Moreover, some of the features in original data set may have insignificant or no relevance with the response variable rendering these useless in predictive modeling; hence, implementing initial feature selection is necessary (Lin et al. 2008). Here, the initial feature selection was performed using nonlinear (MPR) methods (Singh et al. 2012). Variables exhibiting significant relationship with the response variable were retained while dropping the others. The insignificant variables then dropped one by one and the prediction error and correlation coefficient were recorded. Finally the T, pH, EC, SO4, NO3, Na, COD, and BOD were retained as independent set of variables and DO as the dependent one. The basic statistics of the selected measured hydro-chemical variables is given in Table 1.

Table 1 Basic statistics of the selected hydro-chemical variables (N = 1,070)
Full size table

The data were partitioned into training, validation, and test sets using the Kennard–Stone (K-S) approach. The K-S algorithm designs the model set in such a way that the objects are scattered uniformly around the training domain. Thus, all sources of the data variance are included into the training model (Daszykowski et al. 2007; Basant et al. 2010). In the present study, the complete data set (1,070 samples × 9 variables) was partitioned as training (749 samples × 9 variables); validation (161 samples × 9 variables), and test (160 samples × 9 variables) set, thus, comprising of 70, 15, and 15 % samples, respectively. Prior to implement the KRR, KPCR, and KPLS algorithms, the data were mean-centered (Kramer 1998). In case of SVR, the raw data were normalized to an interval by transformation. Here, all the variables were transformed to the same ground-uniform distributions on −1, +1. Since the data were pre-processed, these were transformed back to the original form prior to the post-modeling computations.

Nonlinearity in data

Nonlinearity in data is an important factor to be considered prior to the selection of the model. Nonlinearity in the data was tested using the Brock–Dechert–Scheinkman (BDS) statistics (Brock et al. 1996). BDS is a two-tail nonparametric method for testing the serial independence and nonlinear structure in a data based on the correlation integral. It tests the null hypothesis of independent and identically distributed (I.I.D.) data against an unspecified alternative. For a scalar time series {x t } of length N, and embed it into m-dimensional space generating a new series {X t },  X t  ∈ R m, the correlation integral may be calculated as (Brock et al. 1996)

$$ {C}_{\varepsilon, \kern0.5em m}=\frac{1}{N_m\ \left({N}_m-1\right)}\ {\displaystyle {\sum}_{i\ne j}{I}_{i,j,\varepsilon }} $$
(1)

where,  I i,j,ε  = 1 if ‖x m i  − x m j ‖ ≤ ε;  I i,j,ε   = 0 otherwise. The correlation integral measures the spatial correlation among the points, by adding the number of pairs of points (i, j), where 1 ≤ i ≤ N and 1 ≤ j ≤ N, in the m-dimensional space which are “close” in the sense that the points are within a radius or tolerance ε of each other. Finally, the BDS statistics can be defined (Brock et al. 1996) as:

$$ {\mathrm{BDS}}_{\varepsilon, m}=\sqrt{N}\ \frac{\left[{C}_{\varepsilon, \kern0.5em m}-{\left({C}_{\varepsilon, \kern0.5em m}\right)}^m\right]}{\sigma_{\varepsilon, \kern0.5em m}} $$
(2)

where σ ε, m is the standard deviation of C ε, m . If the computed BDS statistics exceeds the critical value at the conventional level, the null hypothesis of linearity is rejected, which reveals the presence of nonlinear dependence in the data (Anoruo 2011).

Kernel regression modeling

In nonparametric kernel regression, linear regression model is constructed in a high-dimensional feature space F to which the d-dimensional input pattern vectors x i are nonlinearly mapped, φ : x ∈ Rd → φ(x) ∈ F, which corresponds to a nonlinear regression model in the original space.

$$ f(x)={\displaystyle {\sum}_{i=1}^T{\mathbf{B}}_{\mathrm{i}}{\upvarphi}_{\mathrm{i}}\left(\mathbf{x}\right)+{\boldsymbol{b}}_r} $$
(3)

where T is the dimensionality size of the feature space, φ is the nonlinear mapping function, B i and b r are the regression coefficient vector and residuals, respectively. In certain feature spaces (reproducing kernel Hilbert space), the transformed input data φ(x) appear as dot products < φ(x i ),  φ(x j ) > and it is not necessary to explicitly define the mapping. Kernel methods can be used to avoid direct calculation of computationally expensive nonlinear mapping φ, but rather make use of the so called kernel-trick which uses kernel matrix of the training data to achieve nonlinear regression (Cao et al. 2011).

Since the form of the nonlinear mapping function is generally not known in advance and is difficult to determine, the feature space is constructed implicitly by invoking a generic kernel function, operating on two input vectors as:

$$ \mathbf{K}\left({\mathbf{x}}_{\mathrm{i}},{\mathbf{x}}_{\mathrm{j}}\right)=\left(\varphi \left({\mathbf{x}}_{\mathbf{i}}\right),\varphi \left({\mathbf{x}}_{\mathbf{j}}\right)\right) $$
(4)

where x i and x j are two objects in the data set, and φ is the actual nonlinear mapping function. While using a kernel function, it is not necessary to know the actual underlying feature map to construct a linear model. Many different kernel functions can be used in this context, including the polynomial, Gaussian (radial basis functions, RBF), and sigmoid (Jemwa and Aldrich 2005). However, the kernel function when applied results in a square symmetric matrix, the kernel matrix K. A kernel function transforms the data matrix (n × m) of n samples and m variables in to a kernel matrix (n × n). The optimal values of the selected kernel function parameters are determined by optimizing the regression performance. A specific choice of kernel function implicitly determines the mapping φ and the feature space F. The selection of kernel function is dependent on the distribution of the data. Research has shown that RBF is not only theoretically well founded but also superior in some practical applications (Zhang et al. 2010). Here in our study, we have used the Gaussian kernel function.

A conceptual diagram of the feature extraction using kernel-based algorithms is shown in Fig. 2. It shows the steps involved in the implementation of kernel methods. The training samples are firstly represented using a kernel function to create a kernel matrix, and subsequently the kernel matrix obtained is modeled by a linear algorithm to produce a complex model. The model is finally used to predict the unseen samples. In the process, the linear algorithms are naturally combined with the specific kernel function to produce a more complex algorithm in a high dimensional feature space. For a set of vectors, x 1, x 2, …x n , a kernel method constructs the kernel or Gram matrix, K. The basic structure gives all the information about the relation between the points (Fig. 2a). Thus, kernelizing a given algorithm amounts to reformulating it in terms of inner products. Such a matrix is positive, semi-definite, which means that for every real vector x, the real number x T Kx ≥0. Now, when a new pattern is presented, we construct all the inner (kernel) products of the pattern with the training set objects that are closer to it (Fig. 2b). The results are afterward combined with the weights obtained from the training stage and this sum is fed to the regression function (Taylor and Cristianini 2004).

Fig. 2
figure 2

Schematic diagram of the a general steps for implementing kernel methods, b feature extraction using kernel-based algorithm

Full size image

Here, we have constructed KRR, KPCR, KPLSR, and SVR approaches to construct the models to predict the DO levels in water using set of independent hydro-chemical variables.

Kernel ridge regression

KRR is an extension of RR to allow for nonlinear prediction function y = f(x). At the same time, it provides a way to avoid the computational complication involved in producing the ridge forecast when the number of predictors becomes very large. Thus, in KRR, the goal is to built a linear model in the higher dimensional feature space F. and the matrix product XX T in RR is replaced by the new matrix product φ(x)φ(x)T (=K(x i ,x j )) using the kernel trick, which allows for the calculation of dot product in the higher dimensional feature space using simple dot product function defined on input pairs (i, j). The KRR function in a reproducing kernel Hilbert space (RKHS) can be shown as (Cristianini and Taylor 2000),

$$ f(x)={\mathbf{y}}^T\kern0.5em {\left(\mathbf{K}+\lambda \mathbf{I}\right)}^{-1}\mathbf{k} $$
(5)

where k = k(x i ,x), i = 1,2,… n; K is the kernel matrix, λ is the regularization constant, I is n-dimensional identity matrix, and y is the response vector. KRR has the major advantage of obtaining the so-called kernel analytically and subsequently allows the number of basis functions to be virtually infinite (Zhang et al. 2007).

Kernel principal component regression

KPCR, a nonlinear regression technique uses the nonlinear kernel principal component analysis (KPCA) to extract the principal components (PCs) in the independent data. In KPCA, the training data X = [x 1, x 2, …. x n ]T ∈ Rp is mapped into a high dimensional feature space F (M = [φ(x 1), φ(x 2), …, φ(x n )]T). Use of an appropriate kernel function, provides K = MM T ∈ Rn × n. Features of the training and unknown test samples can be extracted using KPCA through projecting the mapped samples φ(x) on to the first k projections P k (Cao et al. 2011);

$$ {\mathbf{P}}_{\mathrm{k}}\varphi \left(\mathbf{x}\right)={\displaystyle {\sum}_{i=1}^n{\upalpha}_i^k<\varphi \left({\mathbf{x}}_i\right),\upvarphi \left(\mathbf{x}\right)>}={\displaystyle {\sum}_{i=1}^n{\upalpha}_i^{k\ }\mathbf{k}\left({\mathbf{x}}_i,\mathbf{x}\right)={\mathbf{k}}_{\mathrm{test}}{\alpha}^k} $$
(6a)

where k test = Mφ(x) = [k(x 1,x), k(x 2,x), …   …, k(x n ,x)]. Now, the scores vectors of

PCs extracted by the KPCA are regressed with the dependent variable vector (training data) and the regression coefficient vector, so obtained, is then used to predict the responses in unknown samples. The KPCR model for the prediction of response variable any input vector x can be expressed as (Rosipal et al. 2001);

$$ f\left(\mathbf{x}\right)={\displaystyle {\sum}_{k=1}^p{\mathrm{w}}_k}{\displaystyle {\sum}_{i=1}^M{\alpha}_i^k\mathbf{K}\left({\mathbf{x}}_{i,}\ \mathbf{x}\right)+\mathbf{b}} $$
(6b)

where, p is number of PCs retained in the KPCR model and K(x i ,x) can be estimated using the kernel function. The variables α k i are computed by the diagonalization of kernel matrix of the input variables and wk are the least square estimates of regression coefficients. For the centralized regression model bias, b is zero. KPCR requires only two parameters (number of PCs and width of the kernel function) to be tuned for its model selection.

Kernel partial least squares regression

KPLSR is a nonlinear extension of linear PLSR (Rosipal and Trejo 2001) in which training samples are transformed into a feature space F, x i  ∈ Rn → φ(x i ) ∈ F, where φ(.) is nonlinear mapping function that projects the input vectors from the input space to F. The dimensionality of the feature space is arbitrarily large, and can even be infinite. Through the kernel trick, φ(x i )T, φ(x j ) = K(x i ,x j ), both the nonlinear mapping and computation of dot products can be avoided in the feature space. M, M T represents the kernel matrix, K of the inner products between all mapped samples. The estimated regression coefficient, B in KPLSR can be given by (Zhang and Teng 2010);

$$ \mathbf{B}={\mathbf{M}}^T\mathbf{U}{\left({\mathbf{T}}^T\mathbf{KU}\right)}^{-1}{\mathbf{T}}^T\mathbf{y} $$
(7)

where T and U are the scores and loadings matrices, respectively. y is the response vector. For an unknown test data consisted of n t samples, the following equation can be used to predict the training and test data, respectively:

$$ \mathbf{y}=\mathbf{MB}=\mathbf{KU}{\left({\mathbf{T}}^T\mathbf{KU}\right)}^{-1}{\mathbf{T}}^T\mathbf{y}\kern0.5em $$
(8a)
$$ {\mathbf{y}}_{\mathbf{test}}={\mathbf{M}}_{\mathrm{new}}\mathbf{B}={\mathbf{K}}_{\mathrm{new}}\mathbf{U}{\left({\mathbf{T}}^T\mathbf{KU}\right)}^{-1}{\mathbf{T}}^T\mathbf{y}\kern0.5em $$
(8b)

where M new is the matrix of the mapped test points and K new is the (n new × n) test kernel matrix whose elements are k(x i , x j ), where x i is the ith test sample and x j is the jth training sample.

Support vector regression

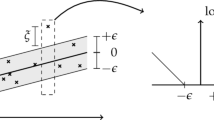
In SVR approach, the original data points from the input space are mapped into a high dimensional or even infinite dimensional feature space using a suitable kernel function, where a linear regression is performed. For a training data set, (x i ,y i ), x i ЄR n, i = 1,..,m, y Є{+1, −1}, where y i denotes the target property of an already known ith case, the aim is to find the linear function f(x) = wx + b, wx ЄRn, b ЄR for which the difference between the actual measured value y i and estimated value f(x i ) would be at most equal to ε or [y i  − f(x i )] < ε, where ε is the insensitive loss function, w is the weight vector and b is the bias. These parameters define the location of separating plain and are determined during the training process (Vapnik 1999; Pan et al. 2008). Introducing the slack variables (ξ, ξ*) to take the error of estimation into account and the penalty parameter C yields a quadratic programming problem:

$$ \begin{array}{l}\begin{array}{c}\hfill \min \hfill \\ {}\hfill \mathbf{w},\mathrm{b},\xi, {\xi}^{*}\hfill \end{array}\ \frac{1}{2}\ {\mathbf{w}}^T\mathbf{w}+\mathrm{C}{\displaystyle {\sum}_{i=1}^{\mathrm{l}}\left({\xi}_i+{\xi}_i^{*}\right)}\hfill \\ {}\mathrm{subject}\ \mathrm{to}\kern1.25em \left({\mathbf{w}}^T\ \phi \left({\mathbf{x}}_i\right)+b\right)-{y}_i\le \int +{\xi}_i,\hfill \\ {}{y}_i-\left({\mathbf{w}}^T\ \phi \left({\mathbf{x}}_i\right)+b\right)\le \upepsilon +{\xi}_i^{*},\hfill \\ {}{\xi}_{i,}{\xi}_i^{*}\ge 0,i=1,\dots, \mathrm{l}.\hfill \end{array} $$
(9a)

which may be transformed to its corresponding dual optimization form. With the help of kernel function nonlinear optimal regression function can be obtained (Vapnik 1999; Cherkassky and Ma 2004) as;

$$ f(x)={\displaystyle {\sum}_{i=1}^N\left({\alpha}_i-{\alpha}_i^{*}\right)\mathbf{K}\left({\mathbf{x}}_i,\mathbf{x}\right)}+\mathbf{B} $$
(9b)

where α i α * i  = 0,  α i α * i , ≥ 0,  i = 1,.., N.  α i and α * i (with 0 ≤ α i α * i  ≥ C) are the Lagrange multipliers, K(x i,x) represents the kernel function, and B are the coefficients of the linear model. The data points with nonzero α i and α * i values are the support vectors (SVs).

The performance of SVR depends on the combination of several factors, such as the kernel function type and its corresponding parameters, capacity parameter, C, and ε-insensitive loss function (Pan et al. 2008). For the RBF kernel, the most important parameter is the width σ of the RBF, which controls the amplitude of the kernel function and, hence, the generalization ability of SVR (Noori et al. 2011). C is a regularization parameter that controls the trade-off between maximizing the margin and minimizing the training error. If C is too small, then insufficient stress will be placed on fitting the training data. If C is too large, then the algorithm will over fit the training data (Wang et al. 2007).

Model selection and optimization of parameters

The generalization performance of the regression methods depend on proper setting of several model parameters. In kernel-based methods, choice of kernel parameters has a crucial effect on the performance. Moreover, the appropriate numbers of PCs in KPCR and KPLSR methods and a regularization term in KRR have to be considered. In SVR, these include the capacity parameter C, the insensitive loss function ε, and the kernel function-dependent parameter (Ustun et al. 2005). The parameter C determines the trade-off between the smoothness of the regression function and the amount up to which deviations larger than ε are tolerated. The parameter ε regulates the radius of the ε tube around the regression function and thus, the number of SVs that finally will be selected to construct the regression function (leading to a space solution). A too large value of ε results in less SVs and consequently, the resulting regression model may yield large prediction errors on unseen future data (Singh et al. 2011).

In the present study, a cross-validation (CV) method based on the predicted mean squared error (MSE) in training and validation data was used to select the Gaussian kernel parameter (σ), regularization parameter (λ) in KRR, and number of PCs for the KPCR and KPLSR models. MSE was calculated as;

$$ \mathrm{MSE}=\frac{1}{N}{\displaystyle {\sum}_{i=1}^N{\left({\mathrm{y}}_{\mathrm{pred},i}-{\mathrm{y}}_{\mathrm{meas},i}\right)}^2} $$
(10)

where y pred,i and y meas,i represent the predicted and measured values of the response variable in ith sample, and N represents the total number of observations. CV selects the algorithm with the smallest estimated risk. Compared to the re-substitution error, CV avoids over-fitting because the training sample is independent from the validation sample (Arlot and Celisse 2010). In SVR, the model parameters (C, ε, and σ) were optimized using the grid and pattern searches over a wide space employing the V-fold cross-validation (Hsu and Chang 2003). The accuracy of grid search optimization depends on the parameter range in combination with the chosen interval size. In V-fold cross-validation, the data in training set are divided into V subsets of equal size. Subsequently one subset is tested using the model trained on the remaining V − 1 subsets. Thus, each instance of the whole training set is predicted once. The cross-validation procedure prevents the over-fitting problem (Hsu and Chang 2003).

Model performance criteria

The performance of each of the models used here was evaluated using different statistical criteria parameters, such as the mean absolute error (MAE), root mean squared error (RMSE), and the correlation coefficient (R) between the measured and model predicted values of the response computed for all the three (training, validation, and test) data sets (Singh et al. 2010). The MAE measured the average magnitude of the error in a set of predictions, without considering their direction. It is a linear score which means that all the individual differences between predictions and corresponding measured values are weighted equally in the average. The RMSE represents the error associated with the model. It is a measure of the goodness-of-fit, best describes an average measure of the error in predicting the dependent variable. However, it does not provide any information on phase differences (Singh et al. 2013). Each performance criteria term described above conveys specific information regarding the predictive performance efficiency of a specific model. Goodness of fit of the selected models was also checked through the analysis of the residuals.

Results and discussion

Basic statistics of the raw hydro-chemical data used here is presented in Table 1. Concentration of both the dependent and independent set of variables showed large variations between the samples, with a high coefficient of variation (CoV). The CoV, a measure of statistical dispersion of data, is the mean normalized standard deviation of the given data set. The hydro-chemical variables showed a CoV between 4.4 % (pH) and 149.2 % (NO3). The large variation in concentration of the variables corresponds to the nature and types (point and non-point) of sources distributed in the large geographical area of the river basin and large variations in climate and seasonal influences in the study region. pH showed lowest variation and it may be due to the buffering capacity of the river. Variables of anthropogenic origin showed larger variations as compared to those of the natural origin variables (Table 1). It may be attributed to the fact that the geogenic processes are almost in equilibrium state, whereas, the anthropogenic processes are time-dependent in nature.

The nonlinear dependence of the data was calculated using the BDS statistics. BDS extracts linear structure in the data by use of an estimated linear filter. The BDS statistics was calculated using Eq. 2 (m = 2 to 5 and ε = 0.5). In BDS test, the null hypothesis of linearity is rejected if the computed test statistics exceeds the critical value at the conventional level. The rejection of the null hypothesis reveals the presence of nonlinear dependence in the data (Anoruo 2011). In our case, the BDS statistics exceeded the significance level (p < 0.01), thus suggesting for severe nonlinear data structure and hence a nonlinear model is required for developing an appropriate regression function. Nonlinear kernel-based regression models were therefore constructed here.

Kernel regression modeling

Model selection and parameterization

For determining the optimum values of various unknown parameters in different kernel methods used here, CV technique was employed. Optimum values of the model parameters were selected on the basis of MSE values obtained in training as well as validation data. First, optimal ranges of the model parameters values (λ and σ in KRR, number of PCs and σ in KPCR and KPLSR models) were decided by varying them simultaneously. Subsequently, these were finely tuned and finally, values of λ in KRR and number of PCs in KPCR and KPLSR models were varied keeping the value of σ constant (close to optimum value). Initially lower values of λ or PCs were taken which were subsequently varied to higher values. For all combinations of model parameters, corresponding MSE values were calculated both for the training and validation data. An increase in λ value or number of PCs in respective models resulted in consistently lowering of MSE values as well as narrowing the difference between two MSEs in training and validation data, which afterwards, although continued declining further, their difference widened. Optimal values of model parameters were finally determined on the basis of a reasonable difference in MSE values in two sets. Larger differences in the MSEs in training and validation sets were considered due to the over-fitting of the respective model in training set. To check any over-fitting of these models in the training data, these were applied to predict the independent test data. SVR model parameters were optimized using a 10-fold CV. Accordingly, the training data were partitioned in to 10-folds and iterations of training and validation were performed such that, within each iteration a different fold of data held-out for validation while the remaining 9-folds were used for learning and subsequently the learned models are used to make predictions about the data in the validation fold. Thus, each time, a model was constructed and tested with an unseen dataset. Model parameters (C and σ) yielding minimum MSE in training and validation data were finally selected.

Kernel ridge regression

The regularization term λ and the kernel width σ are two important model parameters determining the performance of KRR method. CV procedure applied to the training and validation data sets yielded the optimum values of 2.5 and 600 for the regularization and width parameters, respectively. Value of λ modifies the regression criterion, as the fitting quality is bound within this predefined threshold (Zhang et al. 2007). Further, it controls the trade-off between the sum square error function and a quadratic penalty term. The first term enforces closeness to the data while the second ensures smoothness of the solution. The optimal value of σ depends on the input data variance (Kim et al. 2005). The selected optimum KRR model yielded MSE of 0.45 and 0.61 in the training and validation sets, respectively. The model was then applied to the test data (MSE = 0.41) and its performance was evaluated by estimating various criteria parameters (Table 2). The optimal KRR model yielded the MAE, RMSE, and R values of 0.53, 0.67, 0.961 in training, 0.60, 0.78, 0.850 in validation and 0.50, 0.64, 0.655 in test data. From the model diagnostics, it is evident that KRR predicted the response variable closer to the measured values (Fig. 3).

Table 2 Values of the performance criteria parameters for various kernel regression models
Full size table
Fig. 3
figure 3

Plot of measured and KRR model predicted values of the DO in river water in a training, b validation, and c test set

Full size image

Kernel principal component regression

KPCR models were generated using different combinations of PCs and σ parameters. Prior to the regression, KPCA was used to extract the significant PCs. KPCA method of feature extraction produce nonlinear PCs which are substantially higher (up to the number of data points, n) than the PCA. This is advantageous in situations where the dimensionality of the input data points is smaller than the data points and the data structure is spread over all the eigen directions (Rosipal et al. 2001). The extracted features by KPCA are then projected on the original training and testing datasets. For studying the effect of model selection criteria on the performance of DO prediction, different sets of training, validation and test data were used. Simulations were carried out with different model parameters employing the training data, and the set of parameters that predicted the least MSE on validation data was selected as the optimal set of parameters and further used for the prediction of the unseen test data. In the present case, the optimum number of the PCs and value of σ were 280 and 600, respectively. Comparable values of σ have been reported in other studies based on kernel regression methods (Jade et al. 2003; Postama et al. 2011). This combination of model parameters yielded the lowest MSE values of 0.36, 0.62 and 0.43 in training, validation, and test sets. Different performance diagnostic parameters as obtained for the training, validation, and test data sets using the selected KPCR model are presented in Table 2. The optimal KPCR model yielded the MAE, RMSE, and R values of 0.45, 0.60, 0.964 in training, 0.60, 0.79, 0.844 in validation and 0.51, 0.65, 0.647 in test data. Low prediction errors in all the three sets suggest for the adequacy of the KPCR in DO level prediction. Plots of the model predicted and measured values of DO concentration in training, validation and test sets are given in Fig. 4, showing a close pattern of variations.

Fig. 4
figure 4

Plot of measured and KPCR model predicted values of the DO in river water in a training, b validation, and c test set

Full size image

Kernel partial least squares regression

KPLSR model was developed to predict the DO levels in water. Both the width parameter σ and the number of PCs in the feature space were determined to optimize the KPLSR model using the CV method. The selection of the optimal number of PCs was either based on the first increase of the MSE during CV, or if no increase was observed by the method. Parameter optimization was performed using the training and validation sets. The optimal number of the PCs and value of σ were determined as 11 and 600, respectively. The model yielded the MSE values of 0.34 and 0.62 in the training and validation data, respectively. The selected KPLSR model was then used to predict the unseen test samples (MSE = 0.42). Comparable values of the two parameters in KPLSR are reported by others (Postama et al. 2011). For a smaller σ value the input data with greater distance will be too spread in feature space and intended localization may be lost. Further, such values of σ will lead to memorizing of the training data structure. A high noise level in the input data has the tendency to increase the optimal value for σ which coincides with the intuitive assumption about smearing out the local structure. The performance of the selected KPLSR model was evaluated by several statistical parameters (Table 2). The optimal KPLSR model yielded the MAE, RMSE, and R values of 0.45, 0.58, 0.966 in training, 0.60, 0.78, 0.846 in validation and 0.50, 0.65, 0.659 in test data. A closely followed pattern of variation in measured and predicted response values (Fig. 5) and relatively low prediction errors suggest for the adequacy of the selected model in predicting the DO levels. KPLSR models have widely been applied in multivariate data modeling (Rosipal et al. 2001; Zhang and Teng 2010; Postama et al. 2011; Zhang and Ma 2011). Performance diagnostics for the KPLSR model (Table 2) suggested for its good performance in predicting the DO levels. Similar findings are also reported by other studies (Rosipal et al. 2001; Postama et al. 2011).

Fig. 5
figure 5

Plot of measured and KPLSR model predicted values of the DO in river water in a training, b validation, and c test set

Full size image

Support vector regression

Cross-validation procedure yielded the optimal values of the SVR model parameters, C, ε, and σ as 11.13, 0.001, and 1.88, respectively, and the number of SVs was 669. The selected model yielded MSE of 0.35 and 0.41 in the training and validation data, respectively. The model was then applied to the test data (MSE = 0.37). Under the assumptions of Gaussian function, the value of C can be related to the range of the response values in the training data. From Eq.(9b), the regularization parameter C defines the range of values 0 ≤ α i ,α i * ≤ C assumed by dual variables used as linear coefficients in SVR solution. Hence, a good value of C can be chosen equal to the range of output values of the training data (Mattera and Haykin 1999). However, such a selection of C is sensitive to possible outliers in the training data. Cherkassky and Ma (2004) proposed an approach to determine value of C based on mean and standard deviation values of the output variable in the training data. Optimum value of C in our case coincides with the one computed using this method (Cherkassky and Ma 2004). Values of the model performance criteria parameters as computed for the training, validation and test sets are presented in Table 2. The optimal SVR model yielded the MAE and RMSE values of 0.39, 0.59 in training, 0.47, 0.64 in validation, and 0.46, 0.61 in test data. A reasonably high correlation between the predicted and measured values of the response variable in training (0.964), validation (0.899), and test set (0.701), and low errors of prediction suggest for the good-fit of the selected model to the dataset and its predictive ability for the new future samples (Singh et al. 2010). SVR also predicted the response variable closer to the measured values in the training, validation and test data (Fig. 6).

Fig. 6
figure 6

Plot of measured and SVR model predicted values of the DO in river water in a training, b validation, and c test set

Full size image

The response values predicted by different kernel-based regression models and the residuals corresponding to the training, validation and test sets show almost complete independence and random distribution (figures not shown due to brevity). Residuals versus predicted value plots can be more informative regarding model fitting to a data set. If the residuals appear to behave randomly (low correlation), it suggests that the model fits the data well. On the other hand, if non-random distribution is evident in the residuals, the model does not fit the data adequately (Singh et al. 2010).

From the modeling results (Table 2), it is evident that the performances of the kernel regression modeling methods (KRR, KPCR, KPLSR, and SVR) were satisfactory (Fig. 7). The kernel methods mapped the nonlinear input space into a high dimensional feature space, where the data structure is likely to be linear (Woo et al. 2009). Moreover, projection of the original data to the components with higher eigenvalues discards the noise component in the original data (Rosipal et al. 2001). The kernel methods could capture the nonlinearities in the original data space benefitting from the linear data structure in the feature space. However, the predictive performance of all the kernel regression methods used here were comparable. Other study (Rosipal and Trejo 2001) also reported very closely comparable correlations between the measured and model predicted values obtained by KRR, KPCR, and KPLSR methods. An equal value (600) of σ was obtained for KRR, KPCR, and KPLSR models, whereas it was significantly different in case of SVR model. It may be probably due to the normalization of the variables (+1, −1) used in SVR, whereas in other kernel methods mean-centered data were used. Similar pattern for σ values in SVR and KPLSR models has been reported earlier (Postama et al. 2011). Plot of MSE values as computed for different optimal kernel models (Fig. 7) suggests that SVR model is relatively more robust to over-fitting as compared to other kernel methods. SVR avoids under- and over-fitting the training data by minimizing the training error C  ∑  1i = 1 (ξi + ξ *i ) as well as the regularization term, ½ w T w in Eq. (9a).

Fig. 7
figure 7

Plot of the MSE values in training, validation and test sets showing performance of different kernel regression models

Full size image

From the results, it is evident that the kernel regression methods used here successfully predicted the dependent variable. These methods intrinsically cope with nonlinearities in a very flexible way, are robust to uncertainty and noise, and are effective when dealing with low numbers of high dimensional samples. The crucial advantage of KRR is that it requires a single matrix inversion and deals with multi-collinearity by assuming linear regression model (Cortes et al. 2005). KPCR has a priori advantage that it gives the possibility to extract more PCs than linear PCR. Moreover, it does not require nonlinear optimization, but just the solution of an eigenvalue problem (Scholkopf et al. 1996). However, its main drawback is that no simple method is available to reconstruct patterns from their PCs. The main advantage of KPLSR is that it avoids nonlinear optimization by utilizing the kernel function corresponding to the inner product in the feature space (Rosipal and Trejo 2001). SVR although, avoids over-fitting of data, it uses limited data points while building the model. The major disadvantage of kernel methods is that the correlation between the obtained regression model and the original input space is lost. Therefore, it is not directly possible to see which variable contribute to the final regression and a direct interpretation of the model is not straightforward (Postama et al. 2011).

Conclusions

In this work, kernel-based regression models, such as KRR, KPCR, KPLSR, and SVR were constructed and applied to the nonlinear hydro-chemical data collected over 10 years for predicting the DO concentration. Cross-validation method was employed to determine the optimum values of the model parameters. The kernel methods mapped the nonlinear input into a high-dimensional feature space where the data structure is likely to be linear. These methods require only linear algebra to develop the process models, whereas other nonlinear modeling methods involve nonlinear optimization. All the kernel regression models constructed here performed well with the nonlinear hydro-chemical data demonstrating excellent predictive and generalization abilities. A comparable performance of these models could be attributed to the fact that these successfully captured the nonlinearities in the data. Among these SVR approach provided relatively robust model less prone to over-fitting due to minimized error and regularization terms. The successful application of the kernel methods to the nonlinear data of a dynamic system considered here demonstrated the feasibility and effectiveness of the kernel-based algorithms in predicting the response variable. The presented simple methodologies could be applied to model various chemical, biological, and other such systems