Introduction

Dissolved oxygen concentration (DO) is the amount of molecular oxygen dissolved in water and plays a crucial role in determination of water quality. Among all other water quality variables that must be regularly measured and monitored, DO is practically the most important. The importance given to DO concentration is not only for itself, but also for its influence on so many other water quality variables and several other processes. DO provides regular information about water quality in rivers, streams, and lakes and is required for the survival of the aerobic aquatic organisms. Understanding the variation of DO is therefore a major priority for water resource managers. In addition to the traditional methods used for measuring DO concentration, previous attempts have been conducted to propose alternative methods to estimate DO concentrations mainly based on mathematical modeling.

To date, several researchers worldwide have attempted to develop effective and robust models for DO concentration. These studies can be divided into two categories: (i) estimation models and (ii) forecasting models. For the first category, the following three subgroups exist: (1) artificial neural network (ANNs) models, including multilayer perceptron neural network (MLPNN), radial basis function neural network (RBFNN), generalized regression neural network (GRNN), cascade correlation artificial neural networks (CCNN), and Elman neural networks (ELNN) (Akkoyunlu et al. 2011; Ay and Kisi 2012; Heddam 2014a, 2016a; Diamantopoulou et al. 2007; Liu et al. 2012); (2) fuzzy logic and neuro-fuzzy models (Ranković et al. 2012; Heddam 2014b; Ay and Kisi 2016); (3) evolutionary models (Kisi et al. 2013; Heddam 2014c, 2016b); (4) artificial neural network and wavelet decomposition conjunction models (Xu and Liu 2013; Evrendilek and Karakaya 2014a, b, 2015); (5) support vector machines (SVM) (Liu et al. 2013; Liu et al. 2014). For the second category, the objective is the development of models capable estimating DO concentrations using only antecedent values of DO without inclusion of water quality variables as inputs (Alizadeh and Kavianpour 2015; Wang et al. 2013; Faruk 2010; Heddam 2016b).

Akkoyunlu et al. (2011) compared MLPNN and RBFNN to estimate DO at different depths in Lake Ecosystem in Turkey. Ay and Kisi (2012) attempted to estimate DO at the upstream station of Foundation Creek, Colorado, USA, using data from the downstream and vice versa, using two models; MLPNN and RBFNN. Heddam (2014a) demonstrated that GRNN model was a good and powerful tool for estimating hourly DO concentration. Heddam (2016a) applied RBFNN for estimating DO using four water quality variables. Diamantopoulou et al. (2007) firstly presented a CCNN model for predicting DO at a monthly time step. The application of the ELNN was reported by Liu et al. (2012). In all the above studies, the authors selected several water quality variables as inputs at different time steps, from hourly to monthly. Adaptive neuro-fuzzy inference system (ANFIS) is another well-known model that widely reported as a powerful tool for modeling DO concentration. Ranković et al. (2012) were firstly demonstrated that the ANFIS model could be successfully applied for modeling DO concentration using monthly data from Gruža Reservoir, Serbia. Heddam (2014b) and Ay and Kisi (2016) compared two ANFIS models, (i) grid partition-based fuzzy inference system, named ANFIS_GRID, and (ii) subtractive clustering-based fuzzy inference system, named ANFIS_SUB, for estimating DO, at hourly and monthly time steps, respectively.

Few studies in the literature have focused on the application of the evolutionary models for modeling DO concentration. Kisi et al. (2013) demonstrated that gene expression programming (GEP) provided better results compared to the standard MLPNN and ANFIS models. Heddam (2014c) applied two dynamic evolving neural-fuzzy inference systems, (i) offline-based system named DENFIS-OF and (ii) online-based system, named DENFIS-ON, for modeling DO at an hourly time step, and demonstrated that the DENFIS were the best in comparison to the MLPNN and multiple linear regression (MLR) models. Heddam (2016b) proposed evolving fuzzy neural network (EFuNN) for estimating DO and demonstrated that the EFuNN was more accurate than the MLR model.

Combined wavelet transforms (WT) and ANNs and sometimes MLR models, is another kind of approach adopted in the literature for estimating DO concentration. Meanwhile, Xu and Liu (2013) applied a wavelet neural network (WNN) conjunction models for DO estimation using monthly data from Jishan Lake in Duchang County, Jiangxi Province, China. Evrendilek and Karakaya (2014a) selected the orthogonal wavelet families for denoising time series of water quality variables, and applied three ANN models for estimating DO, at Yenicaga Lake, Bolu, in Turkey. Evrendilek and Karakaya (2014b, 2015) applied DWT and MLR conjunction models for estimating DO concentration using data from Lake Abant, Turkey. Support vector machines (SVM) based on kernel function is largely used in the area of water science; however, it is relatively a new form of models used for modeling DO. Liu et al. (2013) compared least squares support vector regression (LSSVR), SVM and MLPNN for modeling DO in river crab culture ponds, China, and demonstrated that LSSVR was the best. In another study, Liu et al. (2014) demonstrated that particle swarm optimization (PSO) significantly improves the predictive capabilities of the LSSVR model in predicting DO. A particular type of model called the extended stochastic harmonic analysis (ESHA) was developed by Abdul-Aziz and Ishtiaq (2014) and compared with the classical harmonic analysis (CHA) for estimating hourly DO concentration, and found that the ESHA model was better when compared to CHA model.

Forecasting DO concentration models were rarely presented in the literature. This kind of models adopt antecedent values as input to forecast the future DO value at a specific horizon. Faruk (2010) investigated the capabilities of the MLPNN in forecasting monthly DO concentration in the Buyuk Menderes basin, Turkey. Wang et al. (2013) applied three models, namely, bootstrapped wavelet neural network (BWNN), MLPNN, and WNN, for forecasting monthly DO. Alizadeh and Kavianpour (2015) compared two forecasting models: MLPNN and WNN models in DO forecasting. The authors demonstrated that using four antecedent values of DO as inputs, the model provided better results at hourly time step when compared to the model at daily time step. Heddam (2016c) used the OP-ELM for forecasting DO in 7 days ahead, using previous values of DO measured at an hourly time step.

An analysis of the works reported above revealed that most of the works focused on the prediction of DO without water quality variables (category of forecasting models), is rarely adopted. Recently, Heddam (2016d) proposed a new kind of model for predicting DO without water variables. The author compared RBFNN and MLR for modeling DO using the components of the Gregorian calendar that are: (i) year number, (ii) number of months from 1 to 12, (iii) number of days from 1 to 31, and (iv) number of hours from 0:00 to 24:00. To the best of the authors’ knowledge, there is no such study in the literature which examines the potential of extreme learning machines (ELM)-based approach, for modeling DO concentration with water quality variables as predictor. Hence, this study aims to introduce new kind of models for estimating DO concentration in river. The proposed ELM models were first applied for estimating DO using four water quality variables as inputs, and second, they were applied for forecasting DO without water quality variables and using only the component of the Gregorian calendar as input. Finally, we investigated whether the proposed ELM models can outperform the well-known multilayer perceptron neural network (MLPNN) and multiple linear regression (MLR) approaches for modeling DO concentration with and without water quality variables as predictors.

Methods

ELM is a new data-driven model, first presented by Huang et al. (2004) and developed later by Huang et al. (2006a, b). ELM has been introduced to improve the learning ability of the standard single hidden layer feedforward neural networks (SLFN). As a result, several attempts have been made over the past few years, with success, to improve the original algorithm; consequently, some changes were made and several types of ELM have been introduced. The present work aims to compare four ELM categories: the standard ELM with sigmoid activation function called S-ELM, the ELM with radial basis activation function (R-ELM), the online sequential extreme learning machine (OS-ELM), and the optimally pruned extreme learning machine (OP-ELM) for the first time. The four ELM models were also compared with the standard multilayer perceptron neural network (MLPNN) and multiple linear regression (MLR) models. Detailed descriptions of the proposed models are presented below.

Extreme learning machines

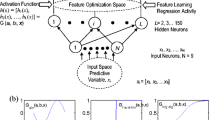
In order to improve the performance and the learning ability of the SLFN, Huang et al. (2006a, b) introduced the ELM as a new learning algorithm. In ELM, parameters of hidden nodes are randomly selected and the output weights are analytically determined using least squares method (Huang et al. 2006a, b; Huang et al. 2012). Details of the mathematical formulation of the ELM can be summarized as follows (Fig. 1):

Fig. 1
figure 1

ELM structure (Huang 2015)

Full size image

For N arbitrary training samples represented by (x i, y i), where x i = [x i1, x i2, … , x iD] T∈RD and [y i1, y i2, …, y iD]T∈RD; The output of an SLFN with N hidden nodes can be represented by (Huang et al. 2006a, b):

$$ {f}_N(x)=\sum_{i=1}^N{\beta}_i{f}_i\left({x}_j\right)=\sum_{i=1}^N{\beta}_i{f}_i\left({w}_i\cdot {x}_j+{b}_i\right)={o}_j\kern0.5em x\in {R}^n,{w}_i\in {R}^n $$
(1)

where w i is the weight vector connecting the input layer to the ith hidden node, β i is the weight connecting the ith hidden node to the output node, and f is the hidden node’s activation function. Consequently, (w i  × x) denotes the inner product of vectors w i and the input x. Here, w i  = [w i1, w i2, …, w iD]T is the weight vector connecting the ith hidden node to the input nodes, β i = [β i1, β i2, …, β ik ] T is the weight vector connecting the ith hidden node to the output nodes, and b i is the threshold of the ith hidden node. The standard SLFN with N hidden nodes with activation function f(x) can be written as (Huang et al. 2015):

$$ H\beta = T $$
(2)

where

$$ H=\left[\begin{array}{ccc}\hfill {f}_1\left({w}_1\cdot {x}_1+{b}_1\right)\hfill & \hfill \cdots \hfill & \hfill {f}_N\left({w}_N\cdot {x}_1+{b}_N\right)\hfill \\ {}\hfill \vdots \hfill & \hfill \vdots \hfill & \hfill \vdots \hfill \\ {}\hfill {f}_1\left({w}_1\cdot {x}_N+{b}_1\right)\hfill & \hfill \cdots \hfill & \hfill {f}_N\left({w}_N\cdot {x}_N+{b}_N\right)\hfill \end{array}\right] $$
(3)
$$ \beta =\left[\begin{array}{c}\hfill {\beta}_1^T\hfill \\ {}\hfill \vdots \hfill \\ {}\hfill {\beta}_N^T\hfill \end{array}\right]\ \mathrm{and}\ \mathrm{T}=\left[\begin{array}{c}\hfill {t}_1^T\hfill \\ {}\hfill \vdots \hfill \\ {}\hfill {t}_N^T\hfill \end{array}\right] $$
(4)

ELM simply solves the function by:

$$ \beta ={H}^{+} T $$
(5)

where H + is the Moore-Penrose generalized inverse of matrix H. In the present study, we applied two types of ELM; S-ELM with sigmoid activation function and R-ELM with radial basis activation function. Two activation functions are presented below (Huang 2015; Liang et al. 2006).

The sigmoid function:

$$ f\left( w, b, x\right)=\frac{1}{1+{e}^{-\left( w\cdot x+ b\right)}} $$
(6)

The radial basis functions with the popular Gaussian function:

$$ f\left( w, b, x\right)={e}^{- b{\left\Vert x- w\right\Vert}^2} $$
(7)

ELM has been successfully applied for modeling reference evapotranspiration (ET0) at the north, mid, and southern parts of Iraq (Abdullah et al. 2015); prediction of monthly effective drought index in eastern Australia (Deo and Şahin 2015); simulation of monthly mean streamflow water level in eastern Queensland (Deo and Şahin 2016); forecasting monthly streamflow discharge rates in the Tigris River, Iraq (Yaseen et al. 2016); and prediction of daily water level in the Urmia Lake, Iran (Shiri et al. 2016).

Online sequential extreme learning machine

Online sequential extreme learning machine (OS-ELM) was first proposed by Liang et al. (2006) as a variant ELM algorithm. OS-ELM is a modified version of the original ELM, developed for single hidden layer feedforward networks (SLFNs) with additive or radial basis function (RBF) hidden nodes (Liang et al. 2006). In the original ELM, the learning algorithm starts only if all the training samples are ready, consequently, when new data are available, the ELM must be retrained (Liang et al. 2006). Contrary to the ELM, OS-ELM is capable of learning the available data one-by-one or “chunk-by-chunk” with a fixed or varying chunk size (Liang et al. 2006; Huang et al. 2011); when the learning procedure for any particular observation is completed, the observation is discarded from the pattern (Liang et al. 2006; Huang et al. 2011). The OS-ELM algorithm is implemented in two stages: (i) the initialization and (ii) the online sequential learning phase. The learning algorithm is summarized as follows (Singh et al. 2016): (i) Training data are sequential one-by-one or block-by-block, (ii) only a new data sample is presented to the learning algorithm for training; the data samples are not used for training again and again; (iii) once finished with the data sample, it will be discarded from the pattern; and (iv) prior knowledge about the length of the data samples to be presented to the learning algorithm is not necessary (Singh et al. 2016).

If a new chunk of data is received, it results in a problem of minimizing (Liang et al. 2006):

$$ \left\Vert \left[\begin{array}{c}\hfill {H}_0\hfill \\ {}\hfill {H}_1\hfill \end{array}\right] w-\left[\begin{array}{c}\hfill {T}_0\hfill \\ {}\hfill {T}_1\hfill \end{array}\right]\right\Vert $$
(8)

Consequently, the connecting weight w becomes:

$$ {w}^{(1)}={K}_1^{-1}{\left[\begin{array}{c}\hfill {H}_0\hfill \\ {}\hfill {H}_1\hfill \end{array}\right]}^T\left[\begin{array}{c}\hfill {T}_0\hfill \\ {}\hfill {T}_1\hfill \end{array}\right] $$
(9)

where

$$ {K}_1={\left[\begin{array}{c}\hfill {H}_0\hfill \\ {}\hfill {H}_1\hfill \end{array}\right]}^T\left[\begin{array}{c}\hfill {H}_0\hfill \\ {}\hfill {H}_1\hfill \end{array}\right]={K}_0+{H}_1^T{H}_1 $$
(10)

In order to increase the efficiency of sequential learning, w (1) must be calculated as a function of w (0), K 1 , H 1 , and T 1 :

$$ {\left[\begin{array}{c}\hfill {H}_0\hfill \\ {}\hfill {H}_1\hfill \end{array}\right]}^T\left[\begin{array}{c}\hfill {T}_0\hfill \\ {}\hfill {T}_1\hfill \end{array}\right]={H}_0^T{T}_0+{H}_1^T{T}_1={K}_1{w}^{(0)}-{H}_1^T{H}_1{w}^{(0)}+{H}_1^T{T}_1 $$
(11)

w (1) can be expressed as follows by combining (10) and (11):

$$ {w}^{(1)}={K}_1^{-1}{\left[\begin{array}{c}\hfill {H}_0\hfill \\ {}\hfill {H}_1\hfill \end{array}\right]}^T\left[\begin{array}{c}\hfill {T}_0\hfill \\ {}\hfill {T}_1\hfill \end{array}\right]={w}^{(0)}{+{K}_1^{-1} H}_1^T\left({T}_1-{H}_1{w}^{(0)}\right) $$
(12)

Iteratively, when the (k + 1) new chunk of data arrives, the recursive method is implemented for acquiring the updated solution. w (k+1) can be updated by:

$$ {w}^{\left( k+1\right)}={w^{(k)}+ K}_{k+1}^{-1}{H}_{k+1}^T\left({T}_{k+1}-{H}_{k+1}{w}^{(k)}\right) $$
(13)

with

$$ {K}_{k+1}^{-1}={K}_k^{-1}-{K}_k^{-1}{H}_{k+1}^T{\left( I+{H}_{k+1}{K}_k^{-1}{H}_{k+1}^T\right)}^{-1}\times {H}_{k+1}{K}_k^{-1} $$
(14)

OS-ELM has been successfully applied for many engineering problems (Lima et al. 2016; Yadav et al. 2016; Wang and Han 2014).

Optimally pruned extreme learning machine

Optimally pruned extreme learning machine (OP-ELM) was first proposed by Miche et al. (2008a, b) and presented later by Miche et al. (2010). OP-ELMs accepts multiple types of functions, i.e., Gaussian, sigmoid, and linear (Pouzols and Lendasse 2010a, b). Using a real-world data set on a toy example (Miche et al. 2008b) demonstrated in a clear and effective manner that the original ELM suffers from an important drawback that lead to a decrease in the accuracy of the algorithm, when irrelevant or correlated variables are presented in the training data set (Sovilj et al. 2010). OP-ELM is presented as a good solution for pruning away irrelevant variables. (Miche et al. 2008a, 2010). The OP-ELM is achieved in three steps (Moreno et al. 2014; Grigorievskiy et al. 2014): (i) an over-parameterized ELM is built with initially large number of neurons; (ii) an appropriate ranking of the hidden neurons is made upon based on their contribution to the linear explanation of the ELM output, using the multi-response sparse regression (MRSR) (Similä and Tikka 2005) or least angle regression (LARS) (Efron et al. 2004) if the output is one-dimensional; (iii) leave-one-out (LOO) validation is used to decide how many neurons to prune. Presented as a good alternative to solve complex problems, OP-ELM has been successfully applied for many engineering problems (Sorjamaa et al. 2008; Sovilj et al. 2010; Moreno et al. 2014; Grigorievskiy et al. 2014; Akusok et al. 2015; Heddam 2016c).

Multilayer perceptron neural network

Multilayer perceptron neural network (MLPNN) (Rumelhart et al. 1986) is a well-known ANNs model and mainly adopted for solving problems in environmental science. MLPNN is a universal approximator (Hornik et al. 1989; Hornik 1991). MLPNN is composed of layers of units called neurons. MLPNN has three types of layers: an input layer, one or more hidden layers, and an output layer. In the present study, we have used a model with only one hidden layer with sigmoid activation function and a linear activation function also called identity function in the output layer. The number of neurons in the hidden layer is determined with trial and error. The input layer contains the predictors (pH, TE, SC, and TU) for models with water quality variables, and the year, month, day, and hour numbers for the models without water quality variables. Finally, the output layer contains only one neuron; the DO concentration. More details about MLPNN can be found in Haykin (1999).

Multiple linear regression)

Multiple linear regression (MLR) is a method adopted to provide a simple linear relation between a set of predictors (x i ), and one variable called response (Y); the model can be presented as follow:

$$ Y= f\left({x}_i\right)={\beta}_0+{\beta}_1{x}_1+{\beta}_2{x}_2{+\beta}_3{x_3+\beta}_4{x}_4+{\beta}_i{x}_i $$
(15)

where Y is the response (DO); x i is the water quality variables (pH, TE, SC, and TU); and β i is the parameters of the models.

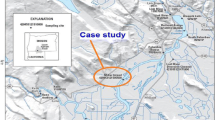
Case studies

DO modeling in river ecosystems with and without water quality variables was demonstrated using eight different datasets from different basins in USA: Clackamas, Willamette, Umpqua, Tualatin, Delaware, and Cumberland basins. Detailed presentation of the rivers with the identification code of each station (ID) at different basins is reported in Table 1. For the eight stations, data are available at the United States Geological Survey (USGS) website:http://or.water.usgs.gov/cgi-bin/grapher/table_setup.pl?site_id. The water quality data used in this study consisted of measured water temperature (TE, °C), turbidity (TU FNU), pH (std. unit), specific conductance (SC, μS/cm) and dissolved oxygen (DO, mg/L). Water quality variables were measured at 1-h time interval. For each station, we selected a period of record for four calendar years. Detailed descriptions of the data set with the period of records are reported in Table 2. Each data set is divided into two subsets: (i) a training subset (70%) and (ii) a validation subset (30%); results for each station are reported in Table 3. Table 4 represents the statistical parameters of water quality variables in the study area. In the table, the terms X mean, X max, X min, S x , C v , and R denote the mean, maximum, minimum, standard deviation, coefficient of variation, and the coefficient of correlation between the variable and the DO, respectively.

Table 1 Geographical location of the selected stations
Full size table
Table 2 Data set presentation for all stations
Full size table
Table 3 The number of data used in training (70%) and validation (30%) subsets for all stations
Full size table
Table 4 Statistical parameters of the used data sets for all stations
Full size table

Application and results

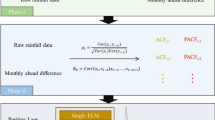
The aim of this study is to demonstrate the capability and usefulness of the ELM models for the prediction of DO concentration in river ecosystems with and without water quality variables as inputs. The investigation was conducted in three phases. First, by selecting four water quality variables (TE, pH, SC, and TU), several combinations were selected and six scenarios (Table 5) (i) TE, pH, SC, and TU; (ii) TE, pH, and SC; (iii) TE, SC, and TU; (iv) TE and SC; (v) TE and pH; and (vi) TE and TU were compared. The selection of the six combinations is mainly based on the correlation coefficient. Second, an attempt is made to predict DO concentration without water quality variables as input. Within this context, we have selected four inputs variables that are (i) year number, (ii) month number from 1 to 12, (iii) day number of the month from 1 to 31, and (iv) hour number from 0:00 to 24:00. For example, the inputs of the pattern that correspond to 15 December 2010 at 22:00 are described as below:

  1. 1.

    Input 1: year number, i.e., “2010”.

  2. 2.

    Input 2: month number, i.e., “12”.

  3. 3.

    Input 3: day number, i.e., “15”.

  4. 4.

    Input 4: hour number, i.e., “22.00”.

Table 5 The input combinations of different models
Full size table

Flowchart of the proposed approaches with and without water quality variables is presented in Fig. 2.

Fig. 2
figure 2

Flowchart of the two proposed modeling scenarios: scenario 1 using water quality variables as predictor and scenario 2 without water quality variables as predictors

Full size image

Similar to the models with water quality variables, the models without water quality always have four input variables. Third, the best ELM models are evaluated by training with validation dataset and testing with training dataset, with and without water quality variables.

In order to remove the effect of different units of measurement, the data were standardized using the Z score method (Gulgundi and Shetty 2016):

$$ {x}_{ni, k}=\frac{x_{i, k}-{m}_k}{Sd_K} $$
(16)

where x ni, k is the normalized value of the variable k (input or output) for each sample i. x i , k is the original value of the variable k. m k and S dk are the mean value and standard deviation of the variable k. According to Gulgundi and Shetty (2016), the Z score method is mainly adopted in the studies based on statistical analysis; furthermore, the effect of different units of measurement was completely eliminated. It has been demonstrated that the Z score method (Gulgundi and Shetty 2016; Heddam 2016c, d, e) improves the performances and the accuracy of the models. In this study, four statistical indices were selected to evaluate the different ELM models. These indices are the coefficient of correlation (R), the Nash-Sutcliffe efficiency (NSE), the root mean squared error (RMSE), and the mean absolute error (MAE), calculated as follows (Legates and McCabe 1999):

$$ R=\left[\frac{\frac{1}{N}\sum \left({O}_i-{O}_m\right)\left({P}_i-{P}_m\right)}{\sqrt{\frac{1}{N}\sum_{i=1}^n{\left({O}_i-{O}_m\right)}^2}\sqrt{\frac{1}{N}\sum_{i=1}^n{\left({P}_i-{P}_m\right)}^2}}\right] $$
(17)
$$ \mathrm{NSE}=1-\frac{\sum_{i=1}^N{\left[{O}_i-{P}_i\right]}^2}{\sum_{i=1}^N{\left[{O}_i-{O}_m\right]}^2} $$
(18)
$$ \mathrm{RMSE}=\sqrt{\frac{1}{N}\sum_{i=1}^N{\left({O}_i-{P}_i\right)}^2} $$
(19)
$$ \mathrm{MAE}=\frac{1}{N}\sum_{i=1}^N\left|{O}_i-{P}_i\right| $$
(20)

where N is the number of data points, O i is the measured value, and P i is the corresponding model prediction. O m and P m are the average values of O i and P i . For applying the ELM models, we used the following Matlab codes: (i) for OP-ELM model, we used the code available at http://research.ics.aalto.fi/eiml/software.shtml and for the OS-ELM, S-ELM, and R-ELM we used the code available at http://www.ntu.edu.sg/home/egbhuang/elm_codes.html.

Predicting DO using water quality variables as predictors

Table 6 shows the evaluation of the OP-ELM1, OS-ELM1, S-ELM1, R-ELM1, MLPNN1, and MLR1 models in training and validation phases for each station. It should be noted that Table 6 contains only the best models. The complete results, including the best and the worst models developed are reported in Tables A1–A6 as supplementary materials.

Table 6 Performances of different models in modeling DO at all stations using water quality variables as predictors
Full size table

According to the obtained results, some important conclusions can be drawn. First, among the six OP-ELM models, the OP-ELM1 is always the best followed by the OP-ELM2 in the second place, the OP-ELM3 and OP-ELM4 ranked as third. Second, it is clear from Table A1 that inclusion of turbidity in the models does not help to significantly improve the performances of the proposed models, and the accuracy of the models is slightly improved. However, the TU is not suitable as input variable and may not be a predictor of DO concentration. Third, water TE and pH are the most important predictors of DO. According to Table A1, the R varies with different combinations in the training phase. The best R value (0.990) was obtained using OP-ELM1 at two stations: USGS 14211720 and USGS 14317450. Similarly, the best NSE value (0.980) was obtained using OP-ELM1 at the USGS 14317450 station. In terms of the RMSE and MAE, the best performances were obtained using OP-ELM1, with RMSE equal to 0.152 mg/L and MAE equal to 0.110 mg/L, at the USGS 14316460 station. In addition, the results for the six OP-ELM models in the validation phase are also summarized in Table A1. As shown in Table A1, the OP-ELM1 and OP-ELM2 provide the best accuracy at eight stations, with high R and NSE, and low RMSE and MAE. Furthermore, the results obtained in the validation phase indicate that: (i) inclusion of the TU as input does not help to improve the accuracies of the proposed models (ii) OP-ELM5 model with TE and pH as inputs provides good results at four stations with R values ranging from 0.914 to 0.987; NSE values range from 0.835 to 0.975. The validation results for the best OP-ELM1 models show smaller RMSE and MAE with values equal to 0.172 mg/L and 0.116, respectively. Measured and predicted DO concentrations with OP-ELM1 at the eight stations in the validation phase, using water quality variables as inputs are presented in Fig. 3. The scatterplots apparently illustrate that the estimates of the OP-ELM1 model closely follow the corresponding measured DO values (especially the extreme values).

Fig. 3
figure 3

Scatterplot of measured vs calculated DO using OP-ELM1 models in the validation period

Full size image

Results obtained using the six OS-ELM models in the training and validation phases at all eight stations are summarized in Table A2. It should be observed here that the six OS-ELM models give high accuracy and the OS-ELM1 performs better than the other models by showing lower RMSE and MAE values, and higher NSE and R values. The results indicate that the OS-ELM1 and OS-ELM2 are the best among the all six models. These models relatively give the high R and NSE, and low RMSE and MAE values. It can be observed that the OS-ELM models yield results worse than those obtained using the OP-ELM models. When comparing these two models taking into account the increasing importance of the input variables from two to four inputs, the OP-ELM models perform superior to the OS-ELM models. According to Table A2, the R and NSE values obtained using OS-ELM1 model in the validation phase, lie in an interval between 0.923 and 0.987 and 0.852 and 0.974, respectively. Similarly, the validation results of the best OS-ELM1 models, respectively, show smaller RMSE and MAE with values equal to 0.179 and 0.134 mg/L when compared to other models. The RMSE and MAE accuracies of the best OS-ELM1 model were increased by 25.40 and 26.60% using OP-ELM1, respectively. Measured and predicted DO concentrations with OS-ELM1, at the eight stations in the validation phase, using water quality variables as inputs are presented in Fig. 4. Scatterplots apparently illustrate that the estimates of the OS-ELM1 model closely follows the corresponding measured DO values.

Fig. 4
figure 4

Scatterplot of measured vs calculated DO using OS-ELM1 models in the validation period

Full size image

Table A3 shows the model evaluation of the six S-ELM models in the training and validation phases at all eight stations. According to Table A3, in the validation phase, the S-ELM1 is the best model for the all stations, with the highest R and NSE values, and the lowest RMSE and MAE values. The R and NSE values of the best S-ELM1 model are 0.988, and 0.977, respectively. Based on the RMSE and MAE as seen in Table A3, the S-ELM1 is selected as the best model in approximating hourly DO with the values equal to 0.179 and 0.140 mg/L, respectively. Furthermore, it can be observed that the S-ELM1 models yield results worse than those obtained using the OP-ELM1 model and yield results better than those obtained using the OS-ELM1 models. In the validation phase, the OP-ELM1 improves the S-ELM1 model with 18.60 and 57.14% reductions in RMSE and MAE, respectively. By contrast, the accuracy of the S-ELM1 model in respect to the RMSE and MAE was increased by 21.83 and 59.40%, respectively, against the OS-ELM1 model. Among the two-input models (combination 5, TE and pH inputs), the S-ELM5 is the best model with R, NSE, RMSE, and MAE values equal to 0.987, 0.974, 0.192, and 0.152 mg/l, respectively. Measured and predicted DO concentrations with S-ELM1 models at eight stations in the validation phase, using water quality variables as predictors are presented in Fig. 5. It is obvious from the parameters of the fit line equations in scatterplots that the S-ELM1 model estimates are close to corresponding DO values.

Fig. 5
figure 5

Scatterplot of measured vs calculated DO using S-ELM1 models in the validation period

Full size image

Table A4 shows the model evaluation of the six R-ELM models in the training and validation phases at all eight stations. Similar to the results obtained using OP-ELM, OS-ELM, and S-ELM, the R-ELM1 is the best model at the all stations, with the highest R and NSE values, and the lowest RMSE and MAE values. The best results is obtained using the R-ELM1 at the USGS 14317450 with R, NSE, RMSE, and MAE values equal to 0.988 and 0.976, respectively. In addition, R-ELM1 has the minimum value of RMSE (0.189 mg/L) and MAE (0.150 mg/L) values. As seen in Table A4, the R-ELM5 with only two water quality variables as inputs (TE and pH) is the best model with R, NSE, RMSE, and MAE values equal to 0.987, 0.974, 0.189, and 0.150 mg/L, respectively. The R-ELM1 model clearly performs worse than the OP-ELM1 and S-ELM1 models; however, the R-ELM1 provides better results than the OS-ELM1 model. In the validation phase, OP-ELM1 improves the OS-ELM1, S-ELM1, and R-ELM1 models, with the 10.41, 3.91, and 5.49% reductions in RMSE, respectively. In addition, the accuracy of the OP-ELM1 model in respect to the MAE is increased by 12.50, 5.00, and 6.33% against the OS-ELM1, S-ELM1, and R-ELM1, respectively. Measured and predicted DO concentrations with R-ELM1 models at eight stations in the validation phase, using water quality variables as predictors are presented in Fig. 6. It is obvious from the parameters of the fit line equations in scatterplots that the DO estimates by the R-ELM1 models closely follow the measured values.

Fig. 6
figure 6

Scatterplot of measured vs calculated DO using R-ELM1 models in the validation period

Full size image

Table A5 shows the model evaluation of the six MLPNN models in the training and validation phases at all eight stations. According to Table A5, MLPNN1 have the best accuracy and performed the best in comparison to the all other five models. In the validation phase, the R varies with different combinations. The best R and NSE values (0.989 and 0.978) were obtained using MLPNN1 at the USGS 14317450station. In terms of the RMSE and MAE, the best performances were obtained using MLPNN1, with RMSE equal to 0.177 mg/L and MAE equal to 0.138 mg/L. Although the results obtained using MLPNN at the eight stations are very satisfactory, we also conclude that OP-ELM1 is performing better compared to the MLPNN1 in all stations, and the MLPNN1 ranks only second, third, and fourth, in terms of the performance criteria. Measured and predicted DO concentrations with MLPNN1 models at eight stations in the validation phase, using water quality variables as predictors are presented in Fig. 7.

Fig. 7
figure 7

Scatterplot of measured vs calculated DO using MLPNN1 models in the validation period

Full size image

Results using MLR are presented herein to draw a robust conclusion about the results obtained using the ELM and MLPNN models. Results using MLR are tabulated in Table A6. According to Table A6, both MLR1 and MLR2 perform well for modeling DO in all stations. On the other hand, MLR1 provided the best results compared to all other models. By comparing the results obtained using MLR1 and all ELM and MLPNN1 models, MLR1 presents the worst overall performances and rank in the last place. Measured and predicted DO concentrations with MLR1 models at eight stations in the validation phase, using water quality variables as predictors are presented in Fig. 8.

Fig. 8
figure 8

Scatterplot of measured vs calculated DO using MLR1 models in the validation period

Full size image

Finally, we compared the results obtained using the OP-ELM1, OS-ELM1, S-ELM1, R-ELM1, MLPNN1, and MLR1 models. The performances of the six models are tabulated in Table 6. As shown in Table 6, the six models are ranked according to the performances of each model in the validation phase at all eight stations. According to Table 6, OP-ELM1 model provides the best performance and is ranked in the first place at seven stations and in the second place at one station. R-ELM1 is ranked in the first place in one station, in the second place in four stations, and it is third at only one station. MLPNN is ranked in the second place at two stations, in the third place in four stations, and finally, in the fourth place in two stations. OS-ELM1 and S-ELM1models are ranked either third, fourth, and fifth, except at two stations where OS-ELM1 model is ranked in the second place, as reported in Table 6. Finally, according to Table 6, we can conclude that the MLR1 is the worst model among all the compared models, and ranked in the sixth place. Details comparison and ranking of the six models is reported in Table 7.

Table 7 Ranking and comparison of different six models in modeling DO at all stations using water quality variables as predictors
Full size table

Finally, in order to illustrate the capabilities and usefulness of the best obtained models OP-ELM1, OS-ELM1, S-ELM1, R-ELM1, MLPNN1, and MLR1 having TE, pH, SC, and TU variables as inputs, the models were also evaluated by interchanging the training and validation datasets by setting the training dataset (30%) and validation dataset (70%) and the results are summarized in Table 8. As seen from the table, the results are always good and the models provide high accuracy, with the exception of the R-ELM1 at the USGS 3431083 station, in which the performances of the model are dramatically decreased. For the 30% training and 70% validation case, the major parts of the results approximate the results obtained at 70% training and 30% validation case, which may mean that the models are capable to predict DO with a high accuracy. Comparing the performances of the four models, OP-ELM1 yields the best results and ranks in the first place at six stations, while the MLR1 presents the worst overall performances.

Table 8 Evaluation of the optimal models trained with validation dataset and tested with training dataset by using water quality variables as predictors
Full size table

Predicting DO without water quality variables as predictors

Table 9 shows the model evaluation of the four ELM, MLPNN, and MLR models without water quality variables as predictors, at all eight stations. In the validation phase, as seen in Table 9, all the ELM models provide good approximates with respect to four statistical indices. R-ELM is the best model and ranks first at seven stations while the MLPNN ranks in the second place at five stations, followed by the S-ELM and the OS-ELM in the third and fourth places, respectively. Without water quality variables as predictors, MLR presents the worst overall performances. Using MLR, the R and NSE values never exceed 0.44 and 0.186, respectively. Table 9 also shows that RMSE and MAE were found to be very high, and in some case, they reached to 2.573 and 2.104 mg/L, respectively. The R-ELM model yields low RMSE and MAE values (0.223 and 0.171 mg/L) at the USGS 14316460 and it is better than the all other models. As can be seen from the comparison made in Table 9, the models’ accuracies in estimating hourly DO values decrease by using the components of the Gregorian calendar as predictors instead of water quality parameters. Ranking accuracy of the four models is reported in Table 9 according to the performances of each model in the validation phase at all eight stations.

Table 9 Performances of the proposed models in modeling DO at all stations without water quality variables as predictors
Full size table

Table 10 shows the model evaluation of the four ELM models trained using validation dataset (30%) and tested using training dataset (70%) without water quality variables as inputs. A first analysis of the obtained results reveals that: (i) the performance accuracy of the developed models was decreased and (ii) the R-ELM provides the best results in all training and validation phases at all eight stations, followed by the MLPNN in the second place, S-ELM in the third place, OS-ELM in the fourth place, OP-ELM in the fifth place, and finally, MLR with the lowest accuracy ranks in the last place. In the validation phase, R-ELM yields the lowest RMSE (0.186 mg/L) and MAE (0.243 mg/L), and the highest R (0.975) and NSE (0.920) indices. Based on these results, it is clear that none of the proposed models are able to provide the performances achieved using the R-ELM.

Table 10 Evaluation of the optimal models trained with validation dataset and tested with training dataset without water quality variables as predictors
Full size table

Conclusions

In the present study, an attempt was made to estimate DO concentration using four different ELM models; also, the paper investigated whether ELM can outperform MLPNN and MLR, for modeling DO with and without water quality variables as predictors. Various water quality datasets obtained from eight different stations; USA were used for developing the models. The novelty of the present work lies on one hand in the application of the ELM approaches at the first time, and in the other hand, an attempt to estimate DO concentration without water quality variables and using the components of the Gregorian calendar as inputs. From the results obtained, we can draw the following conclusions. First, in the first application using the four water quality variables as inputs, the OP-ELM was found to be more accurate than the OS-ELM, S-ELM, and R-ELM at seven stations and provided the best accuracy in the validation phase, with high R and NSE values (from 0.924 to 0.989) and (from 0.853 to 0.933), respectively. Comparison of the best OP-ELM models suggests that the OP-ELM models are superior to the MLPNN and MLR at all stations, and the MLR is the worst models in all stations. Therefore, the OP-ELM model is a very promising tool for modeling DO concentration. Second, in the second application using the components of the Gregorian calendar as inputs, the R-ELM performed the best at seven stations and provided the best accuracy in the validation phase, with high R and NSE values (from 0.884 to 0.969) and (from 0.781 to 0.939), respectively. The MLPNN is ranked in the second place at five stations, while the MLR results suggest that the linear model is very poor with very low accuracy, which leads to the conclusion that the MLR is insufficient for mapping a good relation between DO and the components of the Gregorian calendar; hence, the selection of nonlinear models like ELM and MLPNN are highly recommended. In addition, the important conclusion could be drawn that, in some cases, the inclusion of the turbidity as input did not improve the accuracies of the proposed models; on the contrary, it made them worse. The study also indicated that the hourly DO might be successfully estimated by the ELM models using only components of the Gregorian calendar as inputs when water quality data are missing or do not exist.