Introduction

A versatile simulation model for streamflow water level can assist with the dissemination of lead time information on temporal evolution of local catchment hydrology and, therefore, is of paramount importance to water management, environmental monitoring, agriculture, ecosystems, and resource management (Ni et al. 2010). In Australia, streamflow has decreased since 1970 (IPCC 2001). As such, meteorological (rainfall-related) and hydrological (streamflow-related) drought and its impact on water security are a significant cross-cutting issue. The Murray-Darling Basin, Australia’s largest and economically sensitive river system that accounts for 70 % of irrigated crops and pastures, is likely experiencing decline in streamflow by 10–25 % by 2050 and 16–48 % by 2100, and little is known about future impacts on groundwater (Hennessy et al. 2007). Therefore, a prior knowledge of streamflow as a first-order integrator of rainfall conditions in a local catchment is appealing to the end users particularly for informed decision-making process (Chiew et al. 1998).

In Australia, the primary indicators of streamflow water level (e.g., rainfall or evaporation regime) are highly variable (Verdon et al. 2004) and respond rapidly to radiative perturbations (Deo et al. 2009; McAlpine et al. 2007; McAlpine et al. 2009). With a naturally variable climate influenced by El Nino Southern Oscillation, positive and negative aberrations in streamflow have pronounced impact on meteorological and hydrological disasters (Deo et al. 2009; Nicholls et al. 1997). However, streamflow is impacted by inter-annual variability of river flows (McMahon et al. 1992), which culminates added challenges in managing risks with irrigations, ecosystems, and marine life (Chiew et al. 1998). Although flood and drought are linked mainly to ENSO (Kiem and Franks 2004; Kiem et al. 2003), application of teleconnections driven by climate indices and sea surface temperatures (SSTs) for forecasting streamflow is an evolving area of interest.

The modeling of streamflow water levels should consider rainfall as an input as the variability of streamflow is influenced by surplus or deficit of rain water as a primary source of environmental flow. Therefore, the causal relationships between the current and the antecedent rainfall, river flow, and climate indices that affect these parameters should be employed for simulation of streamflow (Chiew and McMahon 2002; Chiew et al. 1998; Dettinger and Diaz 2000; Dettinger et al. 2000; Ouyang et al. 2014; Piechota et al. 2001; Simpson et al. 1993). Often, lagged relationship of streamflow with rainfall and climate indices such as Southern Oscillation Index, Indian Ocean Dipole, ENSO Modoki Index, and Pacific Decadal Oscillation Index is used (Zubair and Chandimala 2006). Hydrological droughts that are reflected by aberrations in streamflow are intrinsically linked to oceanic–atmospheric processes (Drosdowsky 1993; Kiem and Franks 2001; McBride and Nicholls 1983) and so are the Pacific Decadal Oscillation (PDO) (Power et al. 1999; Risbey et al. 2009) and Indian Ocean Dipole (IOD) indices (Saji et al. 1999; Saji and Yamagata 2003). Also importantly, ENSO hydroclimatic links is known to foster below-normal streamflow discharge during El Niño and above normal during La Niña events. For example, a study found that sea surface temperatures (SSTs) can play a pivotal role in the prediction of January–March and April–June streamflow levels (Chiew and McMahon 2002). Therefore, the pivotal, yet crucial role of the inter-related inputs must be considered carefully for development of accurate and reliable streamflow models.

In general, data-driven models of streamflow that identify patterns and trends in historical observations use three primary approaches. First, historical changes in streamflow partitioned into training and testing datasets are utilized for predictive modeling as streamflow displays high degree of serial correlation (or persistence) arising from soil and groundwater storage and recharge that acts to delay the response of rainfall–runoff processes. This provides streamflow a memory of several months, which can represent the initial catchment hydrology to act as a source of prediction (Chiew et al. 1998). Second, concurrent or lagged correlations between rainfall and climate indices (McBride and Nicholls 1983) and streamflow (Chiew et al. 1998) can be utilized in a purely statistical sense. Third, probabilistic predictions are made, for example, by the Bureau of Meteorology with Bayesian joint probability where antecedent streamflow, rainfall, and climate indices are used as predictors to forecast streamflow (Robertson and Wang 2008; Wang and Robertson 2011; Wang et al. 2009). Recently, physically based approaches were also applied for monthly and seasonal forecasting of streamflow using rainfall–runoff models and historical dataset (Wang et al. 2011; Chowdhury et al. 2010).

The aforementioned methods have adopted statistical tools where artificial intelligence (AI) algorithms were used to extract predictive features embedded in historical input data. AI is a popular tool that is able to capture linear as well as non-linear relationships between streamflow and rainfall, climate indices, and related inputs (Asefa et al. 2006; Chang et al. 2002; Holland 1975; Koza 1992; Patterson 1998). It analyzes complex relationships between predictors and objective variable (Deo and Şahin 2015a; Deo et al. 2015; Salcedo-Sanz et al. 2015). Artificial neural network (ANN) is a popular model for simulation of hydroclimatic variables (Abbot and Marohasy 2012; Abbot and Marohasy 2014; Deo and Şahin 2015a; Masinde 2013; Nastos et al. 2014; Ortiz-García et al. 2014; Ortiz-García et al. 2012; Shukla et al. 2011; Tran et al. 2011). Despite its widespread use, a bottleneck of the ANN is the iterative tuning of model parameters, slow response of gradient-based learning algorithm utilized by hidden neurons and low accuracy compared to more advanced algorithms (Acharya et al. 2013; Şahin et al. 2014). Alternative models based on relevance vector machine and multivariate adaptive regression spline model have also been developed (Deo et al. 2015).

In this study, we applied the extreme learning machine (ELM) model for the simulation of streamflow in eastern Queensland. While its application for streamflow simulation is rarely found in literature for this particular region, the ELM model has successfully been applied elsewhere, for example in drought (Deo and Şahin 2015b) and evaporative loss (Deo et al. 2015) simulation, downscaling global climate model (Acharya et al. 2013), and solar and wind prediction (Şahin et al. 2014; Salcedo-Sanz et al. 2014). Despite its advantages over conventional data-driven model (e.g., ANN) and successful application in context of drought and evaporative modeling (Deo and Şahin 2015a; b; Deo et al. 2015; Samui and Dixon 2012), to our best knowledge, no study has tested the ELM for streamflow simulation in our region although the importance of streamflow as an environmental parameter (e.g., creek hydrology and ecosystems health) has been overstated (Chowdhury et al. 2010). As such, the adoption of ELM as an improved class of models in eastern Queensland is an original contribution of this research.

The novelty of our research is to develop and validate the utility of an ELM model for simulation of monthly streamflow water levels (Q WL) using predictors from set of nine variables for three hydrological catchments (Gowrie Creek: 18.44° S, 145.85° E; Mary River 25.95° E, 152.49° E, and Albert River 28.05° S. 153.05° E). The objective was to demonstrate the ability of the ELM for simulation of Q WL using hydrometeorological data, climate indices (Southern Oscillation Index (SOI), IOD, PDO, and ENSO Modoki Index (EMI)), and SSTs (Nino 3.0; Nino 3.4, and Nino 4.0). A selection of inputs was performed using cross correlation analysis, and the sensitivity of developed ELM model for simulation of Q WL based on single inputs (rainfall and periodicity) and all nine inputs was performed. In order to provide a benchmark, an ANN model with optimum input variables was also developed to elucidate the predictive accuracy of ELM model for simulation of Q WL.

Theory of machine learning model

Extreme learning machine

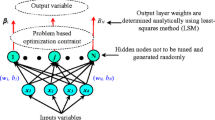
The extreme learning machine (ELM) algorithm was developed by Huang et al. (2006)). It is a state-of-art AI algorithm developed under single-layer feedforward neural network (SLFN) (Fig. 1) and since has widely been used in prediction problems (Acharya et al. 2013; Belayneh and Adamowski 2012; Deo and Şahin 2015b; Şahin et al. 2014). As the ELM is easy to use with no requirement for parameters to be tuned except the predefined network architecture, the algorithm avoids complications faced by the gradient-based algorithms (e.g., ANN) in terms of their relatively slow learning, difficulty with learning epochs, and the problems encountered by the local minima within the predictive data. Importantly, ELM learning process is faster compared to other conventional learning algorithms such as ANN or support vector machine (SVM) (Deo and Şahin 2015b; Rajesh and Prakash 2011).

Fig. 1
figure 1

a A schematic view of the ELM algorithm with input space, optimization space, hidden neuron parameters (a, b), and output space. Inputs are defined by nine predictor variables (x) while single output has the objective variable (y). Hidden neurons have different type of computational nodes (Huang and Chen 2007). b A sample plot of activation functions, G (a, b, x), tried in this study

Full size image

In the ELM model, the training of input data is accomplished in time span of seconds and minutes, even for large dataset and even complex applications, which are not achievable using conventional techniques. Besides, ELM model has good generalization performance compared to the ANN, SVM, and the singular value decomposition (SVD) algorithms in various classification and regression problems (Acharya et al. 2013; Deo and Şahin 2015b; Huang et al. 2015; Sánchez-Monedero et al. 2014). Consequently, the ELM is used as an ideal algorithm for forecasting atmospheric variables such as solar energy, air temperatures, and rainfall (Deo and Şahin 2015b; Leu and Adi 2011; Şahin 2012; Şahin et al. 2013; Şahin et al. 2014; Sánchez-Monedero et al. 2014; Wu and Chau 2010

In Fig. 1a, the schematic structure of ELM is exemplified. Consider a set of N distinct samples (x i , y i ) ∈ R n × R m, n, m are the domains and i = 1, 2… N. The SLFNs with L hidden neurons and activation function, G (a i, b i, x) is described viz (Huang et al. 2006; Şahin et al. 2014):

$$ {f}_L(x)={\displaystyle \sum_{i=l}^L{\beta}_i{h}_i(x)} $$
(1)

where β = [β 1, β 2, …, β L]T is the output weight matrix between hidden layer of L nodes to the m > 1 output nodes, and h(x) = [h 1(x), h 2(x), …, h L(x)] is the non-linear mapping space, which comprised the output row vector with respect to input x. Note that h i (x) is the output of the ith hidden node output. In optimization space, ELM model analyses input data to “learn” the natural patterns or trends present in the time series in order to simulate the objective variable, which is intrinsically related to the input space. According to Huang and Chen (2007)), the output function of hidden nodes may not be unique and different functions are used with various neuron arrangements to finalize the optimum model.

In this study, a number of h i(x) (Eqs. (7–12)) were tried in terms of the following:

$$ {h}_i(x)=G\left({a}_i.{b}_i.x\right),\kern1em {a}_i\in {R}^N,{b}_i\in R,i=\left[1,\kern0.5em 2,\kern0.5em \dots, \kern0.5em L\right] $$
(2)

where G (a, b, x) is the activation function for ELM model with hidden parameters (a, b). The G (a, b, x) is a non-linear piecewise continuous function that satisfies the ELM universal approximation capability theorem (Huang and Chen 2007; Huang et al. 2006), and therefore, it may be optimized for the best unsupervised learning outcome. In the ELM model, the hidden node parameters (a, b) are randomly generated without any interference from the predictor data and may be deduced by continuous probability distribution instead of being explicitly trained. This leads to remarkable computational efficiency compared to traditional neural network (e.g., SVM or ANN) (Huang et al. 2006; Huang et al. 2015).

The optimum ELM model was deduced by trailing activation functions with several model runs. Figure 1b shows a sample of the plots for G (a, b, x). In this study, the activation functions were defined by sine (G sin), hard-limit (G hard-lim), logarithmic sigmoid (G log sig), tangent sigmoid (G tan sig), radial basis (G rad bias), and triangular basis (G tri basis) equations viz

$$ {G}_{\sin}\left(a,b,x\right)= \sin \left( ax+b\right) $$
(7)
$$ {G}_{\mathrm{hard}\hbox{-} \lim}\left(a,b,x\right)=\left\{\frac{1, if\; ax+b<0}{0,\kern0.24em \mathrm{otherwise}}\right. $$
(8)
$$ {G}_{\mathrm{logsig}}\left(a,b,x\right)=\frac{1}{1+ \exp \left(-\left( ax+b\right)\right)} $$
(9)
$$ {G}_{\mathrm{tansig}}\left(a,b,x\right)=\frac{2}{1+ \exp \left(-2\left( ax+b\right)\right)-1} $$
(10)
$$ {G}_{\mathrm{rad}\kern0.5em \mathrm{bias}}\left(a,b,x\right)= \exp \left(-{\left( ax+b\right)}^2\right) $$
(11)
$$ {G}_{\mathrm{tribasis}}\left(a,b,x\right)=\left\{\frac{1-\left| ax+b\right.\left|,\; if-1\le \left( ax+b\right)\le 1\right.}{0\kern2.28em ,\;\mathrm{otherwise}}\right. $$
(12)

The trialing of the activation functions was necessary to develop a robust model that considers the best equation(s) for extracting features within the input data to simulate Q WL. Upon selecting the suitable G (a, b, x) and deducing weights for hidden and output layer (β), simulation of Q WL was performed by minimizing the approximation error

$$ \underset{\beta \in {R}^L}{ \min }{\left\Vert H\beta -T\right\Vert}^2 $$
(13)

where ||.|| denotes the Frobenius norm and H is the hidden layer (randomized) matrix produced by the activation function, mathematically defined viz

$$ H=\left[\begin{array}{l}h\left({x}_1^L\right)\\ {}\kern1em \vdots \\ {}h\left({x}_N^L\right)\end{array}\right]=\left[\begin{array}{l}{h}_1\left({x}_1\right)\cdots \cdots {h}_L\left({x}_1\right)\\ {}\kern1em \vdots \\ {}{h}_1\left({x}_N\right)\cdots \cdots {h}_L\left({x}_N\right)\end{array}\right] $$
(14)

Note that T is the target output matrix that in our case represents the simulated variable, y (≡ Q WL):

$$ T=\left[\begin{array}{l}{t}_1^L\\ {}\kern1em \vdots \\ {}{t}_m^L\end{array}\right]=\left[\begin{array}{l}{t}_{11}\cdots \cdots {t}_{1m}\Big)\\ {}\kern1em \vdots \\ {}{t}_{N1}\cdots \cdots {t}_{Lm}\Big)\end{array}\right] $$
(15)

Finally, the optimal solution to Eq. (13) is given by

$$ \beta *={H}^{+}T $$
(16)

where H + is the Moore–Penrose generalized inverse of the hidden layer matrix H.

Artificial neural network

In order to benchmark the performance of the ELM model, an artificial neural network (ANN) model was also developed. The ANN model is a computational paradigm composed of non-linear elements (neurons) operating in parallel and massively connected by networks characterized by different weights. A single neuron computes the sum of its inputs, adds a bias term, and drives the simulation results through a generally non-linear activation function to produce a single output termed as the activation level of the neuron. ANN models are specified by network topology, neuron characteristics, and training or learning rules (Lippman 1987) with inputs, output, and hidden layers with interconnections. The fundamental processing unit is a neuron, which computes a weighted sum of its input signals, x i , for i = 0, 1, 2. . . N, hidden layers, w ij , and then applies a non-linear activation function to produce an output signal u j (Deo and Şahin 2015a; Şahin 2012).

A neuronal model consists of an externally applied bias, b k, which has the effect of increasing or decreasing the net input of activation function depending on whether it is positive or negative. Mathematically, it is described by

$$ {y}_k=\varPhi \left({u}_k+{b}_k\right),\;\mathrm{where}\kern0.24em {U}_k={\displaystyle \sum_{j=1}^m{W}_k{X}_j} $$
(17)

where x 1, x 2, . . ., x m are the inputs signals; w k1, w k2, . . ., w km are the synaptic weights of neuron k; u k is the linear combiner output due to input signals; b k is the bias; Φ(.) is the activation function; and y k is the output signal of the neuron. Bias b k has the effect of applying an affine transformation to the output u k of the linear combiner viz

$$ {v}_k={u}_k+{b}_k $$
(18)

In particular, depending on whether the b k is positive or negative, the relationship between the induced local field or activation potential v k of neuron k and linear combiner output u k can be modified. Note that as a result of this affine transformation, the graph of v k versus u k no longer passes through the origin. The bias b k is an external parameter of artificial neuron k (Deo and Şahin 2015a; Şahin 2012).

Equivalently, combinations of Eqs. (17) and (18) may be formulated as follows (Haykin 2010)

$$ {v}_k={\displaystyle \sum_{j=0}^m{w}_{kj}{x}_j} $$
(19)
$$ {y}_k=\varPhi \left({v}_k\right) $$
(20)

The tangent sigmoid, ϕ(x), logarithmic sigmoid, ψ(x), and linear, χ(x), transfer function are described as follows (Vogl et al. 1988)

$$ \varphi (x)=\frac{2}{1+{e}^{-2x}}-1 $$
(21)
$$ \psi (x)=\frac{1}{1+{e}^{-x}} $$
(22)
$$ \chi (x)= linear(x)=x $$
(23)

Thus, Eqs. (21–23) were trialed in order to determine the best ANN model.

In this study, we have also optimized the ANN-based simulation models by utilizing a number of learning algorithms including the quasi-Newton, resilient, scaled conjugate gradient, Levenberg–Marquardt, conjugate gradient with Powell–Beale restarts, conjugate gradient with Fletcher–Reeves updates, conjugate gradient with Polak-Ribiére updates, one-step secant and the gradient descent with momentum and adaptive learning rate, following earlier studies (Deo and Şahin 2015a; Şahin 2012). Therefore, based on the lowest mean square error, the optimum ANN model with most appropriate transfer function and the best machine learning algorithm was adopted for the final simulation of the monthly Q WL.

Materials and method

Study area and model dataset

In order to develop a simulation model based on the ELM algorithm, this study has utilized eight predictor time series (plus the month as additional indicator of periodicity) where the rainfall (P) was the primary meteorological input and streamflow water level (Q WL) was the objective (or simulated) output. Figure 2 plots a geographic map of the present study site, namely Gowrie Creek (Abergowrie), Mary River (Miva Road), and Albert River (Lumeah number 2). Table 1 lists characteristics of the hydrological stations used for simulation of Q WL. Shown also are the closest meteorological stations that provided the matching P data for simulation of Q WL.

Fig. 2
figure 2

The hydrological sites from the Queensland Water Monitoring Portal (red circles) and the Australian Bureau of Meteorology's high-quality rainfall sites (blue asterisks). The approximate distance between the hydrological and meteorological stations is shown in Table 1

Full size image
Table 1 The characteristics of hydrological (streamflow) and meteorological (rainfall) stations for study sites in eastern Queensland
Full size table

The monthly values of Q WL data were acquired from the Water Monitoring Data Portal (Dept of Environment & Resource Management), http://watermonitoring.dnrm.qld.gov.au/host.htm (DNRM 2014). Since reliable monthly P time series were not available for the streamflow sites, measurements of rainfall from the closest meteorological site (Macknade Sugar Mill, 44.96 km from Gowrie Creek; Cowal 0.99 km from Mary River; Harrisville 45.89 km from Albert River) were extracted from Bureau of Meteorology website (http://www.bom.gov.au/climate/data-services/) (Haylock and Nicholls 2000). Also, despite the availability of the Q WL data from 1953 for Gowrie Creek and Albert River and from 1910 for Mary River, a number of quality control indicators had showed that the earlier period has significantly fragmented time series and, therefore, was considered unreliable.

Consequently, the monthly P data for the period 1960–2012 were used as the predictor variables for both the ELM and the ANN models. Any missing P and Q WL in this period were recovered from calendar averaged values within the monthly hydrological period. Figure 3a–c compares the monthly pattern of Q WL for Gowrie Creek, Mary River, and Albert River and the corresponding P for Macknade Sugar Mill, Cowal, and Harrisville. For all hydrological stations, there was good correspondence with their monthly cycle of rainfall. The overall trends showed generally high streamflow (and also rainfall) values from the month of January–April and lower from August–November. Also, since the P data were acquired some distance away from actual hydrological site and that the hydrological peaks can be slightly delayed compared to the rainfall cycle (Brodie et al. 2008), there was a subtle but notable lag between the peak value of Q WL and the corresponding P time series as the recharge component of rainfall may not be returned as streamflow water immediately.

Fig. 3
figure 3

The pattern of monthly cycle of streamflow, Q WL (m), and precipitation, P (mm), for the period 1960–2012. Note that the P data are from nearest meteorological station specified in Table 1

Full size image

In addition to the monthly P data used as the primary variable for simulation of the mean monthly Q WL, training datasets utilized the monthly variation in the climate mode indices (SOI, PDO, EMI, and IOD) and SSTs (Nino 3.0 5° N–5° S, 150° W–90° W; Nino 3.4 5° N–5° S, 170° W–120° W; Nino 4.0 5° N–5° S, 160° W–150° W) (Table 2). The SOI and IOD data were acquired from Australian Bureau of Meteorology (Trenberth 1984), and the PDO index was acquired from the Joint Institute of the Study of Atmosphere and Ocean (Mantua et al. 1997; Zhang et al. 1997). In its original form, the SOI was calculated by the Troup’s method using the differences in mean sea-level pressure between Tahiti and Darwin, while the PDO index was created using the UKMO Historical SST dataset for 1900–1981, Reynolds Optimally Interpolated SST (Morid et al. 2007) for January 1982–Dec 2001, and OI.v2 SST fields from January 2002 onward.

Table 2 The cross correlation coefficients (r cross) computed for input (x) and objective variable (y ≡ Q WL) at zero lag
Full size table

In this study, we employed the monthly EMI as a predictor variable, which represented the first two dominant modes of variation in the EOF analysis of SST anomalies area-averaged over (165° E–140° W, 10° S–10° N), (110° W–70° W, 15° S–5° N), and (125° E–145° E, 10° S–20° N), respectively. Data were acquired from Japanese Agency for Marine-Earth Science and Technology (https://www.jamstec.go.jp/frcgc/research/d1/iod/e/index.html). It is imperative to note that the EMI reflects coupled ocean–atmosphere interactions in the Pacific Ocean (Ashok et al. 2003, 2007; Weng et al. 2007). Several studies have shown that the EMI is prominent for identifying teleconnection pattern arising from tropical Pacific (Cai and Cowan 2009; Taschetto 2009). Therefore, considering the impacts of large-scale climate drivers and SSTs on rainfall (and streamflow) variability in Australia, the climate mode indices used in the ELM and ANN model development were considered appropriate, as they have also been employed in previous models (Abbot and Marohasy 2012; Abbot and Marohasy 2014; Deo and Şahin 2015a, b; Mekanik et al. 2013; Morid et al. 2007

Development of predictive model and performance assessment

All experiments were performed under MATLAB programming platform on a Pentium 4, 2.93GHz CPU. Table 3 details the ELM and its comparative (ANN) model used for simulation of Q WL. As a first step, the 53 years of data (1960–2012) were partitioned in two segments: one for training phase (1960–2005) where monthly rainfall, climate indices, and SSTs were used as predictor variables and the other set had testing phase (2006–2012) where the simulated Q WL was validated with site-specific measurements. The training dataset was used to develop the appropriate ELM and ANN models. After training the networks, a weight matrix was obtained for each parameter in consideration and applied to the independent input parameters in “test” set. The simulations were compared with the observed streamflow.

Table 3 The ELM and ANN models with best input combinations as per Table 2
Full size table

Crucial for any robust predictive model is the consideration of the pertinent factors such as the proper selection of input variables, training of these inputs while ensuring minimum level of over-fitting, selecting the best training algorithm and activation function, ensuring smallest generalization error, and using the best performance metrics (Maier and Dandy 2000; Maier et al. 2010; Tiwari and Adamowski 2013). Unlike previous studies that have utilized a prescribed set of predictor variables (e.g., rainfall, temperature, climate index, etc.) without a prior selection process (Deo and Şahin 2015a, b; Salcedo-Sanz et al. 2015), in this study, we have deduced the input signal(s) by the correlation with Q WL in order to develop a robust model.

As there is no “rule of thumb” to determine significant inputs (Adamowski 2008; Tiwari and Adamowski 2013), the input signal patterns were analyzed by correlation statistics using a cross correlation function (Adamowski et al. 2012). The cross correlation function measured the statistical similarity between inputs (x) and shifted (lagged) copies of Q WL as a function of lag. For a discrete signal, correlation of time series, x i = (x 1, x 2… x M − 1) and y = (y 1, y 2… y N − 1), is

$$ {\varphi}_{xy,k}={\displaystyle \sum_{j= \max \left(0,k\right)}^{\min \left(M-1+k,N-1\right)}{x}_{j-k},\kern1em k=-\left(M+1\right),\dots, 0,\dots, \left(N-1\right)} $$
(24)

and the normalized correlation coefficient, r cross, is defined as

$$ {r}_{\mathrm{cross}}(t)=\frac{\varphi_{xy}(t)}{\sqrt{\varphi_{xx}(0)\kern1em {\varphi}_{yy}(0)}} $$
(25)

such that the quantity r cross(t) will vary between −1 and 1. A value r cross(t) = 1 indicates that at alignment t, the two time series have the same exact shape (although amplitudes may be different) while −1 indicates the same shape with opposite sign. However, when r cross(t) = 0, the two signals are uncorrelated but if r cross(t) ≥0.70, a good match is evident between x (inputs) and y (Q WL).

Subsequently, a set of input combinations were deduced by analyzing r cross of each variable with Q WL. Figure 4 plots correlogram of Q WL with inputs (i.e., rainfall, SSTs, and climate indices). In this plot, the statistically significant r cross at 95 % confidence levels is located outside the blue lines. Evidently, the level of correlation of the P data with Q WL acquired the highest magnitude for all stations at zero lag (r cross ≈ 0.306–0.718) which was also statistically significant (Table 2) (note that the cross correlation of streamflow with inputs was also significant at various other lags; however, in this study, only the zero lag has been used as the r cross attained the highest magnitude). Except for the EMI and SOI which had statistically significant r cross from (−0.237) to (−0.328) and (0.241 to 0.277), respectively, for all three stations, cross correlation of Q WL with the other input variables varied quite significantly. That is, for Gowrie Creek, a statistically significant value of r cross ≈ 0.341 was obtained for Q WL with Nino 3.0 SST, but a very low statistically insignificant value was obtained for Albert and Mary River. Furthermore, Nino 3.4 SST correlated well with Q WL for Mary River (r cross ≈ −0.201), but it was poorly correlated with streamflow measurements for Gowrie Creek and Albert River. For the PDO and IOD indices, the correlation with Q WL was statistically significant only for Albert Creek station (r cross ≈ 0.134–0.174) (Table 2).

Fig. 4
figure 4

A set of correlogram of streamflow water levels (Q WL) and its predictor variable as the rainfall (P), sea surface temperatures (Nino 3.0 SST, Nino 3.4 SST; Nino 4.0 SST), Southern Oscillation Index (SOI), Pacific Decadal Oscillation Index (PDO), Indian Ocean Dipole (IOD), and ENSO Modoki Index (EMI). a Albert River, b Gowrie Creek, and c Mary River. Statistically significant cross correlation coefficients (r cross) at 95 % confidence level are outside the blue lines

Full size image

Taken together, discernible differences in cross correlations of streamflow with prescribed inputs showed the significance of selecting input combinations rather than using all variables. Consequently, in this study, three sets of ELM models were developed: (1) an optimum model with unique combinations of inputs (x) where x = [month, P, Nino 3.0 SST, Nino 4.0 SST, SOI, EMI] for Gowrie Creek station, x = [month, P, SOI, PDO, IOD, EMI] for Albert River station, and x = [month, P, Nino 3.4 SST, Nino 4.0 SST, SOI, EMI] for Mary River station, (2) trial ELM model 1 with the month and rainfall as inputs, and (3) trial ELM model 2 nine input variables. The latter were utilized to check the response of ELM algorithm for simulating streamflow when no feature selection process was incorporated. It is also imperative to note that a follow-up study could incorporate appropriate lagged signals with statistically significant cross correlations.

A three-layer neuron arrangement with input space (where input variables were fed in), learning space (where activation or transfer functions were applied to formulate the best neuronal arrangements with lowest mean square error), and output space (where streamflow was simulated as objective variable) was designed. Table 3 provides details of the ELM and ANN models. For both cases, the maximum number of input neurons (x) was 9 (denoted as x 1, x 2, x 3 …, x 9), where one neuron was assigned for month (to account for periodicity), one neuron for meteorological inputs (rainfall), four neurons for climate indices (SOI, IOD, EMI, and PDO), and remainder three neurons for sea surface temperatures (Nino SSTs). In the learning space, the activation functions defined by Eqs.(7–12) were applied to simulate the Q WL based on the sine, log-sigmoid, hyperbolic tangent sigmoid, radial bias, triangular bias, hyperbolic tangent sigmoid, and the hard-limit equations.

In each trial, the number of nodes in hidden layer was increased gradually by an interval of five with different activation functions tried (Eq. (7–12)) and subsequent adjustments of the model’s parameters were performed to deduce the optimum ELM architecture (Table 3). Then, the nearly optimal node determined by lowest mean square error, which was intrinsically disparate for each site, was adopted. For ANN model, two sets of simulations were performed: (1) with optimum combination of predictor variables and (2) with the month and rainfall as the prescribed inputs. The simulations were compared with an equivalent ELM model. The tuning of hidden layer for the ANN model was performed using 5 to 50 neurons with different machine learning algorithms. Table 3 shows the architecture of ELM and ANN models used for simulation of monthly streamflow.

Based on simulated and observed Q WL, model performance was assessed using mean absolute error (MAE), coefficient of determination (R 2) (Paulescu et al. 2011; Ulgen and Hepbasli 2002), Willmott’s Index (d) (Acharya et al. 2013; Willmott 1981; Willmott 1982), and the Nash–Sutcliffe coefficient (E) (Krause et al. 2005; Nash and Sutcliffe 1970) viz the following mathematical equations:

$$ \mathrm{M}\mathrm{A}\mathrm{E}=\frac{1}{N}{\displaystyle \sum_{i=1}^n\left|{\left({Q}_{{{\mathrm{WL}}_{\mathrm{pred}}}_{\mathrm{i}}}-{Q}_{{{\mathrm{WL}}_{\mathrm{obs}}}_{\mathrm{i}}}\right)}_t\right|} $$
(26)
$$ {R}^2={\left(\frac{{\displaystyle \sum_{i=1}^n\left({Q}_{{\mathrm{WL}}_{\mathrm{obs},\mathrm{i}}}-{\overset{\_\_}{Q}}_{{\mathrm{WL}}_{\mathrm{obs}}}\right)\left({Q}_{{\mathrm{WL}}_{\mathrm{pred},\mathrm{i}}}-{\overset{\_\_}{Q}}_{{\mathrm{WL}}_{\mathrm{pred}}}\right)}}{\sqrt{{\displaystyle \sum_{i=1}^n{\left({Q}_{{\mathrm{WL}}_{\mathrm{obs},\mathrm{i}}}-{\overset{\_\_}{Q}}_{{\mathrm{WL}}_{\mathrm{obs}}}\right)}^2}}\sqrt{{\displaystyle \sum_{i=1}^n{\left({Q}_{{\mathrm{WL}}_{\mathrm{pred},\mathrm{i}}}-{\overset{\_\_}{Q}}_{{\mathrm{WL}}_{\mathrm{pred}}}\right)}^2}}}\right)}^2 $$
(27)
$$ d=1-\left[\frac{{\displaystyle \sum_{i=1}^N{\left({Q}_{{\mathrm{WL}}_{\mathrm{obs},\mathrm{i}}}-{Q}_{{\mathrm{WL}}_{\mathrm{pred},\mathrm{i}}}\right)}^2}}{{\displaystyle \sum_{i=1}^N{\left(\left|{Q^{\hbox{'}}}_{{\mathrm{WL}}_{\mathrm{pred},\mathrm{i}}}-{\overset{\_\_}{Q}}_{{\mathrm{WL}}_{\mathrm{obs}}}\right|-\left|{Q^{\hbox{'}}}_{{\mathrm{WL}}_{\mathrm{obs},\mathrm{i}}}-{\overset{\_\_}{Q}}_{{\mathrm{WL}}_{\mathrm{obs}}}\right|\right)}^2}}\right],\kern0.5em 0\le d\le 1 $$
(28)
$$ E=1-\left[\frac{{\displaystyle \sum_{i=1}^N{\left({Q}_{{\mathrm{WL}}_{\mathrm{obs},\mathrm{i}}}-{Q}_{{\mathrm{WL}}_{\mathrm{pred},\mathrm{i}}}\right)}^2}}{{\displaystyle \sum_{i=1}^N{\left({Q}_{{\mathrm{WL}}_{\mathrm{obs},\mathrm{i}}}-{\overset{\_\_}{Q}}_{{\mathrm{WL}}_{\mathrm{obs}}}\right)}^2}}\right],\kern0.5em 0\le E\le 1 $$
(29)

where \( {Q}_{{{\mathrm{WL}}_{\mathrm{p}}}_{\mathrm{i}}} \) and \( {Q}_{{{\mathrm{WL}}_{\mathrm{o}}}_{\mathrm{i}}} \) were the ith monthly value of simulated and observed Q WL in the test period t, respectively, i is the month of the test data, \( {\overset{\_}{Q}}_{{\mathrm{WL}}_{\mathrm{obs}}} \) and \( {\overset{\_}{Q}}_{{\mathrm{WL}}_{\mathrm{p}}} \) are the overall mean parameters, and N (=84) is the length (number of samples in the test set) for period t (2006 to 2012).

Results and discussion

The relationship between simulation and observed streamflow water levels obtained from the ELM and ANN models with optimum input combinations (Fig. 4; Tables 2 and 3) is shown in Fig. 5a. Also shown are the simulation results for trial ELM model using month and rainfall as the predictor dataset (Fig. 5b). Undoubtedly, the predictive ability of the ELM and the ANN models varied greatly between the different stations and the input combinations used to simulate the monthly Q WL. In fact, for all three stations considered, the ELM model appeared to be accurate than the ANN model since its level of scatter was the lowest. However, when optimum input combinations for each station (Table 3) were used, the degree of scatter was lower for both the ELM and ANN models compared to the simulations when only rainfall and corresponding month were inputted into the model.

Fig. 5
figure 5

A scatter plot of simulated and observed streamflow (Q WL) in test period (2006–2012) with best fit line of the form Q pred = mQ obs + C. a Optimum ELM model with best input combinations specified in Table 3. b Trial ELM model with rainfall (P) and corresponding month as input variables

Full size image

Among the three stations tested, the simulation for Mary River for both input cases was the best whereas simulations for Gowrie Creek were the least accurate. Interestingly, when only the rainfall and the month were considered as inputs for Albert River site (Fig. 5b), the scatterplot appeared to be consistently shifted to higher simulated Q WL for ELM model. Although the actual cause of this is currently unclear, the lesser scatter for the ELM model showed its better performance even with less number of predictor datum points.

In order to check the performance of the ELM model with nine input variables, Fig. 6 shows the simulated and observed mean streamflow water levels for the trial ELM model. The square of the correlation coefficient (R 2) and the best-fit equations are shown for each station. Also, Table 4 lists the statistical metrics of regression analysis performed between predicted streamflow (Q WL pred) and observed streamflow (Q WL obs) by ELM and ANN models, assessed by a simple regression equation, Q WL pred = mQ WL obs + C. Note that regression coefficient (r) and maximum deviation (maxDev) of simulations from observed index with gradient (m) of linear regression plot, regression coefficient (r), and the y-intercept (C) are included.

Fig. 6
figure 6

A scatter plot of simulated and observed mean streamflow (Q WL) for the trial ELM model with all nine inputs, x = [month; P; Nino 3.0 SST; Nino 3.4 SST; Nino 4.0 SST; SOI; PDO; IOD; EMI] in test period (2006–2012). For each station, the square of correlation coefficient (R 2) and best-fit equation have been shown

Full size image
Table 4 Statistical metrics of regression analysis for simulated (Q WL pred) and observed streamflow (Q WL obs) based on regression equation: Q WL pred = mQ WL obs + C
Full size table

Comparing Fig. 6 with Fig. 5, it was noticeable that the inclusion of irrelevant input variables seems to deteriorate the performance of the ELM model. For example, for the case of Gowrie Creek, the gradient and correlation coefficients were 0.969 and 0.964, respectively, for the optimum model with six inputs, but with the inclusion of nine inputs in the trial ELM model, there was a reduction in m and r by about 19.3 and 24.1 %, respectively. Likewise, the y-intercept (whose ideal zero value is expected to show the best fit of observed and simulated water levels) increased from 0.003 to 0.203 when all nine inputs were incorporated into the trial ELM model. Likewise, the maximum deviation increased from 0.188 to 0.523. However, it was imperative to note that the trial ELM model with only rainfall and the corresponding month yielded better results compared to the trial ELM model with all nine input variables.

According to the results of Fig. 6 and Table 4, the inclusion of irrelevant inputs into the ELM model inadvertently deteriorated the accuracy of the simulated Q WL. Also, based on the scatterplot, it was evident that the optimum ELM model simulations for Mary River yielded the best results (with m ≈ 0.979 and r ≈ 0.990). However, simulations by the optimum ANN model provided the best results for Albert River (m ≈ 0.936, r ≈ 0.830) followed by Mary River (m ≈ 0.917, r ≈ 0.892) and the worst for Gowrie Creek (m ≈ 0.729, r ≈ 0.732). Notwithstanding this, the performance indicators remained smaller in magnitude compared those of the optimum ELM model (Table 4), thus demonstrating the superiority of the ELM over ANN model for monthly streamflow simulation.

In addition to inspecting the visual agreement between simulated and observed Q WL, it was important to assess the actual model prediction error (PE) for each month where the quantity PE = Q WL pred − Q WL obs was calculated over the test period. Figure 7 shows the absolute value of PE for the optimum ELM model. For comparison, the results of the optimum ANN model were also included. There was unambiguous evidence that the simulated value of Q WL was in much better agreement with the observed values of Q WL for the optimum ELM model, as this model yielded much smaller error values compared to the optimum ANN model. For all three stations, the performance of the ELM model outweighed the performance of the ANN, as it resulted in significantly large values of PE.

Fig. 7
figure 7

The prediction error (PE = Q WL pred–Q WL obs) using optimum ELM model shown as the difference between observed (Q WL obs) and simulated streamflow (Q WL pred) for a Gowrie Creek, b Albert River, and c Mary River in test period (2006–2012)

Full size image

In Table 5, we assess the overall model PE, standard deviation (σ), and the number of datum points within the ± (0–1)σ, ± (1–2)σ, ± (2–3)σ, and >±3.0σ for the optimum ELM and ANN models. Indeed, the metrics showed that for all stations considered, the optimum ELM model was more accurate with |PE| ≈ 0.0278–0.0793 compared to the optimum ANN model with |PE| ≈ 0.0489–0.2493. It was also noteworthy that the range of standard deviations for the ELM model simulations was smaller (σ ≈ 0.0218–0.0725) relative to the larger range of 0.0407–0.2381 (for the ANN model). This suggested that the optimum ELM model was not only more accurate but also stable and, therefore, exhibited lower fluctuations in the simulated value of Q WL. Another interesting observation can be made by checking the number of error values within the ± (0–1), ± (1–2), ± (2–3), and ± (>) 3 standard deviations. When the PE was considered within ± (>) 3σ, a maximum of 1 datum point was located within this error range for the ELM model whereas for the ANN model, up to 3 data points within the test period had model errors located within ± (>) 3σ. Consequently, this also concurs with the deduction that the optimum ELM model was highly accurate compared to the optimum ANN model.

Table 5 An assessment of model prediction error, |PE|, standard deviation, σ, and number of datum points in ± (0–1)σ, ± (1–2)σ, ± (2–3)σ, and >±3.0σ for optimum models
Full size table

In Table 6, we show the model performance metrics defined by Eqs. (17–20) computed within the test period (2006–2012). Note that performance metrics for the optimum ELM model with six best input combinations, trial ELM models with only rainfall and month as input variable, and the trial ELM model with all nine inputs have been shown. For comparison purposes, the optimum ANN (best inputs) and trial ANN model (all nine inputs) results have also been tabulated. In interpreting these performance metrics, one must be mindful that the magnitude of MAE for the best model is expected to be as small as possible in order to demonstrate that the simulated streamflow exhibits the lowest deviation from the observed values. As MAE is considered to be less sensitive to extreme values in the simulated data than the root mean square error (Fox 1981), we have ignored the latter metric in our analysis. Also, for best model with most reliable simulations, the magnitude of R 2 which was determined from a scatter plot of observed and simulated Q WL is expected to be close to unity, and d and E should be unity for a perfect fit (Krause et al. 2005). In model assessment, a disadvantage of the R 2 and E NS arises from the fact that the differences of observed and predicted streamflow parameters use the squared values. Consequently, large errors in time series can be overestimated whereas small values can be neglected (Legates and McCabe 1999). This insensitivity was overcome using Willmott’s Index, d (Willmott 1981). where the ratio of mean square error and potential error was considered for ELM model assessment instead of the squared differences between simulated and observed parameters (Willmott 1984).

Table 6 The model performance based on coefficient of determination (R 2), Willmott’s Index (d), Nash–Sutcliffe coefficient (E NS), peak percentage deviation (P dv), and mean absolute error (MAE) in the test period (2006–2012)
Full size table

The statistical metrics (Table 6) provided undisputed evidence that the optimum ELM was highly accurate compared to the optimum ANN model. In comparison with the ANN model, the ELM model yielded correlation statistics that were very high (R 2 ≈ 0.957–0.994) and so were the magnitudes of Willmott’s Index and Nash–Sutcliffe efficiency (d ≈ 0.968–0.986 and E NS ≈ 0.955–0.989). Importantly, the peak percentage deviation for the ELM model was also quite low (P dv ≈ −0.091–1.993) compared to P dv ≈ −0.254–18.080 for the ANN model. This showed that the ELM model generated much reliable results compared to the ANN, which also concurred emphatically with relatively lower magnitudes of the MAE for the former model.

In terms of the simulation of Q WL from the trial models with only rainfall and month as inputs, the ELM yielded better results than the ANN, albeit its overall performance was worse compared to the optimum ELM with selected inputs. For example, simulations for the trial ELM model with rainfall and month as input yielded R 2 that was lower by 18.98 % (Gowrie Creek), 28.42 % (Albert River), and 8.08 % (Mary River), and the magnitudes of d were by 17.15, 44.18, and 11.77 %, respectively. Likewise, the peak percentage deviation and MAE values were significantly higher when trial ELM model was simulated with only rainfall and month as the input variable. Similar observations were made when the ELM model was executed with all nine inputs rather than the selected optimum input combinations.

It was noteworthy that for all models tested, the overall simulation accuracy over the test period represented by Eqs. (18–20) had better performance for Mary River compared to the other two stations, although PE represented by Eq. (17) was higher. That is, for Mary River, the r 2, d, and E NS registered approximately 0.990, 0.986, and 0.989, respectively, but the MAE was 0.079 m (optimum ELM) compared to 0.964, 0.968, and 0.963 (Gowrie Creek) and 0.957, 0.962, and 0.955 (Albert River). This was also confirmed by simulations obtained from the optimum ANN as well as the trial ELM and ANN models. As confirmed later (Figs. 8 and 9), the distribution of simulated Q WL was closer to the observed and the magnitude of statistically significant cross correlation coefficients was larger for Mary River (Table 2; Fig. 4). Taken together, it is conclusive that among the other stations, simulations for Mary River were more accurate than Gowrie Creek and Albert River. This was perhaps attributable to the closer distance (which was <0.99 km) of rainfall station (Cowal) to the (hydrological) station (Mary River) where simulations were performed. By contrast, rainfall stations used for Gowrie Creek and Albert River were inadvertently 45 km away (Table 1) and, therefore, were unresponsive to changes in hydrological flow. It was perhaps this reason, and others, that the simulations for Mary River yielded the best agreement with observed Q WL.

Fig. 8
figure 8

Boxplot of distributions of predicted (Q obs) and simulation streamflow (Q pred) for a Gowrie Creek, b Albert River, and c Mary River. Whiskers are used to show extremities of predicted and observed flow properties

Full size image
Fig. 9
figure 9

A histogram of relative frequency of absolute prediction error (PE) (m) in error bracket for the optimum ELM model compared with the trial ELM model with month and rainfall (P) as inputs for a Gowrie Creek, b Albert River, and c, d Mary River. The numbers on each bar show the actual count of months in test period

Full size image

A boxplot with the distribution of simulated and observed streamflow in the prescribed test period is shown in Fig. 8. Note that the whiskers in boxplot were used to show the extremities of predicted and observed streamflow properties using their respective quartile values where the lower end of each boxplot was at the lower quartile, p 25 (25th percentile), and upper end for the upper quartile, p 75 (75th percentile), and the second quartile, p 50 (50th percentile), was the median. Two horizontal whiskers were extended from the top and bottom of the box, where the bottom whisker extends from p 25 to the smallest non-outlier in the dataset, whereas the other one goes from p 75 to the largest non-outlier. Table 6 summarizes the statistical properties for simulated and observed streamflow.

According to Fig. 8, the distribution of simulated streamflow was close to the observed values for all three stations when the optimum ELM model was utilized. This confirmed that the ELM model was more accurate in simulating the monthly Q WL. However, when the optimum ANN model was used, there was a very significant discrepancy between the distribution of Q WL pred and Q WL obs especially for Gowrie Creek. Quite clearly, the extreme values of streamflow were poorly represented in the ANN simulation model for this site. In fact, the simulated Q WL pred was highly underpredicted as most of the simulated values were lower than the observed. For the case of Albert River, the optimum ANN model was more responsive and, therefore, yielded more accurate simulations despite the presence of a notable outlier in Q WL pred. The most accurate streamflow simulations were obtained for Mary River both by optimum ELM and ANN models.

In order to inspect the model simulation skill more closely, the differences in distribution of error statistics in terms of maximum, minimum, lower quartile (Q 25), median (Q 50), upper quartile (Q 75), range, skewness, and flatness of streamflow for the optimum ELM and the optimum ANN models are shown in Table 7. Also shown are the error statistics of the trial ELM and trial ANN models with month and rainfall as the input variables. Again, these statistics confirmed more accurate simulations for the ELM compared to the ANN model for both the optimum and the dual input (rainfall and month) case. In terms of the maximum simulated and observed streamflow, the optimum ELM model yielded a value of 0.16 m whereas the optimum ANN model had 0.57 m for Gowrie Creek. Likewise, for Albert River, the optimum ELM model generated a difference of 0.07 m whereas the ANN model had 0.18 m, and for Mary River, it was 0.39 versus 1.13 m. Similar deduction was made when the minimum, lower quartile, median, upper quartile, and the range of simulated and observed Q WL were analyzed for the optimum ELM and ANN models, as well as the trial ELM and ANN models. This demonstrated the efficacy of the ELM model for reliable simulation of extreme values of streamflow compared to the ANN model.

Table 7 Difference in distribution of error statistics in terms of maximum, minimum, lower quartile (Q 25), median (Q 50), upper quartile (Q 75), range, skewness, and flatness of streamflow in the test period
Full size table

Figure 9 shows a histogram of the relative frequency of prediction error (PE) in various error brackets for the optimum ELM compared to the trial ELM model with only month and rainfall (P) as the inputs. Also shown are numbers on each bar representing the actual percentage values for the particular error bin. When the results for the optimum ELM model (left) were considered, almost 44 % of simulations were in ±0.05-m bin width (Gowrie Creek) whereas that for Albert River was 71 % and Mary River was 37 %. This confirmed that the optimum ELM model yielded the most simulation of streamflow for Albert River, which was also consistent with earlier results (Figs. 5 and 6). It was also noticeable that the next error bin (± (0.05–0.10) m) was only 12 % and (± (0.10–0.15) m) was only 1 % compared to about 28 and 11 % (Gowrie Creek) and 24 and 11 % (Mary River), respectively.

Based on this analysis, it is axiomatic to conclude that ELM model simulations for Albert River generated the smaller PE when compared with the other two stations. In fact, a closer assessment showed that for the case of Mary River, the optimum ELM model yielded relatively small yet notable error values in larger error bins (cumulative frequency was approximately 5.0 % for error of ± (0.2–0.4) m)), which concurred with earlier the results (Fig. 7c). It is therefore conclusive that the trial ELM model with only the month and rainfall as input variables was more inaccurate compared to the optimum ELM model (Figs. 8 and 9, right).

For all stations considered, the frequency distribution of model simulation errors for trial models (with unselected inputs and with only rainfall and month as input) was inherently located in larger error bins compared to the optimum ELM model where errors were concentrated in smaller bin. This was also the true for the comparative trial ANN model with nine inputs (not shown here). Therefore, an ostensible deduction is made: that streamflow modeling requires selection of the most relevant input variables by a careful and robust assessment of statistical dependence of input(s) and target (objective) variable (Table 2; Fig. 4). This is necessary for accurate modeling since relationship between inputs and outputs needs to be better identified and irrelevant variables whose features are not useful for the simulation of the objective variable are eliminated (Tiwari and Adamowski 2013). Consequently, proper selection of variables tends to achieve better simulation accuracy compared to models with no selection of variables, as was evident for the case of trial ELM and ANN models developed in this study.

Summary and conclusion

In the twenty-first century where environmental challenges are exacerbated by the underlying consequences of climate shift, the appraisal of streamflow using efficient models as a useful stratagem for applications in environmental monitoring, adaptive water resources planning, sustainable agriculture, and ecosystem management. In this study, we exemplified the utility of ELM model for simulating streamflow in eastern Queensland and results were validated with the ANN model. In order to develop the ELM model, hydrological data were utilized for Gowrie Creek (18.44° S; 145.85° E), Albert (28.05° S; 153.05° E), and Mary River (25.95° S; 152.49° E) for the period 1960–2012. The rainfall data were acquired from weather stations, namely Macknade Sugar Mill (18.58° S; 146.25° E), Harrisville Post Office (27.81° S; 152.67° E), and Cowal (25.95° S; 152.50° E) with climate indices (SOI, PDO, IOD, EMI), and SST (Nino 3.4 SST, Nino 3.4 SST, and Nino 4.0 SST). In order to determine significant inputs, cross correlation of streamflow with input series was performed.

Based on the statistically significant correlations (r cross), three sets of models were developed that included a trial ELM model with month (to consider periodicity) and eight input variables, a trial ELM model with only month and rainfall as input, and an optimum ELM model with selection of best inputs for each station. All predictive models were trained using data for the period 1960–2005, tested over 2006–2012, and the model’s performance was assessed using statistical measures to verify its ability to simulate the streamflow. The findings are enumerated as follows.

  • A cross correlation analysis of observed streamflow with each of the eight inputs revealed a statistically significant dependence on rainfall (r cross ≈ 0.306–0.718), SOI (r cross ≈ 0.141–0.215), and EMI (r cross ≈ −0.237 to −0.314) for all stations. However, cross correlation of streamflow with time series of PDO, EMI, IOD, and SSTs was different for different hydrological stations.

  • For ELM model, trial and error experiments were performed using activation functions (sigmoid, sine, hard-limit, triangular basis, radial basis, logarithmic sigmoid, and tangent sigmoid functions) and randomly assigned weights and incrementally varying hidden neurons (2 to 150). Therefore, the optimum ELM was designed with hard-limit activation equation and neuronal architecture of 6-106-1 (Gowrie Creek), 6-74-1 (Albert River), and 6-146-1 (Mary River) corresponding to its input–hidden–output arrangements.

  • The comparative ANN model was trialed using tangent and logarithmic sigmoid transfer functions with several learning algorithms. This resulted in best ANN model with Levenberg–Marquardt algorithm and a neuronal architecture of 6-28-1 (Gowrie Creek), 6-18-1 (Albert River), and 6-20-1 (Mary River).

  • For all stations considered for simulation of mean monthly streamflow, the optimum ELM outperformed the ANN model. For Gowrie Creek, performance metrics yielded a value of R 2 ≈ 0.964, d ≈ 0.968, and E NS ≈ 0.963 (ELM) compared to 0.732, 0.802, and 0.698 (ANN), while for Albert River, a value of R 2 ≈ 0.957, d ≈ 0.962, and E NS ≈ 0.955 (ELM) was obtained compared to 0.830, 0.863, and 0.816 (ANN). Similarly, a value of R 2 ≈ 0.990, d ≈ 0.986, and E NS ≈ 0.989 (ELM) was obtained compared to 0.892, 0.855, and 0.891 (ANN).

  • Given correlation of streamflow with rainfall for all stations, trial models using rainfall and month as inputs yielded good performance for the ELM compared to the ANN model. However, simulation accuracy of both models was worse compared to the optimum models with selected input. When all nine inputs were incorporated into the trial ELM model without selection of variables, the performance deteriorated quite significantly.

  • An analysis of the relative frequency of simulation errors in different error brackets showed that the trial ELM with month and rainfall as inputs resulted in a higher frequency for the wider error brackets (>±0.10 m)) compared to the optimum ELM model that produced the highest frequency of all errors in the larger ± (0–0.05) m bracket.

Based on our findings, it is ascertained that the ELM model with selected input variables has a good ability to simulate streamflow water level and its performance is comparatively better than the ANN model. It is therefore advocated that the ELM algorithm is a useful utility for environmental monitoring where predictive modeling of parameters (e.g., streamflow) is required. Finally, the ELM-based streamflow model can be employed to implicate or analyze trends in hydrological parameters (e.g., rainfall), assessing the viability of irrigation systems, river flows, or lakes as well as sustainable use of water for agriculture and developing flood and drought response strategies.