1 Introduction

Dissolved oxygen (DO) concentration is an important water quality parameter, which consists an important indicator of water pollution in rivers (Mohan and Pavan Kumar 2016). DO is used to assess the trophic state of rivers, canals and lakes (Gikas 2014; Chamoglou et al. 2014; Mellios et al. 2015). During the last decade, much effort has been devoted to the modelling of DO in river, lake and stream ecosystems using artificial intelligence (AI) techniques, and much work has been done on this subject. Of course, and not surprisingly, regarding the capabilities and usefulness of the AI techniques, the overwhelming attention given to their application is not just luck. Motivation for using AI techniques in DO modelling has received considerable attention in the last few years and an in-depth literature review suggests that the following four types of AI techniques have been broadly applied on the subject:

  1. 1.

    Artificial neural networks based approach (ANNs): generally, there are the following three types of ANNs that are widely used in modelling DO: (i) generalized regression neural network (GRNN) (Heddam 2014a; Antanasijević et al. 2013, 2014); (ii) radial basis function neural network (RBFNN) (Akkoyunlu et al. 2011; Ay and Kisi 2012; Emamgholizadeh et al. 2014); and (iii) multilayer perceptron neural network (MLPNN) (Ranković et al. 2010; Areerachakul et al. 2013).

  2. 2.

    Fuzzy logic and neurofuzzy system: generally, the famous adaptive neuro-fuzzy inference system (ANFIS) is the broadly reported model in modelling DO (Heddam 2014b; Nemati et al. 2015).

  3. 3.

    Evolutionary models: generally, gene expression programming (GEP) (Kisi et al. 2013), dynamic evolving neural-fuzzy inference system (DENFIS) (Heddam 2014c), Particle Swarm Optimization (PSO) (Liu et al. 2014), and genetic algorithm (GA) (Liu et al. 2013) are the widely used models.

  4. 4.

    Wavelet decomposition models (Evrendilek and Karakaya 2014, 2015).

Although the already developed models for estimating DO have shown good precision and accuracy, and they offer a good alternative in the absence of direct in situ measurements, these models suffer from a number of shortcomings and limitations. First, the models are linked to the water quality variables which already have been used in the calibration of the models; these will typically involve maintaining the input variables available regularly. Second, the models cannot be applied without timely and reliable water quality data. It would be interesting to investigate the capabilities of the AI models in forecasting DO at different level in advance using only the time series of DO and without the need for water quality variables as input to the models. Forecasting DO in river ecosystems is a relatively difficult task, since the concentration of DO varies significantly over different time periods of the day, especially between morning and evening, within the seasons, and from year to year. Hence, according to what was stated above, we can define three categories of forecasting models: short-term, medium-term and long-term forecasting models. Long-term forecasting refers to more than 5 days in advance (120 h) and refers to one of two horizons, one is 5 days in advance (120 h), the other is 7 days in advance (168 h). In medium-term forecasting, the horizon is usually three to four days in advance (72 h to 96 h). Finally, short-term forecasting involves a period of about one to two days (24 h to 48 h). Obviously, for the long-term forecasting horizon, using a long historical data set, may improve the accuracy of the developed models.

Understanding the concentration and change of DO in freshwater ecosystems is necessary and of great importance. DO varies depending on many factors, including salinity, temperature and pressure (USGS 2008). These factors can be classified as follows (Cox 2003a, 2003b): (i) reaeration from the atmosphere; (ii) enhanced aeration at weirs and other structures; (iii) photosynthetic oxygen production; and (iv) the introduction of DO from other sources such as tributaries. The primary causes of DO depletion are: (i) the oxidation of organic material in the water column; (ii) degassing of oxygen in supersaturated water; (iii) respiration by aquatic plants; (iv) oxygen demand exerted by river bed sediments (Cox 2003a, 2003b). Low levels of DO in the water are accompanied by hypoxia (HY) and anoxia (AX) (Nürnberg 2004). Anoxia is defined as a condition of zero (a total loss of DO) or very low DO concentrations, while hypoxia is defined as a condition of low DO. Seasonal hypoxia, and eventual anoxia, can be caused by high anthropogenic nutrient loadings (Breitburg et al. 2003). Hypoxia profoundly affects ecosystem functioning, with strong implications for all ecosystem components, i.e., biodiversity, biological and cause physiological stress, and even death, to associated aquatic organisms, which indicate a stressed environment (Friedrich et al. 2014). Regarding the importance of the HY and AX processes, it will be very interesting to develop a model that will be used as an early warning system, and will have the ability to deliver more accurate and time sensitive information during stress events.

Few studies have attempted to develop forecasting models for DO time series without the need of using the water quality variable as input to the models. Alizadeh and Kavianpour (2015) compared two ANNs models, the standard MLPNN and wavelet-neural network (WNN), in forecasting DO at hourly and daily time steps, at the Hilo Bay on the east side of the Big Island of Hawaii, Pacific Ocean. DO at different time lags were considered as input variables for the MLPNN and WNN models. They have tested four forecasting models having different input combinations: DO(t-1), DO(t-2), DO(t-3) and DO(t-4). The models developed had only one output: the DO at (t + 1). The t corresponds to the DO at the present time (day or hour), and the (t-1) until (t-4) correspond to the four previous values of DO. As a result of the study, for the models at daily time step, they have obtained a correlation coefficient (R) of 0.66 and 0.72 for the models having two inputs (i.e., (t-1) and (t-2)) and the models having four inputs (i.e., (t-1), (t-2), (t-3) and (t-4)), respectively. At hourly time step, the authors reported excellent results with an R of 0.94 in the validation phase. An et al. (2015) proposed a new forecasting model using the nonlinear grey Bernoulli model (NGBM (1, 1)) in forecasting DO in the Guanting reservoir (inlet and outlet), located at the upper reaches of the Yongding River in northwest Beijing, China. The authors used DO at weekly time step. Altunkaynak et al. (2005) examined the potential of fuzzy logic-based model (FL) to forecast monthly DO in the Golden Horn in Istanbul, Turkey. The authors have used two inputs (i.e., DO(t-1) and DO(t-2)) and one output (DO(t)). As a result of the study, it was seen that one can forecast the next month’s DO concentration from antecedent measurements within acceptable relative error limits. Wang et al. (2013) compared the bootstrapped wavelet neural network (BWNN) as a new tool in forecasting monthly DO in Harbin, China. The proposed BWN model has been compared with the standard MLPNN and the wavelet neural network models (WNN). They have compared three types of models: using only DO(t-1) as input; using only DO(t-3) as input and using DO(t-1) and DO(t-3) as inputs. In all three developed models the output was the DO(t). As a result of the study the authors reported a high Nash-Sutcliffe efficiency (NSE) value equal to 0.85 in the validation phase. Faruk (2010) applied the MLPNN in forecasting monthly DO time series using the data for the period between 1996 and 2004 from the Büyük Menderes basin, Turkey, and has obtained a NSE coefficient equal to 0.91.

As indicated above, a literature review demonstrates that modelling DO is broadly discussed and several kinds of models have been developed worldwide. However, few studies have been devoted to forecasting DO and many more are needed. In the previous forecasting studies, we can report the following drawbacks: (i) the time-step chosen is often constrained by the availability of DO data, and the majority of the models use data at monthly, weekly or infrequently daily time step, which is not really efficient as the amount of DO varies rapidly; (ii) in all reported models, the forecast horizon is generally the value at the next time (t + 1), and none of the studies has investigated a long term forecasting horizon. Therefore, in this paper we present the OP-ELM as a new and powerful tool in forecasting hourly dissolved oxygen concentration (DO) several hours in advance. The proposed model is compared to the standard MLPNN in order to demonstrate its superiority and usefulness. We test this new model with data from the Klamath River at Miller Island Boat Ramp, Oregon, USA, to illustrate how the proposed model can forecast DO very well. To the author’s knowledge, DO forecasting with OP-ELM is the first study in the literature. Therefore, the present study investigates the use of OP-ELM in the development of a robust model for DO forecasting.

2 Materials and Methods

2.1 Study Area and Data Set

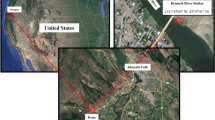
Historical hourly DO data from 1 January 2004 to 31 December 2013 were used in this study; they are available at the United States Geological Survey (USGS) website: http://or.water.usgs.gov/cgi-bin/grapher/table_setup.pl?site_id. Two stations were chosen: at Klamath, River Miller Island Boat Ramp, Oregon USA [Top] (USGS ID: 420,853,121,505,500; Latitude 42°08′53″N; Longitude 121°50′55″E; NAD83); and at Klamath, River Miller Island Boat Ramp, Oregon USA [Bottom] (USGS ID:420,853,121,505,501). Figure 1 shows the locations of the stations. For the two stations, the data set was divided into two sub-data sets: (i) training set (70 %); and (ii) validation set (30 %). Hence, the first seven years (2004 to 2010) were chosen for training and the last three years (2011–2013) for validation. Data were stored in a table, in which each row corresponded to one hour (one pattern) and contained a measured DO value. In some hours, the DO variable was not available, in which case we removed the incomplete patterns. A detailed description of the original and final patterns is reported in Table 1. From Table 1, for the top station a total of 1047 patterns were missing and for the bottom station a total of 3763 patterns were missing. Figures 2 and 3 show the plot of the DO time series for the training and validation, for the two stations. Table 2 summarizes the descriptive statistics of the data set, where Xmean, Xmax, Xmin, Sx and Cv denote the mean, the maximum, the minimum, the standard deviation, and the coefficient of variation, respectively. All the data derived were normalized to have zero mean and unit variance using the Z-score method, calculated by the following formula:

$$ {x}_{ni,k}=\frac{{\displaystyle {x}_{i,k}}-{\displaystyle {m}_k}}{{\displaystyle {Sd}_K}} $$
(1)
Fig. 1
figure 1

Map showing the study area, Klamath River at Miller Island Boat Ramp [Top and Bottom] stations, Oregon, USA. (Adopted from Sullivan et al. 2012, 2013a, 2013b)

Full size image
Table 1 Dataset presentation includes years of available data, the description of the starting and ending dates covering the period of the study, the total patterns available, the incomplete patterns removed from the table, the final patterns used, and separating the data to the subset for training and validation
Full size table
Fig. 2
figure 2

Time series plot of dissolved oxygen concentration (DO) for the USGS [Top] (420,853,121,505,500) station, covering the period of the study. Here the beginning and ending dates are in the training phase from to 01/01/2004 at 01:00 until 12/31/2010 at 24:00; and in the validation phase from to 01/01/2011 at 01:00 until 12/31/2013 at 24:00

Full size image
Fig. 3
figure 3

Time series plot of dissolved oxygen concentration (DO) for the USGS 420853121505501 [Bottom] station, covering the period of the study. Here the beginning and ending dates are in the training phase from to 01/01/2004 at 01:00 until 12/31/2010 at 24:00; and in the validation phase from to 01/01/2011 at 01:00 until 12/31/2013 at 24:00

Full size image
Table 2 Statistical parameters of data set for forecasting models
Full size table

where x ni, k is the normalized value of the variable k (input or output) for each sample i. x i , k is the original value of the variable k (input or output). m k and S dk are the mean value and standard deviation of the variable k (input or output). Normalization is an important process, which increases significantly the performance of the models (Kingston et al. 2005; Heddam et al. 2011, 2012, 2016; Heddam 2016a, 2016b).

2.2 Multilayer Perceptron Neural Network (MLPNN)

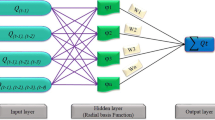
Artificial neural networks (ANNs) are an information processing system which belongs to the category of nonlinear models (Haykin 1999). ANNs are inspired from the function of the human brain. In ANNs, the neurons are tightly interconnected and organized into different layers. There are three types of layers, i.e., an input layer, one or more hidden layers, and an output layer. The layers are connected by weights (Haykin 1999). Multilayer perceptron neural network (MLPNN) (Rumelhart et al. 1986) is the most widely used type of ANNs reported in the literature, considered as a powerful tool in modeling nonlinear processes. The number of neurons contained in the input and output layers, is related to the problem that must be resolved. Each neuron in the input layer corresponds to a single variable, and the output neurons represent the solution of the problem being solved. Figure 4 presents the structure of the MLPNN models used in the present study. It consist of three layers: the input layer with six variables, denoted as x 1 to x 6 and corresponding to the DO at (t-5), (t-4), (t-3), (t-2), (t-1) and (t); the hidden layer with a number of neurons defined by trial and error; and finally, the output layer with only one neuron: the DO at (t + 24) to (t + 168), according to the model developed. The MLPNN are capable of approximating any function with a finite number of discontinuities (Hornik et al. 1989) and are considered as a universal approximator (Hornik et al. 1989; Hornik 1991). Let us denote with k the number of input variables, and m the number of neurons in the hidden layer; the mathematical structure of the MLPNN from the input to the output can be formulated as follows:

$$ {\displaystyle {A}_j}={\displaystyle {\beta}_j}+{\displaystyle \sum_{i=1}^k{\displaystyle {w}_{ij}}\times {\displaystyle {x}_i}} $$
(2)
Fig. 4
figure 4

Multilayer Perceptron Neural Network (MLPNN) structure used in forecasting dissolved oxygen concentration. The structure in this figure is valid for the two stations

Full size image

where A j is the weighted sum of the j hidden neuron, k is the total number of inputs, w ij denotes the weight characterising the connection between the n th input to the m th hidden neuron, and β j is the bias term of each hidden neuron. The output of the m th hidden neuron is given by

$$ {\displaystyle {Y}_j}=f\left({\mathrm{A}}_j\right) $$
(3)

The activation function f adopted in the present study was the sigmoid, given by Eq. (4):

$$ f(A)=\frac{1}{1+{\displaystyle {e}^{-A}}} $$
(4)

The neural network output is then given by:

$$ {\displaystyle {O}_k}={\displaystyle {\beta}_0}+{\displaystyle \sum_{j=1}^m{w}_{jk}\times {Y}_j} $$
(5)

where w jk denotes the weight characterising the connection between the m th hidden neuron to the p th output neuron, m the total number of hidden neurons, and β 0 is the bias term. A linear activation function is most commonly applied to the output layer.

During the last few years, AI techniques are largely used by scientists in developing different kind of models, and the ANNs are the most applied form of AI. Typical applications include the following, among many others: predicting the dispersion coefficient (D) in a river ecosystem (Antonopoulos et al. 2015); modelling the permeability losses in permeable reactive barriers (Santisukkasaem et al. 2015); estimating the reference evapotranspiration (ET0) in India (Adamala et al. 2015); calculating the dynamic coefficient in porous media (Das et al. 2015); predicting Indian monsoon rainfall (Azad et al. 2015); modeling of arsenic (III) removal (Mandal et al. 2015); predicting effluent biochemical oxygen demand (BOD) in a wastewater treatment plant (Heddam et al. 2016); modeling Secchi disk depth (SD) in river (Heddam 2016a); and predicting phycocyanin (PC) pigment concentration in river (Heddam 2016b).

Unsurprisingly, regarding the high capabilities of ANNs in developing environmental models, they have rapidly gained much popularity. But even with this, ANNs models are not without criticism. The performance of the ANNs models depends mainly on (Maier and Dandy 2000; Maier et al. 2010): (i) the selection of the appropriates input; (ii) data division (the best selection of the splitting ratio between training and validation); (iii) the model structure (the number of hidden neurons, number of hidden layers and the type of transfer function); (iv) model calibration; and finally (v) model evaluation using different kind of statistical metrics. Some important details about the appropriate application of the ANN models can be found in: Bowden et al. (2005a, 2005b); Maier and Dandy (2000); and Maier et al. (2010).

2.3 Optimally Pruned Extreme Learning Machine (OP-ELM)

Extreme learning machine (ELM) has been proposed by Huang et al. (2006a, 2006b) for training single hidden layer feedforward neural networks (SLFN) (Huang et al. 2015). ELM is a universal function approximator (Huang and Chen 2007, 2008). In SLFN, we have two weight matrices, from the input layer to the hidden layer (input layer weights) and from the hidden layer to the output layer (output layer weights). These two matrices must be optimized during the training process, generally using the backpropagation training algorithm. According to Huang et al. (2006a, 2006b), when using the ELM algorithm, the input layer weights do not need to be tuned iteratively and to be generated randomly; however, the output layer weights are determined analytically using least-squares method (Huang et al. 2015). The ELM algorithm is presented briefly below.

Let be N arbitrary training samples represented by (x i, y i), where x i = [x i1, x i2,…, x iD]T∈RD and [y i1, y i2,…, y iD]T∈RD. Single hidden layer feedforward neural networks with L hidden nodes and activation function f(x) are mathematically presented as (Huang et al. 2006a, 2006b):

$$ {\displaystyle \sum_{i=1}^L{\displaystyle {\beta}_i}}{\displaystyle {f}_i}\left({\displaystyle {x}_j}\right)={\displaystyle \sum_{i=1}^L{\displaystyle {\beta}_i}}{\displaystyle {f}_i}\left({w}_i\cdot {x}_j+{b}_i\right)={o}_j $$
(6)

where j = 1, 2,…, N. Here w i = [w i1, w i2,…, w iD]T is the weight vector connecting the ith hidden node and the input nodes, β i = [β i1, β i2,…, β ik]T is the weight vector connecting the ith hidden node and the output nodes, and b i is the threshold of the ith hidden node (Zeng et al. 2013). The standard SLFN with L hidden nodes with activation function f(x) can be written as:

$$ H\beta =T $$
(7)

where:

$$ H=\left[\begin{array}{ccc}\hfill {f}_1\left({w}_1\cdot {x}_1+{b}_1\right)\hfill & \hfill \cdots \hfill & \hfill {f}_L\left({w}_L\cdot {x}_1+{b}_L\right)\hfill \\ {}\hfill \vdots \hfill & \hfill \vdots \hfill & \hfill \vdots \hfill \\ {}\hfill {f}_1\left({w}_1\cdot {x}_N+{b}_1\right)\hfill & \hfill \cdots \hfill & \hfill {\displaystyle {f}_L}\left({w}_L\cdot {x}_N+{b}_L\right)\hfill \end{array}\right] $$
(8)
$$ \beta =\left[\begin{array}{c}\hfill {\beta}_1^T\hfill \\ {}\hfill \vdots \hfill \\ {}\hfill {\beta}_L^T\hfill \end{array}\right]\ \mathrm{and}\ \mathrm{T}=\left[\begin{array}{c}\hfill {t}_1^T\hfill \\ {}\hfill \vdots \hfill \\ {}\hfill {t}_L^T\hfill \end{array}\right] $$
(9)

Different from the conventional gradient-based solution of SLFN, ELM simply solves the function by:

$$ \beta ={H}^{+}T $$
(10)

where H+ is the Moore-Penrose generalized inverse of matrix H (Zeng et al. 2013). More details about ELM can be found in: Huang et al. (2006a, 2006b); Huang et al. (2011, 2015); and Huang (2015).

Since it was proposed, ELM has received much popularity and several modifications were proposed to the original algorithm. Among them, we could name: the optimally pruned extreme learning machine (OP-ELM) (Miche et al. 2008, 2010); online sequential extreme learning machine (OS-ELM) (Liang et al. 2006); Bidirectional extreme learning machine B-ELM (Yang et al. 2012); Evolutionary extreme learning machine SaDE-ELM (Cao et al. 2012); Fully Complex Extreme Learning Machine C-ELM (Li et al. 2005); and others. In the present study we focused on the famous OP-ELM.

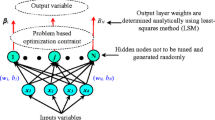
The optimally pruned extreme learning machine was developed by Miche et al. (2008, 2010). It is simply called OP-ELM (Miche et al. 2008, 2010; Sorjamaa et al. 2008), and is a modified version of the original extreme learning machines (ELM). According to Pouzols and Lendasse (2010a, 2010b), OP-ELM is designed for use for up to three different types of kernel functions, i.e., Gaussian, sigmoid and linear kernels, and the creation of an OP-ELM model occurs in three stages. Considering the fact that the original ELM suffer from an important drawback, which is the presence of irrelevant or correlated variables in the training data set, Miche et al. (2008, 2010) introduced the OP-ELM model as a good solution for pruning away irrelevant variables, thereby, further improving the reliability and efficiency of the ELM approach.

Given a training set (x i, y i), x i∈Rd1 and y i∈Rd2; OP-ELM implies three important steps (Grigorievskiy et al. 2014): (i) build a regular ELM model with initially large number of neurons; (ii) rank neurons using multiresponse sparse regression (MRSR) (Similä and Tikka 2005) or least angle regression (LARS) (Efron et al. 2004) if the output is one-dimensional; and (iii) use leave-one-out (LOO) validation to decide how many neurons to prune (Fig. 5). In the first step, a construction of a SLFN using the original ELM algorithm with a large number of neurons is made (by default one hundred neurons). It is important to note that while the ELM use only sigmoid kernels, the OP-ELM offers three possibilities of kernel types: sigmoid, Gaussian and linear (Pouzols and Lendasse 2010a, 2010b). Ranking the hidden neurons according to their accuracy is done in the second step using the MRSR algorithm. Hereafter, we present the MRSR algorithm briefly, according to Similä and Tikka (2005). Suppose that the targets are denoted by an n × p matrix T = [t 1 … t p ] and the regressors are denoted by an n × m matrix X = [x 1 … x m ]. The MRSR algorithm adds sequentially active regressors to the model:

$$ {\displaystyle {Y}^k}={XW}^k $$
(11)
Fig. 5
figure 5

The important steps in developing an OP-ELM (From Sorjamaa et al. 2008)

Full size image

such that the n × p matrix Y k = [y 1 k… y p k] models the targets T appropriately. The m × p weight matrix Wk includes k nonzero rows at the beginning of the kth step. Each step introduces a new nonzero row and, thus, a new regressor to the model. It is reported that MRSR is a variable ranking rather than selection algorithm (Pouzols and Lendasse 2010a). Finally, the third and last step in OP-ELM is the application of the leave-one-out (LOO) validation method where the decision over the actual best number of neurons for the model is taken. According to Grigorievskiy et al. (2014), using the so-called application of the PRESS (PREdiction Sum of Squares) statistic, provides an exact LOO.

Since it was proposed, OP-ELM has gained much popularity in engineering applications during the past few years. Moreno et al. (2014) compared the ELM and the OP-ELM for the classification of remote sensing hyperspectral data; Grigorievskiy et al. (2014) compared the OP-ELM with the linear model and the Least-Squares Support Vector Machines (LS-SVM) for long-term time series prediction; Akusok et al. (2015) applied the OP-ELM for the identification of the likeliest samples in a dataset to be mislabelled; and Sovilj et al. (2010) compared the OP-ELM and optimally pruned k-nearest neighbors OP-KNN for long-term time series prediction.

2.4 Model Performance Indices

In the present study, we used seven performance indices in order to evaluate performance and compare the developed models. These seven indices are: the coefficient of correlation (R) (Eq. 12) (Legates and McCabe 1999), the Willmott index of agreement (d) (Eq. 13) (Willmott 1982; Willmott et al. 1985), the Nash-Sutcliffe efficiency (NSE) (Eq. 14) (Nash and Sutcliffe 1970; Dawson and Wilby 2001), the root mean squared error (RMSE) (Eq. 15) (Chai and Draxler 2014; Dawson et al. 2002), the mean absolute error (MAE) (Eq. 16) (Dawson et al. 2002; Gebremariam et al. 2014), the bias error (Bias) (Eq. 17) (Dawson et al. 2007), and the mean absolute percentage error (MAPE) (Dawson et al. 2007) (Eq. 18):

$$ NSE=1-\frac{{\displaystyle \sum_{i=1}^N{\displaystyle {\left[{\displaystyle {O}_i}-{\displaystyle {P}_i}\right]}^2}}}{{\displaystyle \sum_{i=1}^N{\displaystyle {\left[{\displaystyle {O}_i}-{\displaystyle {O}_m}\right]}^2}}} $$
(12)
$$ d=1-\frac{{\displaystyle \sum_{i=1}^N{\displaystyle {\left({\displaystyle {P}_i}-{\displaystyle {O}_i}\right)}^2}}}{{\displaystyle \sum_{i=1}^N{\displaystyle {\left(\left|{\displaystyle {P}_i}-{\displaystyle {O}_m}\right|+\left|{\displaystyle {O}_i}-{\displaystyle {O}_m}\right|\right)}^2}}} $$
(13)
$$ R=\left[\frac{\frac{1}{N}{\displaystyle \sum \left({\displaystyle {O}_i}-{\displaystyle {O}_m}\right)\left({\displaystyle {P}_i}-{\displaystyle {P}_m}\right)}}{\sqrt{\frac{1}{N}{\displaystyle \sum_{i=1}^n{\displaystyle {\left({\displaystyle {O}_i}-{\displaystyle {O}_m}\right)}^2}}}\sqrt{\frac{1}{N}{\displaystyle \sum_{i=1}^n{\displaystyle {\left({\displaystyle {P}_i}-{\displaystyle {P}_m}\right)}^2}}}}\right] $$
(14)
$$ RMSE=\sqrt{\frac{1}{N}{\displaystyle \sum_{i=1}^N{\displaystyle {\left({\displaystyle {O}_i}-{\displaystyle {P}_i}\right)}^2}}} $$
(15)
$$ MAE=\frac{1}{N}{\displaystyle \sum_{i=1}^N\left|{\displaystyle {O}_i}-{\displaystyle {P}_i}\right|} $$
(16)
$$ Bias=\frac{1}{N}{\displaystyle \sum_{i=1}^N\left({\displaystyle {O}_i}-{\displaystyle {P}_i}\right)} $$
(17)
$$ MAP\mathrm{E}=\frac{1}{N}{\displaystyle \sum_{i=1}^N\left|\frac{{\displaystyle {O}_i}-{\displaystyle {P}_i}}{{\displaystyle {O}_i}}\right|} $$
(18)

where N is the number of data points, O i is the measured value and P i is the corresponding model prediction, and O m and P m are the average values of O i and P i . The Willmott index of agreement (d) is an indicator of model performance. It carries a value from 0 to 1, where a value of 1 indicates perfect agreement (Willmott 1982). The bias error (Bias), also reported as the mean error (ME), for a perfect match has the value zero. A bias index expresses the tendency of the model to underestimate (positive value) or overestimate (negative value). According to Dawson et al. (2007), a low value for the Bias does not necessarily indicate a good model in terms of accurate forecasts, since positive and negative errors will tend to cancel out each other; for this reason, MAE is often preferred to Bias. The Nash-Sutcliffe efficiency (NSE) is a measure of statistical association, which indicates the percentage of the observed variance that is explained by the predicted data (Nash and Sutcliffe 1970). NSE ranges between -∞ and 1, with NSE = 1 being the optimal value (Moriasi et al. 2007). The R statistic describes the degree of colinearity between the observed and predicted values. A perfect model has an R equal to 1; typically, values greater than 0.70 are considered acceptable (Moriasi et al. 2007). Both RMSE and MAE describe the difference between model simulations and observations in the units of the variable. For both, values close to zero indicate perfect fit. Some advantages of MAE over RMSE in the evaluation and comparison of model performance can be found in Willmott and Matsuura (2005). The MAPE, also called MARE (Dawson et al. 2007) or average absolute percentage error (AAPE) (Maier and Dandy 1996; Bowden et al. 2002), is one of the most widely used measures of forecast accuracy for developing models (Kim and Kim 2016; Deo et al. 2016). The MAPE has no upper bound and for a perfect match the result would be zero (Dawson et al. 2007). Although some researchers worldwide already recommend the use of the MAPE as a measure of forecast accuracy, the MAPE has some advantages and disadvantages. One of the most important disadvantages of the MAPE is that it produces infinite or undefined values for zero or close-to-zero measured (observed) values (Kim and Kim 2016), which is the case in many environmental case studies. According to Dawson et al. (2007), the MAPE is subject to “potential fouling by small numbers in the observed record”. The MAPE is susceptible to outliers and it tends to overstate forecast error (Tayman and Swanson 1999; Rayer 2007). If the observed values are very small, MAPE yields extremely large percentage errors (outliers), while zero actual values result in infinite MAPE (Kim and Kim 2016). Hence, when the observed values are close to zero, the MAPE value can explode to a huge number, and if averaged with the other values, it can give a distorted image of the magnitude of the error (Chase 2013).

In addition to all the reported seven performance indices, we also calculated the so-called RPD (Eq. 19) (ratio of standard deviation to RMSE), the scatter index (SI) (Eq. 20), also reported as the normalized objective function (NOF) (Gikas 2014), and the ratio of the mean absolute error to the standard deviation (RMAE) (Eq. 21). The RPD is an important index of model accuracy; in general, RPD values less than one are unacceptable while values greater than 3 are considered excellent (Chang et al. 2001; Ackerson et al. 2015). A value of the RMAE less than 0.5 may be considered low, acceptable and appropriate for model evaluation (Singh et al. 2004; Moriasi et al. 2007). For the scatter index (SI), a perfect model has a SI equal to 0.0 (Gikas 2014), and for values between 0.0 and 1.0, the model predictions are acceptable (Boskidis et al. 2010, 2011; Gikas et al. 2006; Pisinaras et al. 2010).

$$ RPD=\frac{S_X}{RMSE} $$
(19)
$$ SI=\frac{RMSE}{{\mathrm{O}}_m} $$
(20)
$$ RMAE=\frac{MAE}{S_X} $$
(21)

Finally, we report a comparison between measured and calculated mean and standard deviation of DO, in the training and validation phases.

3 Results and Discussion

An attempt has been made in this study to develop a robust model for forecasting DO several hours in advance, in the Klamath River, USA, using OP-ELM model. To draw robust conclusions, it is interesting to compare the results using OP-ELM with the results obtained using the standard MLPNN. We have developed six forecasting models called FM1 to FM6 using the same input data and having different outputs. The structures are shown in Table 3. The six models correspond to three different horizons: short-term (FM1 and FM2), medium-term (FM3 and FM4) and long-term forecasting horizons (FM5 and FM6). Forecasting DO time series refers to estimating the future values at different hour intervals by using a set of previous observed values. This will be interesting, as we use only the time series of DO without any other input variables. For the OP-ELM, we used the implementation available from www.cis.hut.fi/projects/tsp/index.php. In the present study, we applied the OP-ELM with all possible kernels, i.e., linear, sigmoid, and Gaussian, using a maximum number of 100 neurons (Fig. 6). For all the six models developed, the relationship among the inputs and the output can be defined by Eq. (22):

$$ DO\left(t+n\right)=f\left[ DO\left(t-5\right), DO\left(t-4\right), DO\left(t-3\right), DO\left(t-2\right), DO\left(t-1\right), DO(t)\right] $$
(22)
Table 3 Combinations of input variables considered in developing forecasting models
Full size table
Fig. 6
figure 6

Block diagram of the OP-ELM Toolbox (From Miche et al. 2008)

Full size image

For example, for model FM1, the output corresponds to DO at (t + 24), and the forecasting process is the following: with the N observations of the time series of DO at (t = 1, t = 2, t = 3, t = 4,…, t = N), using a model with n input nodes (6 inputs in our study), we have a training data composed of N-n training patterns, in which the first patterns will be composed of DO at (t = 1, 2, 3,…, n) as inputs and DO (n + 24) as the output; the second pattern will contain DO at (t = 2, 3, 4,…, n + 1) as inputs and DO (n + 25) as the output, and the last pattern will be DO (N-(n-6 + 24), N-(n-5 + 24), N-(n-4 + 24),…,N-(n-1 + 24)) as inputs and DO (N) as the output, where N is the total number of patterns. It is clear from the proposed structure that for the FM6 model that has DO at (t + 168) as output, we have a training data composed of (N-168) training patterns, in which the first patterns will be composed of DO at (t = 1, 2, 3, 4, 5,6) as inputs and DO (t = 172) as the output. This structure is valuable for the all six developed models. Therefore, all the six developed models are basically approximators of the general equation (19). In the following sections, the forecasting capabilities of the two proposed models (OP-ELM and MLPNN) are presented and compared.

3.1 Forecasting DO Concentration at the USGS 420853121505500 [Top] Station

According to the seven indices for assessing the performance of the models, the optimal model should have the lowest RMSE, MAE, MAPE and Bias, and the values of NSE, R and d should be close to 1. Table 4 displays the RMSE, MAE, MAPE, Bias, NSE, R and d model performance statistics for both the training and validation sets. The two models (OP-ELM and MLPNN) displayed the highest level of accuracy for both training and validation. For the OP-ELM model, in the training phase, the RMSE, MAE and Bias ranged from 1.081 to 1.785, 0.648 to 1.268, and 0, respectively. The NSE, R and d ranged from 0.779 to 0.919, 0.883 to 0.959, and 0.935 to 0.979, respectively. Likewise, for MLPNN, the RMSE, MAE and Bias ranged from 1.054 to 1.741, 0.635 to 1.241, and −0.0001 to 0.0033, respectively. The NSE, R and d ranged from 0.790 to 0.923, 0.889 to 0.961, and 0.938 to 0.980, respectively. From Table 4, it can be observed that model FM1, whose output is the DO at (t + 24), performed better than the other models in training; while the worst results were obtained for FM6 model, whose output is the DO at (t + 168). In the validation phase, both MLPNN and OP-ELM models performed quite well in forecasting hourly DO. According to Table 4, for the OP-ELM model, the RMSE, MAE and Bias ranged from 1.225 to 1.930, 0.665 to 1.258, and 0.0430 to 0.0920, respectively. The NSE, R and d ranged from 0.621 to 0.848, 0.794 to 0.922, and 0.887 to 0.959, respectively. Likewise, for MLPNN, the RMSE, MAE and Bias ranged from 1.270 to 1.933, 0.697 to 1.264, and 0.0479 to 0.1055. The NSE, R and d ranged from 0.619 to 0.836, 0.791 to 0.919, and 0.883 to 0.958, respectively. From Table 4, we conclude that the accuracies of the OP-ELM model predictions were usually slightly better than those of the MLPNN model. This demonstrates that the OP-ELM model is more suitable for forecasting DO.

Table 4 Performance indices for the OP-ELM and MLPNN forecasting models in the training and validation phases several hours in advance for USGS 420853121505500 [Top] station
Full size table

For reasons explained earlier in the section on model performance indices, an analysis of the MAPE is required to be presented. In the training phase, as shown in Table 4, the values of the MAPE ranged from 0.337 % to 0.784 % for OP-ELM and from 0.315 % to 0.750 % for MLPNN. For all the models, the MAPE of the OP-ELM shows slightly larger value than that of MLPNN models. In the validation phase, as shown in Table 4, the MAPE values ranged from 0.176 % to 0.333 % for OP-ELM and from 0.201 % to 0.342 % for MLPNN. For all the models, the MAPE values of the MLPNN were slightly larger than those of OP-ELM models. However, generally OP-ELM models performed better than MLPNN in the validation phase. To sum up, among the six forecasting models (FM1 to FM6), OP-ELM models showed the best performances in the validation phase. Examination of the MAPE values is another way to evaluate the developed models, and an important question must be answered: although the performances of the models are good according to the others six performance criteria (i.e., RMSE, MAE, Bias, R, NSE and d), why the values of the MAPE are very high, especially in the training phase? First, using the MAPE, the performance of the model can be easily judged. The MAPE is only 0.5 % if the measured value is 0.10 mg/L and the predicted value is 0.105 mg/L. But MAPE is 84 % if the measured value is 0.10 mg/L and the predicted value 0.184 mg/L. Second, as mentioned, the disadvantages of the MAPE include that it can assume a very high value (the case of the present study) if the actual measured value is very small (Kim and Kim 2016; Dawson et al. 2007; Tayman and Swanson 1999; Rayer 2007). For example, for a measured DO of 0.10 mg/L, which is frequently observed in the present study, and a calculated DO value of 8.567 mg/L, the MAPE is 8467 %, which is very high and unacceptable.

In order to demonstrate the capabilities and usefulness of the proposed approaches, we present in Table 5 a comparison between measured and calculated mean and standard deviation, the RPD index, the SI and the RMAE. Values of the RMSE and MAE less than half of the standard deviations (SD) of the observations may be considered low (Singh et al. 2004; Moriasi et al. 2007). As stated above, all RPD values less than one are unacceptable while values greater than 3 are considered excellent. According to Table 5, for both training and validation, there were small differences between model estimates and measured DO values, according to the mean and standard deviation. All RMAE values were less than half of the standard deviation and all RPD values were higher than 1.60. It can be seen from Table 5, in the validation phase, for the MLPNN and OP-ELM models, that all the differences between the mean of the measurements and the corresponding calculated DO values are less than 1.0 %. However, it is worth noting that there are only 5 cases in which the difference between the measured and the corresponding calculated standard deviations are higher than 10 % with a maximum of 13.72 % and a minimum of 0.6 %. This finding implies that the proposed models are very good with a high level of accuracy and robustness.

Table 5 Comparison between Mean and Standard deviation of the measured (Mes) and forecasted (Cal) DO values, ratio of standard deviation (Sx) to RMSE (RPD), scatter index (SI) and ratio of the mean absolute error to standard deviation (RMAE), for USGS 420853121505500 [Top] station
Full size table

For a final verification of the accuracy of the developed forecasting models, we also present in Table 5 the values of the SI index in the training and validation phases, for both MLPNN and OP-ELM models. In the training phase, the SI of the six developed models (FM1 to FM6) ranged between 0.144 and 0.238 for the OP-ELM models, and between 0.140 and 0.232 for the MLPNN models. Furthermore, for all the developed models, the SI was less than 0.240 which indicates excellent modeling results. Similarly, in the validation phase, the SI of the six models ranged between 0.144 and 0.206 for the OP-ELM models, and between 0.187 and 0.227 for the MLPNN models. Furthermore, for all developed models, the SI was less than 0.230, which indicates excellent modeling results. Once again, according to the SI, the OP-ELM is again better. In conclusion, according to the results obtained in the validation phase, the OP-ELM models must be ranked as best. Figures 7 and 8 show scatter plots of the calculated versus observed DO for the OP-ELM and MLPNN models, respectively, in the validation phase. Figures 9 and 10 show the comparison between the calculated and measured DO for OP-ELM and MLPNN models, respectively, in the validation phase.

Fig. 7
figure 7

Scatterplots of calculated versus measured values of dissolved oxygen (DO) in the validation phase, using OP-ELM model for the USGS 420853121505500 [Top] Station: a +24 h, b +48 h, c +72 h, d +96 h, e +120 h, and f +168 h

Full size image
Fig. 8
figure 8

Scatterplots of calculated versus measured values of dissolved oxygen (DO) in the validation phase, using MLPNN model for the USGS 420853121505500 [Top] Station: a +24 h, b +48 h, c +72 h, d +96 h, e +120 h, and f +168 h

Full size image
Fig. 9
figure 9

Comparison between the calculated and measured data of dissolved oxygen (DO) in the validation phase, using OP-ELM model for the USGS 420853121505500 [Top] Station: a +24 h, b +48 h, c +72 h, d +96 h, e +120 h, and f +168 h

Full size image
Fig. 10
figure 10

Comparison between the calculated and measured data of dissolved oxygen (DO) in the validation phase, using MLPNN model for the USGS 420853121505500 [Top] Station: a +24 h, b +48 h, c +72 h, d +96 h, e +120 h, and f +168 h

Full size image

3.2 Forecasting DO Concentration at the USGS 420853121505501 [Bottom] Station

The MLPNN and OP-ELM models with the same input and different outputs were compared based on their performance in training and validation sets. The results are summarized in Tables 6 and 7. It is observed that all models generally gave low values of the RMSE, MAE and bias, and high values of R, d and NSE. Generally, the performances of both the MLPNN and OP-ELM models in DO forecasting were very satisfactory. The first important conclusion is that the two models (MLPNN and OP-ELM) showed higher accuracy in prediction and performed better compared to the results obtained in Top station. Overall, they deliver a higher degree of reliability. It can be seen from the results that the values of all seven performance indices change with respect to the step ahead. Therefore, the two models appear to be performing at the same level of accuracy, but the OP-ELM offers more accuracy in the validation phase. In the training phase, for the OP-ELM model, the RMSE, MAE, and bias ranged from 0.662 to 1.534, 0.425 to 1.084, and 0, respectively. The NSE, R, and d ranged from 0.860 to 0.974, 0.927 to 0.987, and 0.961 to 0.993, respectively. Likewise, for MLPNN, the RMSE, MAE, and bias ranged from 0.656 to 1.502, 0.421 to 1.065, and −0.0042 to 0.0198, respectively, and the NSE, R, and d ranged from 0.865 to 0.974, 0.930 to 0.987, and 0.963 to 0.993, respectively. In the validation phase, both MLPNN and OP-ELM models performed quite well in forecasting hourly DO. According to Table 6, for the OP-ELM model, the RMSE, MAE, and bias ranged from 0.708 to 1.454, 0.425 to 0.995, and 0.00 to −0.0736, respectively, and the NSE, R and d ranged from 0.829 to 0.960, 0.911 to 0.980, and 0.952 to 0.990, respectively. Likewise, for MLPNN, the RMSE, MAE, and bias ranged from 0.730 to 1.489, 0.455 to 1.057, and −0.0582 to −0.1224, respectively, and the NSE, R and d ranged from 0.821 to 0.957, 0.906 to 0.979, and 0.948 to 0.989, respectively. According to Table 6, for all six models, the performance in the training phase was better than the performance in the validation phase. Nevertheless, the FM1 model DO output at (+24 h) must be considered as the best model developed. The FM6 model (+168 h) performed poorer than all the other models in terms of the seven performance indices. For the OP-ELM models, in the training phase, the lowest values of the RMSE, MAE, and Bias of forecasting models were 0.662 (mg/L), 0.425 (mg/L), and 0.00 (mg/L) (for OP-ELM FM1), and the highest values of the NSE, R and d were 0.974, 0.987 and 0.993 (for OP-ELM FM1). Table 6 indicates that the OP-ELM (FM1) had the lowest values of the RMSE and MAE (0.708 mg/L, 0.425 mg/L), and the highest NSE, R and d (0.960, 0.980, and 0.990) in the validation phase. According to Table 6, for the MLPNN models, the lowest values of the RMSE, MAE, and Bias of forecasting models were 0.656 (mg/L), 0.421 (mg/L), and −0.0042 (mg/L) (in MLPNN FM1), and the highest values of the NSE, R, and d were 0.974, 0.987 and 0.993 (in MLPNN FM1). Table 6 indicates that the MLPNN (FM1) had the lowest values of the RMSE and MAE (0.730 mg/L, 0.455 mg/L), and the highest NSE, R and d (0.957, 0.979 and 0.989) in the validation phase. From the results of training and validation, all six models developed in this study were evaluated all together, and results are conspicuous. In the validation phase, the OP-ELM models outperformed MLPNN models in terms of the various performance criteria. Finally, we report again the MAPE values in the training and validation phases. In the training phase, as shown in Table 6, MAPE values ranged from 0.243 % to 0.825 % for OP-ELM and from 0.244 % to 0.783 % for MLPNN. MAPE values for all OP-ELM models were slightly larger than those for MLPNN models. In the validation phase, as shown in Table 6, MAPE values ranged from 0.118 % to 0.278 % for OP-ELM and from 0.134 % to 0.295 % for MLPNN. MAPE values for all MLPNN models were slightly larger compared to those for OP-ELM models. However, generally OP-ELM performed better than MLPNN in the validation phase. To sum up, among the six forecasting models (FM1 to FM6), OP-ELM models showed better performances in the validation phase. In conclusion, the OP-ELM models are better for DO forecasting.

Table 6 Performance of the OP-ELM and MLPNN forecasting models in the training and validation phases several hours in advance for USGS 420853121505501 [Bottom] station
Full size table
Table 7 Comparison between Mean and Standard deviation of the measured (Mes) and forecasted (Cal) values of DO, ratio of standard deviation (Sx) to RMSE (RPD), scatter index (SI), and ratio of the mean absolute error to standard deviation (RMAE), for USGS 420853121505501 [Bottom] station
Full size table

We present in Table 7 a comparison between measured and calculated mean and standard deviation, the RPD index, the SI and the ratio of the RMAE. According to Table 7, for both training and validation there were small differences between model estimates and measured DO values, based on the mean and standard deviation. In the training phase, all the ratios of RMAE were less than 0.5 and all the RPD were higher than 3, except for the FM6 model for both OP-ELM and MLPNN. It can be seen from Table 7, in the validation phase, for both MLPNN and OP-ELM models, that all the difference between the mean of the measurements and the corresponding calculated DO values were less than 1.0 %. However, it is worth noting that there were only 2 cases were the difference between the measured and its corresponding calculated standard deviation were higher than 10 % (FM5 and FM6 for MLPNN), with a maximum of 11.81 % and a minimum of 2 %. This finding implies that the proposed models are very good with a high level of accuracy and robustness. We also present in Table 7 the SI index values in the training and validations phases, for both MLPNN and OP-ELM models. In the training phase, the SI of the six developed models (FM1 to FM6) ranged between 0.101 and 0.183 for OP-ELM models, and between 0.159 and 0.229 for MLPNN models. Furthermore, for all developed models, the SI was less than 0.240, which corresponds to excellent modeling. Similarly, in the validation phase, the SI of the six developed models ranged between 0.097 and 0.160 for OP-ELM models, and between 0.148 and 0.204 for MLPNN models. Furthermore, for all developed models, the SI was less than 0.210, which corresponds to excellent modeling. Once again, according to the SI values, the OP-ELM is better. In conclusion, according to the results obtained in the validation phase, the OP-ELM model must be ranked as better model. Figures 11 and 12 show scatter plots of the calculated versus observed DO for OP-ELM and MLPNN models, respectively, in the validation phase. Figures 13 and 14 show the comparison between the calculated and measured DO for OP-ELM and MLPNN models, respectively, in the validation phase.

Fig. 11
figure 11

Scatterplots of calculated versus measured values of dissolved oxygen (DO) in the validation phase, using OP-ELM model for the USGS 420853121505501 [Bottom] Station: a +24 h, b +48 h, c +72 h, d +96 h, e +120 h, and f +168 h

Full size image
Fig. 12
figure 12

Scatterplots of calculated versus measured values of dissolved oxygen (DO) in the validation phase, using MLPNN model for the USGS 420853121505501 [Bottom] Station: a +24 h, b +48 h, c +72 h, d +96 h, e +120 h, and f +168 h

Full size image
Fig. 13
figure 13

Comparison between the calculated and measured data of dissolved oxygen (DO) in the validation phase, using OP-ELM model for the USGS 420853121505501 [Bottom] station: a +24 h, b +48 h, c +72 h, d +96 h, e +120 h, and f +168 h

Full size image
Fig. 14
figure 14

Comparison between the calculated and measured data of dissolved oxygen (DO) in the validation phase, using MLPNN model for the USGS 420853121505501 [Bottom] station: a +24 h, b +48 h, c +72 h, d +96 h, e +120 h, and f +168 h

Full size image

4 Conclusions

In this paper, we presented and compared two models to forecast DO several hours in advance, MLPNN and OP-ELM, which are based on artificial intelligence paradigm. To show the applicability of the proposed methods, actual values of measured DO in Klamath River at Miller Island Boat Ramp, Oregon, USA were used. The data were collected from 2004 to 2013, at an hourly time step. The study showed the development of a powerful tool, forecasting DO values at good accuracy (R between 0.91 and 0.98) in the validation phase. The results are very encouraging because the development of these tools was undertaken to support the actual methods and models for estimating DO in rivers without using other water quality parameters. This is the first publication that we are aware of, which demonstrates the use of OP-ELM and MLPNN, in forecasting DO several hours in advance up to (7 days). In the validation phase, the results show that for both stations, Top and Bottom, the OP-ELM model ensured more accurate forecasting than the MLPNN model.