Introduction

Optical methods in experimental stress analysis such as photoelasticity, thermoelasticity and a wide variety of interferometric methods are useful and valuable techniques because they provide whole-field information on a specimen surface or the area of interest. However, it is sometimes difficult to extract desired quantities from the quantities obtained by these methods. For example, moiré interferometry provides surface displacements and then strains are obtained by differentiating the displacements spatially. However, the differentiation of measured displacements has the difficulties that the errors in the measured values give rise to even greater errors in their derivatives. Thus, various studies have been performed to obtain strains from measured displacements [1–4].

In the case of photoelasticity, it is well known that the fringe patterns represent the principal stress difference and the principal direction, and thus the stress components themselves cannot be obtained directly. Conventionally, a method based on the equilibrium equation such as a shear difference method has been used for the stress separation in photoelasticity [5, 6]. Several stress separation techniques based on the integration of the equilibrium equations have been developed [7–9]. The major drawback of the conventional methods is that the stresses obtained by these methods usually suffer from error accumulation arising by finite difference approximation. On the other hand, various techniques for determining stress components have also been reported. Patterson and coworkers [10, 11], and Sakagami et al. [12] developed a hybrid method of photoelasticity and thermoelasticity. In this method, the difference and the sum of principal stresses are measured separately, and then, they are combined for obtaining stress components. The difference and the sum of principal stresses can also be obtained by combining photoelasticity and interferometry [13–16]. The disadvantage of the hybrid methods of photoelasticity and another experimental method is that the measurement can be complicated and cumbersome. On the other hand, several hybrid methods with theoretical analysis or numerical analysis, and inverse analysis methods have also been proposed for the stress separation. Chang et al. [17] determined the coefficients of Airy stress function from photoelastic fringes for determining stresses. Berghaus [18] proposed a hybrid method with a finite element method. In this method, displacement boundary condition along the axis of symmetry and free boundary for a finite element method is determined by photoelasticity. Hayabusa et al. [19] and Chen et al. [20] proposed a hybrid method with a numerical method such as a boundary element method. They determined boundary conditions by inverse analysis from photoelastic fringes and then stresses are determined by direct analysis.

The stress separation can be performed by the methods mentioned above. Particularly it can be considered that the use of numerical methods such as a finite element method or a boundary element method for the stress separation is useful because the data processing is easy and full-field stresses and strains can be obtained easily. However, inverse boundary value problems are often ill-posed. Therefore, various additional techniques should be introduced to the inverse analysis for obtaining stable and accurate results. In the present study, an alternative and simple hybrid method for stress separation in photoelasticity is proposed. Boundary conditions for a local finite element model, that is, tractions along the boundaries are determined from photoelastic fringes inversely. Two algorithms are presented. One is linear algorithm in which the tractions are determined from the principal stress difference and the principal direction using the method of linear least-squares. In another algorithm, on the other hand, the tractions are determined only from the principal stress difference using nonlinear least-squares. After determining the tractions, the stress components are obtained by finite element direct analysis. The effectiveness of the proposed method is validated by analyzing the stresses around a hole in a plate under tension and the contact stresses under normal and shear load. Results show that the boundary conditions of the local finite element model can be determined from the photoelastic fringes and then the individual stresses can be obtained by the proposed method. Furthermore, the stresses can be determined even if the boundary condition is complicated such as at the contact surface. It is expected that the proposed method can be powerful tool for stress analysis.

Inversion of Boundary Conditions

Basic Principle

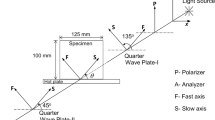
Figure 1 shows a typical optical setup for photoelasticity, that is, a circular polariscope. A birefringent specimen is placed in the polariscope, and then, photoelastic fringes appear when the specimen is loaded. The angle φ of the principal axis of the specimen is interpreted as the principal direction, i.e., the isoclinic parameter. Similarly, the retardation δ of the specimen, that is, the isochromatic parameter is related to the principal stress difference as [21]

$$ {\sigma_1} - {\sigma_2} = \frac{{\delta {f_s}}}{{2\pi h}}, $$
(1)

where f s is the material fringe value, h is the thickness of a specimen, and σ1 and σ2 express the principal stresses, respectively. Various techniques such as a phase-stepping method can be used for obtaining the isochromatic and isoclinic parameters [22–25]. Therefore, the principal stress difference and the principal direction are obtained in the region of interest or the whole field of the specimen by introducing one of the data acquisition and processing techniques.

Fig. 1
figure 1

Typical optical setup for photoelasticity

Full size image

In a finite element method, on the other hand, it can be considered that the reasonably accurate stress distributions are obtained when the appropriate boundary conditions are given, provided that appropriate finite element model is used and material properties are known. In the proposed method, therefore, the boundary conditions of the analysis region, that is, the tractions along the boundaries, are inversely determined from photoelastic fringes. Then, the stresses are determined by finite element direct analysis by applying the computed boundary conditions.

Figure 2 schematically shows a two-dimensional finite element model of the analysis region. The displacements of some nodes are fixed so that the rigid body motion is not allowed. Then, a unit force along one of the direction of the coordinate system is applied to a node at the boundary of the model. That is, the finite element analysis is performed under the boundary condition of the unit force on the boundary. The analysis is repeated by changing the direction of the unit force and the node at which the unit force is applied. The stress components at a point (x i , y i ) for the applied unit force P j = 1 (j = 1~N) are represented as (σ x ′) ij , (σ y ′) ij , and (τ xy ′) ij . Here, i (= 1~M) is the data index, j is the index of the applied force, M is the number of the data points, and N is the number of the forces to be determined at the nodes along the boundary of the model. The stress components (σ x ) i , (σ y ) i , and (τ xy ) i at the point (x i , y i ) under the actual applied forces F j (j = 1~N) can be expressed using the principle of superposition as

$$ \left. {\begin{array}{*{20}{c}} {{{\left( {{\sigma_x}} \right)}_i} = {{\left( {\sigma_x^{\prime }} \right)}_{{ij}}}{F_j}} \hfill \\ {{{\left( {{\sigma_y}} \right)}_i} = {{\left( {\sigma_y^{\prime }} \right)}_{{ij}}}{F_j}} \hfill \\ {{{\left( {{\tau_{{xy}}}} \right)}_i} = {{\left( {\tau_{{xy}}^{\prime }} \right)}_{{ij}}}{F_j}} \hfill \\ \end{array} } \right\}\left( {i = 1 \sim M,j = 1 \sim N} \right), $$
(2)

where the summation convention is used. That is, for example,

$$ \begin{array}{*{20}{c}} {{{\left( {{\sigma_x}} \right)}_i} = }{{{\left( {\sigma_x^{\prime }} \right)}_{{ij}}}{F_j}\left( {i = 1 \sim M,j = 1 \sim N} \right)} \\ = {\sum\limits_{{j = 1}}^N {{{\left( {\sigma_x^{\prime }} \right)}_{{ij}}}{F_j}\left( {i = 1 \sim M} \right)} } \\ = {{{\left( {\sigma_x^{\prime }} \right)}_{{i1}}}{F_1} + {{\left( {\sigma_x^{\prime }} \right)}_{{i2}}}{F_2} + \ldots + {{\left( {\sigma_x^{\prime }} \right)}_{{iN}}}{F_N}\left( {i = 1 \sim M} \right).} \\ \end{array} $$
Fig. 2
figure 2

Finite element model with boundary condition of unit force

Full size image

In equation (2), F j is the nodal forces along the boundary. Therefore, the tractions along the boundaries are determined and subsequent stress analysis can be performed if the values of F j are determined.

Linear Algorithm

From the principal stress difference σ1−σ2 and the principal direction φ obtained by photoelasticity, the normal stress difference σ x −σ y and the shear stress τ xy are obtained as

$$ \begin{array}{*{20}{c}} {{\sigma_x} - {\sigma_y} = \left( {{\sigma_1} - {\sigma_2}} \right)\cos 2\varphi, } \\ {{\tau_{{xy}}} = \frac{1}{2}\left( {{\sigma_1} - {\sigma_2}} \right)\sin 2\varphi .} \\ \end{array} $$
(3)

Therefore, the relationships between the values obtained by photoelasticity and the nodal forces F j along the boundary can be expressed as

$$ \begin{array}{*{20}{c}} {{{\left( {{\sigma_x} - {\sigma_y}} \right)}_i} = \left[ {{{\left( {\sigma_x^{\prime }} \right)}_{{ij}}} - {{\left( {\sigma_y^{\prime }} \right)}_{{ij}}}} \right]{F_j}\left( {i = 1 \sim M,j = 1 \sim N} \right),} \\ {{{\left( {{\tau_{{xy}}}} \right)}_i} = {{\left( {\tau_{{xy}}^{\prime }} \right)}_{{ij}}}{F_j}\left( {i = 1 \sim M,j = 1 \sim N} \right),} \\ \end{array} $$
(4)

where (σ x −σ y ) i and (τ xy ) i express the normal stress difference and the shear stress at the point (x i , y i ) obtained by photoelasticity. Equation (4) expresses linear equations in the unknown coefficients F j . For numerous data points, an over-determined set of simultaneous equations is obtained. In this case, the nodal forces F j along the boundary can be estimated using linear least-squares as

$$ {\mathbf{F}} = \left( {{{\mathbf{A}}^T}{{\mathbf{A}}^{{ - 1}}}} \right){{\mathbf{A}}^T}{\mathbf{S}}, $$
(5)

where F, A and S are the nodal force, stresses under the boundary condition of the unit force and the values obtained by photoelasticity, respectively. They are expressed as

$$ {\mathbf{F}} = \left[ {\begin{array}{*{20}{c}} {{F_1}} \hfill \\ \vdots \hfill \\ {{F_N}} \hfill \\ \end{array} } \right],{\mathbf{A}} = \left[ {\begin{array}{*{20}{c}} {{{\left( {\sigma_x^{\prime }} \right)}_{{11}}} - {{\left( {\sigma_y^{\prime }} \right)}_{{11}}}} & \ldots & {{{\left( {\sigma_x^{\prime }} \right)}_{{1N}}} - {{\left( {\sigma_y^{\prime }} \right)}_{{1N}}}} \\ \vdots & \ddots & \vdots \\ {{{\left( {\sigma_x^{\prime }} \right)}_{{M1}}} - {{\left( {\sigma_y^{\prime }} \right)}_{{M1}}}} & \ldots & {{{\left( {\sigma_x^{\prime }} \right)}_{{MN}}} - {{\left( {\sigma_y^{\prime }} \right)}_{{MN}}}} \\ {{{\left( {\tau_{{xy}}^{\prime }} \right)}_{{11}}}} & \ldots & {{{\left( {\tau_{{xy}}^{\prime }} \right)}_{{1N}}}} \\ \vdots & \ddots & \vdots \\ {{{\left( {\tau_{{xy}}^{\prime }} \right)}_{{M1}}}} & \ldots & {{{\left( {\tau_{{xy}}^{\prime }} \right)}_{{MN}}}} \\ \end{array} } \right],{\mathbf{S}} = \left[ {\begin{array}{*{20}{c}} {{{\left( {{\sigma_x} - {\sigma_y}} \right)}_1}} \\ \vdots \\ {{{\left( {{\sigma_x} - {\sigma_y}} \right)}_M}} \\ {{{\left( {{\tau_x}_y} \right)}_1}} \\ \vdots \\ {{{\left( {{\tau_x}_y} \right)}_M}} \\ \end{array} } \right]. $$

After determining the nodal force F along the boundary using equation (5), the stress components can be obtained by the finite element direct analysis by using the nodal force F as the boundary condition.

Nonlinear Algorithm

As is well known, it is difficult to obtain the accurate values of the principal direction by photoelasticity. The measured principal direction is sometimes affected by the isochromatics and the accuracy of quarter-wave plates. In order to obtain accurate values of the principal direction, various techniques have been proposed [26, 27]. Because the accurate values of the principal direction cannot always be obtained, a method for determining the boundary condition without the principal direction is also described below.

The principal stress difference is expressed using the stress components as

$$ {\sigma_1} - {\sigma_2} = \sqrt {{{{\left( {{\sigma_x} - {\sigma_y}} \right)}^2} + 4\tau_{{xy}}^2.}} $$
(6)

Therefore, the relationship between the experimentally obtained values of the principal stress difference and the nodal forces F j along the boundary can be expressed as

$$ {\left[ {{{\left( {{\sigma_1} - {\sigma_2}} \right)}_i}} \right]^2} = {\left[ {{{\left( {\sigma_x^{\prime }} \right)}_{{ij}}}{F_j} - {{\left( {\sigma_y^{\prime }} \right)}_{{ij}}}{F_j}} \right]^2} + 4{\left[ {{{\left( {\tau_{{xy}}^{\prime }} \right)}_{{ij}}}{F_j}} \right]^2}\left( {i = 1 \sim M,j = 1 \sim N} \right), $$
(7)

where (σ1−σ2) i is the principal stress difference obtained by photoelasticity at the point (x i , y i ). Equation (7) is nonlinear in the unknown parameters F j . To solve these parameters, an iterative procedure based on Newton–Raphson method is employed. Equation (7) is rewritten as

$$ {h_i} = {\left[ {{{\left( {\sigma_x^{\prime }} \right)}_{{ij}}}{F_j} - {{\left( {\sigma_y^{\prime }} \right)}_{{ij}}}{F_j}} \right]^2} + 4{\left[ {{{\left( {\tau_{{xy}}^{\prime }} \right)}_{{ij}}}{F_j}} \right]^2} - {\left[ {{{\left( {{\sigma_1} = {\sigma_2}} \right)}_i}} \right]^2}\left( {i = 1 \sim M,j = 1 \sim N} \right), $$
(8)

A series of iterative equations based on Taylor’s series expansions of equation (8) yields the following equations.

$$ {\left( {{h_i}} \right)_{{k + 1}}} = {\left( {{h_i}} \right)_k} + {\left( {\frac{{\partial {h_i}}}{{\partial {F_1}}}} \right)_k}\Delta {F_1} + \ldots + {\left( {\frac{{\partial {h_i}}}{{\partial {F_N}}}} \right)_i}\Delta {F_N}\left( {i = 1 \sim M} \right), $$
(9)

where subscript k denotes the kth iteration step, and ΔF 1, …, ΔF N are the corrections to the previous estimation of F 1, …, F N . The desired results (h i ) k+1 = 0 yield the following simultaneous equations with respect to the corrections.

$$ - {h_i} = \left( {\frac{{\partial {h_i}}}{{\partial {F_1}}}} \right)\Delta {F_1} + \ldots + \left( {\frac{{\partial {h_i}}}{{\partial {F_N}}}} \right)\Delta {F_N}\left( {i = 1 \sim M} \right), $$
(10)

The solution of equation (10) in the least-squares sense is

$$ {\mathbf{D}} = {\left( {{{\mathbf{B}}^T}{\mathbf{B}}} \right)^{{ - 1}}}{{\mathbf{B}}^T}{\mathbf{H}}. $$
(11)

In that equation,

$$ {\mathbf{D}} = \left[ {\begin{array}{*{20}{c}} {\Delta F} \\ \vdots \\ {\Delta {F_N}} \\ \end{array} } \right],{\mathbf{B}} = \left[ {\begin{array}{*{20}{c}} {\frac{{\partial {h_1}}}{{\partial {F_1}}}} & \ldots & {\frac{{\partial {h_1}}}{{\partial {F_N}}}} \\ \vdots & \ddots & \vdots \\ {\frac{{\partial {h_M}}}{{\partial {F_1}}}} & \ldots & {\frac{{\partial {h_M}}}{{\partial {F_N}}}} \\ \end{array} } \right],{\mathbf{H}} = \left[ {\begin{array}{*{20}{c}} { - {h_1}} \\ \vdots \\ { - {h_M}} \\ \end{array} } \right]. $$

The solution of the matrix equation gives the correction terms for prior estimates of the coefficients. Accordingly, an iterative procedure must be used to obtain the best-fit set of coefficients. Then, the estimates of the unknowns are revised. This procedure is repeated until the corrections become acceptably small. After determining the nodal forces along the boundary, the stress components can be obtained by the finite element direct analysis by using the nodal forces as the boundary condition. That is, the stress separation can be performed. It is noted that because the method described here uses only the principal stress difference, the sign of the applied forces along the boundary cannot be determined. In other words, the proposed nonlinear algorithm cannot judge whether the traction is tension or compression. Therefore, the appropriate initial values should be provided for the calculation of the nonlinear least-squares.

Experimental Verification of the Proposed Method

A simple static problem is analyzed to verify the proposed method. A perforated plate made of epoxy resin, 228 mm in height, 50 mm in width and 3 mm in thickness, having a hole of diameter of 10 mm, is subjected to the tensile load of P = 398 N as shown in Fig. 3. The material fringe value f s of the material is determined as 11.48 kN/m by a calibration test. The specimen is placed in a circular polariscope with the quarter-wave plates matched for the wavelength of 560 nm. Three monochromatic lights of wavelengths of 500 nm, 550 nm, and 600 nm emitted from a halogen lamp with interference filters are used as the light source in order to apply the absolute phase analysis method with tricolor images [28]. The phase-stepped photoelastic fringes are collected by a monochromatic CCD camera with the resolution of 640 × 480 pixels and 256 Gy levels. Then, the fringe pattern is analyzed, the ambiguity of isochromatic phase is corrected and the phase unwrapping is performed by the method proposed previously [28].

Fig. 3
figure 3

Perforated plate specimen used for verifying the proposed method

Full size image

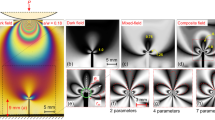
Figure 4(a) shows an example of the photoelastic fringe pattern around the hole. Applying the phase-stepping method with 7 images [28, 29], the wrapped phases of the retardation and the principal direction are obtained as shown in Fig. 4(b) and (c). The phase map of the retardation in Fig. 4(b) contains the region of ambiguity where the mathematical sign of the retardation is wrong. In addition, the values of the retardation in Fig. 4(b) are lying in the range of the −π to π rad. On the other hand, the principal direction in Fig. 4(c) lies in the range from −π/4 to π/4 rad whereas the actual value should be in the range from −π/2 to π/2 rad. The ambiguity of the retardation is corrected using the phase maps obtained for the three monochromatic wavelengths as shown in Fig. 4(d). Then, the unwrapped phases of the retardation and the principal direction are obtained, as shown in Fig. 4(e) and (f). The principal stress difference and the principal direction at the number of the data points M = 2394 on the specimen surface are extracted and used as the data input into the algorithm by the proposed method.

Fig. 4
figure 4

(a) Photoelastic fringe pattern; (b) wrapped retardation with ambiguity of sign; (c) wrapped principal direction; (d) wrapped retardation; (e) unwrapped retardation; (f) unwrapped principal direction

Full size image

The stress separation is performed in the 20 mm × 20 mm region around the hole, indicated by ABCD, shown in Fig. 3. Figure 5 shows the finite element model of the 20 mm × 20 mm region used for the proposed method. In this model, 8-noded isoparametric elements are used. The numbers of the elements and the nodes are 200 and 680, respectively. In order to obtain the stresses under the unit force at a point on the boundary, the displacements at some nodes must be fixed to prevent the rigid body motion. In this study, the x and y components of the displacement at the point A and the y directional displacement at the point B are assumed not to move though these points are displaced actually. This assumption is valid because the rigid body translation and the rotation of the analysis region do not affect the stress distribution. The nodal forces at the other nodes on the boundary are obtained by the proposed method. The number of the nodes along the boundary is 80 and thus the number of the nodal forces along the boundary is 160. That is, the number of the nodal forces to be determined is N = 157 because the three displacement components at the points A and B are fixed.

Fig. 5
figure 5

Finite element model of analysis region

Full size image

The nodal forces are determined using both linear and nonlinear algorithms. These calculations, not only the least-squares but also finite element analysis, are performed using C language programs made by the authors. In the analysis by nonlinear algorithm, the arbitrary initial values of −1 N are given at all nodes at which the nodal forces are to be determined. Then, the iteration is stopped when the values of the correction are smaller than 0.001 N. Figure 6 shows an example of the variation of nodal force at a point during iteration process in the nonlinear algorithm. The value of the nodal force is corrected by the Newton–Raphson method. Then, the value converges to a constant value as shown. Because the nodal forces at 157 points are simultaneously determined in the iteration process, the convergence is not fast and the number of iteration of about 40 is required in this example.

Fig. 6
figure 6

Example of the variation of nodal force during iteration process in nonlinear algorithm

Full size image

The tractions along the boundary CD determined from the nodal forces obtained by the linear and nonlinear algorithms are shown in Fig. 7. In this figure, solid curves represent the values obtained by finite element direct analysis. As shown in this figure, the tractions on the boundary of the analysis area obtained by the proposed method show good agreement with the values obtained by the direct analysis. In addition, the significant difference between the tractions obtained using the linear and nonlinear algorithms is not observed. The average differences between the values obtained by the proposed method and the direct analysis are 0.13 N for the linear algorithm and 0.26 N for the nonlinear algorithm. Using the nodal forces obtained by the proposed method as the input data to finite element analysis, the stresses are computed. Figures 8 and 9 show the stresses around the hole obtained by the linear and nonlinear algorithms, respectively. The stresses obtained by finite element direct analysis are also shown in Fig. 10 for comparison. As shown in these figures, the stress components are obtained from the photoelastic fringes by the proposed linear to nonlinear algorithms. The average difference between the y directional normal stresses σ y obtained by the linear algorithm and direct ones is 0.11 MPa, the maximum difference is 0.66 MPa, and the standard deviation is 0.10 MPa. On the other hand, the average difference, the maximum difference and the standard deviation between the values by the nonlinear algorithm and those by the direct analysis are 0.28 MPa, 0.68 MPa, and 0.12 MPa, respectively. It seems that the results obtained by the linear algorithm are better than those by the nonlinear algorithm. However, in the linear algorithm, the principal stress difference as well as the principal direction is used for obtaining the shear stress and the normal stress difference. Therefore, the results of the stress separation are affected by the accuracy of the principal direction. The principal stress difference can be accurately evaluated in photoelasticity. The principal direction is also accurately evaluated in this result employing the three wavelengths technique. As mentioned, however, it is known that the accurate evaluation of the principal direction is difficult even if a phase-stepping method is introduced. In this case, therefore, the nonlinear algorithm should be used for obtaining the better results. The drawback of the nonlinear algorithm is that the sign of the nodal force cannot be determined. Therefore, appropriate initial values of the nodal force are determined by the linear algorithm and then the nonlinear algorithm is used for determining the tractions if the accurate result of the principal direction is not obtained. Then, the stresses with appropriate sign can be obtained.

Fig. 7
figure 7

Tractions along the boundary CD

Full size image
Fig. 8
figure 8

Stresses obtained by the proposed linear algorithm: (a) σ x ; (b) σ y ; (c) τ xy

Full size image
Fig. 9
figure 9

Stresses obtained by the proposed nonlinear algorithm: (a) σ x ; (b) σ y ; (c) τ xy

Full size image
Fig. 10
figure 10

Stresses obtained by finite element direct analysis: (a) σ x ; (b) σ y ; (c) τ xy

Full size image

Contact Stress Analysis

As is well known, it is difficult to evaluate contact stresses accurately by numerical or theoretical methods because actual condition at the contact surface, for example, the coefficient of friction, the area of contact, the area of slip and stick, cannot be known. Thus, photoelasticity has been used for the contact stress analysis [30, 31], and the results of the contact stress analysis by a numerical method have been validated by experiments [32]. Therefore, contact stress analysis is one of the best examples of the application of photoelasticity.

Figure 11 shows the specimen and the loading condition used in this study. A disk specimen of 25 mm radius and 3 mm thickness is placed in a wide groove between two inclined side-walls and is compressed into contact at the top of the specimen in the normal direction. Not only the disk specimen but the inclined walls and the indenter at the top are made of epoxy resin. This setup can realize three types of contact state including compression and sliding. The compressive load of P = 62 N is applied to the specimen, then, the photoelastic fringes at the contact surfaces A, B and C are observed by a CCD camera (640 × 480 pixels × 8 bits). The phase-stepping method with three monochromatic lights is again used for the fringe pattern analysis [28].

Fig. 11
figure 11

Specimen and loading condition for contact stress analysis

Full size image

The examples of the photoelastic fringes near the contact surfaces A, B and C are shown in Figure 12. As shown in these figures, the maximum fringe order does not appear at the contact surface but a small distance from it. This is the typical fringe pattern of contact problems [30–33]. The eccentric fringe pattern is observed at the contact surface B under the normal and the tangential loads unlike the fringe pattern at the contact surface A under the normal load. On the other hand, the complicated fringe pattern where the small fringe loops appear at the contact surface is observed at the contact surface C. It can be considered that the small fringe loops at the contact surface is generated by the influence of not only the tangential load but the slip between contact surfaces.

Fig. 12
figure 12

Photoelastic fringe patterns and region for analysis: (a) contact surface A; (b) contact surface B; (c) contact surface C

Full size image

The stress separations are performed by the proposed method in the 3 mm × 1 mm regions inside the disk specimen at the contact surfaces A, B and C. The regions for analysis are indicated in Fig. 12 as aAbAcAdA for the contact surface A, aBbBcBdB for the contact surface B, and aCbCcCdC for the contact surface C. The local coordinate systems, shown in Fig. 11, are used for the subsequent analysis. Figure 13 shows the finite element model of the 3 mm × 1 mm region used for the stress separation. The 8-noded isoparametric elements are again used for the finite element model. It is noted that the linear algorithm is used at first, then, the results of the nodal forces obtained by the linear algorithm are used as the initial values for the nonlinear algorithm for obtaining the final results in order to avoid the influence of the inaccuracies of the principal direction.

Fig. 13
figure 13

Finite element model for contact stress analysis

Full size image

Figure 14 shows the subsurface stress components at the contact surfaces A, B and C obtained by the proposed method. At the contact surfaces A and B, the reasonable stress distributions under the normal load at A and the normal and tangential loads at B are obtained. It is observed that the compressive stress σ y is higher than the stress σ x on the contact surface A even if the magnitudes of these stresses are identical in Hertz contact theory where the friction at the contact surface is ignored [33]. The stress distributions at the contact surface B are distorted by the effect of the load of the tangential direction. On the other hand, the complicated stress distributions are observed at the contact surface C reflecting the complicated fringe pattern at the contact surface. It can be considered that there are the regions of stick and slip on the contact surface C because the stresses vary drastically along the contact surface. The maximum shear stresses in plane, that are proportional to the isochromatics fringe order are also computed from the stress components in Fig. 14. Comparing the distributions of the maximum shear stresses in Fig. 15 with the isochromatics fringes in Fig. 12, it can be considered again that the reasonable results are obtained by the proposed method.

Fig. 14
figure 14

Subsurface stresses: (a)~(c) σ x , σ y and τ xy at contact surface A; (d)~(f) σ x , σ y and τ xy at contact surface B; (g)~(i) σ x , σ y and τ xy at contact surface C

Full size image
Fig. 15
figure 15

Maximum shear stress τ1 in plane: (a) contact surface A; (b) contact surface B; (c) contact surface C

Full size image

Conclusions

In this study, an experimental-numerical hybrid method for determining stress components in photoelasticity is proposed. Boundary conditions for a local finite element model are inversely determined from the principal stress difference and the principal direction in linear algorithm. On the other hand, the boundary conditions can be determined from the principal stress difference if the nonlinear algorithm is used. Then, the stresses are obtained by finite element direct analysis using the computed boundary conditions. The effectiveness is validated by applying the proposed method to a plate with a hole under tension and contact problems. Results show that the boundary conditions of the local finite element model can be determined from the photoelastic fringes and then the individual stresses can be obtained by the proposed method. It is expected that the proposed method can be powerful tool for stress analysis.