Introduction

Nearly all mechanical components are subjected to interacting stress fields during service which deteriorate their performance and design life. These interactions could occur between cracks or cracks with nearby discontinuities such as holes, etc., or crack and contact stresses. Studies have focussed on interacting cracks [1,2,3,4,5,6] under various configurations using experiments and simulations to understand effects like stress amplification and shielding. The effect of discontinuities like holes on the crack path have also been studied [7,8,9,10,11].

Researchers have also investigated cracks developed at the bi-material interface, experimentally and numerically, in various configurations over time [12,13,14,15,16]. In the case of interaction problems, photoelastic fringes have provided a wealth of information in both qualitative as well as quantitative sense.

The corrected multiparameter crack-tip solution given by Atluri and Kobayashi [17, 18] has been widely used in experimental fracture mechanics to study complex mixed-mode problems. Similarly, the analytical equations with elliptical contact stress distribution given by Smith and Liu [19] have been used to understand contact developed between two elastic bodies even if friction is present at the contact. Further, in conjunction with the experimental technique of photoelasticity which gives isochromatics (contours of σ1-σ2) as output, the over deterministic non-linear least squares method has been used to study fracture problems [3, 4, 20, 21] and contact problems [22,23,24,25], separately. These have been used to evaluate fracture parameters including SIFs and contact parameters, namely, contact length and friction coefficient. Photoelastic fringes have also assisted in understanding mode dominance in fracture problems [26, 27] and effect of friction in contact stress fields [22, 23].

There has been no work till date to study the interaction of crack and contact stress field. Studies have mostly been limited to extraction of SIFs using only a two-parameter solution for a crack close to contact stresses [28] or analysing only a single crack-contact configuration [29]. There is a need for a systematic study to draw meaningful conclusions. The evaluation of SIFs for cracks in the presence of contact stresses is important to characterise cracks and the focus of this study is to address this aspect.

Crack-tip isochromatics show, on careful scrutiny, certain geometric features even when the contact loads are sufficiently away from the crack-tip which is demonstrated in this paper for a moderately-deep beam with a small vertical crack. The multi-parameter crack-tip solution is explored to capture the geometric features of the isochromatics. In the presence of multiple contact loads, use of superposition method is suggested in ref [30]. Following this, the beam problem is again studied using the superposition of singular crack-tip and contact stress equations.

A moderately-deep beam (L/d ~ 2.4) with a small bottom vertical crack (a/d ~ 0.08) is studied by subjecting it to three-point bending with the contact load sufficiently far away. The experimental isochromatics near the crack-tip are processed to obtain the SIFs using the over-deterministic non-linear least squares method using the multiparameter solution. These results are compared against similar cases modelled using finite elements as a form of verification. Since beams are members which often have to support moving contact loads like rail roads, these are suitable candidates for interaction studies once a crack develops in them. Multiple configurations with varying load positions and magnitudes are considered for a moderately-slender beam (L/d ~ 4.91 and a/d ~ 0.14). Fracture parameters are evaluated from the experimental results using the over deterministic least squares method.

Method of Analysis

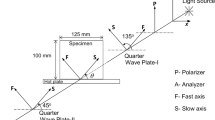
Photoelastic experiments are carried out on transparent epoxy specimens with thickness, h = 5.5 mm and material stress-fringe value, Fσ = 11.86 N/mm/fringe. Dark-field circular polariscope arrangement is used along with white light source. The isochromatic fringes are captured using a Canon EOS 850D CMOS DSLR camera.

The fracture parameter evaluation from experimental isochromatics involves the following steps as elaborated next.

Obtaining Whole Field Fringe Order (N) Using Twelve Fringe Photoelasticity (TFP)

The fringe order at every pixel of the isochromatic image (i.e., test image) is obtained using single-image based processing algorithms [31, 32]. These sophisticated algorithms involve pixel-wise colour matching of the test image against a calibration colour image obtained from a known problem to get N at every pixel. With advancements in computer vision, processing of images with fringe orders as high as twelve is now possible making it suitable for a wide variety of problems.

The colour matching scan is performed using a colour difference formula (CDF) and error minimisation in the pixel-wise RGB (red–green–blue) and HSV (hue-saturation-value) values given by:

$$e=\sqrt{{({R}_{t}-{R}_{c})}^{2}+{({G}_{t}-{G}_{c})}^{2}+{({B}_{t}-{B}_{c})}^{2}+{({H}_{t}-{H}_{c})}^{2}+{({S}_{t}-{S}_{c})}^{2}+{({V}_{t}-{V}_{c})}^{2}}$$
(1)

where subscripts ‘t’ and ‘c’ denote values for test and calibration images, respectively.

Based on minimum error, each pixel in the test image is assigned the corresponding fringe order (N). The pixel-wise fringe orders obtained are further refined using the advanced fringe resolution guided scanning (FRSTFP) scheme [33] to eliminate any jumps due to colour repetition or other error sources. The refined results are smoothened to obtain the whole field fringe order data [31]. These steps are carried out using an in-house developed software DigiTFP® [34].

Data Collection for SIF Evaluation

Stress intensity factor evaluation using regression requires inputs from experiments in the form of positional coordinates (r, θ) with the crack-tip as the origin along with the corresponding fringe order (N). With the availability of whole field fringe order data as discussed in "Obtaining Whole Field Fringe Order (N) Using Twelve Fringe Photoelasticity (TFP)", one can obtain contours of any choice such as bright (N = 0.5, 1.5, 2.5…) or dark field (N = 0, 1, 2…) as well as mixed-field isochromatics (N = 0.25, 0.75, 1.25…) or even composite field isochromatics (N = 0.25, 0.5, 0.75…). The necessity and advantage of using mixed-field and composite field isochromatic fringes is highlighted in several cases analysed in the subsequent sections. Several studies have shown that it is better to collect data along fringe contours that capture the salient geometrical features of the crack-tip fringe field for improved convergence rather than at random locations in the fringe field [4, 5, 16, 32, 35]. By specifying the zone of data collection and the fringe order tolerance, the datapoints are collected automatically from the experimental fringes. Use of mixed-field or composite field facilitates better data collection in case of poor photoelastic response. In this paper, composite field fringes are used for the case discussed in "Evaluation of Stress Intensity Factors" and for all the remaining cases, mixed-field fringes are found to be adequate.

Over-deterministic Non-linear Least Squares Method

The (r, θ, N) data collected in "Data Collection for SIF Evaluation" serve as inputs for the over-deterministic non-linear least squares method whose salient details are discussed next.

Multiparameter crack-tip stress field equations

The corrected equations of Atluri and Kobayashi [18] for a general mixed-mode condition in terms of positional coordinates (r, θ) with the crack-tip as the origin are given as:

$$\begin{array}{r}\left\{\begin{array}{c}{\sigma }_{x}\\ {\sigma }_{y}\\ {\tau }_{xy}\end{array}\right\}=\sum\limits_{n=1}^{\infty }\dfrac{n}{2}{A}_{{\text{I}}n}{r}^{\frac{n-2}{2}}\left\{\begin{array}{c}\left(2+\dfrac{n}{2}+{\left(-1\right)}^{n}\right){\text{cos}}\left(\dfrac{n}{2}-1\right)\theta -\left(\dfrac{n}{2}-1\right){\text{cos}}\left(\dfrac{n}{2}-3\right)\theta \\ \left(2-\dfrac{n}{2}-{\left(-1\right)}^{n}\right){\text{cos}}\left(\dfrac{n}{2}-1\right)\theta +\left(\dfrac{n}{2}-1\right){\text{cos}}\left(\dfrac{n}{2}-3\right)\theta \\ \left(\dfrac{n}{2}-1\right){\text{sin}}\left(\dfrac{n}{2}-3\right)\theta -\left\{\dfrac{n}{2}+{\left(-1\right)}^{n}\right\}{\text{sin}}\left(\dfrac{n}{2}-1\right)\theta \end{array}\right\}\\ -\sum\limits_{n=1}^{\infty }\dfrac{n}{2}{A}_{{\text{II}}n}{r}^{\frac{n-2}{2}}\left\{\begin{array}{c}\left(2+\dfrac{n}{2}-{\left(-1\right)}^{n}\right){\text{sin}}\left(\dfrac{n}{2}-1\right)\theta -\left(\dfrac{n}{2}-1\right){\text{sin}}\left(\dfrac{n}{2}-3\right)\theta \\ \left(2-\dfrac{n}{2}+{\left(-1\right)}^{n}\right){\text{sin}}\left(\dfrac{n}{2}-1\right)\theta +\left(\dfrac{n}{2}-1\right){\text{sin}}\left(\dfrac{n}{2}-3\right)\theta \\ -\left(\dfrac{n}{2}-1\right){\text{cos}}\left(\dfrac{n}{2}-3\right)\theta -\left\{-\dfrac{n}{2}+{\left(-1\right)}^{n}\right\}{\text{cos}}\left(\dfrac{n}{2}-1\right)\theta \end{array}\right\}\end{array}$$
(2)

where AIn and AIIn represent the mode-I and mode-II parameters, respectively. The SIFs and T-stress are related to the respective coefficients as \({K}_{{\text{I}}}={A}_{{\text{I1}}}\sqrt{2\pi }, {K}_{{\text{II}}}=-{A}_{{\text{II1}}}\sqrt{2\pi } {\text{ and }} {\sigma }_{ox}=-{4A}_{\text{I2}}\) The nonlinear regression analysis is carried to fit the experimental data to Equation (2) iteratively by suitable addition of parameters for SIF evaluation. Fringe order error minimisation is used as the convergence criterion for the iterations [18] which is deemed satisfied if

$$\frac{\sum \left|{N}_{theory}-{N}_{exp}\right|}{\mathrm{Total\;no.\;of\;data\;points}}\le \mathrm{convergence\;error}$$
(3)

where Ntheory is the theoretical fringe order obtained at every datapoint from the iterated parameters and Nexp is the actual fringe order obtained experimentally at the point of interest. Initially, for a two-parameter modelling of the stress field, a convergence error of 0.5 is taken and the value is progressively reduced as the number of parameters is increased. Achieved convergence error of 0.05 or less is considered as a good solution.

The experimental datapoints are echoed back on the theoretically simulated isochromatics to ensure that the stress field is indeed reconstructed as desired in addition to monitoring the convergence error. This verification based on fringe order minimisation along with satisfactory theoretical reconstruction of the fringe field has been emphasized in fracture mechanics literature to ensure acceptable results [32, 36].

The data collection and regression analysis are carried out using an in-house software PSIF [37]. The implementation of all the steps elaborated is presented in detail for one sample case in Appendix-A.

Isochromatic Fringe Features at a Crack-tip in the Presence of Contact Stress and SIF Evaluation

A rectangular epoxy beam of dimensions 150 \(\times\) 50 \(\times\) 5.5 mm is taken with a 9 mm vertical crack on the bottom edge. The beam is supported fully on aluminium at the bottom. An epoxy disc of 30 mm radius is used to apply a contact load (P) of 419 N on the top, symmetrical to the crack axis. The dark field isochromatics captured in colour is shown in Fig. 1(a). One observes prominent forward tilting of the crack-tip fringes. The whole field fringe order data for the portion inside the black square in Fig. 1(a) is obtained and the dark, mixed and composite field fringes are presented in Fig. 1(b-d), respectively.

Fig. 1
figure 1

(a) Experimental dark field isochromatics in colour recorded using white light with the region of interest highlighted using black square; grayscale fringes for region of interest as (b) dark field, (c) mixed-field, (d) composite field with near-tip zone marked in red square, (e) close-up of the near-tip zone showing green circle of size 5 times the permissible data collection zone in two-parameter method. Theoretical composite field reconstruction with 55 red experimental datapoints echoed back for (f) 2 parameters, (g) 4 parameters and (h) converged 7 parameter solution

Full size image

It is observed from the crack-tip isochromatic fringes in Fig. 1(b) that in addition to a forward tilt, there is a prominent frontal loop formed ahead of the crack due to the presence of a contact loading applied far away from the crack-tip. Such features get better highlighted using mixed and composite field fringes (Fig. 1(c and d)).

Evaluation of Stress Intensity Factors

In 1957, Irwin, while discussing the results of Post and Wells [38, 39], commented that Westergaard’s solution is inadequate in modelling the observed experimental isochromatics and suggested adding a correction term (-σox) to σx for analysis of finite bodies [40], which is now known as T-stress in fracture literature. This addition explained the forward tilt in the photoelastic fringes, near the crack-tip, as observed in the experiments [38]. Consequently, he showed that the SIF could be theoretically calculated using just one datapoint lying at the farthest point from a photoelastic fringe loop, which is known as Irwin’s two-parameter method.

If one overlooks the presence of the frontal loop in Fig. 1(a), one will attempt to evaluate the SIF using Irwin’s two-parameter method. However, to obtain valid results, Irwin’s two-parameter method requires the farthest datapoint to lie within an extremely small circular zone of radius rm near the crack-tip (rm/a < 0.03) and the angular orientation of this farthest point on the fringe (θm) to lie in the range 73° < θm < 139° [41]. The near-tip zone marked using a red square in Fig. 1(d) is magnified and presented in Fig. 1(e) showing rm and θm labelled with respect to the crack axis. It is not possible to comply with these requirements for the fringes shown in view of the crack-contact interaction. To impress upon this point further, Fig. 1(e) also shows a circle in green having a radius of 1.35 mm which is 5 times the radius of the permissible zone for data collection as per ref. [41]. Even within this circle, there are no discernible fringes for data collection. On considering the closest fringe to the crack-tip from the composite field (N = 1.25), the respective measures for rm and θm are 2.286 mm and 69.58°. The computed values of KI and σox using the two-parameter method are 0.010 MPa√m and 2.612 MPa, respectively. The predicted SIFs change sharply with a small change in the measure of θm which would not give reliable results. Hence, Irwin’s two parameter method is found unsuitable for studying this case.

Sanford [42] observed that Irwin’s correction of Westergaard’s solution is only valid for specific cases. He observed that in experiments, several fringes can cross the crack axis, such as frontal loops for a long crack in an SEN specimen and obtained generalised Westergaard's solution of the crack-tip stress field involving multiple parameters whose coefficients need to be evaluated experimentally. Reference [43] brought out that the various multi-parameter solutions reported are identical and noted that the one by Atluri and Kobayashi [17] is the most elegant one to use.

The present problem (Fig. 1(d)) is initially analysed using the least squares method with the multiparameter crack-tip stress field equations (for a detailed description, see one sample case in Appendix -A). The theoretical reconstruction of the fringe field at 2 parameters, 4 parameters and the converged solution with 7 parameters are presented in Fig. 1(f–h). Even within the multiparameter framework, just two parameters do not reconstruct the fringe field correctly even though it utilises whole field data and not just a point as in case of Irwin’s two-parameter method. It requires 7 parameters to get an acceptable reconstruction. The mode-I SIF (KI) and T-stress evaluated from the converged solution are 0.160 MPa√m and 1.20 MPa within an uncertainty of 0.0024 and 0.009, respectively. The errors between the evaluated values using the multiparameter solution and Irwin’s two-parameter method are 94% and 118% for KI and T-stress, respectively.

Analytical Superposition of Singular Crack and Contact Stress Field

In Ref. [30], to analyse the isochromatics in the presence of adjacent contacts, they have used a linear superposition of the individual stress fields. Following the superposition method suggested in ref. [30], an attempt to understand the interaction analytically is made using a simple superposition of singular crack-tip stress field (KI = 0.160 MPa√m, (Fig. 1(h)) and contact stress field equations. The combined equations required for plotting simulated isochromatics are presented in Appendix – B. The contact stress field corresponding to Fig. 1(a) is modelled using the following inputs: E = 2.3 GPa, v = 0.34, μ = 0, R1 = 30 mm, R2 = ∞ and P = 419 N.

The experimental dark field isochromatics and the composite field in grayscale for the crack-tip region are reproduced in Fig. 2(a and b) with the features highlighted for clarity. To better understand the influence of contact stress, the results using the equations are presented separately in a stepwise manner.

Fig. 2
figure 2

Experimental isochromatics (a) dark field using white light with the region of interest marked using black square, (b) composite field in grayscale for region of interest with fringe features highlighted. Plots for dark field isochromatics in colour with region of interest marked and composite field in grayscale for the region of interest for qualitative comparison using (c-d) only singular term, (e–f) only contact field and (g-h) superposed equations of singular term and contact field for an a/w ratio of 0.18

Full size image

Initially, the isochromatics are plotted using only a singular term crack-tip stress field presented in Fig. 2(c and d). Observing the composite field fringes for the region of interest in Fig. 2(d) shows that the fringes are symmetric about the horizontal. Next, the isochromatics are plotted using only the contact stress field appropriately placed as presented in Fig. 2(e and f). Upon superimposing the singular crack-tip stress field with this contact stress field, one can observe marked changes in the isochromatic features at the crack-tip (Fig. 2(g and h)). It can be seen from Fig. 2(h) that a prominent frontal loop appears in addition to a forward tilt qualitatively capturing the geometric features observed in the experiment. The presence of such features, particularly the frontal loop, can be attributed to a crack-contact stress interaction.

In the interest of further understanding this interaction, qualitative isochromatic plots using the superposed equations for two more cases of smaller crack lengths, 6 mm (a/w = 0.12) and 3 mm (a/w = 0.06), are presented in Fig. 3(a-d). Frontal loops are observed even for very small cracks (a/w = 0.06) which can only be attributed to the interaction with the contact stress field.

Fig. 3
figure 3

Plots for dark field isochromatics in colour and composite field in grayscale using the superposed equations for qualitative visualisation of fringe features for a/w ratio of (a and b) 0.12 and (c and d) 0.06

Full size image

The results using the superposed equations are presented here only to appreciate the presence of these geometric features and not the exact sizes. The sizes of the fringes will only match once the appropriate fracture parameters are evaluated for this problem from the experimental fringes in Fig. 2(a). The evaluation of these parameters using the superposed solution approach is taken up next and the procedure is discussed in the subsequent sections.

While the contact stress field is global in nature, the crack-tip solution is essentially a near-field solution. Hence, SIF evaluation using the superposed equations requires a two-step approach – (i) evaluation of the contact stress parameters, namely, semi-contact length (ac) and friction coefficient (µ) using a least-squares analysis and (ii) evaluation of SIFs using the superposed equations (with ac and µ in (i)) with appropriate weights for the individual crack-tip and contact stress fields which is presented next.

Evaluation of contact stress parameters (a c and μ) from experimental results

From the experimental image, the whole field fringe order data is obtained. It should be noted that the contact stress field is defined with the centre of load application taken as the origin. With this appropriate origin, the data points for the least squares analysis are collected from the dark field fringes. Since the centre of the load application point in experiments is user-specified, it is error-prone much like the user-defined crack-tip in experiments (See Appendix—A). Hence, the process of contact stress origin refinement is carried out to identify the origin of the contact stress (centre of the load application) accurately. The isochromatic fringe field is then theoretically reconstructed with experimental datapoints echoed back for verification as presented in Fig. 4.

Fig. 4
figure 4

(a) Experimental dark field isochromatics recorded in white light (P = 419 N), (b) dark field fringes in grayscale and (c) reconstructed fringe field with data points echoed back in red (50 Nos.)

Full size image

The values of contact parameters obtained from processing the experimental results are ac = 1.51 mm and \(\mu\)  = 0.006. These values are used for the evaluation of SIFs in step-II.

Evaluation of stress intensity factors using the superposed equations

The least squares analysis is carried out using the superposed equations with the contact parameters taken from "Evaluation of Contact Stress Parameters (ac and μ) From Experimental Results" and user-specified constant weights for the contact stress field as well as the crack-tip stress field. Given that the analysis is done near the crack-tip with the contact load far away, the weights are chosen to be higher for the crack-tip stress field and lower for the contact stress field.

Typical results from the analysis for 1 parameter, 4 parameters and 7 parameters are presented for two cases of weights considered (wcontact and wcrack) are presented in Fig. 5.

Fig. 5
figure 5

Composite field reconstruction using superposed solution approach for 1 parameter, 4 parameters and 7 parameters (left to right) using two different weights for stress fields (a-c) wcontact = 0.05; wcrack = 0.95 and (d-f) wcontact = 0.02; wcrack = 0.98 with experimental datapoints echoed back in red

Full size image

The evaluated SIFs for the cases presented in Fig. 5 along with the corresponding convergence errors (CE) are tabulated in Table 1.

Table 1 Results from least squares analysis using superposed solution approach
Full size table

The analysis shows that one parameter solution even with superposition is unable to capture the geometric features of the experimental fringes. While using a four-parameter solution, the geometric features are qualitatively captured and the case requires a seven-parameter solution superposed with contact stress field to capture all the key geometric features ahead of the crack-tip as seen in Fig. 5(f).

It is observed that convergence and proper reconstruction is achieved at lower weights for the contact field (Fig. 5(f)) with a SIF value of 0.156 MPa√m as compared to 0.160 MPa√m (with convergence error of 0.006) using the multiparameter solution presented in "Evaluation of Stress Intensity Factors".

The comparison shows that the results are consistent, provided the choice of weights are appropriate. Evaluation of the appropriate weights may be difficult for a complex problem. Further, the weights for the stress fields for a given problem need not be constants but could also have spatial variation. Hence, although it may be conceptually appealing to compute the SIFs using the superposed analytical equations while approaching such a problem, it is cumbersome from a practical standpoint. The two-step process where the contact stress has to be handled separately followed by the evaluation of appropriate weights for every problem makes this approach unwieldy to implement. On the other hand, given that the crack-tip multiparameter solution is only valid in the neighbourhood of the crack-tip, the self-sufficiency of this solution by suitably choosing the data collection zone is explored in the subsequent sections.

Numerical Verification of the SIFs Evaluated Using the Multiparameter Crack-tip Solution

The configuration shown in Fig. 6 is used for a numerical comparison. To facilitate easy implementation of the boundary conditions in the numerical code, a moderately-deep beam (L/d ~ 2.4) subjected to three-point bending is considered with a very small crack of 4 mm.

Fig. 6
figure 6

Loading schematic for the moderately-deep beam

Full size image

Three load cases are considered for this beam (P1 = 270 N, 308 N and 347 N). The experimental isochromatics recorded using white light are shown in Fig. 7(a) from portion of the beam highlighted in green rectangle in Fig. 6. This portion is considered for further processing.

Fig. 7
figure 7

Results for a moderately-deep beam with column (a) dark field experimental isochromatics with region of interest marked in green, (b) numerically post-processed isochromatics from finite elements (c) mixed-field fringes for the region of interest with data collection zone marked in red rectangle and (d) theoretical reconstruction with datapoints echoed back in red

Full size image

Numerical model is developed in Abaqus® using the XFEM module to model the crack discontinuity. C3D8R 8-noded hexahedral linear brick elements with reduced integration are used. The elliptical distribution of the contact stress is applied using a user-defined analytical field based on the equations from Smith and Liu [19]. Mesh convergence study is carried out and a mesh size of 0.15 mm is used near the crack-tip which gives converged results. The field output from the software is post-processed using an in-house developed method to obtain numerical isochromatics fringes with colours as one would observe in experiments [32]. The numerically post-processed isochromatics for the respective cases closely match with the experimentally obtained fringes (Fig. 7(a and b)).

The red rectangles indicated in the mixed-field fringes (Fig. 7(c)) are used for data collection and SIFs are evaluated using the procedure mentioned in "Methods of Analysis" (an example case presented in Appendix-A). Upon convergence, the fringe field is reconstructed with the datapoints from the experiment echoed back in red (Fig. 7(d)). It can be seen that the reconstruction is good.

Stress intensity factors for the three load cases are evaluated using the multiparameter solution. The mode-I SIFs (KI in MPa√m) are 0.297, 0.341 and 0.376, respectively. The respective mode-II SIFs (KII in MPa√m) are 0.011, 0.013 and 0.016. The solution requires 8, 8 and 9 parameters and the corresponding convergence errors achieved are 0.025, 0.030 and 0.025, respectively that conforms to the recommendation of convergence error less than 0.05. The SIFs are also obtained from the finite element models using the J-integral approach embedded in the software module. The respective SIFs (in MPa√m) for the three load cases from these numerical models are 0.305, 0.348 and 0.392 for mode-I and 0.012, 0.013 and 0.015 for mode-II. The SIF values from experiments and finite elements are compared and a p-value of 0.06 is obtained against a significance level of 0.05 which shows that there is no significant difference in the results.

In view of this, the use of multiparameter crack-tip solution alone is further explored for studying crack-contact stress fields. In the following section, more cases are studied wherein, the contact load is moved closer to crack-tip in stages.

SIF Evaluation for Different Configurations in a Moderately-slender Beam (L/d ~ 4.91)

Since beams are members which often have to support moving contact loads like rail roads, these are suitable candidates for interaction studies once a crack develops in them. Multiple configurations with varying load positions and magnitudes are considered for a moderately-slender beam (L/d ~ 4.91) (Fig. 8(a)). A vertical through-thickness crack of 4 mm length is introduced on the top face of the beam (a/d ~ 0.14). The contact load is applied at different positions using a circular epoxy half-disc of radius 30 mm. The distance between the crack axis and the contact load axis, labelled as S in Fig. 8(a), is decreased from 20 mm, 15 mm, 10 mm, 5 mm, 2 mm to S = 0 in order to increase the influence of contact stress on the crack-tip. The experiments are conducted for two load cases, namely, P2 = 83 N and 125 N. The convention used for discussions in the following sections is shown in Fig. 8(b).

Fig. 8
figure 8

(a) Loading schematic for the moderately-slender beam and (b) convention used for discussion

Full size image

The changes in the fringe features with the moving load can be seen in Fig. 9(a-f) for 83 N contact load. It can be observed that the fringe features on the left side of the crack get modified significantly when the load is moved closer progressively.

Fig. 9
figure 9

Experimental dark field isochromatics for a contact load of 83 N applied using a 30 mm radius circular half-disc with S values of (a) 20 mm, (b) 15 mm, (c) 10 mm, (d) 5 mm, (e) 2 mm and (f) S = 0

Full size image

The experimental isochromatics captured for a similar configuration with an increased contact load of 125 N are shown in Fig. 10(a-f).

Fig. 10
figure 10

Experimental dark field isochromatics for a contact load of 125 N applied using a 30 mm radius circular half-disc with S values of (a) 20 mm, (b) 15 mm, (c) 10 mm, (d) 5 mm, (e) 2 mm and (f) S = 0

Full size image

The experimental isochromatics are processed (as per Appendix A) to obtain the SIFs. The converged results are presented along with results at some intermediate parameters for two typical cases, namely, S = 20 mm (Fig. 11) and S = 5 mm (Fig. 12), respectively.

Fig. 11
figure 11

(a) Experimental dark field isochromatics with the region of interest marked in green, (b) mixed-field fringes for the region of interest with data collection zone marked in red rectangle. Theoretical reconstruction with experimental datapoints echoed back in red for (c) 2 parameters, (d) 5 parameters and (e) converged 9 parameter solution for S = 20 mm and P2 = 83 N

Full size image
Fig. 12
figure 12

(a) Experimental dark isochromatics with region of interest marked in green, (b) mixed-field fringes for the region of interest with data collection zone marked in red rectangle. Theoretical reconstruction with experimental datapoints echoed back at (c) 2 parameters and (d) converged 10 parameter solution for S = 5 mm and P2 = 83 N

Full size image

Figure 11(a) shows the region of interest in the dark field isochromatics captured. The mixed-field fringes for this region are seen in Fig. 11(b) with the red rectangle showing the zone from where data (r, θ, N) has been collected for SIF evaluation. In this case, the ratio of the maximum radius of data collection zone to the crack length (rm/a) is around 1.67 and 1.16 on the right and left side of the crack, respectively (see Fig. 8(b)). The respective theoretical reconstructions at 2 parameters, 5 parameters and the converged solution with 9 parameters are presented in Fig. 11(c–e). While the two-parameter solution is unable to capture the features, by increasing the number of parameters, the multiparameter solution is seen to be very effective in capturing the fringe field. The fringe order error achieved for these cases are 0.077, 0.069 and 0.023, respectively. The error achieved with 9 parameters is well below admissible values (Over-deterministic Non-linear Least Squares Method).

As the contact load is brought closer to the crack, the zone of data collection needs to be adjusted. Figure 12(a) shows the dark field isochromatics for S = 5 mm and P2 = 83 N with the region of interest marked in green and the mixed-field fringes for this region are presented in Fig. 12(b). The red rectangle in Fig. 12(b) shows the data collection zone with rm/a of around 0.8 on the right and in the range of 0.7 to 0.95 on the left of crack. The reconstruction at 2 parameters and the converged 10-parameter solution with convergence errors of 0.14 and 0.03, respectively are shown in Fig. 12(c and d). It can be seen that even complex features due to nearby contact load are effectively getting captured using the multiparameter solution with good reconstruction and satisfactory convergence.

Figure 13 presents the results for the cases S (mm) = 15, 10, 2 and 0 for contact load of 83 N in a consolidated form with the region of interest, mixed-field fringes (with data collection zone in red rectangle), fringe reconstruction at 2 parameters and converged solution shown from left to right.

Fig. 13
figure 13

Experimental dark field isochromatics with the region of interest marked in green, mixed-field fringes for the region of interest with data collection zone marked in red rectangle and theoretical reconstruction with experimental datapoints echoed back at 2 parameters and converged solution (left to right) for P2 = 83 N and (a) S = 15 mm, (b) S = 10 mm (c) S = 2 mm and (d) S = 0

Full size image

For the case of S = 0, due to symmetry, the crack experiences only mode-I loading. However, the problem becomes challenging due to the presence of contact stresses and the useful data collection zone becomes extremely small. The mode-I fringes are confined to a very small zone near the crack tip (~ 1 mm \(\times\) 1 mm) as highlighted by the red square in mixed field fringes (Fig. 13(d)). The fringe order data obtained using sophisticated algorithms developed in photoelasticity data extraction is used advantageously. Using the whole field data, multiple fringes are obtained for data collection as close as ~ 0.5 mm in a zone as small as 1 mm \(\times\) 1 mm to obtain a good reconstruction and effectively evaluate the SIF.

The fringe order errors at convergence for these four cases are 0.014, 0.015, 0.026 and 0.035. The values of the ratio, rm/a for these four cases in the form [right of crack, left of crack] are [1.12, 1.04], [1.24, 0.94], [1.00, 0.75] and [0.25, 0.25], respectively.

It can be seen that as the load moves closer, with suitable reduction in the data collection on the left side of the crack, the multiparameter solution is able to capture the essential features of the fringe field.

Similar configurations have been processed for contact load (P2) of 125 N to introduce variation and assess the performance of the multiparameter solution. The results are presented in a consolidated form for each case of distance S in Fig. 14(a-f). Each case is presented (from left to right) – dark field isochromatics (with region of interest marked in green), mixed-field fringes (with data collection zone in red rectangle), fringe reconstruction at 2 parameters and converged solution.

Fig. 14
figure 14

Experimental dark field isochromatics with the region of interest marked in green, mixed-field fringes for the region of interest with data collection zone marked in red rectangle and theoretical reconstruction with experimental datapoints echoed back at 2 parameters and converged solution (left to right) for P2 = 125 N and (a) S = 20 mm, (b) S = 15 mm, (c) S = 10 mm, (d) S = 5 mm (e) S = 2 mm and (f) S = 0

Full size image

The respective fringe order errors at convergence for these cases are 0.022, 0.027, 0.039, 0.030, 0.047 and 0.042, respectively. The errors are well below the specified criteria for convergence in "Over-deterministic Non-linear Least Squares Method" which shows that the method is very effective in capturing the solution with the suitable addition of parameters. The values of the ratio, rm/a for these cases in the form [right of crack, left of crack] are [1.77, 1.64], [2.09, 1.57], [1.41, 1.22], [1.05, 0.91], [0.98, 0.78] and [0.29, 0.29], respectively. It can be seen that the theoretical reconstruction even in the cases where the contact loading is very close to the crack axis is good using the multiparameter solution (Fig. 14(d-f)).

It is to be noted that all the interaction cases under study are having mode-mixities which is comfortably handled in the form of independent SIFs using the multiparameter solution. The variation of the SIFs obtained with the load positions is presented in Fig. 15.

Fig. 15
figure 15

Variation of evaluated SIFs with varying load positions for the moderately-slender beam

Full size image

The upper and lower bound SIF values obtained from an uncertainty analysis are tabulated in Table 2. Details about the procedures for uncertainty analysis are presented for a sample case in Appendix-A.

Table 2 SIF values for all cases along with corresponding uncertainty values
Full size table

The variation observed in the evaluated SIFs is very less with a range [0.0012, 0.0041] for KI and [2 \(\times\) 10–4, 0.0015] for KII, respectively. Further, there is a reduction observed in the Mode-I SIFs when the contact loading axis and the crack axis coincide with the Mode-II response vanishing due to symmetry.

Conclusion

In this paper, the changes in the geometric features of the isochromatics in the neighbourhood of a crack-tip due to the presence of contact load is brought out. If the presence of the frontal loop is overlooked, one may attempt to evaluate the SIF using the Irwin’s two-parameter solution, which is shown to be not applicable even when a small crack is interacting with a faraway contact load. This implies that a multi-parameter solution is basically needed to handle problems dealing with a crack interacting with the contact load.

Although one may be interested in the first two parameters of Mode-I (KI and T-stress) and the first parameter for Mode-II (KII), to evaluate these from the isochromatic field, a multi-parameter solution is needed, which effectively captures the fringe features upon convergence. The applicability of the use of crack-tip multi-parameter stress field equations being sufficient to extract the SIF is verified by results from FEM for the case of a moderately-deep beam under three-point bending.

Following this, different interaction configurations in a moderately-slender beam are systematically checked by increasing the proximity of the contacts stress relative to the crack-tip. The geometric features of the fringe field are quite complex and it is observed that with appropriate data collection, the multiparameter solution gives fracture parameters for all cases with well-reconstructed fringe field. The evaluated SIFs are reported along with an uncertainty analysis carried out with different datasets. This study demonstrates that the multiparameter solution is very effective in studying problems having interacting between crack-tip and contact stress fields. The applicability of this approach can be extended to study crack-contact interactions found in problems like rail-wheel interaction, mating gears, etc.