Keywords

10.1 Background

Hybrid-experimental approaches facilitate the determination of fundamentally important separate stresses through coupling full-field experimental data with an analytical expression. Full-field experimental methods such as thermoelastic stress analysis (TSA), photoelastic stress analysis (PSA), digital image correlation (DIC), moiré, etc., result in data that are discrete and whose resolution depends on the experimental setup (sensor resolution, lens used, focal distance, grid analyzer, etc.). Moreover, data near geometric singularities such as near holes, notches, and edges are in general unreliable due to different edge effects specific to the experimental approach. Most importantly, raw data often offer one piece of information, e.g. isopachic stresses for TSA, isochromatic stresses for PSA, and displacements for DIC, as opposed to individual separate stress information in the case of analytical solutions and finite element methods. The present study focuses on TSA, where output data are proportional to the summation of the first two principal stresses when considering a two-dimensional plane-stress loading situation as described in Eq. 10.1:

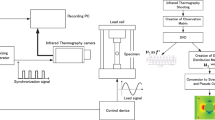
$$ {S}^{\ast }= K\varDelta S= K\varDelta \left({\sigma}_1+{\sigma}_2\right) $$
(10.1)

where S* is the measured TSA image, S the calibrated TSA image, and K the calibration coefficient related to the relevant physical properties of the material of interest, surface condition and TSA system parameters [1], often obtained from a test on a separate uniform coupon. A typical TSA test setup is shown in Fig. 10.1. With failure analysis being essential in engineering design, the separation of TSA coupled stresses becomes necessary – and this has been the topic of interest for many research efforts to date. The first determination of individual thermoelastic stresses was presented in [2] by taking into account the boundary conditions and the expected form of the stress distribution. More work was done in the following decade with the focus on performing such separation on structures with various discontinuities: structure with a circular hole [3], beneath concentrated loads [4], elliptical cutout [5], irregularly-shaped discontinuities [6], pinned structures [7] and more recently on unsymmetrical loading condition often encountered in real life structures [8]. A good review of hybrid thermoelastic stress analysis (Hybrid-TSA) approaches and their different timeline of events are presented in [9] in a special issue of the Journal of Experimental Mechanics on Infrared Imaging and Thermomechanics.

Fig. 10.1
figure 1

Hybrid-TSA test setup

Full size image

10.2 Analytical Component

Individual stress components can be determined by combining TSA thermal data of Eq. 10.1. with relevant analytical information. Many such schemes process the recorded thermal information with equations based on an Airy stress function. For plane-stress isotropy [10], the Airy stress function satisfying conditions of equilibrium and compatibility is given by Eq. 10.2 below:

$$ \begin{array}{l}\phi ={a}_0+{b}_0\operatorname{ln}r+{c}_0{r}^2+{d}_0{r}^2\operatorname{ln}r+\left({A}_0+{B}_0\operatorname{ln}r+{C}_0{r}^2+{D}_0{r}^2\operatorname{ln}r\right)\theta +\left({a}_1r+{b}_1r\operatorname{ln}r+\frac{c_1}{r}+{d}_1{r}^3\right)\operatorname{sin}\theta \\ {}\hspace*{6pt}\quad+\left({a}_1^{\prime}r+{b}_1^{\prime}r\operatorname{ln}r+\frac{c_1^{\prime}}{r}+{d}_1^{\prime}{r}^3\right)\operatorname{cos}\theta +\left({A}_1r+{B}_1r\operatorname{ln}r\right)\theta \operatorname{sin}\theta +\left({A}_1^{\prime}r+{B}_1^{\prime}r\operatorname{ln}r\right)\theta \operatorname{cos}\theta +{\sum}_{n=2}^{\infty}\left({a}_n{r}^n+{b}_n{r}^{n+2}\right. \\ \hspace*{6pt}\quad\left. +\operatorname{ln}r+{c}_n{r}^{-n}+{d}_n{r}^{2-n}\right)\operatorname{sin} n\theta + {\sum}_{n=2}^{\infty}\left({a}_n^{\prime}{r}^n+{b}_n^{\prime}{r}^{n+2}+{c}_n^{\prime}{r}^{-n}+{d}_n^{\prime}{r}^{2-n}\right)\operatorname{cos} n\theta \end{array} $$
(10.2)

where S in Eq. 10.2 can be expressed in terms of the Airy stress function coefficients since

$$ {\sigma}_1+{\sigma}_2=\frac{1}{r}\frac{\partial \phi }{\partial r}+\frac{1}{r^2}\frac{\partial^2\phi }{\partial {\theta}^2}+\frac{\partial^2\phi }{\partial {r}^2} $$
(10.3)

To date, some work has been done aiming at determining the effects of: the number of Airy coefficients, the number of TSA data points, and the level of noise on the overall accuracy of Hybrid-TSA; but without exploring the potential of filtration of TSA images. While TSA data acquisition software (e.g. DeltaTherm by StressPhotonics [11]) does offer different types of filter, the work presented here is focused on the effectiveness of TSA image filtration in the context of Hybrid-TSA.

10.3 Reconstructing TSA Image

The study here is performed on an isotropic disk that is compressed along its diameter as shown in Fig. 10.1. The isopachic stress expression was simulated using the exact analytical solution given in [12] as shown in Eq. 10.4:

$$ {S}_{exact}={\sigma}_1+{\sigma}_2=\frac{-2P}{\pi t}\left[\frac{{\left(R-y\right)}^3+\left(R-y\right){x}^2}{{\left({x}^2+{\left(R-y\right)}^2\right)}^2}+\frac{{\left(R+y\right)}^3+\left(R+y\right){x}^2}{{\left({x}^2+{\left(R+y\right)}^2\right)}^2}-\frac{1}{R}\right] $$
(10.4)

The analytical expression, Eq. 10.4, was used to simulate experimental parameters such as number of data points and more importantly, introduce multiple noise levels. Due to symmetry, only the first quadrant was examined: see Cartesian and polar coordinate systems in Fig. 10.2. The Airy expression of S in Eq. 10.3 was reduced to Eq. 10.5 below for the symmetry and location of the origin:

$$ {S}_{Airy}=4{c}_0+{\sum}_{n=2,4,\dots}^{\infty}\left[4{b}_n^{\prime}\left(n+1\right){r}^n\operatorname{cos} n\theta \right] $$
(10.5)
Fig. 10.2
figure 2

Diametrically loaded disk

Full size image

The solution to the Hybrid-TSA involves solving an over-determined linear-least squares problem where S Airy is equated to S TSA , given in Eq. 10.6:

$$ {\left\{{S}_{Airy}\right\}}_{m\times 1}={\left[A\right]}_{m\times k}\ {\left\{\mathrm{coef}\right\}}_{k\times 1}={\left\{{S}_{TSA}\right\}}_{m\times 1} $$
(10.6)

where: m is the number of TSA data points used, k the number of coefficients, and [A] the Airy matrix. The latter quantity is composed of m 1st stress invariant expressions of the form of Eq. 10.5 in terms of r and θ associated with the m TSA data points used. Upon solving for the coefficients in Eq. 10.6, those are then substituted back into Eq. 10.5 such that the TSA stress field can be reconstructed using Eq. 10.7.The reconstructed image is referred to as S hybrid and is the result of this Hybrid-TSA method.

$$ {\left\{{S}_{hybrid}\right\}}_{m\times 1}={\left[A\right]}_{m\times k}\ \left\{{\left[A\right]}_{m\times k}\backslash {\left\{{S}_{TSA}\right\}}_{m\times 1}\right\} $$
(10.7)

10.4 Simulated Experiments

10.4.1 Methodology

For each test case, a single synthetic S exact image is constructed from Eq. 10.4 as an initial step. Second step, 50 white noise images are masked onto the original one for a given white noise level (expressed in percentage being a study parameter). Numerous noisy images are indeed necessary to extract a global trend about the influence of the filter. Step three, filtration is applied to each of the 50 noisy images with the filter kernel size (in pixel being a processing parameter). Step four, all the 50 S noisy and 50 S filtered are pushed into the Hybrid-TSA approach where they are combined with S Airy of Eq. 10.5, and ultimately reconstructed using Eq. 10.7. For every reconstructed image, the error indicators in Eqs. 10.8 and 10.9 below have been used as a metric for the improvement, or in some cases the lack of improvement, experienced from the image filtration.

$$ {\mathrm{E}}_{filter}=\sum \left[\frac{\left|\frac{S_{exact}}{S_{max}}\right|\times {\left({S}_{hybrid\_ filter}-{S}_{exact}\right)}^2}{N}\right] $$
(10.8)
$$ {\mathrm{E}}_{no\_ filter}=\sum \left[\frac{\left|\frac{S_{exact}}{S_{max}}\right|\times {\left({S}_{hybrid\_ no\_ filter}-{S}_{exact}\right)}^2}{N}\right] $$
(10.9)

where N is the number of pixels used. In addition, a local error at a pixel located at (x, y) can be defined as follows:

$$ {\mathrm{E}}_{\%}\left(x,y\right)=\frac{{\boldsymbol{S}}_{\boldsymbol{hybrid}}\ \left(\boldsymbol{x},\boldsymbol{y}\right)\hbox{--} {\ \boldsymbol{S}}_{\boldsymbol{exact}}\left(\boldsymbol{x},\boldsymbol{y}\right)}{{\boldsymbol{S}}_{\boldsymbol{exact}}\ \left(\boldsymbol{x},\boldsymbol{y}\right)}\times 100\% $$
(10.10)

Note that E filter and E no_filter have no unit, and can be thought of as “normalized” global error indicators. Indeed, they take into account the magnitude S exact of each pixel relative to the maximum magnitude S max over the disk (excluding the zone affected by boundary effects, see Sect. 4.3) in computing the root mean square, as opposed to E% of Eq. 10.10 which is a “straight forward” local percentage error. As calculation is performed for 50 copies of noise, it is then possible to do a statistical analysis on the output data (E filter , E no_filter and E%).

Figure 10.3 describes the flow of the simulated experiment described above. Note that the color bars of the stress contour plots are not shown here as this is for illustration purposes only. The level of white noise in that figure is set here to 10 % such that the differences between S exact , S noisy and S filtered is visually obvious. One immediate observation from the flow chart of Fig. 10.3 is the fact that the hybrid approach itself provides what can be thought of as an “implicit” filter to the noisy image, as the reconstructed fields are built from (analytical) continuous functions. This is evident when comparing the reconstructed image S hybrid_no_filter and the noisy image S noisy in Fig. 10.3. All S results can be then normalized with respect to S origin , which is the value at x = y = 0, see Eq. 10.4:

$$ {S}_{origin}=\frac{-2P}{\pi t}\left[\frac{1}{R}\right]\vspace*{-18pt} $$
(10.11)
Fig. 10.3
figure 3

Numerical experiment flow chart

Full size image

10.4.2 Filtration Approach

A Gaussian filtering is applied to each of the 50 noisy images S noisy . In practice, it is performed by convolution of a Gaussian kernel: see Fig. 10.2. A circular kernel is considered with a diameter equal to six times the standard deviation of the Gaussian function, enabling us to capture the main part of the Gaussian (note however that a normalization of the kernel values is required in order to keep a sum of the kernel values equal to one [13]). As a consequence, the filter can be governed by only one parameter: the diameter of the kernel, which is here expressed in pixel (see parameter filter_kernel_size in Fig. 10.2). An uneven number is required for filter_kernel_size to keep the symmetry of the kernel.

10.4.3 Boundary Effects

Pixels outside the disk are not usable. Different strategies are available to define the filtered values near the boundaries. For the present study, it was chosen to simply exclude the zone affected by boundary effects. In practice, a layer equal to half the kernel diameter is removed from the analysis: see Fig. 10.2. This clearance distance is thus linked to the filter kernel size chosen. Note that the values of the synthetic TSA data S exact near to the very top and bottom (location of point compressive loads) tends to infinity. The clearance zone enables us to exclude also these two stress concentration zones. This is done prior to combining the S exact from Eq. 10.4 with S Airy from Eq. 10.5, such that the linear least square operation of Eq. 10.7 is accomplished without any numerical issues. Still, this simulated test does mimic a real experimental one as it is not uncommon to remove experimental TSA data near edges of cutouts and discontinuities. This is mainly due to the boundary temperature effects as well as boundary vibration effects when the specimen is cyclically loaded while the data is recorded. More information on boundary effects and ways to amend them are discussed in [14].

10.4.4 Results

In a previous study, it was shown that the number of points m has an important impact on the quality of the Hybrid-TSA results. In fact, and contrary to what may seem obvious, the greater the number of TSA points used does not render the hybrid-reconstructed results better (regardless of the Airy coefficients used). Moreover, it was revealed that the level of white noise had no influence on the optimal number k of Airy stress function coefficients to use [15].

10.4.4.1 Effect of Noise Level

In this numerical test, the number m of data points is fixed to 30,000 points, a typical number to use when using a 256 × 256 TSA sensor camera, and the number of Airy stress function coefficients is fixed here to k = 11. Moreover, the kernel filter size is fixed to filter kernel size = 7, and thus the only variable in this numerical experimental is the white noise level. Figure 10.4 below displays both errors E filter and E no_filter with respect to various noise levels varying from 1 % to 10 %. The statistical bar chart reveals that an improvement is achieved by employing the filter prior to the image reconstruction for all noise levels. As mentioned earlier, each test configuration (e.g. noise level = 5 %, m = 30,000, k = 11, filter kernel size = 7) is performed on 50 synthetic noisy TSA images. That being said, Fig. 10.4 also reveals that the standard deviation of both errors E filter and E no_filter increases with higher noise levels. The stress function effect is quite substantial such that the reconstructed hybrid results are almost independent on the level of the noise. This explains why raw image filtering was never applied for Hybrid-TSA approaches.

Fig. 10.4
figure 4

Error bar comparing results pre- VS post- filtration for different white noise levels

Full size image

Figure 10.5 is a map of the local error Ε%(x, y), Eq. 10.10, for a given test scenario with noise level = 5 %. Note that the very high percentage error magnitudes at the edges are at locations of low stress magnitude, where a small change would reflect a high error. This is the main reason why Eqs. 10.8 and 10.9 with weighted rms error is more meaningful and representative in these numerical experiments. Also note the fluctuating sinusoidal trend in the error which is a reflection of the stress function expression of Eq. 10.4.

Fig. 10.5
figure 5

Map of local Ε %(x, y) post-filtration with 5 % noise

Full size image

10.4.4.2 Effect of Kernel Size

With the effect of the filtration being small compared to the natural filter due to the stress reconstructing approach based on analytical expression; a few other parameters have been varied, such as the filter kernel size parameter and the number of points selected out of the total field to be used in the hybrid approach, denoted m′ in the following. Figure 10.6 below is one set of numerical experiments for which the white noise was fixed to 10 %, number of stress function coefficients, k, set to 11, while the filter kernel size is varied for different number of points used, m′. Contrary to what was expected, even for a fairly few number of noisy data points, the stress function had an enough influence to steer the reconstructed image to its correct exact one with the filter kernel size having a minimal effect when looking at the magnitudes of the unitless errors E filter and E no_filter on the y-axis of Fig. 10.6. Similar to the previous numerical experiments, a set of 50 noisy images were used for each test configuration with their corresponding average error being the one plotted in Fig. 10.6.

Fig. 10.6
figure 6

Effects of filter kernel size for different m′

Full size image

The study thus far has shown a small influence of a Gaussian filtering to processing of TSA data in the context of Hybrid-TSA, as a consequence of the implicit filtration that the stress function introduces to the hybrid result. Other filters are available for the processing of thermal-based data [16] and will be considered in further work as well as the effects of the point location.