1 Introduction

Catastrophic floods and mudflows caused by the destruction of the dam can usually lead to significant property damage and casualties downstream. Because of this, it is important to simulate the design and planning of a dam break and associated damage. On March 11, 2010, intensive snow melting and heavy rains led to the Kyzylagash reservoir dam break in the upper reaches of the Kyzylagash river, Almaty region, Republic of Kazakhstan. As a result of these terrible floods, 43 people were killed, 300 were injured of varying degrees of severity and about 1000 were evacuated, 146 houses were completely demolished, 251 were destroyed and 42 were damaged. On March 31, 2019, a dam in which about 3.8 million m3 of water accumulated occurred in the Akmola region, Republic of Kazakhstan. The flow of water moved towards the city of Kokshetau along the channel of the Kylshakty River. In order to understand the effects of dam failure, extensive research has been conducted in recent years. The prediction of such effects of dam break that lead to catastrophic flooding has been studied by civilian and military researchers for more than a century.

Understanding flow characteristics, such as maximum water level and flood arrival time, is fundamental to engineering design and safety. The study mainly included theoretical solutions, physical experiments and numerical simulation. In the last two decades, special attention has been paid to the numerical modeling of the 2D and 3D dam break flows. For this purpose, many numerical methods have been developed.

Due to the rapid growth of computing power, in recent years, the study of dam break with the help of numerical modeling has become popular. Numerical simulation of dam break flows has been done in many papers (Aliparast 2009; Begnudelli and Sanders 2006; Bermúdez et al. 1998; Bradford and Sanders 2002; Brufau and García-Navarro 2000; Lai and Khan 2012; Leal et al. 2010a; Leal et al. 2010b; Lin et al. 2005; Liska and Wendroff 1998; Ozmen-Cagatay and Kocaman 2011; Ying et al. 2008; Yu and Huang 2014; Tsakiris and Spiliotis 2013). When the dam is destroyed, there is an intensive transfer of sediments, the associated morphological changes may be such that the whole riverbed will be changed. However, most studies are carried out with regard to purely hydrodynamic flows, that is, with disregard for morphological changes. Numerical modeling and understanding of the flow in natural rivers was a big challenge for water engineers and researchers. The 2D, depth-averaged shallow water equations of Saint-Venant (Lai and Khan 2012) were widely used to model shallow water flows in coastal zones, estuaries, lakes and natural rivers. Intensive sediment transfer leads to an increase in the level of the simulation result uncertainties. Although it is generally assumed that the sediment mass conservation equation should be added to the hydrodynamic equations, there are open questions concerning the inertia of moving sediments, closure models for transfer velocity or necessary simplifications for presenting complex reality to the actual interactions of sediment and liquid in a mathematical model.

A simple Riemann type solver of Godunov type with the assumption of two separate waves and three bound states, known as the Riemann HLL solver (solver of Harten, Lax, and van Leer) was proposed in (Harten et al. 1983). The modified the HLL solver with the assumption of three separate waves and four states, known as the Riemann HLLC solver (Toro et al. 1994). For the accuracy of modeling, (Fraccarollo and Toro 1995) developed a model using the Weighted Averaged Flux (WAF) method for the partial destruction of a dam over a fixed bed using shallow water equations. Then, in paper (Fraccarollo and Capart 2002), considered the dam destruction problem above the state of the moving layer, provided a theoretical description of the 1D dam destruction flow above the moving layer. To evaluate the Riemann solvers, which were widely used to solve the dam destruction problems, in paper (Erduran et al. 2002) compared the Riemann solvers in terms of implementation, applicability, accuracy and simulation time ease, and numerical stability.

The eigenvalues were developed for the Saint-Venant-Exner equation on a moving channel using an approximate Riemann HLL solver in a 1D model to study dam failure waves in a moving bed (Goutier et al. 2008). Most of the researchers in this simulation used the shallow water equations and the finite volume method (FVM) in their studies, as well as many of the reservoir load formulas that were used in comparative studies. Following this idea was carried out on a model of shallow water - Exner, which represents the destruction process of an embankment on a dam using six known reservoir loading compositions (Emelen et al. 2015).

Since the FVM could be used to handle dam breaks flow in complex terrain, a number of FVM based numerical methods were developed to solve shallow water equations on unstructured meshes (Yoon and Kang 2004; Song et al. 2010). However, using FVM has identified some non-physical numerical problems in the areas of impact and rupture, and one possible solution is to use a non-linear limiter, such as a flow restrictor (Tseng and Yen 2004) or a slope limiter (Tu and Aliabadi 2005). In the past two decades, most flow limiters have been widely used FVM. And significant progress has been made in the application of FVM, in such processes as dam breaking, coastal wave disturbances and tidal currents (Eskilsson and Sherwin 2010; Aizenger and Dawson 2002), flooding and drainage (Ern et al. 2008; Xing et al. 2010; Schwanenberg and Harms 2004). The study of these geomorphological currents is a difficult problem due to their complex dynamics. The interaction between the solid and liquid phases significantly changes the basic flow parameters, including the wave propagation speed and water levels. To keep a well-balanced property in the schema, it could be used the VOF method.

Dam break flows over a fixed impermeable layer have been carefully studied in many papers (Kleefsman et al. 2005; Bell et al. 2010; Marsooli and Wu 2014; Issakhov et al. 2018; Issakhov and Imanberdiyeva 2019), but with intense flows the lower layer of the flow may be moving, so this stream can transfer or shift to this lower layer, such as clay, mud, sand, etc. This process can lead to the very large amounts transportation of sediment, which leads to a large-scale change in the morphology of the area downstream and dramatically increases the damage to the environment and infrastructure of the city. Therefore, it is very important to take into account this geomorphological process of transfer and destruction of bottom sediments. The transfer of these sediments cannot simply be reproduced by the Newtonian fluid model (Gotoh and Fredsøe 2000) and the non-Newtonian model is usually used to predict the stress-dependent viscosity of the phase. The flows behavior in the fixed and moving layers conditions differ significantly, and they strongly influence the deformations of the free surface and the propagation of flood waves. Therefore, it is of great practical and theoretical interest to study these types of flow (Janosi et al. 2004; Lauber and Hager 1998).

In the papers (Papanicolaou et al. 2008; Fraccarollo and Capart 2002; Leal et al. 2010a; Li et al. 2013; Swartenbroekx et al. 2013) give an idea of future trends and needs in relation to hydrodynamic models and sediment transport models. The numerical results are compared with different sets of experimental data, in the conditions of fixed and moving layers, with different materials of the layer, in order to check the accuracy of modeling in a wide range of cases (Evangelista et al. 2013). A model of shallow water - Exner, representing the break process in the dam was used (Emelen et al. 2015). The paper (Hosseinzadeh-Tabrizi and Ghaeini-Hessaroeyeh 2018) simulates the dam break flow caused by the partial destruction of the dam in a suddenly enlarged area over the moving bed. In the study (Zhang and Duan 2011) used one-dimensional shallow water equations based on the FVM to study the various dam break flows above the moving bed. In paper (Xia et al. 2010) used modified 2D shallow water equations in combination with sediment transport to study the moving bed.

Dam break of pure non-Newtonian fluids, such as liquid clay and gel, have been studied in the works (Ancey and Cochard 2009; Chambon et al. 2009). Considering non-Newtonian fluids makes it possible to better explore native complex natural flows, such as mudflows and impurity flows, than considering only Newtonian liquids, such as water. A dam break is considered as a fracture problem for a mixture of particles and a fluid, which was numerically, investigated using the CFD-DEM approach for two non-Newtonian fluids based on experimental data (Li and Zhao 2018). The results of this work showed that non-Newtonian fluids reduce the kinetic energy of particles during early destruction.

The focus of this study is on the destruction of a dam consisting of water and mud that belongs to non-Newtonian fluid (Coussot 1995). Mud flow usually occurs after soil saturation due to rainfall or due to rapid snow melt. Mud and debris flows occur on steep slopes or mountainous areas. Detailed flow control allows us to distinguish four different stages of wave development: the decline phase, the inertia phase, and the transport phase (Hogg and Woods 2001; Hogg and Pritchard 2004). At each of these stages, different physical mechanisms dominate at different times.

In this paper, the model is tested in several dam break laboratory tests. The paper also examines the effect of rolling sediment on the flow in the winding channel. As a real problem, a breakthrough of the Mynzhylky dam was modeled.

2 Mathematical Model

In the present study, an incompressible flow consisting of three phases was considered: water, air and a phase for deposition (impurity). The equations controlling the flow are simply incompressible Navier-Stokes equations.

$$ \frac{\partial {u}_j}{\partial {x}_j}=0 $$
(1)
$$ \frac{\partial {u}_i}{\partial t}+\frac{\partial {u}_i{u}_j}{\partial {x}_j}=g-\frac{1}{\rho}\frac{\partial P}{\partial {x}_i}+\frac{1}{\rho}\frac{\partial }{\partial {x}_j}\left(\tau +{\mu}_t\right) $$
(2)
$$ \frac{\partial \chi }{\partial t}+{u}_j\frac{\partial \chi }{\partial {x}_j}=0 $$
(3)

where u is the flow rate, t is time, p is pressure, ρ is the density of water, f is the external force of the body, g is the acceleration of gravity, χ is the phase response, and \( \overrightarrow{\tau} \) is the stress tensor.

In incompressible Newtonian fluids, the tensor stress is proportional to the strain rate tensor \( \overrightarrow{D} \):

$$ \overrightarrow{\tau}=\mu \overrightarrow{D} $$
(4)
$$ \overrightarrow{D}=\left(\frac{\partial {u}_j}{\partial {x}_i}+\frac{\partial {u}_i}{\partial {x}_j}\right) $$
(5)

μ - dynamic viscosity, which does not depend on \( \overrightarrow{D} \).

For non-Newtonian liquids, the stress tensor is written

$$ \overrightarrow{\tau}=\eta \left(\overrightarrow{D}\right)\overrightarrow{D} $$
(6)

η is a function of all three invariants of the strain rate tensor \( \overrightarrow{D} \). The non-Newtonian flow is modeled according to the following power law for non-Newtonian viscosity

$$ \eta =k{\gamma}^{n-1}H(T) $$
(7)

k is a measure of the liquid average viscosity (consistency index);

n - is a measure of the fluid deviation from the Newtonian (power index), γ refers to the second invariant \( \overrightarrow{D} \) and is defined as

$$ \gamma =\sqrt{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\overrightarrow{D}:\overrightarrow{D}} $$
(8)

H(T) is a temperature dependence known as the Arrhenius law.

$$ H(T)=\exp \left[\alpha \left(\frac{1}{T-{T}_0}-\frac{1}{T_{\alpha }-{T}_0}\right)\right] $$
(9)

where α is the ratio of the activation energy to the thermodynamic constant and Tα is the medium temperature and T0 is the absolute temperature. Temperature dependence is enabled only when the energy equation is on. When setting the parameter to α=0, the temperature dependence is ignored.

The VOF method was presented by Hirt and Nichols (Hirt and Nichols 1981). The equations for the phases are solved by introducing the function F, defined as the average value of the phase characteristic function over the cell of the computational grid. Therefore, F is the volume fraction occupied by the phase in the grid cell. At the end of each time step, the local volume fraction in the cell is used to calculate the local density and viscosity values needed to solve the Navier-Stokes equations. For “mixed cells” (i.e. containing more than one phase), equivalent density and viscosity are calculated by linear interpolation based on the volume fraction.

3 Numerical Simulation Algorithm

The Reynolds-averaged Navier-Stokes equations (RANS) are sampled on a fixed Cartesian grid using the finite volume method. To close the RANS, the SST k-ω turbulent model was used. The PISO algorithm was chosen as the numerical method for solving the presented equations (Issa 1986; Issakhov 2016; Issakhov et al. 2018). This is an extension of the Semi-Implicit Method for Pressure Linked Equations (SIMPLE) algorithm used in computational fluid dynamics to solve the Navier-Stokes equations. The PISO is a procedure for calculating the pressure velocity for the Navier – Stokes equations, which was originally developed for non-iterative calculation of a nonstationary compressible flow, but was successfully adapted to stationary problems. The PISO includes one prediction step and two corrector steps and is designed to provide mass conservation using predictor-corrector steps. The choice of a numerical PISO algorithm is due to the fact that the PISO scheme has an additional level of corrector that ensures the continuity of the obtained solutions. The PISO numerical scheme differs from other tested schemes (Issakhov et al. 2018) in terms of reliability, accuracy, and the required processing time. In papers (Barton 1998; Issakhov et al. 2018), numerical calculations were performed to compare the PISO and SIMPLE algorithms for various test problems.

4 Model Verification

To demonstrate the computational efficiency and numerical accuracy of the present model described above for the dam break problems, several classic test cases were used. These control tests include: (a) dam break flow in the L-shaped channel; (b) partial dam break flow above the moving bed.

4.1 Problem 1. Partial Dam Break Flow above the Moving Bed

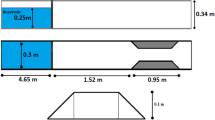
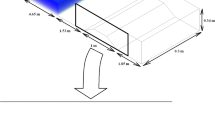
In this test problem, the flow is simulated, caused by the partial destruction of the dam by a suddenly enlarged section over the moving bed. The measurement results (Soares-Frazão et al. 2012) is used to evaluate the proposed model. The tests were carried out in a tank whose width is 3.6 m and a length of 36 m, of which the useful length was about 27.6 m (Fig. 1a). At the same time, the main channel is divided into two channels, between which there is some narrowing. This narrowing is located almost 12 m from the beginning of the stream in the upstream, and the second part of the channel after the narrowing has a length of 15.5 m. Thus, in these two channels on a fixed base, they are covered with a layer of coarse and saturated sand with a thickness of 85 mm. The total length of this coating is 10 m, while the length for the first channel (the channel before the narrowing) is 1 m and the length for the second channel (the channel after the narrowing) is 9 m. A structured mesh was used to simulate the problems. A computational grid was used, consisting of 5,888,841 tetrahedral elements. The computational grid consists of a uniform grid with side dimensions 0.05 m. The time step was set as Δt = 0.005 sec.

Fig. 1
figure 1figure 1

Geometry and dimensions of the experiment (Soares-Frazão et al. 2012) and comparison of the model results with measurement results from (Soares-Frazão et al. 2012) and numerical data (Hosseinzadeh-Tabrizi and Ghaeini-Hessaroeyeh 2018) for the water surface profile on the sensors US1, US2, US5, US6

Full size image

In this experiment, homogeneous coarse sand with a density ratio (ρs/ρw = 2.63) was used as the bottom layer, while the density of water is taken as 998.2 kg/m3. The model for the sediment phase is treated as a non-Newtonian fluid. For a non-Newtonian fluid, the effective viscosity is calculated using eq. (7). At the initial moment, the height of the water in the tank was 0.47 m. The origin of coordinates along the X = 0 axis represents the position of the gate. All upstream boundaries, bounded by a closed wall, at the end of the stream downstream there is an overflow to keep the saturated sediment in its original state and separate the two parts in the lower stream. The channel has four hydrometric sensors (US1, US2, US5 and US6), which determine the changes in the water level after the gate has been opened for 20 s. The exact location of these measuring sensors is like that: US1(0.64 m, −0.5 m), US2(0.64 m, −0.165 m), US5(1.94 m, −0.99 m), US6(1.94 m, −0.33 m). Fig. 1(b,c,d,e) shows a comparison of the numerical data with the results of experimental tests and numerical data (Soares-Frazão et al. 2012) for evaluating the reliability. Figure 2 shows the behavior of the water mass with a moving layer for different times.

Fig. 2
figure 2figure 2

Snapshots of a dam break flow with mudflow for different times (0 s, 1 s, 2 s, 3 s, 4 s, 5 s, 6 s, 7 s, 8 s, 9 s, 10 s, 15 s, 20 s) for sediment heights of 0.085 m

Full size image

As shown in Fig. 1(b,c,d,e), three different experimental data are used for sensors US1 and US6 (Soares-Frazão et al. 2012). Different profiles were presented for three different runs of the experiment. So in this paper, the results were presented comparing the present model with three experimental run data (Soares-Frazão et al. 2012) and numerical data (Hosseinzadeh-Tabrizi and Ghaeini-Hessaroeyeh 2018). Also shown in Fig. 1(b,c,d,e) are the numerical results that were obtained in paper (Hosseinzadeh-Tabrizi and Ghaeini-Hessaroeyeh 2018). As can be seen from the obtained computational data, these results are well described by experimental data (Soares-Frazão et al. 2012). In some sensors, the results obtained even better describe the experimental data for changes in water level than the obtained numerical results in the paper (Hosseinzadeh-Tabrizi and Ghaeini-Hessaroeyeh 2018).

However, it is also possible to note some discrepancy between the obtained results and experimental data (Soares-Frazão et al. 2012). These discrepancies can be seen on the US2 sensor after 13 s. One of the possible causes of the deviation is related to the fact that the shutter instantly rises by releasing the mass, although in the real case this process takes some time. The second of the possible causes is deviations, related to the initial conditions, roughness coefficients and sediment characteristics. And the appearance of these anomalous sawtooth forms is due to the fact that during the water interface movement air bubbles appear in the water and sediment, and used the numerical algorithm does not cope with an empty isolated cell surrounded by water cells. The air bubbles themselves occur when the progressing wave hits the front part of the walls, and begins to rise and when this water falls into the walls, empty, isolated cells are created. And the difference between the numerical data and the experimental data as a percentage for the points US1, US2, US5 and US6 are different: US1–3.02%, US2–7.09%, US5–4.19%, US6–2.43%. Since the presence of a moving layer (non-Newtonian fluid) helps to reduce the flow rate and begins to affect the overall distribution of water. Also the presence of such natural transportable sediments can significantly influence the flow behavior. In case of severe flooding, for example, due to the dam or dam breaking through, the influence of such sediments is even more pronounced, especially in the first moments after the dam is broken and in the immediate vicinity of the dam.

It should be noted that the obtained computational results display that the simulation of this model is reliable and accurate to describe the flooding process during the destruction of the dam over natural rivers with a complex geometry of channels. The flooding effect on this complex reservoir topography is properly modeled using the VOF method. All the above results confirm that the transfer of viscous deposits during dam breakthrough greatly influences the behavior of the entire flow, because the interaction between different phases (Newtonian and non-Newtonian) leads to complex flow behavior. Since in real conditions, the flow at a dam break does not consist only of water and often contains some impurities, and these impurities play a very important role in general when transporting the entire volume of water.

5 Simulation of the Mynzhylky Dam Breaks Flow

The Mynzhylky Plateau is located at the source of the Malaya Almatinka River, 28 km on the south of Almaty. The tract is surrounded by Tuyuksu glaciers. The climate is mountainous, with an average annual temperature of −2.7 °C, snow lasts 237 days a year, and 743 mm of precipitation falls annually. Here, at an altitude of 3020 m above sea level, the Mynzhylky dam protection dam blocks the Small Almatinka River (Fig. 3). The dam was built in 1958 as a protective structure for Almaty. But it was destroyed by the mudflow in 1973, subsequently restored. Dam length 300 m, height 17 m. Near the dam there is a hydro-meteorological station Mynzhylky leading its observations since 1936. This study area is presented in Fig. 3.

Fig. 3
figure 3

Investigated area and location of sensors for measurement

Full size image

This dam in Mynzhylky, in its current state, is unlikely to withstand a powerful mudflow, such as in 1973. The lake now has a volume of 220 thousand m3 of water, but this will not be enough if the situation develops according to the most negative scenario and the interglacial waters breakthrough, which can form mudflows of two million m3. In this problem, the reservoir contains 50 thousand m3 of water, behind the tank there is a movable layer with different heights (1.0 m and 2.0 m). The length of the river bed of the study area is 1317 m, the area is 17,000 m2. The water level is measured using six water level sensors, as illustrated in Fig. 3. The dimensions and geometry of the area are illustrated in Fig. 3. In this experiment, homogeneous coarse sand with a density of 2400 kg/m3 was used as the mud layer. The sediment phase is treated as a non-Newtonian fluid. For a non-Newtonian fluid, the effective viscosity is calculated using eq. (7). A structured mesh was used to simulate the problems. A computational grid was used, consisting of 2,433,550 tetrahedral elements. The computational grid consists of a uniform grid with side dimensions 0.5 m. The time step was set as Δt = 0.01 sec.

Figure 4 shows a comparison of the free-surface profiles on the G1, G2, G3, G4, G5 and G6 sensors with mud flow at a dam break for sediment heights of 1.0 m. Figure 5 shows two-dimensional and three-dimensional shots of a dam break with a mud flow for different times (0 s, 5 s, 10 s, 15 s, 20 s, 25 s, 30 s, 35 s, 40 s, 45 s, 50 s, 55 s, 60 s) for deposit heights of 1.0 m. Figure 4 illustrates a comparison of the free surface profiles on the G1, G2, G3, G4, G5 and G6 sensors with mud flow at the dam break for the sediment heights 2.0 m. Figure 5 shows 2D and 3D images of a dam break flow with mud flow for various times (0 s, 5 s, 10 s, 15 s, 20 s, 25 s, 30 s, 35 s, 40 s, 45 s, 50 s, 55 s, 60 s) for sediment heights of 2.0 m. As can be seen from the obtained results, some sensors recorded water height close to 10 m. However, it should also be noted that in sensors G2 and G5 the height of water surfaces have a value greater than the value of previous sensors. This phenomenon could be explained by the fact that in narrow sections of the river the water surface height increases, compared with wide sections of the river. Despite the long distance, the level of flooding on the G5 sensor is higher than on the G4 due to the smaller channel width.

Fig. 4
figure 4

Comparison of the free-surface profiles on the G1, G2, G3, G4, G5 and G6 sensors with mud flow at the dam break for different of sediment heights: (a) 1.0 m, (b) 2.0 m

Full size image
Fig. 5
figure 5figure 5

Two-dimensional and three-dimensional images modeling of a dam break with mud flow for various times (0 s, 5 s, 10 s, 15 s, 20 s, 25 s, 30 s, 35 s, 40 s, 45 s, 50 s, 55 s, 60 s) for different sediment heights: (a-b) 1.0 m, (c-d) 2.0 m

Full size image

Under the above conditions, the break flow of the Mynzhylky dam reaches an extreme point of 535 m at 49 s, which means the average flow velocity of the impurity into the rivers was approximately 10.92 m/s. In addition to the study of flooding, all other significant effects of flooding should be predicted, including transportation of mobile precipitation. After the shutter opened, a water wave and sediment spread downstream along a wider area. Reflection from the outer wall and curvature of the flow path create blur along the outer side wall of the river. A huge part of the moving layer is transferred to a wide stretch of the river and begins to slowly settle in the area and create a new relief and riverbed. This phenomenon leads to a further change in the relief, as well as in the whole riverbed.

Also, for studying the volume effect of the moving layer, the second formulation of the problem was modeled with a mudflow height of 2.0 m. From the results of Fig. 5, it can be noted that an increase in the volume of sediment slows down the overall water flow. Under these conditions, the flow of water breakthrough reaches the extreme point of the study area already at 52 s after the dam breakthrough, which is 3 s more than it was at a mudflow height of 1.0 m and the average flow rate of impurity into the rivers was approximately 10.29 m/s. As expected, an increase in the viscous moving bed leads to a slowdown in the dam break flow. It was found that in nature with strong flows, the upper layer of the earth is destroyed and transferred, forming a mud and mudflow. Also, to nature, the amount of precipitation transported depends on many factors, such as the type of flow, the type of soil, and so on. Since the increase in these transported sediments leads to a slower flow, increasing the volume of the moving bed, it can be significantly reduce the damage to the dam breakthrough. It is possible to artificially increase the volume of these transported sediments. For example, a certain amount and height of sand or other effective substances that can be carried by the stream poured behind the dam, reducing the shock pressure, which in turn leads to a decrease in the pressure value on the obstacle itself. Regardless of the presence and thickness of the moving layer, the position of the fluid front is almost the same at the beginning of the flow when the dam collapses, but then the flow mixes with the moving layer over time and this layer begins to influence the position of the fluid and causes braking, and this process can be seen in the front parts of the obstacle after t = 5.0 s (Figs. 5). Over time, the difference between the position of the fluid front increases until the fluid front reaches the end of the river bed.

It should also be noted that with an increase in the volume of the moving bed, the water flow in general leads to inhibition. However, these moving layers downstream begin to subside and begin to change the topography and the river beds, which can further lead to an artificial narrowing of the river and an increase in water height in these areas.

6 Conclusions

The proposed model is used for numerical simulation of flooding during the destruction of a dam over natural rivers with complex channel topography. A well-balanced property between different phases is achieved through the VOF method. The tests of this model were made by comparing with extensive laboratory test data and other numerical simulation results. The reliability and accuracy of the model are demonstrated on several test examples, laboratory tests of dam breakthrough in the L-shaped channel and dam breaks over the moving bed. Based on the simulated and compared results of various types of cases, it has been established that the model is reliable and accurate to simulate floods in natural rivers with complex geometry. Predictions using numerical simulation showed good agreement with the experiment and the numerical data of other authors, in particular, the global behavior of the fluid and trends in changes in the height of the water surface were well reproduced. The computational data give greater confidence in the effectiveness of the method.

Taking into account the presence of many uncertainties in real dam destruction, such as topography, channel erosion, partial dam destruction, to implement a realistic dam breakthrough flow, this paper examined the use of Newtonian and non-Newtonian models to model waves caused by the destruction of the dam above the moving bed for real reliefs of the terrain behind the mud-protection dam “Mynzhylky”, which can be transferred by unsteady turbulent flow. In this case, the lower moving layer is considered as a non-Newtonian fluid. In the first moments after the dam breakthrough and near the dam, a huge exchange of momentum between water and the mobilized sediments is the main driving mechanism of morphological modifications. Later and further from the dam, significant morphological changes also occur. These changes mainly occur where the river geometry has local variations in width. In areas where the river bed is expanding, huge sediments were observed, forcing the river to create a new flow through the sediment layer. In the areas where the river bed was narrowed, the level of flooding with water was several times higher than in other areas. The arrival time and average flow rates of the mixture towards the end of the river at various deposition heights were also determined.

In this work, the water and mud movement was simulated during a dam break using the VOF model. In order to simulate this problem, a modification of the standard VOF model was carried out and a combination of Newtonian and non-Newtonian models was used. The validity of this model was verified using several test problems. A modified mathematical model that takes into account the movement of Newtonian and non-Newtonian fluids was used for the real terrain behind the Mynzhylki mudflow dam. For this problem, the duration of the flooding process at various thicknesses of the mud and the calculation of the breakthrough wave during the collapse of hydraulic structures taking into account the terrain were precisely determined.