1 Introduction

Risk assessment studies are often carried out at the design stage for the construction of a new dam or during the testing of the health of an existing dam. Recent dam failures and the anticipated changes in climatic extremes indicate that more emphasis should be given by the scientific community to the causes of such failures and the accurate simulation procedures of dam failure.

In particular in case of embankment dam failure two common causes of failure can be studied in depth based on the findings of the last decades. These causes are the overtopping and the piping. It has been now understood that the most crucial cause mainly with respect to time of failure is the overtopping.

Two are the main processes are of great importance when simulating the failure of an embankment dam: the simulation of breach formation and subsequently the development of outflow hydrograph from the breach. Once this hydrograph is obtained, the peak outflow through the breach and the corresponding critical time are also known. Then the outflow hydrograph is routed through the downstream valley up to the final receptor.

This paper deals with the mathematical simulation of the breach formation and the calculation of the resulting outflow hydrograph through the breach of an embankment dam caused by overtopping. The paper presents a semi-analytical procedure for calculating the outflow hydrograph based on the parabolic shape of the breach and several considerations concerning the breach formation derived from the analysis of historic embankment dam failures.

Embankment breach formation by overtopping has been simulated by complex two-dimensional flow models combined with soil erosion and slope failure algorithms or by one dimensional flow calculations combined with various soil erosion and sediment transport formulations.

Representative efforts of the above latter approach are the works of Christofano (1965); Brown and Rogers (1981); Lou (1981); Ponce and Tsivoglou (1981); Nogueira (1984); Fread (1984) and others.

The increased computational capabilities which are available during the last few decades enabled researchers to use these models in practical applications. This gave the opportunity to formulate physically-based algorithms for simulating the breach formation and the resulting hydrograph. The models BREACH (Fread 1988) and BEED (Singh and Quiroga 1987a, b) belong also to this category of analytical physically-based models.

In order to facilitate the calculation procedure, the National Weather Service of USA presented the package DAMBRK (Fread 1984) and later FLDWAV (Fread 1993) which were widely accepted and used as standard methods in risk assessment studies throughout the world. The main features which made the above software packages popular are that a) they include the breach formation and the outflow hydrograph development together with the routing procedure of the outflow hydrograph through the downstream valley, b) In order to reach a practical solution simplified equations are used which describe the phenomenon without detailed representation of the complex hydrodynamic and erosion procedures.

A detailed review of the methods proposed for describing the breach formation and the development of the outflow hydrograph is included in the book «Dam breach modelling technology» (Singh 1996).

Recently the emphasis of the researchers was focussed on the statistical analysis of some basic parameters using real historic dam failures. Froehlich (1995, 2008), Walder and O’Connor (1997), Wahl (2004), Tsakiris et al. (2010) derived useful conclusions on the range of values which can be examined in risk assessment studies related to dam failures. Given the usefulness of the results of these studies it should be stressed that in most of the cases the conclusions were derived either from a small number of failure events or from incidents under very diverse conditions. Therefore when these recommendations are to be used they should be used with caution.

Apart from the above assistance the need for simulating the process of breach formation and the development of outflow hydrograph remains. Therefore analytical or semi-analytical methods are of importance in the light of the findings of the previous studies.

Previous analytical models were based on two assumptions: a)the reservoir is prismatic and b) the shape of the breach is rectangular or trapezoidal. The proposed methods in this paper examine apart from the prismatic reservoir also the reservoir in which the capacity is a power function of the water depth in the reservoir. Also the paper adopts the assumption of recent findings in the subject underlining that the breach shape is parabolic. For instance Coleman et al. 2002 suggested that cross sections along the developing breach channel are curved in elevation below the waterline. Based on a number of experiments, Coleman et al. 2002 proposed the use of the parabolic breach shape.

2 Basic Notions

2.1 Breach Formation

The simulation of the breach formation of an embankment dam due to overtopping is a very complicated task since it depends on a large number of factors including the dam and the weir geometry, the construction materials and methods, the slope protection cover, the reservoir dimensions, and the inflow hydrograph during the dam failure. Now it is understood that the embankment failure is realised in three phases. In the first phase the flow overtops the dam and may erode the downstream slope of the dam without creating a breach through the dam. Since the erosion starts from the downstream slope it is of outmost importance to protect this slope against erosion. Several materials have been used in practice for reinforcing the downstream slope of the embankment dams.

In the second phase a breach is formed and enlarged through erosion vertically and horizontally. The second phase ends when the breach reaches its final dimensions. The time required for the final formation of the breach is referred to as time of failure. From the analysis of historical and few experimental data it is concluded that for large embankment dam failure the final level of the bottom of the breach is expected to reach the base of the dam (Tsakiris et al. 2010). According to Froehlich (2008) the maximum height and width of the breach are reached simultaneously. It is also expected that the time of failure is approximately equal to the time of peak outflow from the breach.

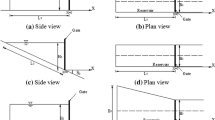
Most investigators have agreed that the shape of the breach of an embankment dam can be approximated successfully by a trapezoidal cross-section, the side slopes (1:m) of which vary from 1:1 to 1:2 (v:h). The variables involved in the trapezoidal dam breach approximation appear in Fig. 1. H b is the height of the breach, \( \overline B \)is the mean width and H 0 is the initial level of the water in the reservoir with respect of the level of the bottom of the final breach (Z min ).

Fig. 1
figure 1

Final dimensions of a trapezoidal dam breach approximation

Full size image

2.2 The Hydraulics of the Breach

The flow through the breach can be approximated as a flow over a broad crest weir (e.g. Powledge et al. 1989). The broad-crested weir has a finite crest length parallel to the flow. In addition the crest is long enough that parallel flow and critical depth occur at some point along the crest (Sturm 2001) (Fig. 2).

Fig. 2
figure 2

Flow regimes in embankment overtopping

Full size image

The critical conditions are derived by differentiating the total energy head H (which is equal to the specify energy at the critical section according to Fig. 2- where datum level for Energy Equation is the dam crest level):

$$ \frac{{dH}}{{dy}} = 1 - \frac{{u_c^2{{B}_c}}}{{g{{A}_c}}} = 0 $$
(1)

In which B c is the width at the water surface, A c is the wetted area and u c is the velocity for the critical conditions.

If energy losses and the kinetic head are considered negligible the conservation of energy leads to the following equation:

$$ Q = {{A}_c}\sqrt {{2g\left( {h\prime - {{y}_c}} \right)}} $$
(2)

in which h’ (“hydraulic head”) is the upstream water depth above the level of breach bottom Z, (h΄ = h – Z) and y c is the critical depth.

In case of a parabolic shape of the cross-section the geometric parameters are linked with the following formula:

$$ {{x}^2} = 2p{{y}_c} $$
(3)

in which p is the characteristic parameter of the parabola.

Finally for the parabolic section according to Bos (1977) the keys determinants are calculated as follows (Fig. 3):

$$ {{A}_c} = \frac{2}{3}{{B}_c}{{y}_c},{{B}_c} = 2\sqrt {{2p{{y}_c}}}, \frac{{u_c^2}}{{2g}} = \frac{{{{A}_c}}}{{2{{B}_c}}} = \frac{1}{3}{{y}_c},{{y}_c} = \frac{3}{4}h\prime,Q = \sqrt {{\frac{3}{4}pg}} {{\left( {h - Z} \right)}^2} $$
(4)
Fig. 3
figure 3

The dimensions of a parabolic dam breach approximation

Full size image

In reality the uniform velocity distribution and the absence of energy losses do not hold and therefore a discharge correcting coefficient C d should be inserted. In addition another coefficient C V is inserted to account for the negligence of the upstream velocity head (Bos 1977).

$$ Q = {{C}_d}{{C}_V}\sqrt {{\frac{3}{4}pg}} {{\left( {h - Z} \right)}^2} $$
(5)

It should be noted that for a variety of conditions, C d ∙C v approaches one and for simplicity may be omitted in the previous equation.

Needless to say that Z (the level of the bottom of the breach) is a function of time determined by the rate of vertical erosion.

3 Methodology

The proposed methodology is based on two phases:

  1. (i)

    The breach is increasing up to its final size. The hydrograph through the breach is produced based on the integration of the differential equation between the level of water in the reservoir behind the dam and the level of the breach bottom, both dependent on time t (t < t f ) .

  2. (ii)

    The outflow continues after the final formation of the breach up to the total depletion of water from the reservoir. During this phase the remaining part of the hydrograph is produced based on the integration of the differential equation between the instantaneous level of the water in the reservoir and the constant level of the bottom of the final breach.

3.1 Phase I : Breach Development

3.1.1 Prismatic Reservoir

To simplify the entire simulation of breach development we assume that the measure of the rate of vertical erosion v (starting from the top of the breach) is constant and can be expressed by the following equation:

$$ {\text{v}} = - \frac{{dZ}}{{dt}} = \frac{{{{H}_b}}}{{{{t}_f}}},\;{\text{or}} $$
(6)
$$ Z = {{Z}_0} - {\text{v}}t $$
(7)

where Z is the level of breach bottom at time t after the beginning of breach formation, H b is the elevation difference from the crest of the dam up to the final level of the breach bottom, t f is the time period required for the final formation of the breach, and Z 0 is the elevation of the crest. All these symbols appear in Fig. 3.

By applying the water- balance equation, the following equation can be written:

$$ {{A}_s}dh = - Qdt $$
(8)

provided that we neglect the additional inflow in the reservoir and that the water surface area remains constant during the breach formation.

As explained in the previous paragraph the flow through the breach can be described as the flow through a broad-crested weir. The system of equations to be solved comprises the Eqs. (6), (8) and (5). Solving the first two equations we derive:

$$ \frac{{dh}}{{dZ}} = \frac{{{{C}_d}{{C}_V}{{{\left( {\frac{3}{4}pg} \right)}}^{{0.5}}}}}{{{\text{v}}\;{{A}_s}}}{{\left( {h - Z} \right)}^2} $$
(9)

By using the “hydraulic head” h’, the above equation is written:

$$ \frac{{dh\prime }}{{dZ}} = M \cdot {{h}^{{\prime 2}}} - 1 \Leftrightarrow \frac{{dh\prime }}{{M{{{\left( {h\prime } \right)}}^2} - 1}} = dZ $$
(10)

in which M stands for the fraction of the left hand side of the equation.

The general solution of the above equation is:

$$ - \frac{{{\text{arctanh}}\left[ {\sqrt {M} \cdot h\prime } \right]}}{{\sqrt {M} }} = Z + C\mathop{ \Leftrightarrow }\limits^{{(7)}} h\prime = \frac{{{ \tanh }\left[ { - \sqrt {M} \left( {\left( {{{Z}_0} - {\text{v}}t} \right) + C} \right)} \right]}}{{\sqrt {M} }} $$
(11)

Taking into account the initial condition Z = Z 0 , h = H 0 for t = 0, the constant C is calculated as follows:

$$ C = - \frac{{{\text{arctanh}}\left[ {\sqrt {M} \cdot \left( {{{H}_0} - {{Z}_0}} \right)} \right]}}{{\sqrt {M} }} - {{Z}_0} $$
(12)

Therefore the final solution is derived as follows:

$$ \left. {\matrix{{*{20}{c}} {Z = {{Z}_0} - {\text{v}}t} \hfill & {} \hfill \\ {h\prime = \frac{{{ \tanh }\left[ { - \sqrt {M} \left( \left( {{{Z}_0} - {\text{v}}t} \right) - \frac{{{\text{arctanh}} \left[ {\sqrt {M} \cdot \left( {{{H}_0} - {{Z}_0}} \right)} \right]}} {{\sqrt {M} }} - {{Z}_0} \right)} \right]}} {{\sqrt {M} }},} \hfill & {h = h\prime + Z} \hfill \\ {M = \frac{{{{C}_d}{{C}_V}{{{\left( {\frac{3}{4}pg} \right)}}^{{0.5}}}}}{{{\text{v}}\;As}}} \hfill & {} \hfill \\ } } \right\} $$
(13)

3.1.2 Reservoir Capacity as a Function of Water Depth

The above methodology was based on the simplifying assumption that the reservoir is prismatic (A S = constant). However it is generally accepted that such a simplification is not sufficiently realistic. In general the capacity of a reservoir can be expressed as a power function of the water depth. It is observed that in the majority of cases the reservoir capacity can be approximated by a cubic function of the water depth. This can be written:

$$ V(h) = k{{h}^3} $$
(14)

Following the same procedure as before we derive:

$$ \frac{{dh}}{{dZ}} = \frac{{{{C}_d}{{C}_V}\sqrt {{\frac{3}{4}pg}} }}{{v3k}}{{\left( {\frac{{h - z}}{h}} \right)}^2} $$
(15)

The above differential equation is homogeneous and therefore the standard transformation can be applied:

$$ \left[ {\matrix{{*{20}{c}} {u = \frac{h}{Z} \Rightarrow h = uZ \Rightarrow \frac{{dh}}{{dZ}} = \frac{{du}}{{dZ}}Z + u,} & {N = \frac{{{{C}_d}{{C}_V}\sqrt {{\frac{3}{4}pg}} }}{{3vk}}} \\ } } \right] $$
(16)
$$ (15)\mathop{ \Leftrightarrow }\limits^{{(16)}} \frac{{du}}{{dZ}}Z + u = N{{\left( {1 - \frac{1}{u}} \right)}^2} \Leftrightarrow $$
$$ \Leftrightarrow \frac{{{{u}^2}}}{{N{{u}^2} - 2Nu + N - {{u}^3}}}du = \frac{{dZ}}{Z} $$
(17)

The latter is a differential equation with separable variables. The difficulty for solving this equation is focused on the integration of the left-hand side which can be determined analytically as an integration of explicit functions.

It should be noticed that the general solution of Eq. 17 is dependent upon the N factor which changes from case to case.

3.2 Phase II: Water Depletion After the Final Formation of the Breach

3.2.1 Prismatic Reservoir

In this second phase the breach has reached its final dimensions. Therefore the following equations can be written:

$$ \left. {\matrix{{*{20}{c}} {{{A}_s}dh = - Qdt} \\ {{{C}_d}{{C}_V}{{{\left( {\frac{3}{4}pg} \right)}}^{{0.5}}}{{{\left( {h - {{Z}_{{\min }}}} \right)}}^2} = Q} \\ {{{Z}_{{\min }}} = const} \\ } } \right\} \Leftrightarrow \frac{{dh}}{{dt}} = - {{\left( {h - {{Z}_{{\min }}}} \right)}^2}\frac{{{{C}_d}{{C}_V}{{{\left( {\frac{3}{4}pg} \right)}}^{{0.5}}}}}{{{{A}_s}}} \Leftrightarrow \frac{{dh}}{{ - {{{\left( {h - {{Z}_{{\min }}}} \right)}}^2}\frac{{{{C}_d}{{C}_V}{{{\left( {\frac{3}{4}pg} \right)}}^{{0.5}}}}}{{{{A}_s}}}}} = dt $$
(18)

then by integrating the above equation we conclude that:

$$ P\frac{1}{{\left( {h - {{Z}_{{\min }}}} \right)}} + C = t,P = \frac{{{{A}_s}}}{{{{C}_d}{{C}_V}{{{\left( {\frac{3}{4}pg} \right)}}^{{0.5}}}}} $$
(19)

The constant of integration C can be calculated from the initial condition for this phase; that is for t = t f , h = h(t f ). Finally after some algebraic operations the following equation is derived:

$$ h = \frac{P}{{\left( {t - {{t}_f} + P\frac{1}{{\left( {h\left( {{{t}_f}} \right) - {{Z}_{{\min }}}} \right)}}} \right)}} + {{Z}_{{\min }}} $$
(20)

3.2.2 Reservoir Capacity as a Function of Water Depth

If the reservoir capacity is represented by a function of the third power of the water depth V(h) = kh 3, a similar procedure as previously may be followed:

$$ \left. {\matrix{{*{20}{c}} {\frac{{dV}}{{dt}} = - Q \Leftrightarrow - 3k{{h}^2}\frac{{dh}}{{dt}} = Q \Leftrightarrow dt = - 3k{{h}^2}\frac{{dh}}{Q}} \\ {{{C}_d}{{C}_V}{{{\left( {\frac{3}{4}pg} \right)}}^{{0.5}}}{{{\left( {h - {{Z}_{{\min }}}} \right)}}^2} = Q} \\ {{{Z}_{{\min }}} = const} \\ } } \right\} $$
(21)

which is equivalent to:

$$ \frac{{dh}}{{dt}} = \frac{{{{C}_d}{{C}_V}{{{\left( {\frac{3}{4}pg} \right)}}^{{0.5}}}}}{{ - 3k}}\frac{{{{{\left( {h - {{Z}_{{\min }}}} \right)}}^2}}}{{{{h}^2}}} $$
(22)

Further as explained earlier for a large number of cases V(h) can be approximated by a cubic function of h. Assuming that Z min   = 0, the following simple linear relationship between the h and t is derived:

$$ h = \frac{{{{C}_d}{{C}_V}{{{\left( {\frac{3}{4}pg} \right)}}^{{0.5}}}}}{{ - 3k}}t + C $$
(23)

The constant of integration C can be calculated from the initial condition for the second phase. That is for t = t f , h(t f ) = known and therefore for t ≥ t f :

$$ h = h\left( {{{t}_f}} \right) - \frac{{{{C}_d}{{C}_V}{{{\left( {\frac{3}{4}pg} \right)}}^{{0.5}}}}}{{3k}}\left( {t - {{t}_f}} \right) $$
(24)

4 Application and Discussion

4.1 Data

The proposed methodology was applied in a risk assessment study of a new embankment dam at the design stage. The data concerning the dam geometry are:

  • Capacity of the reservoir at the crest of the dam: 56.7 × 106 m3

  • Height of the dam: 72 m

  • Mean surface water area in the reservoir: 787,500 m2

  • Elevation of the bottom of the final breach: +0 m

For the simulation of breach formation the following assumptions were adopted:

  • The final breach height is equal to the height of the dam.

  • One meter head above the crest is initially assumed.

  • The shape of the breach is parabolic with p calculated for \( \overline B /{{H}_b} = 3 \)

  • Constant rate of vertical erosion is assumed throughout the breach formation 84 m/h.

4.2 Estimation of Parameter p of the Parabola

Since most of the models presented in the past used a trapezoidal shape of the breach it would be wise to adapt the parabolic shape to the corresponding best fit trapezoidal section. Among the criteria which can be used in this case is that both shapes the area remains the same. This means that the unique determinant p of the parabola can be calculated based on the equal area between trapezoidal and parabolic section.

According to Tsakiris and Spiliotis (2012) the value of the parameter p of the parabolic shape of the breach can be determined based on the relationship of \( \overline B \) and H b. From the review of the historical dam failures it was concluded that \( 2{{H}_b} \leqslant \overline B \leqslant 5.5{{H}_b} \)(Tsakiris et al. 2010). Further there is the recommendation of the Bureau of Reclamation 1982, for \( \overline B = 3{{H}_w} \), in which H w is the height of water above the final breach bottom at the time of failure. For this application we assumed \( \overline B = 3{{H}_b} \) and the determinant p was calculated equal to 182.25 m.

4.3 Phase I (Prismatic Reservoir)

The phase 1 finishes when the time t reaches the failure time t f . For each time step the flow is calculated using Eq. 5: The maximum hydraulic head (h-Z) is achieved when the failure time is reached. The procedure of the analysis is shown at Table 1.

Table 1 Equations for prismatic and non-prismatic reservoir
Full size table

Further to this initial phase I, the phase II follows according to the methodology presented above. By combining phase I and II, the resulting entire outflow hydrograph is illustrated in Fig. 4. The corresponding hydraulic head is presented at Fig. 5.

Fig. 4
figure 4

The outflow hydrograph as a result of phases I and II

Full size image
Fig. 5
figure 5

The hydraulic head as a result of phases I and II

Full size image

4.4 Phase I (Non – prismatic Reservoir)

The capacity of the reservoir V is expressed as a function of the third power of the water depth h. In this application this function is:

$$ \matrix{{*{20}{c}} {V(h) = 113.71{{h}^3}} & {\left( {{\text{V}}\;{\text{in}}\;{{\text{m}}^3}\;{\text{and}}\;{\text{h}}\;{\text{in}}\;{\text{m}}} \right)} \\ } $$
(25)

Τhe Eq. 17, taking into account the initial condition reduces to the following algebraic equation:

$$ Z = \exp \left\{ {\matrix{{*{20}{c}} {1.72774\arctan \left( {1.19366 - 0.614735{\text{u}}} \right) - 0.123974{\text{Ln}}\left( { - 0.716962 + {\text{u}}} \right){ }} \hfill \\ { - 0.438013{\text{Ln}}\left( {6.41659 - 3.88349{\text{u}} + {{\text{u}}^2}} \right) + 3.77984564} \hfill \\ } } \right\} $$
(26)

Starting from u(0) = (73/72) and inserting values of u, the Z values are determined from the above equation and finally h = u∙z. The procedure of the solution is presented in Table 1.

As can be seen from Table 1 the maximum outflow discharge is max Q = 25516 m 3 /s, max h’ =26.39 m at t = 0.5 h

The results obtained are obviously valid if the reservoir capacity can be successfully represented by a function of the third power of the water depth. If the exponent of the function is significantly different than 3, a suitable correction could be incorporated in the calculation of the constant k.

As can be seen if a prismatic reservoir is assumed (and the mean surface area is calculated by dividing the total volume by the height of the dam), the peak outflow from the breach is significantly smaller than in the case in which the reservoir capacity is a third power of the water depth. Similar underestimation of the peak outflow was observed for several applications of the real world. Therefore it is concluded that the results of the «prismatic» assumption are indicative and could be used only in preliminary studies.

As the height of the dam is getting smaller however, the results of the above two solutions tend to be closer. Therefore the assumption of prismatic reservoir could be used for dam breaks of small embankment dams. For large dams though, this assumption seems to influence the results significantly.

Another remarkable point is that by considering a prismatic reservoir the peak outflow occurs at the end of the failure time while in the latter case the peak outflow occurs before the end of the time of failure.

Finally solving the above problem for various values of the ratio \( {{{\overline B }} \left/ {{{{H}_b}}} \right.} \)from 2 to 5.5 it was observed that the peak outflow was not practically influenced for the prismatic reservoir whereas it was positively influenced for the latter case.

Apart from the hypothesis that the rate of vertical erosion is constant other more sophisticated assumptions regarding the pattern of erosion can be further investigated. For example, Singh and Scarlatos 1988 proposed an erosion pattern in which the erosion rate can be considered as a function of flow velocity. However for adopting a different erosion pattern the need of some experimental data is imperative. Unfortunately no such data are available to support the calibration of this type of erosion models.

5 Concluding Remarks

The breach formation and the resulting outflow hydrograph are critical processes for the flood risk assessment studies related to dam failure. This study focussed on the derivation of a semi-analytical method for simulating the above processes in the case of an embankment dam failure due to overtopping.

The main advantage of the method compared to the numerical solutions lies in the fact that it is exact and fulfils the mass conservation principle. However the assumption of «prismatic reservoir» in the case of large dam failures seems to underestimate considerably the peak outflow.

Furthermore one of the uses of the present semi-analytical model is to provide data to test numerical models.