1 Introduction

Accident at hydraulic structures - an emergency associated with the decommissioning (destruction) of a hydraulic structure or its part and the uncontrolled movement of large volumes of water, causing destruction and flooding of the downstream area. Prediction of the dam breaks time, as well as information about the characteristics of the dam break wave and the flood zone of the terrain are necessary for carrying out rescue evacuation operations. Such preliminary prediction of potential hazards, and hence their minimization, can be performed through laboratory experiments and numerical simulations.

Due to the urgency of the problem, there is a considerable number of works considering the experimental dam break flows in laboratory conditions (Kocaman et al. 2020; Wang et al. 2020; Spinewine and Zech 2007; Kamra et al. 2019; Bellos et al. 1992; Aureli et al. 2000). Such works make it possible to check the performed numerical studies, the developed numerical models, and also make it possible to better understand the dynamics of the flow. Thus, laboratory experiments were carried out to study the movement of water flow along straight and curved channels (Miller and Chaudhry 1989; Bell et al. 1992). Experimental studies for channels with complex geometry with lateral contraction - expansion of the configuration are presented in (Goutiere et al. 2011; Soares-Frazao et al. 2012). In the paper (Soares-Frazão and Zech 2008) there is an experiment on the movement of dam break flows through an idealized urban area. The idealized city map is an arrangement of buildings in a 5 × 5 square. In the second case, the “city” was turned at an angle of 22.5° relative to the direction of the flow. In (Oguzhan and Aksoy 2020), the influence of vegetation on the propagation of dam break waves in the event of dam destruction of various shapes was experimentally investigated. There are also works in the scientific literature that provide experimental data on the study of the reservoir geometry effect on the behavior of water flow during the destruction of a hydraulic structure (Feizi Khankandi et al. 2012; Hu et al. 2020). Laboratory experiments have also made it possible to determine the difference between bottom sediments of different and similar diameters (Khosravi et al. 2021).

Another approach for studying the problem of dam break is numerical modeling. In order to check the developed models for reliability and accuracy, very often the numerical results are compared with experimental data (Kamra et al. 2018; Xia et al. 2010). The authors of the article (Ozmen-Cagatay et al. 2014; Ozmen-Cagatay and Kocaman 2012; Bahmanpouri et al. 2021) investigated experimentally and numerically the nature of the dam break wave flows. The work considered a rectangular installation with obstacles at the bottom of the channel. (Zhang et al. 2018) developed a 3D model using finite element methods in an unstructured mesh to simulate the process of dam break. A study (Li et al. 2020) numerically investigated the interaction between free surface deformation caused by dam failure and various obstacles shapes using 3D conjugate level method (CLSVOF) and submerged boundary methods. In the paper (Zhang et al. 2020), the numerical simulation of dam break flow in a channel having a ledge in the form of a step on its bottom was carried out. According to the data provided the presence of a scarp at the bottom of the channel increases the maximum horizontal impulse of water flow. A triangular-shaped setup, instead of the traditional rectangular one, with a shallow water layer downstream has been explored in studies (Yang et al. 2020a, b; Tajnesaie et al. 2020). Another innovation in the paper is a new approach to assessing the gate opening time.

The computational meshless Lagrangian method SPH (Smoothed Particle Hydrodynamics), widely used to simulate free surface flows in many areas (Monaghan et al. 2012), is also popular in modeling dam breaks (Mirauda et al. 2020; Hosseini et al. 2019; Memarzadeh et al. 2018; Razavitoosi et al. 2014; Ghaeini-Hessaroeyeh et al. 2021; Shahheydari et al. 2015; Barati et al. 2018). This method is based on dividing a liquid into discrete elements - particles. (Demir et al. 2019) conducted an experimental study in which the configuration is similar to the setup in (Koshizuka et al. 1995). The authors recorded the pressure readings on the bottom wall, and also provided a numerical implementation of the experiment obtained using the Smoothed Particle Hydrodynamics (SPH) and Finite element method (FEM) methods. Based on the three-dimensional Navier–Stokes equations and the SPH method, the authors of (Luo et al. 2017) studied by numerical modeling of dam failure in a complex cascade channel. There were three dams in the path of the water flow, the destruction of which took place one after another, as a large impulsive force approached. An experimental and numerical study (using the SPH method) of dam break was studied in the paper (Kocaman and Dal 2020). The study was carried out in an inclined rectangular installation with two reservoirs without a gate between them. A dam break in a cascade installation was also considered in a study (Yang et al. 2020a, b). The steep inclined canal was equipped with a group of natural landslide dams that change the behavior of the water flow.

The computational accuracy of the SPH method can be improved by the combined use of smoothed particle hydrodynamics with other grid methods (He et al. 2018; Crespo et al. 2015). For example, the combined Smoothed Particle Hydrodynamics Discrete Element Method (SPH-DEM) approach based on locally averaged Navier–Stokes equations is presented in (Robinson et al. 2014). The advantage of the described method can be considered indisputable convenience in the simulation of complex flow around moving objects in the absence of the need for a grid. The only drawback of SPH compared to mesh methods is that for certain cases it may be necessary to simulate a large number of particles.

In (Hirt and Nichols 1981), it was proposed to introduce a special function f instead of calculating a large number of particles (Gerlach et al. 2006; Pilliod and Puckett 2004). In the presence of a phase at a point, the value of this function is equal to one, in the absence of a zero. At VOF = 1 the cell is completely filled with liquid, at VOF = 0 - with gas, at 0 < VOF < 1 it contains a free surface. (Marsooli and Wu 2014; Issakhov and Imanberdiyeva 2019) simulated a dam break in an area with an uneven bottom. Numerical calculations were performed using the three-dimensional Reynolds-averaged Navier–Stokes equations (RANS), and the VOF method was applied to fix the movement of the water surface. The volume of fluid (VOF) method and the RANS with a turbulent eddy viscosity model k-ε RNG to close the system of equations have been widely used to direct flow through complex geometries (Formentin et al. 2016; Vashahi et al. 2019). A sophisticated 3D non-hydrostatic model developed by (Munoz and Constantinescu 2020) and demonstrating a dam break in real terrain was also constructed using the VOF method.

The three-dimensional numerical model proposed in this study simulates the hydraulic structure break under the influence of a large volume of water and the action of gravity. However, the real dam break is not only the water flow moving at high speed. The natural process of dam break is a transportable mixture of water, mud and stones. It is impossible to characterize the behavior of bottom sediments using only Newtonian fluid; therefore, the multiphase model introduced in the study (Shakibaeinia and Jin 2011) considers the sedimentary layer as a non-Newtonian fluid. A similar approach was used in this paper. There is other works in which it is necessary to use the non-Newtonian fluid model: for example, in order to establish the dependence of fluid viscosity on stress (Gotoh and Fredsøe 2000). The mixing of the water phases and bottom sediments upon opening the gate, as well as the subsequent transfer of the mobile formation caused by the collapsed water flow, is shown in the study (Castro et al. 2008). This process takes place in a channel with a slight slope (0.052%). To minimize the consequences of a dam failure, it is important to study the stability of landslide dams, the failure of which could lead to repeated geological disasters. In the work (Wu et al. 2020), the geometry of a landslide dam of various shapes is considered for various combinations of the installation inclination angles and the dip angles of the sliding surface. The most common cause of failure of earth or earth dams is reservoir overflow (Gregoretti et al. 2010). In (Van Emelen et al. 2014), a trapezoidal sand dam blocks the path of the water flow, and bottom sediments below the dam allow to study the potential erosion downstream of the pile. (Rowan and Seaid 2020) carried out two-dimensional modeling of shallow water flows over a multilayer moving channel, taking into account the various properties of the sediments that form the reservoir.

The main goal of the study is to investigate the process of water flow propagation during a dam break in a channel with a trapezoidal narrowing (Kocaman et al. 2020). The paper also demonstrates the mixing of water flow and sediment downstream. In this paper, it was numerically investigated the behavior of a rapidly moving water flow reaching an urbanized area, taking into account different thicknesses of mud. For calculations, the movement of the flow of water and mud is carried out using Newtonian and non-Newtonian models. For this purpose, a modification of the mathematical model was carried out, since the Newtonian model was used to model the water flow, while the non-Newtonian model was used to model the mud flow. This modification of the mathematical model was described in (Issakhov and Zhandaulet 2020; Issakhov and Borsikbayeva 2021). The correctness of the constructed mathematical model and numerical algorithm is verified using experimental and numerical works of other authors. A distinctive feature of this work is the use of a modified mathematical model for the problem of the behavior of a rapidly moving water flow in an urbanized area with a natural expansion–contraction of the river bed, which is closer to reality. In this study, this area has been idealized as 5 × 5 square “buildings” (Soares-Frazão and Zech 2008). Different thicknesses of mud and different types of mud placement in front of buildings were used to slow down the water flow and reduce the shock pressure against the building. The following summarizes the potential hazard to urbanized areas.

2 Mathematical Model

To describe this process, three-dimensional RANS equations for incompressible flows of two immiscible phases are used, which looks like in the following vector form

$$\nabla u=0$$
(1)
$$\frac{\partial u}{\partial t}+(\nabla u)u=\frac{1}{\rho }f-\frac{1}{\rho }\nabla p+\frac{1}{\rho }\nabla ({\mu }_{eff}\nabla u)$$
(2)
$$\frac{\partial \chi }{\partial t}+{u}_{j}\frac{\partial \chi }{\partial {x}_{j}}=0$$
(3)

where \({\mu }_{eff}=\tau +{\mu }_{t}\), t is the time, p is the pressure, u is the flow rate, \(\rho\) is the density. The considered external force of the body (f), in this case gravitational forces, so that f = \(\rho g\), where g is the gravitational force.

For incompressible Newtonian fluids, the stress tensor is proportional to the strain rate tensor \(\overrightarrow{D}\):

$$\overrightarrow{\tau }=\mu \overrightarrow{D}$$
(4)
$$\overrightarrow{D}=(\frac{\partial {u}_{j}}{\partial {x}_{i}}+\frac{\partial {u}_{i}}{\partial {x}_{j}})$$
(5)

\(\mu\) - dynamic viscosity, which does not depend on \(\overrightarrow{D}\).

For non-Newtonian fluids, the stress tensor is written

$$\overrightarrow{\tau }=\eta (\overrightarrow{D})\overrightarrow{D}$$
(6)

\(\eta\) is a function of all three invariants of the strain rate tensor \(\overrightarrow{D}\). The non-Newtonian flow is modeled according to the following power law for the non-Newtonian viscosity

$$\eta =k{\gamma }^{n-1}H(T)$$
(7)

where n - is a measure of fluid deviation from Newtonian (power index), k is a measure of the average viscosity of a liquid (consistency indicator), γ refers to the second invariant \(\overrightarrow{D}\) and determined like

$$\gamma =\sqrt{{{^1/_2}}\overrightarrow{D}:\overrightarrow{D}}$$
(8)

H(T) - is found by Arrhenius's law.

$$H(T)=\mathrm{exp}[\alpha (\frac{1}{T-{T}_{0}}-\frac{1}{{T}_{\alpha }-{T}_{0}})]$$
(9)

where \({T}_{a}\) is the medium temperature, \({T}_{0}\) is the absolute temperature, α is the ratio of the activation energy to the thermodynamic constant. Temperature dependence is only enabled when the energy equation is enabled. When the parameter is set to α = 0, the temperature dependence is ignored.

To close the RANS, the RNG k-ε turbulent model with two additional partial differential equations for two variables k and ε is used.

$$\frac{\partial \rho k}{\partial t}+\frac{\partial \rho {u}_{j}k}{\partial {x}_{j}}=\frac{\partial }{\partial {x}_{j}}\left(\left(\mu +\frac{{\mu }_{t}}{{\sigma }_{k}}\right)\frac{\partial k}{\partial {x}_{j}}\right)+{P}_{k}-\rho \varepsilon$$
$$\frac{\partial \rho \varepsilon }{\partial t}+\frac{\partial \rho {u}_{j}\varepsilon }{\partial {x}_{j}}=\frac{\partial }{\partial {x}_{j}}\left(\left(\mu +\frac{{\mu }_{t}}{{\sigma }_{\varepsilon }}\right)\frac{\partial \varepsilon }{\partial {x}_{j}}\right)+{C}_{{1}_{\varepsilon }}\frac{\varepsilon }{k}{P}_{k}-{C}_{{2}_{\varepsilon }}^{*}\rho \frac{{\varepsilon }^{2}}{k}$$

where

$${\mu }_{t}={C}_{\mu }\rho \frac{{k}^{2}}{\varepsilon }$$
$${P}_{k}={\mu }_{t}\left(\frac{\partial {u}_{i}}{\partial {x}_{j}}+\frac{\partial {u}_{j}}{\partial {x}_{i}}\right)\frac{\partial {u}_{i}}{\partial {x}_{j}}-\frac{2}{3}\frac{\partial {u}_{k}}{\partial {x}_{k}}\left(3{\mu }_{t}\frac{\partial {u}_{k}}{\partial {x}_{k}}+\rho k\right)$$
$$C_{2_\varepsilon}^\ast=C_{2_e}+\frac{C_\mu\eta^3\left(1-{\displaystyle\frac\eta{\eta_0}}\right)}{1+\beta\eta^3},\;\mathrm{here}\;\mathrm\eta=\frac{Sk}{\mathrm\varepsilon}\;\mathrm{and}\;\mathrm S=\sqrt{S_{\mathit i\mathit j}S_{\mathit i\mathit j}}$$

The constants have the following meanings: \({C}_{\mu }=0.0845\), \({\sigma }_{k}=0.7194\), \({\sigma }_{\varepsilon }=0.7194\), \({C}_{{1}_{\varepsilon }}=1.42\), \({C}_{{2}_{\varepsilon }}=1.68\), \({\eta }_{0}=4.38\).

3 Numerical Algorithm

For the numerical solution of this system of Eqs. (1) - (3), the Pressure-Implicit with Splitting of Operators (PISO) algorithm was chosen (Issa 1986; Jang et al. 1986; Issakhov and Imanberdiyeva 2019; Issakhov et al. 2018; Issakhov and Omarova 2021; Issakhov, Abylkassymova et al. 2022a, 2022b Issakhov et al. 2021). The PISO is originally developed for non-iterative simulation of non-steady compressible flow, but can be usefully adjusted to steady problems and a pressure–velocity calculation procedure for the Navier–Stokes equations. The PISO consists of a totally three steps, which were constructed to ensure mass conservation.

  1. 1.

    The predictor step

Initialization of the pressure p* and find velocity components u*, v* and w*.

  1. 2.

    The corrector step 1

From first step determines correction factors for pressure and velocity (p’, u’, v’, w’), then solve momentum equation by placing corrected pressure p** and get corrected velocity components u**, v** and w**.

$$p\;^{\prime}=p^{\ast\ast}-p^{\ast}$$

Next by determining p’, u’, v’, w’ it places by corrected pressure term p** in discretized momentum equation, then find the corrected velocity component u**, v** and w**. By determining pressure correction p’ it can be calculate correction component for the velocity u’, v’ and w’.

  1. 3.

    The corrector step 2

$$p^{\ast\ast\ast}=p^{\ast\ast}+p\;^{\prime\;\prime};\;p\;^{\prime}=p+p^{\ast}$$
$$u^{\ast\ast\ast}=u^{\ast\ast}+u\;^{\prime\;\prime};\;u\;^{\prime\;\prime}=u\;^{\prime}+u^{\ast}$$
$$v^{\ast\ast\ast}=v^{\ast\ast}+v\;^{\prime\;\prime};\;v\;^{\prime\;\prime}=v\;^{\prime}+v^{\ast}$$
$$w^{\ast\ast\ast}=w^{\ast\ast}+w\;^{\prime\;\prime};\;w\;^{\prime\;\prime}=w\;^{\prime}+w^{\ast}$$

here p***, u***, v***, w*** – corrected pressure and velocity components, respectively, p**, u**, v**, v** – second correction for pressure and velocity components. By setting p = p***, u = u***, v = v***, w = w*** where p, u, v, w – corrected pressure and velocity components.

The equation for volume fraction was found by explicit time discretization. In this method the standard finite-difference interpolation schemes were used to the volume fraction values that were found at the previous time step. All numerical calculations were done using ANSYS Fluent.

4 Test Problem

The configuration of this test problem, according to the experiment presented in (Kocaman et al. 2020), was a rectangular horizontal channel with a length, width, and height of 8.9 m, 0.3 m, and 0.34 m, respectively. The volume of water is restrained by a vertical gate located at a distance of 4.65 m from the beginning of the reservoir. The initial water level was \({h}_{o}=0.25\) m. The rest of the canal, downstream of the gate, was initially dry. At a distance of 1.52 m from the vertical gate, there were symmetrical trapezoidal obstacles. Such barriers were set up to simulate the natural expansion–contraction of the river bed and natural or man-made barriers. The length of the barrier was 0.95 m, and the compression width was 0.1 m. Since the water flow does not enter the reservoir, the upper boundary was designated as “wall”. Since the reservoir was open downstream, the lower boundary was designated as “outlet”. The side walls of the channel and the bottom have also been defined as "walls". The experimental results were compared with the calculations obtained during the development of this numerical model. The calculated data were obtained using the VOF method, and the system of RANS was included in the basis of the mathematical model. The RNG k-ε turbulent model was used to close the system of equations. The time step was ∆t = 0.005 s (Fig. 1).

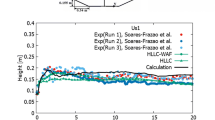
The change in the water level was measured using eight different sensors \({P}_{1}, {P}_{2},{P}_{3},{P}_{4},{P}_{5}, {P}_{6},{P}_{7},{P}_{8}\), the location of which is shown in Fig. 2. Comparison of the obtained numerical results with experimental data, as well as with the numerical results of other authors is shown in the Fig. 3. The results in the comparative plots in Fig. 3 are presented in dimensionless form: the initial water depth h0 was taken as the denominator of the horizontal distance (X = \(\frac{x }{{h}_{o}}\)) and flow depth (\(\frac{h }{{h}_{o}}\)), while the dimensionless time has the form \({T=t(^g/_{h_0})^{^1/_2}}\). To obtain such a dimensionless form, the time t was multiplied by \((^g/_{h_0})^{^1/_2}\). As soon as the vertical gate rises, there is an instantaneous drop in the water level at the P1 control point upstream of the gate. In contrast to this, in the P2 sensor, which is symmetrically relative to the P1 sensor, there is a jump in the water level at T = 5. Further, in the interval T = 5 - 30, the water level remains almost unchanged. At the measurement point P3 (X = 2.80), the overall rise of the water flow is observed noticeably slower, since the wave of the dam break flow reaches only T = 20. A sharp increase in the water level is observed when the water flow reaches the control points. A gradual decrease in water depth occurs when the reflected wave, which is already moving upward, reaches the axis of the dam. The numerical results of the authors (Kocaman et al. 2020), which were obtained using RANS, show good agreement with the experiment, while when using SWE, the water level rises significantly. The proposed numerical model in this paper also shows the successful agreement of the obtained numerical results with experimental data, which proves the reliability and efficiency of the method used.

Fig. 1
figure 1

Channel configuration in the test problem

Full size image
Fig. 2
figure 2

Location of sensors \({P}_{1}, {P}_{2},{P}_{3},{P}_{4},{P}_{5}, {P}_{6},{P}_{7},{P}_{8}\) on the channel geometry

Full size image
Fig. 3
figure 3

Change in water level over time at control points

Full size image

Figure 4 shows comparative plots of numerical data and measured free surface profiles at different points in time after opening the vertical gate. At T = 11.28, in the region of trapezoidal compression of the channel, one can notice a sharp increase in the height of the water level and the resulting reflected wave. The reflected wave is finally formed at T ≥ 21.92. Figure 5 shows the profiles of the propagation of a water column at certain points in time in a three-dimensional view. The reflected dam break wave described above can also be clearly seen in this figure.

Fig. 4
figure 4figure 4

Change in the water height level at certain control points in time

Full size image
Fig. 5
figure 5

The nature of the propagation of the water flow at a certain control point in time, three-dimensional view

Full size image

5 Dam-Break Flow Through an Idealized City

In this section, the behavior of a rapidly moving flow of water reaching an urbanized area was investigated. The movement of the water flow was caused by the instantaneous hydraulic structure break. The process of spreading the volumes of water was also hampered by the transverse compression of the channel in the form of a trapezoidal shape. To study the nature of the water flow, several cases were considered:

  1. 1.

    Case 1 - there is a layer of bottom sediments 0.025 m high behind the trapezoidal narrowing of the channel

  2. 2.

    Case 2 - there is a layer of bottom sediments 0.05 m high behind the trapezoidal narrowing of the channel

  3. 3.

    Case 3 - the bottom sediment layer was located by alternating mud and dry land: one row of the sedimentary layer was 0.025 m high, the next 0.05 m, then again 0.025 m and finally the height of the last row was also 0.05 m.

To carry out numerical modeling, the computational geometry was specified as in the test problem (Kocaman et al. 2020) with some changes in it. Urbanized terrain in this case was imitated by symmetrical square projections of 5 × 5 dimensions (Soares-Frazão and Zech 2008). “Buildings”, having a square form with a side of 0.05 m and a height of 0.1 m at the base, were at a distance of 0.0375 m from each other. The dimension of the calculated configuration for all three cases is shown in Figs. 6 and 7. As in the test problem, the length, width and height of the water reservoir were 4.65 m, 0.3 m and 0.25 m, respectively. Similar to the test problem to close the system of equations was used an RNG k-ε turbulent model was with a spatial step of 0.0075 m, as a result of which the computational grid consisted of 2,074,866 elements and, finally, a time step dt = 0.005 s was used. The density of the sedimentary layer was taken as 2683 kg/m3.

Fig. 6
figure 6

Calculation scheme for Case 1 and Case 2, top view

Full size image
Fig. 7
figure 7

Design scheme for Case 3, top view

Full size image

Figure 8 illustrates the graphs of changes in the water level during the whole time of the computational experiment (t = 19.2 s). From the figures presented below, it can be concluded that even a small increase in the height of bottom sediments can reduce the water flow rate, namely, by 0.2 s under the conditions considered in this problem. Also, none of the four measuring sensors noticed an increase in the height of the water column - it did not rise higher than 0.16 m. Starting at about t = 16.4 s, the shock wave completely covers the buildings and until the end of the computational experiment, the height of the water column is unstable (Table 1).

Fig. 8
figure 8

Change in the height of the water level in the calculated sensors over time

Full size image

Figure 9 illustrates the changes in pressure over time at control points G1, G2 and G3, the coordinates of which can be seen in Table 2. According to the results of numerical simulations, Case-1 and Case-3 observed the lowest pressure level in the first two seconds (~ 500 Pa) at G1 control point. In contrast to this, the maximum pressure value is observed at t = 2.28 s, namely ~ 2000 Pa. After the described sharp jump (t = 2.28 s) at the point G1, the pressure level changes insignificantly in three cases and, finally stops fluctuating from 12 to 19 s. At point G2, a similar phenomenon is observed, with a few exceptions: the maximum pressure value is observed at t = 3 s, which means about ~ 1900 Pa. Finally, the last G3 point shows similar pressure change results with the G1 indicator gauge.

Fig. 9
figure 9

Change in pressure in the calculated sensors over time

Full size image
Table 1 Coordinates of the location of the calculated sensors
Full size table
Table 2 Coordinates of the location of the calculated sensors for measuring pressure
Full size table

The maximum pressure value (almost 2000 Pa) in the case of a sediment height of 0.05 m. This can be explained by the fact that these control points (G1 and G3) are located on the walls of the building, which are close to the walls of the channel, so the reflected water wave against these walls forms an additional pressure on these walls. However, this effect is not observed at the control point (G2), since the action of the reflected water wave almost does not affect the walls of the building, which is located in the middle of the channel. Since the measurement of the pressure level was carried out on the outermost buildings of the "city", such a sharp jump can cause the destruction of the building and, therefore, lead to possible human casualties. Avoiding death by reducing the flow rate and maximum shock pressure is one solution to this problem. Figures 10, 11 and 12 show the motion profiles of the free surface at times taken when solving the test problem (Kocaman et al. 2020) for all three cases. Since the end of the channel was open, after some time a gradual decrease in the volume of water in the installation is observed.

Fig. 10
figure 10

Three-dimensional view of the process of water flow propagation at different points in time at the depth of the mud layer 0.025 m

Full size image
Fig. 11
figure 11

Three-dimensional view of the process of water flow propagation at different points in time at the depth of the mud layer 0.05 m

Full size image
Fig. 12
figure 12

Three-dimensional view of the process of water flow propagation at different points in time in the "mixed" case

Full size image

So from the obtained results, it can be observed that both the propagation of the water wave and the distribution of pressure on the walls of the building have symmetrical results. It can be seen, in such conditions, the most susceptible to destruction are the outermost buildings, since according to the data obtained in these buildings it shows the maximum pressure than in the central building. However, it should be noted that the influence of the thickness of the deposit and even the location of the deposit play a huge role. So, according to the location and thickness of the sediment proposed in this work, it can be seen that at all control points there is a decrease in the maximum pressure. However, it should be noted that the higher the deposit thickness, the higher the maximum pressure on the walls of the building. The results show that the best results are deposits with a thickness of 0.025 m and a mixed location of the deposit. This is due to the fact that the greater thickness of the sediment, together with the water moving downstream, forms a large mass, which, colliding with the building, forms a greater shock pressure. In general, the existence of deposits of a certain thickness has a beneficial effect on the formation of mud flow and the slowing down of the flow itself.

So after the water break, it can be observed that the water level begins to fall very sharply, and when passing through the trapezoidal compression region of the channel, one can notice a sharp increase in the water level height, as well as the formation of many reflected waves. An additional rise in the water level is observed after the area of compression of the channel in front of the buildings, this is due to the collision of the main flow with the buildings. So these collisions form additional humps in the progressive waves while significantly increasing the depth of flood waves. However, it should be noted that this process does not take place for a long time and after 2.5 s the water level gradually begins to fall to 16.1 s, since by this time the process of water break ends. After 16.1 s, as can be seen from all control points, a sharp rise in the water level appears. It should be noted that the closer the control point located upstream, so the process is faster, whereas for the points that are located downstream of the process takes place with some delay in 0.6 s. Also, depending on the location of the control points, changes in the water height level occur in different ways. As can be seen from the figures, the further the control point located downstream, the hanging of the water level occurs less rapidly. However, the growth process does not take long and begins to fall almost immediately. The obtained results show a strong influence of flood water downstream on the progressing wave. So after the deposition layer, a significant decrease in the speed of the driving wave is noticeable, which can have a beneficial effect on urbanized buildings, since a decrease in the speed of the driving wave has led to a decrease in the value of the maximum pressure exerted on the walls of the building.

6 Conclusion

The proposed study shows the computational results of a three-phase flow during a break of a hydraulic structure (water, air and phase for the sedimentary layer). The imitation of the motion of a free surface (water) was achieved using a Newtonian fluid, while the propagation of a moving layer was achieved using a non-Newtonian fluid. This approach is based on the VOF method. The three-dimensional incompressible Navier–Stokes equations with modification were solved using the PISO numerical algorithm. The developed numerical model was tested for reliability by comparing the calculated results with measurement values and numerical data of other authors. In the course of approbation, the obtained values displayed good agreement with experimental calculations.

By analyzing the numerical results, it can be concluded that an increase in the height of the mud layer leads to deceleration of the moving water flow. Thus, the artificial superposition of low-altitude sediments gives a gain in time, which can subsequently be used for the timely evacuation of the population. It should be noted that the analysis of comparative graphs showed the deceleration of the water flow by more than 0.2 s for a moving layer depth of 0.025 m and when using a mixed arrangement of the sediment. From the obtained results, it can be noticed a decrease in the maximum pressure value by almost 2 times.

Despite the fact that in this three-dimensional numerical model of dam break some conditions were idealized (urban configuration, installation geometry, etc.), the results of this study can significantly help in a deeper understanding of the real break of hydraulic structures processes. The method of water break flow proposed in this work is a kind of protection for the population in real time. The obtained results in the course of the proposed numerical modeling can serve as a good promise in the future by modeling the real natural landscape of river channels.

However, it should be noted that there are some limitations to this study. First, it can be noted that a large computational grid is required to simulate real large-scale problems. However, due to the large size of the computational grid, even the most powerful supercomputers cannot carry out simulations in an adequate time. Secondly, it should be noted that the analysis of the obtained results and the conduct of experimental work during the dam break of the water flow, taking into account the mud impurities. Thirdly, to maximize the approximation of the problem to the real case, it will be necessary to take into account many factors, such as the presence of various particles in the impurity flow, complex terrain reliefs, etc.

Further research will be directed, firstly, to improve the obtained numerical results by increasing the computational grid. Secondly, by adding the most important factors that will bring the problem as closely as possible to the real case.