1 Introduction

The dam break problem is one of the most devastating floods in the history of the modern world. Intensive snow melting, heavy rains, as well as human factors, such as carelessness, can lead to a dam break, which in turn can lead to flooding and destruction of neighboring settlements. Despite the fact that there has been a lot of research on the destruction of the dam, this phenomenon remains one of the most important problems in the field of hydraulic engineering because of its danger to human society. Therefore, dam breakthrough is a classic problem of great engineering importance (Chanson 2006).

This problem is also acute in the Republic of Kazakhstan. There have been similar natural disasters, which resulted in the death of many local residents. For example, in 2010, the dam break of the Kyzylagash reservoir in the Almaty region killed 43 people, hundreds were injured, about a thousand people had to be evacuated from flooded places. In the summer of 1921, heavy rains fell in Almaty, and intensive melting of snow and glaciers began in the mountainous areas. Because of these natural leashes along the river Small Almatinka, the mudflow reached actually the center of the city. Within five hours, a significant part of Alma-Ata was turned into ruins and covered with a mud mass. More than 500 people were killed. Because of such acutely pressing issues, it is very important to investigate all aspects of the dam break problem.

The scientific value of dam breakthrough has long been recognized as an idealized problem for evaluation and testing for a number of theories and approaches, both in mathematics and in physics (Wang et al. 2000). In most past studies, dam failure was considered as a collapse of water, and only a few of them were in mixtures of particles with water (Razavitoosi et al. 2014; Spinewine and Zech 2007). With the advancement of computing technology, numerical methods have become an excellent research tool in various fields. For example, the popular numerical method for tracking and locating a free surface, the volume of fluid (VOF) method (Hirt and Nichols 1981), based on Eulerian meshes, and made it possible to simulate free surface deformations. Using such numerical methods, many works were done to describe the flow behavior after the dam was broken. A realistic model of a dam break was introduced by (Issakhov and Imanberdiyeva 2019) above a fixed bed with different reliefs. Also, using the VOF method (Issakhov et al. 2018), dam breaks were modeled for various forms of obstacles. In study (Ying et al. 2009) developed a reliable and accurate computational model based on a conservative form using the finite volume discretization on unstructured triangular grids for flows with broken sections that can flow over difficult terrain. Also, there are studies related to the use of RANS equations, which include turbulence models (Abdolmaleki et al. 2004; Quecedo et al. 2005; Shigematsu et al. 2004). An improved SPH approach to solving three-dimensional free-surface problems was demonstrated (Xu 2016), where three complex numerical problems were modeled, 1) three-dimensional dam break to a vertical wall, 2) an obstacle with a cubic shape and 3) an obstacle with a cylindrical shape, which was compared with the available numerical data and experimental data. The numerical code developed by (Celis et al. 2017) based on the finite difference method (FDM) showed good results of destruction and splashing when the dam is broken. In paper (Li and Yu 2019), a flood wave caused by a dam break acting on the vertical lower wall of the channel, which was numerically investigated using VOF and LS (Level Set) models, where it was shown that VOF model has an excellent ability to work with interface modeling, especially with the waves destruction and the deformation of the free surface with a large amplitude, compared with the LS model. A complete understanding of the water flow spreading process was presented by (Yang et al. 2018) when a dam is broken through with different depths of water downstream above a fixed bed.

However, it is necessary to take into account that in real conditions the flow at a dam break does not consist only of water and often contains some impurities and particles. When the dam is broken, these impurities play a very important role, since the transportation of this mixture will have a different movement pattern. In this case, this mixture can be described as a non-Newtonian flow. This flow can be defined as a dense flow of fluid and impurities, in which direct interactions between impurities are the dominant feature that determines the nature of the flow.

Intense flows that arise during the dam break and often cause morphological evolution and sediment transport, which, in turn, contributes to the change in flows. Interactive processes of flow, sediment transport and morphological evolution are a hierarchy of considerable physical problems interest in the fields of hydraulics and geomorphology. A good understanding of these processes is important not only from an application point of view, but also for effective flood risk management and the environmental well-being of the region (Frey and Church 2009).

The dam destruction flows above a fixed impermeable layer have been carefully studied in many papers (Issakhov et al. 2018; Kleefsman et al. 2005; Marsooli and Wu 2014), but with intensive flows the lower layer of the flow can be mobile, therefore this flow can transfer or shift to this lower layer, such as clay, mud, sand, etc. This process can lead to the transportation of very large amounts of sediment, which leads to a large-scale change in the morphology of the area downstream and dramatically increases the damage to the environment and infrastructure of the city. Also, due to friction, inertial effects and pulse exchanges, the lower layer can significantly affect the flood wave development. Therefore, it is very important to take into account this geomorphological process of transfer and destruction of bottom sediments. The transfer of these sediments cannot simply be reproduced by the model of Newtonian fluid (Gotoh and Fredsøe 2000). Consequently, a non-Newtonian model is necessary in order to be able to predict the stress-dependent viscosity of the phase. Thus, it is important to accurately simulate the geomorphological changes associated with dam break flows. The flow behavior in the fixed conditions and moving layers differ significantly, and they strongly influence the deformations of the free surface and the propagation of flood waves. Therefore, it is of great practical and theoretical interest to study these types of flow (Janosi et al. 2004; Lauber and Hager 1998).

In study (Papanicolaou et al. 2008) provide insights into future trends and needs regarding hydrodynamic and sediment transport models. Before attention to the effects of sediments was primarily focused on quasi-analytical solutions (Fraccarollo and Capart 2002), and then using computational models including shallow-water two-layer models (Leal et al. 2010; Li et al. 2013; Swartenbroekx et al. 2013). The bilayer models have been significantly improved in terms of the sediment transport description, from partial connection between sediment and flow to full connection. In paper (Evangelista et al. 2013), the numerical results are compared with different sets of experimental data, in fixed conditions and moving layers, with different materials of the layer, in order to verify the simulation accuracy in a wide range of cases. In paper (Emelen et al. 2015) a model of shallow water - Exner, representing the dam break process was used. This paper analyzes the ability of the classical model of shallow water to model a complex sediment transfer process. In study (Hosseinzadeh-Tabrizi and Ghaeini-Hessaroeyeh 2018), the dam break flow caused by the partial destruction of the dam in a suddenly enlarged area above the moving bed was simulated. In this paper the model was used to simulate two laboratory tests.

Numerical simulations have been widely used as a reliable tool for studying various dam break flows above a moving bed. One-dimensional shallow water equations was used by (Zhang and Duan 2011) based on the finite volume method. In paper (Xia et al. 2010) used modified 2D shallow water equations in combination with the sediment transfer equation to study the moving layer, and an unstructured finite volume discretization was used to solve the basic equations.

The dam break of pure non-Newtonian liquids, such as liquid clay and gel, was studied in papers (Ancey and Cochard 2009; Chambon et al. 2009). Considering non-Newtonian fluids really allows for a better exploration of native complex natural flows, such as mudflows and impurity flows, than considering only Newtonian fluids, such as water. A dam breakthrough is considered as a fracture problem for a mixture of particles and a fluid (Li and Zhao 2018), which was numerically, investigated using the CFD-DEM approach for two non-Newtonian fluids based on experimental data. The numerical data were carefully compared to several control cases, including the particles and water mixture, a dry granular system, as well as three pure liquids (Herschel-Bulkley liquid, Bingham liquid and water). This work showed that non-Newtonian fluids can reduce the kinetic energy of particles during early destruction. In paper (Lin and Chen 2013) investigated the number of particles effect on the flows behavior and momentum on the flow structure. The flow rate increased with decreasing concentration, while the impulse decreased. The results of this work (Lin and Chen 2013) illustrated that the friction coefficient has an obvious effect on the flow. However, the parameters considered in this study were limited, and only the forward position of the mixture flow was compared to investigate their effects. In previous studies related to dam break flows, the effect of the moving lower layer was not shown in detail. Because sediments are very viscous, they can affect flow in general. Their friction and elastic recovery coefficients can affect the flow behavior due to the interaction between the fluids.

The focus of this study is on the destruction of a dam consisting of water and mud, which is a non-Newtonian fluid (Coussot 1995). Mud flow usually occurs after soil saturation due to rainfall or due to rapid snow melt. Mud and debris flows occur on steep slopes or mountainous areas. Detailed flow control allows us to distinguish three different stages of wave development: the decline phase, the inertia phase, and the transport phase (Hogg and Woods 2001; Hogg and Pritchard 2004). At each of these stages, different physical mechanisms dominate at different times.

Based on a numerical approach, this study aims to provide new data of computational calculation of pressure peaks value during a dam break, taking into account the mud flow. More specifically, this paper discusses the value of maximum pressure relative to different forms of obstacles. Numerical simulation was performed using VOF using the ANSYS Fluent.

2 Mathematical Model

In the present study, an incompressible flow consisting of three phases was considered: water, air and a phase for deposition (impurity). The equations controlling the flow are simply incompressible Navier-Stokes equations.

$$ \frac{\partial {u}_j}{\partial {x}_j}=0 $$
(1)
$$ \frac{\partial {u}_i}{\partial t}+\frac{\partial {u}_i{u}_j}{\partial {x}_j}=g-\frac{1}{\rho}\frac{\partial P}{\partial {x}_i}+\frac{1}{\rho}\frac{\partial }{\partial {x}_j}\left(\tau +{\mu}_t\right) $$
(2)
$$ \frac{\partial \chi }{\partial t}+{u}_j\frac{\partial \chi }{\partial {x}_j}=0 $$
(3)

where u is the flow rate, ρ is the density of water, p is pressure, t is time, f is the external force of the body, g is the acceleration of gravity, χ is the phase response, and \( \overrightarrow{\tau} \) is the stress tensor.

In incompressible Newtonian fluids, the tensor stress is proportional to the strain rate tensor \( \overrightarrow{D} \):

$$ \overrightarrow{\tau}=\mu \overrightarrow{D} $$
(4)
$$ \overrightarrow{D}=\left(\frac{\partial {u}_j}{\partial {x}_i}+\frac{\partial {u}_i}{\partial {x}_j}\right) $$
(5)

μ - dynamic viscosity, which does not depend on \( \overrightarrow{D} \).

For non-Newtonian liquids, the stress tensor is written

$$ \overrightarrow{\tau}=\eta \left(\overrightarrow{D}\right)\overrightarrow{D} $$
(6)

η is a function of all three invariants of the strain rate tensor \( \overrightarrow{D} \). The non-Newtonian flow is computed by power law for non-Newtonian viscosity

$$ \eta =k{\gamma}^{n-1}H(T) $$
(7)

k is the average viscosity measure of a liquid (consistency index);

n - is the fluid deviation measure from the Newtonian (power index), γ refers to the second invariant \( \overrightarrow{D} \) and is defined as

$$ \gamma =\sqrt{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\overrightarrow{D}:\overrightarrow{D}} $$
(8)

H(T) found by the Arrhenius law.

$$ H(T)=\exp \left[\alpha \left(\frac{1}{T-{T}_0}-\frac{1}{T_{\alpha }-{T}_0}\right)\right] $$
(9)

where α is the ratio of the activation energy to the thermodynamic constant and Tα is the medium temperature and T0 is the absolute temperature. Temperature dependence is enabled only when the energy equation is on. When setting the parameter to α=0, the temperature dependence is ignored.

The VOF method was first introduced by Hirt and Nichols (Hirt and Nichols 1981). The equations for the phases are solved by introducing the function F, determined as the average value of the phase characteristic function over the cell of the computational grid. Therefore, F is the volume fraction occupied by the phase in the grid cell. At the end of each time step, the local volume fraction in the cell is used to compute the local viscosity and density values needed to solve the Navier-Stokes equations. For “mixed cells” (i.e. containing more than one phase), equivalent viscosity and density are computed by linear interpolation based on the volume fraction.

To close the Reynolds-averaged Navier-Stokes equations (RANS), the SST k-ω turbulent model with two additional partial differential equations for two variables k and ω was used.

3 Numerical Simulation Algorithm

The Reynolds-averaged Navier-Stokes equations (RANS) are sampled on a fixed Cartesian grid using the finite volume method approximation. The PISO algorithm for numerical algorithm (Issa 1986; Issakhov and Mashenkova 2019; Issakhov, 2016) was chosen. The PISO was developed to provide mass conservation using predictor-corrector steps, which includes one prediction and two corrector steps.

4 Verification of the Mathematical Model

Problem 1 The initial stage of the dam break

The study of the flow impact was carried out taking into account the dam break in which the water flow column created by the destruction of the dam faces a vertical obstacle. Therefore, improving the description of this particular flow of exposure is of great interest. For verification of the 3D model, experimental dam break data from the Netherlands Marine Research Institute (MARIN) (Kleefsman et al. 2005) were used. This measurement could be considered as a simple model of water flow. The geometry of the experiment is shown in Fig. 1.

Fig. 1
figure 1

Geometry of the experiment (Kleefsman et al. 2005)

Full size image

A large tank 3.22 × 0.993 × 1.0 m is used with an open roof. In one part of the tank, water with a volume of 0.67 m3 is held by the shutter. When the shutter instantly rises by releasing a mass, a water flow is created that moves due to gravitational forces. A box representing a scale model of an obstacle with a size of 0.403 × 0.161 × 0.161 m was placed in the tank. The obstacle was covered with pressure sensors (P1, P3, P5, P7) and two water level indicators (H2, H4).

The interaction of intensive water flows with the structure is a key problem in hydraulic, oceanic and coastal construction. This interaction is presented in Fig. 2, which includes a very fast impulsive force (i.e. a stroke), followed by a more stationary stage. Obtained numerical results from the VOF model as shown in Fig. 3, the obtained numerical results from the developed model show acceptable accuracy compared with experimental data. Fig. 4 shows snapshots of numerical results for the total flow at time points of 0.4 and 0.56 s compared with experimental values (Kleefsman et al. 2005).

Fig. 2
figure 2

Pressure profiles at different control points (P1, P3, P5, P7)

Full size image
Fig. 3
figure 3

Vertical heights of water in a tank on lines H4 and H2

Full size image
Fig. 4
figure 4

Snapshots of dam break simulation with experiment at time points of 0.4 and 0.56 s

Full size image

As can be displayed from Fig. 2 at the moment when the wave hits an obstacle, the pressure distribution on the surface of this obstacle is perfectly described using modeling. This figure shows the pressure distribution at points P1 and P3 at the front of the box, as well as at the top of the box at points P5 and P7 (the locations of the sensors are marked in Fig. 1). The shock pressure magnitude is the same for both the numerical data and the data from the measurement at point P1 (the lowest point on the box) (Kleefsman et al. 2005). The moment when the backward wave hits the obstacle again (approximately 4.7 s) also well characterized using modeling (Fig. 2). In the lower part of Fig. 2, where diagrams of pressure distribution over time are shown in the upper part of the box, there is a clear difference between the data of simulation and data from the measurement (Kleefsman et al. 2005). This anomalous pressure distribution appears several times in the bursts form, which can be seen at whole control points P1, P3, P5 and P7 (Fig. 2) at the same moment (approximately 1.3 s). The appearance of these bursts is due to the fact that small droplets of water after a given impact on an obstacle fall into empty cells that are completely surrounded by cells with a liquid, and these empty cells change to cells of the computational area with a liquid in one time interval. This intermittent change leads to the appearance of an anomalous peak pressure value in the entire pressure field.

From this figure, it could be noticed that there is an appropriate match between the computational snapshots and the measurement snapshots, when the water falls into the box for the first time at 0.4 s. In the second figure, the data from measurement and numerical data are illustrated for 0.56 s. From this picture, the shape of the water free surface could be outlined which goes around an obstacle and goes a little forward. The computational data are in appropriate agreement with measurement results (Kleefsman et al. 2005). The global behavior of water is the same, and the impact peak of pressure is in appropriate agreement, especially in the lower part of the obstacle.

Problem 2. The dam break flow above the movable layer of sediment

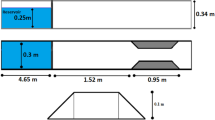
In order to verify the proposed model, in this section this model is applied to the control test of the dam break flow above the moving sediment layer. The laboratory measurement (Spinewine and Zech 2007) includes a water tank separated by valves in the middle, and the bottom of the tank is covered with a layer of mobile sediments. The experimental area has a height of 0.7 m and a total length of 6 m, that is, 3 m on both sides of the central gate, simulating an idealized dam. The width of the channel was set to 25 cm along the entire length of the channel. The water depth of this experiment is 35 cm as shown in Fig. 5. In this experiment, homogeneous coarse sand with a density of 2683 kg/m3 and polyvinyl chloride with a density of 1580 kg/m3 were used as the bottom layer.

Fig. 5
figure 5

Geometry and dimensions of the experiment (Spinewine and Zech 2007)

Full size image

The simulation snapshots in Fig. 6 show that a significant amount of precipitation is being destroyed by the dam break flow. This in turn leads to sediment loss, changing the flow depth. Ultimately, in the viscous phase, the flow becomes dominant and is slowed down by friction. Due to the presence of coarse sand, the flow at breakthrough slows down and leads to sediment transport and decreases. Also, the proposed model is compared with the results of other authors (Ran et al. 2015).

Fig. 6
figure 6

Simulation and experiment images (Spinewine and Zech 2007) of dam break with geomorphological changes at various times t = 0.25, 0.5, 0.75, 1 s

Full size image

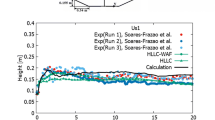
Figure 6 illustrates the simulation and experiment images (Spinewine and Zech 2007) when a dam is broken through with geomorphological changes at various points (t = 0.25, 0.5, 0.75, 1.0 s). Comparisons in Fig. 7 showed that the calculated free surface profiles are in appropriate agreement with the results of measurement (Spinewine and Zech 2007) and the numerical data of other authors (Ran et al. 2015).

Fig. 7
figure 7

Comparison of free surface profiles

Full size image

In general, in Fig. 8 from the obtained results, it can be seen that the observed flood wave differs from typical dam failure waves over fixed beds, showing that the very presence of a moving bed greatly affects the transport of water flow. The results showed that the dam break flow above the moving bed is much softer compared to the dam break flow above the fixed rigid layer. This is due to the fact that the transfer process of the lower layer reduces the energy flow. Thus, the presence of a moving layer increased the flow area and, consequently, reduced the flow rate.

Fig. 8
figure 8

Comparison of free surface profiles with mobile and immobile beds

Full size image

5 Numerical Study of Dam Breaks with Mudflow for Various Forms of Obstacle

To estimate the pressure distribution on the surface of a dam with mud flow during a dam break, a moving mud layer is added to the second experiment (Kleefsman et al. 2005), as shown in Fig. 9. The moving layer consisted of homogeneous sand with a density of 2683 kg/m3. In our model, the sediment phase is treated as a non-Newtonian fluid. For a non-Newtonian fluid, the effective viscosity is calculated using eq. (7).

Fig. 9
figure 9

Geometry modeling mud flow

Full size image

Figure 9 shows that the three-dimensional computing area consists of length, width and height with dimensions of 3.22 m, 0.993 m, 1.0 m as in the second experiment. Whereas the original water column is formed with a length, width and height with dimensions of 1.228 m, 0.993 m, 0.55 m, respectively. A moving layer with different heights (0.01 m, 0.02 m, 0.05 m) is laid between the water column and the obstacle, which has a size of 1.167 m. The air occupies the remaining space. Figure 10 shows the pressure distribution profiles on pressure gauges P1, P3, P5 and P7 of the obstacle surface with mud flow during the dam break for different deposition heights. For this model, Figs. 11, 12 and 13 are represented by snapshots of numerical results at time 0.4 and 0.56 s with mudflow at the dam break for different sediment heights. The liquid column extends to the opposite wall, and as can be seen from all the figures, the deposition front moves more slowly than the water front. Figures 11, 12 and 13 show that, due to the presence of the mud deposit, the free surface movement of the water begins to slow down and as the mud deposit height increases, this movement becomes slower. Since the water free surface is mixed with gravity deposits, and becomes more viscous, this leads to a general inhibition of all impurities.

Fig. 10
figure 10

Profiles of pressure distribution on pressure gauges P1, P3, P5 and P7 of the obstacle surface with mudflow during the dam break for different deposition heights

Full size image
Fig. 11
figure 11

Snapshots of a dam break with mudflow at time points of 0.4 and 0.56 s for sediment heights of 0.01 m

Full size image
Fig. 12
figure 12

Snapshots of a dam break with mudflow at time points of 0.4 and 0.56 s for sediment heights of 0.02 m

Full size image
Fig. 13
figure 13

Snapshots of a dam break with mudflow at time points of 0.4 and 0.56 s for sediment heights of 0.05 m

Full size image

From the presented pressure profiles in Fig. 10, it can be noted that at all control points the maximum pressure value decreases due to mud deposits. The decrease in pressure value is the result of a decrease in flow rate. The effect of viscous clay deposition is qualitatively confirmed from the results shown in Fig. 10, where it can be seen a decrease in the maximum shock pressure for the P1 control point almost 2 times, whereas for the P3, P5, P7 control points, it can be seen that the pressure value does not change very much. It should be noted that the first impact is the most dangerous for the integrity of the dam structure, and the use of viscous grease deposits has a beneficial effect on the dam structure itself during the first impact.

Below are the results of a dam break simulation for different heights of the moving bed. From the obtained results in Figs. 12 and 13, it can be noted that the moving layer helps to reduce the flow velocity, which in turn leads to a decrease in the pressure value on the obstacle itself. Regardless of the presence and thickness of the moving layer, the fluid front position is almost the same at the beginning of the flow when the dam collapses, but then the flow mixes with the moving layer over time and this layer begins to influence the position of the fluid and causes braking, and this process can be seen in the front part of the obstacle after t = 0.56 s (Figs. 11, 12 and 13). Over time, the difference between the front position of the liquid increases until the front of the liquid touches the opposite wall.

To further reduce the pressure values on the dam surface the different forms of dams were used. Thus, in paper (Issakhov et al. 2018), optimal obstacle shapes were proposed for reducing the shock pressure values. For the 3D model, the same optimal forms as in paper (Issakhov et al. 2018), obstacles with a slope of 30° and an arched obstacle with a central arc angle of 45° (Fig. 14) were used, since these forms showed the best results for reducing the impact pressure value (Issakhov et al. 2018). Figure 15 shows the pressure profiles on the P1, P3, P5, P7 pressure gauges with different forms of obstacles. However, in this work, muddy deposits were added. Figure 16 shows the pressure profiles on the P1, P3, P5, P7 pressure gauges for the arched shape at different deposition heights. In paper (Issakhov et al. 2018), the arched shape of the obstacle made it possible to reduce the shock pressure by almost 3.7 times as compared with the rectangular shape of the obstacle. From the obtained results in Fig. 16, it can be seen that under the influence of a non-Newtonian fluid and the optimal shape of the obstacle, the maximum shock pressure at point P1 was reduced more than 6 times comparing with the rectangular shape of the obstacle. However, it should be noted that for the remaining control points P3, P5, P7, the pressure value does not actually change. The whole process of moving the immobile layer and water in case of dam break with different heights of mudflows for different times from the arched form of an obstacle is shown in Figs. 17, 18 and 19. All the above results confirm that the transfer of viscous deposits during dam break greatly influences the behavior of the entire flow, because the interaction between different phases (Newtonian and non-Newtonian) leads to complex flow behavior. Since in real conditions, the flow at a dam break does not consist only of water and often contains some impurities, and these impurities play a very important role in general movements when transporting the entire volume of water.

Fig. 14
figure 14

Optimal obstacle shapes for a 3D problem

Full size image
Fig. 15
figure 15

Pressure profiles on pressure gauges P1, P3, P5, P7 with different forms of obstacles

Full size image
Fig. 16
figure 16

Pressure profiles on pressure gauges P1, P3, P5, P7 for the arched shape at different mud heights

Full size image
Fig. 17
figure 17

Snapshots from modeling of a dam break with mudflow for various time points with an arching obstacle for 0.01 m sediment heights

Full size image
Fig. 18
figure 18

Snapshots from modeling of a dam break with mudflow for various time points with an arching obstacle for 0.02 m sediment heights

Full size image
Fig. 19
figure 19

Snapshots from modeling of a dam break with mudflow for various time points with an arching obstacle for 0.05 m sediment heights

Full size image

6 Conclusions

This paper presented the numerical results of an incompressible dam break flow simulation, consisting of three phases: water, air and a phase for deposition (impurity). The water free surface movement has been carried out using the Newtonian fluid model, and the movement of mud impurity has been performed by the non-Newtonian fluid model based on the VOF method. The pressure and speed relationship was reached using the PISO algorithm. Computational modeling of the dam break problem using the VOF method has been satisfied in ANSYS Fluent, which significantly reduced numerical effort.

Verification of the mathematical model was performed on two test problems. Although from the obtained numerical data a definite difference in the shock distribution of pressure with results of measurement could be noticed, however, using this model, it will be possible to carry out computational modeling with acceptable accuracy. Predictions using computational modeling illustrated appropriate agreement with the experiment and the computational data of other authors, in particular, the global fluid behavior and pressure trends on the dam walls were well reproduced. The data from the computation give greater confidence in the effectiveness of the method.

This study proposes the use of Newtonian and non-Newtonian models for modeling waves caused by the dam destruction above the moving bed. In this case, the lower moving layer has been considered as a non-Newtonian fluid. The simulation data are in appropriate agreement with the data of measurement. The obtained results show that with the modeling it is possible to accurately predict the dynamic sediment transfer process. Also, the calculation data are in good agreement with other numerical results. It was found that the transfer of the lower layer began near the initial dam section and spread downstream. This study emphasizes the importance of carrying out numerical simulation of dam failure at moving earth layers, because this condition could be found in natural flows. In the future, these computational data and estimated mudflow heights may be used to predict 3D problems with actual complex terrain when the dam is broken.