1 Introduction

Water is a critical ecological element because it is scarce in an arid environment (Kim et al. 2003). Therefore, water source has severely restricted the sustainable development in the arid region of northwest China. For the arid region in northwest China, the water resource which can be utilized is mainly from the streamflow of inland rivers. So the runoff variation of an inland river has aroused more and more attention (Chen et al. 2009; Hao et al. 2008; Li et al. 2008; Xu et al. 2008a, 2009a; Wang et al. 2013).

As a scientific base for water utilization planning, hydrological prediction has been paid attention by the scientists in various countries. One of the traditional forecasting methods for hydrology system is the regressive analysis (Ding and Deng, 1988). But in the recent 20 years, various methods such as grey model (Deng 1989), functional-coefficient time series model (Shao et al. 2009), wavelet analysis (Smith et al. 1998; Chou 2007; Sang 2012), artificial neural network (Hsu et al. 1995; Hu et al. 2008), fractal and chaotic theory (Wilcox et al. 1991; Xu et al. 2008a, 2009a) have been widely applied in the hydrological prediction. Specially, some hybrid models (Kim et al. 2003; Lin 2006; Wang and Ding 2003; Sahay and Srivastava 2014; Yarar 2014) have been used.

Because the hydrology process is closely interconnected with climatic process, and greatly influenced by climate change, the key of hydrological prediction is to understand the hydro-climatic process. Theoretically, hydro-climatic process can be evaluated to determine if they comprise an ordered, deterministic system, an unordered, random system, or a chaotic, dynamic system, and whether change patterns of periodicity or quasi-periodicity exist. Many case studies in different countries and regions have suggested that the hydro-climatic process is a complex system, with nonlinearity as its basic characteristic (Ibbitt and Woods 2004; Sivakumar 2007; Wang et al. 2008; Xu et al. 2011a, 2013a). But it is difficult to achieve a thorough understanding of the complex mechanism of nonlinear hydro-climatic process (Xu et al. 2010).

In the last 10 years, many studies have been conducted to evaluate climatic change and hydrological processes in the arid regions of northwestern China (Chen and Xu 2005; Wang et al. 2010; Xu et al. 2011a, 2011b; Zhang et al. 2010). A number of studies have indicated that there was a visible transition in the hydro-climatic processes in the past half-century (Chen and Xu 2005; Chen et al. 2006; et al. 2007; Wang et al. 2010). This transition was characterized by a continual increase in temperature and precipitation, added river runoff volumes, increased lake water surface elevation and area, and elevated groundwater levels. This transition may bring a series questions if these changes represent a localized transition to a warm and wet climate type in response to global warming, or merely reflect a centennial periodicity in hydrological dynamics. To date, these questions have not received satisfactory answers; therefore, more studies are required to understand the nonlinear hydro-climatic process from different perspectives by using different methods (Xu et al. 2013a).

To further understand the change of runoff in an inland river and its response to regional climate change in northwest China at different time scales, we selected the Yarkand River as a typical representative to analyze the variation patterns of annual runoff (AR), annual average temperature (AAT) and annual precipitation (AP) by using wavelet analysis (WA), and constructed an integrated model to simulate the variation of AR with AAT and AP by integrating wavelet decomposition (WD) and back propagation artificial neural network (BPANN).

2 Study Area and Data

2.1 Study Area

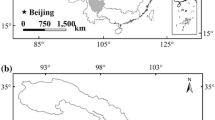
Originating from the surrounding mountains, one of the headwaters of the Tarim River, the Yarkand River is a typical inland river in northwest China, which has been relatively undisturbed by human activities. Therefore, to understand the response of runoff in an inland river to regional climate change in northwest China, we specially selected the Yarkand River as a case for modelling and demonstration in this study.

The Yarkand River (Fig. 1) is located in the southeastern region of Xinjiang Uygur Autonomous Region, with a length of 1097 km. The Yarkand River (35°40′ ~ 40°31′N,74°28′ ~ 80°54′E) has a total basin area of 9.89 × 104 km2, including 6.08 × 104 km2 as the mountain area, which accounts for 61.5 %, and 3.81 × 104 km2 as the plain area, which takes up 38.5 % (Sun et al. 2006). The main stream of the Yarkand River originates from Karakoram Pass in the north slope of Karakoram Mountain, where is full of towering peaks and glaciers. The Yarkand River is a typical inland river, and there is rare precipitation and no water recharge to the stream in the plain area. The multi-year average runoff in the Yarkand River consists of 64.0 % from glacial ablation, 13.4 % from rain and snow supply, and 22.6 % from groundwater supply, respectively (Sabit and Tohti 2005; Liu et al. 2008).

Fig. 1
figure 1

Location of the study area

Full size image

2.2 Data

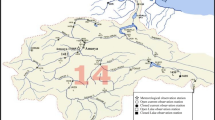
As a headwater of the Tarim River, the streamflow is rarely disturbed by human activities, whereas mainly affected by climatic factors, especially temperature and precipitation in the mountainous (Hao et al. 2008; Tao et al. 2011). In order to analyze the stream flow of the Yarkand River and its response to regional climate change, we use the data of runoff as well as temperature and precipitation. The runoff data were from the Kaqun hydrological station, and temperature and precipitation data were from Tash Kurghan meteorological station. The two stations are located in the source areas of the river; the amount of water used by humans is minimal compared to the total discharge. Therefore, the observed hydrological and meteorological records reflect the natural conditions.

To investigate the annual variation of runoff and its relation with regional climate change, this study used the raw data of annual runoff (AR), annual average temperature (AAT) and annual precipitation (AP) from 1957 to 2008, which were revealed in Fig. 2.

Fig. 2
figure 2

The raw data of AR, AAT and AP for the study period

Full size image

3 Methods

In order to simulate the annual runoff and its response to regional climate change at different time scales, we constructed an integrated model by integrating wavelet analysis (WA) and artificial neural network (ANN). We firstly identified the variation pattern of annual runoff and its related climatic factors by using WA at a given time scale, and then simulated the variation of annual runoff with its related climatic factors by using ANN based on WA at the corresponding time scale.

3.1 Wavelet analysis

Wavelet transformation has been shown to be a powerful technique for characterizing the frequency, intensity, scale, and duration of variations in hydro-climatic process (Labat 2005; Chou 2007; Xu et al. 2009b; Sang 2012). Wavelet analysis can also reveal localized time and frequency information without requiring the signal time series to be stationary, as required by the Fourier transform and other spectral methods (Farge 1992; Torrence and Compo 1998).

One of our tasks in this paper is to approximate the variation patterns of runoff and its related climatic factors by using wavelet decomposition and reconstruction at different time scales.

The principle of wavelet decomposition and reconstruction is as follows (Mallat 1989; Farge 1992; Torrence and Compo 1998). Considering a given signal X(t), such as AR, AAT and AP, etc., which can be built up as a sequence of projections onto Father and Mother wavelets indexed by both k {k = 1, 2, ......} and s {s = 2j, j = 1, 2, ......}. The coefficients in the expansion are given by the projections

$$ \left\{\begin{array}{c}\hfill {s}_{J,k}={\displaystyle \int X(t){\varPhi}_{J,k}(t) dt\begin{array}{ccc}\hfill \begin{array}{cc}\hfill \begin{array}{cc}\hfill \hfill & \hfill \hfill \end{array}\hfill & \hfill \hfill \end{array}\hfill & \hfill \hfill & \hfill \hfill \end{array}}\hfill \\ {}\hfill {d}_{j,k}={\displaystyle \int X(t){\varPsi}_{j,k}}(t) dt\begin{array}{cc}\hfill \hfill & \hfill j=1,2,\dots, J\hfill \end{array}\hfill \end{array}\right. $$
(1)

where J is the maximum scale sustainable by the number of data points, \( {\varPhi}_{j,k}={2}^{-j/2}\varPhi \left(\frac{t-{2}^jk}{2^j}\right) \) is father wavelet, and \( {\varPsi}_{j,k}={2}^{-j/2}\varPsi \left(\frac{t-{2}^jk}{2^j}\right) \) is mother wavelet. Generally, father wavelet is used for the lowest-frequency smooth components, which requires wavelet with the widest support; mother wavelet is used for the highest-frequency detailed components. In other words, father wavelet is used for the major trend components, and mother wavelet is used for all deviations from the trend.

Once a mother wavelet is selected, the wavelet transform can be used to decompose a signal according to scale, allowing separation of the fine-scale behavior (detail) from the large-scale behavior (approximation) of the signal (Bruce et al. 2002). The relationship between scale and signal behavior is designated as follows: a low scale corresponds to compressed wavelet as well as rapidly changing details, namely high frequency, whereas a high scale corresponds to stretched wavelet and slowly changing coarse features, namely low frequency. Signal decomposition is typically conducted in an iterative fashion using a series of scales such as a = 2, 4, 8, ......, 2L, with successive approximations being split in turn so that one signal is broken down into many lower resolution components.

The representation of the signal X (t) now can be given by:

$$ X(t)={S}_J+{D}_J+{D}_{J-1}+\dots +{D}_j+\dots +{D}_1 $$
(2)

where \( {S}_J={\displaystyle \sum_k{s}_{J,k}{\varPhi}_{J,k}(t)} \) and \( {D}_j={\displaystyle \sum_k{d}_{j,k}{\varPsi}_{j,k}(t)},\mathrm{j}=1,2,\dots, \mathrm{J} \)

In general, we have the relationship as

$$ {S}_{j-1}={S}_j+{D}_j $$
(3)

where {S J , S J − 1, …, S 1} is a sequence of multi-resolution approximations of the function X (t) at ever-increasing levels of refinement. The corresponding multi-resolution decomposition of X (t) is given by {S J , D J , D J − 1, …, D j , …, D 1}.

Selecting a proper wavelet function is a prerequisite for wavelet analysis. The actual criteria for wavelet selection include self-similarity, compactness, and smoothness (Ramsey 1999; Xu et al. 2004). Choosing the Symmlet as the basic wavelet, we experimented with alternative choices of scaling functions, and found the qualitative results from ‘Sym8’ are robust. Therefore, ‘Sym8’ were used for approximating the variation patterns of AR, AAT and AP at different time scales in this study.

3.2 Back Propagation Artificial Neural Network Based on Wavelet Decomposition

In order to simulate the variation of annual runoff with regional climate change at different time scales, we constructed an integrated approach, a back propagation artificial neural network based on wavelet decomposition (BPANNBWD). We first approximated the variation patterns of AR, AAT and AP by using wavelet decomposition on the basis of the discrete wavelet transform (DWT) at a given time scale, and then simulated the variations of AR with AAT and AP by using the back propagation artificial neural network based on the wavelet approximation at the corresponding time scale.

In the back-propagation artificial neural networks, a number of smaller processing elements (PEs) are arranged in layers: an input layer, one or more hidden layers, and an output layer (Hsu et al. 1995). The input from each PE in the previous layer (x i) is multiplied by a connection weight (w ji). These connection weights are adjustable and may be likened to the coefficients in statistical models. At each PE, the weighted input signals are summed and a threshold value (θj) is added. This combined input (I j) is then passed through a non-linear transfer function (f (∙)) to produce the output of the PE (y j). The output of one PE provides the input to the PEs in the next layer. This process can be summarized in equations as follows (Maier and Dandy 1998):

$$ {I}_j={\displaystyle \sum {w}_{ji}{x}_i+}{\theta}_j $$
(4)
$$ {y}_i=f\left({I}_j\right) $$
(5)

Our ANN model is a three-tier structure: an input X with two variables (i.e. AAT and AP) is linearly mapped to intermediate variables (called hidden neurons) H, which are then nonlinearly mapped to the output y (i.e. AR).

By comparing the advantages and disadvantages of artificial neural network transfer functions (Dorofki et al. 2012), we selected the activation function as hyperbolic tangent sigmoid transfer function as follows:

$$ f\left(\mathrm{I}\right)=\frac{\left(1-{e}^{-I}\right)}{\left(1+{e}^{-I}\right)} $$
(6)

where f(⋅) represents transfer function, and I represents input

As mentioned above, this is achieved by repeatedly presenting examples of the input/output relationship to the model and adjusting the model coefficients (i.e. the connection weights) in an attempt to minimize an error function between the historical outputs and the outputs predicted by the model. This calibration process is generally referred to as ‘training’. The aim of the training procedure is to adjust the connection weights until the global minimum in the error surface has been reached.

The back-propagation process is commenced by presenting the first example of the desired relationship to the network. The input signal flows through the network, producing an output signal, which is a function of the values of the connection weights, the transfer function and the network geometry. The output signal produced is then compared with the desired (historical) output signal with the aid of an error (cost) function.

The model parameters are optimized by minimizing the mean square error given by the cost function:

$$ E=<||y-{y}^{obs}||{}^2> $$
(7)

where y obs is the observed data, < ⋅ > denotes a sample or time mean

Because it can train any network as long as its weight, net input, and transfer functions have derivative functions (Kermani et al. 2005), we selected Levenberg-Marquardt (trainlm) as the training function in the computing environment of MATLAB.

It is evident that the BPANNBWD model is a multivariable simulation model for cause and effect, which is different from the hybrid models for hydrologic prediction of a time series such as the wavelet network (Wang and Ding 2003), wavelet neuro fuzzy model (Yarar 2014) and wavelet transform-genetic algorithm-neural network model (Sahay and Srivastava 2014). In the BPANNBWD model, variations of AAP and AP are regarded as the causes of the variation of AR, namely the variation of annual runoff is its response to regional climate change.

3.3 Test for Simulation Effect

To further compare the simulation effect of BPANNBWD with that of traditional statistics model such as multiple linear regression (MLR) at different time scales, we also constructed the multiple linear regression based on wavelet decomposition (MLRBWD). The principle of MLRBWD is as follows (Xu et al. 2008b, 2013c): the data series of AR, AAT and AP were firstly approximated by using wavelet decomposition (DW) at a chosen time scale; then the variations of AR with AAT and AP were estimated by using the multiple linear regression (MLR) based on the wavelet approximation at the corresponding time scale.

At each time scale, the variation of annual runoff with regional climate change was simulated by the multiple linear regression equation (MLRE) as follows:

$$ y={a}_0+{a}_1{x}_1+{a}_2{x}_2+\cdots +{a}_k{x}_k $$
(8)

where, y is dependent variable, x i the independent variables; a i is the regression coefficient, which is generally calculated by method of least squares (Xu 2002). In this study, the dependent variable is the annual runoff (AR) and the independent variables are related climatic factors, such as the annual average temperature (AAT) and annual precipitation (AP), etc.

In order to identify the uncertainty of the estimates for a given simulation model, the coefficient of determination was calculated as follows:

$$ \mathrm{CD}=1-\frac{ RSS}{ TSS}=1-\frac{{\displaystyle \sum_{i=1}^n{\left({y}_i-{\widehat{y}}_i\right)}^2}}{{\displaystyle \sum_{i=1}^n{\left({y}_i-\overline{y}\right)}^2}} $$
(9)

where CD is the coefficient of determination; \( {\widehat{y}}_i \) and y i are the simulate value and actual data of runoff respectively; \( \overline{y} \) is the mean of y i (i = 1, 2, …, n); \( RSS={\displaystyle \sum_{i=1}^n{\left({y}_i-{\widehat{y}}_i\right)}^2} \) is the residual sum of squares; \( TSS={\displaystyle \sum_{i=1}^n{\left({y}_i-\overline{y}\right)}^2} \) is the total sum of squares. The CD value is a measure of how well the simulate results represent the actual data.

Statistics tells us that a bigger CD indicates a higher certainty and lower uncertainty of the simulation model (Xu 2002).

To compare the relative goodness of models at different time scales, we also used the measure of Akaike information criterion (AIC). The formula of AIC is as follows (Anderson et al. 2000):

$$ AIC=2k+n \ln \left( RSS/n\right) $$
(10)

where k is the number of parameters estimated in the model; n is the number of samples; RSS is the same as in formula (9)

Akaike information criterion means that a smaller AIC indicates a better model.

For small sample sizes (i.e., n/K ≤ 40), the second-order Akaike Information Criterion (AICc) should be used instead

$$ AI{C}_c= AIC+\frac{2k\left(k+1\right)}{n-k-1} $$
(11)

where n is the sample size. As the sample size increases, the last term of the AICc approaches zero, and the AICc tends to yield the same conclusions as the AIC (Burnham and Anderson 2002).

4 Results and discussion

4.1 Variation patterns of annual runoff and its related regional climate factors

Our previous study indicated that (Xu et al. 2010, 2011a), the annual average temperature (AAT) and annual precipitation (AP) are the most important two factors that related with the annual runoff (AR). The result was also supported by the other studies for the headwaters of the Tarim River Basin (Hao et al. 2008; Chen et al. 2009; Ling et al. 2013).

Because the original signal series of AR, AAT and AP presented fluctuations with high frequency, it is hard to identify any variation patterns from the raw data (Xu et al. 2011a, 2013a). For mining out the variation patterns of AR, AAT and AP, we need to represent the signal series by wavelet analysis at different time scales (Xu et al. 2008b, 2009b).

For computing the wavelet decomposition of AR, AAT and AP, the five time scales are designated as S1 to S5, which represent 2- year, 4-year, 8-year, 16-year and 32-year time scale respectively. We used the method described in section 3.1 to represent the signal series of AR, AAT and AP, and the results are shown as Fig. 3.

Fig. 3
figure 3

Variation patterns of AR, AAT, and AP at different time scales

Full size image

Figure 3a revealed the five variation patterns for AR at the time scale of S1, S2, S3, S4, and S5 respectively. The S1 curve retains a large amount of residual noise from the raw data (see Fig. 2 for a comparison), and drastic fluctuations along the entire time span. Furthermore, the S1 curve also indicates that, although the annual runoff varied greatly throughout the study period, there was a hidden slightly increasing trend. The S2 curve still retains a considerable amount of residual, as indicated by the presence of 4 peaks and 4 valleys. However, the S2 curve is much smoother than the S1 curve, which allows the hidden increasing trend to be more apparent. The S3 curve retains much less residual, as indicated by the presence of 2 peaks and 2 valleys. Compared to S2, the increase in runoff over time is more apparent in S3. Finally, the S5 curve presents an ascending tendency, whereas the increasing trend is obvious in the S4 curve.

Accordingly, Fig. 3b and Fig. 3c provide us the cognition for comparing the variation patterns of AAT and AP at different time scales. Similar to AR, AAT and AP also presented five variation patterns at the time scale of S1, S2, S3, S4, and S5 respectively. The S1 and S2 curve showed a hidden slightly increasing trend with drastic fluctuations, whereas the curves are getting much smoother and the increasing trend becomes even more obvious with the time scale increases. It is evident that the S4 and S5 curve for AAT and AP exhibited a visible monotonically increasing trend similar to that for AR.

In conclusion, the results as Fig. 3 revealed a fact that the pattern of hydro-climatic process is scale-dependent in time. At 16-year and 32-year time scale, AR presented a monotonically increasing trend with the similar trend of AAT and AP. But at 2-year, 4-year, and 8-year time scale, AR presented a nonlinear variation with fluctuations of AAT and AP.

4.2 Simulation for Annual Runoff With Regional Climate Change

To simulate the variation of annual runoff with regional climate change at different time scales, we used the BPANNBDW method described in section 3.2 to individually construct a 3-layer back-propagation artificial neural network based on the wavelet decomposition results of AR, AAT and AP for each time scale.

The network structure of the 3-layer back-propagation artificial neural network is “2-1-1”, which indicates that there is an input layer with two variables (i.e. AAT and AP), an output layer with one variables (i.e. AR), and a hidden layer in the network. The neuron number of the hidden layer in the network for each time scale is not same, which is 3, 5, 5, 5 and 4 at the time scale of S1, S2, S3, S4 and S5 respectively (Table 1).

Table 1 Optimized parameters of BPANN at different time scales
Full size table

Using the computing software, MATLAB, we selected the transfer function as tansig, and training function as trainlm to train network.

Based on wavelet decomposition results of AR, AAT and AP from 1957 to 2008, we randomly extracted 80 %, 10 % and 10 % of the data as training, validation and testing samples, respectively. The results show that, at the time scales of S1, S2, S3, S4 and S5, the all network models have reached the expected error target (0.001) with learning rate of 0.01. The optimized parameters of the BPANN to simulate the annual runoff with regional climate change at different time scales are showed in Table 1.

Table 2 listed the simulation error of BPANNBWD at the 2-year, 4-year 8-year, 16-year, and 32-year time scale. The results showed that, as the time scale increased from S1 to S5, the smaller the estimated error is, and the better the simulation effect is.

Table 2 Simulation errors of BPANNBWD at different time scales
Full size table

Figure 4 shows the simulated results by BPANNBWD on the five time scales, which take input variables: annual average temperature (AAT) and annual precipitation (AP), to simulate output variable: annual runoff (AR). In this figure, sub-figure (a), (b), (c), (d) and (e) show the comparison between original data of annual runoff and its simulation, at the 2-year, 4-year 8-year, 16-year, and 32-year time scale, respectively.

Fig. 4
figure 4

Comparison between simulated values for AR and its original data at different time scale

Full size image

By comparing the CD and AIC value in Table 3, we can know the effect (good or bad) of different models at different time scales.

Table 3 CD and AIC values of BPANNBWD at different time scales
Full size table

The CD value at the time scale of S1 and S2 (i.e. 2-year and 4-year scale) is 0.2103 and 0.4924 respectively, which is relatively lower; but that at the time scale of S3, S4 and S5 (i.e. 8-year, 16-year and 32-year scale) is high as 0.9904, 0.9955 and 0.9986 respectively. These results indicated that the certainty of estimates at the larger time scale (i.e. 8-year, 16-year and 32-year scale) are markedly higher than the smaller time scale (i.e. 2-year and 4-year scale).

The AIC value at each time scale also tells us the similar results, the model at time scale of S5 is the best, that at time scale of S4 is better, that at time scale of S3 is moderate, that at time scale of S2 is the penult, and that at time scale of S1 is the worst.

In fact, our related study (Xu et al. 2008b, 2011a, 2011b, 2013b) revealed that the hydro-climatic process at a large time scale (e.g. 16-year or 32-year scale) is basically a linear process with monotonic trend, but at a small time scale (e.g. 2-year or 4-year scale) the process is essentially a nonlinear process with complicated causations. Therefore, the estimated precision at a large time scale (e.g. 16-year or 32-year scale) is high, whereas it is difficult to accurately predict at a small time scale (e.g. 2-year or 4-year scale).

4.3 Comparing the Simulation Effect With the Traditional Statistics Method

To compare the simulation effect of BPANNBWD with that of the traditional statistics method such as multiple linear regression (MLR), we also used the MLRBWD method described in section 3.3 to fit a group of multiple linear regression equations (MLREs) for simulating the variations of AR with AAT and AP at the five time scales. Table 4 showed the four indices, average absolute error, average relative error, CD and AIC for the MLRBWD at the time scale of S1, S2, S3, S4 and S5 respectively.

Table 4 Simulation effect of MLRBWD at different time scales
Full size table

Comparing table 2 to table 4, we found that the simulation errors, average absolute error and average relative error of BPANNBWD are both smaller than those of MLRBWD at every time scale. Comparing table 3 to table 4, we found that the CD value of BPANNBWD is bigger than that of MLRBWD at every time scale. Moreover, the AIC value of BPANNBWD is smaller than that of MLRBWD at every time scale. That is to say, all the four indices, average absolute error, average relative error, CD and AIC indicate that the simulated effect from BPANNBWD is better than that from MLRBWD at every time scale.

5 Conclusions

Selecting the Yarkand River as a typical representative, this study identified the variation pattern of annual runoff (AR), annual average temperature (AAT) and annual precipitation (AP) by using wavelet analysis (WA), and constructed an integrated model, i.e. the back propagation artificial neural network based on wavelet decomposition (BPANNBWD), to simulate the change of AR with AAT and AP at different time scales.

The main conclusions of this study are as follows:

  1. 1.

    The integrated approach combining wavelet analysis (WA) and artificial neural network (ANN) provides a way to understand the relationship between the runoff of an inland river and its related climatic factors in northwest China from a multi-scale perspective.

  2. 2.

    Variations of annual runoff (AR) with annual average temperature (AAT) and annual precipitation (AP) are scale-dependent in time. The variation patterns of AR, AAT and AP present basically linear trends at 16-year and 32-year time scale, but they exhibit nonlinear fluctuations at 2-year, 4-year and 8-year time scale.

  3. 3.

    The BPANNBWD well simulated the variation of AR with AAT and AP at the all five time scales. Compared to the traditional statistics method, the simulation effect of BPANNBWD is better than that of multiple linear regression (MLR) at every time scale. Moreover, the simulation effect at a larger time scale (e.g. 16-year or 32-year scale) is better than that at a smaller time scale (e.g. 2-year or 4-year scale).