1 Introduction

Many case studies in different countries and regions have suggested that the hydro-climatic process is a complex system, with nonlinearity as its basic characteristic (Ibbitt and Woods 2004; Kantelhardt et al. 2003; Livina et al. 2003; Strupezewski et al. 2006; Sivakumar 2007; Wang et al. 2008; Liu 2008). Therefore, more studies are required to explore the nonlinear characteristics of hydro-climatic process from different perspectives and using different methods. As a result, the hydro-climatic process has been explored using various nonlinear analytical methods, including wavelets, artificial neural networks, and the fractal theory (Wilcox et al. 1991; Smith et al. 1998; Cannon and McKendry 2002; Chou 2007; Hu et al. 2008; Wang et al. 2006). However, it has proven difficult to achieve a thorough understanding of the nonlinear hydro-climatic process by any individual method (Xu et al. 2010).

In the last 20 years, many studies have been conducted to evaluate climatic change and hydrological processes in the arid and semi-arid regions in northwestern China (Chen and Xu 2005; Wang et al. 2010; Zhang et al. 2010). A number of studies have indicated that there was a visible transition in the hydro-climatic processes in the past half-century (Chen and Xu 2005; Chen et al. 2006; Shi et al. 2007; Wang et al. 2010). This transition was characterized by a continual increase in temperature and precipitation, added river runoff volumes, increased lake water surface elevation and area, and elevated groundwater levels. These changes have led to increased water resources, providing immediate relief to the local water shortage. However, the climatic change has also caused the accelerated retreat of glaciers, which are important natural water reservoirs for the ecosystems in inland China.

The Yarkand River, mainly recharged by seasonal glacier melt and snowmelt, is one of headwaters of the Tarim River in arid area of northwestern China, and relatively, it has not been disturbed by more human activities. So, how the hydro-climatic process of the Yarkand River has changed during the past half-century? Was it really that the runoff has increased going with temperature and precipitation increase? To series of these changes, such inquiries may be designed to determine if these changes represent a localized transition to a warm and wet climate type in response to global warming, or merely reflect a centennial periodicity in hydrological dynamics. To date, these questions have not received satisfactory answers.

Based on the observed climatic and hydrological data series from hydrologic and meteorological stations in source area of the Yarkand River, this study applied a comprehensive method including Mann–Kendall (MK) test, wavelet analysis, regression analysis, and correlation dimension to investigate the nonlinear variations of annual runoff and its response to climate changes, as well as the fractal characteristics of hydro-climatic process.

2 Materials and methods

2.1 Study area

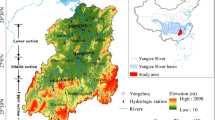
The Yarkand River (Fig. 1) is located in the southeastern of Xinjiang Uygur autonomous region, with a length of 1,097 km. The Yarkand River (35°40′–40°31′N, 74°28′–80°54′E) has a total basin area of 9.89 × 104 km2, including 6.08 × 104 km2 as the mountain area, which accounts for 61.5 %, and 3.81 × 104 km2 as the plain area, which takes up 38.5 % (Sun et al. 2006). The main stream of Yarkand River originates from Karakoram Pass in the north slope of Karakoram Mountain, where is full of towering peaks and developmental glaciers, as well as the extremely rare precipitation in plain. Due to the special geographical conditions, the accumulation of ice and snow in high mountain is the only supply for runoff. Therefore, the Yarkand River is a typical ice and snow supply river, in which the multi-year average runoff in Kaqun hydrometric station consists of 64.0 % from mean volume of glacial ablation, 13.4 % from rain and snow supply, and 22.6 % from groundwater supply, respectively (Sabit and Tohti 2005; Liu et al. 2008).

Fig. 1
figure 1

Location of the Yarkand River

Full size image

2.2 Data

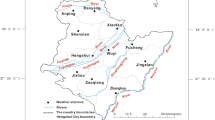
Some studies have shown that the river’s runoff is influenced by exogenous variables in time series analysis, such as matter and energy constants (Chen and Kumar 2004; Shao et al. 2009). For the Yarkand River is an inland river, with no water recharge in the plain area, its stream flow mainly comes from mountainous area, i. e. the Pamir Mountains. In other words, the runoff of the Yarkand River is in turn mainly fed by glacier, snowmelt and precipitation in the Pamir Mountains. Therefore, the climatic factors, especially temperature and precipitation, directly affect the annual changes in the runoff. So we use the runoff as well as temperature and precipitation data to analyze the nonlinearity of annual runoff process in Yarkand River. The runoff data were from the Kaqun hydrologic station, and temperature and precipitation data were from Tash Kurghan meteorological station. The two stations are located in the source areas of the river and the amount of water used by humans is minimal compared to the total discharge. Therefore, it was assumed that the observed hydrological and meteorological records reflect the natural conditions.

Long-term climate changes can alter the runoff production pattern, the timing of hydrological events, and the frequency and severity of floods, particularly in arid or semi-arid regions. Therefore, a small change in precipitation and temperature may result in marked changes in runoff (Gan, 2000). To investigate the runoff and its related climatic effect, this study used the time series data of annual runoff, annual average temperature and annual precipitation from 1957 to 2008.

2.3 Methodology

In order to understand the nonlinear hydro-climatic process in the Yarkand River, this paper conducted a comprehensive method including MK test, the wavelet analysis, wavelet regression analysis and correlation dimension step by step. Firstly, MK test was employed to identify trends for runoff and climatic factors. Secondly, the wavelet analysis was used to reveal the nonlinear variations in the runoff and its related climatic factors at different time scales. Thirdly, the relationship between the runoff and its related climatic factors was revealed by the regression analysis based on the wavelet analysis at different time scales. Finally, the fractal character of the hydro-climatic process related climatic factors was revealed by the correlation dimension method.

2.3.1 MK trend test

There are many statistical methods available to detect trends within the time series and each method has its own strength and weakness (Xu 2002). Whatever, non-parametric trend detection methods are less sensitive to outliers than the parametric statistics such as Pearson’s correlation coefficient. Moreover, the rank-based nonparametric MK test (Kendall 1975; Mann 1945) can test trends in a time series without requiring normality or linearity, and is therefore highly recommended for general use by the World Meteorological Organization (Mitchell et al. 1966). The MK trend test has been widely used in detecting trends in meteorological and hydrological series (Chen et al. 2006; Burn 2008; Xu et al. 2009b; Zhang et al. 2010). This paper also uses MK test method to analyze trends in the temperature, precipitation and runoff series in the Yarkand River basin.

The statistic of the MK trend test, \( Z_{c} \), is expressed as:

$$ Zc = \left\{ {\begin{array}{*{20}c} {\frac{S - 1}{{\sqrt {\text{var} (S)} }},} & {S > 0} \\ {0,} & {S = 0} \\ {\frac{S + 1}{{\sqrt {\text{var} (S)} }},} & {S < 0} \\ \end{array} } \right. $$
(1)

where

$$ S = \sum\limits_{i = 1}^{n - 1} {\sum\limits_{k = i + 1}^{n} {\text{sgn} (x_{k} - x_{i} )} } , $$
(2)
$$ \text{sgn} (\theta ) = \left\{ {\begin{array}{*{20}c} {1,} & {\theta > 0} \\ {0,} & {\theta = 0} \\ { - 1,} & {\theta < 0} \\ \end{array} } \right., $$
(3)
$$ \text{var} (S) = n(n - 1)(2n + 5)/18 $$
(4)

where \( x_{k} \) and \( x_{i} \) are the sequential data values for runoff, temperature and precipitation, and n is length of the data.

The index for measurement of trend, i.e., the inclination is expressed as follows:

$$ \beta = {\text{Median}}\left( {\frac{{x_{i} - x_{j} }}{i - j}} \right) $$
(5)

where 1 < j < i < n. A positive β denotes a rising trend, while a negative β means a decreasing trend.

The MK test can be used in the following manner: for the null hypothesis of \( H_{0} :\beta = 0 \), if \( |Z_{c} | > Z_{1 - \alpha /2} \), then the null hypothesis is rejected, where, \( Z_{1 - \alpha /2} \) is the standard normal variance, and \( \alpha \) is the significance level for the test.

2.3.2 Wavelet analysis

Wavelet transformation has shown to be a powerful technique for characterization of the frequency, intensity, time position, and duration of variations in climate and hydrological time series (Smith et al. 1998; Labat et al. 2005; Chou 2007; Xu et al. 2009b). Wavelet analysis can also reveal the localized time and frequency information without requiring the time series to be stationary, which is required by the Fourier transform and other spectral methods (Torrence and Compo 1998).

A continuous wavelet function \( \Uppsi (\eta ) \) that depends on a nondimensional time parameter \( \eta \) can be written as (Labat 2005):

$$ \Uppsi (\eta ) = \Uppsi (a,b) = |a|^{ - 1/2} \Uppsi \left( {\frac{t - b}{a}} \right) $$
(6)

where t denotes time, a is the scale parameter and b is the translation parameter. \( \Uppsi (\eta ) \) must have a zero mean and be localized in both time and Fourier space (Farge 1992). The continuous wavelet transform (CWT) of a discrete signal, \( x(t) \), such as the time series of runoff, temperature or precipitation, is expressed by the convolution of \( x(t) \) with a scaled and translated \( \Uppsi (\eta ) \),

$$ W_{x} (a,b) = |a|^{ - 1/2} \int\limits_{ - \infty }^{ + \infty } {x(t)\Uppsi^{*} \left( {\frac{t - b}{a}} \right)dt} $$
(7)

where, * indicates the complex conjugate, and W x (a, b) denotes the wavelet coefficient. Thus, the concept of frequency is replaced by that of scale, which can characterize the variation in the signal, \( x(t) \), at a given time scale.

Selecting a proper wavelet function is a prerequisite for time series analysis. The actual criteria for wavelet selection include self-similarity, compactness, and smoothness (Ramsey 1999; Xu et al. 2004). For the present study, symlet 8 was chosen as the wavelet function according to these criteria.

The nonlinear trend of a time series, \( x(t) \), can be analyzed at multiple scales through wavelet decomposition on the basis of the discrete wavelet transform (DWT). The DWT is defined taking discrete values of a and b. The full DWT for signal, \( x(t) \), can be represented as (Mallat 1989):

$$ x(t) = \sum\limits_{k} {\mu_{{j_{0} ,k}} } \varphi_{{j_{0} ,k}} (t) + \sum\limits_{j = 1}^{{j_{0} }} {\sum\limits_{k} {\omega_{j,k} \psi_{j,k} (t)} } $$
(8)

where \( \phi_{{j_{0} ,k}} (t) \) and \( \psi_{j,k} (t) \) are the flexing and parallel shift of the basic scaling function, \( \phi (t) \), and the mother wavelet function, \( \psi (t) \), and \( \mu_{{j_{0} ,k}} (j < j_{0} ) \) and \( \omega_{j,k} \) are the scaling coefficients and the wavelet coefficients, respectively. Generally, scales and positions are based on powers of 2, which is the dyadic DWT (Sun et al. 2006).

Once a mother wavelet is selected, the wavelet transform can be used to decompose a signal according to scale, allowing separation of the fine-scale behavior (detail) from the large-scale behavior (approximation) of the signal (Bruce et al. 2002). The relationship between scale and signal behavior is designated as follows: low scale corresponds to compressed wavelet as well as rapidly changing details, namely high frequency; whereas high scale corresponds to stretched wavelet and slowly changing coarse features, namely low frequency. Signal decomposition is typically conducted in an iterative fashion using a series of scales such as a = 2, 4, 8,…, 2L, with successive approximations being split in turn so that one signal is broken down into many lower resolution components.

The wavelet decomposition and reconstruction were used to approximate the nonlinear trend of annual runoff and its related factors over the entire study period at the selected different time scales.

2.3.3 Wavelet regression analysis

To understand the change trend of runoff and its causes during the past decades, this paper also employed a wavelet regression analysis to examine the nonlinear trend of runoff in the Yarkand River and its climatic effect factors. The analysis steps are as follows (Xu et al. 2008b, 2011a, b): (1) firstly, nonlinear variations of runoff and climate factors, such as annual runoff, annual average temperature and annual precipitation were approximated by using wavelet decomposition on the basis of the DWT at different time scales; (2) then, the statistical relationship between runoff and temperature and precipitation were revealed by using regression analysis method based on the wavelet approximation.

2.3.4 Correlation dimension

The correlation dimension method is usually applied to determine whether the hydro-climatic process exhibits a chaotic dynamic characteristic (Wang et al. 2006; Sivakumar 2007; Sivakumar and Chen 2007; Xu et al. 2008a, 2009a).

Consider \( x(t) \), a time series of annual runoff or its related factor (such as temperature, precipitation), and suppose it is generated by a nonlinear dynamic system with m degrees of freedom. To restore the dynamic characteristic of the original system, it is necessary to construct an appropriate series of state vectors, \( X^{(m)} (t) \), with delay coordinates in the m-dimensional phase space according to the basic ideas initiated by Grassberger and Procaccia (1983):

$$ X^{(m)} (t) = \left\{ {x(t),x(t + \tau ), \ldots ,x(t + (m - 1)\tau )} \right\} $$
(9)

where \( m \) is the embedding dimension and τ is an appropriate time delay.

The trajectory in the phase space is defined as a sequence of m dimensional vectors. If the dynamics of the system can be reduced to a set of deterministic laws, the trajectories of the system converge toward a subset of the phase space, which is called an “attractor”. Many natural systems do not conform with time to a cyclic trajectory. Some nonlinear dissipative dynamic systems tend to shift toward the attractors for which the motion is chaotic, i.e. not periodic and unpredictable over long times. The attractors of such systems are called strange attractors. For the set of points on the attractor, using the G-P method (Grassberger and Procaccia 1983), the correlation-integrals are defined to distinguish between stochastic and chaotic behaviors.

The correlation-integrals can be defined as follows:

$$ C(r) = \frac{1}{{N_{R}^{2} }}\sum\limits_{j = 1}^{{N_{R} }} {\sum\limits_{i = 1}^{{N_{R} }} {\Uptheta \left( {r - |X_{i} - X_{j} |} \right)} } $$
(10)

where r is the surveyor’s rod for distance, N R is the number of reference points taken from N, and N is the number of points. The relationship between N and N R is N R  = N − (m − 1)τ. \( \Uptheta (x) \) is the Heaviside function, which is defined as:

$$ \Uptheta (x) = \left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 & {x \le 0} \\ \end{array} } \\ {\begin{array}{*{20}c} 1 & {x > 0} \\ \end{array} } \\ \end{array} } \right. $$
(11)

The expression counts the number of points in the dataset that are closer than the radius, r, within a hypersphere of the radius, r, and then divides this value by the square of the total number of points (because of normalization). As r → 0, the correlation exponent, d, is defined as:

$$ C(r) \propto r^{d} $$
(12)

It is apparent that the correlation exponent, d, is given by the slope coefficient of \( \ln C(r) \) versus \( \ln r \). According to (\( \ln r,\ln C(r) \)), d can be obtained by the least squares method (LSM) using a log–log grid.

To detect the chaotic behavior of the system, the correlation exponent has to be plotted as a function of the embedding dimension (as shown in Fig. 6). If the system is purely random (e.g. white noise) the correlation exponent increases as the embedding dimension increases, without reaching the saturation value (Grassberger and Procaccia 1983).

If there are deterministic dynamics in the system, the correlation exponent reaches the saturation value, which means that it remains approximately constant as the embedding dimension increases. The saturated correlation exponent is called the correlation dimension of the attractor. The correlation dimension belongs to the invariants of the motion on the attractor. It is generally assumed that the correlation dimension equals the number of degrees of freedom in the system, and higher embedding dimensions are therefore redundant. For example, to describe the position of the point on the plane (two-dimensional system), the third dimension is not necessary because it is redundant. In addition, the correlation dimension is often fractal and represented as a non-integral dimension, which is typical for chaotic dynamical systems that are very sensitive to initial conditions (Grassberger and Procaccia 1983).

The correlation dimension provides information regarding the dimension of the phase-space required for embedding the attractor. It is important for determining the number of dimensions necessary to embed the attractor and the number of variables present in the evolution of the process.

3 Results and discussion

The raw data of annual runoff, annual average temperature and annual precipitation showed in fluctuating patterns for the period of 1957 to 2008 (Fig. 2). However, it is difficult to identify any trends (e.g. periodicity) simply based on the surface of the oscillation pattern. In order to reveal the nonlinearity of the hydro-climatic process in the Yarkand River, we analyzed it step by step using MK test, wavelet variance analysis, wavelet regression analysis, and correlation dimension method.

Fig. 2
figure 2

Original data of annual runoff, annual average temperature and annual precipitation

Full size image

3.1 The results of MK trend test

Some research results (Shi et al. 2007; Chen et al. 2006, 2009) show that, since the latter twentieth century, there is an obvious change about hydro-climatic process in arid area of northwestern China, such as rising temperature, added precipitation and increased river runoff, and so on. Thus, under this background, if the Yarkand River Basin has the similar trend or not? Perhaps the MK trend test can explain the problem.

Though the raw data in Fig. 2 has shown obvious fluctuations and nonlinear changes, the results of nonparametric MK test reveals the annual trend of runoff, temperature and precipitation (Table 1).

Table 1 Mann–Kendall trend test for annual runoff, annual average temperature and annual precipitation
Full size table

The results of MK trend test for the time series of annual runoff denote that the original assumption is rejected during the period from 1957 to 2008. The results indicate that there was a significant (α = 0.1) increasing trend of annual runoff from 1957 to 2008.

Similarly, the results of MK trend test for the time series of annual average temperature reveal that the original assumption is rejected during the period from 1957 to 2008. The results mean that there was an increasing trend of annual temperature from 1957 to 2008 at significant level of 0.01.

Moreover, the results of MK trend test for the time series of annual precipitation show that the original assumption is rejected at significant level of 0.1 during the period from 1957 to 2008. The results suggest that there was a significant decreased trend of annual precipitation from 1957 to 1985, but a significant (α = 0.1) precipitation increase during 1986 to 2008.

In addition, the results in Table 1 are not only indicate the remarkable increasing trend of runoff, temperature and precipitation in Yarkand River Basin, during the period of 1957–2008, but also show that average increase extent in annual runoff is 2.234 × 108 m3/10 year, average increase extent in annual average temperature is 0.223 °C/10 year, and average increase extent in annual precipitation is 4.453 mm/10 year.

3.2 Nonlinear variation of runoff and climate factors

The nonlinear variation for the annual runoff process and the related climate factors were analyzed at multiple-year scales through wavelet decomposition on the basis of the DWT.

The wavelet decomposition for the time series of annual runoff at five time scales resulted in five variants of nonlinear variations (Fig. 3). The S1 curve retains a large amount of residual noise from the raw data (see Fig. 2 for a comparison), and drastic fluctuations along the entire time span. These characteristics indicate that, although the runoff varied greatly throughout the study period, there was a hidden increasing trend. The S2 curve still retains a considerable amount of residual noise, as indicated by the presence of four peaks and four valleys. However, the S2 curve is much smoother than the S1 curve, which allows the hidden increasing trend to be more apparent. The S3 curve retained much less residual noise, as indicated by the presence of two peaks and two valleys. Compared to S2, the increase in runoff over time was more apparent in S3. Finally, the S5 curve presents an ascending tendency, whereas the increasing trend is obvious in the S4 curve.

Fig. 3
figure 3

Nonlinear variations for annual runoff at the different time scales

Full size image

Accordingly, Figs. 4, 5 provide us a method for comparing the nonlinear variations of annual average temperature and annual precipitation at different time scales. The wavelet decomposition for the time series of annual average temperature and annual precipitation at five time scales resulted in five nonlinear variations respectively. These five time scales are also designated as S1 to S5. The curves present an ascending tendency although drastic fluctuations in S1 and S2. Then, the curves are getting much smoother and the increasing trend becomes even more obvious as the scale level increases (see Figs. 4, 5 for a comparison).

Fig. 4
figure 4

Nonlinear variations for annual average temperature at the different time scales

Full size image
Fig. 5
figure 5

Nonlinear variations for annual precipitation at the different time scales

Full size image

The upper analysis showed that the nonlinear variations of runoff, temperature and precipitation of the Yarkand River basin were dependent on time scales.

3.3 The response of stream flow to climate change

Some studies have shown that stream flows can also be influenced by other variables (called exogenous variables in time series analysis), such as matter and energy, and that such influences might not be constants (Chen and Kumar 2004; Shao et al. 2009). Especially in an arid inland river basin, the river’s flow mainly comes from mountainous watershed (Chen et al. 2009). Indeed, the runoff of the Yarkand River primarily comes from the Pamir Mountains, which is in turn fed by snowmelt and precipitation in mountain area. Therefore, the dynamics of regional climate, especially temperature and precipitation, directly affect the annual changes in the runoff. For this reason, it is important to determine whether there is a relationship in the time-series of the annual runoff, annual average temperature and annual precipitation during the study period.

To verify this relationship, the following linear regression model was developed using the annual average temperature and annual precipitation as two independent variables and the annual runoff as the dependent variable:

$$ \begin{gathered} AR = 3.5AAT - 0.037AP + 56.75 \hfill \\ R^{2} = 0.1983;\;F = 2.517;\;\alpha = 0.1 \hfill \\ \end{gathered} $$
(13)

where AR denotes the annual runoff, AAT is the annual average temperature, and AP represents the annual precipitation.

The test results showed that the above regression was significant at α = 0.1. Furthermore, Eq. (13) revealed a positive correlation between the annual runoff and the annual average temperature, which was expected. These results are readily supported by the fact that the majority of streamflow comes from glacial melt and snow melt, which have been occurring at increased rates as the temperature increases. These results have been confirmed by other studies (Wang et al. 2006). However, Eq. (13) also indicates the existence of a weak, negative correlation between the annual runoff and the annual precipitation, which does not seem reasonable. Indeed, this finding conflicts with the results of other studies (Chen and Xu 2005; Chen et al. 2006), which have suggested that both the temperature and precipitation series in the Tarim basin have been increasing in a pattern similar to that of annual runoff over the past 50 years. It is possible that this inconsistency is caused by noise in the raw time-series data, which should be filtered out via wavelet decomposition based on the discrete wavelet transform (Xu et al. 2008a).

The covariability between runoff and climate factors on multiple time scales can be examined via regression analysis based on the results of wavelet decomposition (Xu et al. 2008b). For the purpose to understand the response of the runoff to regional climate change, based on the results of wavelet decomposition at different time scales (Figs. 3, 4 5), regression equations were fitted for describing the relationship among annual runoff, annual average temperature and annual precipitation (Table 2).

Table 2 Regression equations describing the relationship between annual runoff and annual average temperature and annual precipitation at different time scales
Full size table

As is shown in Table 2, the binary linear regression equations on each time scale have passed the significant test.

On the time scales of 2-year, the linear regression equation shows that the dependent variable, annual runoff positively correlated only with the independent variable, temperature at a significant level of 0.01. Because another independent variable, annual precipitation did not appear in the regression equation on the time scales of 2-year, we can say that the temperature is the major factor influencing the runoff of the Yarkand River.

Moreover, on the time scales of 4-, 8-, 16- and 32-year, annual runoff has positive correlations with both annual average temperature and annual precipitation at a high significant level of 0.001. In another word, although the runoff, temperature and precipitation appeared nonlinear variations, the runoff presented a linear correlation with the temperature and precipitation.

Based on the above-mentioned wavelet regression analysis at different time scales, the results can be summarized as that the increasing trend of runoff in Yarkand River is resulted from the raised temperature and added precipitation, especially much closer to raised temperature. This is due to be that the Yarkand River is mainly supplied by meltwater from the ice and snow in the Pamirs, which resulted in that the runoff is on increasing tendency with the raised temperature (Chen et al. 2009; Zhang et al. 2010).

In conclusion, in the view of multi-scales and statistical significance, the annual runoff change of Yarkand River is related to the change of regional climate, especially to the ascending annual average temperature. In another word, the runoff variation is the result for responding regional climate. With the raised temperature and added precipitation, the annual runoff of Yarkand River presented a nonlinear increasing trend. Furthermore, this conclusion is agreed with the research results for runoff change trend under the other background of climatic change in Tarim basin, i.e. in the recent 50 years, the change is corresponding with the raised temperature and added precipitation in Tarim basin (Liu et al. 2008; Chen et al. 2009; Xu et al. 2010).

3.4 The chaotic dynamic system of hydro-climatic process

The annual runoff time series of the Yarkand River was used to reconstruct the phase space, while the correlation dimension of the attractor was calculated. Different values for the radius, r, were first selected to compute the values of the correlation-integrals, \( C(r) \), which were used to plot the curves within a dual logarithmic coordinate system (Fig. 6). This diagram shows the relationship between \( \ln C(r) \) and \( \ln \;(r) \) for the annual runoff with a number of different embedding dimensions, m. The slope coefficient of \( \ln C(r) \) versus \( \ln r \), i.e. the correlation exponent, \( d \), which was used to embed dimension \( m = 1,\;2,\; \ldots \), was calculated using the least square method (LSM).

Fig. 6
figure 6

A plot of ln C(r) versus ln (r)

Full size image

The diagram in Fig. 7 shows the gradual saturation process of the correlation exponent. It is evident that the correlation exponent increases with embedding dimension, \( m \), and a saturated correlation exponent, the correlation dimension of attractor (\( D \)), was obtained when \( m \ge 7 \).

Fig. 7
figure 7

The correlation exponent (d) versus embedding dimension (m)

Full size image

The same procedure was used to calculate the correlation dimensions of the attractors for annual average temperature and annual precipitation.

The correlation dimensions for the annual runoff, annual average temperature and annual precipitation are shown in Table 3. Because correlation dimension for the annual runoff is above 3, at least four independent variables are needed to describe the dynamics of the hydrological process of the Yarkand River. Furthermore, correlation dimensions for annual average temperature and annual precipitation are close to 3, which also indicates that it need three independent variables to describe the dynamics of temperature as well as precipitation process.

Table 3 The correlation dimensions for the annual runoff, annual average temperature and annual precipitation
Full size table

Moreover, the fact that none of the correlation dimensions is an integer indicates that the hydro-climatic process in the Yarkand River has the fractal characteristics.

4 Conclusions

The present study employed several different methods to analyze hydro-climatic process of the Yarkand River, and the results led to a few recognizable conclusions. Due to the complexity of the phenomena evaluated here, as well as the limitations of this study, it is difficult to understand the physical mechanism in details. Nevertheless, these results provide valuable information that provides an understanding of the nonlinear characteristics of the hydro-climatic process of the Yarkand River from different perspectives.

Summarizing the above results and discussion, we elicited the basic conclusions as follows:

  1. (1)

    The annual runoff, annual average temperature and annual precipitation in the Yarkand River Basin showed an increasing trend during the period of 1957–2008 at a significant level of 0.1, 0.01 and 0.01 respectively. The average increase extent of annual runoff, annual average temperature and annual precipitation was 2.234 × 108 m3/10 year, 0.223 °C/10 year, and 4.453 mm/10 year, respectively.

  2. (2)

    The nonlinear pattern of runoff, temperature and precipitation in the Yarkand River Basin during the period of 1957–2008 was scale-dependent with time. The wavelet decomposition for the time series of annual runoff, annual average temperature and annual precipitation at five time scales resulted in five patterns of nonlinear variations respectively. The curves were getting much smoother and the increasing tendency became even more obvious as the time scales increased.

  3. (3)

    The annual runoff of Yarkand River positively correlated only with the independent variable, i.e. annual average temperature with a significant level of 0.01 at the time scales of 2-year, whereas it has positive correlations with both annual average temperature and annual precipitation a significant level of 0.001 at the time scales of 4-, 8-, 16- and 32-year. The results indicate that although the runoff, temperature and precipitation presented nonlinear variations at different time scales, the runoff has a linear correlation with the temperature and precipitation.

  4. (4)

    The hydro-climatic process of the Yarkand River is a chaotic dynamic system, in which the correlation dimension of annual runoff, annual average temperature and annual precipitation is 3.2118, 2.999 and 2.992 respectively. Moreover, the fact that none of the correlation dimensions is an integer indicates that the hydro-climatic process has the fractal characteristics.