1 Introduction

Due to the advantages of quantum mechanics overcoming the limitations of classical computation, quantum computation has attracted many researchers [1]. Many quantum algorithms have been proposed [1]. There are two famous quantum algorithms, Shor’s factorization algorithm [2] and Grove’s search algorithm [3]. The former provides a striking exponential speedup over the best known classical factorization algorithms. Therefore, the RSA system [4] will be successfully attacked by Shor’s factorization algorithm. By Grove’s search algorithm, we can obtain selected data from unsorted data in \( {\text{O}}\left( {\sqrt N } \right) \) times, where \( N \) denotes the number of data. Grove’s search algorithm provides a quadratic speedup over the best known classical algorithms.

In addition to computation speedup, quantum systems provide unconditional security based on no-cloning theorem and Hesienberg uncertainty theorem [5]. We can hide the secret information to avoid eavesdropping in the quantum system. The quantum data hiding methods are classified into three categories. First, quantum data hiding (QDH) [6, 7] embeds secret information by the physical of characteristic, local operations, and classical communications (LOCC). Second, narrow quantum steganography (QS) [8] hides secret information in quantum error-correcting code (QECC) or quantum image [9]. Last, quantum covert channels (QCC) [10] are utilized for key conveying in quantum cryptography.

In the second category, we pay attention to quantum images [11, 12]. Although many researchers have presented encryption algorithms [13,14,15,16,17] in quantum images, this paper only focuses on data hiding. In 2015, Wang et al. proposed least significant qubit (LSQb) information hiding algorithm for NEQR quantum image [18]. According to the color information and position information are entangled together in NEQR [19], they embedded the secret information into the least significant qubit of the color information by using the unitary operations. Therefore, like the traditional LSB method [20], LSQb method generates the quantum cover image hiding the secret information in the least significant qubit of the color information. Independently, Jiang et al. [21] proposed two LSB methods: standard LSB method and block LSB method. The standard LSB method hides one message bit in each pixel. In the block LSB method, each block only hides one message bit. In fact, the standard LSB method can be seen as a special case of the block LSB method. Obviously, the block LSB method provides more robustness.

In this paper, we hide the secret information in the \( 2^{n} \times 2^{n} \) NEQR quantum image with \( q \)-qubit color information. According to Yan et al.’s paper [11], the NEQR quantum image provides more accurate information retrieval. The NEQR quantum image and the secret information are transferred to the recipient by using the quantum teleportation scheme. The recipient not only gets the secret information, but also holds the quantum image after one measurement. At first, the third party constructs the \( \left( {4n + 2q + 2m} \right) \)-qubit general Bell state, including two quantum registers \( B_{1} \) and \( B_{2} \). The third party then distributes the registers \( B_{1} \) and \( B_{2} \) to the sender and the recipient, respectively. After getting the quantum register \( B_{1} \), \( \left( {2n + q + m} \right) \)-qubit of half-Bell state, the sender attaches the \( q \)-qubit color register C, the \( 2n \)-qubit position register \( P \), and the \( m \)-qubit secret register M, to construct a \( \left( {4n + 2q + 2m} \right) \)-qubit quantum state. In the register C and the register \( P \), the NEQR quantum image is produced by sub-operations gradually in quantum computation [19, 22, 23]. The sender then puts the secret information \( S \) into the register M by using the quantum operation CNOT. Because the sender and the recipient share \( \left( {4n + 2q + 2m} \right) \)-qubit general Bell state, the sender utilizes the quantum teleportation scheme [24] to transfer the NEQR quantum image and the secret information \( S \) to the recipient. In the quantum teleportation scheme, the sender must measure the register C, the register \( P \), the register M, and the register \( B_{1} \) and send measured values to the recipient by the classical channel. The recipient utilizes the measured values to recover the NEQR quantum image in the first (\( 2n + q) \) qubits of the register \( B_{2} \) and the secret information \( S \) in the last \( m \) qubits of the register \( B_{2} \). Last, the recipient gets information secret S after measuring the last \( m \) qubits of the register \( B_{2} \) and retains a quantum image in the register \( B_{2} \).

The remainder of this paper is organized as follows. In the next section, Zhang et al.’s NEQR and Wang et al.’s method are reviewed. Section 3 describes our method. Section 4 gives an example of our method. The analysis and comparison of the proposed method are given in Sect. 5 and finally the last section, Sect. 6, concludes this paper.

2 Related work

In this section, we review Zhang et al.’s NEQR representation [19] and Wang et al.’s method [18]. In 2013, Zhang et al. proposed a novel enhanced quantum representation of digital images [19]. Their model is more effective than Le et al.’s model [22] in quantum images. In NEQR representation, the color information qubit sequence and the position information qubit sequence are entangled, where the color information denotes color information of the classical image. We set the color information as the binary code \( c_{i} = b_{q - 1}^{i} b_{q}^{i} \ldots b_{0}^{i} \), where \( i \) denotes the position of the image and \( q \) (\( q = 1 \) for binary image, \( q = 8 \) for grayscale, \( q = 24 \) for RGB image, etc.) is the length of the color information. In a \( 2^{n} \times 2^{n} \) NEQR representation, we construct two quantum registers: the \( q \)-qubit color register C and the \( 2n \)-qubit position register \( P \). Then, we apply \( 2n \) Hadamard gates on the position register \( P \) and get

$$ \left| \varphi \right\rangle = \frac{1}{{2^{n} }}\mathop \sum \limits_{i = 0}^{{2^{2n} - 1}} \left( {\left| 0 \right\rangle_{C} \left| i \right\rangle_{P} } \right). $$
(2.1)

We perform the quantum operation \( U_{P} = \prod\nolimits_{i = 0}^{{2^{2n} - 1}} {V_{iP} } \) on \( \left| \varphi \right\rangle \) satisfying \( V_{iP} (\left| 0 \right\rangle_{C} \left| i \right\rangle_{P} ) = \left| {c_{i} } \right\rangle_{C} \left| i \right\rangle_{P} \) and get

$$ \left| {\varphi_{1} } \right\rangle = U_{P} \left( {\left| \varphi \right\rangle } \right) = \frac{1}{{2^{n} }}\mathop \sum \limits_{i = 0}^{{2^{2n} - 1}} \left( {\left| {c_{i} } \right\rangle_{C} \left| i \right\rangle_{P} } \right). $$
(2.2)

We give an example to understand the NEQR representation. Figure 1 gives a classical image. We know that \( n = 1, q = 2. \) The color information \( c_{01} \) is 3. To construct the corresponding NEQR representation, we perform the quantum circuit of Fig. 2.

Fig. 1
figure 1

An example of \( 2 \times 2 \) classical image

Full size image
Fig. 2
figure 2

Quantum circuit of the example

Full size image

According to Fig. 2, we prepare two quantum registers and set an initial state:

$$ \left| \varphi \right\rangle_{0} = \left| {00} \right\rangle_{C} \left| {00} \right\rangle_{P} . $$
(2.3)

We execute two Hadamard gates on the position register \( P \) and get

$$ \begin{aligned} \left| \varphi \right\rangle_{1} & = \left| {00} \right\rangle_{C} \left( {\frac{1}{2}\left( {\left| {00} \right\rangle_{P} + \left| {01} \right\rangle_{P} + \left| {10} \right\rangle_{P} + \left| {11} \right\rangle_{P} } \right)} \right) \\ & = \frac{1}{2}\left( {\left| {00} \right\rangle_{C} \left| {00} \right\rangle_{P} + \left| {00} \right\rangle_{C} \left| {01} \right\rangle_{P} + \left| {00} \right\rangle_{C} \left| {10} \right\rangle_{P} + \left| {00} \right\rangle_{C} \left| {11} \right\rangle_{P} } \right). \\ \end{aligned} $$
(2.4)

Last, we utilize CNOT to control the image color information into the corresponding color register C. Then, we will get

$$ \begin{aligned} \left| \varphi \right\rangle_{2} & = \frac{1}{2}(\left| {\left( {0 \oplus 1} \right)0} \right\rangle_{C} \left| {00} \right\rangle_{P} + \left| {\left( {0 \oplus 1} \right)\left( {0 \oplus 1} \right)} \right\rangle_{C} \left| {01} \right\rangle_{P} \\ & \quad + \left| {0\left( {0 \oplus 1} \right)} \right\rangle_{C} \left| {10} \right\rangle_{P} + \left| {0\left( {0 \oplus 1} \right)} \right\rangle_{C} \left| {11} \right\rangle_{P} ) \\ & = \frac{1}{2}\left( {\left| {10} \right\rangle_{C} \left| {00} \right\rangle_{P} + \left| {11} \right\rangle_{C} \left| {01} \right\rangle_{P} + \left| {01} \right\rangle_{C} \left| {10} \right\rangle_{P} + \left| {01} \right\rangle_{C} \left| {11} \right\rangle_{P} } \right) \\ \end{aligned} $$
(2.5)

Next, we review Wang et al.’s method [18]. Like the traditional LSB method [20], Wang et al.’s method embeds the secret information into the least significant qubit of the color information in the NEQR quantum image. First, the sender prepares an initial state \( \left| \rho \right\rangle_{0} = \left| 0 \right\rangle_{C}^{ \otimes q} \left| 0 \right\rangle_{P}^{ \otimes 2n} \). Then, according to the classical image, the sender constructs the corresponding a \( 2^{n} \times 2^{n} \) NEQR quantum image:

$$ \left| {\rho_{1} } \right\rangle = \frac{1}{{2^{n} }}\mathop \sum \limits_{i = 0}^{{2^{2n} - 1}} \left( {\left| {c_{i} } \right\rangle_{C} \left| i \right\rangle_{P} } \right), $$
(2.6)

where \( c_{i} = \left( {b_{q - 1}^{i} b_{q - 2}^{i} \ldots b_{0}^{i} } \right), i = 0, \, 1 \ldots ,2^{2n} - 1. \)

Now, the sender tries to embed the secret information \( S = s_{{2^{2n} - 1}} s_{{2^{2n} - 2}} \ldots s_{0} \) into the least significant qubit of the color information \( c_{i} \). To embed the secret bit \( s_{m} \) (\( 0 \le m \le 2^{2n} - 1 \)), the sender performs the quantum operation \( V_{jC} \) satisfying

$$ \begin{aligned} V_{jC} \left( {\left| {\rho_{1} } \right\rangle } \right) & = V_{jC} \left( {\frac{1}{{2^{n} }}\mathop \sum \limits_{i = 0}^{{2^{2n} - 1}} \left( {\left| {b_{q - 1}^{i} b_{q - 2}^{i} \ldots b_{0}^{i} } \right\rangle_{C} \left| i \right\rangle_{P} } \right)} \right) \\ & = \frac{1}{{2^{n} }}\left( {\left| {b_{q - 1}^{j} b_{q - 2}^{j} \ldots b_{1}^{j} s_{j} } \right\rangle_{C}\left| j \right\rangle } \right) + \mathop \sum \limits_{i = 0,i \ne j}^{{2^{2n} - 1}} \left| {c_{i} } \right\rangle_{C} \left| i \right\rangle_{P} ). \\ \end{aligned} $$
(2.7)

After performing the quantum operation \( U_{C} = \prod\nolimits_{j = 0}^{{2^{2n} - 1}} {V_{jC} } \), the sender has

$$ \begin{aligned} U_{C} \left( {\left| \rho_{1} \right\rangle} \right) & = \mathop \prod \limits_{j = 0}^{{2^{2n} - 1}} V_{jC} \left( {\frac{1}{{2^{n} }}\mathop \sum \limits_{i = 0}^{{2^{2n} - 1}} \left( {\left| {b_{q - 1}^{i} b_{q - 2}^{i} \ldots b_{0}^{i} } \right\rangle_{C} \left| i \right\rangle_{P} } \right)} \right) \\ & = \frac{1}{{2^{n} }}\mathop \sum \limits_{i = 0}^{{2^{2n} - 1}} \left( {\left| {b_{q - 1}^{i} b_{q - 2}^{i} \ldots b_{1}^{i} s_{i} } \right\rangle_{C} \left| i \right\rangle_{P} } \right). \\ \end{aligned} $$
(2.8)

Obviously, the secret information \( S \) has been embedded into the least significant qubit of the color information \( c_{i} \) in the NEQR quantum image.

We give an example to understand Wang et al.’s method [18]. The sender wants to embed the secret information \( S = \left( {1010} \right)_{2} \) into the NEQR quantum image \( \left| {\rho_{1} } \right\rangle = \frac{1}{2}\left( {\left| {10} \right\rangle_{C} \left| {00} \right\rangle_{P} + \left| {11} \right\rangle_{C} \left| {01} \right\rangle_{P} + \left| {01} \right\rangle_{C} \left| {10} \right\rangle_{P} + \left| {01} \right\rangle_{C} \left| {11} \right\rangle_{P} } \right) \). After performing the quantum operation \( U_{C} = \prod\nolimits_{j = 0}^{{2^{2} - 1}} {V_{jC} } \), the sender has

$$ \begin{aligned} \left| {\rho_{2} } \right\rangle & = U_{C} \left( {\left| {\rho_{1} } \right\rangle } \right) = \mathop \prod \limits_{j = 0}^{{2^{2} - 1}} V_{jC} \left( {\frac{1}{2}\mathop \sum \limits_{i = 0}^{{2^{2} - 1}} \left( {\left| {b_{1}^{i} b_{0}^{i} } \right\rangle_{C} \left| i \right\rangle_{P} } \right)} \right) = \frac{1}{2}\mathop \sum \limits_{i = 0}^{{2^{2} - 1}} \left( {\left| {b_{1}^{i} s_{i} } \right\rangle_{C} \left| i \right\rangle_{P} } \right) \\ & = \frac{1}{2}\left( {\left| {10} \right\rangle_{C} \left| {00} \right\rangle_{P} + \left| {11} \right\rangle_{C} \left| {01} \right\rangle_{P} + \left| {00} \right\rangle_{C} \left| {10} \right\rangle_{P} + \left| {01} \right\rangle_{C} \left| {11} \right\rangle_{P} } \right). \\ \end{aligned} $$
(2.9)

The sender transfers the quantum state \( \left| {\rho_{2} } \right\rangle \) to the recipient. But, how to extract the secret information \( S = \left( {1010} \right)_{2} \) from \( \left| {\rho_{2} } \right\rangle \)? In Wang et al.’s method [18], the recipient directly measures the quantum state \( \left| {\rho_{2} } \right\rangle \). One bit of the secret information \( S \) will be discovered. Here we introduce another extracting algorithm in Sang et al.’s method [25]. The recipient attaches four qubits, say \( M_{0} ,M_{1} ,M_{2} ,{\text{and}} M_{3} \), to the quantum state \( \left| {\rho_{2} } \right\rangle \) and gets

$$ \left| {\rho_{3} } \right\rangle = \frac{1}{2}\left( {\left| {10} \right\rangle_{C} \left| {00} \right\rangle_{P} + \left| {11} \right\rangle_{C} \left| {01} \right\rangle_{P} + \left| {00} \right\rangle_{C} \left| {10} \right\rangle_{P} + \left| {01} \right\rangle_{C} \left| {11} \right\rangle_{P} } \right)\left| 0 \right\rangle_{{M_{0} }} \left| 0 \right\rangle_{{M_{1} }} \left| 0 \right\rangle_{{M_{2} }} \left| 0 \right\rangle_{{M_{3} }} . $$
(2.10)

The recipient then uses the control-swap operation to swap \( M_{i} \) and the least significant qubit of the color information \( c_{i} \). We have

$$ \begin{aligned}\left| {\rho_{4}} \right\rangle & = \frac{1}{2}\left(\left| {{\text{1}}{\mathbf{0}}} \right\rangle_{C} \left| {00} \right\rangle_{P} \left| {\mathbf{0}} \right\rangle_{{M_{0}}} \left| 0 \right\rangle_{{M_{1}}} \left| 0 \right\rangle_{{M_{2}}} \left| 0 \right\rangle_{{M_{3}}} + \left| {{\text{1}}{\mathbf{0}}} \right\rangle_{C} \left| {01} \right\rangle_{P} \left| 0 \right\rangle_{{M_{0}}} \left| {\mathbf{1}} \right\rangle_{{M_{1}}} \left| 0 \right\rangle_{{M_{2}}} \left| 0 \right\rangle_{{M_{3}}} \right.\\ & \quad\left. +\, \left| {{\text{0}}{\mathbf{0}}} \right\rangle_{C} \left| {10} \right\rangle_{P} \left| 0 \right\rangle_{{M_{0}}} \left| 0 \right\rangle_{{M_{1}}} \left| {\mathbf{0}} \right\rangle_{{M_{2}}} \left| 0 \right\rangle_{{M_{3}}} + \left| {{\text{0}}{\mathbf{0}}} \right\rangle_{C} \left| {11} \right\rangle_{P} \left| 0 \right\rangle_{{M_{0}}} \left| 0 \right\rangle_{{M_{1}}} \left| 0 \right\rangle_{{M_{2}}} \left| {\mathbf{1}} \right\rangle_{{M_{3}}} \right). \end{aligned} $$
(2.11)

In the quantum state \( \left| {\rho_{4} } \right\rangle \), the secret information has been extracted in \( M_{0} ,M_{1} ,M_{2} ,\;{\text{and}}\;M_{3} \). If the recipient wants to get the classical secret information, he/she will face the same measurement problem in Wang et al.’s method.

3 Our method

Assume that the sender wants to send \( m \)-bit secret information \( S \) and a \( 2^{n} \times 2^{n} \) NEQR quantum image I to the recipient, where I includes the \( q \)-qubit color register C and the \( 2n \)-qubit position register \( P \). At first, the third party constructs the \( \left( {4n + 2q + 2m} \right) \)-qubit general Bell state \( \frac{1}{{\sqrt {2^{2n + q + m} } }}\sum\nolimits_{j = 0}^{{2^{2n + q + m} - 1}} {\left| j \right\rangle_{{B_{1} }} \left| j \right\rangle_{{B_{2} }} } \), where \( B_{1} \) and \( B_{2} \) are two quantum registers with the same length. The third party distributes the quantum registers \( B_{1} \) and \( B_{2} \) to the sender and the recipient, respectively. After getting the quantum register \( B_{1} \), \( \left( {2n + q + m} \right) \)-qubit of half-Bell state, the sender constructs the quantum state

$$ \left| {\psi_{1} } \right\rangle = \frac{1}{{\sqrt {2^{2n + q + m} } }}\left| 0 \right\rangle_{C}^{ \otimes q} \left| 0 \right\rangle_{P}^{ \otimes 2n} \left| 0 \right\rangle_{M}^{ \otimes m} \left( {\mathop \sum \limits_{j = 0}^{{2^{2n + q + m} - 1}} \left| j \right\rangle_{{B_{1} }} } \right), $$
(3.1)

by attaching the \( q \)-qubit color register C, the \( 2n \)-qubit position register \( P \) and the \( m \)-qubit secret register M. The sender then applies \( 2n \) Hadamard gates on the position register \( P \) and the quantum operation \( U_{P} \) to generate a \( 2^{n} \times 2^{n} \) NEQR quantum image in the color register C and the position register \( P \) according to the classical image. Using Zhang et al.’s NEQR representation, the sender gets the following quantum state

$$ \left| {\psi_{2} } \right\rangle = \frac{1}{{\sqrt {2^{4n + q + m} } }}\left( {\mathop \sum \limits_{i = 0}^{{2^{2n} - 1}} \left| {c_{i} } \right\rangle_{C} \left| i \right\rangle_{P} } \right)\left| 0 \right\rangle_{M} \left( {\mathop \sum \limits_{j = 0}^{{2^{2n + q + m} - 1}} \left| j \right\rangle_{{B_{1} }} } \right), $$
(3.2)

where \( \frac{1}{{2^{n} }}\left( {\sum\nolimits_{i = 0}^{{2^{2n} - 1}} {\left| {c_{i} } \right\rangle_{C} \left| i \right\rangle_{P} } } \right) \) denotes the NEQR quantum image I. Next, the sender performs the operation \( U_{s} \) to put the secret information \( S = s_{m - 1} s_{q - 2} \ldots s_{0} \) into the secret register M and gets

$$ \left| {\psi_{3} } \right\rangle = \frac{1}{{\sqrt {2^{4n + q + m} } }}\left( {\mathop \sum \limits_{i = 0}^{{2^{2n} - 1}} \left| {c_{i} } \right\rangle_{C} \left| i \right\rangle_{P} } \right)\left| S \right\rangle_{M} \left( {\mathop \sum \limits_{j = 0}^{{2^{2n + q + m} - 1}} \left| j \right\rangle_{{B_{1} }} } \right). $$
(3.3)

In \( \left| {\psi_{3} } \right\rangle \), we let \( \left| {c_{i} } \right\rangle_{C} \left| i \right\rangle_{P} \left| S \right\rangle_{M} \) be \( \left| {h_{i} } \right\rangle_{CPM} \) and get

$$ \left| {\psi '_{3} } \right\rangle = \frac{1}{{\sqrt {2^{4n + q + m} } }}\left( {\mathop \sum \limits_{i = 0}^{{2^{2n} - 1}} \left| {h_{i} } \right\rangle_{CPM} } \right)\left( {\mathop \sum \limits_{j = 0}^{{2^{2n + q + m} - 1}} \left| j \right\rangle_{{B_{1} }} } \right). $$
(3.4)

The sender next transfers \( h_{i} \) to the recipient by using the quantum teleportation scheme. The sender utilizes quantum operation \( U_{B} \) (\( 2n + q + m \) qubit of CNOT) to flip the register \( B_{1} \) (the target qubit) according to quantum registers C, P, and M. Then, the sender gets

$$ \begin{aligned} \left| {\psi_{4} } \right\rangle & = \frac{1}{{\sqrt {2^{4n + q + m} } }}U_{B} \left( {\left( {\mathop \sum \limits_{i = 0}^{{2^{2n} - 1}} \left| {h_{i} } \right\rangle_{CPM} } \right)\left( {\mathop \sum \limits_{j = 0}^{{2^{2n + q + m} - 1}} \left| j \right\rangle_{{B_{1} }} } \right)} \right) \\ & = \frac{1}{{\sqrt {2^{4n + q + m} } }}\left( {\mathop \sum \limits_{i = 0}^{{2^{2n} - 1}} \left| {h_{i} } \right\rangle_{CPM} } \right)\left( {\mathop \sum \limits_{j = 0}^{{2^{2n + q + m} - 1}} \left| {h_{i} \oplus j} \right\rangle_{{B_{1} }} } \right). \\ \end{aligned} $$
(3.5)

Actually, the registers \( B_{1} \) and \( B_{2} \) are entangled. Therefore, the quantum system is

$$ \left| {\psi '_{4} } \right\rangle = \frac{1}{{\sqrt {2^{4n + q + m} } }}\left( {\mathop \sum \limits_{i = 0}^{{2^{2n} - 1}} \left| {h_{i} } \right\rangle_{CPM} } \right)\left( {\mathop \sum \limits_{j = 0}^{{2^{2n + q + m} - 1}} \left| {h_{i} \oplus j} \right \rangle _{{B_{1} }} \left| j \right\rangle_{{B_{2} }} } \right). $$
(3.6)

Now, the sender performs \( 2n + q + m \) Hadamard gates on registers C, P, and M and has

$$ \begin{aligned} \left| {\psi_{5} } \right\rangle & = \frac{1}{{\sqrt {2^{4n + q + m} } }}\left( {\mathop \sum \limits_{i = 0}^{{2^{2n} - 1}} H^{{ \otimes \left( {2n + q + m} \right)}} \left| {h_{i} } \right\rangle_{CPM} } \right)\left( {\mathop \sum \limits_{j = 0}^{{2^{2n + q + m} - 1}} \left| {h_{i} \oplus j } \right\rangle_{{B_{1} }} \left| j \right\rangle_{{B_{2} }} } \right) \\ & = \frac{1}{{2^{3n + q + m} }}\left( {\left( {\mathop \sum \limits_{i = 0}^{{2^{2n} - 1}} \mathop \sum \limits_{k = 0}^{{2^{2n + q + m} - 1}} \left( { - 1} \right)^{{h_{i} \cdot k}} \left| k \right\rangle_{CPM} } \right)\left( {\mathop \sum \limits_{j = 0}^{{2^{2n + q + m} - 1}} \left| {h_{i} \oplus j } \right\rangle_{{B_{1} }} \left| j \right\rangle_{{B_{2} }} } \right)} \right). \\ \end{aligned} $$
(3.7)

Set \( l = h_{i} \oplus j \). The above quantum state will be

$$ \begin{aligned} \left| {\psi '_{5} } \right\rangle & = \frac{1}{{2^{3n + q + m} }}\left( {\left( {\mathop \sum \limits_{i = 0}^{{2^{2n} - 1}} \mathop \sum \limits_{k = 0}^{{2^{2n + q + m} - 1}} \left( { - 1} \right)^{{h_{i} \cdot k}} \left| k \right\rangle_{CPM} } \right)\left( {\mathop \sum \limits_{l = 0}^{{2^{2n + q + m} - 1}} \left| l \right\rangle_{{B_{1} }} \left| {h_{i} \oplus l} \right\rangle_{{B_{2} }} } \right)} \right) \\ & = \frac{1}{{2^{3n + q + m} }}\left( {\mathop \sum \limits_{i = 0}^{{2^{2n} - 1}} \mathop \sum \limits_{k = 0}^{{2^{2n + q + m} - 1}} \mathop \sum \limits_{l = 0}^{{2^{2n + q + m} - 1}} \left| k \right\rangle_{CPM} \left| l \right\rangle_{{B_{1} }} \left( { - 1} \right)^{{h_{i} \cdot k}} \left| {h_{i} \oplus l} \right\rangle_{{B_{2} }} } \right). \\ \end{aligned} $$
(3.8)

Now, the sender performs the measurement operation on registers C, P, M, and \( B_{1} \). The resulting quantum state is \( \frac{1}{{2^{n} }}\left( {\left| k \right\rangle_{CPM} \left| l \right\rangle_{{B_{1} }} \mathop \sum \limits_{i = 0}^{{2^{2n} - 1}} \left( { - 1} \right)^{{h_{i} \cdot k}} \left| {h_{i} \oplus l} \right\rangle_{{B_{2} }} } \right). \) The sender gets \( k \) and \( l \) after measurement and sends \( k \) and \( l \) to the recipient by the classical channel. After receiving \( k \) and \( l \) from the sender, the recipient has

$$ \left| {\psi_{6} } \right\rangle = \frac{1}{{2^{n} }}\mathop \sum \limits_{i = 0}^{{2^{2n} - 1}} \left( { - 1} \right)^{{h_{i} \cdot k}} \left| {h_{i} \oplus l} \right\rangle_{{B_{2} }} . $$
(3.9)

The recipient performs the operation CNOT on \( \left| {\psi_{6} } \right\rangle \) according to \( l \) and gets

$$ \left| {\psi_{7} } \right\rangle = \frac{1}{{2^{n} }}\left( {\mathop \sum \limits_{i = 0}^{{2^{2n} - 1}} \left( { - 1} \right)^{{h_{i} \cdot k}} \left| {h_{i} \oplus l \oplus l} \right\rangle_{{B_{2} }} } \right) = \frac{1}{{2^{n} }}\left( {\mathop \sum \limits_{i = 0}^{{2^{2n} - 1}} \left( { - 1} \right)^{{h_{i} \cdot k}} \left| {h_{i} } \right\rangle_{{B_{2} }} } \right). $$
(3.10)

Given \( k = \left( {k_{2n + q + m - 1} k_{2n + q + m - 2} \ldots k_{0} } \right) \), the recipient generates the operation \( U_{z}^{{k_{t} }} \) = \( \left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & {{\text{e}}^{{\pi i \cdot k_{t} }} } \\ \end{array} } \right] \) satisfying \( \left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & {{\text{e}}^{{\pi i \cdot k_{t} }} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & {{\text{e}}^{{\pi i \cdot k_{t} }} } \\ \end{array} } \right] = I \), where \( k_{t} \in \left\{ {0, 1} \right\},0 \le t \le 2n + q + m - 1. \) These \( 2n + q + m \) operations form \( U_{z} = \prod\nolimits_{t = 0}^{2n + q + m - 1} {U_{z}^{{k_{t} }} } \). The recipient performs the operation \( U_{z} \) on \( \left| {\psi_{7} } \right\rangle \) and gets

$$ \begin{aligned} \left| {\psi_{8} } \right\rangle & = \frac{1}{{2^{n} }}U_{z} \left( {\mathop \sum \limits_{i = 0}^{{2^{2n} - 1}} \left( { - 1} \right)^{{h_{i} \cdot k}} \left| {h_{i} } \right\rangle_{{B_{2} }} } \right) = \frac{1}{{2^{n} }}\left( {\mathop \sum \limits_{i = 0}^{{2^{2n} - 1}} \left( { - 1} \right)^{{h_{i} \cdot k}} \left( {{\text{e}}^{{\pi i \cdot h_{i} \cdot k}} } \right)\left| {h_{i} } \right\rangle_{{B_{2} }} } \right) \\ & = \frac{1}{{2^{n} }}\left( {\mathop \sum \limits_{i = 0}^{{2^{2n} - 1}} \left( { - 1} \right)^{{h_{i} \cdot k}} \left( { - 1} \right)^{{h_{i} \cdot k}} \left| {h_{i} } \right\rangle_{{B_{2} }} } \right) = \frac{1}{{2^{n} }}\left( {\mathop \sum \limits_{i = 0}^{{2^{2n} - 1}} \left| {h_{i} } \right\rangle_{{B_{2} }} } \right). \\ & = \frac{1}{{2^{n} }}\left( {\mathop \sum \limits_{i = 0}^{{2^{2n} - 1}} \left| {c_{i} } \right\rangle \left| i \right\rangle \left| S \right\rangle } \right)_{{B_{2} }} \\ \end{aligned} $$
(3.11)

After measuring the last m qubits of the register \( B_{2} \), the recipient gets information secret S and a quantum image

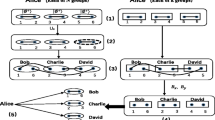
$$ \left| {\psi_{9} } \right\rangle = \frac{1}{{2^{n} }}\left( {\mathop \sum \limits_{i = 0}^{{2^{2n} - 1}} \left| {c_{i} } \right\rangle \left| i \right\rangle } \right)_{{B_{2} }} . $$
(3.12)

In the following, Figs. 3 and 4 show, respectively, the quantum circuits of the sender and recipient. According to these quantum circuits, we design two quantum algorithms: quantum information hiding algorithm and quantum information extracting algorithm. Furthermore, we give the schematic for our method in Fig. 5.

Algorithm 1. Quantum information hiding algorithm

Input:

the \( 2^{n} \times 2^{n} \) classical image (including the q-bit color information \( c_{i} \)), the m-bit secret information \( S = s_{m - 1} s_{q - 2} \ldots s_{0} \) and the quantum register \( B_{1} \) (\( \left( {2n + q + m} \right) \)-qubit of half-Bell state from the third party).

Output:

classical integers k, l, and quantum state \( \left| {\psi_{6} } \right\rangle \).

Step 1.

Construct an initial quantum state

 

\( \left| {\psi_{1} } \right\rangle = \frac{1}{{\sqrt {2^{2n + q + m} } }}\left| 0 \right\rangle_{C}^{ \otimes q} \left| 0 \right\rangle_{P}^{ \otimes 2n} \left| 0 \right\rangle_{M}^{ \otimes m} \left( {\mathop \sum \limits_{j = 0}^{{2^{2n + q + m} - 1}} \left| j \right\rangle_{{B_{1} }} } \right) \),

 

where C, \( P \), M and, \( B_{1} \) denote the \( q \)-qubit color register, the \( 2n \)-qubit position register, the \( m \)-qubit secret register, and the \( \left( {2n + q + m} \right) \)-qubit of half-Bell state, respectively.

Step 2.

Perform \( 2n \) Hadamard gates and the operation \( U_{P} \) to generate an NEQR quantum image in quantum registers C and \( P \) according to the classical image. Then, we get

 

\( \left| {\psi_{2} } \right\rangle = \frac{1}{{\sqrt {2^{4n + q + m} } }}\left( {\mathop \sum \limits_{i = 0}^{{2^{2n} - 1}} \left| {c_{i} } \right\rangle_{C} \left| i \right\rangle_{P} } \right)|0\rangle_{M} \left( {\mathop \sum \limits_{j = 0}^{{2^{2n + q + m} - 1}} \left| j \right\rangle_{{B_{1} }} } \right). \)

Step 3.

Perform the operation \( U_{s} \) to put the secret information \( S = s_{m - 1} s_{q - 2} \ldots s_{0} \) into the secret register M and get

 

\( \left| {\psi_{3} } \right\rangle = \frac{1}{{\sqrt {2^{4n + q + m} } }}\left( {\mathop \sum \limits_{i = 0}^{{2^{2n} - 1}} \left| {c_{i} } \right\rangle_{C} \left| i \right\rangle_{P} } \right)\left| S \right\rangle_{M} \left( {\mathop \sum \limits_{j = 0}^{{2^{2n + q + m} - 1}} \left| j \right\rangle_{{B_{1} }} } \right). \)

Step 4.

Perform quantum operation \( U_{B} \) to produce \( \left| {\psi_{4} } \right\rangle \) by setting register C, P, and M as control bits and register \( B_{1} \) as target bits. We then get

 

\( \left| {\psi_{4} } \right\rangle = \frac{1}{{\sqrt {2^{4n + q + m} } }}\left( {\mathop \sum \limits_{i = 0}^{{2^{2n} - 1}} \left| {h_{i} } \right\rangle_{CPM} } \right)\left( {\mathop \sum \limits_{j = 0}^{{2^{2n + q + m} - 1}} \left| {h_{i} \oplus j} \right\rangle_{{B_{1} }} } \right), \)

 

where \( \left| {h_{i} } \right\rangle_{CPM} = \left| {c_{i} } \right\rangle_{C} \left| i \right\rangle_{P} \left| S \right\rangle_{M} \). Because the sender and the recipient hold the Bell state, this quantum system will be

 

\( \left| {\psi '_{4} } \right\rangle = \frac{1}{{\sqrt {2^{4n + q + m} } }}\left( {\mathop \sum \limits_{i = 0}^{{2^{2n} - 1}} \left| {h_{i} } \right\rangle_{CPM} } \right)\left( {\mathop \sum \limits_{j = 0}^{{2^{2n + q + m} - 1}} \left| {h_{i} \oplus j} \right\rangle_{{B_{1} }} \left| j \right\rangle_{{B_{2} }} } \right). \)

Step 5.

Perform \( \left( {2n + q + m} \right) \) Hadamard gates on registers C, P, and M. We get

 

\( \left| {\psi_{5} } \right\rangle = \frac{1}{{2^{3n + q + m} }}\left( {\left( {\mathop \sum \limits_{i = 0}^{{2^{2n} - 1}} \mathop \sum \limits_{k = 0}^{{2^{2n + q + m} - 1}} \left( { - 1} \right)^{{h_{i} \cdot k}} \left| k \right\rangle_{CPM} } \right)\left( {\mathop \sum \limits_{j = 0}^{{2^{2n + q + m} - 1}} \left| {h_{i} \oplus j} \right\rangle_{{B_{1} }} \left| j \right\rangle_{{B_{2} }} } \right)} \right). \) Set \( l = h_{i} \oplus j \), we have

 

\( \left| {\psi '_{5} } \right\rangle = \frac{1}{{2^{3n + q + m} }}\left( {\mathop \sum \limits_{i = 0}^{{2^{2n} - 1}} \mathop \sum \limits_{k = 0}^{{2^{2n + q + m} - 1}} \mathop \sum \limits_{l = 0}^{{2^{2n + q + m} - 1}} \left| k \right\rangle_{CPM} \left| l \right\rangle_{{B_{1} }} \left( { - 1} \right)^{{h_{i} \cdot k}} \left| {h_{i} \oplus l} \right\rangle_{{B_{2} }} } \right). \)

Step 6.

Perform the measurement operation on registers C, P, M, and \( B_{1} \). We get classical integers k and l after measurement. It is worthy of noting that the recipient has

 

\( \left| {\psi_{6} } \right\rangle = \frac{1}{{2^{n} }}\left( {\mathop \sum \limits_{i = 0}^{{2^{2n} - 1}} \left( { - 1} \right)^{{h_{i} \cdot k}} \left| {h_{i} \oplus l} \right\rangle_{{B_{2} }} } \right). \)

 

At last, the sender transfers the classical integers k and l to the recipient by the classical channel.

Algorithm 2. Quantum information extracting algorithm

Input:

classical integers k, l, and the quantum state \( \left| {\psi_{6} } \right\rangle \).

Output:

secret information S and the quantum image \( \left| {\psi_{9} } \right\rangle \).

Step 1.

Perform the operation CNOT on \( \left| {\psi_{6} } \right\rangle \) according to \( l \) and get

 

\( \left| {\psi_{7} } \right\rangle = \frac{1}{{2^{n} }}\left( {\mathop \sum \limits_{i = 0}^{{2^{2n} - 1}} \left( { - 1} \right)^{{h_{i} \cdot k}} \left| {h_{i} \oplus l \oplus l} \right\rangle_{{B_{2} }} } \right) = \frac{1}{{2^{n} }}\left( {\mathop \sum \limits_{i = 0}^{{2^{2n} - 1}} \left( { - 1} \right)^{{h_{i} \cdot k}} \left| {h_{i} } \right\rangle_{{B_{2} }} } \right). \)

Step 2.

Perform the operation \( U_{z} = \prod\nolimits_{t = 0}^{2n + q + m - 1} {U_{z}^{{k_{t} }} } \) on \( \left| {\psi_{7} } \right\rangle \) according to \( k \) and get

 

\( \left| {\psi_{8} } \right\rangle = \frac{1}{{2^{n} }}\left( {\mathop \sum \limits_{i = 0}^{{2^{2n} - 1}} \left| {h_{i} } \right\rangle_{{B_{2} }} } \right) = \frac{1}{{2^{n} }}\left( {\mathop \sum \limits_{i = 0}^{{2^{2n} - 1}} \left| {c_{i} } \right\rangle \left| i \right\rangle \left| S \right\rangle } \right)_{{B_{2} }} . \)

Step 3.

Measure the last \( m \) qubits of the register \( B_{2} \) to extract secret information S and get a quantum image

 

\( \left| {\psi_{9} } \right\rangle = \frac{1}{{2^{n} }}\left( {\mathop \sum \limits_{i = 0}^{{2^{2n} - 1}} \left| {c_{i} } \right\rangle \left| i \right\rangle } \right)_{{B_{2} }} . \)

Fig. 3
figure 3

Quantum circuit of the sender

Full size image
Fig. 4
figure 4

Quantum circuit of the recipient

Full size image
Fig. 5
figure 5

Schematic for our method

Full size image

4 An example of our method

To understand our method easily, we give an example in this section. First, we construct the quantum image \( \left| \psi \right\rangle = \frac{1}{2}\left( {\left| {10} \right\rangle_{C} \left| {00} \right\rangle_{P} + \left| {11} \right\rangle_{C} \left| {01} \right\rangle_{P} + \left| {01} \right\rangle_{C} \left| {10} \right\rangle_{P} + \left| {01} \right\rangle_{C} \left| {11} \right\rangle_{P} } \right) \) according to Fig. 1. Assume that the sender wants to transfer the secret information \( S = \left( {10} \right)_{2} \) and the quantum image \( \left| \psi \right\rangle \) to the recipient. Figure 6 shows the sender’s quantum circuit which stems from Fig. 3. Similarly, Fig. 7 shows the recipient’s quantum circuit which stems from Fig. 4. The simulation of our example has been implemented in Julia language, as shown in Fig. 8, and has been tested on a Core i7 4790 with 8 GB of RAM. The simulation shows that the recipient extracts the secret information \( S = \left( {10} \right)_{2} \) and the quantum image \( \left| \psi \right\rangle = \frac{1}{2}\left( {\left| {10} \right\rangle_{C} \left| {00} \right\rangle_{P} + \left| {11} \right\rangle_{C} \left| {01} \right\rangle_{P} + \left| {01} \right\rangle_{C} \left| {10} \right\rangle_{P} + \left| {01} \right\rangle_{C} \left| {11} \right\rangle_{P} } \right) \) if measured values \( k = \left( {010101} \right)_{2} \) and \( l = \left( {110011} \right)_{2} \).

Fig. 6
figure 6

An example of the sender’s quantum circuit

Full size image
Fig. 7
figure 7

An example of the recipient’s quantum circuit

Full size image
Fig. 8
figure 8

Simulation of our example in Julia language

Full size image

5 Analysis and comparison

In our method, if the third party is trusted and the classical channel is secure, anyone cannot copy an unknown quantum state according to no-cloning theorem. Therefore, the information cannot be leaked in our method. But if the third party is untrusted, this party may be an eavesdropper who is in possession of a third sub-system that may be entangled with those given to the sender and the recipient [26]. For example, the third party uses the general Bell state \( \frac{1}{{\sqrt {2^{2n + q + m} } }}\sum\nolimits_{j = 0}^{{2^{2n + q + m} - 1}} {\left| j \right\rangle_{{B_{1} }} \left| j \right\rangle_{{B_{2} }} \left| j \right\rangle_{{B_{3} }} } \) instead of \( \frac{1}{{\sqrt {2^{2n + q + m} } }}\sum\nolimits_{j = 0}^{{2^{2n + q + m} - 1}} {\left| j \right\rangle_{{B_{1} }} \left| j \right\rangle_{{B_{2} }} } \), where the quantum register \( B_{3} \) is the third sub-system. We further suppose that the third party can obtain the measured values \( k \) and \( l \) from the classical channel. After the recipient measuring the last \( m \) qubits of the register \( B_{2} \) to extract secret information, the third party can use the sub-system \( \left| j \right\rangle_{{B_{3} }} \) to obtain secret information. To be sure that the third party is completely decoupled from data of the sender and the recipient, the sender and the recipient must share a maximally entangled state, which can be proven by local measurements and public discussion alone [27]. To prove the presence of entanglement in a quantum state that is effectively distributed between the sender and the recipient, the class of entanglement witness operators is used [26, 28]. However, not all entanglement witness operators are useful for the purpose of teleportation. Teleportation witness operators are presented [29, 30]. Therefore, the sender and the recipient must verify the general Bell state \( \frac{1}{{\sqrt {2^{2n + q + m} } }}\sum\nolimits_{j = 0}^{{2^{2n + q + m} - 1}} {\left| j \right\rangle_{{B_{1} }} \left| j \right\rangle_{{B_{2} }} } \) before using it. In our method, the third party must construct \( r \) general Bell states \( \frac{1}{{\sqrt {2^{2n + q + m} } }}\sum\nolimits_{j = 0}^{{2^{2n + q + m} - 1}} {\left| j \right\rangle_{{B_{1} }} \left| j \right\rangle_{{B_{2} }} } \) and distribute them to the sender and the recipient. The sender and the recipient then randomly select \( r - 1 \) general Bell states to see if these general Bell states are verified with the use of teleportation witness operators [29, 30]. Once \( r - 1 \) general Bell states are verified, the sender and the recipient will perform our method by using the remaining general Bell state.

Table 1 gives a comparison of LSQb method, the block LSB method and our method in computational complexity, capacity, key size, the third party, and the number of extracted bits.

Table 1 Comparison of LSQb method, the block LSB method, and our method
Full size table

To analyze the computational complexity of our method, we assume that all one qubit gates and all controlled-V gates are elementary operations [1, 31]. At first, we consider the cost of constructing the \( 2^{n} \times 2^{n} \) NEQR image. In Step 2 of Algorithm 1, we need \( 2n \) Hadamard gates and a quantum operation \( U_{P} = \prod\nolimits_{i = 0}^{{2^{2n} - 1}} {V_{i} } \). Because \( V_{i} (\left| 0 \right\rangle_{C} \otimes \left| i \right\rangle_{P} ) = \left| {c_{i} } \right\rangle_{C} \otimes \left| i \right\rangle_{P} \), one \( V_{i} \) operation requires q \( (2n + 1) \)-qubit Toffoli gates. We know that one (\( 2n + 1) \)-qubit Toffoli gate is implemented by 32 \( \times \)(\( 2n \))- 120 elementary operations and one garbage bit which is passed unchanged [32]. Therefore, we need (\( 2n + 2^{2n} q\left( {64n - 120} \right)) \) elementary operations to construct the \( 2^{n} \times 2^{n} \) NEQR image. In Step 3 of Algorithm 1, we only need \( m \) CNOT gates to perform the operation \( U_{s} \). Step 4 requires \( \left( {2n + q + m} \right) \) CNOT gates to perform the operation \( U_{B} \). In Step 5 of Algorithm 1, we need \( \left( {2n + q + m} \right) \) Hadamard gates. Assuming that \( m < \left( {2n + q} \right) \), Algorithm 1 requires \( {\text{O}}\left( {2^{2n} qn} \right) \) elementary operations. Similarly, in Algorithm 2, Step 1 needs \( \left( {2n + q + m} \right) \) CNOT gates and Step 2 needs \( \left( {2n + q + m} \right) \) \( U_{z}^{{k_{t} }} \) gates. Thus, Algorithm 2 requires \( {\text{O}}\left( {n + q + m} \right) \) elementary operations. Thus, our method requires \( {\text{O}}\left( {2^{2n} qn} \right) \) elementary operations. In LSQb method and the block LSB method, the NEQR image must be constructed. These two methods also require \( {\text{O}}\left( {2^{2n} qn} \right) \) elementary operations.

Next, we compare the hiding capacity of our method with that of LSQb method. Our method hides \( m \) secret bits which is independent of the size of the quantum image. LSQb method can hide \( 2^{n} \) secret bits which depend on the size of the quantum image. According to our assumption \( m < \left( {2n + q} \right) \), LSQb method has higher hiding capacity. However, LSQb method only gets one secret bit with just one measurement. If one wants to get another secret bit, he/she must execute LSQb method again. After measurement, he/she can get another secret bit with the probability \( \left( {1 - 2^{ - n} } \right) \). Therefore, one can get \( m \) secret bits with the probability \( \prod\nolimits_{i = 1}^{m - 1} {\left( {1 - \frac{i}{{2^{n} }}} \right)} \) if he/she executes LSQb method \( m \) times. It is worthy of noting that the quantum image collapses after measurement. In our method, we will extract \( m \) secret bits and a quantum image after measurement with certainty. However, our method must transfer \( \left( {4n + 2q + 2m} \right) \) bits by the classical channel.

6 Conclusion

This paper has proposed a novel information hiding method based on the NEQR quantum image by using the quantum teleportation scheme. In the proposed method, the recipient not only gets the secret information, but also holds the quantum image after measurement. As compared with Wang et al.’s method which hides secret information in the least significant qubit (LSQb), our method will not collapse the quantum image and decrease the computed cost of extracting one secret bit by \( O\left( m \right) \) times.