1 Introduction

Quantum entanglement [1,2,3,4,5,6,7,8] is an essential feature of quantum mechanics. As one of the fundamental differences between quantum entanglement and classical correlations, a key property of entanglement is that a quantum system entangled with one of other subsystems limits its entanglement with the remaining ones. The monogamy relations give rise to the distribution of entanglement in the multipartite setting. Monogamy is also an essential feature allowing for security in quantum key distribution [9].

For a tripartite system A, B and C, the usual monogamy of an entanglement measure \(\mathcal {E}\) implies that [10] the entanglement between A and BC satisfies \(\mathcal {E}_{A|BC}\ge \mathcal {E}_{AB} +\mathcal {E}_{AC}\). In Refs. [11, 12], the monogamy of entanglement for multiqubit W-class states has been investigated, and the monogamy relations for tangle and the squared concurrence have been proved. It gives the general monogamy relations for the x-power [13] of concurrence of assistance for generalized multiqubit W-class states.

In this paper, we show that the monogamy inequalities for concurrence of assistance obtained so far can be made tighter. We establish entanglement monogamy relations for the xth \((x\ge 2)\) and yth \((y<0)\) power of the concurrence of assistance which are tighter than those in [13], which give rise to finer characterizations of the entanglement distributions among the multipartite W-class states. Furthermore, we also present the general monogamy relations for the x-power of negativity of assistance for generalized multiqubit W-class states.

2 Tighter monogamy relations for concurrence of assistance

We first consider the monogamy inequalities related to concurrence. Let \(H_X\) denote a discrete finite-dimensional complex vector space associated with a quantum subsystem X. For a bipartite pure state \(|\psi \rangle _{AB}\) in vector space \(H_A\otimes H_B\), the concurrence is given by [14,15,16]

$$\begin{aligned} C(|\psi \rangle _{AB})=\sqrt{{2\left[ 1-\mathrm {Tr}(\rho _A^2)\right] }}, \end{aligned}$$
(1)

where \(\rho _A\) is the reduced density matrix by tracing over the subsystem B, \(\rho _A=\mathrm {Tr}_B(|\psi \rangle _{AB}\langle \psi |)\). The concurrence for a bipartite mixed state \(\rho _{AB}\) is defined by the convex-roof extension

$$\begin{aligned} C(\rho _{AB})=\min _{\{p_i,|\psi _i\rangle \}}\sum _ip_iC(|\psi _i\rangle ), \end{aligned}$$

where the minimum is taken over all possible decompositions of \(\rho _{AB}=\sum _ip_i|\psi _i\rangle \langle \psi _i|\), with \(p_i\ge 0\) and \(\sum _ip_i=1\) and \(|\psi _i\rangle \in H_A\otimes H_B\).

For a tripartite state \(|\psi \rangle _{ABC}\), the concurrence of assistance is defined by [17, 18]

$$\begin{aligned} C_a(|\psi \rangle _{ABC})\equiv C_a(\rho _{AB})=\mathrm {max}_{\{p_i,|\psi _i\rangle \}}\sum _ip_iC(|\psi _i\rangle ), \end{aligned}$$

where the maximum is taken over all possible decompositions of \(\rho _{AB}=\mathrm {Tr}_C(|\psi \rangle _{ABC}\langle \psi |)=\sum _ip_i|\psi _i\rangle _{AB}\langle \psi _i|.\) When \(\rho _{AB}=|\psi \rangle _{AB}\langle \psi |\) is a pure state, then one has \(C(|\psi \rangle _{AB})=C_a(\rho _{AB})\).

For an N-qubit pure state \(|\psi \rangle _{AB_1\cdots B_{N-1}}\in H_A\otimes H_{B_1}\otimes \cdots \otimes H_{B_{N-1}}\), the concurrence \(C(|\psi \rangle _{A|B_1\cdots B_{N-1}})\) of the state \(|\psi \rangle _{A|B_1\cdots B_{N-1}}\), viewed as a bipartite state under the partition A and \(B_1,B_2,\ldots , B_{N-1}\), satisfies [25]

$$\begin{aligned} C^{\alpha }(\rho _{A|B_1,B_2\cdots ,B_{N-1}})\ge C^{\alpha }(\rho _{AB_1})+C^{\alpha }(\rho _{AB_2})+\cdots +C^{\alpha }(\rho _{AB_{N-1}}), \end{aligned}$$

for \(\alpha \ge 2\), where \(\rho _{AB_i}=\mathrm {Tr}_{B_1\cdots B_{i-1}B_{i+1}\cdots B_{N-1}}(|\psi \rangle _{AB_1\cdots B_{N-1}}\langle \psi |)\). It is further improved that for \(\alpha \ge 2\), one has [19],

$$\begin{aligned}&C^\alpha (\rho _{A|B_1B_2\cdots B_{N-1}})\ge C^\alpha (\rho _{AB_1}) +\frac{\alpha }{2} C^\alpha (\rho _{AB_2})+\cdots +\left( \frac{\alpha }{2}\right) ^{m-1}C^\alpha (\rho _{AB_m})\nonumber \\&\quad +\,\left( \frac{\alpha }{2}\right) ^{m+1}\left( C^\alpha (\rho _{AB_{m+1}}) +\cdots +C^\alpha (\rho _{AB_{N-2}})\right) +\left( \frac{\alpha }{2}\right) ^{m}C^\alpha (\rho _{AB_{N-1}}) \end{aligned}$$
(2)

and

$$\begin{aligned} C^\alpha (\rho _{A|B_1B_2\cdots B_{N-1}})< K\left( C^\alpha (\rho _{AB_1})+C^\alpha (\rho _{AB_2})+\cdots +C^\alpha (\rho _{AB_{N-1}})\right) \end{aligned}$$
(3)

for all \(\alpha <0\), where \(K=\frac{1}{N-1}\).

Dual to the Coffman–Kundu–Wootters inequality, the generalized monogamy relation based on the concurrence of assistance does not satisfy the monogamy relation. But, for an N-qubit generalized W-class states \(|\psi \rangle _{AB_1\cdots B_{N-1}}\in H_A\otimes H_{B_1}\otimes \cdots \otimes H_{B_{N-1}}\), the concurrence of assistance \(C_a(|\psi \rangle _{A|B_1\cdots B_{N-1}})\) of the state \(|\psi \rangle _{AB_1\cdots B_{N-1}}\) satisfies the inequality [13],

$$\begin{aligned} C_a^x(\rho _{A|B_1,B_2\cdots ,B_{N-1}})\ge C_a^x(\rho _{AB_1})+C_a^x(\rho _{AB_2})+\cdots +C_a^x(\rho _{AB_{N-1}}), \end{aligned}$$
(4)

and

$$\begin{aligned} C_a^y(\rho _{A|B_1,B_2\cdots ,B_{N-1}})< C_a^y(\rho _{AB_1})+C_a^y(\rho _{AB_2})+\cdots +C_a^y(\rho _{AB_{N-1}}), \end{aligned}$$
(5)

where \(x\ge 2\), \(y\le 0\).

In fact, as the characterization of the entanglement distribution among the subsystems, the monogamy inequalities satisfied by the concurrence of assistance can be further refined and become tighter.

In the following, we study the monogamy property of the concurrence of assistance for the N-qubit generalized W-class states \(|\psi \rangle \in H_A\otimes H_{B_1}\otimes \cdots \otimes H_{B_{N-1}}\) defined by

$$\begin{aligned} |\psi \rangle =a|00\cdots 0\rangle +b_1|10\cdots 0\rangle +\cdots +b_N|00\cdots 1\rangle , \end{aligned}$$
(6)

with \(|a|^2+\sum _{i=1}^N|b_i|^2=1\). For N-qubit generalized W-class states (6), one has [13],

$$\begin{aligned} C(\rho _{AB_i})=C_a(\rho _{AB_i}),~~~~i=1,2,\ldots ,N-1, \end{aligned}$$
(7)

where \(\rho _{AB_i}=\mathrm {Tr}_{B_1\cdots B_{i-1}B_{i+1}\cdots B_{N-1}}(|\psi \rangle \langle \psi |)\).

Theorem 1

For the N-qubit generalized W-class states \(|\psi \rangle \in H_A\otimes H_{B_1}\otimes \cdots \otimes H_{B_{N-1}}\), let \(\rho _{AB_{j_1}\cdots B_{j_{m-1}}}\) denote the m-qubit, \(2\le m\le N\), reduced density matrix of \(|\psi \rangle \). If \(C(\rho _{AB_{j_i}})\ge C(\rho _{AB_{j_{i+1}}\cdots B_{j_{m-1}}})\) for \(i=1,2,\ldots t\), and \(C(\rho _{AB_{j_k}})\le C(\rho _{AB_{j_{k+1}}\cdots B_{j_{m-1}}})\) for \(k=t+1,\ldots ,{m-2}\), \(\forall \) \(1\le t\le {m-3},~m\ge 4\), the concurrence of assistance satisfies

$$\begin{aligned} C_a^x(\rho _{A|B_{j_1}\cdots B_{j_{m-1}}})&\ge C_a^x(\rho _{AB_{j_1}}) \nonumber \\&\quad +\,\frac{x}{2}C_a^x(\rho _{AB_{j_2}})+\cdots +\left( \frac{x}{2}\right) ^{t-1}C_a^x(\rho _{AB_{j_t}}) \nonumber \\&\quad +\,\left( \frac{x}{2}\right) ^{t+1}\left( C_a^x(\rho _{AB_{j_{t+1}}})+\cdots +C_a^x(\rho _{AB_{j_{m-2}}})\right) \nonumber \\&\quad +\,\left( \frac{x}{2}\right) ^tC_a^x(\rho _{AB_{j_{m-1}}}) \end{aligned}$$
(8)

for all \(x\ge 2\).

Proof

For the N-qubit generalized W-class states \(|\psi \rangle \), according to the definitions of \(C(\rho )\) and \(C_a(\rho )\), one has \(C_a(\rho _{A|B_{j_1}\cdots B_{j_{m-1}}})\ge C(\rho _{A|B_{j_1}\cdots B_{j_{m-1}}})\). When \(x\ge 2\), we have

$$\begin{aligned} C_a^x(\rho _{A|B_{j_1}\cdots B_{j_{m-1}}})&\ge C^x(\rho _{A|B_{j_1}\cdots B_{j_{m-1}}}) \ge C^x(\rho _{AB_{j_1}}) \nonumber \\&\quad +\,\frac{x}{2}C^x(\rho _{AB_{j_2}})+\cdots +\left( \frac{x}{2}\right) ^{t-1}C^x(\rho _{AB_{j_t}}) \nonumber \\&\quad +\,\left( \frac{x}{2}\right) ^{t+1}\left( C^x(\rho _{AB_{j_{t+1}}})+\cdots +C^x(\rho _{AB_{j_{m-2}}})\right) \nonumber \\&\quad +\,\left( \frac{x}{2}\right) ^tC^x(\rho _{AB_{j_{m-1}}})\nonumber \\&=C_a^x(\rho _{AB_{j_1}}) +\frac{x}{2}C_a^x(\rho _{AB_{j_2}})+\cdots +\left( \frac{x}{2}\right) ^{t-1}C_a^x(\rho _{AB_{j_t}}) \nonumber \\&\quad +\,\left( \frac{x}{2}\right) ^{t+1}\left( C_a^x(\rho _{AB_{j_{t+1}}})+\cdots +C_a^x(\rho _{AB_{j_{m-2}}})\right) \nonumber \\&\quad +\,\left( \frac{x}{2}\right) ^tC_a^x(\rho _{AB_{j_{m-1}}}), \end{aligned}$$
(9)

where we have used in the first inequality the relation \(a^x\ge b^x\) for \(a\ge b\ge 0,~x\ge 2\). The second inequality is due to (2). The equality is due to (7). \(\square \)

As for \(x\ge 2\), \((x/2)^t\ge 1\) for all \(1\le t\le j_{m-3}\), comparing with the monogamy relations for concurrence of assistance (4), our formula (8) in Theorem 1 gives a tighter monogamy relation with larger lower bounds. In Theorem 1 we have assumed that some \(C(\rho _{AB_{j_i}})\ge C(\rho _{AB_{j_{i+1}}\cdots B_{j_{m-1}}})\) and some \(C(\rho _{AB_k})\le C(\rho _{AB_{k+1}\cdots B_{m-1}})\) for the N-qubit generalized W-class states. If all \(C(\rho _{AB_{j_i}})\ge C(\rho _{AB_{j_{i+1}}\cdots B_{j_{m-1}}})\) for \(i=1, 2, \ldots , {m-2}\), then we have the following conclusion:

Theorem 2

If \(C(\rho _{AB_{j_i}})\ge C(\rho _{AB_{j_{i+1}}\cdots B_{j_{m-1}}})\) for \(i=1, 2, \ldots , {m-2}\), then we have

$$\begin{aligned} C_a^x(\rho _{A|B_{j_1}\cdots B_{j_{m-1}}})\ge C_a^x(\rho _{AB_{j_1}}) +\frac{x}{2}C_a^x(\rho _{AB_{j_2}})+\cdots +\left( \frac{x}{2}\right) ^{m-2}C_a^x(\rho _{AB_{j_{m-1}}})\nonumber \\ \end{aligned}$$
(10)

for all \(x\ge 2\).

Example 1

Let us consider the 4-qubit generalized W-class states,

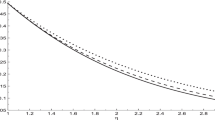
$$\begin{aligned} |W\rangle _{AB_1B_2B_3}=\frac{1}{2}(|1000\rangle +|0100\rangle +|0010\rangle +|0001\rangle ). \end{aligned}$$
(11)

We have \(C_a^x(|\psi \rangle _{A|B_1B_2B_3})=\left( \frac{\sqrt{3}}{2}\right) ^x\). From our result (8) we have \(C_a^x(|\psi \rangle _{A|B_1B_2B_3})\ge \left[ 1+\frac{x}{2}+\left( \frac{x}{2}\right) ^2\right] \left( \frac{1}{2}\right) ^x\), and from (4) one has \(C_a^x(|\psi \rangle _{A|B_1B_2B_3})\ge 3\left( \frac{1}{2}\right) ^x\), \(x\ge 2\). One can see that our result is better than that in [13] for \(x\ge 2\), see Fig. 1.

Fig. 1
figure 1

y is the value of \(C_a(|\psi \rangle _{A|B_1B_2B_3})\). Solid (red) line is the exact value of \(C_a(|\psi \rangle _{A|B_1B_2B_3})\), dashed (blue) line is the lower bound of \(C_a(|\psi \rangle _{A|B_1B_2B_3})\) in (8), and dot-dashed (green) line is the lower bound in [13] for \(x\ge 2\) (Color figure online)

Full size image

We can also derive a tighter upper bound of \(C_a^y(\rho _{A|B_1\cdots B_{N-1}})\) for \(y<0\).

Theorem 3

For the N-qubit generalized W-class states \(|\psi \rangle \in H_A\otimes H_{B_1}\otimes \cdots \otimes H_{B_{N-1}}\), let \(\rho _{AB_{j_1}\cdots B_{j_{m-1}}}\) be the m-qubit, \(2\le m\le N\), reduced density matrix of \(|\psi \rangle \) with \(C(\rho _{AB_{j_i}})\ne 0\) for \(1\le i\le m-1\), we have

$$\begin{aligned} C_a^y(\rho _{A|B_{j_1}\cdots B_{j_{m-1}}})< \tilde{M} \left( C_a^y(\rho _{AB_{j_1}})+C_a^y(\rho _{AB_{j_2}})+\cdots +C_a^y(\rho _{AB_{j_{m-1}}})\right) \quad \end{aligned}$$
(12)

for all \(y<0\), where \(\tilde{M}=\frac{1}{m-1}\).

Proof

For \(y< 0\), we have

$$\begin{aligned} C_a^y(\rho _{A|B_{j_1}\cdots B_{j_{m-1}}})&\le C^y(\rho _{A|B_{j_1}\cdots B_{j_{m-1}}}) \nonumber \\&<\tilde{M} \left( C^y(\rho _{AB_{j_1}})+C^y(\rho _{AB_{j_2}})+\cdots +C^y(\rho _{AB_{j_{m-1}}})\right) \nonumber \\&= \tilde{M} \left( C_a^y(\rho _{AB_{j_1}})+C_a^y(\rho _{AB_{j_2}})+\cdots +C_a^y(\rho _{AB_{j_{m-1}}})\right) ,\qquad \end{aligned}$$
(13)

where we have used in the first inequality the relation \(a^x\le b^x\) for \(a\ge b\ge 0,~x\le 0\). The second inequality is due to (3). The equality is due to (7). \(\square \)

As the factor \(\tilde{M}=\frac{1}{m-1}\) is less than one, inequality (12) is tighter than the one in [13]. This factor \(\tilde{M}\) depends on the number of partite N. Namely, for larger multipartite systems, inequality (12) gets even tighter than the one in [13].

Example 2

Let us consider again 4-qubit generalized W-class states (11). We have \(C_a^y(|\psi \rangle _{A|B_1B_2B_3})=\left( \frac{\sqrt{3}}{2}\right) ^y\). From our result (12) we have \(C_a^y(|\psi \rangle _{A|B_1B_2B_3})\le \left( \frac{1}{2}\right) ^y\), while from (5) one gets \(C_a^y(|\psi \rangle _{A|B_1B_2B_3})\le 3\left( \frac{1}{2}\right) ^y\). It can be seen that our result is better than that in [13] for \(y<0\), see Fig. 2.

Fig. 2
figure 2

f(y) is the value of \(C^y_a(|\psi \rangle _{A|B_1B_2B_3})\). Solid (red) line is the exact value of \(C^y_a(|\psi \rangle _{A|B_1B_2B_3})\), dashed (blue) line is the upper bound of \(C^y_a(|\psi \rangle _{A|B_1B_2B_3})\) in (12), and dot-dashed (green) line is the upper bound in [13] (Color figure online)

Full size image

Remark 1

In (12) we have assumed that all \(C(\rho _{AB_{j_i}})\), \(i=1,2,\ldots ,m-1\), are nonzero. In fact, if one of them is zero, the inequality still holds by removing this term from the inequality. Namely, if \(C(\rho _{AB_{j_i}})=0,\) then one has \(C_a^y(\rho _{A|B_{j_1}\cdots B_{j_{m-1}}})<\frac{1}{2}C_a^y(\rho _{AB_{j_1}})+\cdots +\left( \frac{1}{2}\right) ^{i-1}C_a^y(\rho _{AB_{j_{i-1}}})+\left( \frac{1}{2}\right) ^{i}C_a^y(\rho _{AB_{j_{i+1}}})+\cdots +\left( \frac{1}{2}\right) ^{m-3}C_a^y(\rho _{AB_{j_{m-2}}})+\left( \frac{1}{2}\right) ^{m-3} C_a^y(\rho _{AB_{j_{m-1}}})\). By cyclically permuting the subindices in \(B_{j_1}\cdots B_{j_{m-1}}\), we can get a set of inequalities. Summing up these inequalities we have \(C_a^y(\rho _{A|B_{j_1}\cdots B_{j_{m-1}}})<\frac{1}{m-1}\left( C_a^y(\rho _{AB_{j_1}})+\cdots +C_a^y(\rho _{AB_{j_{i-1}}})+C_a^y(\rho _{AB_{j_{i+1}}})+\cdots +C_a^y(\rho _{AB_{j_{m-2}}})+ C_a^y(\rho _{AB_{j_{m-1}}})\right) \) for \(y<0\).

3 Monogamy relations for negativity of assistance

Another well-known quantifier of bipartite entanglement is the negativity. Given a bipartite state \(\rho _{AB}\) in \(H_A\otimes H_B\), the negativity is defined by Vidal and Werner [20], \(N(\rho _{AB})=\left( \left| \left| \rho _{AB}^{T_A}\right| \right| -1\right) /2\), where \(\rho _{AB}^{T_A}\) is the partial transpose with respect to the subsystem A; ||X|| denotes the trace norm of X, i.e., \(||X||=\mathrm {Tr}\sqrt{XX^\dag }\). Negativity is a computable measure of entanglement and is a convex function of \(\rho _{AB}\). It vanishes if and only if \(\rho _{AB}\) is separable for the \(2\otimes 2\) and \(2\otimes 3\) systems [21]. For the purpose of discussion, we use the following definition of negativity, \( N(\rho _{AB})=\left| \left| \rho _{AB}^{T_A}\right| \right| -1\). For any bipartite pure state \(|\psi \rangle _{AB}\), the negativity \( N(\rho _{AB})\) is given by \(N(|\psi \rangle _{AB})=2\sum _{i<j}\sqrt{\lambda _i\lambda _j}=(\mathrm {Tr}\sqrt{\rho _A})^2-1\), where \(\lambda _i\) are the eigenvalues for the reduced density matrix of \(|\psi \rangle _{AB}\). For a mixed state \(\rho _{AB}\), the convex-roof extended negativity (CREN) is defined as

$$\begin{aligned} N_c(\rho _{AB})=\mathrm {min}\sum _ip_iN(|\psi _i\rangle _{AB}), \end{aligned}$$
(14)

where the minimum is taken over all possible pure state decompositions \(\{p_i,~|\psi _i\rangle _{AB}\}\) of \(\rho _{AB}\). CREN gives a perfect discrimination of positive partial transposed bound entangled states and separable states in any bipartite quantum systems [22, 23]. For a mixed state \(\rho _{AB}\), the convex-roof extended negativity of assistance (CRENOA) is defined as [24]

$$\begin{aligned} N_a(\rho _{AB})=\mathrm {max}\sum _ip_iN(|\psi _i\rangle _{AB}), \end{aligned}$$
(15)

where the maximum is taken over all possible pure state decompositions \(\{p_i,~|\psi _i\rangle _{AB}\}\) of \(\rho _{AB}\).

Let us consider the relation between CREN and concurrence. For any bipartite pure state \(|\psi \rangle _{AB}\) in a \(d\otimes d\) quantum system with Schmidt rank 2, \(|\psi \rangle _{AB}=\sqrt{\lambda _0}|00\rangle +\sqrt{\lambda _1}|11\rangle \), one has \(N(|\psi \rangle _{AB})=\parallel |\psi \rangle \langle \psi |^{T_B}\parallel -1=2\sqrt{\lambda _0\lambda _1} =\sqrt{2(1-\mathrm {Tr}\rho _A^2)}=C(|\psi \rangle _{AB})\). In other words, negativity is equivalent to concurrence for any pure state with Schmidt rank 2, and consequently it follows that for any two-qubit mixed state \(\rho _{AB}=\sum p_i|\psi _i\rangle _{AB}\langle \psi _i|\),

$$\begin{aligned} N_c(\rho _{AB})&=\mathrm {min}\sum _ip_iN(|\psi _i\rangle _{AB})\\ \nonumber&=\mathrm {min}\sum _ip_iC(|\psi _i\rangle _{AB})\\ \nonumber&=C(\rho _{AB}), \end{aligned}$$
(16)
$$\begin{aligned} N_a(\rho _{AB})&=\mathrm {max}\sum _ip_iN(|\psi _i\rangle _{AB})\\ \nonumber&=\mathrm {max}\sum _ip_iC(|\psi _i\rangle _{AB})\\ \nonumber&= C_a(\rho _{AB}), \end{aligned}$$
(17)

where the minimum and the maximum are taken over all pure state decompositions \(\{p_i,~|\psi _i\rangle _{AB}\}\) of \(\rho _{AB}\).

Combining (7), (16) and (17), we can get the following lemma.

Lemma 1

For N-qubit generalized W-class states (6), we have

$$\begin{aligned} N_c(\rho _{AB_i})=N_a(\rho _{AB_i}). \end{aligned}$$
(18)

As is already known, the negativity satisfies the monogamy relation for N-qubit pure state [24]. In fact, for any N-qubit state, the monogamy relation of the negativity always holds. Therefore, we can get the following lemma.

Lemma 2

For any N-qubit state \(\rho \in H_A\otimes H_{B_1}\otimes \cdots \otimes H_{B_{N-1}}\), we have

$$\begin{aligned} N_c^x(\rho _{A|B_1\cdots B_{N-1}})\ge \sum _{i=1}^{N-1}N_c^x(\rho _{AB_i}),~~~~x\ge 2. \end{aligned}$$
(19)

Proof

From Ref. [24], one has

$$\begin{aligned} N_c^2(|\psi \rangle _{A|B_1\cdots B_{N-1}})\ge \sum _{i=1}^{N-1}N_c^2(\rho _{AB_i}), \end{aligned}$$
(20)

for N-qubit pure state. Applying the similar approach in Ref. [25], one can get

$$\begin{aligned} N_c^x(|\psi \rangle _{A|B_1\cdots B_{N-1}})\ge \sum _{i=1}^{N-1}N_c^x(\rho _{AB_i}), \end{aligned}$$
(21)

for N-qubit pure state with \(x\ge 2\).

Let \(\rho =\sum _ip_i|\psi _i\rangle _{AB_1\cdots B_{N-1}}\langle \psi _i|\) be the optimal decomposition of \(N_c(\rho _{A|B_1\cdots B_{N-1}})\) for the N-qubit mixed state, we have

$$\begin{aligned} N_c^x(\rho _{A|B_1\cdots B_{N-1}})&= \left( \sum _{i=1}p_iN_c(|\psi \rangle _{A|B_1\cdots B_{N-1}})\right) ^x\\ \nonumber&\ge \left( \sum _{i=1}p_i\sqrt{\sum _{k=1}^{N-1}N_c^2(\rho _{AB_k})}\right) ^x\\ \nonumber&\ge \left[ \sum _k\left( \sum _ip_iN_c(\rho _{AB_k})\right) ^2\right] ^\frac{x}{2}\\ \nonumber&\ge \sum _{i=1}^{N-1}N_c^x(\rho _{AB_i}), \end{aligned}$$
(22)

where the first inequality is due to (20). The second inequality is due to Minkowski inequality: \((\sum _k(\sum _ix_{ik}))^\frac{1}{2}\le \sum _i(\sum _kx_{ik}^2)^\frac{1}{2}\). The last inequality is due to \((\sum _ia_i)^\alpha \ge \sum _ia_i^\alpha \) for \(a_i\ge 0,~\alpha \ge 1\). \(\square \)

In the following, we can derive a better monogamy relation for CREN.

Lemma 3

For any N-qubit state \(\rho \in H_A\otimes H_{B_1}\otimes \cdots \otimes H_{B_{N-1}}\), if \(N_c(\rho _{AB_i})\ge N_c(\rho _{A|B_{i+1}\cdots B_{N-1}})\) for \(i=1, 2, \ldots , m\), and \(N_c(\rho _{AB_j})\le N_c(\rho _{A|B_{j+1}\cdots B_{N-1}})\) for \(j=m+1,\ldots ,N-2\), \(\forall \) \(1\le m\le N-3\), \(N\ge 4\), we have

$$\begin{aligned} N^x_c(\rho _{A|B_1B_2\cdots B_{N-1}})&\ge N^x_c(\rho _{AB_1})\\\nonumber&\quad +\,\frac{x}{2} N^x_c(\rho _{AB_2})+\cdots +\left( \frac{x}{2}\right) ^{m-1}N^x_c(\rho _{AB_m})\\\nonumber&\quad +\,\left( \frac{x}{2}\right) ^{m+1}(N^x_c(\rho _{AB_{m+1}}) +\cdots +N^x_c(\rho _{AB_{N-2}}))\\\nonumber&\quad +\,\left( \frac{x}{2}\right) ^{m}N^x_c(\rho _{AB_{N-1}}) \end{aligned}$$
(23)

for all \(x\ge 2\).

Proof

From (19), one has \(N^2_c(\rho _{A|BC})\ge N^2_c(\rho _{AB})+N^2_c(\rho _{AC}).\) If \(N_c(\rho _{AB})\ge N_c(\rho _{AC})\), we have

$$\begin{aligned} N^x_c(\rho _{A|BC})&\ge (N^2_c(\rho _{AB})+N^2_c(\rho _{AC}))^{\frac{x}{2}}=N^x_c(\rho _{AB})\left( 1+\frac{N^2_c(\rho _{AC})}{N^2_c(\rho _{AB})}\right) ^{\frac{x}{2}} \\\nonumber&\ge N^x_c(\rho _{AB})\left[ 1+\frac{x}{2}\left( \frac{N^2_c(\rho _{AC})}{N^2_c(\rho _{AB})}\right) ^{\frac{x}{2}}\right] =N^x_c(\rho _{AB})+\frac{x}{2}N^x_c(\rho _{AC}), \end{aligned}$$
(24)

where the second inequality is due to the inequality \((1+t)^x\ge 1+xt \ge 1+xt^x\) for \(x\ge 1,~0\le t\le 1\).

By using inequality (24) repeatedly, one gets

$$\begin{aligned} N^x_c(\rho _{A|B_1B_2\cdots B_{N-1}})&\ge N^x_c(\rho _{AB_1})+\frac{x}{2}N^x_c(\rho _{A|B_2\cdots B_{N-1}})\\\nonumber&\ge N^x_c(\rho _{AB_1})+\frac{x}{2}N^x_c(\rho _{AB_2}) +\left( \frac{x}{2}\right) ^2N^x_c(\rho _{A|B_3\cdots B_{N-1}})\\\nonumber&\ge \cdots \ge N^x_c(\rho _{AB_1})+\frac{x}{2}N^x_c(\rho _{AB_2}) +\cdots +\left( \frac{x}{2}\right) ^{m-1}N^x_c(\rho _{AB_m})\\\nonumber&\quad +\,\left( \frac{x}{2}\right) ^m N^x_c(\rho _{A|B_{m+1}\cdots B_{N-1}}). \end{aligned}$$
(25)

As \(N_c(\rho _{AB_j})\le N_c(\rho _{A|B_{j+1}\cdots B_{N-1}})\) for \(j=m+1,\ldots ,N-2\), by (24) we get

$$\begin{aligned} N^x_c(\rho _{A|B_{m+1}\cdots B_{N-1}})&\ge \frac{x}{2}N^x_c(\rho _{AB_{m+1}})+N^x_c(\rho _{A|B_{m+2}\cdots B_{N-1}})\nonumber \\&\ge \frac{x}{2}(N^x_c(\rho _{AB_{m+1}})+\cdots +N^x_c(\rho _{AB_{N-2}}))+N^x_c(\rho _{AB_{N-1}}). \end{aligned}$$
(26)

Combining (25) and (26), we have Lemma 3. \(\square \)

We can also derive a bound of \(N_c^x(\rho _{A|B_1B_2\cdots B_{N-1}})\) for \(x<0\).

Lemma 4

For any N-qubit state \(\rho \in H_A\otimes H_{B_1}\otimes \cdots \otimes H_{B_{N-1}}\), we have

$$\begin{aligned} N_c^x(\rho _{A|B_1B_2\cdots B_{N-1}})< M' \left( N_c^x(\rho _{AB_1})+N_c^x(\rho _{AB_2})+\cdots +N_c^x(\rho _{AB_{N-1}})\right) \end{aligned}$$
(27)

for all \(x<0\), where \(M'=\frac{1}{N-1}\).

Proof

For arbitrary tripartite state, from (19) we have

$$\begin{aligned} N^x_c(\rho _{A|B_1B_2})&\le \left( N_c^2(\rho _{AB_1})+N_c^2(\rho _{AB_2})\right) ^{\frac{x}{2}}\\\nonumber&= N_c^x(\rho _{AB_1})\left( 1+\frac{N_c^2(\rho _{AB_2})}{N_c^2(\rho _{AB_1})}\right) ^{\frac{x}{2}}<N_c^x(\rho _{AB_1}), \end{aligned}$$
(28)

where the first inequality is due to \(x<0\) and the second inequality is due to \(\left( 1+\frac{N_c^2(\rho _{AB_2})}{N_c^2(\rho _{AB_1})}\right) ^{\frac{x}{2}}<1.\) On the other hand, we have

$$\begin{aligned} N_c^x(\rho _{A|B_1B_2})&\le \left( N_c^2(\rho _{AB_1})+N_c^2(\rho _{AB_2})\right) ^{\frac{x}{2}}\\\nonumber&= N_c^x(\rho _{AB_2})\left( 1+\frac{N_c^2(\rho _{AB_1})}{N_c^2(\rho _{AB_2})}\right) ^{\frac{x}{2}}<N_c^x(\rho _{AB_2}). \end{aligned}$$
(29)

From (28) and (29) we obtain

$$\begin{aligned} N_c^x(\rho _{A|B_1B_2})< \frac{1}{2}(N_c^x(\rho _{AB_1})+N_c^x(\rho _{AB_2})). \end{aligned}$$
(30)

By using inequality (30) repeatedly, one gets

$$\begin{aligned} N_c^x(\rho _{A|B_1B_2\cdots B_{N-1}})&< \frac{1}{2}\left( N_c^x(\rho _{AB_1})+N_c^x(\rho _{A|B_2\cdots B_{N-1}})\right) \\ \nonumber&<\frac{1}{2}N_c^x(\rho _{AB_1})+\left( \frac{1}{2}\right) ^2N_c^x(\rho _{AB_2}) +\left( \frac{1}{2}\right) ^2N_c^x(\rho _{A|B_3\cdots B_{N-1}})\\ \nonumber&<\cdots < \frac{1}{2}N_c^x(\rho _{AB_1})+\left( \frac{1}{2}\right) ^2N_c^x(\rho _{AB_2})+\cdots \\ \nonumber&\quad +\,\left( \frac{1}{2}\right) ^{N-2}N_c^x(\rho _{AB_{N-2}}) +\left( \frac{1}{2}\right) ^{N-2} N_c^x(\rho _{AB_{N-1}}). \end{aligned}$$
(31)

By cyclically permuting the subindices \(B_1, B_2, \ldots , B_{N-1}\) in (31) we can get a set of inequalities. Summing up these inequalities we obtain (27). \(\square \)

In the following, we study the monogamy property of the CRENOA for N-qubit generalized W-class states (6). We can obtain the following theorem.

Theorem 4

For the N-qubit generalized W-class states \(|\psi \rangle \in H_A\otimes H_{B_1}\otimes \cdots \otimes H_{B_{N-1}}\), with \(\rho _{AB_{j_1}\cdots B_{j_{m-1}}}\) the m-qubit, \(2\le m\le N\), reduced density matrix of \(|\psi \rangle \). If \(N_c(\rho _{AB_{j_i}})\ge N_c(\rho _{AB_{j_{i+1}}\cdots B_{j_{m-1}}})\) for \(i=1,2,\ldots t\), and \(N_c(\rho _{AB{j_k}})\le N_c(\rho _{AB_{j_{k+1}}\cdots B_{j_{m-1}}})\) for \(k=t+1,\ldots ,{m-2}\), \(\forall \) \(1\le t\le {m-3},~m\ge 4\), then the CRENOA satisfies

$$\begin{aligned} N_a^x(\rho _{A|B_{j_1}\cdots B_{j_{m-1}}})&\ge N_a^x(\rho _{AB_{j_1}}) \nonumber \\&\quad +\,\frac{x}{2}N_a^x(\rho _{AB_{j_2}})+\cdots +\left( \frac{x}{2}\right) ^{t-1}N_a^x(\rho _{AB_{j_t}}) \nonumber \\&\quad +\,\left( \frac{x}{2}\right) ^{t+1}\left( N_a^x(\rho _{AB_{j_{t+1}}})+\cdots +N_a^x(\rho _{AB_{j_{m-2}}})\right) \nonumber \\&\quad +\,\left( \frac{x}{2}\right) ^tN_a^x(\rho _{AB_{j_{m-1}}}) \end{aligned}$$
(32)

for all \(x\ge 2\).

Proof

For the N-qubit generalized W-class states \(|\psi \rangle \), according to the definitions of \(N_c(\rho )\) and \(N_a(\rho )\), one has \(N_a(\rho _{A|B_{j_1}\cdots B_{j_{m-1}}})\ge N_c(\rho _{A|B_{j_1}\cdots B_{j_{m-1}}})\). When \(x\ge 2\), we have

$$\begin{aligned} N_a^x(\rho _{A|B_{j_1}\cdots B_{j_{m-1}}})&\ge N_c^x(\rho _{A|B_{j_1}\cdots B_{j_{m-1}}}) \ge N_c^x(\rho _{AB_{j_1}}) \nonumber \\&\quad +\,\frac{x}{2}N_c^x(\rho _{AB_{j_2}})+\cdots +\left( \frac{x}{2}\right) ^{t-1}N_c^x(\rho _{AB_{j_t}}) \nonumber \\&\quad +\,\left( \frac{x}{2}\right) ^{t+1}\left( N_c^x(\rho _{AB_{j_{t+1}}})+\cdots +N_c^x(\rho _{AB_{j_{m-2}}})\right) \nonumber \\&\quad +\,\left( \frac{x}{2}\right) ^t N_c^x(\rho _{AB_{j_{m-1}}})\nonumber \\&=N_a^x(\rho _{AB_{j_1}}) +\frac{x}{2}N_a^x(\rho _{AB_{j_2}})+\cdots +\left( \frac{x}{2}\right) ^{t-1}N_a^x(\rho _{AB_{j_t}}) \nonumber \\&\quad +\,\left( \frac{x}{2}\right) ^{t+1}\left( N_a^x(\rho _{AB_{j_{t+1}}})+\cdots +N_a^x(\rho _{AB_{j_{m-2}}})\right) \nonumber \\&\quad +\,\left( \frac{x}{2}\right) ^tN_a^x(\rho _{AB_{j_{m-1}}}), \end{aligned}$$
(33)

where we have used in the first inequality the relation \(a^x\ge b^x\) for \(a\ge b\ge 0,~x\ge 2\). Using the result of Lemma 3, one gets the second inequality. The equality is due to Lemma 2. \(\square \)

In Theorem 4 we have assumed that some \(N_c(\rho _{AB_{j_i}})\ge N_c(\rho _{AB_{j_{i+1}}\cdots B_{j_{m-1}}})\) and some \(N_c(\rho _{AB_{j_k}})\le N_c(\rho _{AB_{j_{k+1}}\cdots B_{j_{m-1}}})\) for the N-qubit generalized W-class states. If all \(N_c(\rho _{AB_{j_i}})\ge N_c(\rho _{AB_{j_{i+1}}\cdots B_{j_{m-1}}})\) for \(i=1, 2, \ldots , {m-2}\), then we have the following conclusion:

Theorem 5

If \(N_c(\rho _{AB_{j_i}})\ge N_c(\rho _{AB_{j_{i+1}}\cdots B_{j_{m-1}}})\) for \(i=1, 2, \ldots , {m-2}\), we have

$$\begin{aligned} N_a^x(\rho _{A|B_{j_1}\cdots B_{j_{m-1}}})\ge N_a^x(\rho _{AB_{j_1}}) +\frac{x}{2}N_a^x(\rho _{AB_{j_2}})+\cdots +\left( \frac{x}{2}\right) ^{m-2}N_a^x(\rho _{AB_{j_{m-1}}})\nonumber \\ \end{aligned}$$
(34)

for all \(x\ge 2\).

We can also derive a tighter upper bound of \(N_a^y(\rho _{AB_1\cdots B_{N-1}})\) for \(y<0\).

Theorem 6

For the N-qubit generalized W-class states \(|\psi \rangle \in H_A\otimes H_{B_1}\otimes \cdots \otimes H_{B_{N-1}}\) with \(N_c(\rho _{AB_{j_i}})\ne 0\) for \(1\le i\le m-1\), we have

$$\begin{aligned} N_a^y(\rho _{A|B_{j_1}\cdots B_{j_{m-1}}})< \tilde{M} \left( N_a^y(\rho _{AB_{j_1}})+N_a^y(\rho _{AB_{j_2}})+\cdots +N_a^y(\rho _{AB_{j_{m-1}}})\right) \nonumber \\ \end{aligned}$$
(35)

for all \(y<0\), where \(\tilde{M}=\frac{1}{m-1}\).

Proof

For \(y< 0\), we have

$$\begin{aligned} N_a^y(\rho _{A|B_{j_1}\cdots B_{j_{m-1}}})&\le N_c^y(\rho _{A|B_{j_1}\cdots B_{j_{m-1}}}) \nonumber \\&<\tilde{M} \left( N_c^y(\rho _{AB_{j_1}})+N_c^y(\rho _{AB_{j_2}})+\cdots +N_c^y(\rho _{AB_{j_{m-1}}})\right) \nonumber \\&= \tilde{M} \left( N_a^y(\rho _{AB_{j_1}})+N_a^y(\rho _{AB_{j_2}})+\cdots +N_a^y(\rho _{AB_{j_{m-1}}})\right) ,\nonumber \\ \end{aligned}$$
(36)

where we have used in the first inequality the relation \(a^x\le b^x\) for \(a\ge b\ge 0,~x\le 0\). The second inequality is based on Lemma 4. The equality is due to the Lemma 2. \(\square \)

Remark 2

In (35) we have assumed that all \(N_c(\rho _{AB_{j_i}})\), \(i=1,2,\ldots ,m-1\), are nonzero. In fact, if one of them is zero, the inequality still holds if one simply removes this term from the inequality. Namely, if \(N_c(\rho _{AB_{j_i}})=0,\) then one has \(N_a^y(\rho _{A|B_{j_1}\cdots B_{j_{m-1}}})<\frac{1}{2}N_a^y(\rho _{AB_{j_1}})+\cdots +\left( \frac{1}{2}\right) ^{i-1}N_a^y(\rho _{AB_{j_{i-1}}})+\left( \frac{1}{2}\right) ^{i}N_a^y(\rho _{AB_{j_{i+1}}})+\cdots +\left( \frac{1}{2}\right) ^{m-3}N_a^y(\rho _{AB_{j_{m-2}}})+\left( \frac{1}{2}\right) ^{m-3} N_a^y(\rho _{AB_{j_{m-1}}})\). By cyclically permuting the subindices in \(B_{j_1}\cdots B_{j_{m-1}}\), we can get a set of inequalities. Summing up these inequalities we have \(N_a^y(\rho _{A|B_{j_1}\cdots B_{j_{m-1}}})<\frac{1}{m-1}\left( N_a^y(\rho _{AB_{j_1}})+\cdots +N_a^y(\rho _{AB_{j_{i-1}}})+N_a^y(\rho _{AB_{j_{i+1}}})+\cdots +N_a^y(\rho _{AB_{j_{m-2}}})+ N_a^y(\rho _{AB_{j_{m-1}}})\right) \), for \(y<0\).

4 Conclusion

Entanglement monogamy is a fundamental property of multipartite entangled states. We have presented tighter monogamy inequalities for the x-power of concurrence of assistance \(C_a^x(\rho _{A|B_{j_1}\cdots B_{j_{m-1}}})\) of the m-qubit reduced density matrices, \(2\le m \le N\), for the N-qubit generalized W-class states, when \(x\ge 2\). A tighter upper bound of y-power of concurrence of assistance is also derived for \(y<0\). The monogamy relations for the x-power of negativity of assistance for the N-qubit generalized W-class states have been also investigated for \(x\ge 2\) and \(x<0\), respectively. These relations give rise to the restrictions of entanglement distribution among the qubits in generalized W-class states.