1 Introduction

Quantum entanglement [1,2,3,4,5,6] is an essential feature of quantum mechanics that distinguishes the quantum from the classical world. It is one of the fundamental differences between quantum entanglement and classical correlations that a quantum system entangled with one of the other systems limits its entanglement with the remaining others. This restriction of entanglement shareability among multiparty systems is known as the monogamy of entanglement. The monogamy relations give rise to the structures of entanglement in the multipartite setting. For a tripartite system A, B, and C, the monogamy of an entanglement measure \(\varepsilon \) implies that the entanglement between A and BC satisfies \(\varepsilon _{A|BC}\ge \varepsilon _{AB}+ \varepsilon _{AC}\).

In Ref. [7, 8], the monogamy of entanglement for multiqubit W-class states has been investigated, and the monogamy relations for tangle and the squared concurrence have been proved. In this paper, we show the general monogamy relations for the x-power of concurrence of assistance, the entanglement of formation, and the entanglement of assistance for generalized multiqubit W-class states.

2 Monogamy of concurrence of assistance

For a bipartite pure state \(|\psi \rangle _{AB}\) in vector space \(H_A\otimes H_{B}\), the concurrence is given by [9,10,11]

$$\begin{aligned} C\left( |\psi \rangle _{AB}\right) =\sqrt{2\left[ 1-\hbox {Tr}\left( \rho ^2_A\right) \right] }, \end{aligned}$$
(1)

where \(\rho _A\) is reduced density matrix by tracing over the subsystem B, \(\rho _{A}=\hbox {Tr}_{B}(|\psi \rangle _{AB}\langle \psi |)\). The concurrence is extended to mixed states \(\rho =\sum _{i}p_{i}|\psi _{i}\rangle \langle \psi _{i}|\), \(p_{i}\ge 0\), \(\sum _{i}p_{i}=1\), by the convex roof construction,

$$\begin{aligned} C\left( \rho _{AB}\right) =\min _{\{p_i,|\psi _i\rangle \}} \sum _i p_i C\left( |\psi _i\rangle \right) , \end{aligned}$$
(2)

where the minimum is taken over all possible pure-state decompositions of \(\rho _{AB}\).

For a tripartite state \(|\psi \rangle _{ABC}\), the concurrence of assistance (CoA) is defined by [12]

$$\begin{aligned} C_a\left( |\psi \rangle _{ABC}\right) \equiv C_a\left( \rho _{AB}\right) =\max _{\{p_i,|\psi _i\rangle \}}\sum _ip_iC\left( |\psi _i\rangle \right) , \end{aligned}$$
(3)

for all possible ensemble realizations of \(\rho _{AB}=\hbox {Tr}_{C}(|\psi \rangle _{ABC}\langle \psi |)=\sum _i p_i |\psi _i\rangle _{AB} \langle \psi _i|\). When \(\rho _{AB}=|\psi \rangle _{AB}\langle \psi |\) is a pure state, then one has \(C(|\psi \rangle _{AB})=C_{a}(\rho _{AB})\).

For an N-qubit state \(|\psi \rangle _{AB_1\ldots B_{N-1}}\in H_A\otimes H_{B_1}\otimes \ldots \otimes H_{B_{N-1}}\), the concurrence \(C(|\psi \rangle _{A|B_1\ldots B_{N-1}})\) of the state \(|\psi \rangle _{A|B_1\ldots B_{N-1}}\), viewed as a bipartite with partitions A and \(B_1B_2\ldots B_{N-1}\), satisfies the following inequality [13]

$$\begin{aligned} C^\alpha _{A|B_1B_2\ldots B_{N-1}}\ge C^\alpha _{AB_1}+C^\alpha _{AB_2}+\cdots +C^\alpha _{AB_{N-1}}, \end{aligned}$$
(4)

and

$$\begin{aligned} C^\beta _{A|B_1B_2\ldots B_{N-1}}< C^\beta _{AB_1}+C^\beta _{AB_2}+\cdots +C^\beta _{AB_{N-1}}, \end{aligned}$$
(5)

where \(\alpha \ge 2\), \(\beta \le 0\), \(C_{AB_i}=C(\rho _{AB_i})\) is the concurrence of \(\rho _{AB_i}=\hbox {Tr}_{B_1\ldots B_{i-1}B_{i+1}\ldots B_{N-1}}(\rho )\), \(C_{A|B_1B_2\ldots B_{N-1}}=C(|\psi \rangle _{A|B_1\ldots B_{N-1}})\). Due to the monogamy of concurrence, the generalized monogamy relation based on the concurrence of assistance has been proved in Ref. [14],

$$\begin{aligned} C^2\left( |\psi \rangle _{A|B_1\ldots B_{N-1}}\right) \le \sum _{i=1}^{N-1}C^2_a\left( \rho _{AB_i}\right) . \end{aligned}$$
(6)

In the following, we study the monogamy property of the concurrence of assistance for the n-qubit generalized W-class states \(|\psi \rangle \in H_{A_1}\otimes H_{A_2}\otimes \cdots \otimes H_{A_n}\) defined by

$$\begin{aligned} |\psi \rangle =a|000\ldots \rangle +b_1|01\ldots 0\rangle +\cdots +b_n|00\ldots 1\rangle , \end{aligned}$$
(7)

with \(|a|^2+\sum _{i=1}^{n}|b_i|^2=1\).

Lemma 1

For n-qubit generalized W-class states (7), we have

$$\begin{aligned} C\left( \rho _{A_1A_i}\right) =C_a\left( \rho _{A_1A_i}\right) , \end{aligned}$$
(8)

where \(\rho _{A_1A_i}=\mathrm{Tr}_{A_2\ldots A_{i-1}A_{i+1}\ldots A_{n}}(|\psi \rangle \langle \psi |)\).

Proof

It is direct to verify that [7], \(\rho _{A_1A_i}=|x\rangle _{A_1A_i}\langle x|+|y\rangle _{A_1A_i}\langle y|\), where

$$\begin{aligned} |x\rangle _{A_1A_{i}}= & {} a|00\rangle _{A_1A_{i}} +b_1|10\rangle _{A_1A_{i}}+b_i|01\rangle _{A_1A_{i}},\\ |y\rangle _{A_1A_{i}}= & {} \sqrt{\sum _{k\ne i}|b_k|^2}|00\rangle _{A_1A_{i}}. \end{aligned}$$

From the Hughston–Jozsa–Wootters theorem Ref. [7], for any pure-state decomposition of \(\rho _{A_1A_{i}}=\sum _{h=1}^{r}|\phi _h\rangle _{A_1A_{i}}\langle \phi _h|\), one has \(|\phi _h\rangle _{A_1A_{i}} =u_{h1}|x\rangle _{A_1A_{i}}+u_{h2}|y\rangle _{A_1A_{i}}\) for some \(r\times r\) unitary matrices \(u_{h1}\) and \(u_{h2}\) for each h. Consider the normalized state \(|\tilde{\phi _h}\rangle _{A_1A_{i}}=|\phi _h\rangle _{A_1A_{i}}/\sqrt{p_h}\) with \(p_h=|\langle \phi _h|\phi _h\rangle |\). One has the concurrence of each two-qubit pure \(|\tilde{\phi _h}\rangle _{A_1A_{i}}\),

$$\begin{aligned} C^2\left( |\tilde{\phi _h}\rangle _{A_1A_{i}}\right) =\frac{4}{p_h^2}|u_{hi}|^4|b_1|^2|b_i|^2. \end{aligned}$$

Then for the two-qubit state \(\rho _{A_1A_{i}}\), we have

$$\begin{aligned} \sum _hp_hC\left( |\tilde{\phi _h}\rangle _{A_1A_{i}}\right) =\sum _hp_h\frac{2}{p_h}|u_{hi}|^2|b_1||b_i| =2|b_1||b_i|. \end{aligned}$$

Thus, we obtain

$$\begin{aligned} C(\rho _{A_1A_i})= & {} \min _{p_h,|\tilde{\phi _h}\rangle _{A_1A_{i}}} \sum _hp_hC\left( |\tilde{\phi _h}\rangle _{A_1A_{i}}\right) \\= & {} \max _{p_h,|\tilde{\phi _h}\rangle _{A_1A_{i}}} \sum _hp_hC\left( |\tilde{\phi _h}\rangle _{A_1A_{i}}\right) \\= & {} C_a\left( \rho _{A_1A_i}\right) . \end{aligned}$$

\(\square \)

Specifically, in Ref. [8], the same result \(C(\rho _{A_1A_i})=C_a(\rho _{A_1A_i})\) has been proved for the generalized W-class states (7) with \(a=0\).

Theorem 1

For the n-qubit generalized W-class states \(|\psi \rangle \in H_{A_1}\otimes H_{A_2}\otimes \cdots \otimes H_{A_n}\), the concurrence of assistance satisfies

$$\begin{aligned} C_a^x\left( \rho _{A_1|A_{j_1}\ldots A_{j_{m-1}}}\right) \ge \sum _{i=1}^{{m-1}}C^x_a\left( \rho _{A_1A_{j_i}}\right) , \end{aligned}$$
(9)

where \(x\ge 2\) and \(\rho _{A_1A_{j_1}\ldots A_{j_{m-1}}}\) is the m-qubit, \(2\le m\le n\), reduced density matrix of \(|\psi \rangle \).

Proof

For the n-qubit generalized W-class state \(|\psi \rangle \), according to the definitions of \(C(\rho )\) and \(C_a(\rho )\), one has \(C_a(\rho _{A_1|A_{j_1}\ldots A_{j_{m-1}}})\ge C(\rho _{A_1|A_{j_1}\ldots A_{j_{m-1}}})\). When \(x\ge 2\), we have

$$\begin{aligned} C^x_a\left( \rho _{A_1|A_{j_1}\ldots A_{j_{m-1}}}\right)\ge & {} C^x\left( \rho _{A_1|A_{j_1}\ldots A_{j_{m-1}}}\right) \\\ge & {} \sum _{i=1}^{m-1}C^x\left( \rho _{A_1A_{j_i}}\right) \\= & {} \sum _{i=1}^{m-1}C^x_a\left( \rho _{A_1A_{j_i}}\right) . \end{aligned}$$

Here, we have used in the first inequality the relation \(a^x\ge b^x\) for \(a\ge b>0\) and \(x\ge 0\). The second inequality is due to the monogamy of concurrence (4). The last inequality is due to the Lemma 1. \(\square \)

Theorem 2

For the n-qubit generalized W-class state \(|\psi \rangle \in H_{A_1}\otimes H_{A_2}\otimes \cdots \otimes H_{A_n}\) with \(C(\rho _{A1A_{j_i}})\ne 0\) for \(1\le i\le m-1\), we have

$$\begin{aligned} C_a^y\left( \rho _{A_1|A_{j_1}\ldots A_{j_{m-1}}}\right) <\sum _{i=1}^{{m-1}}C^y_a\left( \rho _{A_1A_{j_i}}\right) , \end{aligned}$$
(10)

where \(y\le 0\) and \(\rho _{A_1A_{j_1}\ldots A_{j_{m-1}}}\) is the m-qubit reduced density matrix as in Theorem 1.

Proof

For \(y\le 0\), we have

$$\begin{aligned} C^y_a\left( \rho _{A_1|A_{j_1}\ldots A_{j_{m-1}}}\right)\le & {} C^y\left( \rho _{A_1|A_{j_1}\ldots A_{j_{m-1}}}\right) \\< & {} \sum _{i=1}^{m-1}C^y\left( \rho _{A_1A_{j_i}}\right) \\= & {} \sum _{i=1}^{m-1}C^y_a\left( \rho _{A_1A_{j_i}}\right) . \end{aligned}$$

We have used in the first inequality the relation \(a^x\le b^x\) for \(a\ge b>0\) and \(x\le 0\). The seconder inequality is due to the monogamy of concurrence (5). The last inequality is due to Lemma 1.

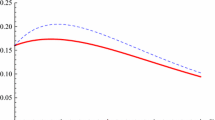
According to (9) and (10), we can also obtain the lower bounds of \(C_a(\rho _{A_1|A_{j_1}\ldots A_{j_{m-1}}})\). As an example, consider the 5-qubit generalized W-class states (7) with \(a=b_2=\frac{1}{\sqrt{10}}\), \(b_1=\frac{1}{\sqrt{15}}\), \(b_3=\sqrt{\frac{2}{15}}\), \(b_4=\sqrt{\frac{3}{5}}\). We have

$$\begin{aligned} C_a\left( \rho _{A_1|A_{2}A_{3}}\right) \ge \frac{2}{\sqrt{15}}\root x \of {\left( \frac{1}{\sqrt{10}}\right) ^x +\left( \sqrt{\frac{2}{15}}\right) ^x} \end{aligned}$$

and

$$\begin{aligned} C_a\left( \rho _{A_1|A_{2}A_{3}A_{4}}\right) \ge \frac{2}{\sqrt{15}}\root x \of {\left( \frac{1}{\sqrt{10}}\right) ^x +\left( \sqrt{\frac{2}{15}}\right) ^x+\left( \sqrt{\frac{3}{5}}\right) ^x} \end{aligned}$$

with \(x\ge 2\). The optimal lower bounds can be obtained by varying the parameter x, see Fig. 1, where for comparison the upper bounds are also presented by using the formula \(C_a(\rho _{AB})\le \sqrt{2(1-\hbox {Tr}(\rho _{A}^2))}\) [15], namely \(C_a(\rho _{A_1|A_{2}A_{3}})\le \frac{2}{\sqrt{18}}\) and \(C_a(\rho _{A_1|A_{2}A_{3}A_{4}}) \le \frac{2}{\sqrt{18}}\). From Fig. 1, one gets that the optimal lower bounds of \(C_a(\rho _{A_1|A_2A_3})\) and \(C_a(\rho _{A_1|A_2A_3A_4})\) are 0.249 and 0.471, respectively, attained at \(x=2\). \(\square \)

Fig. 1
figure 1

Solid line is the lower bound of \(C_a(\rho _{A_1|A_2A_3})\), dashed line is the lower bound of \(C_a(\rho _{A_1|A_2A_3A_4})\) as functions of \(x\ge 2\), and dotted line is the upper bound of \(C_a(\rho _{A_1|A_2A_3})\) and \(C_a(\rho _{A_1|A_2A_3A_4})\)

Full size image

3 Monogamy of entanglement of formation

The entanglement of formation of a pure state \(|\psi \rangle \in H_A\otimes H_B\) is defined by

$$\begin{aligned} E\left( |\psi \rangle \right) =S\left( \rho _A\right) , \end{aligned}$$
(11)

where \(\rho _A=\hbox {Tr}_{B}(|\psi \rangle \langle \psi |)\) and \(S(\rho )=\hbox {Tr}(\rho \log _2\rho )\). For a bipartite mixed state \(\rho _{AB}\in H_A\otimes H_B\), the entanglement of formation is given by

$$\begin{aligned} E\left( \rho _{AB}\right) =\min _{\{p_i,|\psi _i\rangle \}}\sum _ip_iE\left( |\psi _i\rangle \right) , \end{aligned}$$
(12)

with the infimum taking over all possible decompositions of \(\rho _{AB}\) in a mixture of pure states \(\rho _{AB}=\sum _ip_i|\psi _i\rangle \langle \psi _i|\), where \(p_i\ge 0\) and \(\sum _ip_i=1\).

It has been shown that the entanglement of formation does not satisfy the inequality \(E_{AB}+E_{AC}\le E_{A|BC}\) [16]. Rather it satisfies [13],

$$\begin{aligned} E^\alpha _{A|B_1B_2\ldots B_{N-1}}\ge E_{AB_1}^\alpha +E_{AB_2}^\alpha +\cdots +E^\alpha _{AB_{N-1}}, \end{aligned}$$
(13)

where \(\alpha \ge \sqrt{2}.\)

The corresponding entanglement of assistance (EoA) [17] is defined in terms of the entropy of entanglement [18] for a tripartite pure state \(|\psi \rangle _{ABC}\),

$$\begin{aligned} E_a\left( |\psi \rangle _{ABC}\right) \equiv E_a\left( \rho _{AB}\right) =\max _{\{p_i,|\psi _i\rangle \}}\sum _ip_iE\left( |\psi _i\rangle \right) , \end{aligned}$$
(14)

which is maximized over all possible decompositions of \(\rho _{AB}=\hbox {Tr}_{C}(|\psi \rangle _{ABC})=\sum _ip_i|\psi _i\rangle \langle \psi _i|\), with \(p_i\ge 0\) and \(\sum _ip_i=1\). For any N-qubit pure state \(|\psi \rangle \in H_A \otimes H_{B_1}\otimes \cdots \otimes H_{B_{N-1}}\), it has been shown that the entanglement of assistance satisfies [13],

$$\begin{aligned} E\left( |\psi \rangle _{A|B_1B_2\ldots B_{N-1}}\right) \le \sum _{i=1}^{N-1}E_a\left( \rho _{AB_i}\right) . \end{aligned}$$
(15)

In fact, generally we can prove the following results for the n-qubit generalized W-class states about the entanglement of formation and the entanglement of assistance.

Theorem 3

For the n-qubit generalized W-class states \(|\psi \rangle \in H_{A_1}\otimes H_{A_2}\otimes \cdots \otimes H_{A_n}\), we have

$$\begin{aligned} E\left( |\psi \rangle _{A_1|A_2\ldots A_{n}}\right) \le \sum _{i=2}^{{n}}E\left( \rho _{A_1A_{i}}\right) , \end{aligned}$$
(16)

where \(\rho _{A_1A_i}\), \(2\le i\le n\) is the 2-qubit reduced density matrix of \(|\psi \rangle \).

Proof

For the n-qubit generalized W-class states \(|\psi \rangle \), we have

$$\begin{aligned} E\left( |\psi \rangle _{A_1|A_2\ldots A_{n}}\right)= & {} f\left( C^2\left( |\psi \rangle _{A_1|A_2\ldots A_{n}}\right) \right) \\= & {} f\left( \sum _{i=2}^{n}C^2\left( \rho _{A_1A_{i}}\right) \right) \\\le & {} \sum _{i=2}^{n}f\left( C^2\left( \rho _{A_1A_{i}}\right) \right) \\= & {} \sum _{i=2}^{n}E\left( \rho _{A_1A_{i}}\right) , \end{aligned}$$

where for simplify, we have denoted \(f(x)=h\left( \frac{1+\sqrt{1-x}}{2}\right) \) with \(h(x)=-x\log _2(x)-(1-x)\log _2(1-x).\) We have used in the first and last equalities that the entanglement of formation obeys the relation \(E(\rho )=f(C^2(\rho ))\) for a bipartite \(2\otimes D\), \(D\ge 2\), quantum state \(\rho \) [19]. The second inequality is due to the fact that \(C^2(|\psi \rangle _{A_1\ldots A_{n}})=\sum _{i=2}^{n}C^2(\rho _{A_1A_{i}}).\) The inequality is due to the fact \(f(x+y)\le f(x)+f(y)\). \(\square \)

As for the entanglement of assistance, we have the following conclusion.

Theorem 4

For the n-qubit generalized W-class states \(|\psi \rangle \in H_{A_1}\otimes H_{A_2}\otimes \cdots \otimes H_{A_n}\), we have

$$\begin{aligned} E\left( \rho _{A_1|A_{j_1}\ldots A_{j_{m-1}}}\right) \le \sum _{i=1}^{{m-1}}E_a\left( \rho _{A_1A_{j_i}}\right) , \end{aligned}$$
(17)

where \(\rho _{A_1|A_{j_1}\ldots A_{j_{m-1}}}\) is the m-qubit reduced density matrix of \(|\psi \rangle \), \(2\le m\le n\).

Proof

From the Lemma 2 of Ref. [7], one has \(\rho _{A_1|A_{j_1}\ldots A_{j_{m-1}}}\) of \(|\psi \rangle \) is a mixture of a generalized W class state and vacuum. Then, we have

$$\begin{aligned} E\left( \rho _{A_1|A_{j_1}\ldots A_{j_{m-1}}}\right)\le & {} \sum _hp_hE\left( |\psi \rangle ^h_{A_1|A_{j_1}\ldots A_{j_{m-1}}}\right) \\\le & {} \sum _hp_h\sum _{i=1}^{m-1}E\left( \rho ^h_{A_1A_{j_i}}\right) \\= & {} \sum _{i=1}^{m-1}\left[ \sum _hp_hE\left( \rho ^h_{A_1A_{j_i}}\right) \right] \\\le & {} \sum _{i=1}^{m-1}\left[ \sum _hp_h\left( \sum _jq_jE\left( |\psi _j\rangle ^h_{A_1A_{j_i}}\langle \psi _j|\right) \right) \right] \\= & {} \sum _{i=1}^{m-1}\sum _{hj} p_hq_jE\left( |\psi _j\rangle ^h_{A_1A_{j_i}}\langle \psi _j|\right) . \end{aligned}$$

We obtain the first inequality by noting that \(|\psi \rangle ^h_{A_1|A_{j_1}\ldots A_{j_{m-1}}}\) is a generalized W class state or vacuum [7]. When \(|\psi \rangle ^h_{A_1|A_{j_1}\ldots A_{j_{m-1}}}\) is a generalized W class state, then we have \(E(|\psi \rangle ^h_{A_1|A_{j_1}\ldots A_{j_{m-1}}})\le \sum _{i=1}^{m-1}E(\rho ^h_{A_1A_{j_i}})\); When \(|\psi \rangle ^h_{A_1|A_{j_1}\ldots A_{j_{m-1}}}\) is a vacuum, then we have \(E(|\psi \rangle ^h_{A_1|A_{j_1}\ldots A_{j_{m-1}}})=0\le \sum _{i=1}^{m-1}E(\rho ^h_{A_1A_{j_i}})\). The second inequality is due to the definition of the entanglement of formation (12) for mixed quantum states. Since \(\sum _{hj}p_hq_j=1\) and \(\sum _{hj} p_hq_j|\psi _j\rangle ^h_{A_1A_{j_i}}\langle \psi _j|\) is a pure decomposition of \(\rho _{A_1A_{j_i}}\), we have (17). \(\square \)

4 Conclusions and remarks

Entanglement monogamy is a fundamental property of multipartite entangled states. We have shown the monogamy for the x-power of concurrence of assistance \(C_a(\rho _{A_1|A_{j_i}\ldots A_{j_{m-1}}})\) of the m-qubit reduced density matrices, \(2\le m\le n\), for the n-qubit generalized W-class states. The monogamy relations for the entanglement of formation and the entanglement of assistance the monogamy relation for the n-qubit generalized W-class states have been also investigated. These relations give rise to the restrictions of entanglement distribution among the qubits in generalized W-class states.