Tighter Monogamy Relations for the Tsallis-q and Rényi-α Entanglement in Multiqubit Systems

Abstract

Monogamy relations characterize the distributions of quantum entanglement in multipartite systems. In this work, we present some tighter monogamy relations in terms of the power of the Tsallis-q and Rényi-α entanglement in multipartite systems. We show that these new monogamy relations of multipartite entanglement with tighter lower bounds than the existing ones. Furthermore, three examples are given to illustrate the tightness.

1 Introduction

Quantum entanglement is an essential feature in terms of quantum mechanics, which distinguishes quantum mechanics from the classical world and plays a very important role in communication, cryptography, and computing. A key property of quantum entanglement is the monogamy relations [1, 2], which is a quantum systems entanglement with one of the other subsystems limits its entanglement with the remaining ones, known as the monogamy of entanglement (MoE) [2, 3]. For any tripartite quantum state ρ_A∣BC, MoE can be expressed as the following inequality $\mathcal {E}(\rho _{A|BC})\geq \mathcal {E}(\rho _{AB})+\mathcal {E}(\rho _{AC})$, where ρ_AB = tr_C(ρ_A|BC), ρ_AC = tr_B(ρ_A|BC), and $\mathcal {E}$ is an quantum entanglement measure. Furthermore, Coffman, Kundu and Wootters expressed that the squared concurrence also satisfies the monogamy relations in multiqubit states [1]. Later the monogamy relations are widely promoted to other entanglement measures such as entanglement of formation [4], entanglement negativity [5], the Tsallis-q and Rényi-α entanglement [6, 7]. These monogamy relations will help us to have a further understanding of the quantum information theory [8], even black-hole physics [9] and condensed-matter physics [10]. In [11, 12], the authors prove that the η th power of Tsallis-q entanglement satisfies monogamy relations for 2 ≤ q ≤ 3, the power η ≥ 1, the Rényi-α entanglement also satisfies monogamy relations for α ≥ 2, the power η ≥ 1, and $2>\alpha \geq \frac {\sqrt {7}-1}{2}$, the power η ≥ 2.

Our paper is organized as follows. In Section 2, we review some basic preliminaries of concurrence, Tsallis-q, and Rényi-α entanglement. In Section 3, we develop a class of monogamy relations in terms of the Tsallis-q entanglement, they are tighter than the results in [11]. In Section 4, we explore a class of monogamy relations based on the Rényi-α entanglement which are tighter than the results in [12]. In Section 5, we summarize our results.

2 Basic Preliminaries

We first recall the definition of concurrence. For a bipartite pure state |φ〉_AB, the concurrence can be defined as [13,14,15]

$$C(|\varphi\rangle_{AB})=\sqrt{2(1-tr{{\rho}_{A}^{2}})},$$

(1)

where ρ_A = tr_B(|φ〉_AB〈φ|).

For any mixed state ρ_AB, its concurrence is defined via the convex-roof extension in [16]

$$C(\rho_{AB})=min\sum\limits_{j} p_{j} C(|\varphi_{j}\rangle_{AB}),$$

(2)

where the minimum is taken over all possible pure state decompositions of $\rho _{AB}= \sum \limits _{j}p_{j}| \varphi _{j}\rangle _{AB}\langle \varphi _{j}|$, and $\sum \limits _{j}p_{j}=1$.

It has been proved that the concurrence $C(\rho _{A|B_{1}{\cdots } B_{N-1}})$ of mixed state $\rho _{A| B_{1}{\cdots } B_{N-1}}$ has an important property such that [17]

$$C^{2}(\rho_{A|B_{1}{\cdots} B_{N-1}})\geq C^{2}(\rho_{A|B_{1}})+C^{2}(\rho_{A|B_{2}{\cdots} B_{N-1}})\geq {\cdots} \geq\sum\limits_{i=1}^{N-1} C^{2}(\rho_{A|B_{i}}),$$

(3)

where $\rho _{A|B_{i}}=\text {tr}_{B_{1}{\cdots } B_{i-1}B_{i+1}{\cdots } B_{N-1}}(\rho _{A|B_{1}{\cdots } B_{N-1}})$.

Quantum entanglement plays an important role in quantum information. Another well-known quantum entanglements are Tsallis-q entanglement and Rényi-α entanglement. For any bipartite pure state |φ〉_AB, the Tsallis-q entanglement is defined as [18].

$$T_{q}(|\varphi\rangle_{AB})=S_{q}(\rho_{A})=\frac{1}{q-1}(1-tr{\rho_{A}^{q}}),$$

(4)

where q ≥ 0, q≠ 1, and ρ_A = tr_B(|φ〉_AB〈φ|). When q tends to 1, the Tsallis-q entropy converges to the von Neumann entropy.

For a mixed state ρ_AB, the Tsallis-q entanglement is defined by its convex-roof extension, which can be expressed as

$$T_{q}{(\rho_{AB})}=min \sum\limits_{i} p_{i} T_{q}(|\varphi_{i}\rangle_{AB}),$$

(5)

where the minimum is taken over all possible pure state decomposition of $\rho _{AB}= \sum \limits _{i}p_{i}| \varphi _{i}\rangle _{AB}\langle \varphi _{i}|$.

When $\frac {5-\sqrt {13}}{2}\leq q\leq \frac {5+\sqrt {13}}{2}$, for any bipartite pure state |φ〉_AB, it has been explored that the Tsallis-q entanglement T_q(|φ〉_AB) has an analytical formula [19],

$$T_{q}(|\varphi\rangle_{AB})=g_{q}(C^{2}(|\varphi\rangle_{AB})),$$

(6)

where the function g_q(x) is defined as

$$g_{q}(x)=\frac{1}{q-1}\left[1-\left( \frac{1+\sqrt{1-x}}{2}\right)^{q} -\left( \frac{1-\sqrt{1-x}}{2}\right)^{q}\right],$$

(7)

for 0 ≤ x ≤ 1, and g_q(x) is an increasing monotonic and convex function in [20]. Specially, for 2 ≤ q ≤ 3, the function g_q(x) has an important property [18]

$$g_{q}({x^{2}+y^{2}})\geq g_{q}(x^{2})+g_{q}(y^{2}).$$

(8)

When $\frac {5-\sqrt {13}}{2}\leq q\leq \frac {5+\sqrt {13}}{2}$, for any two-qubit mixed state ρ, the Tsallis-q entanglement can be expressed as T_q(ρ) = g_q(C²(ρ)) [20].

Now, we recall some preliminaries of the Rényi-α entanglement. For a bipartite pure state |φ〉_AB, the Rényi-α entanglement can be defined as [21]

$$E_{\alpha}(|\varphi\rangle_{AB})=\frac{1}{1-{\alpha}}log_{2}(tr{\rho}_{A}^{\alpha}),$$

(9)

where α > 0, and α≠ 1, ρ_A = tr_B(|φ〉_AB〈φ|). When α tends to 1, the Rényi-α entropy converges to the von Neumann entropy.

For a bipartite mixed state ρ_AB, the Rényi-α entanglement can be defined as

$$E_{\alpha}(\rho_{AB})=min\sum\limits_{i} p_{i} E_{\alpha}(|\varphi_{i}\rangle_{AB}),$$

(10)

where the minimum is taken over all possible pure state decompositions $\{p_{i},\varphi _{AB}^{i}\}$ of ρ_AB.

When $\alpha \geq \frac {\sqrt {7}-1}{2}$, for any two-qubit state ρ_AB, the Rényi-α entanglement has an analytical formula [21, 22]

$$E_{\alpha}(\rho_{AB})=f_{\alpha}(C(\rho_{AB})),$$

(11)

where f_α(x) can be expressed as

$$f_{\alpha}(x)=\frac{1}{1-\alpha}log_{2}\bigg[\bigg(\frac{1-\sqrt{1-x^{2}}}{2}\bigg)^{\alpha}+\bigg(\frac{1+\sqrt{1-x^{2}}}{2}\bigg)^{\alpha}\bigg],$$

(12)

0 ≤ x ≤ 1, and f_α(x) is a monotonically increasing convexity function.

For α ≥ 2, the function f_α(x) satisfies the following inequality [22],

$$f_{\alpha}\left( \sqrt{x^{2}+y^{2}}\right)\geq f_{\alpha}(x)+f_{\alpha}(y).$$

(13)

For $\frac {\sqrt {7}-1}{2}\leq \alpha <2$, the function f_α(x) has an important property such that [23]

$${f}_{\alpha}^{2}\left( \sqrt{x^{2}+y^{2}}\right)\geq {f}_{\alpha}^{2}(x)+ {f}_{\alpha}^{2}(y).$$

(14)

3 Tighter Monogamy Relations in Terms of the Tsallis-q Entanglement

To present the tighter monogamy relations of the Tsallis-q entanglement in multipartite systems, we introduce three lemmas as follows.

Lemma 1

For 0 ≤ x ≤ 1 and μ ≥ 1, we have

$$\begin{array}{@{}rcl@{}} (1+x)^{\mu}&\geq& 1+\frac{\mu^{2}}{\mu+1}x+\left( 2^{\mu}-\frac{\mu^{2}}{\mu+1}-1\right)x^{\mu} \\ &\geq& 1+\frac{\mu}{2}x+\left( 2^{\mu}-\frac{\mu}{2}-1\right)x^{\mu}\geq1+(2^{\mu}-1)x^{\mu}. \end{array}$$

(15)

Proof

If x = 0, then the inequality is trivial. Otherwise, let $f(\mu ,x)=\frac {(1+x)^{\mu }-\frac {\mu ^{2}}{\mu +1}x-1}{x^{\mu }}$, then, $\frac {\partial f}{\partial x}=\frac {\mu x^{\mu -1}\left [1+\frac {\mu (\mu -1)}{\mu +1}x-(1+x)^{\mu -1}\right ]}{x^{2\mu }}$. When μ ≥ 1 and 0 ≤ x ≤ 1, it is obvious that $1+\frac {\mu (\mu -1)}{\mu +1}x\leq (1+x)^{\mu -1}$. Thus, $\frac {\partial f}{\partial x}\leq 0$, and f(μ,x) is a decreasing function of x, i.e. $f(\mu ,x)\geq f(\mu ,1)=2^{\mu }-\frac {\mu ^{2}}{\mu +1}-1$. Consequently, we have $(1+x)^{\mu }\geq 1+\frac {\mu ^{2}}{\mu +1}x+\left (2^{\mu }-\frac {\mu ^{2}}{\mu +1}-1\right )x^{\mu }$. Since $\frac {\mu ^{2}}{\mu +1}\geq \frac {\mu }{2}$, for 0 ≤ x ≤ 1 and μ ≥ 1, one gets $1+\frac {\mu ^{2}}{\mu +1}x+\left (2^{\mu }-\frac {\mu ^{2}}{\mu +1}-1\right )x^{\mu }=1+ \frac {\mu ^{2}}{\mu +1}(x-x^{\mu })+(2^{\mu }-1)x^{\mu }\geq 1+\frac {\mu }{2} x+\left (2^{\mu }-\frac {\mu }{2}-1\right )x^{\mu }=1+\frac {\mu }{2}(x-x^{\mu })+(2^{\mu }-1)x^{\mu }\geq 1+(2^{\mu }-1)x^{\mu }$.

Lemma 2

For any 2 ≤ q ≤ 3, μ ≥ 1, g_q(x) defined on the domain D = {(x,y)|0 ≤ x,y ≤ 1}, if x ≥ y, then we have

$$g_{q}^{\mu}({x^{2}+y^{2}}) \geq g_{q}^{\mu}(x^{2})+\frac{\mu^{2}}{\mu+1}g_{q}^{{\mu}-1}(x^{2})g_{q}(y^{2})+\left( 2^{\mu}-\frac{\mu^{2}}{\mu+1}-1\right)g_{q}^{\mu}(y^{2}).$$

(16)

Proof

For 2 ≤ q ≤ 3, μ ≥ 1, according to inequality (8), we have

$$\begin{array}{@{}rcl@{}} g_{q}^{\mu}(x^{2}+y^{2})&\geq& (g_{q}(x^{2})+g_{q}(y^{2}))^{\mu}\\ &=&{g}_{q}^{\mu}(x^{2})(1+\frac{g_{q}(y^{2})}{g_{q}(x^{2})})^{\mu}\\ &\geq& {g}_{q}^{\mu}(x^{2})+\frac{\mu^{2}}{\mu+1}g_{q}^{{\mu}-1}(x^{2})g_{q}(y^{2})+(2^{\mu}-\frac{\mu^{2}}{\mu+1}-1)g_{q}^{\mu}(y^{2}), \end{array}$$

(17)

where the first inequality is due to inequality (8) and the second inequality is due to Lemma 1.

Lemma 3

For any N-qubit mixed state $\rho _{A|B_{1}{\cdots } B_{N-1}}$, we have

$$T_{q}{(\rho_{A|B_{1}{\cdots} B_{N-1}})}\geq g_{q}(C^{2}(\rho_{A|B_{1}{\cdots} B_{N-1}})).$$

(18)

Proof

Suppose that $\rho _{A|B_{1}{\cdots } B_{N-1}}=\sum \limits _{i} p_{i} |\varphi _{i}\rangle _{A|B_{1}{\cdots } B_{N-1}}$ is the optimal decomposition for $T_{q}{(\rho _{A|B_{1}{\cdots } B_{N-1}})}$, then we have

$$\begin{array}{@{}rcl@{}} T_{q}{(\rho_{A|B_{1}{\cdots} B_{N-1}})} & =& \sum\limits_{i} p_{i} T_{q}(|\varphi_{i}\rangle_{A|B_{1}{\cdots} B_{N-1}})\\ & =& \sum\limits_{i} p_{i} g_{q}(C^{2}(|\varphi_{i}\rangle_{A|B_{1}{\cdots} B_{N-1}}))\\ &\geq& g_{q} (\sum\limits_{i} p_{i} C^{2}(|\varphi_{i}\rangle_{A|B_{1}{\cdots} B_{N-1}}))\\ &\geq& g_{q} ((\sum\limits_{i} p_{i} C(|\varphi_{i}\rangle_{A|B_{1}{\cdots} B_{N-1}}))^{2})\\ &\geq& g_{q}(C^{2}(\rho_{A|B_{1}{\cdots} B_{N-1}})), \end{array}$$

(19)

where the first inequality is due to that g_q(x) is a convex function, the second inequality is due to the Cauchy-Schwarz inequality: $(\sum \limits _{i}{a_{i}^{2}})(\sum \limits _{i}{b_{i}^{2}})\geq (\sum \limits _{i}a_{i}b_{i})^{2}$, with $a_{i}=\sqrt {p_{i}}$, and $b_{i}=\sqrt {p_{i}}C(|\varphi _{i}\rangle _{A|B_{1}{\cdots } B_{N-1}})$, and the third inequality is due to the minimum property of $C(\rho _{A|B_{1}{\cdots } B_{N-1}})$.

Now, we give the following theorems of the monogamy inequalities in terms of the Tsallis-q entanglement.

Theorem 1

For any 2 ≤ q ≤ 3, the power η ≥ 1, and N-qubit mixed state $\rho _{A|B_{1}{\cdots } B_{N-1}}$, if $C(\rho _{A|B_{i}})\geq C(\rho _{A|B_{i+1}{\cdots } B_{N-1}}), i=1,2,\cdots ,N-2$, N > 3, we have

$$\begin{array}{@{}rcl@{}} {T}_{q}^{\eta}(\rho_{A|B_{1}{\cdots} B_{N-1}}) \geq \sum\limits_{i=1}^{N-3}h^{i-1}T_{q}^{\eta}(\rho_{A|B_{i}}) +h^{N-3}Q_{AB_{N-2}}, \end{array}$$

(20)

where h = 2^η − 1, $Q_{AB_{N-2}}=T_{q}^{\eta }(\rho _{A|B_{N-2}})+\frac {\eta ^{2}}{\eta +1}T_{q}^{\eta -1}(\rho _{A| B_{N-2}})T_{q}(\rho _{A|B_{N-1}})+\left (2^{\eta }-\frac {\eta ^{2}}{\eta +1}-1\right )T_{q}^{\eta }(\rho _{A|B_{N-1}})$.

Proof

Let $\rho _{A|B_{1}{\cdots } B_{N-1}}$ be an N-qubit mixed state, from Lemma 3 and inequality (3), we have

$$\begin{array}{@{}rcl@{}} T_{q}^{\eta}(\rho_{A|B_{1}{\cdots} B_{N-1}}) & \geq& g_{q}^{\eta}({C^{2}(\rho_{A|B_{1}})+C^{2}(\rho_{A|B_{2}{\cdots} B_{N-1}})})\\ & \geq& g_{q}^{\eta}(C^{2}(\rho_{A|B_{1}}))+\frac{\eta^{2}}{\eta+1} g_{q}^{\eta-1}(C^{2}(\rho_{A| B_{1}}))g_{q}(C^{2}(\rho_{A|B_{2}{\cdots} B_{N-1}}))\\ && \quad+(2^{\eta}-\frac{\eta^{2}}{\eta+1}-1)g_{q}^{\eta}(C^{2}(\rho_{A|B_{2}{\cdots} B_{N-1}}))\\ & \geq& g_{q}^{\eta}(C^{2}(\rho_{A|B_{1}}))+hg_{q}^{\eta}(C^{2}(\rho_{A|B_{2}{\cdots} B_{N-1}})), \end{array}$$

(21)

where the first inequality is due to the monotonically increasing property of the function g_q(x) and inequality (3), the second inequality is due to Lemma 2, and the third inequality is due to the fact that $C^{2}(\rho _{A|B_{1}})\geq C^{2}(\rho _{A|B_{2}{\cdots } B_{N-1}})$.

Similar calculation procedure can be used to the term $g_{q}^{\eta }(C^{2}(\rho _{A|B_{2}{\cdots } B_{N-1}}))$, by iterative method we can get

$$\begin{array}{@{}rcl@{}} && g_{q}^{\eta}(C^{2}(\rho_{A|B_{2}{\cdots} B_{N-1}}))\\ &\geq & g_{q}^{\eta}(C^{2}(\rho_{A|B_{2}}))+hg_{q}^{\eta}({C^{2}(\rho_{A|B_{3}{\cdots} B_{N-1}})})\geq \cdots\\ &\geq & g_{q}^{\eta}(C^{2}(\rho_{A|B_{2}}))+hg_{q}^{\eta}(C^{2}(\rho_{A|B_{3}})) +\cdots+h^{N-5}g_{q}^{\eta}(C^{2}(\rho_{A|B_{N-3}}))\\ &&\quad+h^{N-4}\bigg\{g_{q}^{\eta}(C^{2}(\rho_{A|B_{N-2}})) +\frac{\eta^{2}}{\eta+1}g_{q}^{\eta-1}(C^{2}(\rho_{A|B_{N-2}}))g_{q}(C^{2}(\rho_{A|B_{N-1}}))\\ &&\quad+(2^{\eta}-\frac{\eta^{2}}{\eta+1}-1)g_{q}^{\eta}(C^{2}(\rho_{A|B_{N-1}}))\bigg\}. \end{array}$$

(22)

According to the fact T_q(ρ) = g_q(C²(ρ)) for any two qubit mixed state ρ, and combining inequality (21) and (22), we complete the proof.

Theorem 2

For any 2 ≤ q ≤ 3, the power η ≥ 1, and N-qubit mixed state $\rho _{A|B_{1}{\cdots } B_{N-1}}$, if $C(\rho _{A|B_{i}})\geq C(\rho _{A|B_{i+1}{\cdots } B_{N-1}}), i=1, 2, \cdots ,m$, $C(\rho _{A|B_{j}})\leq C(\rho _{A|B_{j+1}{\cdots } B_{N-1}}), j=m+1, m+2, {\cdots } N-2$, N > 3, we have

$$T_{q}^{\eta}(\rho_{A|B_{1}{\cdots} B_{N-1}}) \geq \sum\limits_{i=1}^{m}h^{i-1}T_{q}^{\eta}(\rho_{AB_{i}})+h^{m+1}\sum\limits_{j=m+1}^{N-3}T_{q}^{\eta}(\rho_{AB_{j}})+h^{m}{{Q}_{AB_{N-1}}},$$

(23)

where h = 2^η − 1, ${{Q}_{AB_{N-1}}}=T_{q}^{\eta }(\rho _{A|B_{N-1}})+\frac {\eta ^{2}}{\eta +1}T_{q}^{\eta -1}(\rho _{A| B_{N-1}})T_{q}(\rho _{A|B_{N-2}}) +(2^{\eta }-\frac {\eta ^{2}}{\eta +1}-1)T_{q}^{\eta }(\rho _{A|B_{N-2}})$.

Proof

For 2 ≤ q ≤ 3, η ≥ 1, we obtain

$$\begin{array}{@{}rcl@{}} && T_{q}^{\eta}(\rho_{A|B_{1}{\cdots} B_{N-1}})\\ &\geq & \sum\limits_{i=1}^{m}h^{i-1}T_{q}^{\eta}(\rho_{AB_{i}})+h^{m}g_{q}^{\eta}({C^{2}(\rho_{A|B_{m+1}{\cdots} B_{N-1}})})\\ &\geq & \sum\limits_{i=1}^{m}h^{i-1}T_{q}^{\eta}(\rho_{AB_{i}})+h^{m}\bigg\{ g_{q}^{\eta}(C^{2}(\rho_{A|B_{m+2}{\cdots} B_{N-1}}))+(2^{\eta}-\frac{\eta^{2}}{\eta+1}-1)g_{q}^{\eta}(C^{2}(\rho_{A|B_{m+1}}))\\ && +\frac{\eta^{2}}{\eta+1}g_{q}^{\eta-1}({C^{2}(\rho_{A|B_{m+2}{\cdots} B_{N-1}})})g_{q}(C^{2}(\rho_{A|B_{m+1}}))\bigg\}\\ &\geq & \sum\limits_{i=1}^{m}h^{i-1}T_{q}^{\eta}(\rho_{AB_{i}})+h^{m+1}g_{q}^{\eta}(C^{2}(\rho_{A|B_{m+1}}))+h^{m}g_{q}^{\eta}(C^{2}(\rho_{A|B_{m+2}{\cdots} B_{N-1}}))\geq \cdots\\ &\geq & \sum\limits_{i=1}^{m}h^{i-1}T_{q}^{\eta}(\rho_{AB_{i}})+h^{m+1}\sum\limits_{j=m+1}^{N-3}g_{q}^{\eta}(C^{2}(\rho_{AB_{j}}))+h^{m}\bigg\{ (2^{\eta}-\frac{\eta^{2}}{\eta+1}-1)g_{q}^{\eta}(C^{2}(\rho_{A|B_{N-2}}))\\ && \quad+g_{q}^{\eta}(C^{2}(\rho_{A| B_{N-1}}))+\frac{\eta^{2}}{\eta+1}g_{q}^{\eta-1}(C^{2}(\rho_{A| B_{N-1}}))g_{q}(C^{2}(\rho_{A|B_{N-2}}))\bigg\}, \end{array}$$

(24)

where the first inequality is due to Theorem 1, and the second inequality is due to Lemma 2 and the fact that $C(\rho _{A| B_{j}})\leq C(\rho _{A|B_{j+1}\cdots B_{N-1}})$ for j = m + 1,m + 2,⋯N − 2, N > 3. According to the denotation of $Q_{AB_{N-1}}$ and combining inequality (24), we obtain inequality (23).

Remark 1

We consider a particular case of N = 3. Note that when 2 ≤ q ≤ 3, the power η ≥ 1, if $T_{q}(\rho _{AB_{1}})\geq T_{q}(\rho _{AB_{2}})$, then we get the following result,

$$\begin{array}{@{}rcl@{}} T_{q}^{\eta}(\rho_{A|B_{1}B_{2}}) &\geq& T_{q}^{\eta}(\rho_{AB_{1}})+\frac{\eta^{2}}{\eta+1}T_{q}^{\eta-1}(\rho_{AB_{1}})T_{q}(\rho_{AB_{2}})\\ && \quad+\left( 2^{\eta}-\frac{\eta^{2}}{\eta+1}-1\right)T_{q}^{\eta}(\rho_{AB_{2}}). \end{array}$$

(25)

If $T_{q}(\rho _{AB_{1}})\leq T_{q}(\rho _{AB_{2}})$, then

$$\begin{array}{@{}rcl@{}} T_{q}^{\eta}(\rho_{A|B_{1}B_{2}}) &\geq& T_{q}^{\eta}(\rho_{AB_{2}})+\frac{\eta^{2}}{\eta+1}T_{q}^{\eta-1}(\rho_{AB_{2}})T_{q}(\rho_{AB_{1}})\\ && \quad+\left( 2^{\eta}-\frac{\eta^{2}}{\eta+1}-1\right)T_{q}^{\eta}(\rho_{AB_{1}}). \end{array}$$

(26)

To see the tightness of the Tsallis-q entanglement directly, we give the following example.

Example 1

Under local unitary operations, the three-qubit pure state can be written as [24, 25]

$$|\psi\rangle_{A|BC}=\lambda_{0}|000\rangle+\lambda_{1}e^{i{\varphi}}|100\rangle+\lambda_{2}|101\rangle +\lambda_{3}|110\rangle+\lambda_{4}|111\rangle,$$

(27)

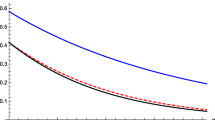
where 0 ≤ φ ≤ π, λ_i ≥ 0,i = 0,1,2,3,4, and ${\sum }_{i=0}^{4}{\lambda _{i}^{2}} =1$, set $\lambda _{0}=\frac {\sqrt {5}}{3}$, λ₁ = 0, λ₄ = 0, $\lambda _{2}=\frac {\sqrt {3}}{3}$, $\lambda _{3}=\frac {1}{3}$, q = 2. From the definition of the Tsallis-q entanglement, after simple computation, we can get $T_{q}(\rho _{A| BC})=g_{q}[(2\lambda _{0}\sqrt {(\lambda _{2})^{2}+(\lambda _{3})^{2}+(\lambda _{4})^{2}})^{2}]$, T_q(ρ_AB) = g_q[(2λ₀λ₂)²], and T_q(ρ_AC) = g_q[(2λ₀λ₃)²], then we have T_q(ρ_A|BC) = 0.49383, T_q(ρ_AB) = 0.37037, and T_q(ρ_AC) = 0.12346. Consequently, $T_{2}^{\eta }(\rho _{A|BC})=(0.49383)^{\eta }\geq T_{2}^{\eta }(\rho _{AB})+(2^{\eta }-\frac {\eta ^{2}}{\eta +1}-1)T_{2}^{\eta }(\rho _{AC})+\frac {\eta ^{2}}{\eta +1}T_{2}^{\eta -1}(\rho _{AB})T_{2}(\rho _{AC})= (0.37037)^{\eta }+\frac {\eta ^{2}}{\eta +1}(37037)^{\eta -1}(0.12346)+(2^{\eta }-\frac {\eta ^{2}}{\eta +1}-1)(0.12346)^{\eta }$. While the result in [11] is $T_{2}^{\eta }(\rho _{AB})+(2^{\eta }-1)T_{2}^{\eta }(\rho _{AC})+\frac {\eta }{2}T_{2}(\rho _{AC})((T_{2}^{\eta -1}(\rho _{AB}))-(T_{2}^{\eta -1}(\rho _{AC})))=(0.37037)^{\eta }+(2^{\eta }-1)(0.12346)^{\eta }+\frac {0.12346{\eta }}{2}((0.37037)^{\eta -1}-(0.12346)^{\eta -1})$. One can see that our result is tighter than the ones [11] for η ≥ 1. See Fig. 1.

Fig. 1

The axis T stands the Tsallis-q entanglement of |ψ〉_A|BC, which is a function of η (1 ≤ η ≤ 3). The dotted line stands the value of $T_{2}^{\eta }(\rho _{A|BC})$. The dashed line stands the lower bound given by our improved monogamy relations. The solid black line represents the lower bound given by [11]

4 Tighter Monogamy Relations in Terms of the Rényi-α Entanglement

In order to present the tighter monogamy relations of the Rényi-α entanglement in multiqubit systems, we introduce three lemmas as follows.

Lemma 4

For any N-qubit mixed state $\rho _{A|B_{1}{\cdots } B_{N-1}}$, we have

$$E_{\alpha}{(\rho_{A|B_{1}{\cdots} B_{N-1}})}\geq f_{\alpha}(C(\rho_{A|B_{1}{\cdots} B_{N-1}})).$$

(28)

Proof

Suppose that $\rho _{A|B_{1}{\cdots } B_{N-1}}=\sum \limits _{i} p_{i} |\varphi _{i}\rangle _{A|B_{1}{\cdots } B_{N-1}}$ is the optimal decomposition for $E_{\alpha }({\rho _{A|B_{1}{\cdots } B_{N-1}}})$, then we have

$$\begin{array}{@{}rcl@{}} E_{\alpha}({\rho_{A|B_{1}{\cdots} B_{N-1}}}) & =& \sum\limits_{i} p_{i} E_{\alpha}(|\varphi_{i}\rangle_{A|B_{1}{\cdots} B_{N-1}}) \\ & =& \sum\limits_{i} p_{i} f_{\alpha}(C(|\varphi_{i}\rangle_{A|B_{1}{\cdots} B_{N-1}}))\\ &\geq& f_{\alpha} (\sum\limits_{i} p_{i} C(|\varphi_{i}\rangle_{A|B_{1}{\cdots} B_{N-1}}))\\ &\geq& f_{\alpha}(C(\rho_{A|B_{1}{\cdots} B_{N-1}})), \end{array}$$

(29)

where the first inequality is due to the convexity of f_α(x) and the last inequality follows from the definition of concurrence for mixed state.

Lemma 5

For any α ≥ 2, μ ≥ 1, suppose that the function f_α(x) defined on the domain D = {(x,y)|0 ≤ x,y ≤ 1,0 ≤ x² + y² ≤ 1}, if x ≥ y, then we have

$$f_{\alpha}^{\mu}(\sqrt{x^{2}+y^{2}})\geq f_{\alpha}^{\mu}(x)+\frac{\mu^{2}}{\mu+1}f_{\alpha}^{{\mu}-1}(x)f_{\alpha}(y)+\left( 2^{\mu}-\frac{\mu^{2}}{\mu+1}-1\right)f_{\alpha}^{\mu}(y).$$

(30)

Proof

For μ ≥ 1, and α ≥ 2, we have

$$\begin{array}{@{}rcl@{}} f_{\alpha}^{\mu}(\sqrt{x^{2}+y^{2}})&\geq& (f_{\alpha}(x)+f_{\alpha}(y))^{\mu}\\ &\geq& f_{\alpha}^{\mu}(x)+\frac{\mu^{2}}{\mu+1}f_{\alpha}^{{\mu}-1}(x)f_{\alpha}(y)+\left( 2^{\mu}-\frac{\mu^{2}}{\mu+1}-1\right)f_{\alpha}^{\mu}(y), \end{array}$$

(31)

where the first inequality is due to inequality (13), and the second inequality is due to Lemma 1.

Lemma 6

For any $\frac {\sqrt {7-1}}{2} \leq \alpha < 2$, μ ≥ 1, ${\mu }=\frac {\gamma }{2}$, the function f_α(x) defined on the domain D = {(x,y)|0 ≤ x,y ≤ 1,0 ≤ x² + y² ≤ 1}, if x ≥ y, then we have

$$f_{\alpha}^{\gamma}(\sqrt{x^{2}+y^{2}})\geq f_{\alpha}^{\gamma}(x)+\frac{\mu^{2}}{\mu+1}f_{\alpha}^{{\gamma}-2}(x)f_{\alpha}^{2}(y) +\left( 2^{\mu}-\frac{\mu^{2}}{\mu+1}-1\right)f_{\alpha}^{\gamma}(y).$$

(32)

Proof

For μ ≥ 1, and ${\mu =\frac {\gamma }{2}}$, we have

$$\begin{array}{@{}rcl@{}} f_{\alpha}^{\gamma}(\sqrt{x^{2}+y^{2}})&\geq& (f_{\alpha}^{2}(x)+f_{\alpha}^{2}(y))^{\mu}\\ & \geq& f_{\alpha}^{\gamma}(x)+\frac{\mu^{2}}{\mu+1}f_{\alpha}^{{\gamma}-2}(x)f_{\alpha}^{2}(y)+(2^{\mu}-\frac{\mu^{2}}{\mu+1}-1)f_{\alpha}^{\gamma}(y), \end{array}$$

(33)

where the first inequality can be assured by inequality (14), and the second inequality is due to Lemma 1.

Now, we give the following theorems of the tighter monogamy inequality in terms of the Rényi-α entanglement.

Theorem 3

For any α ≥ 2, the power μ ≥ 1, and N-qubit mixed state $\rho _{A|B_{1}{\cdots } B_{N-1}}$, if $C(\rho _{A|B_{i}})\geq C(\rho _{A|B_{i+1}{\cdots } B_{N-1}}), i=1,2,\cdots ,N-2$, N > 3, then we have

$$E_{\alpha}^{\mu}(\rho_{A|B_{1}{\cdots} B_{N-1}}) \geq \sum\limits_{i=1}^{N-3}h^{i-1}E_{\alpha}^{\mu}(\rho_{A|B_{i}}) +h^{N-3}Q_{AB_{N-2}},$$

(34)

where h = 2^μ − 1, $Q_{AB_{N-2}}=E_{\alpha }^{\mu }(\rho _{A|B_{N-2}})+\frac {\mu ^{2}}{\mu +1}E_{\alpha }^{\mu -1}(\rho _{A| B_{N-2}})E_{\alpha }(\rho _{A|B_{N-1}}) +(2^{\mu }-\frac {\mu ^{2}}{\mu +1}-1)E_{\alpha }^{\mu }(\rho _{A|B_{N-1}})$.

Proof

We consider an N-qubit mixed state $\rho _{A|B_{1}{\cdots } B_{N-1}}$, from Lemma 4, we have

$$\begin{array}{@{}rcl@{}} E_{\alpha}^{\mu}(\rho_{A|B_{1}{\cdots} B_{N-1}}) & \geq& f_{\alpha}^{\mu}\bigg(\sqrt{C^{2}(\rho_{A|B_{1}})+C^{2}(\rho_{A|B_{2}{\cdots} B_{N-1}})}\bigg)\\ & \geq& f_{\alpha}^{\mu}(C(\rho_{A|B_{1}}))+\frac{\mu^{2}}{\mu+1} f_{\alpha}^{\mu-1}(C(\rho_{A| B_{1}}))f_{\alpha}(C(\rho_{A|B_{2}{\cdots} B_{N-1}}))\\ && \quad+\left( 2^{\mu}-\frac{\mu^{2}}{\mu+1}-1\right)f_{\alpha}^{\mu}(C(\rho_{A| B_{2}{\cdots} B_{N-1}}))\\ & \geq& f_{\alpha}^{\mu}(C(\rho_{A|B_{1}}))+hf_{\alpha}^{\mu}(C(\rho_{A| B_{2}{\cdots} B_{N-1}}))\\ & \geq& \cdots\\ & \geq& f_{\alpha}^{\mu}(C(\rho_{A|B_{1}}))+hf_{\alpha}^{\mu}(C(\rho_{A|B_{2}}))+\cdots+h^{N-4}f_{\alpha}^{\mu}(C(\rho_{A|B_{N-3}}))\\ && \quad+h^{N-3}\bigg\{f_{\alpha}^{\mu}(C(\rho_{A|B_{N-2}})) +\frac{\mu^{2}}{\mu+1}f_{\alpha}^{\mu-1}(C(\rho_{A|B_{N-2}}))f_{\alpha}(C(\rho_{A|B_{N-1}}))\\ & & \quad+\left( 2^{\mu}-\frac{\mu^{2}}{\mu+1}-1\right)f_{\alpha}^{\mu}(C(\rho_{A|B_{N-1}}))\bigg\}, \end{array}$$

(35)

where the first inequality is due to the monotonically increasing property of the function f_α(x) and inequality (3), the second inequality is due to Lemma 5, and the third inequality is due to the fact that $C(\rho _{A|B_{i}})\geq C(\rho _{A|B_{i+1}{\cdots } B_{N-1}})$, i = 1,2,⋯ ,N − 2. Then, according to the denotation of $Q_{AB_{N-2}}$ and the definition of the Rényi-α entanglement, we complete the proof.

Theorem 4

For any α ≥ 2, the power μ ≥ 1, and N-qubit mixed state $\rho _{A|B_{1}{\cdots } B_{N-1}}$, if $C(\rho _{A|B_{i}})\geq C(\rho _{A|B_{i+1}{\cdots } B_{N-1}})$, i = 1,2,⋯ ,m, $C(\rho _{A|B_{j}})\leq C(\rho _{A|B_{j+1}{\cdots } B_{N-1}})$, j = m + 1,m + 2,⋯N − 2, N > 3, then we have

$$E_{\alpha}^{\mu}(\rho_{A|B_{1}{\cdots} B_{N-1}}) \geq \sum\limits_{i=1}^{m}h^{i-1}E_{\alpha}^{\mu}(\rho_{AB_{i}})+h^{m+1}\sum\limits_{j=m+1}^{N-3}E_{\alpha}^{\mu}(\rho_{AB_{j}})+h^{m}{{Q}_{AB_{N-1}}},$$

(36)

where h = 2^μ − 1, ${{Q}_{AB_{N-1}}}=E_{\alpha }^{\mu }(\rho _{A|B_{N-1}})+\frac {{\mu }^{2}}{\mu +1}E_{\alpha }^{\mu -1}(\rho _{A| B_{N-1}})E_{\alpha }(\rho _{A|B_{N-2}}) +(2^{\mu }-\frac {{\mu }^{2}}{\mu +1}-1)E_{\alpha }^{\mu }(\rho _{A|B_{N-2}})$.

Proof

For any α ≥ 2, μ ≥ 1, $C(\rho _{A|B_{i}})\geq C(\rho _{A|B_{i+1}{\cdots } B_{N-1}})$, i = 1,2,⋯ ,m, from Theorem 3, we know that

$${E}_{\alpha}^{\mu}(\rho_{A|B_{1}{\cdots} B_{N-1}}) \geq \sum\limits_{i=1}^{m}h^{i-1}E_{\alpha}^{\mu}(\rho_{AB_{i}})+h^{m}f_{\alpha}^{\mu}(C(\rho_{A|B_{m+1}{\cdots} B_{N-1}})).$$

(37)

When $C(\rho _{A|B_{j}})\leq C(\rho _{A|B_{j+1}{\cdots } B_{N-1}}), j=m+1, m+2, {\cdots } N-2$, N > 3, we get that

$$\begin{array}{@{}rcl@{}} {f}_{\alpha}^{\mu}(C(\rho_{A|B_{m+1}{\cdots} B_{N-1}})) & \geq& {f}_{\alpha}^{\mu}\bigg(\sqrt{{C^{2}(\rho_{A|B_{m+1}})+C^{2}(\rho_{A|B_{m+2}{\cdots} B_{N-1}})}}\bigg)\\ &\geq& {f}_{\alpha}^{\mu}({C(\rho_{A|B_{m+2}{\cdots} B_{N-1}})})+\left( 2^{\mu}-\frac{\mu^{2}}{\mu+1}-1\right)f_{\alpha}^{\mu}(C(\rho_{A|B_{m+1}}))\\ &&\quad+\frac{\mu^{2}}{\mu+1}f_{\alpha}^{\mu-1}({C(\rho_{A|B_{m+2}{\cdots} B_{N-1}})})f_{\alpha}(C(\rho_{A|B_{m+1}}))\\ &\geq& f_{\alpha}^{\mu}({C(\rho_{A|B_{m+2}{\cdots} B_{N-1}})})+hf_{\alpha}^{\mu}(C(\rho_{A|B_{m+1}}))\\ & \geq&\cdots\\ & \geq& h\{f_{\alpha}^{\mu}(C(\rho_{A|B_{m+1}}))+\cdots+f_{\alpha}^{\mu}(C(\rho_{A| B_{N-3}}))\}\\ && \quad+\bigg\{f_{\alpha}^{\mu}(C(\rho_{A| B_{N-1}}))+\frac{\mu^{2}}{\mu+1}f_{\alpha}^{\mu-1}(C(\rho_{A| B_{N-1}}))f_{\alpha}(C(\rho_{A|B_{N-2}}))\\ && \quad +(2^{\mu}-\frac{\mu^{2}}{\mu+1}-1)f_{\alpha}^{\mu}(C^{2}(\rho_{A|B_{N-2}}))\bigg\}, \end{array}$$

(38)

where the first inequality is due to the monotonically increasing property of the function f_α(x) and inequality (3), the third inequality is from the fact that $C(\rho _{A| B_{j}})\leq C(\rho _{A|B_{j+1}{\cdots } B_{N-1}})$, j = m + 1,m + 2,⋯N − 2, N > 3. According to the definition of the Rényi-α entanglement, and combining inequality (37) and (38), we obtain inequality (36).

Remark 2

We consider a particular case of N = 3. Note that when α ≥ 2, the power μ ≥ 1, if $E_{\alpha }(\rho _{AB_{1}})\geq E_{\alpha }(\rho _{AB_{2}})$, then we get the following result,

$$\begin{array}{@{}rcl@{}} E_{\alpha}^{\mu} (\rho_{A|B_{1}B_{2}})&\geq& E_{\alpha}^{\mu}(\rho_{AB_{1}})+\frac{\mu^{2}}{\mu+1}E_{\alpha}^{\mu-1}(\rho_{AB_{1}})E_{\alpha}(\rho_{AB_{2}})\\ && \quad+\left( 2^{\mu}-\frac{\mu^{2}}{\mu+1}-1\right)E_{\alpha}^{\mu}(\rho_{AB_{2}}), \end{array}$$

(39)

if $E_{\alpha }(\rho _{AB_{1}})\leq E_{\alpha }(\rho _{AB_{2}})$, then

$$\begin{array}{@{}rcl@{}} E_{\alpha}^{\mu}(\rho_{A|B_{1}B_{2}}) &\geq& E_{\alpha}^{\mu}(\rho_{AB_{2}})+\frac{\mu^{2}}{\mu+1}E_{\alpha}^{\mu-1}(\rho_{AB_{2}})E_{\alpha}(\rho_{AB_{1}})\\ && \quad+\left( 2^{\mu}-\frac{\mu^{2}}{\mu+1}-1\right)E_{\alpha}^{\mu}(\rho_{AB_{1}}). \end{array}$$

(40)

To see the tightness of the Rényi-α entanglement directly, we give the following example.

Example 2

Let us consider the state in (27) given in Example 1. Set $\lambda _{0}=\frac {\sqrt {5}}{3}$, λ₁ = λ₄ = 0, $\lambda _{2}=\frac {\sqrt {3}}{3}$, $\lambda _{3}=\frac {1}{3}$, where α = 2. From definition of the Rényi-α entanglement, after simple computation, we get E₂(φ_A|BC) = 0.98230, E₂(φ_AB) = 0.66742, E₂(φ_AC) = 0.19010, and $E_{2}^{\mu }(\rho _{A|BC})=(0.98230)^{\mu }\geq E_{2}^{\mu }(\rho _{AB})+(2^{\mu }-\frac {\mu ^{2}}{\mu +1}-1)E_{2}^{\mu }(\rho _{AC})+\frac {\mu ^{2}}{\mu +1}E_{2}^{\mu -1}(\rho _{AB})E_{2}(\rho _{AC})$$=(0.66742)^{\mu }+\frac {\mu ^{2}}{\mu +1}(0.66742)^{\mu -1}(0.19010)+(2^{\mu }-\frac {\mu ^{2}}{\mu +1}-1)(0.19010)^{\mu }$. While the formula in [12] is $E_{2}^{\mu }(\rho _{AB})+\frac {\mu }{2}E_{2}^{\mu -1}(\rho _{AB})E_{2}(\rho _{AC})+(2^{\mu }-\frac {\mu }{2}-1)E_{2}^{\mu }(\rho _{AC})=(0.66742)^{\mu }+\frac {\mu }{2}(0.66742)^{\mu -1}(0.19010)+(2^{\mu }-\frac {\mu }{2}-1)(0.19010)^{\mu }$. One can see that our result is tighter than the ones in [12] for μ ≥ 1. See Fig. 2.

Fig. 2

The axis E stands the Rényi-α entanglement of |ψ〉_A|BC, which is a function of μ (1 ≤ μ ≤ 4). The dotted line stands the value of $E_{2}^{\mu }(\rho _{A|BC})$. The dashed line stands the lower bound given by our improved monogamy relations. The solid black line represents the lower bound given by [12]

Theorem 5

For any $\frac {\sqrt {7-1}}{2} \leq \alpha < 2$, the power μ ≥ 1, ${\mu }=\frac {\gamma }{2}$, and N-qubit mixed state $\rho _{A|B_{1}{\cdots } B_{N-1}}$, if $C(\rho _{A|B_{i}})\geq C(\rho _{A|B_{i+1}{\cdots } B_{N-1}}), i=1,2,\cdots ,N-2$, N > 3, then we have

$$E_{\alpha}^{\gamma}(\rho_{A|B_{1}{\cdots} B_{N-1}}) \geq \sum\limits_{i=1}^{N-3}h^{i-1}E_{\alpha}^{\gamma}(\rho_{A|B_{i}}) +h^{N-3}Q_{AB_{N-2}},$$

(41)

where h = 2^μ − 1, $Q_{AB_{N-2}}=E_{\alpha }^{\gamma }(\rho _{A|B_{N-2}})+\frac {\mu ^{2}}{\mu +1}E_{\alpha }^{\gamma -2}(\rho _{A| B_{N-2}})E^{2}_{\alpha }(\rho _{A|B_{N-1}}) +(2^{\mu }-\frac {\mu ^{2}}{\mu +1}-1)E_{\alpha }^{\gamma }(\rho _{A|B_{N-1}})$.

Proof

For $\frac {\sqrt {7-1}}{2} \leq \alpha < 2$, μ ≥ 1, and ${\mu }=\frac {\gamma }{2}$, we consider an N-qubit mixed state $\rho _{A|B_{1}{\cdots } B_{N-1}}$, from Lemma 4, we have

$$\begin{array}{@{}rcl@{}} E_{\alpha}^{\gamma}(\rho_{A|B_{1}{\cdots} B_{N-1}})& \geq& f_{\alpha}^{2\mu} \bigg(\sqrt{C(\rho_{A|B_{1}})+C^{2}(\rho_{A|B_{2}{\cdots} B_{N-1}})}\bigg)\\ & \geq& f_{\alpha}^{\gamma}(C(\rho_{A|B_{1}}))+\frac{\mu^{2}}{\mu+1} f_{\alpha}^{\gamma-2}(C(\rho_{A| B_{1}}))f_{\alpha}^{2}(C(\rho_{A|B_{2}{\cdots} B_{N-1}}))\\ && \quad+(2^{\mu}-\frac{\mu^{2}}{\mu+1}-1)f_{\alpha}^{\gamma}(C(\rho_{A|B_{2}{\cdots} B_{N-1}})\\ & \geq& f_{\alpha}^{\gamma}(C(\rho_{A|B_{1}}))+hf_{\alpha}^{\gamma}(C(\rho_{A|B_{2}\cdot B_{N-1}}))\\ & \geq& \cdots\\ & \geq& f_{\alpha}^{\gamma}(C(\rho_{A|B_{1}}))+hf_{\alpha}^{\gamma}(C(\rho_{A|B_{2}}))+\cdots+h^{N-4}f_{\alpha}^{\gamma}(C(\rho_{A|B_{N-3}}))\\ && \quad+h^{N-3}\bigg\{f_{\alpha}^{\gamma}(C(\rho_{A|B_{N-2}}))+\frac{\mu^{2}}{\mu+1}f_{\alpha}^{\gamma-2}(C(\rho_{A|B_{N-2}}))f_{\alpha}^{2}(C(\rho_{A|B_{N-1}}))\\ && \quad+(2^{\mu}-\frac{\mu^{2}}{\mu+1}-1)f_{\alpha}^{\gamma}(C(\rho_{A|B_{N-1}}))\bigg\}, \end{array}$$

(42)

where the first inequality comes from the monotonically increasing property of the function f_α(x) and inequality (3), the second inequality is due to Lemma 6, and the third inequality is due to the fact that $C(\rho _{A|B_{i}})\geq C(\rho _{A|B_{i+1}{\cdots } B_{N-1}})$, i = 1,2,⋯ ,N − 2. According to the definition of the Rényi-α entanglement and the denotation of $Q_{AB_{N-2}}$, we obtain inequality (41).

Theorem 6

For $\frac {\sqrt {7-1}}{2} \leq \alpha < 2$, the power μ ≥ 1, ${\mu }=\frac {\gamma }{2}$, and N-qubit mixed state $\rho _{A|B_{1}{\cdots } B_{N-1}}$, if $C(\rho _{A|B_{i}})\geq C(\rho _{A|B_{i+1}{\cdots } B_{N-1}}), i=1,2,\cdots ,m$, $C(\rho _{A|B_{j}})\leq C(\rho _{A|B_{j+1}{\cdots } B_{N-1}})$, j = m + 1,m + 2,⋯N − 2, N > 3, then we have

$$\begin{array}{@{}rcl@{}} E_{\alpha}^{\gamma}(\rho_{A|B_{1}{\cdots} B_{N-1}}) \geq \sum\limits_{i=1}^{m}h^{i-1}E_{\alpha}^{\gamma}(\rho_{AB_{i}})+h^{m+1}\sum\limits_{j=m+1}^{N-3}E_{\alpha}^{\gamma}(\rho_{AB_{j}})+h^{m}{{Q}_{AB_{N-1}}}, \end{array}$$

(43)

where h = 2^μ − 1, ${{Q}_{AB_{N-1}}}=E_{\alpha }^{\gamma }(\rho _{A|B_{N-1}})+\frac {{\mu }^{2}}{\mu +1}E_{\alpha }^{\gamma -2}(\rho _{A| B_{N-1}})E^{2}_{\alpha }(\rho _{A|B_{N-2}})+(2^{\mu }-\frac {{\mu }^{2}}{\mu +1}-1)E_{\alpha }^{\gamma }(\rho _{A|B_{N-2}})$.

Proof

When $C(\rho _{A| B_{i}})\geq C(\rho _{A|B_{i+1}{\cdots } B_{N-1}})$, i = 1,2,⋯ ,m, from Theorem 5, we have

$$\begin{array}{@{}rcl@{}} E_{\alpha}^{\gamma}(\rho_{A|B_{1}{\cdots} B_{N-1}}) & \geq & f_{\alpha}^{\gamma}(C(\rho_{A|B_{1}}))+hf_{\alpha}^{\gamma}(C(\rho_{A|B_{2}}))+\cdots+h^{m-1}f_{\alpha}^{\gamma}(C(\rho_{A|B_{m}}))\\ && \quad +h^{m}f_{\alpha}^{\gamma}(C(\rho_{A|B_{m+1}{\cdots} B_{N-1}}))\\ &&= \sum\limits_{i=1}^{m}h^{i-1}E_{\alpha}^{\gamma}(\rho_{AB_{i}})+h^{m}f_{\alpha}^{\gamma}(C(\rho_{A|B_{m+1}{\cdots} B_{N-1}})). \end{array}$$

(44)

When $C(\rho _{A|B_{j}})\leq C(\rho _{A|B_{j+1}{\cdots } B_{N-1}}), j=m+1, m+2, {\cdots } N-2$, N > 3, from Lemma 6, we get

$$\begin{array}{@{}rcl@{}} f_{\alpha}^{\gamma}(C(\rho_{A|B_{m+1}{\cdots} B_{N-1}}))&\geq& f_{\alpha}^{2\mu} \bigg(\sqrt{C^{2}(\rho_{A|B_{m+1}})+C^{2}(\rho_{A|B_{m+2}{\cdots} B_{N-1}})}\bigg)\\ &\geq& f_{\alpha}^{\gamma}(C(\rho_{A|B_{m+2}{\cdots} B_{N-1}}))+\left( 2^{\mu}-\frac{\mu^{2}}{\mu+1}-1\right)f_{\alpha}^{\gamma}(C(\rho_{A|B_{m+1}}))\\ &&\quad +\frac{\mu^{2}}{\mu+1}f_{\alpha}^{\gamma-2}(C(\rho_{A|B_{m+2}{\cdots} B_{N-1}}))f_{\alpha}^{2}(C(\rho_{A|B_{m+1}}))\\ &\geq& f_{\alpha}^{\gamma}(C(\rho_{A|B_{m+2}{\cdots} B_{N-1}}))+hf_{\alpha}^{\gamma}(C(\rho_{A|B_{m+1}}))\\ &\geq& \cdots\\ &\geq& hf_{\alpha}^{\gamma}(C(\rho_{A| B_{m+1}}))+\cdots+hf_{\alpha}^{\gamma}(C(\rho_{A| B_{N-3}}))\\ &&\quad+\bigg\{f_{\alpha}^{\gamma}(C(\rho_{A| B_{N-1}}))+\frac{\mu^{2}}{\mu+1}f_{\alpha}^{\gamma-2}(C(\rho_{A|B_{N-1}}))f_{\alpha}^{2}(C(\rho_{A|B_{N-2}}))\\ &&\quad+\left( 2^{\mu}-\frac{\mu^{2}}{\mu+1}-1\right)f_{\alpha}^{\gamma}(C(\rho_{A|B_{N-2}}))\bigg\}, \end{array}$$

(45)

where the first inequality comes from the monotonically increasing property of the function f_α(x) and inequality (3), the second inequality is due to Lemma 6, and the third inequality is due to the fact that $C(\rho _{A|B_{j}})\leq C(\rho _{A|B_{j+1}{\cdots } B_{N-1}})$, j = m + 1,m + 2,⋯N − 2, N > 3. According to the denotation of $Q_{AB_{N-1}}$ and combining inequality (44) and (45), we complete the proof.

Remark 3

We consider a particular case of N = 3. Note that when $\frac {\sqrt {7}-1}{2}\leq \alpha <2$, the power μ ≥ 1 and $\mu =\frac {\gamma }{2}$, if $E_{\alpha }(\rho _{AB_{1}})\geq E_{\alpha }(\rho _{AB_{2}})$, then we get the following result,

$$\begin{array}{@{}rcl@{}} E_{\alpha}^{\gamma}(\rho_{A|B_{1}B_{2}})& \geq& E_{\alpha}^{\gamma}(\rho_{AB_{1}})+\frac{\mu^{2}}{\mu+1}E_{\alpha}^{\gamma-2}(\rho_{AB_{1}})E_{\alpha}^{2}(\rho_{AB_{2}})\\ && \quad+\left( 2^{\mu}-\frac{\mu^{2}}{\mu+1}-1\right)E_{\alpha}^{\gamma}(\rho_{AB_{2}}), \end{array}$$

(46)

if $E_{\alpha }(\rho _{AB_{1}})\leq E_{\alpha }(\rho _{AB_{2}})$, then

$$\begin{array}{@{}rcl@{}} E_{\alpha}^{\gamma}(\rho_{A|B_{1}B_{2}})& \geq& E_{\alpha}^{\gamma}(\rho_{AB_{2}})+\frac{\mu^{2}}{\mu+1}E_{\alpha}^{\gamma-2}(\rho_{AB_{2}})E_{\alpha}^{2}(\rho_{AB_{1}})\\ && \quad+\left( 2^{\mu}-\frac{\mu^{2}}{\mu+1}-1\right)E_{\alpha}^{\gamma}(\rho_{AB_{1}}). \end{array}$$

(47)

To see the tightness of the Rényi-α entanglement directly, we give the following example.

Example 3

Let us consider the state in (27) given in Example 1. Suppose that $\lambda _{0}=\frac {\sqrt {5}}{3}$, λ₁ = λ₄ = 0, $\lambda _{2}=\frac {\sqrt {3}}{3}$, $\lambda _{3}=\frac {1}{3}$, and $\alpha =\frac {\sqrt {7}-1}{2}$. From definition of the Rényi-α entanglement, we have E_α(|ψ〉_A|BC) = 0.99265, E_α(|ψ〉_AB) = 0.83477, E_α(|ψ〉_AC) = 0.41466, and $E_{\alpha }^{\gamma }(\rho _{A|BC})=(0.99265)^{\gamma }\geq E_{\alpha }^{\gamma }(\rho _{AB})+\frac {\gamma ^{2}}{4+2\gamma }E_{\alpha }^{\gamma -2}(\rho _{AB})E_{\alpha }^{2}(\rho _{AC}) +\left .(2^{\frac {\gamma }{2}}-\frac {\gamma ^{2}}{4+2\gamma }-1)E_{\alpha }^{\gamma }(\rho _{AC})\right .=(0.83477)^{\gamma }+\frac {\gamma ^{2}}{4+2\gamma }(0.83477)^{\gamma -2}(0.41466)^{2}$$+\left .(2^{\frac {\gamma }{2}}-\frac {\gamma ^{2}}{4+2\gamma }-1)(0.41466)^{\gamma }\right ..$ While the formula in [12] is $E_{\alpha }^{\gamma }(\rho _{AB})+\frac {\gamma }{4}E_{\alpha }^{\gamma -2}(\rho _{AB})E_{\alpha }^{2}(\rho _{AC})+(2^{\frac {\gamma }{2}}-\frac {\gamma }{4}-1)E_{\alpha }^{\gamma }(\rho _{AC})=(0.83477)^{\gamma }+\frac {\gamma }{4}(0.83477)^{\gamma -2}(0.41466)^{2}+(2^{\frac {\gamma }{2}}-\frac {\gamma }{4}-1)(0.41466)^{\gamma }.$ One can see that our result is tighter than the result in [12] for $\mu =\frac {\gamma }{2}$, γ ≥ 2. See Fig. 3.

Fig. 3

The axis E stands the Rényi-α entanglement of |ψ〉_A|BC, which is a function of γ (2 ≤ γ ≤ 6). The dotted line stands the value of $E_{\frac {\sqrt {7}-1}{2}}^{\gamma }(\rho _{A|BC})$. The dashed line stands the lower bound given by our improved monogamy relations. The solid black line represents the lower bound given by [12]

5 Conclusion

Multipartite entanglement can be regarded as a fundamental problem in the theory of quantum entanglement. Our results may contribute to a fuller understanding of the Tsallis-q and Rényi-α entanglement in multipartite systems. In this paper, we have explored some tighter monogamy relations in terms of η th power of the Tsallis-q entanglement $T_{q}^{\eta }(\rho _{A|B_{1}{\cdots } B_{N-1}})$ (η ≥ 1, 2 ≤ q ≤ 3) and the Rényi-α entanglement $E_{\alpha }^{\mu }(\rho _{A|B_{1}{\cdots } B_{N-1}})$ (μ ≥ 1, α ≥ 2 ) and $E_{\alpha }^{\gamma }(\rho _{A|B_{1}{\cdots } B_{N-1}})$ (γ ≥ 2, $\frac {\sqrt {7}-1}{2}\leq \alpha <2$ ). We show that these new monogamy relations of multiparty entanglement have larger lower bounds and are tighter than the existing results [11, 12]. Our approach may also be applied to the study of monogamy properties related to other quantum correlations.