Quantum computation for large-scale image classification

Abstract

Due to the lack of an effective quantum feature extraction method, there is currently no effective way to perform quantum image classification or recognition. In this paper, for the first time, a global quantum feature extraction method based on Schmidt decomposition is proposed. A revised quantum learning algorithm is also proposed that will classify images by computing the Hamming distance of these features. From the experimental results derived from the benchmark database Caltech 101, and an analysis of the algorithm, an effective approach to large-scale image classification is derived and proposed against the background of big data.

1 Introduction

In the context of big data, how to make full use of images, the maximum quantity of unstructured big data in the internet, is a problem worthy of thorough consideration. At present, tagging images (i.e., classifying them automatically into different classes) is the first step to further use. The end of this step can be understood by a simple application scenario: A man wants to select some images from an image dataset to make a web page, in that case selecting from a classified image dataset would be more efficient than doing the same work from an unclassified dataset. However, when the number of images exceeds 100,000, the time required to classify such a large number of images becomes unwieldy. According to the related literature on this subject [1, 2], the total time of the classification task, including extracting image features and training the classifier, would amount to several days or even as much as a week. This problem of time consumption may be eased to a certain degree by taking advantage of the computational power of cloud computing or distributed systems [3, 4]. But doing this would not solve the problem completely, because other related problems (the cost of communication, memory constraints, and file I/O bottlenecks) would remain. Is there a more efficient way to accomplish the task of large-scale image classification?

In recent years, image processing via quantum computation, known as quantum image processing (QIP), and machine learning via quantum computation, known as quantum learning (QL), have brought a new perspective to large-scale image processing. The present study shows that using quantum properties to encode images has significantly improved the storage efficiency and time efficiency of certain operations, such as rotation. However, due to the lack of an effective way to get the main information (the features) from the quantum images, we still lack effective methods for accomplishing certain other complicated operations, such as image classification or recognition.

In this paper, for the first time, we address the problem of large-scale image classification using quantum computation. We discover that Schmidt decomposition, in addition to its well-known function of describing entanglement, can condense the main information of a quantum image into a few large coefficients; these can be deemed to be global features of the quantum image. Meanwhile, we analyze the quantum learning algorithm [5] and discuss its drawbacks. This algorithm judges the class to which the quantum object (state) belongs by computing the Hamming distance. However, the algorithm becomes less efficient when the number of categories that require classification is large. We redesign the key steps of the algorithm and propose a more efficient algorithm for image classification by computing the selected Schmidt coefficients (features). From our experiments on the benchmark image data set Caltech101 [6] and our analysis of the algorithm, we argue that the new algorithm, combined with the feature extraction method, presents an effective scheme for large-scale image classification.

The remainder of the paper is organized as follows. Section 2 describes the related works of QIP and QL and depicts a QL algorithm [5] in more detail. Section 3 describes the proposed method to extract quantum image features based on Schmidt decomposition. Section 4 analyzes the drawbacks of the algorithm [5] and proposes a revised version. Section 5 shows the experimental results and discusses them in detail. Finally, conclusions and directions for possible future work are provided in Sect. 6.

2 Related works

2.1 Quantum image processing

Quantum image processing first appeared in 1997, when Vlasov proposed a method of using quantum computation to recognize so-called orthogonal images [7]. However, in the years that followed, few scholars noted this research and only a few related articles were written. Then, in approximately 2010, this topic suddenly attracted active research again and gradually developed into an independent research subfield. At present, the research of QIP focuses primarily on how to define and represent images using quantum states and on how to implement operations based on these states. Qubit Lattice [8], Real Ket [9] and FRQI [10] are three principal quantum image formats. In addition to these three, there are many others, most of which can be considered to be variants of the three principal formats.

Taking Real Ket as an example, we note that it uses the probability amplitude of each component of a superposition state to map and store the value of each pixel. The representation method can be visualized via the model shown in Fig. 1, if we ignore its renormalization procedure in classical-to-quantum construction. Equation (1) provides its quantum representation format.

The Dirac representation of the quantum ground states corresponds to the pixel’ s row and column coordinates. $C_{ij}$ is the probability amplitude of $|i\rangle \otimes |j\rangle$, which stores the pixel normalized gray level value of the ith row and jth column.

$$\begin{aligned} |\hbox {image}\rangle = \sum _i\sum _j C_{ij}|i\rangle \otimes |j\rangle \qquad \hbox {st}.\sum _i\sum _j |C_{ij}|^2=1 \end{aligned}$$

(1)

Fig. 1

Real Ket quantum image

Let us compare the storage efficiency of Real Ket to a classical image format. For a classical image of $2^n\times 2^n$, if the gray level value of one pixel is represented by 8 bits, then the total number of bits needed will be $2^n\times 2^n\times 8$. However, Real Ket requires only 2n qubits. For an image of $512\times 512$, the classical method requires 2,097,152 bits, but quantum method only requires 18 qubits. These numbers suggest the significant efficiency of quantum storage.

The reason for this remarkable improvement in efficiency of quantum over classical methods of storage lies in the superposition property of quantum states. This property can also lead to quantum parallel computing, which improves the execution efficiency of many image operations. For example, the rotations of an image that can be realized by one unitary operation on all components of the $|\hbox {image}\rangle$ are exponentially faster than their classical counterparts.

Besides Real Ket, most of the other image representation schemes also use the superposition property of quantum states. But Real Ket holds the highest storage efficiency [11]. Thus, we select Real Ket to be the quantum image representation in depicting our scheme.

2.2 Quantum learning

Compared to quantum image processing, the combination of quantum computation and machine learning could be wider and deeper. The term “quantum learning” evolves from the term “quantum machine learning,” and it suggests a more independent sub-discipline [12], which has had fruitful influential research results [13–16]. The success rests on two aspects: Machine learning has many applications in the context of big data, so it has aroused intense research interest when infused the properties of quantum computation. On the other hand, previous quantum information studies, such as Quantum State Discrimination [17], have established a solid theoretical foundation for QL.

A full discussion of QL is beyond the scope of this article. The following section describes a concrete QL algorithm [5], the revised version of which will be used in our scheme.

This QL algorithm is intended to determine a new object belongs to which class in the training set. The new object is indicated by a quantum state $|x\rangle$ (a normalized n-dimensional feature vector $|x_1\ldots x_n\rangle$ ). The training set is indicated by N feature vectors $|v^p\rangle ,\,p=1,\ldots ,N$ and the corresponding class $c^p\in \{1,\ldots ,l\}$. This can be written as $\{|v_{1}^{p}\ldots v_{n}^{p},c^{p}\rangle \}\in \mathbb {H}_2^{\otimes n}\otimes \mathbb {H}_l$.

This algorithm uses Hamming distances to compute the distance between two objects. The Hamming distance is defined as counting the number of positions at which the corresponding symbols of two strings of equal length are different. For example, the Hamming distance: $0110 \leftrightarrow 0001$ has a distance of 3, while the Hamming distance: $0110 \leftrightarrow 1110$ has a distance of 1.

• Step 1: Construct a “training set superposition.”

  $$\begin{aligned} |\mathcal {T}\rangle =\frac{1}{\sqrt{N}} \sum _p{|v_1^p\ldots v_n^p,c^p\rangle } \end{aligned}$$

  (2)

• Step 2: Prepare the unclassified quantum state $|x_1\ldots x_n\rangle$ in the first register, prepare the training set $|\mathcal {T}\rangle$ in the second register and prepare an ancilla qubit $|0\rangle$ in the last register. The result can be written as $|\phi _0\rangle$ .

  $$\begin{aligned} |\phi _0\rangle =\frac{1}{\sqrt{N}} \sum _p{|x_1\ldots x_n;v_1^p\ldots v_n^p,c^p;0\rangle } \end{aligned}$$

  (3)

• Step 3: Put the ancilla qubit into a Hadamard gate, leading to Eq. (4).

  $$\begin{aligned} |\phi _1\rangle =\frac{1}{\sqrt{N}} \sum _p{|x_1\ldots x_n;v_1^p\ldots v_n^p,c^p\rangle }\otimes \frac{1}{\sqrt{2}} \bigl (|0\rangle +|1\rangle \bigr ) \end{aligned}$$

  (4)

• Step 4: Compute the Hamming distance between $|x_1\ldots x_n\rangle$ and each $|v_1^p\ldots v_n^p\rangle$ in the training set, store the result $|d_1^p\ldots d_n^p\rangle$ in the second register and reverse the value.

  $$\begin{aligned} \begin{aligned} |\phi _2\rangle&=\prod _k X(x_k)\hbox {CNOT}(x_k,v_k^p)|\phi _1\rangle \\&=\frac{1}{\sqrt{N}} \sum _p{|x_1\ldots x_n;d_1^p \ldots d_n^p,c^p\rangle }\otimes \frac{1}{\sqrt{2}} \bigl (|0\rangle +|1\rangle \bigr )\\ \end{aligned} \end{aligned}$$

  (5)

  $\hbox {CNOT}(a, b)$-gate overwrites the second entry b with 0 if $a = b$ else with 1. X gate is used to reverse the value.

• Step 5: Construct the unitary operator U as Eq. (6) and apply it on $|\phi _2\rangle$.

  $$\begin{aligned} U= & {} \mathrm{e}^{-i\frac{\pi }{2n}H} \quad \hbox {with} \quad H=\mathbbm {1}\otimes \sum _k{\left( \frac{\sigma _z+\mathbbm {1}}{2}\right) }_{d_k}\otimes \mathbbm {1}\otimes (\sigma _z)_c \end{aligned}$$

  (6)
  $$\begin{aligned} |\phi _3\rangle= & {} U|\phi _2\rangle =\frac{1}{\sqrt{2N}} \sum _p\biggl ( {\mathrm{e}^{i\frac{\pi }{2n}\bar{d}(x,v^p)}|x_1\ldots x_n;d_1^p\ldots d_n^p,c^p;0\rangle }\nonumber \\&+\,{\mathrm{e}^{-i\frac{\pi }{2n}\bar{d}(x,v^p)}|x_1\ldots x_n;d_1^p\ldots d_n^p,c^p;1\rangle }\biggr ) \end{aligned}$$

  (7)

• Step 6: Apply the Hadamard gate on the last register, yielding the final state $|\phi _4\rangle$.

  $$\begin{aligned} \begin{aligned} |\phi _4\rangle&=\mathbbm {1}\otimes \mathbbm {1}\otimes \mathbbm {1}\otimes H |\phi _3\rangle \\&= \frac{1}{\sqrt{N}} \sum _p\biggl ( {\cos {\frac{\pi }{2n}\bar{d}(x,v^p)}|x_1\ldots x_n;d_1^p\ldots d_n^p,c^p;0\rangle }\\&\quad +{\sin {\frac{\pi }{2n}\bar{d}(x,v^p)}|x_1\ldots x_n;d_1^p\ldots d_n^p,c^p;1\rangle }\biggr ) \end{aligned} \end{aligned}$$

  (8)

Measure the last register. If the input $|x\rangle$ is far away from most training patterns, the probability of the ancilla qubit being in the state $|1\rangle$ is much higher. Else if the input is close to many patterns, the ancilla qubit ends up in state $|0\rangle$. This algorithm is valid in the case of small categories, but it becomes inefficient when the categories grow. In Sect. 4, we will give the reason for this assertion via a detailed analysis and we will propose a revised version to overcome this drawback.

3 Feature extraction of quantum image

3.1 Acquire the main energy of a quantum image

In classical image processing, transformations such as K_L, DCT and wavelet change image data from the spatial domain to the frequency domain or the transform domain. After transformation, the main energy of the image is concentrated upon a limited number of coefficients, while other coefficients are equal to 0 or close to 0. A typical method used for pattern recognition is to select the nonzero coefficients as the global features of the image. The idea behind this method is also named as the principal component analysis, which was used in the well-known Eigenface method 20 years ago for human face recognition [18].

In quantum image processing, how to perform effective transformation on quantum images (quantum states) to achieve a condensed form is an open question. We find that Schmidt decomposition(SD), which is a basic tool used to study the entanglement properties of composite systems, can do work that is similar to what classical transformations can do.

The SD can be described as such a theorem [19]. Suppose $|\varphi \rangle$ is a pure state of a composite system, AB. Then, there exist orthonormal states $|\varPhi _\mathrm{A}\rangle$ for system A and orthonormal states $|\varPhi _\mathrm{B}\rangle$ of system B such that

$$\begin{aligned} |\varphi \rangle =\sum _i\lambda _i|\varPhi _\mathrm{A}\rangle |\varPhi _\mathrm{B}\rangle \end{aligned}$$

(9)

where $\lambda _i$ are nonnegative real numbers satisfying $\sum _i\lambda _i^2=1$ known as Schmidt coefficients.

The base $|\varPhi _\mathrm{A}\rangle$ and $|\varPhi _\mathrm{B}\rangle$ are called the Schmidt bases for A and B, respectively, and the number of nonzero value $\lambda _i$ is called the Schmidt number for the state $|\varphi \rangle$. The Schmidt number is an important property of a composite quantum system, which in some sense quantifies the amount of entanglement between systems A and B.

For example, the SD of Bell state $\frac{1}{\sqrt{2}} \bigl (|00\rangle + |11\rangle \bigr )$ is shown in Eq. (10) .

$$\begin{aligned} \frac{1}{\sqrt{2}}\bigl (|00\rangle + |11\rangle \bigr )=\frac{1}{\sqrt{2}}|00\rangle +\frac{1}{\sqrt{2}} |11\rangle \end{aligned}$$

(10)

where the coefficient of Schmidt bases $\lambda _1=\frac{1}{\sqrt{2}}$ and $\lambda _2=\frac{1}{\sqrt{2}}$. The Schmidt bases are ${\{|0\rangle , |1\rangle \}}$, and the Schmidt number is 2, which indicates the maximum entanglement between two qubits.

Accomplishing the SD requires skills that are described in detail in [11]. Here, we depict concisely the basic steps to perform the SD on the Real Ket image. For convenient depiction, we rewrite the Real Ket image [Eq. (1)) as Eq. (11)].

$$\begin{aligned} |\hbox {image}\rangle = \sum ^1_{j_1=0}\sum ^1_{j_2=0}\ldots \sum ^1_{j_n=0}C_{j_1j_2\ldots j_n}|j_1\rangle \otimes |j_2\rangle \otimes \cdots \otimes |j_n\rangle \end{aligned}$$

(11)

We select the first qubit ($|j_1\rangle$) as system A and the $n-1$ remaining qubits ($|j_2\rangle \otimes \cdots \otimes |j_n\rangle$) as system B. Then, we execute the SD.

$$\begin{aligned} |\hbox {image}\rangle = \sum _{\alpha _1}\lambda _{\alpha _1}|\varPhi _{\alpha _1}\rangle |\varPhi ^{[2\ldots n]}_{\alpha _1}\rangle \end{aligned}$$

(12)

where $\alpha _1$ corresponds to the first SD and the superscript of the Schmidt base $|\varPhi ^{[2\ldots n]}_{\alpha _1}\rangle$ indicates the qubits of sub-system B. We go on to compute the SD by splitting $|\varPhi ^{[2\ldots n]}_{\alpha _1}\rangle$ into qubit 2 and the n-2 remaining qubits; this is shown in Eq. (13).

$$\begin{aligned} |\hbox {image}\rangle = \sum _{\alpha _1}\lambda _{\alpha _1}|\varPhi _{\alpha _1}\rangle \biggl (\sum _{\alpha _2}\lambda _{\alpha _2}|\varPhi _{\alpha _2}\rangle |\varPhi ^{[3\ldots n]}_{\alpha _2}\rangle \biggr ) \end{aligned}$$

(13)

We continue to perform the SD on $|\varPhi ^{[3\ldots n]}_{\alpha _2}\rangle$, $|\varPhi ^{[4\ldots n]}_{\alpha _3}\rangle ,\ldots$ via the same bipartite splitting, until we finally derive equation (14).

$$\begin{aligned} |\hbox {image}\rangle = \sum _{\alpha _1} \sum _{\alpha _2}\ldots \ \sum _{\alpha _{n-1}}\lambda _{\alpha _1}\lambda _{\alpha _2}\ldots \lambda _{\alpha _{n-1}}|\varPhi _{\alpha _1\alpha _2\ldots \alpha _{n-1}}\rangle \end{aligned}$$

(14)

Now, we obtain $2^{2n-1}$ Schmidt coefficients, which correspond to a quantum state of 2n qubits prepared from the image of $2^n\times 2^n$. In the experiments depicted in Sect. 5, we find that most of these coefficients are 0 or close to 0. That is to say, after the SD, the main energy (information) of the quantum image is condensed into a few large coefficients, which can be understood as global features of the quantum image. Therefore, using them to classify images is reasonable. The key to this approach is to determine how many coefficients should be selected to perform classification reliably. That is to say, we should choose neither too many nor too few. What then is the optimal value of k, the number of large coefficients to be selected? We will achieve this value based on another experiment in Sect. 5.

Once we find the optimal value of k, we can use the Schmidt bases to construct a projector operator such as $\sum _{i\in \{\lambda _i\ge \lambda _k\}}|\varPhi _i\rangle \langle \varPhi _i|$, and we can apply it on $|\hbox {image}\rangle$ to extract the global features of the quantum image.

$$\begin{aligned} |\widetilde{\hbox {image}}\rangle = \sum _{i\in \{\lambda _i\ge \lambda _k\}}|\varPhi _i\rangle \langle \varPhi _i||\hbox {image}\rangle \end{aligned}$$

(15)

Now, $|\widetilde{\hbox {image}}\rangle$ can be used for the next step of image classification.

3.2 Feature coding

Before we execute the algorithm of image classification, we need to encode each $|\widetilde{\hbox {image}}_i\rangle$ to another form for convenient calculation of the Hamming distance of each class. That is to say, we must map $\Gamma \bigl (|\widetilde{\hbox {image}}_i\rangle \bigr )$ from $|\widetilde{\hbox {image}}_i\rangle$ to a new vector $|v^p\rangle$. A well-designed coding demands $|v^p\rangle$ should be sparse. Usually the dimensionality of $|v^p\rangle$ is higher than original $|\widetilde{\hbox {image}}_i\rangle$ and the mapping $\Gamma (x)$ is nonlinear. According to the theory of LCC [20], the nonlinear mapping can be relaxed as $|\widetilde{\hbox {image}}_i\rangle \approx B|v^p\rangle$, where $B=\mathbb {R}^{d \times n}$ is a real matrix of $d \times n$ named as the codebook, as long as it satisfies the following conditions:

• The approximation $|\widetilde{\hbox {image}}_i\rangle \approx B|v^p\rangle$ is sufficiently accurate;

• The coding $|v^p\rangle$ should be sufficiently local such that only those bases close to $|\widetilde{\hbox {image}}_i\rangle$ are activated.

Usually we can map different classes of images to different orthogonal feature vectors $|v^p\rangle$. If the B is known, the rest of the work is to solve the Moore–Penrose pseudo-inverse $B^{-1}$. Then, we can derive the final feature code $|v^p\rangle$. This work can be done using an existing quantum algorithm, which has exponentially higher speed than its classical counterparts [21].

4 The algorithm for image classification

Now, we have the feature vector $|v^p\rangle$ for each class in the image training set. If a Real Ket image $|X\rangle$ were to be classified, we would first use the SD to obtain the largest k Schmidt coefficient and approximate it as $|\widetilde{X}\rangle$. Then, we would encode it as the feature vector $|x_1\ldots x_n\rangle$ according to the method described in Sect. 3.2. Finally, we would use the revised version of Schuld’s algorithm to perform image classification.

The original Schuld’s algorithm is described in Sect. 2.2. In the following subsections, we will firstly analyze the drawbacks of the original algorithm as well as the tricks used in the algorithm. Based on this, we further explain why the algorithm is invalid for classification when the image scale is large. Then, we propose the revised version to deal with such case.

4.1 The drawbacks of Schuld’s algorithm

The key of Schuld’s algorithm is the design of the operator U in step (5). The key part of U is $\mathrm{e}^{\sum _k\bigl (\frac{\sigma _z+\mathbbm {1}}{2} \bigr )_{d_k}}$. When executing spectral decomposition on $\frac{\sigma _z+{\mathbbm {1}}}{2}$, we get:

$$\begin{aligned} \frac{\sigma _z+\mathbbm {1}}{2}= \begin{pmatrix} 1 &{} 0 \\ 0 &{} 0 \end{pmatrix}= 1|0 \rangle \langle 0|+0 |1 \rangle \langle 1| \end{aligned}$$

(16)

Then, according to the operational rule of operator functions, we get:

$$\begin{aligned} \mathrm{e}^{\frac{\sigma _z+\mathbbm {1}}{2}}= \mathrm{e}^1|0 \rangle \langle 0|+|1 \rangle \langle 1| \end{aligned}$$

(17)

In step (4), after the original algorithm has executed $\prod _k X(x_k)\hbox {CNOT}(x_k,v_k^p)$, the second register is overwritten by $|d_1^p\ldots d_n^p\rangle$, which records the difference of $|x_1\ldots x_n\rangle$ with each feature vector $|v_1^p\ldots v_n^p\rangle$. Note that $|d_1^p\ldots d_n^p\rangle$ uses ones-complement code. That is to say that, if $x_i=v_i^p\ \hbox {then}\ d_i^p=1;\ \hbox {else}\ d_i^p=0$. So, the operational result of $\mathrm{e}^{\frac{\sigma _z+\mathbbm {1}}{2}}$ on each $|d_i^p\rangle$ is $\mathrm{e}^1$ when $d_i^p=0$, and otherwise, it is 1. Hence, the summation $\mathrm{e}^{\sum _k\bigl (\frac{\sigma _z+\mathbbm {1}}{2} \bigr )_{d_k}}$ stores the Hamming distance of $|x_1\ldots x_n\rangle$ with each feature vector $|v_1^p\ldots v_n^p\rangle$ in the exponent of “e.”

This step is a key step to the final state $|\phi _4\rangle$ [Eq. (8)], in which the probability amplitude of each class $|c^p\rangle$ corresponds to the Hamming distance of $|X\rangle$ with each class.

From the above analysis, we find two drawbacks:

• The original algorithm has prepared three registers. Among these registers, the second one stores the data of the training set. In step (4), these data are overwritten by $|d_1^p\ldots d_n^p\rangle$. That means, the training set (database) should be reconstructed in each run, which is a waste of time and unnecessary.

• In the final state $|\phi _4\rangle$, the probability amplitude of the component $|c^p\rangle$ corresponds to the Hamming distance. As long as we determine which $|c^p\rangle$ has the largest probability amplitude, we can determine to which class $|X\rangle$ actually belongs. For the purpose of further analysis, we reduce $|\phi _4\rangle$ to a simple form by ignoring other parts:

  $$\begin{aligned} |\phi _4\rangle =\alpha _1|c^1\rangle +\alpha _2|c^2\rangle +\cdots +\alpha _p|c^p\rangle +\cdots +\alpha _l|c^l\rangle , \quad \hbox {st.} \sum \alpha _i^2=1 \end{aligned}$$

  (18)

The remaining work is to determine which $\alpha _p$ is the largest amplitude. This work is quantum state tomography [22], and the precision (standard deviation) is in proportion to the measurement time m. Reference [19] gives the standard deviation for estimating the $\alpha _p$ as $O(\frac{1}{\sqrt{m}})$. That is to say that if we want to determine the classification of $|x\rangle$, such inequality must meet:

$$\begin{aligned} \frac{1}{\sqrt{m}} < \min { |\alpha _i-\alpha _j|} \end{aligned}$$

(19)

where $\alpha _i$ is the largest $\alpha _p, p=1,\ldots ,l$ and $j \ne i$.

Reference [5] gives the time efficiency of the algorithm as $O(TPn)^6$, where n is the size of the feature vectors, P is the number of training examples and T is times to get a sufficiently precise picture from the measurement results.

Now, we can estimate the value of T according to this inequality (Eq. 19). It is straightforward that if there is just one $\alpha _p = 1\ (p=1,\ldots ,l)$, then $T=1$. This scenario occurs with limited classes, and each class is very different from the other classes. However, as the number of classes increases, the difference between the largest $\alpha _i$ and the second largest $\alpha _j$ would be narrow. This would significantly increase the run time T. Moreover, coupled with the exponential growth in the measurement settings with the number of qubits, the total run time T would become unworkably large. Thus, this algorithm is unrealistic for use in classifying large-scale images.

4.2 The revision of Schuld’s algorithm

Aiming to solve the two drawbacks discussed above, we propose two modifications:

• In step 4, the difference between each $x_i$ and $v_i^p$ is computed by a CNOT gate. As we know, with the CNOT gate, swapping the control end and the controlled end does not affect the operation result, but the controlled end will be overwritten by the result. In the original algorithm, $|x_1,\cdots ,x_n\rangle$ is the control end and $|v_1^p,\cdots ,v_n^p\rangle$ is controlled end. After CNOT operation, $|v_1^p,\cdots ,v_n^p\rangle$ is overwritten by $|x_1 \oplus v_1^p,\cdots , x_n \oplus v_n^p\rangle$, which is namely $|d_1^p,\cdots ,d_n^p\rangle$.

  Therefore, if we change $\prod _k X(x_k)\hbox {CNOT}(x_k,v_k^p)\Longrightarrow \prod _kX(v_k^p)\hbox {CNOT}(v_k^p,x_k)$, the $|x_1\ldots x_n\rangle$ rather than $|v_1^p\ldots v_n^p\rangle$ is overwritten to be $|d_1^p\cdots d_n^p\rangle$. That means, in the next run, the $|v_1^p\ldots v_n^p\rangle$ is unchanged and we do not need to redo step 1. This modification is straightforward, but improves the time efficiency.

• We propose to overcome too many run times T by setting the largest $\alpha _i=1$ and the other $\alpha _j=0$ by executing an if statement as follows:

The purpose of this step is to distinguish the nearest $|v_1^p\ldots v_n^p\rangle$ from the other feature vectors, so that the final measurement can determine the correct classification of $|X\rangle$ with a probability of 1 provided the appropriate t is set.

The if condition of “hamming distance $\le t$” can be written as $\hbox {COND}^p$:

$$\begin{aligned}&\hbox {COND}\_0^p= d_1^p\wedge d_2^p\wedge \cdots \wedge d_n^p\\&\hbox {COND}\_1^p\\&\quad = (\lnot d_1^p\wedge d_2^p\wedge \cdots \wedge d_n^p)\vee ( d_1^p\wedge \lnot d_2^p\wedge \cdots \wedge d_n^p)\vee \cdots \vee (d_1^p\wedge d_2^p\wedge \cdots \wedge \lnot d_n^p)\\&\hbox {COND}\_2^p\\&\quad = (\lnot d_1^p\wedge \lnot d_2^p\wedge \cdots \wedge d_n^p)\vee ( \lnot d_1^p\wedge d_2^p\wedge \lnot d_3^p\wedge \cdots \wedge d_n^p)\vee \cdots \vee (\lnot d_1^p\wedge d_2^p\\&\wedge \cdots \wedge d_{n-1}^p\wedge \lnot d_n^p)\vee ( d_1^p\wedge \lnot d_2^p\wedge \lnot d_3^p\wedge \cdots \wedge d_n^p)\vee \cdots \vee ( d_1^p\wedge \lnot d_2^p\wedge d_3^p\wedge \\&\cdots \wedge \lnot d_n^p)\vee \cdots \vee ( d_1^p\wedge d_2^p\wedge d_3^p\wedge \cdots \wedge \lnot d_{n-1}^p \wedge \lnot d_n^p)\\&\ldots \\&\hbox {COND}^p= \hbox {COND}\_0^p\vee \hbox {COND}\_1^p\vee \hbox {COND}\_2^p\vee \cdots \vee \hbox {COND}\_t^p \end{aligned}$$

In classical computing, this logic can be realized by AND gates, NOT gates and OR gates. In quantum computing, we need to transform these gates to reversible gates to meet quantum-mechanical properties. A quantum AND gate can be realized with a Toffoli gate, and a quantum NOT gate can be realized with a X gate. These are shown in Fig. 2. Meanwhile, because $x \vee y = \overline{ \bar{x} \wedge \bar{y} }$, a quantum OR gate can be realized using a quantum AND gate and a quantum NOT gate. So the entire $\hbox {COND}^p$ logic can be realized by the cascade of these reversible gates.

Fig. 2

a Quantum_AND gate and b quantum_NOT gate

However, the cost of such straightforward way to realize $\hbox {COND}^p$ is too high. For each $\hbox {COND}\_i^p\ (i=1,\cdots ,t)$, there are $\begin{pmatrix} n\\ i \end{pmatrix}$ entries for $\vee$. In each entry, there are i items for $\lnot$ and $n-1$ items for $\wedge$. Therefore, the number of logic gates required to realize $\hbox {COND}\_i^p$ is $\begin{pmatrix} n\\ i \end{pmatrix}(n-1+i)$ and the entire $\hbox {COND}^p$ is:

$$\begin{aligned} (n-1) + \begin{pmatrix} n\\ 2 \end{pmatrix}(n-1+2) + \cdots + \begin{pmatrix} n\\ t \end{pmatrix}(n-1+t) \end{aligned}$$

(20)

The complexity will increase tremendously with the Hamming distance t. We need to realize this logic more intelligently.

Given that $d_i^p$ uses ones-complement code to record the difference between $x_i$ and each $v_i^p$ at corresponding position i, we can rewrite the if condition of “hamming distance $\le t$” as follows:

$$\begin{aligned} \sum d_i \ge n - t \end{aligned}$$

(21)

Suppose $2^{k-1} \le n \le 2^k$, then, if we set a variable $l = 2^k - n$, then the above equation can be derived as:

$$\begin{aligned} \sum d_i +l \ge n +l - t \Longrightarrow \sum d_i +l + t \ge 2^k \end{aligned}$$

(22)

This equation means we can use additional circuits to determine whether the “hamming distance $\le t$” or not. Set an initial value $l + t$ to the left end of this circuit, and then determine whether there is one “1” in the highest $\lceil \log t \rceil$ qubits (overflow qubits $\ge 2^k$) in this summation. This determination condition can be achieved with the aid of an incremental circuit, which is proposed by Kaye [23] and shown in Fig. 3.

Fig. 3

Quantum $a+1$ gate

Fig. 4

Quantum circuit of $a+d_i$

The idea of Fig. 3 is as follows: Incrementation by 1 means the flipping of the sub-summation a[0...n-1] from the least significant qubit. If a[i] flips from 1 to 0, the addition would continue. If a[i] flips from 0 to 1, which means no carry qubit is produced, the addition should stop. The ancilla qubit in the circuit can be viewed as a flag which signals the first time a qubit flips from 0 to 1. It should be reset to 1 for the next run of addition. The work flow of this circuit can be depicted as the following pseudo-code:

Fig. 5

Quantum OR circuit

As illuminated by the circuit shown in Fig. 3, we add another control end $d_i$ to realize $a+d_i$, which is shown in Fig. 4a and simplified in Fig. 4b. Once the addition is done, we select the $\lceil \hbox {log}t \rceil$ most significant qubits and use quantum OR gate to get $\hbox {COND}^p$. The quantum OR gate is shown in Fig. 5, and the overall circuit to achieve $\hbox {COND}^p$ is shown in Fig. 6.

Fig. 6

Quantum circuit to generate $\hbox {COND}^p$

Once we get the $\hbox {COND}^p$, we can set $|d_1^p\ldots d_n^p\rangle$ according to its value in the if branches, i.e., we set each $d_i^p$ to $d^{p'}_i$ in accordance with truth Table 1. The logic in Table 1 can be simplified as the derivation of Eq. (23). And the final circuit can be realized by CNOT gates, which are shown in Fig. 7.

$$\begin{aligned} d_i^{p'} = (\hbox {COND}^p \wedge \bar{d}_i^p) \vee (\hbox {COND}^p \wedge d_i^p) = \hbox {COND}^p \end{aligned}$$

(23)

Table 1 Truth table

Fig. 7

Circuit of Table 1

Add another register to record the value of $|d_1^{p'}\ldots d_n^{p'}\rangle$, and replace the original $|d_1^{p}\ldots d_n^{p}\rangle$. Therefore, the $|\phi _2\rangle$ [Eq. (5)] will be:

$$\begin{aligned} |\phi _2\rangle =\frac{1}{\sqrt{N}} \sum _p{|x_1^p\ldots x_n^p;d_1^{p'}\ldots d_n^{p'},c^p\rangle }\otimes \frac{1}{\sqrt{2}} \bigl (|0\rangle +|1\rangle \bigr ) \end{aligned}$$

(24)

Continue to do the remaining steps of the quantum learning algorithm discussed in Sect. 2.2, and through a simple derivation, we find that the final state $|\phi _4\rangle$ will be:

$$\begin{aligned} \begin{aligned} |\phi _4\rangle&= \frac{1}{\sqrt{N}} \biggl (|x_1\ldots x_n;0\ldots 0,c^1;0\rangle +\cdots +|x_1\ldots x_n;1\ldots 1,c^k;1\rangle \\&\quad +\cdots +|x_1\ldots x_n;0\ldots 0,c^N;0\rangle \biggr ) \end{aligned} \end{aligned}$$

(25)

Then, we perform the joint measurement of the $c^p$ and the ancilla qubit, and the classification k can be derived with a probability of 1.

4.3 The analysis of the performance

In our revised algorithm, the main modification is the appending circuit to do if branch statement as shown in Figs. 6 and 7. The cost of the core part (Fig. 4) of this circuit is depicted as the following equation, which is measured by the number of “elementary gates” $\{\hbox {NOT}, \hbox {CNOT}, \hbox {Toffoli}\}$ [23].

$$\begin{aligned} \hbox {the cost of in}\,C_k ={\left\{ \begin{array}{ll} 1, &{} k =1 \\ 10, &{} k=2 \\ 2k^2+k-5, &{} k \ge 3 \end{array}\right. } \end{aligned}$$

(26)

In Fig. 6, the sub-circuit that generates the $\lceil \log t \rceil$ largest qubits calls module $inC_k$ n times. The sub-circuit that generates $\hbox {COND}^p$ has $\lceil \hbox {log}t \rceil +1$ NOT gates and $\lceil \hbox {log}t \rceil -1$ Toffoli gates. In Fig. 7, there are n CNOT gates. Hence, the cost of the total circuit is:

$$\begin{aligned} n(2n^2+n-5)+(\lceil \log t \rceil + 1)+(\lceil \log t \rceil - 1)+n \end{aligned}$$

(27)

The time performance of the original Schuld’s algorithm is $O(TPn)^6$ [23]. When we append a further step to execute Figs. 6 and 7, the extra cost to execute the algorithm is $O(n^3)$ according to formula (27). Hence, the time performance of the revised algorithm improves from $O(TPn)^6$ to $O(Pn)^6$. This improvement would be greater if the number of categories were more. For example, if $\min { |\alpha _i-\alpha _j|} \le 0.1$ [Eq. (19)], then the run time T would be more than 100. However, the revised algorithm need only run one time to obtain the right classification.

5 Experiment and discussion

5.1 Experiments

5.1.1 Experiment 1 obtain the main energy of the image of Lena

At first, we normalize the gray-scale value of every pixel and reshape the $512\times 512$ image of Lena to a vector in this order left to right and top to bottom, which is commensurate with a quantum state of 18 qubits. Then, we execute the SD in the bipartite splitting order according to Sect. 3.1. The SD gives us $2^{17}$ Schmidt coefficients. Then, we select the $2^{16}, 2^{15}, 2^{13}, 2^{11}$ and $2^9$ largest coefficients to reconstruct the quantum state, which ultimately allows us to restore the image of Lena. The original image of Lena and the effect of the restored images are shown in Fig. 8a–f.

Table 1 records the details of the reconstruction of the image of Lena after the SD. Fidelity is a frequently used metric to judge how close two quantum states are. It is defined by the inner product of two states, i.e., $\langle \phi |\varphi \rangle$. Obviously, the closer the value of $\langle \phi |\varphi \rangle$ is 1, the closer $|\phi \rangle$ and $|\varphi \rangle$ will be. Here, we use an approximate value of fidelity to judge the quality of the recovered image.

$$\begin{aligned} \hbox {fidelity}= \sum _{\{\mathrm{the}\, \mathrm{largest}\,k\, \mathrm{coefficients}\}}|\lambda _k|^2 \end{aligned}$$

(28)

With respect to Fig. 8, we discern that Fig. 8b–d shows almost the same as the original Lena image (Fig 8a) as seen with the naked eye, Fig 8e shows a little distortion, and Fig. 8f shows significant distortion. From Table 2, we find that the fidelity of Fig. 8b–d is above 99 %. Given this, and the quality of the reconstruction image, we can draw a conclusion that after the SD, the main energy of the quantum image has been concentrated in a limited number of coefficients.

Fig. 8

Original Lena image and recovery images. a The original image of $512\times 512$. b–f The recovery images by selecting the largest SD coefficients of $2^{16}, 2^{15}, 2^{13}, 2^{11}$ and $2^9$

Table 2 Detail of the SD and reconstruction of Lena image

5.1.2 Experiment 2 find the largest coefficients of the optimal k

The aim of selecting the largest Schmidt coefficients of k is to perform image classification rather than to reconstruct the original image perfectly with fewer coefficients. Thus, we do not need many of these coefficients provided that different classes can be distinguished from each other via the distance computed by these coefficients.

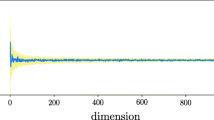
We have conducted experiments on the benchmark image set Caltech101[23], which has five image classes. Beginning with 15 coefficients, we add five coefficients in each successive round to compute the hit rate of each class. Figure 9a–e depicts five sample figures that correspond to 15, 45, 500, 1000 and 2000 coefficients. We find that as the number of Schmidt coefficients increases, the hit rate of almost every class also increases. But, different classes have different hit rates. We also discern that the classification of the class “camera” needs only a few coefficients to reach a very high rate, and the hit rate of the class “cup” is lower even if a lot of coefficients are computed. The class “butterfly” is the only class for which the hit rate decreases after the number of coefficients selected reaches a climax. (Fig. 9c–e) This implies that selecting more coefficients does not yield better results. The reason for this is that too many coefficients may increase the probability of misjudgment, especially for images with dispersive features. Figure 9f shows the average hit rate of all classes, from which we discern that an amount of 13 % of the large coefficients is sufficient for image classification.

Fig. 9

Hit rate of each class. a–e The hit rate of each class corresponding to 15, 45, 500, 1000 and 2000 coefficients selected. f The average hit rate of every class

5.2 Discussion

Few published works have discussed the theme of image classification. However, the technique used in some analogous works may be a potential way to accomplish image classification. In order to highlight our contribution, we list these works for comparison.

Image retrieval is the most relevant topic to image classification and is frequently discussed; please see works [8, 10, 24–27]. In these papers, the technique used to perform image retrieval is the same: Do repeated measurements on identical copies of an images to obtain probability distribution of a group of orthogonal bases, which allow us to estimate the probability amplitude of each component of a quantum image (state) with enough precision for retrieval. This technique (measurement) is also required for quantum image classification, but it should be exploited with more elaboration. In general, the retrieval must obtain complete information via measurements in order to distinguish each different image. However, classification only requires partial information via measurements provided this information is enough to classify similar images into the same category.

Another relevant topic is how to search for simple patterns in binary images. Schützhold proposes an algorithm for the searching of simple patterns, such as a parallel straight line, in binary images. This algorithm takes advantage of quantum Fourier transformation to speed up the process, but it does not search for patterns that have no linear transformation relationship, such as a circle [28]. Venegas-Andraca uses entanglement to describe the relationship among the vertexes of a triangle or a rectangle. Based on this description, he also provides a method taking advantage of Bell inequality to retrieve such simple patterns in binary images [29]. However, these techniques can only be used for searching for simple patterns in binary image, and they are unsuitable for natural images.

Li and Caraiman discuss image segmentation. Li prepares operators to judge the gray-scale value of the pixels that are encoded by the same group of orthogonal bases and speeds up this procedure by taking advantage of the Grover algorithm [24]. Caraiman implements image segmentation based on setting a proper threshold by calculating histogram [30]. These techniques may not be used in image classification, because using raw image data directly to perform classification may lead to high failure rates and low efficiency.

Zhang discusses image registration. He binds a sequence number to different images and then uses these numbers to match images by using the Grover algorithm [31]. The essence of this algorithm is the comparison of the keyword that is bound to the image rather than the content of the image itself.

Compared to these previous works, our method has the following novel features:

• We are the first to put forward the concept of quantum global image features.

Prior to our work, there were no works involving how to acquire the global features of quantum images. The analogous works were all performed directly on the raw image data. We select the large coefficients of the Schmidt decomposition as the global features and use them to perform image classification. These features provide an efficient condensed form that can be used to approximate the original image and may also be used as an effective way to perform image classification.

• We put forward a new method to perform a similarity judgment of image classification.

Prior to our work, the analogous works concerning image retrieval, image segmentation and image registration all use the raw image data to judge the equivalence between two quantum images. However, equivalence judgment (vs. than similarity judgment) is invalid for tasks such as natural image classification. This is because there is very little difference in the backgrounds of two images with the same object, such as the face of the same person in various forms of illumination, and this can lead to misjudging the two images as being two irrelevant images. In classical pattern recognition, there are many ways to judge similarity: Euclidean distance, cosine distance, Manhattan distance and Hamming distance are the most popular forms of distance. In our revised algorithm, we set a threshold value t to judge the greatest similarity by computing the Hamming distance among all the images in the dataset. According to our analysis of the algorithm and the results of our experiments, we argue that the revised algorithm is an effective way to compute similarity among quantum images.

6 Conclusions and future work

Based on our simulated experiments and our analysis of the algorithm, we argue that our scheme is effective for large-scale image classification. The contributions of this paper are:

• We discovered that the Schmidt decomposition doing on quantum image has an effect like classical transformation doing on classical image. Based on this discovery, we firstly defined Schmidt coefficients as the global features of quantum image and extracted big values of these coefficients to encode as feature vectors (states) to do image classification.

• We also analyzed the Schuld’s algorithm and found its vague recognition of the nearest object in the large training set with the unclassified object by computing Hamming distance. Aiming at this drawback, we added an extra step to discriminate the nearest object from others by setting an appropriate threshold. By using a simple trick, the time cost to do the extra step is $O(n^3)$. As a result, the time efficiency of Schuld’s algorithm is improved from $O(TPn)^6$ to $O(Pn)^6$.

Although these contributions are noticeable, the work of this paper is still preliminary. Further work in the future may include:

• Seeking a more natural way to compute distance

Hamming distance is not a natural way to classify images. The main reason to select it as the metric for determining the class of a quantum image is its ability to discriminate among orthogonal quantum states. While orthogonal quantum states can be distinguished reliably, this does not ensure the correct classification of 100 % of quantum images. Because the task of image classification is measuring for similarity, the nature of this task implies that there is no way can be used to correctly classify 100 % of the images studied. Previous studies have already presented certain methods to improve the probability of the discrimination of nonorthogonal quantum states [17]. Thus, it is possible to classify quantum images in a more natural way, such as computing Euclidean distance between quantum images (states).

• Improve the ability of the classifier

The classifier is simple. More powerful tools, such as the quantum support vector machine [13], could be incorporated in our scheme to improve the ability to perform large-scale image classification.

QIP and QL are new research fields full of promise. In this paper, we presented a combination of these two fields and demonstrated a promising application of such a combination. The work of this paper has revealed directions that require further research, and the promising combination of QIP and QL will motivate us to continue this research and explore further.