Protocols of quantum key agreement solely using Bell states and Bell measurement

Abstract

Two protocols of quantum key agreement (QKA) that solely use Bell state and Bell measurement are proposed. The first protocol of QKA proposed here is designed for two-party QKA, whereas the second protocol is designed for multi-party QKA. The proposed protocols are also generalized to implement QKA using a set of multi-partite entangled states (e.g., 4-qubit cluster state and $\Omega$ state). Security of these protocols arises from the monogamy of entanglement. This is in contrast to the existing protocols of QKA where security arises from the use of non-orthogonal state (non-commutativity principle). Further, it is shown that all the quantum systems that are useful for implementation of quantum dialogue and most of the protocols of secure direct quantum communication can be modified to implement protocols of QKA.

1 Introduction

Since Bennett and Brassard [1] proposed the first protocol of unconditionally secure quantum key distribution (QKD), several aspects of secure quantum communication have been explored [2–7]. One such idea is quantum key agreement (QKA) [8–11]. There are two notions of QKA. In the weaker notion of QKA that was followed in [12], a key is generated by two or more parties through the negotiation, which happens in public. Under this weaker notion of QKA, many of the existing protocols of QKD can be viewed as protocols of QKA. For example, well-known BB84 [1], Ekert [2], and B92 [3] protocols of QKD qualify as protocols of QKA if we follow the weaker notion of QKA introduced in [12]. However, we are interested in a stronger notion of QKA that was introduced in Ref. [8] and is subsequently followed in all the recent works on QKA [9, 10, 13–19]. In this notion of QKA, all the parties involved in the key generation process contribute equally to construct the key. This is in contrast to QKD where a single party can control the entire key. Before we introduce new protocols of QKA, it is important to understand the differences between key distribution (KD) and key agreement (KA) in further detail. In a KD protocol, a trusted authority (TA) chooses a secret key that will be used in future for communication and transmits (distributes) it to other parties who want to communicate. In contrast, in a KA scheme (KAS): two or more parties establish a secret key on their own. Thus in two-party scenario, we may say that in protocols of KD, a key is created by Alice and the same is securely transmitted to Bob, while in the protocols of KA, both Alice and Bob contribute information that is subsequently used to derive the shared secret key. Further, in a good KAS, each party contributes equally to the shared key, and a dishonest party or a group of dishonest parties cannot control or completely decide the final key. The last point shows why all the traditional protocols of quantum cryptography, e.g., BB84 [1], B92 [3], ping-pong (PP) [5], and LM05 [6] are not protocols of QKA in their original forms.

Several protocols of classical key agreement are studied since the well-known Diffie–Hellman (DH) key agreement protocol or the exponential key agreement protocol was introduced by Diffie and Hellman in 1976 [20]. A large number of the classical key agreement protocols are actually variant of the DH protocol as they are based on intractability of the DH problem [21] and references therein]. To be precise, security of these protocols depends on the intractability of discrete logarithm (DL) problem, which may be stated as follows: given a generator $g$ of a cyclic group $G$ and an element $g^{x}$ in $G$, determine $x$. Quite similarly, the DH problem is stated as: given $g^{x}$ and $g^{y}$, determine $g^{xy}$ [22]. Clearly if we can solve DL problem in polynomial time then we will be able to solve DH problem in polynomial time. As there is no efficient classical algorithm for DL problem, modified and improved DH protocols have been considered to be secure for long. Interestingly, in 1997, Shor introduced polynomial-time quantum algorithms for prime factorization and discrete logarithms [23]. These two quantum algorithms clearly established that neither the RSA protocol nor the DH-based KA protocols would remain secure if a scalable quantum computer is built. This fact along with the already established unconditional security of QKD enhanced the interest on QKD and QKA.

First protocol of QKA was introduced by Zhou et al. in 2004 [8] using quantum teleportation. Almost simultaneously Hsueh and Chen [24] proposed another protocol of QKA. However, in 2009, Tsai and Hwang [13] showed that quantum teleportation-based Zhou et al. protocol was not a true protocol of QKA as a particular user can completely determine the final (shared) key without being detected. Next year Tsai et al. [14] showed that even protocol of Hsueh and Chen does not qualify as a protocol of QKA. In 2010, Chong and Hwang [9] developed a protocol of QKA using mutually unbiased bases (MUBs). Apparently, Chong Hwang (CH) protocol was the first successful protocol of QKA. They claimed that their protocol is based on BB84. However, a deeper analysis would show that their protocol is closer to LM05 protocol [6]. Of course, the security of both LM05 and BB84 protocols arises from the non-commutativity and nocloning principles. In 2011, Chong, Tsai, and Hwang [15] proposed a modified version of Hsueh and Chen protocol that is free from the limitations of the original protocol mentioned in Ref. [14]. All the successful and unsuccessful efforts of designing protocols of QKA until recent past were limited to two-party case. Recently, an enhanced interest on multi-party QKA schemes has been observed, and several protocols have been reported [10, 16–19]. A systematic review of all these existing works leads us to the following observations.

• 1. The amount of works reported to date on QKA is much less compared with the amount of works reported on other aspects of quantum cryptography, such as QKD, deterministic secure quantum communication (DSQC), quantum secure direct communication (QSDC), and quantum dialogue (QD). Thus, we may conclude that QKA is not yet studied rigorously, and probably many more combinations of quantum states and protocols of QKA can be found. Keeping this in mind, we show that majority of the existing protocols of QSDC, DSQC, and QD can be turned into protocol of QKA by introducing a delayed measurement technique.

• 2. Security of all the protocols of two-party and multi-party QKA reported to date is based on conjugate coding, i.e., the security is obtained using two or more MUBs, and thus, the protocols are essentially of BB84 type. This leads to a question: Is it essential to use non-orthogonal states (2 or more MUBs) for designing of protocols of QKA? The question is not yet answered, but the expected answer is “no” as QKA is related to QKD and a few orthogonal-state-based protocols of QKD (e.g., Goldenberg-Vaidman (GV) protocol [4] and N09 or counter-factual protocol [25]) are known since a few years. Further, some of the present authors have recently shown that protocols of QSDC and DSQC can be designed using orthogonal states [26, 27]. In addition, several exciting experiments on orthogonal-state-based QKD are reported in recent past [28–31]. These recent experimental observations and the recently proposed orthogonal-state-based protocols are very interesting as they are fundamentally different from the traditional conjugate coding-based protocols where two or more MUBs (set of non-orthogonal states) are used to provide security. Keeping these in mind, the present paper aims to provide orthogonal-state-based protocols of two-party and multi-party QKA.

Remaining part of the paper is organized as follows. In the next section, we present a protocol of QKA for two-party scenario. In Sect. 3, we provide a protocol of three-party QKA and discuss the possibilities of extending it to $n$-party ($n>3)$ scenario. Specifically, we have shown that the proposed three-party protocol can be extended to a five-party protocol of QKA that uses 4-qubit $|\Omega \rangle$ state or 4-qubit cluster state. In Sect. 4, security and efficiency of the proposed protocols are discussed and are compared with that of other existing protocols of QKA. In Sect. 5, we investigate the possibilities of transforming the existing protocols of QSDC, DSQC, and QD to protocols of QKA. Finally, the paper is concluded in Sect. 6.

2 Protocol 1: A two-party protocol of QKA

Step 1::

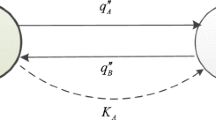
Alice prepares $|\psi ^{+}\rangle ^{\otimes n}$ where $|\psi ^{+}\rangle =\frac{|00\rangle +|11\rangle }{\sqrt{2}}$. She uses first qubits of each Bell state to form an ordered sequence $p_{A}=\{p_{A}^{1},\, p_{A}^{2},\, p_{A}^{3},\ldots ,\, p_{A}^{n}\}.$ Similarly, she forms an ordered sequence $q_{A}=\{q_{A}^{1},\, q_{A}^{2},\, q{}_{A}^{3},\ldots ,\, q_{A}^{n}\}$ with all the second qubits. Here, $p_{A}^{i}$, $q_{A}^{i}$ denote the first and second particles of $i^{th}$ copy of the Bell state $|\psi ^{+}\rangle ,$ for $1\le i\le n$. She also prepares a random sequence $K_{A}=\{K_{A}^{1},\, K_{A}^{2},\, K_{A}^{3},\ldots ,\, K_{A}^{n}\}$, where $K_{A}^{i}$ denotes the $i^{th}$ bit of sequence $K_{A}$ and $K_{A}^{i}$ is randomly chosen from $\{0,1\}.$ $K_{A}$ may be considered as Alice’s key.

Step 2::

Alice prepares a sequence of $\frac{n}{2}$ Bell states ( $|\psi ^{+}\rangle ^{\otimes \frac{n}{2}}$) as decoy qubits and concatenates the sequence with $q_{A}$ to form an extended sequence $q_{A}^{\prime }$. She applies a permutation operator $\Pi _{2n}$ on $q_{A}^{\prime }$ to create a new sequence $\Pi _{2n}q_{A}^{\prime }=q_{A}^{\prime \prime }$ and sends that to Bob.

Step 3::

After receiving the authentic acknowledgment of the receipt of the entire sequence $q_{A}^{\prime \prime }$ from Bob, Alice announces the coordinates of the qubits $(\Pi _{2n}$) sent by her. Using the information, Bob rearranges the qubits and performs Bell measurements on the decoy qubits and computes the error rate. Ideally, in absence of Eve, all the decoy Bell states are to be found in $|\psi ^{+}\rangle .$ If the error rate is found to be within the tolerable limit, they continue to the next step, otherwise they discard the protocol and go back to Step 1.

Step 4::

Bob drops the decoy qubits to obtain $q_{A}$. Now, he prepares a new random sequence $K_{B}=\{K_{B}^{1},\, K_{B}^{2},\, K_{B}^{3},\ldots ,\, K_{B}^{n}\}$, where $K_{B}^{i}$ denote the $i^{th}$ bit of sequence $K_{B}$, for $1\le i\le n$ and $K_{B}^{i}$ is randomly chosen from $\{0,1\}.$ $K_{B}$ may be considered as Bob’s key. He applies a unitary operation on each qubit of sequence $q_{A}$ to encode $K_{B}$. The encoding scheme is as follows: to encode $K_{B}^{i}=0$ and $K_{B}^{i}=1$, he applies $I$ and $X$, respectively, on $q_{A}^{i}$. This forms a new sequence $q_{B}$. After encoding operation, Bob concatenates $q_{B}$ with a sequence of $\frac{n}{2}$ Bell states ( $|\psi ^{+}\rangle ^{\otimes \frac{n}{2}}$) that is prepared as decoy qubits and subsequently applies the permutation operator $\Pi _{2n}$ to obtain an extended and randomized sequence $q_{B}^{\prime }$ which he sends to Alice.

Step 5::

After receiving the authenticated acknowledgment of the receipt of the entire sequence $q_{B}^{\prime }$ from Alice, Bob announces the position of the decoy qubits (note that he does not disclose the actual order of the message qubits), i.e., $\Pi _{n}\in \Pi _{2n}.$ Alice checks the possibility of eavesdropping by following the same procedure as in Step 3. If the error rate is found to be within the tolerable limit, they continue to the next step, otherwise they discard the protocol and go back to Step 1.

Step 6::

Alice publicly announces her key $K_{A}$ and Bob uses that and his own key (sequence) $K_{B}$ to form the shared key: $K=K_{A}\oplus K_{B}$.

Step 7::

Bob announces the actual order of the message qubits $(\Pi _{n}\in \Pi _{2n})$ and Alice uses that information to obtain $q_{B}.$ Now, she combines $p_{A}$ and $q_{B}$ and performs Bell measurements on $p_{A}^{i}q_{B}^{i}$. This would reveal $K_{B}$ as she knows the initial state and the encoding scheme used by Bob.

Step 8::

Using $K_{A}$ and $K_{B}$, Alice prepares her copy of the shared key, i.e., $K=K_{A}\oplus K_{B}$.

The protocol discussed above is an orthogonal-state-based two-party protocol of QKA. However, several multi-party protocols of QKA are introduced in recent past [10, 16–19]. Of course, none of these recently introduced multi-party QKA protocols are based on orthogonal state. Keeping these in mind, we aim to provide a completely orthogonal-state-based protocol of three-party QKA along the line of [10]. Further, the possibility of extending the proposed orthogonal-state-based three-party protocol into $n$-party case with $n>3$ is also discussed in the following section.

3 Protocol 2: A multi-party protocol of QKA

In analogy to the previous protocol Alice, Bob and Charlie produce their secret keys:

$$\begin{aligned} \begin{array}{lc} K_{A} &{} =\{K_{A}^{1},\, K_{A}^{2},\, K_{A}^{3},\ldots ,\, K_{A}^{n}\},\\ K_{B} &{} =\{K_{B}^{1},\, K_{B}^{2},\, K_{B}^{3},\ldots ,\, K_{B}^{n}\},\\ K_{C} &{} =\{K_{C}^{1},\, K_{C}^{2},\, K_{C}^{3},\ldots ,\, K_{C}^{n}\},\end{array} \end{aligned}$$

where $K_{A}^{i},\, K_{B}^{i},\, K_{C}^{i}$ denote $i^{th}$ bit of key of Alice, Bob and Charlie, respectively,¹ and $i=1,\,2,\ldots ,\, n$. We describe a protocol of multi-party QKA in the following steps.

Step 1::

Alice, Bob, and Charlie separately prepare $|\psi ^{+}\rangle _{A}^{\otimes n}$, $|\psi ^{+}\rangle _{B}^{\otimes n}$ and $|\psi ^{+}\rangle _{C}^{\otimes n}$, respectively. As in Step 1 of the previous protocol, Alice prepares two ordered sequences $p_{A}=\{p_{A}^{1},\, p_{A}^{2},\, p_{A}^{3},\ldots ,\, p_{A}^{n}\}$ and $q_{A}=\{q_{A}^{1},\, q_{A}^{2},\, q_{A}^{3},\ldots ,\, q_{A}^{n}\}$ composed of all the first and the second qubits of the Bell states that she has prepared. Similarly, Bob and Charlie prepare $p_{B}=\{p_{B}^{1},\, p_{B}^{2},\, p_{B}^{3},\ldots ,\, p_{B}^{n}\}$, $q_{B}=\{q_{B}^{1},\, q_{B}^{2},\, q_{B}^{3},\ldots ,\, q_{B}^{n}\}$ and $p_{C}=\{p_{C}^{1},\, p_{C}^{2},\, p_{C}^{3},\ldots ,\, p_{C}^{n}\}$, $q_{C}=\{q_{C}^{1},\, q_{C}^{2},\, q_{C}^{3},\ldots ,\, q_{C}^{n}\}$ from $|\psi ^{+}\rangle _{B}^{\otimes n}$ and $|\psi ^{+}\rangle _{C}^{\otimes n}$, respectively.

Step 2::

Each of Alice, Bob, and Charlie separately prepares sequence of $\frac{n}{2}$ Bell states ($|\psi ^{+}\rangle ^{\otimes \frac{n}{2}})_{j}$ with $j\in \{A,\, B,\, C\}$ as decoy qubits and concatenates the sequence with $q_{j}$ to form extended sequences $q_{j}^{\prime }$. Subsequently, user $j$ applies permutation operator $(\Pi _{2n})_{j}$ on $q_{j}^{\prime }$ to create a new sequence $(\Pi _{2n})_{j}q_{j}^{\prime }=q_{j}^{\prime \prime }$ and sends that to user $j+1$. Here, we follow a notation in which $j\in \{A,\, B,\, C\}$ and $A,\, B,C$ follow a modulo $3$ algebra that gives us the relations: $A+3=B+2=C+1=A,$ $A=C+1,\, B=A+1,\,$ $C=B+1$ and so on.

Step 3::

After receiving the authentic acknowledgment of receipt from the receiver (user $j+1$), corresponding sender (user $j$) announces the coordinates of the qubits $(\Pi _{2n})_{j}$ sent by him/her. Each receiver computes error rate as in Step 3 of the previous protocol. If the computed error rates are found to be within the tolerable limit, they continue to the next step, otherwise they discard the protocol and go back to Step 1.

Step 4::

After discarding the decoy qubits, each user $j$ encodes his/her secret bits by applying the unitary operation on each qubit of the sequence received by him (i.e., on $q_{j-1}$) in accordance with his/her key $K_{j}$. The encoding scheme is as follows: If $K_{j}^{i}=0\,(1)$ then user $j$ applies $I\,(X)$ on $q_{j-1}^{i}.$ As a result of encoding operations, user $j$ obtains a new sequence $r_{j}$. After the encoding operation, user $j$ concatenates $r_{j}$ with a sequence of $\frac{n}{2}$ Bell states ( $|\psi ^{+}\rangle ^{\otimes \frac{n}{2}})_{j}$ that is prepared as decoy qubits and subsequently applies the permutation operator $(\Pi _{2n})_{j}$ to obtain an extended and randomized sequence $r_{j}^{\prime }$, which he/she sends to the user $j+1$.

Step 5::

After receiving the authentic acknowledgment of the receipt of the sequence $r_{j}^{\prime }$ from the receiver $j+1$, the sender $j$ announces the coordinates of the decoy qubits, i.e., $(\Pi _{n})_{j}\in (\Pi _{2n})_{j}$. User $j+1$ uses the information for computing the error rate as before and if it is below the threshold value then they go on to the next step, otherwise they discard the communication. In absence of eavesdropping, user $j$ announces the coordinates of the message qubits, i.e., $(\Pi _{n})_{j}\in (\Pi _{2n})_{j}$.

Step 6::

Same as Step 4 with only difference that if $K_{j}^{i}=0$ and $K_{j}^{i}=1$ then user $j$ applies $I$ and $Z$, respectively, on $r_{j-1}^{i}.$ As a result of encoding operations, user $j$ obtains a new sequence $s_{j}$, and after insertion of decoy qubits and applying permutation operator, he/she obtains a randomized sequence $s_{j}^{\prime }$ which he/she sends to the user $j+1$.

Step 7::

Same as Step 5.

Step 8::

After discarding the decoy qubits, each user rearranges the sequence received by him/her. Now each user $j$ has two ordered sequences $p_{j}$ and $s_{j-1}.$ Each of the users $j$ performs Bell measurements on $p_{j}^{i}s_{j-1}^{i}$. According to the output of the Bell measurement and Table 1 each user $j$ can obtain the secret keys of the other two parties. Hence, the shared secret key $K=K_{A}\oplus K_{B}\oplus K_{C}$ can be generated.

Table 1 Transformation of $|\psi ^{+}\rangle$ based on two operations

Here, we note that $\{I,\, X,\, iY,\, Z\}$ is a modified Pauli group² under multiplication and $\{I,\, X\},$ $\{I,\, Z\}$ are its disjoint subgroups. Here, disjoint subgroups refer to two subgroups $g_{i}$ and $g_{j}$ of a group $G$ that satisfy $g_{i}\cap g_{j}=\{I\},$ where $I$ is the identity element. Thus, except identity element $g_{i}$ and $g_{j}$ do not contain any other common element. Now, we assume that $G$ is a group of order $M$ under multiplication and elements of $G$ are $x$-qubit unitary operators. Further, we assume that there exist $n$ mutually disjoint subgroups $g_{i}$ with $i=1,\ldots ,\, n$ of the group $G$ such that $g_{i}$’s are of equal size (say each of the $g_{i}$’s has $2^{y}$ elements) and $\Pi _{i}^{\otimes m}g_{i}=g_{1}\otimes g_{2}\otimes g_{3}\otimes \ldots \otimes g_{m}=\left\{ U_{1},U_{2},\ldots ,U_{(2^{y})^{m}}\right\}$ where $\left( 2^{y}\right) ^{m}\le M$; $U_{i}\in G$ and $U_{i}\ne U_{l}$ $\forall \, i,\, l\in \left\{ 1,2,\ldots ,\left( 2^{y}\right) ^{m}\right\} .$ Now if we have $I^{\otimes \left( N-x\right) }U_{i}|\phi _{0}\rangle =|\phi _{i}\rangle$ and $\langle \phi _{i}|\phi _{l}\rangle =\delta _{i,l}$ where $|\phi _{i}\rangle$ is an $N$-qubit quantum state with $N>x,$ then we can have an $(m+1)$-party version of Protocol 2 of QKA. In this $(m+1)$-party protocol of QKA all the $(m+1)$ parties create quantum state $|\phi _{0}\rangle$ in the beginning. Each user keeps the first $N-x$ qubits of $|\phi _{0}\rangle$ with himself/herself and sends the remaining qubits to the user $j+1$ after following the strategy for eavesdropping checking. Subsequently, user $j$ encodes his/her $y$-bit secret key ($N>x\ge y$) by applying unitary operators from $g_{1}$ on the $x$ qubits that he/she has received from the user $j-1$ in the previous step and sends the key encoded state to user $j+1$. After $m$ rounds of such encoding (in $k^{\mathrm{th}}$ round of encoding operation, all the users encode their keys using elements of $g_{k}$) and communication operations user $j$ measures the $N$ qubits of his/her possession using $\{|\phi _{i}\rangle \}$ basis. From the input state ($|\phi _{0}\rangle$) and output state (say, $|\phi _{\mathrm{\mathrm{final}}}\rangle =|\phi _{k}\rangle )$, he/she would know the unitary operator $U_{k}$ that has converted the initial state into the final state. Now, the condition $\Pi _{i}^{\otimes m}g_{i}=\left\{ U_{1},U_{2},\ldots ,U_{(2^{y})^{m}}\right\}$ where $U_{i}\in G$ and $U_{i}\ne U_{l}$ ensures that every sequence of encoding operations will lead to different $U_{k}$, and this is how user $j$ can know the key encoded by the other users and he/she can use that to create the shared key $K_{1}\oplus K_{2}\oplus \ldots \oplus K_{m},$ where the secret key of the user $j$ is $K_{j}.$

In Protocol 2, we have used modified Pauli group $G=G_{1}=\{I,\, X,\, iY,\, Z\}.$ It has three disjoint subgroups: $g_{1}=\{I,X\},\, g_{2}=\{I,Z\},\, g_{3}=\{I,iY\}$ which satisfy $g_{1}\otimes g_{2}=g_{2}\otimes g_{3}=g_{3}\otimes g_{1}=G_{1}.$ Further, $|\phi _{0}\rangle =|\psi ^{+}\rangle$ and as $G_{1}$ is the set of elements used for dense coding using Bell states so it naturally implies $U_{i}|\phi _{0}\rangle =|\phi _{i}\rangle \forall \, U_{i}\in G:$ $\langle \phi _{i}|\phi _{l}\rangle =\delta _{i,l}$. Thus, Protocol 2 is a special case of a more general scenario described here. Many more examples can be obtained from the properties of Pauli groups discussed in Ref. [33]. Just to provide specific examples, we may note that for the modified Pauli group

$$\begin{aligned} G_{2}&= G_{1}\otimes G_{1}=\{I,\, X,\, iY,\, Z\}\otimes \{I,\, X,\, iY,\, Z\}\nonumber \\&= \left\{ I\otimes I,\, I\otimes X,\, I\otimes iY,\, I\otimes Z,\, X\otimes I,\, X\otimes X,\right. \nonumber \\&X\otimes iY,\, X\otimes Z,\, iY\otimes I,\, iY\otimes X,\, iY\otimes iY,\nonumber \\&\left. iY\otimes Z,Z\otimes I,\, Z\otimes X,\, Z\otimes iY,\, Z\otimes Z\right\} \end{aligned}$$

(1)

we have following disjoint subgroups of order 2: $g_{1}=\left\{ I\otimes I,\, I\otimes X\right\} ,\, g_{2}=\left\{ I\otimes I,\, X\otimes I\right\} ,\, g_{3}=\left\{ I\otimes I,\, I\otimes Z\right\} ,\, g_{4}=\left\{ I\otimes I,\, Z\otimes I\right\} ,$ $g_{5}=\left\{ I\otimes I,\right. \left. I\otimes iY\right\}$, and $g_{6}=\left\{ I\otimes I,\, iY\otimes I\right\}$. Further, these disjoint subgroups satisfy

$$\begin{aligned} g_{1}\otimes g_{2}\otimes g_{3}\otimes g_{4}=g_{1}\otimes g_{2}\otimes g_{5}\otimes g_{6}=g_{3}\otimes g_{4}\otimes g_{5}\otimes g_{6}=G_{2} \end{aligned}$$

(2)

and the elements of $G_{2}$ can be used for dense coding using 4-qubit maximally entangled $|\Omega \rangle$ state and cluster ($|C\rangle )$ state if the elements of $G_{2}$ operate on first and third qubits of these states. Here,

$$\begin{aligned} |\Omega \rangle&= \frac{1}{2}(|0000\rangle +|0110\rangle +|1001\rangle -|1111\rangle ),\\ |C\rangle&= \frac{1}{2}(|0000\rangle +|0011\rangle +|1100\rangle -|1111\rangle ). \end{aligned}$$

The table of dense coding for these states using elements of $G_{2}$ is explicitly shown in our earlier work (see Table 1 of Ref. [33]). As the elements of $G_{2}$ can be used for dense coding using $|\Omega \rangle$ and $|C\rangle$ states, output states obtained on application of the elements of $G_{2}$ on $|\Omega \rangle$ or $|C\rangle$ are mutually orthogonal. This clearly implies that we can construct a five-party protocol of QKA using $|\Omega \rangle$ or $|C\rangle$ state where each user prepares a large number of copies of one of these two states and keeps second and fourth qubit with himself/herself and sends the remaining qubits to next user and later encodes his/her secret key using $g_{i}'$s. In a five-party protocol, encoding operation should take place in 4 rounds and the users would use either $g_{1},g_{2},g_{3},g_{4}$ or $g_{1},g_{2},g_{5},g_{6}$ or $g_{3},g_{4},g_{5},g_{6}.$ We can generate many more examples of multi-party protocols of QKA using similar strategy and properties of modified Pauli group.

4 Security and efficiency analysis

Protocol 2 is designed along the line of existing protocol of Yin, Ma, and Liu [10] with a modified strategy of eavesdropping checking that converts the non-orthogonal-state-based protocol of Yin, Ma, and Liu into an orthogonal-state-based protocol. Unconditional security of the eavesdropping checking using this technique is already shown in our earlier works [26, 27] where we have also established that security of this orthogonal-state-based technique of eavesdropping checking originates from the monogamy of entanglement [27]. Thus, the protocol is secure against external attacks (eavesdropping). Remaining part of the protocol is technically equivalent to Yin Ma Liu (YML) protocol, and consequently, the security of YML protocol against the internal attacks (i.e., the attempts of malicious Alice, Bob, and Charlie to completely control the key either individually or by mutual cooperation of any two users) is applicable here, too. Thus, Protocol 2 is a secure protocol of QKA, and it does not need any separate elaborate discussion. Keeping this in mind in the remaining part of the present section, we have explicitly analyzed the security of Protocol 1.

4.1 Security against eavesdropping

Our Protocol 1 and also the protocol of Chong and Hwang [9] may be viewed as protocols of secure direct communication of $K_{B}$ from Bob to Alice added with a classical communication of $K_{A}$ from Alice to Bob. Specifically, instead of sending a meaningful message, Alice and Bob send random keys to each other. While Bob sends his key $K_{B}$ by using a DSQC or QSDC scheme, Alice announces her key $K_{A}$ publicly. Security proofs of the existing protocols of DSQC and QSDC ensure that the key communicated by Bob (i.e., $K_{B})$ using DSQC or QSDC scheme is unconditionally secure. Thus, Eve has no information about $K_{B}.$ On the other hand, the key communicated by Alice (i.e., $K_{A}$) is a public knowledge. However, it does not affect the secrecy of the shared key as the final shared key to be produced and used is $K_{A}\oplus K_{B},$ knowledge of $K_{A}$ alone does not provide any information about $K_{A}\oplus K_{B}$. Thus, the shared key produced in this manner is secure from external attacks of Eve. However, there may exist insider attacks in which Alice or Bob tries to completely control the shared key. Security of Protocol 1 against such attacks is described below.

4.1.1 Security against dishonest Alice

To communicate $K_{B}$ if Alice and Bob use a standard protocol of DSQC or QSDC (say they use PP protocol), then it would be possible for Alice to know Bob’s secret key before she announces $K_{A}.$ In that case, she will be able to completely control the shared key by manipulating $K_{A}$ as per her wish. To circumvent this attack, we have modified the protocol in such a way that Bob does not announce the coordinates of the message qubits sent by him till he receives $K_{A}.$ This strategy introduces a delay in measurement of Alice, and this delayed measurement strategy ensures that Alice cannot control the key by knowing $K_{B}$ prior to her announcement of $K_{A}$.

4.1.2 Security against dishonest Bob

Alice announces her key only after receiving the message qubits (without their actual order) from Bob. This ensures that Bob cannot control the key by knowing Alice’s key. Only thing that Bob can do after knowing $K_{A}$ is to change/modify the coordinates of $q_{B}^{\prime }$, but any modification in that would lead to entanglement swapping in our case and that would lead to probabilistic outcomes without any control of Bob. Further, Bob will be completely unaware of $K_{B}$ to be generated by Alice in that case and as a consequence any such effort of Bob would lead to different keys at ends of Alice and Bob. Thus, the protocol ensures that Bob cannot control the key. Here, we may note that similar strategy was used in Chong and Hwang [9] protocol. In their protocol, modified QSDC scheme that was used for Bob to Alice communication was equivalent to LM05 [6] protocol. In contrast, here, we have used a modified orthogonal version of PP-type protocol, which may be referred to as $\mathrm{PP^{GV}}$ protocol [27].

5 Turning existing protocols of quantum communication to protocols of QKA

In the previous sections, we have seen that there exist a strong link between protocols of DSQC/QSDC and those of QKA. For example, PP [5] and LM05 [6] protocols of QSDC have already been employed to design protocols of QKA (Protocol 1 presented here and CH protocol [9]). This observation leads to an important question: Is it possible to convert all protocols of secure direct quantum communication into protocols of QKA? In what follows we aim to answer this question. We also aim to study the possibilities of transforming other protocols of quantum communication to protocols of QKA.

5.1 Turning a protocol of QSDC/DSQC to a protocol of QKA

Recently, we have shown that maximally efficient protocols for secure direct quantum communications can be constructed using any arbitrary orthogonal basis [26]. However, all of them will not lead to protocol of QKA. To be precise, eavesdropping can be avoided in all protocols of DSQC and QSDC, and by randomizing the sequence of key encoded bits sent by Bob (i.e., by delaying the measurement to be performed by Alice), we can circumvent the attacks of dishonest Alice, but it is not sufficient to build a protocol of QKA. We also need to avoid the attacks of dishonest Bob. To do so, we need to restrict the information available to Bob. Specifically, Bob must not have complete information of the basis that is used to prepare the qubits on which he has encoded his key. In our Protocol 1 and in all orthogonal-state-based two-way DSQC/QSDC protocols, this can be achieved if Alice keeps some of the qubits of each entangled state with her as that would restrict Bob from changing $K_{B}$ after receiving $K_{A}$. The same can be achieved in a non-orthogonal-state-based protocol by using more than one MUBs. If Alice prepares the state randomly using one of the basis sets and do not disclose the basis set used by her till Bob discloses the sequence then Bob will not have complete access of the basis set used for preparation of the message qubits. As a consequence, he will not be able to control the key. This is shown in a particular case in Ref. [9].

The above discussion shows that the DSQC/QSDC protocol to be used to implement a QKA protocol cannot be one-way as in that case Bob will have complete access to the basis in which the quantum state used for encoding of his key is prepared (since in a one-way protocol Bob himself will prepare the quantum state). Thus, none of the one-way protocol of DSQC or QSDC would lead to QKA. However, most of the two-way protocols of secure quantum communication would lead to QKA. As example, we may note both Deng Long Liu (DLL) protocol [34] and Cai Li (CL) protocol [35] can be viewed as variant of PP protocol [36], but DLL being a one-way protocol would not give us a QKA protocol, but two-way CL protocol would lead to a QKA protocol.

5.2 Turning a protocol of QD to a protocol of QKA

A very interesting two-way quantum communication scheme is QD [33] and references therein]. Since in the above, we have already seen that two-way secure direct communication is useful for QKA and since a large number of alternatives for implementing quantum dialogue are recently proposed by us (see Table 4 of Ref. [33]), it would be worthy to investigate the relation between QKA and QD. In a Ba An-type QD protocol [37], Alice keeps part of an entangled state ($|\phi \rangle _{i})$ with herself and encodes her secret on the remaining qubits by applying unitary operation $U_{A}$ and subsequently sends the message encoded qubits to Bob who applies $U_{B}$ on them and returns the qubits to Alice with appropriate strategy of eavesdropping checking. Now, Alice measures the final state ($|\phi \rangle _{f})$ and announces the outcome. As the states and operators are chosen in such a way that $|\phi \rangle _{i}$ and $|\phi \rangle _{f}$ are mutually orthogonal, from the announcement of Alice we know $U_{A}U_{B}$. As Alice (Bob) knows $U_{A}\,(U_{B})$, she (he) can easily obtain $U_{B}\,(U_{A})$ using $U_{A}U_{B}$ obtained from the announcement of Alice. For a detailed discussion, see Ref. [33] where it is explicitly shown that if we have a set of mutually orthogonal $n$-qubit states $\{|\phi _{0}\rangle ,|\phi _{1}\rangle ,\ldots ,|\phi _{i}\rangle ,\ldots ,|\phi _{2^{n}-1}\rangle \}$ and a set of $m$-qubit unitary operators $\{U_{0},U_{1},U_{2},\ldots ,U_{2^{n}-1}\}$ such that $U_{i}|\phi _{0}\rangle =|\phi _{i}\rangle$ and $\{U_{0},U_{1},U_{2},\ldots ,U_{2^{n}-1}\}$ forms a group under multiplication then it would be sufficient to construct a quantum dialogue protocol of Ba An type. Now assume that $n>m$ and Alice encodes nothing (i.e., she always choose $U_{A}=I_{m}$ ) and keeps $(n-m)$-qubits with herself and sends the remaining $m$-qubits to Bob who encodes his key by applying an $m$-qubit unitary operation $U_{B}$ and sends that back to Alice, but only after changing the order so that Alice cannot measure the final state immediately. Alice announces her key after receiving the key encoded qubits from Bob as in Protocol 1 and subsequently Bob announces the sequence of the message qubits sent by him. In QKA, Alice does not need to disclose her measurement outcome. This modified QD protocol is equivalent to our Protocol 1. This clearly shows that all protocols of QD with $n>m$ would lead to protocols of QKA. It is interesting because in [33], we have shown that a large number of alternative combinations of quantum states and unitary operators can be used to implement QD. All of them (if $n>m$) will be useful for QKA, too.

5.3 Efficiency analysis

A well-known measure of efficiency of secure quantum communication is known as qubit efficiency [38], which is given as

$$\begin{aligned} \eta =\frac{c}{q+b}, \end{aligned}$$

(3)

where $c$ denotes the total number of transmitted classical bits (message bits), $q$ denotes the total number of qubits used, and $b$ is the number of classical bits exchanged for decoding of the message (classical communication used for checking of eavesdropping is not counted). This measure was introduced by Cabello in 2000, and it has been frequently used since then to compare protocols of secure direct communication. As we are not interested in communicating a message here, so we may modify the meaning of $c$ in $\eta$ to make it suitable for comparison of protocols of QKA. In the modified notion, $c$ is the length of the shared key generated by the protocol. Thus, in case of our first protocol, if we generate an $n$-bit shared key then $c=n.$ Further, in the entire protocol, we have used $2n$ Bell states, i.e., $4n$ qubits (of which $n$-Bell states were used as decoy qubits). Thus, $q=4n$. Now, Alice and Bob announce the coordinates of the message qubits and Alice announces $K_{A}$, each of these three steps require communication of $n$ classical bits. Thus, $b=3n.$ All other classical communications incurred in the process are related to the checking of eavesdropping and classical bits exchanged for eavesdropping checking are not counted in $b$. Thus, $b=3n.$ This makes $\eta =\frac{n}{4n+3n}=\frac{1}{7}=14.29\,\%.$ In the similar manner, if an $n$-bit shared key is prepared through Protocol 2 then $c=n$ and $q=3(2n+3n)$ as each party creates $n$ Bell states for key encryption and $\frac{3n}{2}$ Bell states for eavesdropping checking. Further, each party uses $3n$ bits of classical information for the disclosure of coordinates of the message qubits. Thus, $b=3\times 3n=9n$ and consequently $\eta =\frac{n}{15n+9n}=\frac{1}{24}=4.17\%.$ As YML protocol is similar to the Protocol 2 with only difference in the strategy adopted for eavesdropping checking, for YML protocol also we obtain $\eta =4.17\%$. Clearly, Protocol 1 is more efficient than Protocol 2 and YML protocol, but Protocol 1 is less efficient than its QSDC counterpart ($\mathrm{PP^{GV}}$ protocol) whose qubit efficiency as per the unmodified definition is $\eta =\frac{n}{4n+2n}=\frac{1}{6}=16.67\,\%$.³ This is expected as with the increase on number of parties contributing to the key, $q$ and $b$ required to generate the key of same size should also increase. This point can be further established by noting that $\eta$ for the five-party protocol described above will be $\frac{1}{70}=1.43\,\%$ as $q=4n\times 5=20n,$ $b=2n\times 5\times 5=50n$ and $c=n.$

6 Conclusions

In the present work, we have proposed two protocols of QKA. The first one works for two-party case and the second one works for multi-party case. Both the protocols in their original form use only Bell basis for preparation of the encoding states and their measurement for decoding and eavesdropping check. Subsequently, it is shown that the applicability of the proposed protocols can be extended to 4-qubit cluster state and $\Omega$-state. This specific feature that the states are measured and prepared using the same basis implies that conjugate coding (non-commutativity) is not essential for obtaining the required security for QKA, and it is possible to construct completely orthogonal-state-based protocols of QKA. Here, it would be apt to note that the use of entangled states in general and Bell states in particular for implementation of protocols of secure quantum communication is not new. From the early days of secure quantum communication, entangled states were used to implement protocols of QKD, QSDC, and DSQC [2, 5, 34, 35]. However, in all those entangled-state-based protocols (e.g., Ekert’s protocol of QKD [2], CL protocol of QSDC [35] and DLL protocol of DSQC [34]) eavesdropping was checked using two or more MUBs. For example, 3 MUBs were used in Ekert’s protocol and 2 MUBs were used in DLL and CL protocols. As mutually non-orthogonal bases (i.e., MUBs or non-commutativity) were used in these protocols and in the YML protocol of QKA [10] for the eavesdropping check, none of these entangled-state-based protocols are completely orthogonal-state-based protocol and their security arises from conjugate coding. However, the protocols of QKA proposed here use only a single (Bell) basis and consequently establish that conjugate coding is not essential for the implementation of unconditionally secure protocols of QKA. Thus, these protocols essentially establish that the protocols proposed here are completely orthogonal-state-based protocols, and their security is independent of conjugate coding.

The proposed protocols are the first set of orthogonal-state-based protocols of QKA as all the existing protocols of QKA are based on conjugate coding. Thus, the proposed protocols are fundamentally different from all the existing protocols of QKA. As the orthogonal-state-based protocols show that the use of conjugate coding or in other words use of non-commutativity principle is not essentially required for unconditional security, they require lesser quantum resources in a sense. To be precise, monogamy of entanglement is sufficient to protect these protocols [27].

We have also shown that most of the existing protocols of QSDC and DSQC and all the protocols of QD can be turned into protocols of QKA. This is an interesting observation as a protocol of QSDC, DSQC, or QD requires a relatively stricter security compared with a protocol of QKD or QKA. The requirement of relatively stricter security arises from the fact that in a protocol of QKD or QKA, if we obtain signatures of eavesdropping, then we can drop the key and create a new one. Thus, we do not bother about information leakage due to eavesdropping as long as we can detect all attempts of eavesdropping. However, in a protocol of QSDC, DSQC, or QD, we cannot afford to allow information leakage as in contrast to QKD (where a random sequence is sent) a meaningful information is sent in a protocol of QSDC, DSQC, or QD. This point may be elaborated by briefly noting that a protocol of QSDC or DSQC can always be reduced to protocol of QKD, but the converse is not true in general. Just as a simple example, we may consider that Alice and Bob have devices to implement a protocol of QSDC. Thus, Alice is capable of securely communicating a meaningful message to Bob. Now, if we assume that Alice has a random number generator and she uses that to generate a sequence of random numbers and communicates that to Bob as a key (thus a random message is communicated instead of a meaningful message), the key would be secure as any message sent using the QSDC protocol is secure. Thus it is straightforward to reduce a protocol of QSDC to a protocol of QKD. In brief, a protocol requiring stricter security can be reduced to a protocol requiring relatively weaker security if other requirements are satisfied. This fact is intrinsically used in Sect. 5 to establish that most of the existing protocols of QSDC and DSQC and all the protocols of QD can be turned into protocols of QKA. As several schemes of implementing QSDC, DSQC, and QKD are already known, the present work leads to several new options for implementation of QKA. Further, as the orthogonal-state-based protocols of QKD are experimentally implemented in recent past, the protocols proposed here seem to be experimentally realizable.