1 Introduction

Key agreement, also called key exchange, is a cryptographical primitive which allows two participants to interact with each other so that they can share a secret key. The shared key can be used for a secret-key cryptosystem or authentication protocols. These protocols allow parties to share secret keys freely and securely over insecure channel without the need for a previously-established shared secret. Different from the key distribution, in which one party distributes a secret key to the other ones, all involved parties in a key agreement protocol can equally influence the outcome of the protocol, and no one can decide the shared key alone. In other words, in addition to have the same ability of resisting adversaries from the outside world as the key distribution protocol does, a secure key agreement protocol is also required to prevent the participant attacks, i.e., the dishonest party may try to determine the secret key alone. The first practical solution to the key agreement problem was the Deffie-Hellman exponential key exchange in 1976 [1]. Since the pioneering work of Diffie and Hellman, a number of work began to consider the multiparty key agreement. Multiparty key agreement can be seen as a generalization of two-party key agreement. The first multiparty key agreement was proposed by Ingemarsson et al. in 1982 [2], which is a nature extension of the classical Diffe-Hellman key agreement protocol. However, key agreement protocols become increasingly vulnerable with more powerful quantum computation [3, 4] since their security is mostly based on the computation complexity.

On the other hand, quantum cryptography, which is based on the principle of quantum mechanical to perform cryptographic tasks, can provide unconditional security [5]. A lot of attention has focused on the quantum cryptography, and it has been developed quickly since the quantum key distribution protocol (BB84) was proposed by Bennett and Brassard in 1984 [6], such as quantum key distribution [7–11], quantum secret sharing [12–15], quantum secure direct communication [16–26], quantum private comparison [27–32], quantum signature [33, 34] and quantum oblivious transfer [35].

Quantum key agreement (QKA), a new branch of quantum cryptography, was first proposed by Zhou et al. in 2004 [36], which utilizes quantum mechanics to guarantee its security. In their protocol, the quantum teleportation technique [37] was used to generate a secret key over public channels. However, there are some attacks on Zhou et al.’s protocol, e.g., a party can fully determine the shared key alone, i.e., it is not a fair QKA [38], and it is susceptible to the participant attack [39]. Later, Chong and Hwang [40] proposed a new QKA protocol based on BB84 protocol, in which the technique of delayed measurement and the authenticated classical channel were used. Recently, Huang et al.[41] considered the QKA protocol in the collective noise channels. However, only two participants were involved in the above QKA protocols. Recently, an extension of the two-party quantum key agreement was proposed by Shi and Zhong [42], which is based on EPR pairs and entanglement swapping. Unfortunately, Liu et al. [43] found that their protocol was not a fair QKA because a dishonest participant can determine the secret key independently, and they presented a secure multiparty QKA protocol with single particles. Later, the efficiency of their protocol was improved [44].

In this paper, we propose a multi-party quantum key agreement (MQKA) protocol utilizing the genuinely maximally entangled six-qubit state [45] (we call it BPB state for short hereafter). The presented protocol allows participants to share a secret key and preserves the following advantages. The outcome of the protocol is influenced by all parties; no one can determine the shared key alone. And both outside eavesdroppers and inside participants cannot influence the generated key without introducing any error.

The rest of this paper is organized as follows. Section 2 analyzes the structure of the BPB state and shows the excellent properties which are useful for designing our protocol. In Section 3, we present our MQKA protocol by using the BPB state. Then, the security analysis is given in Section 4. Section 5 gives a short conclusion.

2 The Genuinely Maximally Entangled Six-Qubit State

Quantum entanglement, as a physical resource, plays a key role in many applications such as quantum teleportation [37], quantum dense coding [9], quantum key distribution [7], quantum secret sharing [46, 47]. By using a numeric searching program, Borras et al.[45] found the BPB state, which is

$$\begin{array}{@{}rcl@{}} \frac{1}{\sqrt{32}} [ (|000000\rangle &+& |111111\rangle + |000011\rangle + |111100\rangle \\ &+& |000101\rangle + |111010\rangle + |000110\rangle + |111001\rangle \\ &+& |001001\rangle + |110110\rangle + |001111\rangle + |110000\rangle \\ &+& |010001\rangle + |101110\rangle + |010010\rangle + |101101\rangle \\ &+& |011000\rangle + |100111\rangle + |011101\rangle + |100010\rangle) \\ &-&(|010100\rangle + |101011\rangle + |010111\rangle + |101000\rangle \\ &+& |011011\rangle + |100100\rangle + |001010\rangle + |110101\rangle \\ &+& |001100\rangle + |110011\rangle + |011110\rangle + |100001\rangle)]_{123456} \end{array} $$
(1)

We denote this six-qubit state by Ψ6q b . From the above formula, we can see that Ψ6q b includes 32 terms, each of which has even |0〉 and equal coefficient.

To show the entangled property of Ψ6q b , we can rewrite it as

$$\begin{array}{@{}rcl@{}} {\Psi}_{6qb}&=&\frac{1}{2}(|{\Phi}^{+}\rangle_{12}|{\Phi}^{+}\rangle_{36}|{\Phi}^{+}\rangle_{45} +|{\Phi}^{-}\rangle_{12}|{\Psi}^{-}\rangle_{36}|{\Psi}^{+}\rangle_{45} \\ &+&|{\Psi}^{-}\rangle_{12}|{\Psi}^{+}\rangle_{36}|{\Phi}^{-}\rangle_{45} +|{\Psi}^{+}\rangle_{12}|{\Phi}^{-}\rangle_{36}|{\Psi}^{-}\rangle_{45}) \end{array} $$
(2)
$$\begin{array}{@{}rcl@{}} &=&\frac{1}{2}(-|{\Phi}^{-}\rangle_{13}|{\Phi}^{-}\rangle_{24}|{\Phi}^{+}\rangle_{56} +|{\Phi}^{+}\rangle_{13}|{\Psi}^{+}\rangle_{24}|{\Psi}^{+}\rangle_{56} \\ &-&|{\Psi}^{+}\rangle_{13}|{\Psi}^{-}\rangle_{24}|{\Phi}^{-}\rangle_{56} -|{\Psi}^{-}\rangle_{13}|{\Phi}^{+}\rangle_{24}|{\Psi}^{-}\rangle_{56}) \end{array} $$
(3)
$$\begin{array}{@{}rcl@{}} &=&\frac{1}{2}(|{\Phi}^{-}\rangle_{14}|{\Phi}^{+}\rangle_{26}|{\Phi}^{-}\rangle_{35} +|{\Phi}^{+}\rangle_{14}|{\Psi}^{+}\rangle_{26}|{\Psi}^{+}\rangle_{35} \\ &+&|{\Psi}^{-}\rangle_{14}|{\Psi}^{-}\rangle_{26}|{\Phi}^{+}\rangle_{35} +|{\Psi}^{+}\rangle_{14}|{\Phi}^{-}\rangle_{26}|{\Psi}^{-}\rangle_{35}) \end{array} $$
(4)
$$\begin{array}{@{}rcl@{}} &=&\frac{1}{2}(|{\Phi}^{+}\rangle_{15}|{\Phi}^{+}\rangle_{23}|{\Phi}^{+}\rangle_{46} +|{\Phi}^{-}\rangle_{15}|{\Psi}^{+}\rangle_{23}|{\Psi}^{-}\rangle_{46} \\ &+&|{\Psi}^{+}\rangle_{15}|{\Psi}^{-}\rangle_{23}|{\Phi}^{-}\rangle_{46} +|{\Psi}^{-}\rangle_{15}|{\Phi}^{-}\rangle_{23}|{\Psi}^{+}\rangle_{46}) \end{array} $$
(5)
$$\begin{array}{@{}rcl@{}} &=&\frac{1}{2}(|{\Phi}^{-}\rangle_{16}|{\Phi}^{+}\rangle_{25}|{\Phi}^{-}\rangle_{34} +|{\Phi}^{+}\rangle_{16}|{\Psi}^{-}\rangle_{25}|{\Psi}^{-}\rangle_{34} \\ &+&|{\Psi}^{+}\rangle_{16}|{\Psi}^{+}\rangle_{25}|{\Phi}^{+}\rangle_{34} +|{\Psi}^{-}\rangle_{16}|{\Phi}^{-}\rangle_{25}|{\Psi}^{+}\rangle_{34}) \end{array} $$
(6)

From the above (2–6), it is obvious to see that the other four qubits will collapse to the tensor product of two pairs of EPR when any two qubits of Ψ6q b are measured with the Bell Basis {|Φ+〉,|Φ−〉,|Ψ+〉,|Ψ−〉}. The Ψ6q b can also be rewritten as

$$\begin{array}{@{}rcl@{}} {\Psi}_{6qb}=\frac{1}{4}[ |{\Phi}^{+}\rangle_{12}(&|{\Phi}^{+}\rangle_{34}&|{\Phi}^{+}\rangle_{65} +|{\Phi}^{-}\rangle_{34}|{\Phi}^{-}\rangle_{65} \\ +&|{\Psi}^{+}\rangle_{34}&|{\Psi}^{+}\rangle_{65} +|{\Psi}^{-}\rangle_{34}|{\Psi}^{-}\rangle_{65}) \\ +|{\Phi}^{-}\rangle_{12}(-&|{\Phi}^{+}\rangle_{34}&|{\Phi}^{-}\rangle_{65} +|{\Phi}^{-}\rangle_{34}|{\Phi}^{+}\rangle_{65} \\ -&|{\Psi}^{+}\rangle_{34}&|{\Psi}^{-}\rangle_{65} +|{\Psi}^{-}\rangle_{34}|{\Psi}^{+}\rangle_{65}) \\ +|{\Psi}^{+}\rangle_{12}(&|{\Phi}^{+}\rangle_{34}&|{\Psi}^{+}\rangle_{65} +|{\Phi}^{-}\rangle_{34}|{\Psi}^{-}\rangle_{65} \\ -&|{\Psi}^{+}\rangle_{34}&|{\Phi}^{+}\rangle_{65} -|{\Psi}^{-}\rangle_{34}|{\Phi}^{-}\rangle_{65}) \\ +|{\Psi}^{-}\rangle_{12}(-&|{\Phi}^{+}\rangle_{34}&|{\Psi}^{-}\rangle_{65} +|{\Phi}^{-}\rangle_{34}|{\Psi}^{+}\rangle_{65} \\ +&|{\Psi}^{+}\rangle_{34}&|{\Phi}^{-}\rangle_{65} -|{\Psi}^{-}\rangle_{34}|{\Phi}^{+}\rangle_{65})] \end{array} $$
(7)

On the other hand, we know that when one of the Pauli unitary operators {I,σ X ,i σ Y ,σ Z } is applied to one particle of a Bell state, it will be transformed into another Bell state. For instance,

$$\begin{array}{@{}rcl@{}} (I \otimes I)|{\Phi}^{+}\rangle = |{\Phi}^{+}\rangle \\ (\sigma_{Z} \otimes I)|{\Phi}^{+}\rangle = |{\Phi}^{-}\rangle \\ (\sigma_{X} \otimes I)|{\Phi}^{+}\rangle = |{\Psi}^{+}\rangle \\ (i \sigma_{Y} \otimes I)|{\Phi}^{+}\rangle = |{\Psi}^{-}\rangle \end{array} $$
(8)

Local unitary transformation will not change the entanglement of quantum state, so Ψ6q b will be changed into another BPB state. Let us agree on the following encoding:

$$\begin{array}{@{}rcl@{}} &|{\Phi}^{+}\rangle& : 00, \quad |{\Phi}^{-}\rangle : 01 \\ &|{\Psi}^{+}\rangle& : 10, \quad |{\Psi}^{-}\rangle : 11 \end{array} $$
(9)
$$\begin{array}{@{}rcl@{}} &I& : 00, \quad \sigma_{Z} : 01 \\ &\sigma_{X}& : 10, \quad i\sigma_{Y} : 11 \end{array} $$
(10)

We denote the encoding of x as E n c o d(x) where x∈{|Φ+〉,|Φ−〉,|Ψ+〉,|Ψ−〉,I,σ Z ,σ X ,i σ Y }. For example, E n c o d(|Φ−〉)=01 and E n c o d(σ Z )=01. We can let E n c o d(y)=E n c o d(−y) (y∈{|Φ+〉,|Φ−〉,|Ψ+〉,|Ψ−〉}) because the measurement outcome of −y will be y with certainty if it is measured with Bell basis. Actually, we can say that y and −y are the same up to a global phase factor −1.

After the above encoding (9–10) , the (7) tells us that if we measure particle 1,2 , particle 3,4 and particle 6,5 with Bell basis, respectively, then the responding measurement outcomes R 12, R 34 and R 65 satisfy the following equation:

$$ Encod(R_{12}) \oplus Encod(R_{34}) \oplus Encod(R_{65})=00 $$
(11)

Furthermore, if unitary operators U 1, U 2 and U 3 (U 1,U 2,U 3∈{I,σ Z ,σ X ,i σ Y }) are applied to particle 1, particle 3 and particle 6, respectively, and then particle 1,2 , particle 3,4 and particle 6,5 are measured with Bell basis, respectively, the measurement outcomes \(R^{\prime }_{12}\), \(R^{\prime }_{34}\) and \(R^{\prime }_{65}\) satisfy the following equation:

$$\begin{array}{@{}rcl@{}} Encod(U_{1}) \oplus Encod(U_{2}) \oplus Encod(U_{3}) \\= Encod(R^{\prime}_{12}) \oplus Encod(R^{\prime}_{34}) \oplus Encod(R^{\prime}_{65}) \end{array} $$
(12)

3 The Presented Multi-Party Quantum Key Agreement Protocol

In this section, we introduce our MQKA protocol, in which the participants can share a secret key. In our protocol, we assume that the classic channel is authenticated. Suppose that n participants, P 0,⋯ ,P n−1, have secret bit strings K 0,⋯ ,K n−1, respectively. They want to derive a secret key K=K 0⊕⋯⊕K n−1. Here, ⊕ denotes the addition module 2.

$$\begin{array}{@{}rcl@{}} K_{0} &&= (k_{0L}, k_{0(L-1)}, \ldots, k_{01} ) \\ {\ldots} \\ K_{i} &&= (k_{iL}, k_{i(L-1)}, \ldots, k_{i1} ) \\ {\ldots} \\ K_{n-1} &&= (k_{(n-1)L}, k_{(n-1)(L-1)}, \ldots, k_{(n-1)1} ) \\ K_{0} \oplus \ldots \oplus K_{n-1} &&= (k_{0L}\oplus {\ldots} \oplus k_{(n-1)L}, \ldots, k_{01} \oplus {\ldots} \oplus k_{(n-1)1}) \end{array} $$
(13)

where L is even (for simplicity) and represents the length of secret bit string.

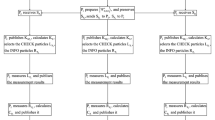
The presented multi-party quantum key agreement protocol can be described as follows.

  1. (S1)

    For each P i , he first prepares \(\frac {L}{2}\) BPB state Ψ6q b , where i∈{0,⋯ ,n−1}. Then he picks up the particles 3, 4 (particles 6, 5) from each Ψ6q b to form an ordered sequence S 34 (S 65). After that P i prepares some decoy particles, each of which is in one of the quantum states {|0〉,|1〉,|+〉,|−〉}. He randomly inserts the decoy particles into the sequence S 34 (S 65) to form a new sequence \(S_{34}^{*}\) (\(S_{65}^{*}\)). Note that only P i know the initial states and positions of the d decoy particles. Then, P i transmits \(S_{34}^{*}\) (\(S_{65}^{*}\)) to P (i−1)m o d n (P (i+1)m o d n ), and only keeps particles 1, 2 in his lab. For simplicity, let us denote P (i−1)m o d n and P (i+1)m o d n as P i−1 and P i+1, respectively.

  2. (S2)

    Confirming that P i−1 and P i+1 have received all the particles of \(S_{34}^{*}\) and \(S_{65}^{*}\), respectively. P i announces the positions and the bases of the decoy particles to P i−1 and P i+1, respectively. In the following, P i−1 and P i+1 measure the decoy particles in the correct bases according to P i ’s announcement and randomly publish half of their measurement outcomes. Then P i announces the initial states of the left half of the decoy particles. At last, they check whether the initial states and the measurement results are consistent. If they are not consistent, this protocol will be aborted and repeat the step (1). Otherwise, the protocol will go to the next step.

  3. (S3)

    P i−1 and P i+1 remove the particles of the sample states. Then they perform operation \(U_{P_{i-1}}\) and \(U_{P_{i+1}}\) (\(U_{P_{i-1}},U_{P_{i+1}} \in \{I, \sigma _{X}, \sigma _{Y}, \sigma _{Z}\}\)) on the particle 3 and particle 6 of each Ψ6q b of the ordered sequence according to their input and the encoding agreement (10), respectively. For example, if the \(jth \left (j=1, 2, \ldots , \frac {L}{2}\right )\) two bits of the input of P i−1 and P i+1 are 11 and 01, respectively. P i−1 and P i+1 will perform operation i σ Y and σ Z on the particle 3 and particle 6 of the jth BPB state Ψ6q b respectively.

  4. (S4)

    If all the participants have finished steps (1)–(3), then they go to the next step.

  5. (S5)

    P i−1 and P i+1 randomly insert the decoy states into the encoded particle sequence S 34 and particle S 65 respectively by the decoy method described in step (1) and step (2), and then send them to P i−2 and P i+2, respectively.

  6. (S6)

    The participants carry out the protocol similar to steps (2)–(5) until participants \(P_{i-\frac {n-1}{2}}\) and \(P_{i+\frac {n-1}{2}}\) have sent the encoded particle sequences to P i if the security checking of quantum channels is passed.

  7. (S7)

    If all the participants have finished steps (1)–(6), then they go to the next step.

  8. (S8)

    After confirming that P i has received the sequence from \(P_{i-\frac {n-1}{2}}\) and \(P_{i+\frac {n-1}{2}}\), they announce the positions and the corresponding bases of the decoy particles. Then for each of the decoy particles, P i measures the decoy particles in the correct bases . After that, he asks \(P_{i-\frac {n-1}{2}}\) and \(P_{i+\frac {n-1}{2}}\) to announce the initial states of the decoy particles respectively. At last, he checks whether the initial states and the measurement results are consistent. If there are consistent with each other, they continue to the next step; otherwise, they abort this protocol and restart from step (1).

  9. (S9)

    After receiving the encoded particle sequence S 34 and particle sequence S 65, P i performs unitary operation \(U_{P_{i}}\) on the particle 1 of each Ψ6q b of the ordered sequence according to his input and the encoding agreement (10), then he measures particles 1,2, particles 3,4 and particles 6,5 of the \(jth {\Psi }_{6qb} \left (j=1, 2, \ldots , \frac {L}{2}\right )\) with the Bell basis. Then he will obtain the final key. Suppose their measurement outcomes of the j t h Ψ6q b are \(R_{12}^{j}\), \(R_{34}^{j}\) and \(R_{65}^{j}\), then he will get the final key of the jth two bits \(K^{j}=Encod\left (R_{12}^{j}\right )\oplus Encod\left (R_{34}^{j}\right ) \oplus Encod\left (R_{65}^{j}\right )\).

4 Analysis of the Presented Protocol

In this section, we will prove that our protocol is secure. Generally speaking, the security analysis of quantum key agreement protocol is more complex than quantum key distribution (QKD) [5, 6, 48–50] and quantum secure direct communication (QSDC) [17, 18, 51–54] because the attacks from all participants have to be considered in quantum key agreement protocols. In other words, the outside eavesdroppers try to obtain the shared key. While, some participants may try to determine the shared key alone. Therefore, the security of quantum key agreement protocol is to prevent both outside and participant attacks. For clarity, we assume that the party P i starts the protocol.

4.1 Outside Attacks

In our protocol, we use the decoy particles to prevent the eavesdropping. This idea is derived from the quantum key distribution protocol [6]. In decoy-state method, besides target states, several other non-orthogonal states as decoy states are used. Since eavesdropper cannot distinguish between the target states and the decoy states, she has to apply the same strategy to all of them. As a result, any eavesdropping attempt by eavesdropper will inevitably modify the photon statistic and expose her [55–57]. Therefore, any eavesdropping will be discovered in the protocol by using the decoy-state method. Without loss of generality, the most general operation U E Eve employed is to cause the intercepted photons to interact coherently with an auxiliary quantum system |E〉. Then she sends the operated photons to the receivers. Suppose that U E satisfies the following conditions.

$$\begin{array}{@{}rcl@{}} U_{E}|0\rangle |E\rangle &=& a|0\rangle |E_{00}\rangle + b|1\rangle |E_{01}\rangle, \end{array} $$
(14)
$$\begin{array}{@{}rcl@{}} U_{E}|1\rangle |E\rangle &=& c|0\rangle |E_{10}\rangle + d|1\rangle |E_{11}\rangle, \end{array} $$
(15)

where |a|2+|b|2=1 and |c|2+|d|2=1. If Eve introduces no error in the eavesdropping check, the general operation U E must satisfy the following conditions.

$$\begin{array}{@{}rcl@{}} U_{E}|0\rangle |E\rangle &=& a|0\rangle |E_{00}\rangle, \\ U_{E}|1\rangle |E\rangle &=& d|1\rangle |E_{11}\rangle, \end{array} $$
(16)
$$\begin{array}{@{}rcl@{}} U_{E}|+\rangle |E\rangle &=&\frac{1}{\sqrt{2}}(a|0\rangle |E_{00}\rangle + b|1\rangle |E_{01}\rangle + c|0\rangle |E_{10}\rangle + d|1\rangle |E_{11}\rangle)\\ &=& \frac{1}{2}(|+\rangle (a|E_{00}\rangle + b|E_{01}\rangle + c|E_{10}\rangle + d|E_{11}\rangle))\\ &+& \frac{1}{2}(|-\rangle (a|E_{00}\rangle - b|E_{01}\rangle + c|E_{10}\rangle - d|E_{11}\rangle))\\ &=& \frac{1}{2}(|+\rangle (a|E_{00}\rangle + b|E_{01}\rangle + c|E_{10}\rangle + d|E_{11}\rangle)) \end{array} $$
(17)
$$\begin{array}{@{}rcl@{}} U_{E}|-\rangle |E\rangle &=&\frac{1}{\sqrt{2}}(a|0\rangle |E_{00}\rangle + b|1\rangle |E_{01}\rangle - c|0\rangle |E_{10}\rangle - d|1\rangle |E_{11}\rangle)\\ &=& \frac{1}{2}(|+\rangle (a|E_{00}\rangle + b|E_{01}\rangle - c|E_{10}\rangle - d|E_{11}\rangle))\\ &+& \frac{1}{2}(|-\rangle (a|E_{00}\rangle - b|E_{01}\rangle - c|E_{10}\rangle + d|E_{11}\rangle))\\ &=& \frac{1}{2}(|-\rangle (a|E_{00}\rangle - b|E_{01}\rangle - c|E_{10}\rangle + d|E_{11}\rangle)). \end{array} $$
(18)

From the above (16), (17) and (18), we have the following Eqs.

$$\begin{array}{@{}rcl@{}} b|E_{01}\rangle &=& 0 \end{array} $$
(19)
$$\begin{array}{@{}rcl@{}} c|E_{10}\rangle &=& 0 \end{array} $$
(20)
$$\begin{array}{@{}rcl@{}} a|E_{00}\rangle - b|E_{01}\rangle + c|E_{10}\rangle - d|E_{11}\rangle &=& 0 \end{array} $$
(21)
$$\begin{array}{@{}rcl@{}} a|E_{00}\rangle + b|E_{01}\rangle - c|E_{10}\rangle - d|E_{11}\rangle &=&0. \end{array} $$
(22)

Here 0 denote a column zero vector. Further, we can get a=d=1, b=c=0 and |E 00〉=|E 11〉. Therefore, we have U E Ψ6q b |E〉=Ψ6q b |E ′〉, i.e., Eve introduce no error in the eavesdropping only when her ancillary state and the target photon are product states. So outside eavesdroppers cannot obtain the shared key without being detected.

Since our protocol transmits the same photons more than once, it may suffer from the Trojan horse attacks. Such kind of circular quantum transmission has been discussed [58–62]. To prevent this type of attacks, participants can install a special quantum optical device such as the wavelength quantum filter and the photon number splitters (PNS) to detect an attack. According to Refs. [58–62], Eve’s invisible photons can be filtered out by using the wavelength quantum filter, and the PNS can split each legitimate photon to discover the delay photons. If there is an irrational high rate of multi-photon signal, then the attack can be detected. As pointed out in Ref. [60], this kind of Trojan horse attack is not an exploit of a weakness of the protocol in itself, but rather an exploit of a weakness in certain imperfect implementations. Without the imperfection of the single-photon detectors, this kind of Trojan horse attack will not exist any longer.

4.2 Participant Attack

Generally speaking, the participant is the most powerful attacker in the multi-party computation protocols [63]. If the presented QKA protocol is secure for the dishonest participants, it is also secure for any eavesdropper.

Because of the decoy-photon technique, eavesdropper’s several kinds of outsider attacks, such as the intercept-resend attack, measurement-resend attack, entanglement-measure attack and the denial-of-service attack can be detected. Notice that if P i is the first one that finishes the protocol, then he will be the first one that gets the shared key. Then he can decide the final key alone. For example, suppose P i has already obtain the shared key k, where k is the bitwise of P 0,⋯ ,P n−1’s keys. Then P i encodes k ′⊕k⊕k i as his secret key, instead of k i , when other participants as senders carry out their protocol, where k ′ is the key that P i desired and k i is P i ’s secret key. Therefore, other participants will accept k ′ as the final shared key. Thus, this protocol is not a fair key agreement in this situation. To avoid this unfairness, all the participant cannot execute the steps (8)-(9) until all the other participants have accomplished the steps (1)-(9). Then P i has no chance to know the share key ahead of the others. Then this attack can be avoided automatically. Notice that the decoy-state method is also used to detect the dishonest of P i in the presented protocol.

4.3 Security Analysis Over Noisy Quantum Channel

The security of our protocol is analyzed under the condition that all quantum channels are noiseless. Since it is hard to build perfect quantum channels in a practical transmission process, the success probability of quantum communication would be decreased under noisy conditions. In this subsection, we show that our protocol is still secure over noisy quantum channel.

Eve may intercept the particles sent from P i to P i−1 and P i+1. She then performs intercept-resend attack or entangle-measure attack, and forwards these tampered particles to P i−1 and P i+1 through an ideal channel (supposed that she has the ability to establish an ideal quantum channel). Eve tries to cover up her attack by the way that it seems for honest participants that the error induced by her attack just like the the noise of the quantum channel. We have learned that the quantum bit error rate of noise (𝜖) is roughly between 2 % and 8.9 % depending on the different channel situations. The above attacks will not be detected if the eavesdropper detection rate of our protocol is smaller than 𝜖. Fortunately, the detection rate using the decoy method in our protocol is 25 % which is greater than 𝜖. Therefore, the presented protocol will be secure even in the noisy quantum channel.

4.4 Efficiency Analysis

Here, the particle efficiency is defined as η=c/q, where, c denotes the length of the final secret key, and q is the number of the transmitted qubits on the quantum channel. In order to generate 2 bits of shared key, each party has to prepare a BPB state and enough decoy particles in our protocol. Hence, the qubit efficiency of our protocol can be computed, \(\eta = \frac {2}{(2\kappa +4)n}=\frac {1}{(\kappa +1)n}\), where κ is the detection rate and n is the number of the participants. While, the qubit efficiency of the improved MQKA in Ref. [44] is \(\frac {1}{(\kappa +1)n}\). Hence, our new protocol is as efficient as it.

5 Conclusions

We present a multi-party quantum key agreement protocol based on the genuinely maximally entangled six-qubit state. In our protocol, participants can agree on a key and no one can determine the shared key alone. We have also shown that it is secure against both outside and participant attacks. Up to now, dealing with a BPB state is far more involved than the counterparts involving two or three particles, so our protocol may be difficult to realize physically. However, utilizing multi-particle entanglement to constructing quantum cryptography protocols is important in theory, and further research on applications of multi-qubit entanglement is need in the future.