1 Introduction

Quantum cryptography has made great progress since the first quantum key distribution protocol (QKD) was proposed by Bennett and Brassard in 1984 [1]. The main goal of this field is to take advantage of quantum effects to provide unconditionally secure information exchange. People have proposed many kinds of quantum cryptographic protocols [2–28], including quantum key distribution, quantum secure direct communication, quantum secret sharing, quantum signature, and so on.

Different from the key distribution, the key agreement protocol is a key establishment technique whereby a shared secret key is derived by two or more specified parties as a function of information contributed by, or associated with, each of these, such that all of them can not predetermine the value of the key [29, 30]. However, the security of classical key agreement based on the computation complexity is strongly challenged by the capability of computation or algorithms, especially since Shor [31] proposed two algorithms for quantum computation, i.e., discrete logarithms and factoring. Therefore, quantum key agreement (QKA) based on the principles of quantum mechanics is a subject worthy of study, in which both parties contribute information and jointly establish the shared secret key by using the quantum channels. In 2004, Zhou et al. [32] first proposed a QKA protocol based on quantum teleportation. However, Zhou et al.’s protocol was pointed out by Tsai et al. [33] that a user can fully determine the shared key alone without being detected. In 2010, Chong and Hwang [34] proposed a QKA protocol based on BB84 [1], in which two parties can negotiate a shared secret key by using the unitary operations and the delayed measurement technique. In 2011, Chong et al. [35] proposed an improvement on Hsueh et al.’s protocol [36] with maximally entangled states. But these QKA protocols [32–36] only involved two parties and can not be used in the multi-party situation. So, in 2013, Shi and Zhong [37] proposed a multi-party QKA based on entanglement swapping with bell states and bell measurements. Unfortunately, Liu et al. [38] pointed out that Shi et al.’s protocol can not be secure in the sense that the key can be totally determined by a dishonest participant alone. In the same paper, Liu et al. proposed a multi-party QKA with single particles, which was the first secure multi-party scheme declared by the authors.

In this paper, we propose a three-party quantum key agreement protocol with two-photon entanglement. We use the idea of quantum dense coding on the four EPR pairs. The three participants are peer entities and they first generate their respective secret keys randomly. Then one party can extract the other two parties’ secret keys by performing Bell measurement on the initial particles in his site and the particles encoded by the other two parties. Thus the shared secret key can been established by using the XOR operation. The rest of our paper is structured as follows. Section 2 describes the present protocol in detail. The security analysis is discussed in Sect. 3. Finally, Sect. 4 concludes our scheme briefly.

2 Description of the Present Protocol

Let us introduce two-qubit entangled states. An EPR pair is one of the four Bell states, i.e., \(|\psi^{+}\rangle = 1/\sqrt{2}(|01\rangle+|10\rangle)\), \(|\psi^{-}\rangle = 1/\sqrt{2}(|01\rangle-|10\rangle)\), \(|\phi^{+}\rangle=1/\sqrt{2}(|00\rangle+|11\rangle)\), and \(|\phi^{-}\rangle= 1/\sqrt{2}(|00\rangle-|11\rangle)\). Where |0〉 and |1〉 are the up and down eigenstates of Pauli operator σ z . Let |+〉 and |−〉 be \((|0\rangle+|1\rangle)/\sqrt{2}\) and \((|0\rangle-|1\rangle)/\sqrt{2}\) respectively. Suppose U 0,U 1, and U 2 are three local unitary operations. That is, U 0≡I=|0〉〈0|+|1〉〈1|, U 1≡σ x =|0〉〈1|+|1〉〈0|, U 2≡σ z =|0〉〈0|−|1〉〈1|. An EPR pair can be transformed into another EPR pair by performing the unitary operation U i , i=0,1,2 on the second particle. The transformation can be shown in Table 1. Furthermore, we perform two consecutive operations on the second qubit of |ψ +〉, i.e., if we take U 0 or U 1 as the first unitary operation, U 0 or U 2 as the second unitary operation, then the transformation can be summarized in Table 2.

Table 1 The transformation of the four EPR pairs
Full size table
Table 2 The transformation of |ψ +〉 based on two operations
Full size table

Suppose that there are three characters, say, Alice, Bob, and Charlie. Three parties want to establish a shared secret key K over the quantum channels. Alice, Bob, and Charlie first generate the random bit strings K A , K B , and K C as their own secret keys, respectively. That is,

$$\begin{aligned} K_A =& \{a_1a_2\cdots a_n\}, \end{aligned}$$
(1)
$$\begin{aligned} K_B =& \{b_1b_2\cdots b_n\}, \end{aligned}$$
(2)
$$\begin{aligned} K_C =& \{c_1c_2\cdots c_n\}, \end{aligned}$$
(3)

where a i ,b i ,c i ∈{0,1}, i=1,2,…,n. In the following, we describe the present quantum key agreement.

Step 1:

Each party prepares n entangled states |ψ +〉 and divides these entangled states into two ordered qubit sequences. Let P A1 and P A2 be Alice’s two sequences, where each particle in P A1 is the first qubit of |ψ +〉 and that in P A2 is the second qubit. Similarly, P B1 and P B2 represent Bob’s sequences, and P C1 and P C2 represent Charlie’s. Moreover, each party prepares enough decoy photons which are randomly in {|0〉,|1〉,|+〉,|−〉}. Then Alice/Bob/Charlie inserts them into P A2/P B2/P C2 randomly. After that, Alice/Bob/Charlie sends the mixed sequence to Bob/Charlie/Alice.

Step 2:

After confirming Bob/Charlie/Alice has received the sequence, Alice/Bob/Charlie announces the positions and the corresponding basis {|0〉,|1〉} or {|+〉,|−〉} of the decoy particles. Then two parties check the quantum channel by comparing the measurement results. If the error rate exceeds the threshold, then this protocol is aborted. Otherwise, it is continued.

Step 3:

Bob/Charlie/Alice first picks out the decoy particles, then performs the unitary operation on each particle in P A2/P B2/P C2 according to b i /c i /a i (i=1,2,…,n), which forms a new sequence \(P^{1}_{A2}/P^{1}_{B2}/P^{1}_{C2}\). The rule is described as following. If b i =0/c i =0/a i =0, Bob/Charlie/Alice chooses U 0; otherwise, chooses U 1. Moreover, Bob/Charlie/Alice prepares enough decoy particles which are chosen from {|0〉,|1〉,|+〉,|−〉} and inserts them into \(P^{1}_{A2}/P^{1}_{B2}/P^{1}_{C2}\) randomly. Then Bob/Charlie/Alice sends the mixed photon sequence to Charlie/Alice/Bob.

Step 4:

After confirming Charlie/Alice/Bob has received the sequence, Bob and Charlie/Charlie and Alice/Alice and Bob perform the second eavesdropping check. If the error rate exceeds the threshold, two parties abort this protocol. Otherwise, they continue this process.

Step 5:

Charlie/Alice/Bob first picks out the decoy particles, then performs the unitary operation on each particle in \(P^{1}_{A2}/P^{1}_{B2}/P^{1}_{C2}\) according to c i /a i /b i (i=1,2,…,n), which forms a new sequence \(P^{2}_{A2}/P^{2}_{B2}/P^{2}_{C2}\). That is, if c i =0/a i =0/b i =0, Charlie/Alice/Bob chooses U 0; otherwise, chooses U 2. Moreover, Charlie/Alice/Bob prepares enough decoy particles which are chosen from {|0〉,|1〉,|+〉,|−〉} and inserts them into \(P^{2}_{A2}/P^{2}_{B2}/P^{2}_{C2}\) randomly. Then Charlie/Alice/Bob returns the mixed photon sequence to Alice/Bob/Charlie.

Step 6:

After confirming Alice/Bob/Charlie has received the sequence, two parties perform the third security check. If they confirm the qubit transmission is insecure, this process is aborted. Otherwise, the protocol is continued.

Step 7:

Alice/Bob/Charlie first picks out the decoy particles. Each party has two particle sequences so far. That is, Alice has P A1 and \(P^{2}_{A2}\); Bob has P B1 and \(P^{2}_{B2}\); Charlie has P C1 and \(P^{2}_{C2}\). Each party performs Bell measurement orderly on the corresponding photon pair in his two sequences. According to Table 2 and measurement results, each party can obtain the other two parties’ secret keys. Thus the shared secret key K=K A ⊕K B ⊕K C .

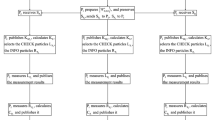
From the above steps, we can see each party transmits his particle sequence to the other two parties simultaneously, which forms a cycle between them. For conciseness, we ignore the security check and illustrate the whole protocol in Fig. 1. Next, we take n=1 for example to explain the establishment of K. Suppose K A =0, K B =1, K C =1. We only consider Alice wants to extract Bob’s secret key K B and Charlie’s secret key K C . Alice prepares |ψ +〉12, and sends particle 2 to Bob. Bob performs U 1 on the particle according to Step 3 and therefore |ψ +〉12 is transformed into |ϕ +〉12 (Table 1). Then he sends this particle to Charlie. Charlie performs U 2 according to Step 5 and therefore |ϕ +〉12 is transformed into |ϕ −〉12 (Table 1). Finally, Charlie sends this particle to Alice. Then Alice performs Bell measurement on this particle and particle 1. The measurement result must be |ϕ −〉12. Thus Alice can extract K B and K C from Table 2. In the same way, if Bob and Charlie prepare |ψ +〉12 respectively, they can also obtain the other two parties’ secret keys. So three parties can establish a shared secret key 0 by computing K A ⊕K B ⊕K C .

Fig. 1
figure 1

Illustration of the present protocol. In Step II, U A , U B , U C represent Alice’s, Bob’s, and Charlie’s unitary operation respectively, and U A ,U B ,U C ∈{U 0,U 1}. “\(U_{A}:P_{C2}\rightarrow P^{1}_{C2}\)” represents Alice applies her unitary operation U A on the particle sequence P C2 to form \(P^{1}_{C2}\) (the others are similar). In Step IV, three parties’ operations \(U'_{A}, U'_{B}, U'_{C}\in\{U_{0}, U_{2}\}\). “BM” in Step VI represents Bell measurement. The solid arrows denote the quantum channels and the dotted lines denote that the three parties execute the procedure simultaneously

Full size image

3 Security Analysis and Discussion

In this section, we will demonstrate the security of our protocol. A secure quantum key agreement protocol can not only prevent the outside eavesdroppers from getting some information about the shared secret key, but also deter the dishonest participants from determining the shared key alone. That is, a PKA protocol can resist against the outsider attack and the insider attack.

We first consider the outsider attack. Suppose Eve is an evil attacker who wants to steal the shared secret key between the three parties. From the seven steps, we can see that the direction of qubit transmission is one-way and it is a separate process that one party obtains the secret keys of the other two parties. Without loss of generality, we consider Alice is a particle generators, and Bob and Charlie are receivers. When the particles are sent form Alice to Bob, Bob to Charlie, and Charlie to Alice, Eve can take an intercept-resend attack. For example, she captures the particles that Alice sent to Bob and replaces her own particles to resend them. However, the decoy particles are randomly inserted into the sequence and Eve can not possibly know the positions and the corresponding measurement basis of decoy particles before Alice announces the relevant information. In addition, each decoy particle is chosen from the four states |0〉, |1〉, |+〉, and |−〉 randomly. Let m be the number of decoy particles, then the probability that Eve could not been detected is 1/4m. Thus, Eve can not pass the eavesdropping check in the condition that the errors occur. The other attack that Eve may employ is the entangle-measure attack. We take the particle 2 of |ψ +〉12 for example. Suppose that Eve prepares an ancilla E, and performs a unitary operation U on the particle E and 2 when the particle 2 passes by. Then we have

$$\begin{aligned} U:\quad |0\rangle|\epsilon\rangle \rightarrow& |0\rangle|\epsilon_{00}\rangle+|1\rangle|\epsilon_{01}\rangle \end{aligned}$$
(4)
$$\begin{aligned} |1\rangle|\epsilon\rangle \rightarrow& |0\rangle|\epsilon_{10}\rangle+|1\rangle|\epsilon_{11}\rangle, \end{aligned}$$
(5)

where |ϵ ij 〉 (i,j∈{0,1}) are pure ancilla states uniquely determined by U. The whole quantum system is in the state

$$\begin{aligned} U\bigl|\psi^+\bigr\rangle_{12}|\epsilon\rangle_E =& U\biggl(\frac{1}{\sqrt{2}}\bigl(|10\rangle+|01\rangle\bigr)_{21}\biggr)|\epsilon\rangle_{E} \end{aligned}$$
(6)
$$\begin{aligned} \rightarrow& \frac{1}{\sqrt{2}}\bigl(|1\rangle_2|u\rangle_{1E}+|0\rangle_2|v\rangle_{1E}\bigr), \end{aligned}$$
(7)

where |u〉→|0〉|ϵ 00〉+|1〉|ϵ 01〉, |v〉→|0〉|ϵ 10〉+|1〉|ϵ 11〉. If Eve wants to avoid introducing error, then 〈1|u〉=0 and 〈0|v〉=0 should be satisfied, i.e., ϵ 01=0 and ϵ 10=0. On the other hand, if two parties check the quantum channel by using the basis {|+〉,|−〉}, then we have

$$\begin{aligned} U:\quad{} |+\rangle|\epsilon\rangle \rightarrow& \frac{1}{2}\bigl(|+\rangle\bigl(|\epsilon_{00}\rangle+|\epsilon_{11}\rangle\bigr)+ |-\rangle\bigl(|\epsilon_{00}-|\epsilon_{11}\rangle\bigr)\bigr) \end{aligned}$$
(8)
$$\begin{aligned} |-\rangle|\epsilon\rangle \rightarrow& \frac{1}{2}\bigl(|+\rangle\bigl(|\epsilon_{00}\rangle-|\epsilon_{11}\rangle\bigr)+ |-\rangle\bigl(|\epsilon_{00}+|\epsilon_{11}\rangle\bigr)\bigr). \end{aligned}$$
(9)

Thus the quantum system is in the state

$$\begin{aligned} U\bigl|\psi^+\bigr\rangle_{12}|\epsilon\rangle_E =& U\biggl(\frac{1}{\sqrt{2}}\bigl(|++\rangle-|--\rangle\bigr)_{21}\biggr)|\epsilon\rangle_{E} \end{aligned}$$
(10)
$$\begin{aligned} \rightarrow& \frac{1}{2\sqrt{2}}\bigl(|+\rangle_2\bigl(|+\rangle_1\bigl(|\epsilon_{00}\rangle+|\epsilon_{11}\rangle\bigr)_E+ |-\rangle_2\bigl(|\epsilon_{00}\rangle-|\epsilon_{11}\rangle\bigr)_E\bigr) \end{aligned}$$
(11)
$$\begin{aligned} &{} - |-\rangle_2\bigl(|+\rangle_1\bigl(|\epsilon_{00}\rangle-|\epsilon_{11}\rangle\bigr)_E+ |-\rangle_2\bigl(|\epsilon_{00}\rangle+|\epsilon_{11}\rangle\bigr)_E\bigr)\bigr). \end{aligned}$$
(12)

Similarly, Eve must ensure that the measurement results |+〉2|−〉1 and |−〉2|+〉1 cannot appear if she wants to avoid introducing error. Thus we have ε 00=ϵ 11 and the whole quantum system is in the state |ψ +〉12|ϵ 00〉 E . That is, Eve can not obtain any useful information from observing the ancilla. Therefore our protocol can resist against the outsider attack from the above discussion.

Next, we consider the insider attack. In our protocol, the three random bit strings K A , K B , and K C are generated as Alice’s, Bob’s, and Charlie’s secret key respectively which are only known to themselves and can not be determined by any part of them alone. Each party has a equal contribution to the establishment of the shared secret key and the three parties are entirely peer entities. The way that all the participants share a secret key by combining each participant’s key is similar to that in Liu et al.’s protocol [38] which is based on single particles. The difference is that the qubit transmission between all the participants is multi-way in Liu et al.’s protocol. Suppose that Alice is honest without loss of generality, and the dishonest parties Bob and Charlie want to determine the shared key alone. To realize this purpose, the dishonest parties need to obtain Alice’s secret key. Thus Bob and Charlie should be particle producers and receive the encoded particles sent from Alice. In Bob’s site he directly sends the particles prepared by himself to Alice with the help of Charlie after performing his unitary operation on the particles instead of Charlie’s operation. After Alice returns the encoded particles, Bob can get Alice’s secret key. In Charlie’s site, when he has sent the particle sequence to Alice, Charlie directly receives Alice’s encoded particles with the help of Bob to get her secret key by performing the unitary operation himself. However, on the other hand, the procedures are executed simultaneously by the three parties. That is, Alice would not extract Bob’s or Charlie’s secret key if the two dishonest parties colluded to cheat her. Therefore, our three-party protocol is secure against the outsider attack and insider attack from the above analysis.

4 Conclusion

In this paper, we propose a three-party quantum key agreement protocol based on EPR pairs. Three parties can establish a shared key in such a way that one party extracts the other two parties’ secret key and all parties perform XOR operations on their secret keys. Moreover, the security analysis shows that our protocol is security against the outsider attack and insider attack. The security of our scheme is considered under the condition of ideal quantum channels. Since noise cannot be disregarded in a practical transmission process, the success probability of quantum communication would be decreased in a noisy channel. This problem may be solved perfectly in the future research.