1 Introduction

The research of quantum correlation or, more precisely, quantum entanglement can date back to a paper [1] in 1935, but we do not get the accurate definition of this at that time. Nowadays, quantum entanglement, which is one of the most significant concepts, has attracted much attention in quantum information processing because of its importance in developing the idea of quantum computers and other quantum information devices [2–8], such as quantum cryptograph, quantum key distribution, and quantum teleportation [2, 9]. However, in recent years, investigations show that entanglement is not a unique measure of quantum correlations because there exist other types of nonclassical correlations which are not captured by entanglement, and it can offer support for lots of quantum tasks. For instance, some separate states are also useful in improving performance in some tasks of quantum computer [9]. Then the quantum discord [10], which is used as a tool to measure nonclassical correlations of quantum states, appeared. Recently, numerous works have been devoted on the study of quantum discord [11–19]. However, it is usually troublesome to calculate quantum discord analytically because of the complicated optimization involved. In view of these facts, Luo introduced a new method to classify and quantify statistical correlations in bipartite states. They use measurement-induced disturbance (MID), which does not involves optimization procedure, to characterize correlations as classical or quantum [20]. In this paper, we will investigate the quantum correlations base on MID in our model.

As we know, the quantum entanglement of condensed matter systems is an important emerging field recently. People have made several investigations of quantum entanglement on thermal equilibrium states of spin chains subject to an external magnetic field at finite temperature [21–25]. In addition, the quantum correlations of two qubits with Dzyaloshinskii–Moriya (DM) interaction, which can influence the phase transition, also have attracted much attention [26–30]. In this paper, in comparison with the thermal quantum discord of two qubits [31–34], we not only expand the study on thermal quantum correlation to mixed-spin (1/2, 1) XXZ model, but also consider the effects of DM interaction and external magnetic field on thermal quantum correlation measured by MID.

The paper is organized as follows. In Sect. 2, we give the model and obtain the expression of the negativity and measurement-induced disturbance (MID) through mathematical calculations and analysis. Then we will investigate quantum phase transitions (QPT) of the ground states in Sect. 3. In Sect. 4, the effects of DM interaction and external magnetic field on \(N\) and MID are given out. Moreover, we will compare the negativity and MID in detail to obtain some significative conclusions. Finally, we will summarize in Sect. 5.

2 One-dimensional two-mixed-spin XXZ model with DM interaction

The Hamiltonian of one-dimensional mixed-spin (1/2, 1) XXZ model with DM interaction in the z direction under an inhomogeneous magnetic field can be written as

$$\begin{aligned} H_\mathrm{XXZ}&= J\sum \limits _{n=1}^{N} {\left[ \vec {s}_n \vec {S}_{n+1} +\vec {S}_{n+1} \vec {s}_{n+2} +(\gamma -1)(s_n^z S_{n+1}^z +S_{n+1}^z s_{n+2}^z )\right] } \nonumber \\&+\,D\sum \limits _{n=1}^N {\Big (s_n^x S_{n+1}^y -s_n^y S_{n+1}^x +S_{n+1}^x s_{n+2}^y -S_{n+1}^y s_{n+2}^x \Big )} \nonumber \\&+\,B\sum \limits _{n=1}^N {\Big [(B-b)s_{2n-1}^z +(B+b)S_{2n}^z\Big ]} \end{aligned}$$
(1)

where \(J\) is the exchange constant and \(J >0\) corresponds with the antiferromagnetic case as well as \(J <0\) is ferromagnetic case; \(\gamma \) is the anisotropy parameter, \(D\) is the strength of DM interaction in the direction of \(\hbox {z}; (B+b)\) and \((B-b)\) are external magnetic field in \(z\) direction; \(s_{1}^{\alpha }\) and \(S_2^{\alpha } (\alpha =x,y,z)\) are the spin operators; \(b\) controls the degree of inhomogeneity of magnetic field.

In this paper, for simplicity, we take the two-qubit case as an example to investigate the given model. So the Hamiltonian in Eq. (1) can be simplified to

$$\begin{aligned} H_\mathrm{XXZ} =J\left[ \left( s_1^{x} S_2^{x} + s_1^{y} S_2^y +\gamma s_1^z S_2^z \right) +D\left( s_1^x S_2^y -s_1^y S_2^x \right) \right] + (B-b)s_1^z +(B+b)S_2^z\quad \end{aligned}$$
(2)

For this model, the spin operators’ components take the form

$$\begin{aligned} s_{1}^x&= \frac{1}{2}\left( {{\begin{array}{l@{\quad }l} 0&{} 1 \\ 1&{} 0 \\ \end{array} }} \right) , \quad s_{1}^y =\frac{1}{2}\left( {{\begin{array}{l@{\quad }l} 0&{} {-i} \\ i&{} 0 \\ \end{array} }} \right) , \quad s_{1}^z =\frac{1}{2}\left( {{\begin{array}{l@{\quad }l} 1&{} 0 \\ 0&{} {-1} \\ \end{array} }} \right) , \nonumber \\ S_2^x&= \frac{1}{\sqrt{2}}\left( {{\begin{array}{l@{\quad }l@{\quad }l} 0&{} 1&{} 0 \\ 1&{} 0&{} 1 \\ 0&{} 1&{} 0 \\ \end{array} }} \right) , \quad S_2^y \!=\!\frac{1}{\sqrt{2}}\left( {{\begin{array}{l@{\quad }l@{\quad }l} 0&{} {-i}&{} 0 \\ i&{} 0&{} {-i} \\ 0&{} i&{} 0 \\ \end{array} }} \right) , \quad S_2^z \!=\!\left( {{\begin{array}{l@{\quad }l@{\quad }l} 1&{} 0&{} 0 \\ 0&{} 0&{} 0 \\ 0&{} 0&{} {-1} \\ \end{array} }} \right) .\quad \end{aligned}$$
(3)

For a system in equilibrium at temperature T, the state can be represented by the density operator,

$$\begin{aligned} \rho (T)=\frac{1}{Z}\exp \left( -\frac{H}{k_B T}\right) \end{aligned}$$
(4)

where \(Z=Tr[\exp (-H/k_B T)]\) is the partition function, T is the thermodynamic temperature, and \(k_B\) is the Boltzmann constant which is considered as unity in the follow for simplicity. In order to obtain the expression of negativity and measurement-induced disturbance, we have to calculate the eigenvalues and the corresponding eigenstates of Hamiltonian equation (2), which are given by

$$\begin{aligned} E_0&= \frac{1}{2}(-b-3B+J\gamma ), \quad \qquad \; \left| {\Psi _0 } \right\rangle =\left| {\frac{1}{2},1} \right\rangle ;\nonumber \\ E_1&= \frac{1}{2}(b+3B+J\gamma ), \qquad \qquad \left| {\Psi _1 } \right\rangle =\left| {-\frac{1}{2},-1} \right\rangle \!; \nonumber \\ E_2&= \frac{1}{4}(2b+2B-J\gamma -v), \qquad \left| {\Psi _2 } \right\rangle =\frac{1}{\sqrt{a_1 a_1^{*} +1}}\left( a_1 \left| {-\frac{1}{2},0} \right\rangle +\left| {\frac{1}{2},-1} \right\rangle \right) \!; \nonumber \\ E_3&= \frac{1}{4}(2b+2B-J\gamma +v), \qquad \left| {\Psi _3 } \right\rangle =\frac{1}{\sqrt{a_2 a_2^{*} +1}}\left( a_2 \left| {-\frac{1}{2},0} \right\rangle +\left| {\frac{1}{2},-1} \right\rangle \right) \!; \nonumber \\ E_4&= \frac{1}{4}(-2b-2B-J\gamma -w), \qquad \left| {\Psi _4 } \right\rangle =\frac{1}{\sqrt{a_3 a_3^{*} +1}}\left( a_3 \left| {-\frac{1}{2},1} \right\rangle +\left| {\frac{1}{2},0} \right\rangle \right) \!; \nonumber \\ E_5&= \frac{1}{4}(-2b-2B-J\gamma +w), \qquad \left| {\Psi _5 } \right\rangle =\frac{1}{\sqrt{a_4 a_4^{*} +1}}\left( a_4 \left| {-\frac{1}{2},1} \right\rangle +\left| {\frac{1}{2},0} \right\rangle \right) \!.\nonumber \\ \end{aligned}$$
(5)

where \(v\!=\!\sqrt{16b^{2}\!+\!8J^{2}\!+\!8D^{2}J^{2}\!-\!8bJ\gamma \!+\!J^{2}\gamma ^{2}}\), \(w\!=\!\sqrt{16b^{2}\!+\!8J^{2}\!+\!8D^{2}J^{2}\!+\!8bJ\gamma \!+\!J^{2}\gamma ^{2}}\), \(a_1 \!=\!\frac{\!-\!4b\!+\!J\gamma \!-\!v}{2\sqrt{2}J(D\!+\!i)}i\), \(a_2 \!=\!\frac{\!-\!4b\!+\!J\gamma \!+\!v}{2\sqrt{2}J(D\!+\!i)}i, \;a_3 =-\frac{4b+J\gamma +w}{2\sqrt{2}J(D+i)}i, \;a_4 =-\frac{4b+J\gamma -w}{2\sqrt{2}J(D+i)}i\).

In the basis \(\left\{ {\vert }- 1/2, - 1\rangle , {\vert }- 1/2, 0\rangle , {\vert }- 1/2,1\rangle , {\vert }1/2, - 1\rangle , {\vert }1/2, 0\rangle , {\vert }1/2,1\rangle \right\} \), we can obtain the density operator of the system as follows

$$\begin{aligned} \rho (T)=\frac{1}{Z}\left( {{\begin{array}{l@{\qquad }l@{\qquad }l@{\qquad }l@{\qquad }l@{\qquad }l} {\rho _{11} }&{} 0&{} 0&{} 0&{} 0&{} 0 \\ 0&{} {\rho _{22} }&{} 0&{} {\rho _{24} }&{} 0&{} 0 \\ 0&{} 0&{} {\rho _{33} }&{} 0&{} {\rho _{35} }&{} 0 \\ 0&{} {\rho _{42} }&{} 0&{} {\rho _{44} }&{} 0&{} 0 \\ 0&{} 0&{} {\rho _{53} }&{} 0&{} {\rho _{55} }&{} 0 \\ 0&{} 0&{} 0&{} 0&{} 0&{} {\rho _{66} } \\ \end{array} }} \right) , \end{aligned}$$
(6)

here, \(\rho _{11} =\delta _1, \rho _{22} =\frac{a_1 a_1^{*} \delta _2 }{a_1 a_1^{*} +1}+\frac{a_2 a_2^{*} \delta _3 }{a_2 a_2^{*} +1}, \rho _{24} =\frac{a_1 \delta _2 }{a_1 a_1^{*} +1}+\frac{a_2 \delta _3 }{a_2 a_2^{*} +1}, \rho _{33} =\frac{a_3 a_3^{*} \delta _4 }{a_3 a_3^{*} +1}+\frac{a_4 a_4^{*} \delta _5 }{a_4 a_4^{*} +1}, \rho _{35} =\frac{a_3 \delta _4 }{a_3 a_3^{*} +1}+\frac{a_4 \delta _5 }{a_4 a_4^{*} +1}, \rho _{44} =\frac{\delta _2 }{a_1 a_1^{*} +1}+\frac{\delta _3 }{a_2 a_2^{*} +1}, \rho _{55} =\frac{\delta _4 }{a_3 a_3^{*} +1}+\frac{\delta _5 }{a_4 a_4^{*} +1}, \rho _{66} =\delta _{0}, \rho _{42} =\rho _{24}^{*}, \rho _{53} =\rho _{35}^{*}, \delta _l =\exp (-E_l /T)(l=0,1,2,3,4,5)\) and the partition function \(Z=\sum \nolimits _{j=0}^5 {\delta _j }\).

It is proven that the negativity, which is based on the partial transpose method [35], is a useful entanglement measure introduced by Vidal and Werner [36], which can be computed effectively for a bipartite system of any dimension. We will use the convention of Ref. [37], which is twice the value of the original definition

$$\begin{aligned} N(\rho )=\sum \limits _{i} {\left| {\mu _i } \right| } , \end{aligned}$$
(7)

where \(\mu _i\) are the negative eigenvalues of the partial transpose \(\rho ^{T_1 }(\rho ^{T_2 })\) of the total state \(\rho \) respect to the first (second) system, and the \(\rho ^{{\mathrm{T}}_{1}}\) can be expressed as

$$\begin{aligned} \rho ^{T_1 }=\frac{1}{Z}\left( {{\begin{array}{l@{\qquad }l@{\qquad }l@{\qquad }l@{\qquad }l@{\qquad }l} {\rho _{_{11}} }&{} 0&{} 0&{} 0&{} {\rho _{_{42}} }&{} 0 \\ 0&{} {\rho _{_{22}} }&{} 0&{} 0&{} 0&{} {\rho _{_{53}} } \\ 0&{} 0&{} {\rho _{_{33}} }&{} 0&{} 0&{} 0 \\ 0&{} 0&{} 0&{} {\rho _{_{44}} }&{} 0&{} 0 \\ {\rho _{_{24}} }&{} 0&{} 0&{} 0&{} {\rho _{_{55}} }&{} 0 \\ 0&{} {\rho _{_{35}} }&{} 0&{} 0&{} 0&{} {\rho _{_{66}} } \\ \end{array} }} \right) . \end{aligned}$$
(8)

Applying these formulas to our model, we can obtain the negativity as follows

$$\begin{aligned} N&= \frac{1}{2Z}\Big \{\max \Big \{0,\sqrt{\rho _{22}^2 +4\rho _{24} \rho _{42} -2\rho _{22} \rho _{44} +\rho _{44}^2 }-\rho _{22} -\rho _{44} \Big \}. \nonumber \\&\Big .+\,\max \Big \{0,\sqrt{\rho _{33}^2 +4\rho _{35} \rho _{53} -2\rho _{33} \rho _{55} +\rho _{55}^2 }-\rho _{33} -\rho _{55} \Big \}\Big \} \end{aligned}$$
(9)

In addition to this, we will investigate the quantum correlation of this model via measurement-induced disturbance in this paper. For a bipartite state \(\rho \), we can apply local measurement \(\{\Pi _{\mathrm{k}} \}\) to it, here \(\Pi _{\mathrm{k}} =\Pi _i^{a} \otimes \Pi _j^b\) and \(\Pi _i^{a}, \Pi _j^b \) are complete projective measurements composed by one-dimensional orthogonal projections for parties a and b. After the measurement, we get a classical state \(\Pi (\rho )=\sum _{i,j} {(\Pi _i^a \otimes \Pi _j^b )\rho } (\Pi _i^a \otimes \Pi _j^b )\). If the spectral resolutions of the reduced states \(\rho ^{a}=\sum _i {p_i^a \Pi _i^a}\) and \(\rho ^{b}=\sum _j {p_j^b \Pi _j^b }\) induce the measurement \(\Pi \), the measurement leaves the marginal information invariant and is in a certain sense the least disturbing. So \(\Pi (\rho )\) is closest to the original state \(\rho \) since this kind of measurement can leave the reduced states invariant. One can use any reasonable distance between \(\rho \) and \(\Pi (\rho )\) to measure the quantum correlation in \(\rho \). According to Luo’s method [20], the quantum correlation can be quantified by the measurement-induced disturbance (MID)

$$\begin{aligned} Q(\rho )=I(\rho )-I[\Pi (\rho )], \end{aligned}$$
(10)

where \(I(\rho )=S(\rho ^{a})+S(\rho ^{b})-S(\rho )\) is quantum mutual information and \(S(\rho )=-tr\rho \log \rho \) denotes the von Neumann entropy.

Based on the definition of MID, the quantum correlation of our model can be expressed as

$$\begin{aligned} Q(\rho )&= -S(\rho )+S[\Pi (\rho )] \nonumber \\&= \lambda _1 \hbox {log}_{2} \lambda _1 +\lambda _2 \hbox {log}_{2} \lambda _2 +\lambda _3 \hbox {log}_2 \lambda _3 +\lambda _4 \hbox {log}_2 \lambda _4 \nonumber \\&-\frac{\rho _{22} }{Z}\log _2 \frac{\rho _{22} }{Z}-\frac{\rho _{33} }{Z}\log _2 \frac{\rho _{33} }{Z}-\frac{\rho _{44} }{Z}\log _2 \frac{\rho _{44} }{Z}-\frac{\rho _{55} }{Z}\log _2 \frac{\rho _{55} }{Z} \end{aligned}$$
(11)

with \(\lambda _{1, 2} \!=\!\frac{\rho _{22} +\rho _{44} +\sqrt{\rho _{22}^2 +4\rho _{24} \rho _{42} \pm 2\rho _{22} \rho _{44} +\rho _{44}^2 }}{2Z}\), and \(\lambda _{3, 4} \!=\!\frac{\rho _{33} +\rho _{55} +\sqrt{\rho _{33}^2 +4\rho _{35} \rho _{53} \pm 2\rho _{33} \rho _{55} +\rho _{55}^2 }}{2Z}\).

3 Quantum phase transitions of the ground states

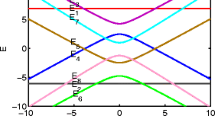
We consider the exchange constant \(J\) as unity and \(\gamma =2\) for simplification. The Fig. 1 describe the eigenvalues of two-mixed-spin (1/2, 1) XXZ model as a function of DM interaction parameter \(D\) for \(B=1\), 4 and \(b=0.2\). As we can see from Fig. 1a, there are no crossing pattern among ground-state eigenvalues so the ground state is always \(\left| {\Psi _4 } \right\rangle \), but the ground-state eigenvalues \(E_4 \) has a sudden change which is called self-avoiding level crossing at the point \(D=0\). Moreover, with the increasing \(B, E_4 \) and \(E_0 \) become closer to each other, and when \(B \) is increased to critical value \(B_m \approx 2.495\) the curves of \(E_4 \) and \(E_0 \) have an intersection at \(D=0\), which means quantum phase transition (QPT) occurs for our system. It is obvious that, these are two symmetrical QPT points about \(D=0\) in this system when \(B>B_m \) as we see in Fig. 1b. The changes of ground states are: entangled \(\left| {\Psi _4 } \right\rangle \rightarrow \) disentangled state \(\left| {\Psi _0 } \right\rangle \rightarrow \) entangled state \(\left| {\Psi _4 } \right\rangle \). In addition to this, comparing Fig. 1a, b, the positions of two QPT points shift with the increasing of \(B\) for the greater \({\vert }D{\vert }\). Figure 2c, d show the evolution of the eigenvalues versus external \(B\) for different \(D\) values at \(b=0.2\). These are three crossing points for each plot, two of which are symmetry about \(B=0\), and another one is zero. Furthermore, the ground state of the system first jumps from a disentangled state \(\left| {\Psi _1 } \right\rangle \) to an entangled state \(\left| {\Psi _2 } \right\rangle \), then it jumps from an entangled state \(\left| {\Psi _4 } \right\rangle \) to a disentangled \(\left| {\Psi _0 } \right\rangle \) at the transformation points, respectively. Similarly, the eigenvalues in terms of \(b\) for different values of \(D\) are plotted in Fig. 3e, f. It can be seen that the existence of \(b\) makes the function curves become asymmetric. From Fig. 3e, we can see the ground state of the system changes from an entangled state \(\left| {\Psi _2 } \right\rangle \) to a disentangled state \(\left| {\Psi _0 } \right\rangle \), then jumps to an entangled state \(\left| {\Psi _4 } \right\rangle \) at the transformation points. Moreover, by comparing Fig. 3e, f, we can get a conclusion that these are only one QPT point when \(D\) is greater than critical point \(D_{m}\), and the change of ground state is from the entangled state \(\left| {\Psi _2 } \right\rangle \) to the entangled state \(\left| {\Psi _4 } \right\rangle \). Through the above analysis, we find that the positions and the level spacing of QPT points can be changed by controlling the DM interaction and external magnetic in our model.

Fig. 1
figure 1

(Color online) The dependence of energy eigenvalues on the DM interaction intensity D in different magnetic field B (we choose the parameters \(J = 1,\gamma =2, b = 0.2\) for simplicity)

Full size image
Fig. 2
figure 2

(Color online) The dependence of Energy eigenvalues on the external \(B\) in different \(D\) values. (\(J = 1,\gamma =2, b = 0.2\))

Full size image
Fig. 3
figure 3

(Color online) The dependence of Energy eigenvalues on \(b\) in different \(D\) values. (\(J = 1,\gamma =2, B = 4\))

Full size image

4 Quantum correlation analyses

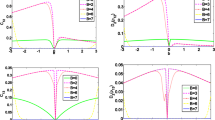
As an example, we investigate the antiferromagnetic case for \(J=1\) and \(\gamma =2\) for simplicity. From Fig. 4, which shows the negativity (\(N\)) and MID as functions of \(T\) and \(D\) when \(B=b=0\), we can see these exists a critical temperature \(T_{m}\), and when the system’s temperature exceeds the critical value the \(N\) and MID disappears, that is to say, the quantum correlation exists only within a certain temperature range. More importantly, the critical temperature of MID is larger than \(N\)’s under the same conditions and critical temperature \(T_{c}\) can increase by increasing the strength of DM interaction. This point implies that the DM interaction may be an effective approach to retain quantum correlation under finite temperature.

Fig. 4
figure 4

(Color online) The negativity (\(N\)) and measurement-induced disturbance (MID) as functions of \(T\) and \(D\) when \(B=b=0\) (\(J = 1,\gamma =2\))

Full size image

The evolution of \(N\) and MID in terms of \(B\) for different values of \(D\) are plotted in Fig. 5. It is obvious that, with the DM interaction \(D\) increasing, the range in which the quantum correlation exists become wider. Moreover, combined with the Fig. 6, which describe the \(N\) and MID as a function of temperature \(T\) for different values of \(D\) at the different external magnetic field \(B\), we can draw a conclusion that \(D\) plays an important role in improving the quantum correlation. In addition to this, we find that \(D\) cannot enlarge the largest negativity alone without the external magnetic field \(B\). When \(B\) exists, \(D\) can improve the largest negativity obviously. But this phenomenon does not occur in measurement-induced disturbance (MID). This point indicates that MID is more stable than negativity under the influence of the external magnetic field, especially when \(B\) closes to zero.

Fig. 5
figure 5

(Color online) The evolution of \(N\) and MID in terms of \(B\) for different values of D (\(J = 1,\gamma =2, T= 0.5, b=0\))

Full size image
Fig. 6
figure 6

(Color online) The \(N\) and MID as a function of temperature \(T\) for different values of \(D\) at the different external magnetic field \(B\) (\(J = 1,\gamma =2, b=0\))

Full size image

Now we begin to discuss the effect of magnetic field on negativity and MID with Dzyaloshinskii–Moriya (DM) interaction, and we will consider DM interaction for \(D=3\) for simplicity. Form Fig. 7, it can be seen obviously that (i) at the case of homogeneous magnetic field, \(N\) and MID vary with the changes of B, but no matter how the B changes, the critical temperature \(T_{c}\) is always a fixed value and (ii) to a certain extent, critical temperature \(T_{c}\) of negativity can be enhanced by the increasing of \(b\) under the inhomogeneous magnetic field. But this phenomenon is not obvious in measurement-induced disturbance because the distinct difference between MID and negativity is that MID vanishes in an asymptotic way, but negativity will be disappeared at critical temperature.

Fig. 7
figure 7

(Color online) The two-dimensional pictures of the \(N\) and MID when \(J=1, \gamma =2\) and \(D=3\). a and b Show \(N\) and MID in terms of \(T\) for different values of \(B\) at the case of homogeneous magnetic field (\(b=0\)), c and d show \(N\) and MID as a function of \(T\) for different values of \(b\) when \(B=1\) for simplicity

Full size image

In the following study, compared with the thermal entanglement measured by negativity, we will investigate the quantum correlation using measurement-induced disturbance (MID) in our system and consider \(B=b=D=0\) for simplicity. In Fig. 8, for the case \(\gamma =1\), the negativity and MID versus the exchange constant \(J\) and temperature \(T\) are plotted. We can observe that both the negativity and MID decrease with the temperature increasing, and MID vanishes in an asymptotic way, but negativity will be disappeared at critical temperature. Moreover, from Fig. 8, we also find that there is no entanglement for the ferromagnetic case (\(J < 0\)), but the MID always exists in both the antiferromagnetic (\(J > 0\)) and ferromagnetic regions, only achieving zero at the critical point \(J = 0\). Through the above discussions, we can get a conclusion that the thermal MID is more robust than thermal entanglement against temperature.

Fig. 8
figure 8

Negativity and MID versus the exchange constant J and temperature T when \(\gamma =1\) and \(B=b=D=0\)

Full size image

In addition to this, when \(J<0\), the ground state is the statistical combination of \(\left| {\Psi _0 } \right\rangle , \left| {\Psi _1 } \right\rangle , \left| {\Psi _2 } \right\rangle \) and \(\left| {\Psi _4 } \right\rangle \) with equal probabilities, but the ground state become to the statistical combination of \(\left| {\Psi _2 } \right\rangle \) and \(\left| {\Psi _4 } \right\rangle \) with equal probabilities when \(J>0\), that is to say, the quantum phase transition (QPT) occurs for our system when \(J=0\). Figure 9 plot the two-dimensional pictures of the negativity and MID versus the exchange constant \(J\) for different values of temperature T. It is obvious that with the decreasing of \(J\), the MID will decrease to zero at the critical point \(J=0\), after which it will enhance to a nearly stable value. This indicates that the MID can detect the critical points of quantum phase transition, while the negativity does not in such circumstances.

Fig. 9
figure 9

(Color online) The two-dimensional pictures of the negativity and MID versus the exchange constant \(J\) for different values of temperature T. (\(\gamma =1\) and \(B=b=D=0\))

Full size image

5 Conclusions

In this paper, we investigate the quantum phase transition (QTP) and quantum correlation in the one-dimensional mixed-spin (1/2, 1) XXZ model with Dzyaloshinskii–Moriya (DM) interaction under an inhomogeneous magnetic field. We discuss the QPT and find that we can change the phase transition points by controlling the value of \(D, B\) and \(b\). Then we calculate the thermal entanglement by negativity and investigate the quantum correlation using measurement-induced disturbance (MID) for our system. Our results show that critical temperature \(T_{c}\) can increase by increasing the strength of DM interaction, and \(D\) plays an important role in improving the quantum correlation. That is to say, we can obtain more correlation at higher temperature by choosing the proper strength of DM interaction. Moreover, we prove that \(D\) cannot enlarge the largest negativity alone without the external magnetic field \(B\), and when \(B\) exists, \(D\) can improve the largest negativity obviously, but this phenomenon does not exist in measurement-induced disturbance (MID). For the magnetic field, the homogeneous magnetic field cannot change the critical temperature \(T_{c}\) alone, but it is shown that the inhomogeneous magnetic parameter \(b\) can suppress the effects of temperature on negativity.

In addition, we compare the negativity and MID in detail and find that MID may reveal more properties about quantum correlations of this system than entanglement, in the sense that MID can be nonzero while there is no thermal entanglement. Furthermore, we discover that MID is more robust than thermal entanglement against temperature \(T\), which behaves that MID decays asymptotically but entanglement vanishes completely at a finite critical temperature \(T_{c}\). Besides, in some circumstances, the MID can detect the critical points of quantum phase transition while the negativity cannot. Through the above discussions, we come to a conclusion that MID may act as a more general tool than negativity for studying quantum correlations quality of quantum systems.