Entanglement in Mixed-Spin (1/2, 3/2) Heisenberg XXZ Model with Dzyaloshinskii-Moriya Interaction

Abstract

In this paper, the entanglement in a mixed-spin (1/2, 3/2) Heisenberg XXZ model with Dzyaloshinskii-Moriya (DM) interaction in an inhomogeneous external magnetic field is studied. We not only calculate the ground-state entanglement but also investigate the behaviors of quantum phase transition following the changes of DM interaction and nonuniform magnetic field. More importantly, we note that the DM interaction improves the critical magnetic field B _c , the critical temperature T _c and broadens the region of entanglement.

1 Introduction

In recent years, the quantum entanglement has become a crucial physical resource in many fields of quantum information processing such as quantum communication [1–3] and quantum computation [4, 5] due to its nonlocal correlation. The Heisenberg chain as the simplest but an operable model has been used for quantum dots [6], cavity QED [7] and so on.

In particular, the thermal entanglement is a natural entanglement, which is different from the other kinds of entanglements by its advantages of stability for the reduction in entanglement of an entangled state due to various sources of decoherence [8, 9]. Recently, lots of studies have devoted to the thermal entanglement in various spin Heisenberg models with or without external magnetic filed [8–21]. As we all know, Dzyaloshinsky and Moriya initially pointed out the Dzyaloshinskii-Moriya interaction [22, 23], which stems from the spin-orbit coupling. By adding DM interaction, many researchers have investigated the thermal entanglement and teleportation [24–31]. In addition, the quantum discord [32] that a more general measure of the quantum correlation with DM interaction also has been studied in Ref. [33, 34]. The above mentioned investigations suggest the thermal entanglement is an important source of mixed entanglement, and the magnetic field and DM interaction play a significant role in various quantum tasks.

It is noteworthy that, in Refs. [19, 20], by using the concept of negativity, Guo et al. have studied the entanglement of mixed-spin (1/2, 3/2) Heisenberg XXY and XX models with the nonuniform magnetic field, and noted that the mixed-spin (1/2, 3/2) Heisenberg chain can generate more entanglement and higher critical temperature T _c than those in spin 1/2 and mixed-spin (1/2, 1) Heisenberg models for the same parameters. It indicates that the mixed-spin (1/2, 3/2) spin chain is a promising system. However, we notice the entanglement in mixed-spin (1/2, 3/2) Heisenberg XXZ chain with DM interaction in an inhomogeneous external magnetic field has not been investigated, and through the above discussions, we realize that this study is essential. In this work, by adding the DM interaction, we not only calculate the ground-state entanglement, but also discuss the behaviors of quantum phase transition (QPT) [35], which takes place in the ground state at zero temperature. In addition, we note that DM interaction not only improves the critical values of the uniform magnetic field and temperature, but also broadens the region of the entanglement.

2 The Model and Calculation

In this paper, the Hamiltonian for the mixed-spin (1/2, 3/2) Heisenberg XXZ model with z−component DM interaction and inhomogeneous magnetic field is given by

$$\begin{array}{@{}rcl@{}} H&=&J\left( {S_{1}^{x}}{S_{2}^{x}}+{S_{1}^{y}}{S_{2}^{y}}+\varDelta {S_{1}^{z}}{S_{2}^{z}}\right)+(B-b){S_{1}^{z}}+(B+b){S_{2}^{z}}\\ &&+D_{z}\left( {S_{1}^{x}}{S_{2}^{y}}-{S_{1}^{y}}{S_{2}^{x}}\right), \end{array} $$

(1)

where J denotes the exchange constant, for J > 0 corresponds to the anti-ferromagnetic case, and J < 0 the ferromagnetic case, Δ is the anisotropy parameter, D _z is DM coupling parameter in the z direction, B describes uniform external magnetic field, and b controls the inhomogeneity of external magnetic field, $S_{1}^{\iota }$ and $S_{2}^{\iota }$ (ι = x, y, z) are the spin operators of spin 1/2 and spin 3/2, respectively.

In order to study the entanglement, we need to obtain the eigenvalues and eigenstates for the mixed-spin (1/2, 3/2) system from Eq. (1). In this work, we choose the standard basis $\left \{\left |\frac {1}{2}, \frac {3}{2}\right \rangle , \left |\frac {1}{2}, \frac {1}{2}\right \rangle , \left |\frac {1}{2}, -\frac {1}{2}\right \rangle , \left |\frac {1}{2}, -\frac {3}{2}\right \rangle , \left |-\frac {1}{2}, \frac {3}{2}\right \rangle , \left |-\frac {1}{2}, \frac {1}{2}\right \rangle , \left |-\frac {1}{2}, -\frac {1}{2}\right \rangle , \left |-\frac {1}{2}, -\frac {3}{2}\right \rangle \right \}$, here |n, m〉 is the eigenstate of ${S_{1}^{z}}$ and ${S_{2}^{z}}$ with the corresponding eigenvalues given by n and m, respectively. Thus the Hamiltonian (1) can be calculated in the matrix form as

$$ H=\left( \begin{array}{cccccccc} a_{11} & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & a_{22} & 0 & 0 & a_{25} & 0 & 0 & 0 \\ 0 & 0 & a_{33} & 0 & 0 & a_{36} & 0 & 0 \\ 0 & 0 & 0 & a_{44} & 0 & 0 & a_{47} & 0 \\ 0 & a_{52} & 0 & 0 & a_{55} & 0 & 0 & 0 \\ 0 & 0 & a_{63} & 0 & 0 & a_{66} & 0 & 0 \\ 0 & 0 & 0 & a_{74} & 0 & 0 & a_{77} & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & a_{88} \end{array} \right), $$

(2)

where $a_{11}=\frac {3}{4}J\varDelta +2B+b$, $a_{22}=\frac {1}{4}J\varDelta +B$, $a_{25}=a_{52}^{\ast }=a_{47}=a_{74}^{\ast }=\frac {\sqrt {3}}{2}J+\frac {\sqrt {3}}{2}Di$, $a_{33}=-\frac {1}{4}J\varDelta -b$, $a_{36}=a_{63}^{\ast }=J+Di$, $a_{44}=-\frac {3}{4}J\varDelta -B-2b$, $a_{55}=-\frac {3}{4}J\varDelta +B+2b$, $a_{66}=-\frac {1}{4}J\varDelta +b$, $a_{77}=\frac {1}{4}J\varDelta -B$ and $a_{88}=\frac {3}{4}J\varDelta -2B-b$. After a mathematical calculation, the eigenvalues are given by

$$\begin{array}{@{}rcl@{}} &&E_{1}=-3\varsigma+2B+b,\\ &&E_{2}=-3\varsigma-2B-b,\\ &&E_{3}=b+B+\varsigma+\tau_{1},\\ &&E_{4}=b+B+\varsigma-\tau_{1},\\ &&E_{5}=-b-B+\varsigma+\tau_{2},\\ &&E_{6}=-b-B+\varsigma-\tau_{2},\\ &&E_{7}=\varsigma+\vartheta,\\ &&E_{8}=\varsigma-\vartheta, \end{array} $$

(3)

where $\varsigma = -\frac {1}{4}J\varDelta$, $\vartheta =\sqrt {{J^{2}} + {b^{2}} + {{D_{z}^{2}}}}$, $\tau _{1}=\frac {1}{2}\sqrt {4b^{2}-4J\varDelta b+J^{2}\varDelta ^{2}+3J^{2}+3{D_{z}^{2}}}$, $\tau _{2}=\frac {1}{2}\sqrt {4b^{2}+4J\varDelta b+J^{2}\varDelta ^{2}+3J^{2}+3{D_{z}^{2}}}$, and the corresponding eigenstates are expressed as

$$\begin{array}{@{}rcl@{}} &&|\Psi_{1}\rangle=\left|\frac{1}{2},\frac{3}{2}\right\rangle,\\ &&|\Psi_{2}\rangle=\left|-\frac{1}{2},-\frac{3}{2}\right\rangle,\\ &&|\Psi_{3}\rangle=\frac{1}{\sqrt{g_{1}g_{1}^{\ast}+1}}\left( g_{1}\left|-\frac{1}{2},\frac{3}{2}\right\rangle+ \left|\frac{1}{2},\frac{1}{2}\right\rangle\right),\\ &&|\Psi_{4}\rangle=\frac{1}{\sqrt{g_{2}g_{2}^{\ast}+1}}\left( g_{2}\left|-\frac{1}{2},\frac{3}{2}\right\rangle+ \left|\frac{1}{2},\frac{1}{2}\right\rangle\right),\\ &&|\Psi_{5}\rangle=\frac{1}{\sqrt{g_{3}g_{3}^{\ast}+1}}\left( g_{3}\left|\frac{1}{2},-\frac{3}{2}\right\rangle+\left|-\frac{1}{2},-\frac{1}{2}\right\rangle\right),\\ &&|\Psi_{6}\rangle=\frac{1}{\sqrt{g_{4}g_{4}^{\ast}+1}}\left( g_{4}\left|\frac{1}{2},-\frac{3}{2}\right\rangle+ \left|-\frac{1}{2},-\frac{1}{2}\right\rangle\right),\\ &&|\Psi_{7}\rangle=\frac{1}{\sqrt{g_{5}g_{5}^{\ast}+1}}\left( g_{5}\left|-\frac{1}{2},\frac{1}{2}\right\rangle+ \left|\frac{1}{2},-\frac{1}{2}\right\rangle\right),\\ &&|\Psi_{8}\rangle=\frac{1}{\sqrt{g_{6}g_{6}^{\ast}+1}}\left( g_{6}\left|-\frac{1}{2},\frac{1}{2}\right\rangle+ \left|\frac{1}{2},-\frac{1}{2}\right\rangle\right), \end{array} $$

(4)

where $g_{1}=\frac {2}{\sqrt 3}\frac {(b+2\varsigma +\tau _{1})(J-D_{z}i)}{J^{2}+{D_{z}^{2}}}$, $g_{2}=\frac {2}{\sqrt 3}\frac {(b+2\varsigma -\tau _{1})(J- D_{z}i)}{J^{2}+{D_{z}^{2}}}$, $g_{3}=\frac {2}{\sqrt 3}\frac {(-b+2\varsigma +\tau _{2})(J-D_{z}i)}{J^{2}+{D_{z}^{2}}}$, $g_{4}=\frac {2}{\sqrt 3}\frac {(-b+2\varsigma -\tau _{2})(J-D_{z}i)}{J^{2}+{D_{z}^{2}}}$, $g_{5}=\frac {(b+\vartheta )(J-D_{z}i)}{J^{2}+{D_{z}^{2}}}$ and $g_{6}=\frac {(b-\vartheta )(J-D_{z}i)}{J^{2}+{D_{z}^{2}}}$.

For a state of system in thermal equilibrium (temperature T), which is described by the density operator $\rho (T) = (1/Z)\exp (-H/k_{B}T)$, where H is the Hamiltonian, $Z=\text {tr}[\exp (-H/k_{B}T)]$ is the partition function, and k _B is Boltzmann constant, for simplicity, we write k _B = 1. The entanglement of states of the system at thermal equilibrium is called thermal entanglement [8, 9]. In the standard basis above-mentioned, the density operator of the system can be given by

$$ \rho(T) = \frac{1}{Z}\left( \begin{array}{cccccccc} \rho_{11} & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & \rho_{22} & 0 & 0 & \rho_{25} & 0 & 0 & 0 \\ 0 & 0 & \rho_{33} & 0 & 0 & \rho_{36} & 0 & 0 \\ 0 & 0 & 0 & \rho_{44} & 0 & 0 & \rho_{47} & 0 \\ 0 & \rho_{52} & 0 & 0 & \rho_{55} & 0 & 0 & 0 \\ 0 & 0 & \rho_{63} & 0 & 0 & \rho_{66} & 0 & 0 \\ 0 & 0 & 0 & \rho_{74} & 0 & 0 & \rho_{77} & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & \rho_{88} \end{array} \right), $$

(5)

where $\rho _{11}=\zeta _{1}, \rho _{22}=\frac {\zeta _{3}}{g_{1}g_{1}^{\ast }+1}+\frac {\zeta _{4}}{g_{2}g_{2}^{\ast }+1}, \rho _{25}=\frac {\zeta _{3}g_{1}^{\ast }}{g_{1}g_{1}^{\ast }+1}+\frac {\zeta _{4}g_{2}^{\ast }}{g_{2}g_{2}^{\ast }+1}, \rho _{33}=\frac {\zeta _{7}}{g_{5}g_{5}^{\ast }+1}+\frac {\zeta _{8}}{g_{6}g_{6}^{\ast }+1}, \rho _{36}=\frac {\zeta _{7}g_{5}^{\ast }}{g_{5}g_{5}^{\ast }+1}+\frac {\zeta _{8}g_{6}^{\ast }}{g_{6}g_{6}^{\ast }+1}, \rho _{44}=\frac {\zeta _{5}g_{3}g_{3}^{\ast }}{g_{3}g_{3}^{\ast }+1}+\frac {\zeta _{6}g_{4}^{\ast }}{g_{4}g_{4}^{\ast }+1}, \rho _{47}=\frac {\zeta _{5}g_{3}}{g_{3}g_{3}^{\ast }+1}+\frac {\zeta _{6}g_{4}}{g_{4}g_{4}^{\ast }+1}, \rho _{52}=\frac {\zeta _{3}g_{1}}{g_{1}g_{1}^{\ast }+1}+\frac {\zeta _{4}g_{2}}{g_{2}g_{2}^{\ast }+1}, \rho _{55}=\frac {\zeta _{3}g_{1}g_{1}^{\ast }}{g_{1}g_{1}^{\ast }+1}+\frac {\zeta _{4}g_{2}g_{2}^{\ast }}{g_{2}g_{2}^{\ast }+1}, \rho _{63}=\frac {\zeta _{7}g_{5}}{g_{5}g_{5}^{\ast }+1}+\frac {\zeta _{8}g_{6}^{\ast }}{g_{6}g_{6}^{\ast }+1}, \rho _{66}=\frac {\zeta _{7}g_{5}g_{5}^{\ast }}{g_{5}g_{5}^{\ast }+1}+\frac {\zeta _{8}g_{6}^{\ast }}{g_{6}g_{6}^{\ast }+1}, \rho _{74}=\frac {\zeta _{5}g_{3}^{\ast }}{g_{3}g_{3}^{\ast }+1}+\frac {\zeta _{6}g_{4}^{\ast }}{g_{4}g_{4}^{\ast }+1}, \rho _{77}=\frac {\zeta _{5}}{g_{3}g_{3}^{\ast }+1}+\frac {\zeta _{6}}{g_{4}g_{4}^{\ast }+1}, \rho _{88}=\zeta _{2}$, $\zeta _{i}=\exp \left (-\frac {E_{i}}{T}\right ),(i=1,2,3...8)$, and $Z={\sum \limits _{1}^{8}} {\zeta _{i}}=2\left [\exp \left (\frac {3\varsigma }{T}\right )\cosh \left (\frac {2B+b}{T}\right )+\exp \left (-\frac {b+B+\varsigma }{T}\right )\cosh \left (\frac {\tau _{1}}{T}\right )+\exp \left (\frac {b+B-\varsigma }{T}\right )\cosh \left (\frac {\tau _{2}}{T}\right )\right .$ $\left .+ \exp \left (-\frac {\varsigma }{T}\right )\cosh \left (\frac {\vartheta }{T}\right )\right ]$.

As is known to all, according to the Peres-Horodecki Criterion [36, 37] which can give a qualitative way for judging whether the state of high dimensional bipartite systems is entangled or not, the negativity was proposed by Vidal and Werner [38] and can be used to effectively compute the entanglement for any mixed state of an arbitrary bipartite system, and it does not increase under local manipulations of the system, thus we use it to study the entanglement in our mixed-spin (1/2, 3/2) system. The negativity of a state ρ is defined as

$$ N(\rho) = \frac{{\|{\rho^{{T_{1}}}}\| - 1}}{2} = \frac{{\|{\rho^{{T_{2}}}}\|-1}}{2} = \sum\limits_{i} {{|u_{i}|}},\\ $$

(6)

where ${\rho ^{{T_{1}}}} \left ({\rho ^{{T_{2}}}}\right )$ denotes the partial transpose of the total state ρ respect to the first (second) subsystem, and u _i is the negative eigenvalue of ${\rho ^{{T_{1}}}} \left ({\rho ^{{T_{2}}}}\right )$. The corresponding partial transpose $\rho ^{T_{1}}$ can be given by

$$ \rho^{T_{1}}=\frac{1}{Z}\left( \begin{array}{cccccccc} \rho_{11} & 0 & 0 & 0 & 0 & \rho_{52} & 0 & 0 \\ 0 & \rho_{22} & 0 & 0 & 0 & 0 & \rho_{63} & 0 \\ 0 & 0 & \rho_{33} & 0 & 0 & 0 & 0 & \rho_{74} \\ 0 & 0 & 0 & \rho_{44} & 0 & 0 & & 0 \\ 0 & 0 & 0 & 0 & \rho_{55} & 0 & 0 & 0 \\ \rho_{25} & 0 & 0 & 0 & 0 & \rho_{66} & 0 & 0 \\ 0 & \rho_{36} & 0 & 0 & 0 & 0 & \rho_{77} & 0 \\ 0 & 0 & \rho_{47} & 0 & 0 & 0 & 0 & \rho_{88} \end{array} \right). $$

(7)

Hence, from Eqs. (6) and (7), one can obtain the expression of negativity as follows

$$\begin{array}{@{}rcl@{}} N=&\frac{1}{2Z}\left\{\max\left\{0,\sqrt{(\rho_{77}-\rho_{22})^{2}+4\rho_{36}\rho_{63}}-\rho_{77}-\rho_{22}\right\}\right.\\ &+\max\left\{0,\sqrt{(\rho_{66}-\rho_{11})^{2}+4\rho_{25}\rho_{52}}-\rho_{66}-\rho_{11}\right\}\\ &+\left.\max\left\{0,\sqrt{(\rho_{88}-\rho_{33})^{2}+4\rho_{47}\rho_{74}}-\rho_{88}-\rho_{33}\right\}\right\}, \end{array} $$

(8)

which is a function of parameters T, J, Δ, B, b and D _z .

3 Ground-State Entanglement and Quantum Phase Transitions (QPT)

In order to investigate the entanglement of ground states and QPT, we analyze the energy eigenvalues behaviour following the change of different parameters. In Fig. 1, we plot the eigenvalues as the functions of the z-component of DM interaction by fixing the rest. Obviously, which eigenstate is the ground state depends on the parameter D _z in this case. It is clear that, when D < D _{z c1} ≈ −2.57, the ground state is the entangled state |Ψ₆〉 with the eigenvalue E ₆, and the corresponding negativity is given by $N=\frac {|\xi |}{|\xi |^{2}+1}$, where $\xi =\frac {\left (2\sqrt {{D_{z}^{2}}+21}+3\right )(D_{z}i-1)}{4\sqrt 3\left ({D_{z}^{2}}+1\right )}$; when D = D _{z c1}, the ground-state eigenvalue E ₆ and the eigenvalue E ₂ with the first excited state |Ψ₂〉 have an intersection, namely, the ground states are doubly degenerate at the intersection, and this suggests that quantum phase transition occurs [35], which is induced by the discontinuous changes in a property of the ground state |Ψ₆〉 and the structure of the first excited state |Ψ₂〉 when the external parameter D _z traverses a critical point D _{z c1}, and in the QPT point, the quantum fluctuations play a dominant role and the thermal fluctuations become frozen. Moreover, when D _{z c1} < D < D _{z c2} ≈ −2.57, the ground-state is the unentangled stat |Ψ₂〉, so the negativity equals to zero; when D _z = D _{z c2}, the ground-state energy eigenvalue E ₂ and the eigenvalue E ₆ with the first excited state |Ψ₆〉 show a crossing point, and the QPT also takes place at D _z = D _{z c2}; when D _z > D _{z c2}, the ground state becomes |Ψ₆〉 again. It is observed that the positions of two QPT points (D _{z c1} ≈ −2.57 and D _{z c2} ≈ 2.57) are symmetric about D _z = 0. In addition, from Fig. 1, we can clearly see the phenomenon that the other energy eigenvalues also display the intersection points, which is caused by the degeneracy of the excited states with the change of DM interaction.

Fig. 1

The eigenvalues E versus the z−copoment of DM interaction D _z , where we assume J = 1, Δ = 0.5, B = 3 and b = 0.5

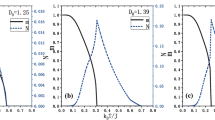
The eigenvalues versus magnetic field B are plotted in Fig. 2. It is easy to find that there are four QPT points (B _c1 ≈ −3.34, B _c2 ≈ −1.48, B _c3 ≈ −0.69 and B _c4 ≈ 3.51), and the ground states can be described by

$$\begin{array}{@{}rcl@{}}&& \Gamma_{GS}=\left\{\begin{array}{ll} |\Psi_{1}\rangle\langle\Psi_{1}| & B<B_{c1},\\ \frac{1}{2}|\Psi_{1}\rangle\langle\Psi_{1}|+\frac{1}{2}|\Psi_{4}\rangle\langle\Psi_{4}| & B=B_{c1},\\ |\Psi_{4}\rangle\langle\Psi_{4}| & B_{c1}<B<B_{c2},\\ \frac{1}{2}|\Psi_{4}\rangle\langle\Psi_{4}|+\frac{1}{2}|\Psi_{8}\rangle\langle\Psi_{8}| & B=B_{c2},\\ |\Psi_{8}\rangle\langle\Psi_{8}| & B_{c2}<B<B_{c3},\\ \frac{1}{2}|\Psi_{8}\rangle\langle\Psi_{8}|+\frac{1}{2}|\Psi_{6}\rangle\langle\Psi_{6}| & B=B_{c3},\\ |\Psi_{6}\rangle\langle\Psi_{6}| & B_{c3}<B<B_{c4},\\ \frac{1}{2}|\Psi_{6}\rangle\langle\Psi_{6}|+\frac{1}{2}|\Psi_{2}\rangle\langle\Psi_{2}| & B=B_{c4},\\ |\Psi_{2}\rangle\langle\Psi_{2}| & B_{c4}<B, \end{array} \right. \end{array} $$

(9)

and the corresponding negativities are obtained as

$$\begin{array}{@{}rcl@{}}&& N=\left\{\begin{array}{ll} 0 & B<B_{c1}, \\ 0.0973 & B=B_{c1} , \\ 0.4979 & B_{c1}<B<B_{c2},\\ 0.2971 & B=B_{c2}, \\ 0.4939 & B_{c2}<B<B_{c3},\\ 0.2931 & B=B_{c3}, \\ 0.4822 & B_{c3}<B<B_{c4},\\ 0.0880 & B=B_{c4}, \\ 0 & B_{c4}<B. \end{array} \right. \end{array} $$

(10)

Fig. 2

The eigenvalues E versus uniform magnetic field B, where we assume J = 1, Δ = 0.5, b = 1 and D _z = 3

By observing Eq. (10), we can find the entanglement of ground state is independent of the uniform magnetic field B when B is in a certain range.

Finally, in Fig. 3, we study the influence of the inhomogeneous magnetic parameter b and note that there are two QPT points (b _c1 ≈ −3.10 and b _c2 ≈ −2.51). It is observed that, with the increasing of b, E ₆ has an abrupt change near b = 0, and the ground state initially changes from the entangled state |Ψ₄〉 (b < b _c1) to the entangled state |Ψ₈〉 (b _c1 < b < b _c2), then jumps to the entangled |Ψ₆〉 (b > b _c2) at the positions of QPT (b = b _c1 and b = b _c2), respectively. The corresponding negativities can be obtained as $N_{|\Psi _{4}\rangle }=\frac {|\sigma _{1}|}{|\sigma _{1}|^{2}+1}$, $N_{|\Psi _{8}\rangle }=\frac {|\sigma _{2}|}{|\sigma _{2}|^{2}+1}$, and $N_{|\Psi _{6}\rangle }=\frac {|\sigma _{3}|}{|\sigma _{3}|^{2}+1}$, where σ ₁ = $-\frac {\sqrt {3}}{60}\left [-4b+1+\sqrt {16b^{2}-8b+121}+\left (12b-3-3\sqrt {16b^{2}-8b+121}\right )i\right ]$, $\sigma _{2}=\frac {1}{10}$ $\left [b-\sqrt {b^{2}+10}-\left (3+3\sqrt {b^{2}+10}\right )i\right ]$, and $\sigma _{3}=-\frac {\sqrt {3}}{60}\left [4b+1+ \sqrt {16b^{2}-8b+121}-\right .$ $\left .\left (12b+3+3\sqrt {16b^{2}-8b+121}\right )i\right ]$. From the above discussions, not only can we change the positions of QPT points, but also obtain the optimal entanglement of ground state by coordinating the parameters D _z , B and b in our model.

Fig. 3

The eigenvalues E versus inhomogeneous magnetic field b, where we assume J = 1, Δ = 0.5, B = 3 and D _z = 3

4 Thermal Entanglement

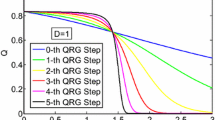
Firstly, we would like to study the effect of the uniform field B on thermal entanglement when DM interaction is included. The N as the functions of T and B are plotted by fixing the parameters J, Δ, b and D _z in Fig. 4. Looking at Fig. 4a, we find that, at zero-temperature limit, the N maintains the maximal value until B arrives at a critical value B _c , above which the N disappears. At the same time, we note that the entanglement also decreases to zero at critical temperature T _c , for the reason that as temperature goes up the mixing of ground state with more excited states acts as a destructive noise that leads to the entanglement decays. In Fig. 4b, six contour lines of N = 0, 0.05, 0.1, 0.2, 0.3, 0.4 are shown, respectively. Beyond the contour line N = 0, there is no entanglement, which also can be seen Eq. (9) the entanglement goes to zero when $\rho _{77}\rho _{22}\geq \rho _{36}^{2}$, $\rho _{66}\rho _{11}\geq \rho _{25}^{2}$, and $\rho _{88}\rho _{33}\geq \rho _{47}^{2}$. Comparing with Ref. [19], where the DM interaction is absent, D _z can enhance the maximal value of N and the critical temperature T _c . For example, by controlling the rest parameters, D _z = 0, $N_{\max }\approx 0.38$, T _c ≈ 1.13 [19]; D _z = 1, $N_{\max }\approx 0.43$, T _c ≈ 1.58. However, we have to note the D _z can’t change the intrinsic nature of the entanglement: when D _z is excluded, observed from the Figures 1 and 3 of Ref. [19] and the Figure 1 of Ref. [20], and when D _z is included, seen from Fig. 4 in our work, we obtain the same result that the critical temperature T _c is completely independent of the uniform magnetic field B.

Fig. 4

The negativity N is plotted as functions of magnetic field B and temperature T when J = 1, Δ = 0.5, b = 0.5 and D _z = 1. (a) The curve of N as functions of B and T. (b) The contour lines of N versus B and T

Secondly, we discuss the role played by the z-component DM interaction in adjusting thermal entanglement. The N as a function of temperature T is plotted for different D _z in Fig. 5, from which one can easily find that the value of N from zero goes up to a maximum with the increases of D _z at zero-temperature limit. Furthermore, when T < T _c and D _z > 1, the higher the temperature is, the smaller the N is, and the value of N decreases due to the destruction of the quantum entanglement by classical thermal fluctuations. However, when 0 < D _z < 1, with the increasing of T, the N goes up gradually to a maximum, then drops slowly to zero. More importantly, it is observed that the larger D _z can improve critical temperature T _c , which means that we can gain the same conclusion with Refs. [25, 28, 29] that the entanglement can be obtained at higher temperature as D _z is raised. In the following, the N versus magnetic field B for different values of D _z is plotted in Fig. 6. When D _z = 0, the N is a small value, and it monotonically decreases to zero with B increasing; when D _z > 1, we find that, as B increases, N goes to a maximum and then decays monotonously to zero at critical uniform magnetic field B _c , and it is easy to see that B _c is broadened by the increasing of D _z . One can also find, for a finite magnetic field B < B _c , the larger D _z can enhance the maximal value of entanglement. Thus one can obtain the conclusion that D _z plays a considerably important role in improving entanglement.

Fig. 5

The negativity N versus temperature T for different z−component of DM interaction D _z , where we assume J = 1, J = 1, Δ=0.5, B = 2 and b = 0.5

Fig. 6

The negativity N versus magnetic B for different z−component of D M interaction D _z , where we assume T = 1, Δ = 0.5 and b = 0.5

In the next step, we discuss how the thermal entanglement behaves as we change the inhomogeneous magnetic field b for various values of D _z . Looking at Fig. 7a and 7b, for $T\rightarrow 0$, it is quite obvious that the parameter b plays a negative role, namely, the higher the b is, the smaller the N is. And as temperature T increases, the N monotonously decreases, the reason is that the maximally entangled state mixes with other excited states. When T is large enough, the all entanglement will be destroyed by classical thermal fluctuations. Comparing Fig. 7a with 7b, the same results can be discovered with Fig. 5 that the larger D _z not only broadens the region of entanglement but also improves the critical temperature T _c . For example, D _z = 0, b = 0, T _c ≈ 1.08, and the same result can be seen in Figure 1(b) of Ref. [19]; D _z = 3, b = 0, T _c ≈ 2.72; D _z = 0, b = 2, T _c ≈ 1.82; D _z = 3, b = 2, T _c ≈ 3.45. At the same time, it is found that the maximal value of N doesn’t have an obvious change when D _z increases for b = 0. Besides, whether or not D _z is considered, we clearly observe that T _c depends on the inhomogeneity of the magnetic field b, and can be improved by the increasing of b. It could be a significant supplement to Refs. [19, 20], in which the same result is obtained in the case that DM interaction is absent.

Fig. 7

The negativity N versus temperature T for different values of inhomogeneous magnetic b, where we assume J = 1, Δ=0.5 and B = 1. (a) D _z = 0; (b) D _z = 3

Ultimately, in Figs. 8 and 9, the N versus temperature for different values of coupling constant J or anisotropy parameter Δ with different D _z values. Looking at Fig. 8a, where D _z = 0, as the temperature increases, the N increases sharply from zero to a peak value, and after the peak value, it decreases monotonously in that the thermal fluctuation gradually dominates the system. It is clear that the maximum value of the N and the critical temperature T _c are enhanced by the increasing of J. In Fig. 8b, where D _z = 3, contrasting with the D _z = 0 case, we find that the larger D _z leads to a result that the maximal value of negativity does not show significant variations as J increases. For the same parameter case, we can obtain more entanglement under higher temperature because of the existence of DM interaction. Moreover, In Fig. 8a and 8b, for different J values, we clearly see that, before N arriving at a maximum, the behaviors of the N are always consistent, which suggests that, in the special region, the temperature is the main factor to affect the entanglement, and the influences of J and D _z can be almost ignored. Looking at Fig. 9a and 9b, we can find, even if the DM interaction is added, the anisotropy parameter Δ still distinctly suppresses the maximal value of N, but it can improve the critical temperature T _c and broaden the region of entanglement for the same Δ. It is also clear that the T _c increases with the increasing of Δ, which agrees with the conclusion of Ref. [19]. In addition, for various Δ values, before the N increasing to a peak value, the behaviors of N are inconsistent, but D _z gradually eliminates this difference.

Fig. 8

The negativity N versus temperature T for different values of coupling constant J, where we assume Δ=0.5, B = 1 and b = 0.5. (a) D _z = 0; (b) D _z = 3

Fig. 9

The negativity N versus temperature T for different values of anisotropy parameter Δ, where we assume J = 1, B = 1 and b = 0.5. (a) D _z = 0; (b) D _z = 3

5 Conclusions

In this article, by using the concept of negativity, we study the effects of the z−component of DM interaction and an inhomogeneous external magnetic field on the entanglement and QPT in mixed-spin (1/2, 3/2) Heisenberg XXZ model. Firstly, we calculate the ground-state entanglement, and note that not only the positions of QPT points can be changed but also the optimal ground-state entanglement can be obtained by coordinating the parameters D _z , B and b in our model. It is noteworthy that, even if the D _z is included, the critical temperature T _c is still completely independent of uniform magnetic B, while D _z can enhances T _c , which means that we can gain more entanglement under higher temperature. It is also observed that D _z improves the critical magnetic field B _c . At the same time, we find that the inhomogeneity of magnetic field b, coupling constant J and the anisotropy parameter Δ play substantially important roles in improving the critical temperature T _c and enhancing the entanglement in our system.