Introduction

Road transport plays a major role in driving both economic development and social activity. However, the presence of negative externalities such as congestion, pollution and accidents brings increasing social and environmental stress, which has emphasized the urgent need for an effective, efficient and socially feasible road transport system (Grant-Muller and Xu 2014). The extraordinarily complex task of introducing developments to the road transport system is well recognised. Efforts to advance policies incrementally or by introducing a single policy measures often fail, leading to calls for ‘integrative’, ‘holistic’ policies that incorporate multiple policy instruments from sectors related to urban mobility. The need for more sustainable and integrative planning processes has been widely recognized, with research including that by Givoni et al. (2013).

The future development and implementation of integrative policies in the road transport sector depend primarily on how well understood they are by decision makers. Road capacity investment and pricing issues have become crucial with an increased demand for the development of new transport infrastructure and the necessity to ensure the infrastructure can be both financed and utilized efficiently (Adler and Proost 2010). Theoretical developments in both the road network design problem (NDP) and road toll pricing have received much attention over a period of time in published research. The NDP involves optimal allocation of budget to the expansion of existing links and/or to the addition of new candidate links so as to maximize the network performance (e.g. minimizing the total travel time or generalized cost, maximizing the social welfare) while accounting for the travellers’ route choice behaviour (LeBlanc 1975). The literature includes several comprehensive reviews of the NDP, examples being Yang and Bell (1998), and Farahani et al. (2013). The road toll pricing problem (as an effective means of both managing road traffic demand and raising additional revenue for road construction) has been studied extensively by both transportation practitioners and economists. Practical implementation has progressed rapidly and electronic road pricing schemes have been proposed and tested worldwide (Meng et al. 2012; Yang and Huang 2005; Yang et al. 2010).

Considering the literature on both NDP and the road toll pricing problem, there have been few published studies concerned with the simultaneous determination of road toll pricing and capacity development, despite the strong connection between them and their importance for the transport system. In the “Literature review” section, a detailed summary of recent studies concerned with the problem of simultaneous determination of road toll pricing and capacity development is provided. In an era of tightly constrained budgets, the analysis of road tolls and capacity provides a useful framework to consider interactions between both decision variables. This is especially the case in developing counties where there may be long term financial constraints on road capacity improvement.

In this paper, we therefore investigate the joint decision making involved in the development of road infrastructure (capacity) alongside introduction of a road toll and the pricing problem. The revenue from a road toll charge is assumed to be a part of the infrastructure financing. In contrast to the case for a build-operate-transfer (BOT) scheme (Xu et al. 2015a), the government will consider road capacity development and road toll pricing together, with the purpose of minimizing total travel time. However the tolled roads established by the government are not necessarily the newly built roads that require financing. In a departure from existing formulations for a continuous network design problem (CNDP), we propose a discrete network design problem (DNDP) approach. This is considered more appropriate for a transport network, as improvements such as lane expansions cannot be delivered in fractional quantities (Boyce and Janson 1980).

We investigate toll pricing and capacity development within a discrete network design framework. Using this approach, different toll pricing and capacity expansion schemes can be compared explicitly, as can variances in total travel time with respect to budget levels and toll revenues. The research uses a new formulation for the joint road toll and capacity DNDP, where the decision variables for toll and capacity are both integer variables. Whilst existing mixed-integer programming formulations generally stipulate a discrete variable for a particular link (of either the toll road or capacity expansion), and a continuous variable for the level of the toll (or capacity quantity), the formulation used in this research is different. It defines discrete capacity variables with respect to the number of additional lanes for capacity expansion and an integer toll level, which lies within a pre-defined toll range. The discrete variable design (with toll pricing and capacity expansion) is more appropriate for use with a transport network, and results show that a road toll on the subset of links provides an approach to the optimal solution with respect to the total travel time.

For the capacity expansion problem with a discrete variable for capacity (i.e. number of additional lanes), Wang et al. (2013) provide a bi-level program formulation and a global optimization algorithm for the DNDP. Hence, this paper can be viewed as extending the state of the art by viewing the road toll as a discrete variable for the joint road toll and capacity DNDP. The issues addressed and problems solved in this paper are as follows. Firstly, the proposed modelling approach can support government decision-makers in identifying how, and under what circumstances, to set the budget levels and the toll pricing levels. It can also assist the public in understanding how the government measures will benefit transport development. Secondly, to solve the proposed bi-level programming problem (with an integer nonlinear program for the upper level problem, and a continuous nonlinear program for the lower level problem), we reformulate it as a single-level mixed-integer nonlinear program with nonlinear complementarity constraints. We then develop a relaxation approach by relaxing the complementarity constraints. The SBB solver in GAMS (2009) is employed to solve the relaxed mixed-integer nonlinear program at each iteration step.

The organization of this paper is as follows: in the “Literature review” section, we provide a brief literature review with respect to the combination/integration of urban road transport management and modelling approaches. The “Problem formulation” section presents the bi-level programming model to describe the DNDP, simultaneously optimizing both road toll charging and road expansion under the fixed Origin Destination (OD) demand case. The “Solution method” section presents a relaxation algorithm, using Solver in GAMS for convenience. In the “Numerical analysis” section, numerical experiments are illustrated using a simple two-node network and the Sioux-Falls network. Finally, conclusions are presented in the “Conclusions” section.

Literature review

The combination or integration of measures for road transport tends to cover certain types of management policies, e.g., the development of sustainable urban transport strategies (Marsden et al. 2010; May et al. 2005a, b), optimal urban transport strategies (May and Still 2000; May et al. 2006; Shepherd et al. 2006; Kelly et al. 2008; Xu et al. 2015b), and more recently, urban transport packages (Givoni 2014). Modelling the combination of measures in the transport network framework is important. Although these management policies have been discussed, relatively few have been based on a transport network modelling process.

Studies into the simultaneous determination of a road toll level and road capacity have taken different approaches. The main studies have focused on investigating whether the revenue from socially optimal pricing on a road can cover the capital cost for constructing and maintaining the road. Mohring and Harwitz (1962) demonstrated that under certain conditions revenues from optimal pricing are just sufficient to cover the cost of optimal supply of road infrastructure. Yang and Meng (2000) considered the selection of toll and capacity for a private highway in a general road network under a BOT scheme. They investigated profitability and social welfare gain together with maximum profit and social welfare solutions in a toll-capacity two-dimensional space. Yang and Huang (2005) dealt with the relationship between pricing, capacity choice and financing in a general network with a single or multiple types of vehicles under the first-best and second-best conditions. Subprasom and Chen (2007) discussed the effects of regulation on highway pricing and capacity choice of a BOT scheme. Dimitriou et al. (2009) addressed the joint optimization of capacity investments and the toll charges problem imposed on multi-group users in monopolistic private highways within general road networks. They provided a game-theoretic formulation that leads to a non-convex bi-level program. With real-application results they demonstrated the importance of considering the spatial heterogeneity of prices, and the trade-off between investments and pricing strategies in regulated private highways. Verhoef et al. (2010) considered second-best cases where only a sub-set of links in a network is subject to tolling and/or capacity choice, and for cases with and without a self-financing constraint. Using the ‘long-run cost functions’ for congested networks they demonstrated that, under certain assumptions, second-best long-run cost (or actually, generalized price) functions can be derived for most cases of interest. These can be used in an applied network model as a substitute for the conventional short-run user cost functions. Recently, building on the works by Tan et al. (2010) and Tan and Yang (2012), Niu and Zhang (2013) discussed the impact of demand uncertainty on the BOT contract design by optimizing a bi-objective problem via three decisions including toll, capacity and concession period.

Concerning development of a modelling approach to simultaneously determine the first and/or second best pricing and road capacity, Koh et al. (2009) investigated the first and second best jointly optimal toll and road capacity investment problems from both the policy and technical perspectives. They emphasized that, as with optimal pricing, optimal investment in capacity could not always be feasible, and therefore a second best optimum investment must be sought. Previous studies to minimize the total travel time or maximize the total social welfare of travellers in transport networks include Zhang and Wee (2012), as they proposed a new bi-level model for the implementation of congestion pricing, with a new objective function for maximizing the reserve capacity of networks. They further formulated this as a single-level optimization program with equilibrium constraints to circumvent the computational difficulty. Recently, Wang et al. (2014b) proposed a bi-level programming model for a joint optimal link-based tradable credit charging scheme and road capacity improvement. Their model integrates the improvement in the urban road network according to improvements in road capacity with a given budget constraint, and decreasing travel demand with the tradable credit scheme. They demonstrated that the tradable credit scheme offers a better combination of cost-effectiveness, administrative flexibility and distributional fairness compared to congestion pricing. To understand the trade-offs between conflicting objectives and to design a financially and environmentally sustainable transport system, Yin et al. (2014) addressed the simultaneous determination of road toll pricing and capacity investment in a congested road network in a multi-criteria decision-making framework. They presented a goal programming approach to follow four major goals including cost recovery, service level, environmental and equity. The multi-objective road toll pricing and capacity investment problem was formulated as a bi-level goal programming model. The numerical results demonstrated that the priority structure of the goals can significantly affect road toll pricing and capacity investment decisions. Research that has focused on the development of algorithms includes work on a sensitivity analysis-based algorithm, a direct search algorithm (introduced in Yang and Huang 2005), and a constraint cutting algorithm (given by Koh et al. 2009). Fan and Gurmu (2014) presented a bi-level genetic algorithm (GA)-based optimization solution methodology that can be used to determine the optimal solution for combined congestion pricing and capacity expansion problems.

Past research into the problem of simultaneous determination of road toll pricing and road capacity development has focused on investigating pricing and self-financing from modelling. Road capacity has been generally assumed to be theoretically continuous, whilst the toll is optimized under given constraints. These studies provide the theoretical background and an important framework for further study. The approach proposed in this paper, with a general DNDP and road toll pricing to minimize the total travel cost under a limited budget is, however, more appropriate for application in the practical transport planning and management contexts.

Problem formulation

Notation

In a given urban road network, we assume that the authority needs to improve the transport network in such a way that the total travel time is minimized. However, the authority faces a shortage of budget and therefore needs to receive revenue from road toll charges. Without loss of generality, we assume constant returns to scale in costs of capacity expansion (Mohring and Harwitz 1962; Strotz 1965; Keeler and Small 1977), and fixed demand in the transport network. It is noted that network design and road pricing are both long-term decisions that impact on demand, and it would therefore be desirable to incorporate demand elasticity. In this study context, one can simply use social welfare instead of total travel time as the design objective function by introducing elastic demand functions. However, incorporating elastic demand and changing the objective function would not fundamentally change the proposed model formulation and the method used to find the solution.Footnote 1

The following symbols are firstly defined:

Sets:

A :

Set of all links in the transport network

D 1 :

Subset of links in the transport network considered for additional lanes, \( D_{1} \subseteq A \)

D 2 :

Subset of links in the transport network considered for the implementation of toll pricing, \( D_{2} \subseteq A \)

LA a :

Set of number of lanes to be added to link \( a \in D_{1} \). For example, LA a  = {0,1,2} means that the transport authority determines to either add zero (do-nothing), one, or two lanes to link \( a \in D_{1} \)

LT a :

Set of values for toll pricing (j a ) imposed by the authority on link \( a \in D_{2} \). For example, \( LT_{a} = \left\{ {j_{a} |j_{ \hbox{min} } \le j_{a} \le j_{ \hbox{max} } ,j_{a} {\text{is integer}} ,a \in D_{2} } \right\} \)

N :

Set of nodes in the transport network

W :

Set of OD pairs

R w :

Set of paths between OD pair \( w \in W \)

Parameters/functions:

\( \delta_{a,r}^{w} \) :

A binary coefficient which equals 1 if path \( r \in R_{w} \) between OD pair \( w \in W \) uses link \( a \in A \), and 0 otherwise

B :

Total available budget

ca(i a ):

Construction cost of adding i lanes to link \( a \in D_{1} \), \( i_{a} \in LA_{a} \); c a (i a ) = 0 if i a  = 0

d w :

Given travel demand for OD pair \( w \in W \)

t a (v a , i a , j a ):

Travel time function on link a when i lanes are added and toll pricing j a are set on link a, \( i_{a} \in LA, j_{a} \in LT_{a} \), \( a \in D_{1} \mathop {\bigcap }\nolimits D_{2} \)

t a (v a , i a ):

Travel time function on link a when i lanes are added on link a, \( i_{a} \in LA_{a} , a \in D_{1} \)

t a (v a , j a ):

Travel time function on link a when toll pricing j a are set on link a, \( j_{a} \in LT_{a} \), \( a \in D_{2} \)

t a (v a ):

Travel time function on link a \( \in A - D_{1} \mathop {\bigcup }\nolimits D_{2} \)

\( \eta \) :

A parameter setting for a more flexible formulation

Decision variables:

\( z1_{a}^{{i_{a} }} \) :

A binary decision variable which equals 1 if and only if i a lanes are added to link \( a \in D_{1} \), \( i_{a} \in LA_{a} \). \( \varvec{z}1 = \left\{ {z1_{a}^{{i_{a} }} , i_{a} \in LA_{a} , a \in D_{1} } \right\} \)

\( z2_{a}^{{j_{a} }} \) :

A binary decision variable which equals 1 if and only if road toll pricing j a is chosen for link \( a \in D_{2} \), \( j_{a} \in LT_{a} \). \( \varvec{z}2 = \left\{ {z2_{a}^{{j_{a} }} , j_{a} \in LT_{a} ,a \in D_{2} } \right\} \)

v a :

Traffic flow on link \( a \in A \),\( v = \left\{ {v_{a} , a \in A} \right\} \)

\( f_{r}^{w } \) :

Traffic flow on path \( r \in R_{w} \) between OD pair \( w \in W \), \( \varvec{f} = \left\{ {f_{r}^{w } ,r \in R_{w} ,w \in W} \right\} \)

Modelling approach

Consider that the authority plans to construct and operate a road under a given budget constraint B (i.e., the available public funding per unit time period). Therefore, the deficit per unit time period for the authority is no more than the budget constraint B, that is,

$$ \mathop \sum \limits_{{a \in D_{1} }} \mathop \sum \limits_{{i_{a} \in LA}} c_{a} \left( {i_{a} } \right)z1_{a}^{{i_{a} }} - \eta \mathop \sum \limits_{{a \in D_{2} }} \mathop \sum \limits_{{j_{a} \in LT}} v_{a} z2_{a}^{{j_{a} }} j_{a} \le B $$

where \( \eta \) is a parameter set to give a more flexible formulation, and the first term is the total construction cost of adding lanes to the network, the second term is the total revenue of toll pricing. Therefore, alongside congestion mitigation, road pricing could also be used for deficit reduction in the case of a limited budget.

The authority aims to minimize the social travel time in the DNDP with road toll pricing scheme \( \varvec{z}2 \). Thus, the upper-level problem can be formulated as

[OP: original problem]:

$$ \left[ {\text{OP}} \right]\quad \quad \begin{array}{*{20}c} {\hbox{min} } \\ {\varvec{z}1,\varvec{z}2} \\ \end{array} \mathop \sum \limits_{a \in A} \mathop \sum \limits_{{i_{a} \in LA}} \mathop \sum \limits_{{j_{a} \in LT}} v_{a} t_{a} \left( {v_{a} ,i_{a} ,j_{a} } \right) $$
(1)

Subject to

$$ \mathop \sum \limits_{{i_{a} \in LA}} z1_{a}^{{i_{a} }} \, = \,1,\quad \forall a \in D_{1} $$
(2)
$$ \mathop \sum \limits_{{j_{a} \in LT}} z2_{a}^{{j_{a} }} \, = \,1,\quad \forall a \in D_{2} $$
(3)
$$ \mathop \sum \limits_{{a \in D_{1} }} \mathop \sum \limits_{{i_{a} \in LA}} c_{a} \left( {i_{a} } \right)z1_{a}^{{i_{a} }} - \eta \mathop \sum \limits_{{a \in D_{2} }} \mathop \sum \limits_{{j_{a} \in LT}} v_{a} z2_{a}^{{j_{a} }} j_{a} \le B $$
(4)
$$ z1_{a}^{{i_{a} }} = \left\{ {0, 1} \right\},\quad \forall a \in A,\,i_{a} \in LA_{a} $$
(5)
$$ z2_{a}^{{j_{a} }} = \left\{ {0, 1} \right\},\quad \forall a \in A,\,j_{a} \in LT_{a} $$
(6)

The objective function (1) represents the total travel time where \( v_{a} \) is determined by the lower-level user equilibrium (UE) problem which will be presented in Eqs. (7)–(10). Constraint (2) ensures that exactly one capacity level is chosen. Constraint (3) ensures that exactly one link toll level is used on each link. Constraint (4) guarantees that the deficit per unit time period of the authority does not exceed the total budget. Constraints (5) and (6) define that \( z1_{a}^{i} \) and \( z2_{a}^{j} \) are binary decision variables separately.

In model [OP], the relation between the capacity and construction cost for each link \( a \in A \) can be any general function (Wang et al. 2013). For example, the cost of adding two lanes, \( c_{a}^{2} \), is not necessarily equal to twice the cost of adding one lane, \( c_{a}^{1} \). This is more reasonable than assuming the construction cost to be a linear function of capacity, as is usually done in the CNDP (Yang and Bell 1998).

As the lower-level of the bilevel programming problem, it is assumed that travel demand is given and fixed, and users’ route choice is characterized by the UE principle. The UE problem with fixed demand can be formulated below (Sheffi 1985):

[UE]

$$ \begin{aligned} &\begin{array}{l} {\hbox{min} } \\ v \\ \end{array} \mathop \sum \limits_{{a \in D_{1} }} \mathop \sum \limits_{{i_{a} \in LA}} z1_{a}^{{i_{a} }} \mathop \smallint \limits_{0}^{{v_{a} }} t_{a} \left( {\omega ,i_{a} } \right)d\omega \\ & \quad+ \mathop \sum \limits_{{a \in D_{2} }} \mathop \sum \limits_{{j_{a} \in LT}} z2_{a}^{{j_{a} }} \mathop \smallint \limits_{0}^{{v_{a} }} t_{a} \left( {\omega ,j_{a} } \right)d\omega \\ &\quad - \mathop \sum \limits_{{a \in D_{1} \cap D_{2} }} \mathop \sum \limits_{{i_{a} \in LA}} \mathop \sum \limits_{{j_{a} \in LT}} z1_{a}^{{i_{a} }} z2_{a}^{{j_{a} }} \mathop \smallint \limits_{0}^{{v_{a} }} t_{a} \left( {\omega ,i_{a} ,j_{a} } \right)d\omega \\ & \quad+ \mathop \sum \limits_{{a \in A - D_{1} \cup D_{2} }} \mathop \smallint \limits_{0}^{{v_{a} }} t_{a} \left( \omega \right)d\omega \\ \end{aligned} $$
(7)

Subject to

$$ \mathop \sum \limits_{{r \in R_{w} }} f_{r}^{w } = d_{w} ,\quad \forall w \in W $$
(8)
$$ v_{a} = \mathop \sum \limits_{w \in W} \mathop \sum \limits_{{r \in R_{w} }} f_{r}^{w } \delta_{a,r}^{w} , \quad \forall a \in A $$
(9)
$$ f_{r}^{w } \ge 0,\quad \forall r \in R_{w} ,\forall w \in W $$
(10)

Constraint (8) defines the demand conservation condition, Constraint (9) defines the relation between link flow and path flow and Constraint (10) requires nonnegative path flows.

In this study, before and after a capacity change and toll setting, it is assumed that link travel time functions \( t_{a} \left( {v_{a} } \right),\;t_{a} \left( {v_{a} ,i_{a} } \right)\;t_{a} \left( {v_{a} ,j_{a} } \right)\;t_{a} \left( {v_{a} ,i_{a} ,j_{a} } \right), \) are always strictly increasing and convex with respect to link flow \( v_{a} \left( {a \in A} \right) \) so that link flow solutions of both the UE and system optimization (SO) traffic assignment problems are unique. With this formulation, we could assume each of these new candidate links already exists by associating it with an infinite (or extremely large) free flow travel time and no toll setting in the initial transport network. If one (or more) lanes is added (\( z1_{a}^{{i_{a} }} , i_{a} \in LA_{a} , a \in D_{1} \)), then it is assumed that the actual free flow travel time is incorporated in the corresponding link travel time function and that a toll scheme will be considered. Compared with the conventional DNDP (that determines whether each link in a set of new candidate links should be added to the transport network), the DNDP formulation here embraces the conventional DNDP as a special case, and simultaneously, the road toll pricing design (\( z2_{a}^{{j_{a} }} , j_{a} \in LT_{a} ,a \in D_{2} \)) is considered for a subset of the set A of all links in the transport network. The purpose of road pricing could be for both congestion mitigation and deficit reduction (in the case of a limited budget).

Solution method

The proposed bilevel programming model is flexible in determining extensions to road infrastructure and the design of road toll pricing from the perspective of government or high level policy makers. However, solving the model is challenging. Potential approaches to solve the model could use existing algorithms to solve the DNDP, for example, the support function method proposed by Gao et al. (2005), the active set technique presented by Zhang et al.(2009), the linear approach technique given by Farvaresh and Sepehri (2011), the branch and bound algorithm given by Farvaresh and Sepehri (2013), and the global optimization recently proposed by Wang et al. (2013). Beside these existing algorithms it would also be possible to reformulate the model then use software from the sector. Here we use the general algebraic modeling system (GAMS, www.gams.com). It is noted that the model [OP] is a mixed-integer nonlinear bilevel programming problem, in which the upper level decision variables are all integer and the lower level decision variables are all continuous. Existing approaches to solve a mixed-integer nonlinear bilevel programming problem include work by Moore and Bard (1990), Jan and Chern (1994), Sahin and Ciric (1998), Gümüş and Floudas (2005) and Mitsos (2010). These greatly expand the range of decision making problems that can be modelled and solved within a bilevel optimization framework. However, little attention is given to bilevel problems involving discrete decisions in the bilevel programming literature. This is primarily because these problems pose major algorithmic challenges in the development of effective solution strategies.

In this paper, a relaxation algorithm is proposed to solve the mixed-integer nonlinear bi-level programming problem. Because the objective and constraints of the lower level problem (UE) satisfy the convexity requirements of the Karush–Kuhn–Tucker (KKT) optimality conditions, the lower level problem can be replaced with its necessary and sufficient KKT optimality conditions. Thus, the bi-level programming model can be reformulated into the following single-level mixed-integer nonlinear optimization problem (MINLP):

[MINLP]

$$ Z = \begin{array}{*{20}c} {\hbox{min} } \\ {\varvec{z}1,\varvec{z}2,\varvec{ v}} \\ \end{array} \mathop \sum \limits_{a \in A} \mathop \sum \limits_{{i_{a} \in LA}} \mathop \sum \limits_{{j_{a} \in LT}} v_{a} t_{a} \left( {v_{a} ,i_{a} ,j_{a} } \right) $$
(11)

Subject to

$$ \mathop \sum \limits_{{i_{a} \in LA}} z1_{a}^{{i_{a} }} \, = \,1,\quad \forall a \in D_{1} $$
(12)
$$ \mathop \sum \limits_{{j_{a} \in LT}} z2_{a}^{{j_{a} }} \, = \,1,\quad \forall a \in D_{2} $$
(13)
$$ \mathop \sum \limits_{{a \in D_{1} }} \mathop \sum \limits_{{i_{a} \in LA}} c_{a} \left( {i_{a} } \right)z1_{a}^{{i_{a} }} - \eta \mathop \sum \limits_{{a \in D_{2} }} \mathop \sum \limits_{{j_{a} \in LT}} v_{a} z2_{a}^{{j_{a} }} j_{a} \le B $$
(14)
$$ z1_{a}^{{i_{a} }} = \left\{ {0, 1} \right\},\quad \forall a \in A,\,i_{a} \in LA_{a} $$
(15)
$$ z2_{a}^{{j_{a} }} = \left\{ {0, 1} \right\},\quad \forall a \in A,\,j_{a} \in LT_{a} $$
(16)
$$ \left[ \begin{aligned} \mathop \sum \limits_{{a \in D_{1} }} \mathop \sum \limits_{{i_{a} \in LA_{a} }} z1_{a}^{{i_{a} }} t_{a} \left( {v_{a} ,i_{a} } \right)\delta_{a,r}^{w} + \mathop \sum \limits_{{a \in D_{2} }} \mathop \sum \limits_{{j_{a} \in LT_{a} }} z2_{a}^{{j_{a} }} t_{a} \left( {v_{a} ,j_{a} } \right)\delta_{a,r}^{w} \hfill \\ - \mathop \sum \limits_{{a \in D_{1} \cap D_{2} }} \mathop \sum \limits_{{i_{a} \in LA_{a} }} \mathop \sum \limits_{{j_{a} \in LT_{a} }} z1_{a}^{{i_{a} }} z2_{a}^{{j_{a} }} t_{a} \left( {v_{a} ,i_{a} ,j_{a} } \right)\delta_{a,r}^{w} + \hfill \\ \mathop \sum \limits_{{a \in A - D_{1} \cup D_{2} }} t_{a} \left( {v_{a} } \right)\delta_{a,r}^{w} - \mu^{w} \hfill \\ \end{aligned} \right]f_{r}^{w } \, = \,0 $$
(17)
$$ \begin{array}{*{20}c} \begin{aligned} & \sum \limits_{{a \in D_{1} }} \sum \limits_{{i_{a} \in LA_{a} }} z1_{a}^{{i_{a} }} t_{a} \left( {v_{a} ,i_{a} } \right)\delta_{a,r}^{w} + \sum \limits_{{a \in D_{2} }} \sum \limits_{{j_{a} \in LT_{a} }} z2_{a}^{{j_{a} }} t_{a} \left( {v_{a} ,j_{a} } \right)\delta_{a,r}^{w} \\ & \quad - \sum \limits_{{a \in D_{1} {\bigcap }D_{2} }} \sum \limits_{{i_{a} \in LA_{a} }} \sum \limits_{{j_{a} \in LT_{a} }} z1_{a}^{{i_{a} }} z2_{a}^{{j_{a} }} t_{a} \left( {v_{a} ,i_{a} ,j_{a} } \right) \delta_{a,r}^{w}\\ & \quad + \sum \limits_{{a \in A - D_{1} {\bigcup }D_{2} }} t_{a} \left( {v_{a} } \right)\delta_{a,r}^{w} - {\mu}^{w} \\ \end{aligned} { \ge 0} \\ \end{array} $$
(18)
$$ f_{r}^{w } \ge 0,\quad \forall r \in R_{w} ,\forall w \in W $$
(19)

Unfortunately, MINLP is non-convex because of the complementarity constraints (17)–(19) (Chen and Florian 1995; Luo et al. 1996; Scheel and Scholtes 2000). To address this difficulty, some algorithmic approaches have been focused on avoiding this formulation (Ban et al. 2006; Bouza and Still 2007; Leyffer 2003). The basic idea of these relaxation schemes is to get rid of the complicated complementarity constraints by replacing these conditions in a suitable way. There are different types of relaxation scheme, for example, Hoheisel et al. (2013) discussed five kinds of relaxation schemes including the global relaxation scheme by Scholtes (2001), the local relaxation scheme by Steffensen and Ulbrich (2010) and the relaxation scheme by Lin and Fukushima (2005), Kadrani et al. (2009), and Kanzow and Schwartz (2010).In this paper, a relaxation algorithm will be adopted to iteratively tackle this MINLP. The main idea of this relaxation algorithm is as follows. The relaxation algorithm presented here introduces auxiliary parameters \( \theta^{w} \) for each OD pair \( \in W \), which can then be used to define relaxed complementarity slackness conditions, rather than the exact ones. We relax the complementarity slackness constraints (17) as follows:

$$ \left[ \begin{aligned} \mathop \sum \limits_{{a \in D_{1} }} \mathop \sum \limits_{{i_{a} \in LA_{a} }} z1_{a}^{{i_{a} }} t_{a} \left( {v_{a} ,i_{a} } \right)\delta_{a,r}^{w} + \mathop \sum \limits_{{a \in D_{2} }} \mathop \sum \limits_{{j_{a} \in LT_{a} }} z2_{a}^{{j_{a} }} t_{a} \left( {v_{a} ,j_{a} } \right)\delta_{a,r}^{w} \hfill \\ - \mathop \sum \limits_{{a \in D_{1} {\bigcap }D_{2} }} \mathop \sum \limits_{{i_{a} \in LA_{a} }} \mathop \sum \limits_{{j_{a} \in LT_{a} }} z1_{a}^{{i_{a} }} z2_{a}^{{j_{a} }} t_{a} \left( {v_{a} ,i_{a} ,j_{a} } \right)\delta_{a,r}^{w} + \hfill \\ \mathop \sum \limits_{{a \in A - D_{1} {\bigcup }D_{2} }} t_{a} \left( {v_{a} } \right)\delta_{a,r}^{w} - {\mu }^{w} \hfill \\ \end{aligned} \right]f_{r}^{w } \le \theta^{w} $$
(20)

The MINLP can then become a relaxed MINLP problem (RMINLP, relaxed mixed-integer nonlinear optimization problem) by replacing Eq. (17) with Eq. (20). In this case, the RMINLP is non-convex and the MFCQ holds (Luo et al. 1996). Consequently, existing MINLP solution algorithms can be adopted to solve the RMINLP. The standard MINLP solver SBB is a GAMS solver for mixed integer nonlinear programming models, based on a combination of the standard Branch and Bound method from Mixed Integer Linear Programming and some of the standard NLP solvers already supported by GAMS (2009). It performs well on models that have difficult nonlinearities and possibly also on models that are fairly non-convex, more details about the SBB solver can refer to http://www.gams.com/dd/docs/solvers/sbb/index.html.

We use SBB to solve the RMINLP. The iterative algorithm can be summarized as follows:

  1. Step 1

    Initialization Choose an initial auxiliary parameter \( \theta_{0}^{w} \) for the complementarity slackness constraint. Set \( \varepsilon \, \ge \,0 \), updating factor \( 0 < \lambda \, < 1 \), and iteration number = 0.

  2. Step 2

    Major iteration By setting \( \theta_{k}^{w} \) as the auxiliary parameter for each complementarity condition in (20), solve the current RMINLP by using the SBB solver in GAMS (2009).

  3. Step 3

    Stop condition If \( \theta_{k}^{w} \ge \varepsilon \), stop and go to Step 4; otherwise set \( \theta_{k + 1}^{w} = \lambda \theta_{k}^{w} \), go to Step 2.

  4. Step 4

    Report solution The optimal solution is achieved from the last run of Step 2.

The relaxation algorithm presented here is straightforward and easily implemented. In particular, many existing solution techniques for the MINLP can be used in Step 2 to tackle RMINLP. Suitable convergence results for the global relaxation scheme have already been known from the discussion given by Hoheisel et al. (2013). The fundamental approach of the relaxation scheme for mixed-integer nonlinear bi-level programming is to replace MINLP by a sequence of the parameterized RMINLP, which is similar to the relaxation method proposed in Scholtes (2001), but extends it to the mixed-integer case.

It is noted that, besides the relaxation methods, there are other ways to deal with the complementarity constraints, for example, dispensing with the complementarity constraints through the introduction of binary variables and a penalty method. All of these approaches have positive and negative features, and none is optimum for all problems. As an example, the binary variables can be used to remove the complementarity constraints as presented in Fortuny-Amat and McCarl (1981) (i.e., rewriting the complementary slackness condition by introducing binary variables and a large positive constant). This transforms the linear bi-level programming problem into a large mixed-integer programming problem. However, it is limited by computational speed due to the large size of the augmented problem (Wen and Hsu, 1991). The penalty method is another important class of algorithms to solve nonlinear bi-level programming problem, however they are generally limited to computing stationary points and local minima (Colson et al. 2005).

Numerical analysis

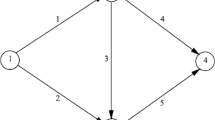
A two link network

We firstly consider a simple two-link network as shown in Fig. 1, consisting of two nodes: node 1 and node 2 and two links: link \( a_{1} \) and link \( a_{2} \). The travel demand \( d_{1} = 100 \). The travel time functions for both links are given by:

$$ t_{a} \left( {v_{a} } \right) = t_{a}^{0} \times \left( {1 + 0.15*\frac{{v_{a} }}{{T_{a} }}} \right),\,a \in \left\{ {a_{1} , a_{2} } \right\} , $$
$$ t_{{a_{1} }}^{0} = 20\,T_{{a_{1} }} = 1.5,\, t_{{a_{2} }}^{0} = 70\, T_{{a_{2} }} = 10.5, $$

where \( T_{a} \) is the current capacity of link \( a \in \left\{ {a_{1} , a_{2} } \right\} \) (i.e. \( t_{a} \left( {v_{{a_{1} }} } \right) = 20 + 2*v_{{a_{1} }} ,\; t_{a} \left( {v_{{a_{2} }} } \right) = 70 + v_{{a_{2} }} \)).

Fig. 1
figure 1

A two-link network

Full size image

We assume the transport authority considers whether there is a need to add 0, 1 or 2 lanes to each link. The binary variables \( z1_{{a_{1} }}^{{i_{{a_{1} }} }} \) and \( z1_{{a_{2} }}^{{i_{{a_{2} }} }} \), \( i_{{a_{1} }} , i_{{a_{2} }} \in \left\{ {0,1,2} \right\} \) can then be used to indicate the multiple capacity level network design decisions. We assume that capacity per lane is 2, that is, \( c_{a}^{1} = 2 \), the total budget \( B = 7000 \) and we set the parameter \( \eta = 1 \).

Concerning the construction cost function, we consider two cases:

  1. (i)

    The construction cost is a linear function of capacity, i.e. \( c_{{a_{1} }} \left( {i_{{a_{1} }} } \right) = 2000i_{{a_{1} }} \, c_{{a_{2} }} \left( {i_{{a_{2} }} } \right) = 3000i_{{a_{2} }} \, i_{{a_{1} }} , i_{{a_{2} }} \in \left\{ {0,1,2} \right\}; \)

  2. (ii)

    The construction cost is a nonlinear function of capacity, i.e. \( c_{{a_{1} }} \left( {i_{{a_{1} }} } \right) = 2000i_{{a_{1} }}^{1/2} \, c_{{a_{2} }} \left( {i_{{a_{2} }} } \right) = 3000i_{{a_{2} }}^{1/3} \, i_{{a_{1} }} , i_{{a_{2} }} \in \left\{ {0,1,2} \right\}. \)

We can also determine the toll level to make the two-link network reach SO.

We now present a comparison of optimal solutions under different models. For the convenience of comparison and demonstration, we firstly present the traffic pattern under different models including: the UE and SO solutions with a traffic assignment problem (TAP) (Sheffi 1985), the first-best toll pricing problem (FBTP) (Hearn and Ramana 1998; Yang and Huang 2005), and DNDP (LeBlanc 1975). The TAP under UE and SO conditions (which determines the UE and SO flow patterns in the transport network with fixed origin–destination demand), demonstrates firstly the traffic situation under the UE assumption that all users minimize their own individual travel costs on transport networks. Secondly it demonstrates the SO assumption that all users cooperate to minimize the total network cost. The UE and SO are two central concepts pertaining to the road pricing, the DNDP and combined DNDP and pricing problems. The FBTPFootnote 2 is solved to demonstrate the best performance under the road pricing scheme. The DNDP is solved to illustrate the optimal effect of increasing road infrastructure under given budget constraints. Finally, the results of our proposed model, which combines road toll pricing and capacity development from the perspective of government or high level decision makers, are presented. The comparisons are focused on the optimal traffic pattern and the objective function values. To avoid any bias during the process comparison, the objective function values of different models are obtained again by the relaxation algorithm given in the “Solution method” section. The results are given in Table 1.

Table 1 Comparison of optimal solutions under different models
Full size table

Table 1 shows the link flow patterns under UE, SO, FBTP, DNDP and a combination of toll and DNDP. With the FBTP, the toll on link \( a_{1} \) (\( j_{{a_{1} }} = 25 \)) changes the traffic flow from UE to SO and the system total travel time decreases from \( Z = 12000 \) to \( Z = 11791 \). Under a budget constraint, \( B = 7000 \) with a linear construction cost (case i), the optimal road development pattern arising from the DNDP is to add two lanes for link \( a_{1} \) and one lane for link \( a_{2} \), in which case the system total travel time will decrease to \( Z = 7275.59 \).

We can further construct the combined first best toll pricing and capacity improvement model (FBTP + DNDP) with the first best toll pricing in the DNDP, as shown in the “Modelling approach” section. The upper level objective function still aims to minimize the total travel time under a budget constraint. With a policy of combined road toll pricing and capacity development, we can set the toll on link \( a_{1} \) (\( j_{{a_{1} }} = 36 \)) and on link \( a_{2} \) (\( j_{{a_{2} }} = 11 \)), and add two lanes for both link \( a_{1} \) and link \( a_{2} . \) The system total travel time will decrease to \( Z = 6766.975 \). Under this case, the total construction cost is \( c_{{a_{1} }} \left( {i_{{a_{1} }} } \right) + c_{{a_{2} }} \left( {i_{{a_{2} }} } \right) = 2000*2 + 3000*2 = 10000 \), the toll revenue on both links is \( v_{{a_{1} }} *j_{{a_{1} }} + v_{{a_{2} }} *j_{{a_{2} }} = 76.728*36 + 23.272*11 = 3018.2 \), therefore the total available budget is \( B + v_{{a_{1} }} *j_{{a_{1} }} = 10018.2 \).

Under a budget constraint, \( B = 5000 \) with a nonlinear construction cost (case ii), as shown in Table 2, the optimal road development pattern arising from the DNDP is to add two lanes on link \( a_{1} \), and the system total travel time will decrease to \( Z = 7275.59 \). With a government policy of combined road toll pricing and capacity development, we can set the toll on link \( a_{1} \) (\( j_{{a_{1} }} = 25 \)) and add two lanes for both link \( a_{1} \) and link \( a_{2} \). In this case the system total travel time will decrease to 6766.975, the total construction cost is \( c_{{a_{1} }} \left( {i_{{a_{1} }} } \right) + c_{{a_{2} }} \left( {i_{{a_{2} }} } \right) = 2000*\sqrt[2]{2} + 3000*\sqrt[3]{2} = 6608.2 \), the toll revenue on link \( a_{1} \) is \( v_{{a_{1} }} *j_{{a_{1} }} = 76.728*25 = 1918.2 \), therefore the total available budget is \( B + v_{{a_{1} }} *j_{{a_{1} }} = 6918.2 \).

Table 2 optimal solutions under a nonlinear construction cost
Full size table

Comparing combined road toll pricing and capacity development with other approaches (DNDP, FBTP, UE, and SO) we find that under the extension of both links, more travellers (\( v_{{a_{1} }} = 7 6. 7 2 8 \)) choose link \( a_{1. } \) With a fixed travel demand assumption, the new links added can reduce the total travel time and improve the level of transport service.

The Sioux-Falls network

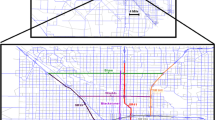
The Sioux-Falls network, as shown in Fig. 2, consists of 24 nodes, 76 links and 528 OD pairs, the parameters can be obtained from http://www.bgu.ac.il/~bargera/tntp/.

Fig. 2
figure 2

The Sioux-Falls network

Full size image

Although it is possible to discuss the first-best toll (as shown for the simple network), it is not necessary for the purposes of the numerical demonstration here. To save space, we use a section of the links as the link toll set and the toll pricing problem therefore becomes a second-best road pricing problem. According to the UE assignment (Wang, et al. 2013; Wang et al. 2014a), we choose the following 10 links: (link 16, 17, 19, 20, 25, 26, 29, 39, 48, 74) as they are the most congested links in terms of the ratio of link flow to capacity. These 10 links are shown by dotted lines in Fig. 2.

We assume the transport authority considers whether it needs to add 0, 1 or 2 lanes to these 10 links and that the capacity is 5 per lane. The budget is \( B \) = 5000. Without loss of generality, we assume a linear construction cost function, i.e., \( c_{a} \left( {i_{a} } \right) = co_{a} *i_{a} \). The coefficients \( co_{a} \) for the 10 links are given in Table 3.

Table 3 construction cost function coefficients
Full size table

We use the SBB to solve the RMINLP in the relaxation algorithm. It performs well on models that have difficult nonlinearities and possibly also on models that are fairly non-convex. The computation time is less than 3 min.

Comparison of optimal solutions under different models

Table 4 presents the link flow pattern (\( v_{a} \)), link cost

Table 4 Comparison of optimal solutions under different models
Full size table

(\( t_{a} \)) and toll \( j_{a} \) on different links, and link capacity extension (\( i_{a} \)) under different models (UE, SO, Second-best toll, DNDP and DNDP + toll). To avoid any bias in the comparisons, the objective function values of different models are obtained again using the relaxation algorithm proposed in this paper. As previously shown, the set of toll links and road capacity links in DNDP are not necessarily the same. It can be seen that in comparison to the UE case (Z = 10062.743), the second-best road pricing brings a reduction in total travel time (Z = 10025.801), however this is still not as low as the SO case (Z = 9826.453). Under the budget (\( B = 5000 \)) and DNDP, Table 4 presents the optimal road expansion with a linear construction cost function given in Table 3 and illustrates the total travel time reducing to a level Z = 7728.312. A toll revenue 332.441 can be achieved with the optimal toll pricing scheme \( j_{a} \) (as shown in Table 4), and with a combination of toll pricing and DNDP the total travel time can reduce to 7029.808.

Relationship between budget, toll pricing and total travel time

To continue the comparison of optimal solutions under different models, we examine the relationship between budget, toll pricing and total network travel time. For the case of the Sioux-Falls network we find that the maximum total investment (i.e., all links given in Table 3 with a two-lane expansion) is 6920, as shown in Table 5. That is, if the government budget is greater than 6920, there is no need for toll pricing and the total travel time will be Z = 6881.759. Table 5 also illustrates the toll revenue and corresponding total travel time (Z) under different budget levels. Generally, the lower the budget level, the higher the toll revenue and the lower the total travel time. However this is not the case when the budget is 5000, where the optimal toll pricing scheme generates 332.441 total revenue. This is higher than the toll revenue of 145.344 with a budget level of 4000. Figure 3 illustrates the rate of reduction in total travel time with respect to the budget level, with the rate of reduction in total travel time declining as the budget level increases. Figure 4 indicates changes in toll revenue with respect to the budget and in contrast, a more erratic rate of decrease is seen as the budget level increases.

Table 5 Total travel time and toll revenue under different budget levels for the Sioux-Falls network
Full size table
Fig. 3
figure 3

Total travel time vs budget constraint for the Sioux-Falls network

Full size image
Fig. 4
figure 4

Toll revenue vs budget level for the Sioux-Falls network

Full size image

Conclusions

Research into (and applications of) packages of measures for transport development and management have received increasing recognition recently. In the context of the development and implementation of integrative measures in an urban road transport equilibrium network, this paper has presented research into the modelling of joint road toll pricing and capacity development, taking the perspective of government or highway authorities. The main contributions of this paper to the state of the art in the literature are as follows:

  • The proposed formulation differs from existing mixed-integer programming formulations which apply where the model decision variables for selected links are discrete for either toll road or capacity expansion, and continuous for the level of toll or capacity. In contrast, the formulation proposed in this paper defines discrete variables for capacity (i.e. the number of additional lanes for capacity expansion) and for the toll level (i.e. an integer toll level within a pre-defined toll range). In the modelling approach described the two sets of links are, in fact, separated so that it is not necessary for D 1 and D 2 to coincide. This allows flexibility according to the policy being designed, allowing, for example, for the revenues from tolling in one part of the network to be used to finance infrastructure improvements elsewhere in the network.

  • To solve the bi-level program (with an integer nonlinear program for the upper level problem and a continuous nonlinear program for the lower level problem), we have first transformed it into a single-level mixed-integer nonlinear program with nonlinear complementarity constraints. A relaxation approach has then been developed to relax the complementarity constraints. At each iteration step, the SBB solver in GAMS was used to solve the relaxed mixed-integer nonlinear program. An existing business software (rather than bespoke software) was used to solve the complex mathematical programming problem, demonstrating that an application of the approach by transport planners/policymakers is practical.

This study further differs from existing analyses in two main aspects. Firstly, the toll pricing and capacity development in a discrete network design framework where different toll pricing and capacity expansion schemes can be compared explicitly. Secondly, the variances in total travel time with respect to the budget level and toll revenues are investigated explicitly. The discrete variable design with toll pricing and capacity expansion is more appropriate for a transport network. The proposed modelling approach can support government decision-makers to identify how, and under what circumstances, to set the budget level and the toll pricing level. It can also help in improving public understanding of how different transport policies can benefit the development of the transport network. Finally, the proposed model can be solved conveniently using existing optimal solvers, making it accessible in principle to the wider transport community and policy makers.

Some other key issues for further study are:

  • Complex behaviour investigation. From the lower model (7–10), given the fixed travel demand, the link toll level and capacity level determined by the upper level, we use the UE principle to investigate the traveler’s route choice behavior. However, network design and road pricing are long-term decisions and thus affect demand. They will also result in optimization of other ways, e.g., departure rates and individual travel mode choice, with the case of regular choices (Xu and Gao 2009). Further model development along these lines is a topic for further study.

  • A multi-modal modelling approach for the additional complexities of the real world. With the proposed model framework, a further additional degree of complexity, i.e. public transport can be integrated. In a modern urban context, a policy that is only designed for cars, without taking public transport into account is largely unthinkable. Integrated transport planning and policy, especially in presence of pricing policies, requires multi-modal thinking.