Introduction

Theoretical developments in road pricing have stemmed from applications of spatial economics and have concentrated on solving the second best optimal toll problem where only a subset of links may be charged (see e.g. Verhoef 2002). In addition to the work on pricing there have been studies into deriving optimal investment in capacity, usually of a single road link (Wheaton 1978; Wilson 1983; d’Ouville and McDonald 1990). Mohring and Harwitz (1962) have shown that under certain conditions revenues from optimal pricing are just sufficient to cover the cost of optimal supply of road infrastructure.

While the relationship between pricing and capacity is well connected, there do not appear many studies in the literature that combine the simultaneous analysis of both variables. In an era of tightly constrained budgets, this analysis provides a useful framework to consider the interactions of both decision variables. However, as with optimal pricing, optimal investment in capacity will not always be feasible, and so a second best optimum investment must be sought.

The focus of this paper is two-fold. Firstly, the paper aims to investigate the policy implications of both the first and second best optimal pricing with capacity investment policies. We consider the theoretical first best case where tolling and investment in capacity is possible on all links, forming a benchmark for our second best cases where we only toll and invest on pre-defined subsets of links. For the first best policy, as discussed it has been shown that the self-financing principle can be achieved under optimal pricing and capacity investment and this has been extended to a general network by Yang and Meng (2002). However, it is also important to analyse the impacts of such policy at the network level in terms of charges and changes to network structure. This is also the case for the second best scenario where constraints on toll and investment locations will naturally lead to a different result. Throughout this paper we consider capacity to be a continuous variable following the extensive literature in Network Design Problem (e.g. Suwansirikul et al. 1987; Yang and Meng 2002).

The second purpose of this paper is to develop a robust algorithm. This problem has a so-called bi-level structure, with the upper and lower levels representing the social objective of the transport planner and the response of the road users, respectively. Such Bi-Level Programming Problems (BLPPs) are recognised as one of the most challenging problems in the optimisation field.

For this reason, a wide range of solution methods have been applied in an attempt to devise an efficient technique, ranging over heuristic iterative methods (Allsop 1974; Suwansirikul et al. 1987; Verhoef and Rowendal 2004), linearisation methods (Ben-Ayed et al. 1988), stochastic search methods (Shepherd and Sumalee 2004), sensitivity-based methods (Friesz et al. 1990; Yang 1997), Karush–Kuhn–Tucker based methods (Marcotte 1986; Verhoef 2002), and recently a marginal function method (Meng et al. 2001) and constraint cutting method (Lawphongpanich and Hearn 2004).

Our own work (Shepherd and Sumalee 2004) looked at the second best optimal toll problem for a small network and showed that the derivative based approach proposed by Verhoef (2002)Footnote 1 failed due to the change in the active path set of the users during the optimisation process. In addition we also found that the algorithm also failed when a perfectly converged UE solution could not be achieved. In this paper, we revisit this numerical example to test the capability of the constraint cutting algorithm (CCA) (Lawphongpanich and Hearn 2004).

The CCA sets up a continuous optimal toll design problem (COTP) as an optimisation problem with the variational inequality (VI) condition of the traffic equilibrium as a constraint. The VI is redefined as a system of inequality constraints in relation to the set of extreme points of the feasible region of the demand and traffic flows. We extend the original algorithm to deal with the joint problem of tolls and capacity investments under elastic demand.

This paper consists of four further sections, the next section deals with the first best conditions for the joint problem (which can be considered as a performance benchmark for the second best solutions). Section three deals with the second best formulation in terms of the extreme point formulation and adapts this to the joint problem. Finally, section four gives a numerical example while section five draws conclusions and looks at further research.

First best tolls and capacity

Since Walters (1961), economists have advocated the first best pricing policy of highways and roads. This requires that all links in a road network are charged with tolls equivalent to the marginal costs of congestion on those links. In addition when capacity is simultaneously considered as a decision variable for the policy maker, Mohring and Harwitz (1962) have shown that under certain conditions revenues from optimal pricing are sufficient to cover the cost of providing the optimal supply of road infrastructure. For a more detailed discussion readers are referred to d’Ouville and McDonald (1990) and Hau (1992). De Borger and Proost (2001) have pointed out that capacity investment may be more attractive when the pricing regime does not take into account congestion costs and that incorrect pricing will in general lead to over investment in infrastructure.Footnote 2 Thus, solving the joint problem of optimal tolls and capacity investments is crucial to an integrated investment decision.

While the conclusions reached by Mohring and Harwitz (1962) were developed for a single link model, Yang and Meng (2002) have shown that this same principle extends to general network formulations with the same conditions of constant returns to capacity expansion and congestion technology. To calculate the first best tolls and capacities we follow Yang and Meng (2002).

Let A be the set of directed links, each link \( a \in A \) is assumed to have a monotonically increasing travel cost function \( c_{a} (v_{a} ,\beta_{a} ) \) of link flow v a for a given link capacity β a (which may be fixed or a variable in the context of the formulations to be discussed). Let K denote the set of origin-destination (O-D) pairs. In addition, we assume that the demand function d k is a continuous and monotonically decreasing function of the generalized travel cost μ k between this OD pair alone.

The feasible region of the flow vectors, Ω, is defined by a linear equation system of flow conservation constraints. Finally, let the unit investment cost for each link be given by i a which is independent of the level of investment following the Mohring and Harwitz (1962) assumptions. Note that cost of capacity is dependent on link length and so has units of Euros per pcu per km. Finally we will assume that the objective of the planner is to maximise the net social welfare defined in Eq. 1 as follows:

$$ \begin{gathered} \psi = \sum\limits_{k \in K} {\int_{0}^{{d_{k} }} {d^{ - 1} \left( \omega \right) - \sum\limits_{a \in A} {c_{a} \left( {v_{a} ,\beta_{a} } \right)v_{a} - \sum\limits_{a \in A} {i_{a} \beta_{a} } } } } \hfill \\ s.t. \hfill \\ \left( {{\mathbf{v}},{\mathbf{d}}} \right) \in \Upomega \hfill \\ \end{gathered} $$
(1)

The first term represents the user benefits, the second user costs and the final term the costs of providing and maintaining the road capacity discounted over its useful life. We shall use this welfare function as a theoretical benchmark against which we compare welfare improvements resulting from second best toll and capacity problems. The convex-nonlinear optimization problem in (1) was solved by the Sequential Quadratic Programming (SQP) algorithm in MATLAB to obtain the first best tolls and capacities for a network.

Second best formulation

This section explains in detail the adaptation of the Cutting Constraint Algorithm (CCA) from Lawphongpanich and Hearn (2004) which was primarily formulated for solving the COTP. Note that Marcotte (1983) proposed a similar method for solving the Continuous Network Design Problem.

Let τ and β be the vector of link tolls and capacities. It is known that the UE condition can be defined as a variational inequality (VI) (Smith 1979):

$$ {\mathbf{c}}\left( {{\mathbf{v}}^{*} ,\tau ,\beta } \right)^{T} \,\cdot \,\left( {{\mathbf{v}} - {\mathbf{v}}^{*} } \right) - {\mathbf{D}}^{{ - {\mathbf{1}}}} \left( {{\mathbf{d}}^{*} ,\tau ,\beta } \right)^{T}\, \cdot \,\left( {{\mathbf{d}} - {\mathbf{d}}^{*} } \right) \ge 0 \quad{\text{for }} \forall \left( {{\mathbf{v}},{\mathbf{d}}} \right) \in \Upomega $$

As mentioned above, Ω is defined by a linear equation system of flow conservation constraints. Thus, Ω is a bounded polyhedral set. From convex set analysis, any point in Ω can be defined by a linear combination of the extreme points (u, q) T of Ω. Let H be the matrix whose columns are the extreme points of Ω, defined by a pair of vectors (u, q) T. Then, for any \( \left( {{\mathbf{v}},{\mathbf{d}}} \right) \in \Upomega \), \( \left( {{\mathbf{v}},{\mathbf{d}}} \right)^{T} = {\mathbf{H}} \cdot \theta \), for some \( \theta \ge 0 \), where θ is a column vector and \( \sum\limits_{i} {\theta_{i} } = 1 \). This condition implies that \( \left( {{\mathbf{v}},{\mathbf{d}}} \right) \in \Upomega \) can be defined as a convex combination of a set of extreme points (for a proof see Theorem 2.1.6 in Bazaraa et al. 2006). Thus, the VI for the UE condition can be redefined as a function of the extreme points of Ω assuming the monotonic condition of c and D −1:

$$ {\mathbf{c}}\left( {{\mathbf{v}}^{*} ,\tau ,\beta } \right)^{T}\, \cdot \,\left( {{\mathbf{u}}^{e} - {\mathbf{v}}^{*} } \right) - {\mathbf{D}}^{{ - {\mathbf{1}}}} \left( {{\mathbf{d}}^{*} ,\tau ,\beta } \right)^{T}\, \cdot \,\left( {{\mathbf{q}}^{e} - {\mathbf{d}}^{*} } \right) \ge 0 \quad {\text{ for }}\forall e \in E $$

where (u e, q e) is the vector of extreme link flow and demand flow indexed by the superscript e, and E is the set of all extreme points of Ω. Thus, the VI or optimisation problem above can be redefined as:

$$ \begin{aligned} &\mathop {\min }\limits_{{\left( {\tau ,\beta ,{\mathbf{v}},{\mathbf{d}}} \right)}} \psi_{1} \left( {\tau ,\beta ,{\mathbf{v}},{\mathbf{d}}} \right) \hfill \\ &s.t. \hfill \\&0 \le \tau_{a} \le \varepsilon_{a}\, \cdot \,\bar{\tau }_{a}\qquad\qquad{\text{ for given }}\varepsilon {\text{ and }}\forall a \in A \hfill \\&0 \le \underset{\raise0.1em\hbox{$\smash{\scriptscriptstyle\cdot}$}}{\beta _{a}}\le \gamma_{a}\, \cdot \,\overline{\beta }_{a}\qquad\qquad {\text{ for given }}\gamma{\text{ and }}\forall a \in A \hfill \\&\left( {{\mathbf{v}},{\mathbf{d}}} \right) \in \Omega \hfill \\&{\mathbf{c}}\left( {{\mathbf{v}}^{*} ,\tau ,\beta } \right)^{T}\, \cdot \,\left( {{\mathbf{u}}^{e} - {\mathbf{v}}^{*} } \right) - {\mathbf{D}}^{{ - {\mathbf{1}}}} \left( {{\mathbf{d}}^{*} ,\tau ,\beta } \right)^{T}\, \cdot \,\left( {{\mathbf{q}}^{e} - {\mathbf{d}}^{*} } \right) \ge 0 \quad{\text{for }} \forall e \in E \hfill \\ \end{aligned} $$
(2)

where ε and γ are binary variables indicating whether a link in the network can be tolled or is subject to capacity enhancement, respectively.

This is the formulation proposed by Lawphongpanich and Hearn (2004). The practical solution algorithm for solving the problem is to sequentially generate and include necessary extreme points into the set E. The problem stated in (2) is referred to as the ‘Master Problem’. The key to the algorithm is the sub-problem used to generate the necessary extreme points from given \( \left( {{\mathbf{v}},{\mathbf{d}},\tau ,\beta } \right) \) from the Master Problem. The strategy adopted is to include the most rapid descent direction (to achieve the UE condition) for given \( \left( {{\mathbf{v}},{\mathbf{d}},\tau ,\beta } \right) \) into the set E. That is to solve the problem:

$$ \begin{aligned} &\mathop {\min }\limits_{{\left( {{\mathbf{u}},{\mathbf{q}}} \right)}} {\mathbf{c}}\left( {{\mathbf{v}},\tau ,\beta } \right)^{T}\, \cdot \,{\mathbf{u}} - \left( {{\mathbf{D}}^{ - 1} \left( {{\mathbf{d}},\tau ,\beta } \right)} \right)^{T}\, \cdot \,{\mathbf{q}} \hfill \\ &s.t. \hfill \\ &\left( {{\mathbf{u}},{\mathbf{q}}} \right) \in \Upomega \hfill \\ \end{aligned} $$
(3)

This problem is referred to as the ‘Sub-problem’. One may notice the similarity between the problem in (3) and the sub-problem in the Simplicial Decomposition Algorithm (Hearn et al. 1987) (or in the Frank–Wolfe algorithm) used in solving the traffic assignment problem.

Indeed, the problem in (3) can be treated in the same manner as the sub-problem in the Simplicial Decomposition Algorithm in which the problem is decomposed into a number of separated problems for each O-D pair and then each problem is solved as a separate shortest path problem to obtain the auxiliary vector of link flow. Next the generalised cost on this shortest path (including the toll) is substituted into the inverse demand function to obtain q. Then, the vector of link flow (u) can be obtained by loading the related row of q to the shortest paths of different OD pairs and summing up the link flows. The CCA can then be summarised as follows:

Algorithm CCA

  1. Step 0:

    Initialise the problem by finding the shortest paths for each O-D pair; set l = 0; define the aggregated link flow and demand flow (u l, q l); and include (u l, q l) into E.

  2. Step 1:

    l = l + 1; Solve the Master Problem with all extreme points in E and obtain the solution vector\( \left( {{\mathbf{v}},{\mathbf{d}},\tau ,\beta } \right) \);then set\( \left( {{\mathbf{v}}^{l} ,{\mathbf{d}}^{l} ,\tau^{l} ,\beta^{l} } \right) \).

  3. Step 2:

    Solve the Sub-problem with \( \left( {{\mathbf{v}}^{l} ,{\mathbf{d}}^{l} ,\tau^{l} ,\beta^{l} } \right) \)and obtain the new extreme point (u l, q l);

  4. Step 3:

    Termination check: If \( {\mathbf{c}}\left( {{\mathbf{v}}^{l} ,\tau^{l} ,\beta^{l} } \right)^{T} \,\cdot \,\left( {{\mathbf{u}}^{l} - {\mathbf{v}}^{l} } \right) - \left( {{\mathbf{D}}^{ - 1} \left( {{\mathbf{d}}^{l} ,\tau^{l} ,\beta^{l} } \right)} \right)^{T} \cdot \left( {{\mathbf{q}}^{l} - {\mathbf{d}}^{l} } \right) \ge 0 \) terminate and \( \left( {{\mathbf{v}}^{l} ,{\mathbf{d}}^{l} ,\tau^{l} ,\beta^{l} } \right) \) is the solution, otherwise include (u l, q l) into E and return to Step 1.

Numerical example

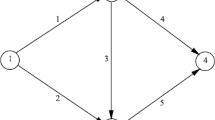
Our numerical example involves the same network (Fig. 1) as in Shepherd and Sumalee (2004) to illustrate how the CCA algorithm overcomes the problem of changes in active path sets between iterations of the optimisation approach and also the poor convergence of the UE assignment problem. The network consists of 18 links, 7 nodes and has 3 origins and 3 destinations (nodes 1, 5 and 7) with 6 OD pairs. While this network is a simplistic abstraction of reality, it embodies a typical mono-centric city centred at node 5 with 1 and 7 being suburbs. Movement from suburbs to the city and suburb to suburb is facilitated by radial movements and two alternative bypass routes. At the same time, this network is more complex than a majority of networks used in the literature and yet not too large to obscure the tractability of results.Footnote 3

Fig. 1
figure 1

Theoretical network used. Source: Shepherd and Sumalee (2004)

Full size image

The cost of travel on each link is given by the usual power law type function of the following form: \( c(v) = c_{0} + a\left( {\frac{v}{\beta }} \right)^{n} \), where c(v) refers to the travel time, c 0 and a are constants and v and β are link flow and capacity, respectively. Please refer to the Appendix for all relevant parameters for this network.

The demand function adopted is based on the power law form: \( d_{k} = d_{k}^{0} \left( {\frac{{\mu_{k} }}{{\mu_{k}^{0} }}} \right)^{{\delta_{k} }} \) where \( d_{k}^{0} ,\mu_{k}^{0} ,\delta_{k} \) are the demand, cost in the no toll equilibrium and elasticity, respectively. All other parameters are as defined previously. In a general case, \( \delta_{k} \) could adopt different values for different OD pairs. For the numerical tests reported in this paper, \( \delta_{k} \) is set to −0.57 for all OD pairs as in Shepherd and Sumalee (2004).

We now discuss the results in terms of the problem being solved starting with the toll only solutions to first and second best and subsequently consider the simultaneous optimisation of capacity and tolls in the first and second best case.

First best tolls

The optimal tolls for the first best solution where all links can be charged to account for marginal costs of congestion were calculated by solving the system optimal equivalent optimisation problem (Sheffi 1985). This first best solution acts as a benchmark for comparing gains in welfare for the second best toll problem. The first best tolls only problem resulted in a gain in welfare of 461 k seconds.

Second best tolls

First we investigate optimal second best single link tolls. As reported in Shepherd and Sumalee (2004) there was no benefit in using positive tolls on links 5, 8, 9, 14 and 15 so these are omitted from this part of the analysis. Table 1 shows the optimal single link tolls, change in welfare and percentage of the first best welfare gain for each link. First of all we can see that the CCA approach provides a solution for all links considered. It can also be seen that tolling links 17 and 13 individually provide the largest increase in welfare.

Table 1 Optimal second best single link tolls and changes in welfare
Full size table

To demonstrate the advantage of the algorithm over the heuristic suggested by Verhoef (2002) and tested in Shepherd and Sumalee (2004) a detailed investigation of the problem with link 4 was conducted. Figure 2 shows the total benefit and lagrangian curves plotted against toll level for this link. The lagrangian in this case represents the welfare or total benefit plus a term for each used path (associated with a Lagrange multiplier) which incorporates the user equilibrium conditions. As discussed in Shepherd and Sumalee (2004) the Lagrangian based approach was disturbed by relatively small convergence errors which become amplified by the Lagrange multipliers. If the error in the convergence of the UE assignment is not significant, then the lagrangian curve should be relatively close to the actual objective function curve. However, as can be seen in Fig. 2 convergence errors for tolls in the range 10–40 s resulted in the optimisation algorithm eventually converging to a toll level of 27 s which is the local optimum of the erroneous lagrangian curve. The jumps in this curve are caused by a combination convergence errors and changes in path set as the toll is varied. For more details see Shepherd and Sumalee (2004).

Fig. 2
figure 2

Optimisation of the toll for link 4. Source: Shepherd and Sumalee (2004)

Full size image

Using the CCA we were able to find the correct optimal toll of approximately 104 s. This demonstrates that the CCA can overcome the issue of convergence error by operating on a relaxed equilibrium condition at each iteration. On the other hand, the Karush–Kuhn–Tucker approach or Sensitivity Analysis approach finds the predicted toll by relying on the perfect satisfaction of the UE condition at each iteration which may not be achieved in a real network. In addition, in the formulation of the CCA there is no explicit requirement for path variables. All variables are related to link flows or demand flows hence avoiding the problem with the change of the active path set.

Pairs of tolls and cordon around the centre

Table 2 shows the tolls and welfare improvement as a result of implementing link tolls on three pairs of links as well as a three link cordon around node 5. The results for the pairs of links increase the benefits but the increase is seen to be additive only, i.e. there is no evidence of synergy from tolling on these pairs of links. In addition the optimal toll levels do not vary much from that obtained from the individual link optimisation.

Table 2 Link Pair and Cordon Toll Solutions with CCA
Full size table

However, the cordon option generates the largest benefit providing nearly 83% of the first best benefits. In this case there is evidence that charging these three links together provides some synergy as the increase in benefits is greater than the sum of the individual increases (382 k seconds compared to 339 k seconds). This result taken with that for link pair 2 demonstrates the inefficiency of leaving a toll free route to the central node. Thus, a cordon around the central area would seem to be a reasonable solution in policy terms for this network.

Joint first best tolls and investment in capacity

Here we present the results of the combined problem whereby we aim to optimise the welfare function by optimising toll levels and investment levels simultaneously under the first best condition. The change in welfare takes into account any changes in the cost of capacity provision compared to the Do-nothing investment as set out in Eq. 1.

First we adopt the approach as detailed in Sect. 2 and solve the joint first best problem. Since we assume a constant cost of capacity expansion (1 generalised second per unit of capacity in this example) and the BPR type travel time function, we can expect to find a solution under the self-financing principle. Table 3 shows the joint first best optimal tolls and capacities compared to the system optimum for the toll only solution and initial values used for the capacities of the links. The joint first best resulted in an increase in welfare of 1.5 million seconds which is more than three times that generated by the first best toll only solution (but obviously this depends on the assumption made about costs of capacity).

Table 3 Joint first best capacities and tolls compared to the toll only system optimal
Full size table

It should be noted that any reduction in capacity leads to cost savingsFootnote 4 on a given link, and indeed some links are removed in our benchmark solution. However, at the same time other links have capacity increased significantly so that the total expenditure on capacity is higher than in the base case. It was also verified that the self-financing result did hold with total revenue equal to total cost of capacity, i.e. 97 k seconds. The optimal configuration of the network found is illustrated in Fig. 3.

Fig. 3
figure 3

Joint toll and capacity optimal network configuration

Full size image

As we can see the capacity has been increased along one main route which corresponds to the shortest free flow paths between the OD pairs. Although this solution would be impractical in most realistic cases it is used as a benchmark and to illustrate the self-financing result (which breaks down if we impose general second best policies such as limited tolling and investment in capacity). In total eight links have been removed by the optimisation as these are routes with a longer free flow travel time than the more direct routes and as such become sub-optimal when capacity investment is allowed. In part this collapse in structure is due to the assumed demand matrix and the fact that there is no source or sink at node 4. We shall investigate what happens with a more fully connected demand structure below.

Notice also that the tolls under joint first best are an order of magnitude smaller than under the toll only system optimal solution. This is of course related to our arbitrary choice of costs of capacity and as capacity has been increased significantly on the remaining links then the marginal costs of congestion are reduced and so the tolls are reduced whilst maintaining the self-financing principle. Further tests showed that as the per unit cost of capacity increases, the structure of the optimised network remains the same but the predicted amounts of capacity were lower as expected. Similarly to achieve the self-financing result, lower tolls were required when capacity was cheap and higher tolls resulted when capacity was more expensive.

Joint first best test with additional origin and destination nodes

Before moving on to the second best tests, as noted above it was thought that the resulting first best structure may be a little unrealistic and that the removal of links may actually be due to the assumed demand structure (only three origin-destination pairs). To investigate this we extended the demand matrix to include origins and destinations at nodes 3 and 4 as well as at 1, 5 and 7. We did not move to a fully connected network as in most practical networks and indeed in reality there does not exist an origin or destination at every node in the network. Figure 4 shows the resulting structure of the joint first best network with the added demand to/from nodes 3 and 4 (see Appendix for full matrix). Note that although links 4 and 9 connected to node 4 are now retained, the four bypass links 5, 8, 14 and 15 are still removed as in the previous case. This is because the free flow costs for these links exceed the combined free flow costs of the routes through node 5 by approximately 100 s. Also these links are physically longer in total and so the first best solution is to invest in the lower free flow cost and shorter physical routes.

Fig. 4
figure 4

First best structure with five origin-destination pairs

Full size image

Table 4 shows the optimal capacities and tolls for the three and five OD pair cases. First note that the optimal capacities cannot be compared directly as we have a different demand matrices/structures. However, apart from the retention of links 4 and 9 to maintain connectivity with node 4 the increases are greater on the more direct routes as in the three OD pair case and as noted above, the longer bypass links are still removed. Notice also that the optimal tolls for those links still active in the three OD pair case are identical to those under the five OD pair case. This is because under first best the tolls are defined by the long run cost functions and provided certain conditions hold are constant and independent from demand (see Verhoef et al. (2008) equation 6e).

Table 4 Joint first best capacities and tolls compared to the toll only system optimal
Full size table

The fact that links are still removed in this case does not come as a surprise as it is in fact similar to the well known Braess paradox (Braess et al. 2005) which says that in some circumstances road closures can improve welfare. Under the Braess paradox we would require that the system shows an increase in welfare with removal of links without increases in capacities on other links, so our case is in fact a weaker version of the paradox as we are also adjusting the network on alternative routes with tolls and changes in capacity.

Whether the Braess paradox is pure theory or whether it can occur in real networks has recently been discussed by Youn et al. (2008) where they show that removal of certain links can improve system efficiency in real networks of London, Boston and New York. This backs up the assertion that investments should be directed at the quickest free flow routes, however, whether the full removal of a link occurs will depend on the network and demand structure. Of course once again the results are also specific to the cost assumptions used for costs of capacity by link.

The most general policy statement which comes from the first best analysis is that if costs of capacity are uniform over a network then this implies investments should be aimed at the most direct routes at the expense of others. Obviously this may not be the case in practice as costs of capacity will vary by link type and area. The most obvious case being where it becomes impossible to add capacity through a town centre without demolishing existing buildings in which case the first best solution may well include bypass links. So whilst we have demonstrated an approach for calculating the benchmark the policy implications are specific to both network and demand structure and to the cost assumptions used.

In the following sections regarding second best strategies we revert to using the three OD pair network demand as we wish to compare results with the previous toll only solutions.

Joint second best tolls and investment in capacity

This section reports the numerical results of the application of the CCA to the joint toll-capacity second best problems. Four sets of tests are conducted. The first set considers the case where we do not allow any reduction in capacity from the base case. This was designed to test the impact on welfare of not allowing any links to be downgraded and was intended as an alternative to the traditional first best benchmark. The second looked at different sets of links optimising their tolls and capacities. The third varies the costs of capacity to demonstrate the impact of cost assumptions on optimal tolls and capacities under the second best regime. The final test investigates different capacity investment strategies under the cordon toll scheme.

Joint second best without capacity reduction

Table 5 shows the results for the first test where no reductions in capacity are allowed. As can be seen where before we removed a link it now remains with capacity set to the base level. However, the tolls in this case became irrelevant and could be set to zero with no flow resulting from the assignment problem on these links. These links are unused as it is better from a system point of view to invest in the shorter (in terms of free flow costs) routes and users choose to use these routes as opposed to the higher free flow costs on the other retained routes.

Table 5 Joint toll and capacity optimization with restrictions on reduction in capacity of links
Full size table

In terms of impact on welfare, there is a 2% reduction compared to the first best solution and this reduction corresponds to the capacity costs of maintaining the unused links.

Joint second best with cordon toll

Table 6 contains the results for the second set of tests. In this test, we consider tolls and capacities on the subset of links forming the cordon under two scenarios.

Table 6 Capacity and toll optimisation results for scenarios 1 and 2 (capacity cost of 1 s)
Full size table

  • Scenario 1 allows capacity to be enhanced on link 17 only.

  • Scenario 2 allows capacity to be changed on all three cordon links.

Comparing back with the toll only solution for the cordon in Table 2 we can see that varying capacity has the effect of increasing the welfare significantly from 382 k seconds to 588 k seconds and 606 k seconds for increases in capacity on link 17 and all three cordon links, respectively. We can also observe that when capacity is increased the optimal toll is slightly reduced. Overall the relative gains in welfare are around 40% of the joint first best. In terms of comparisons with the joint first best, the investment in capacity was lower but the toll revenue generated much higher. Obviously this result is dependent on our assumptions about costs of capacity which will be discussed next.

Joint second best with cordon toll with varying investment cost

To illustrate the impacts of changes in capacity costs, we varied the unit cost of capacity from 1 s to 50 and 100 s. Table 7 shows that as the cost of capacity increases tolls are increased and capacity may be reduced. In the base case, all three links had a capacity of 1,100 pcus/h. With the higher cost of capacity, there was a reduction in the capacities of links 7 and 10 but not that of link 17, though the total inbound capacity has been reduced.

Table 7 Scenario 2: Impacts of different capacity cost assumptions
Full size table

In terms of impacts on second best toll levels we can see from Tables 6 and 7 that with low costs of capacity the tolls are only slightly reduced, whereas with increased costs the tolls are increased significantly when capacity is reduced except for link 17 where capacity is still increased and so the toll is reduced slightly. This would suggest that although costs of capacity play an important role in determining whether tolls will rise or fall compared to the toll only case, it is in fact the resulting direction of capacity enhancement which determines the direction of change in the toll level.

It is also important to point out that there are potential synergies that can be harnessed to increase social welfare. As shown previously in the toll only situation, the tolling of links 7, 10 and 17 produced welfare gains greater than the sum of the individual elements. The same can be said for the simultaneous toll and capacity case. The sum of the social welfare gains from further tests (not shown) with tolling and optimising capacities on links 7, 10 and 17 in turn amount to 550 k seconds. However, when they are tolled and optimised simultaneously as was done in Test 2, the social welfare achieved was 606 k seconds, representing an increase of approximately 10%.

Joint second best with cordon toll and alternative investment strategies

Finally, we consider an alternative investment strategy whereby we consider tolls on the cordon (Links 7, 10 and 17) and capacity enhancements on the peripheral links. These peripheral links form a bypass around the city centre area centred on Node 5. It is designed to simulate the policy of charging tolls around a cordon of a city centre while devoting resources to the expansion of a bypass. It is evident that the social welfare is higher than that achieved in Scenario 2 (667 k seconds or 44% of joint first best) as shown in Table 8. This is primarily attributed to the fact that the optimised capacity would generally benefit a larger proportion of the users determined by the demand matrix. However, it is also noticeable that links 8 and 15 are effectively removed and that this solution is starting to resemble that of the joint first best network.

Table 8 Capacity and toll optimisation results: Scenario 3 (capacity cost of 1 s)
Full size table

Table 9 summarises the revenues from tolls and capacity costs of obtaining the structure prescribed by the above second best scenarios. From Table 9, it appears that there is a budgetary surplus in all cases. However, this would be clearly dependent on the cost of capacity assumed.

Table 9 Impacts on revenues and capacity costs
Full size table

Whether there is a deficit or surplus depends on the location of tolls and investments and using the CCA algorithm it is possible to investigate possible alternative strategies as we have done here. In our simple network we have demonstrated that a simple cordon plus investments in some of the bypass links is a reasonable strategy resulting in around 44% of the joint first best benchmark. This strategy is not necessarily the best second best strategy available and the ranking of strategies tested here again depends on the costs of capacity.

Conclusions

This paper has demonstrated the application of the constraint cutting approach due to Lawphongpanich and Hearn (2004), to the second best toll problem for pre-defined candidate links. This extreme point formulation was shown to work even when there exist discontinuities due to changes in path sets or lack of perfect convergence of the UE solution, thus improving on our attempts with a derivative based method. The algorithm has also been adapted to deal with the joint toll and capacity problem with elastic demand bringing in non-linear functions and added complexity. The results showed the algorithm to be robust in all cases with only minor changes in the bounds required for a couple of single link optimisations to find the global optimum.

In terms of possible policy conclusions, the joint first best solution implies more investment in direct routes should be made where costs of capacity are uniform over a network. Initially our test network collapsed to a single route due to the limited demand structure used. Further tests with a more fully connected demand structure showed that connectivity of the network is maintained under first best, but that removal of links could still be warranted. Removal of a link can be theoretically optimal if it is assumed that costs of the existing capacity are sunk.

This finding is consistent with the Braess Paradox but with a more general setting (variables including both toll and capacity). However, we also recognised that this may not be practical and so investigated the case where existing capacity cannot be downgraded. In this case we saw that the previously removed links were now retained but unused even with no toll applied. Our policy conclusion from the first best tests is that we should invest in the quickest free flow routes when costs of capacity are assumed to be uniform across the network.

For the second best cases, there are potential synergies to be exploited by considering tolling and capacity expansion on a subset of links simultaneously. In our case presented we have illustrated that investing in the bypass links while tolling the cordon around the city centre was the best second best policy, among those investigated here, to pursue. This result crucially depends on the constituent components of the demand matrix and on assumptions regarding the capacity costs.

The finding from the second best tests in fact contrasts with the finding from the first best tests which suggested removal of bypass routes. This contrast in finding shows a complex interaction between the toll and capacity under the second best case in which it is crucial to analyse them simultaneously as illustrated in the paper.

As more links in the network are simultaneously tolled and capacity optimised, the results tend to the joint first best situation. In terms of impact on second best tolls it was seen that tolls are not significantly affected when costs of capacity are low, but that as costs are increased and capacities reduced then tolls for these links can be increased significantly.

Whilst it has been difficult to draw out more general policy implications we have demonstrated that unless costs of capacity are known to be low then tolls should be analysed in conjunction with investments in the network. Furthermore, we have shown that the CCA can be used for such an analysis for pre-defined options of where to toll and invest. Our current research presented in this paper is limited to the case of optimal continuous toll and capacity with a given set of tolled and invested links. For a more practical application, our future research will investigate the issue of discrete toll and capacity as well as location of tolled and invested links. In addition, in a more general case the toll operator and highway planner/authority may not necessarily be the same. Under such a situation future research should look into aspects of competition and differing objectives between these authorities.